Complexity of Maxmin-$\omega$ Cellular Automata

Abstract

We present an analysis of an additive cellular automaton (CA) under asynchronous dynamics. The asynchronous scheme employed is maxmin-$\omega$, a deterministic system, introduced in previous work with a binary alphabet. Extending this work, we study the impact of a varying alphabet size, i.e., more than the binary states often employed. Far from being a simple positive correlation between complexity and alphabet size, we show that there is an optimal region of $\omega$ and alphabet size where complexity of CA is maximal. Thus, despite employing a fixed additive CA rule, the complexity of this CA can be controlled by $\omega$ and alphabet size. The flavour of maxmin-$\omega$ is, therefore, best captured by a CA with a large number of states.

1 Introduction

The maxmin-$\omega$ system was introduced in [9] as a model of asynchronous dynamics on networks. Each node in this system updates its state upon receiving a proportion $\omega$ of inputs from neighbourhood nodes. Cellular automata are reknowned for their modelling capabilities of a variety of complex systems – be they biological, computational or physical. CA consist of a lattice of identical automata, or “cells”, where each cell takes one of a finite set of states. Classical CA update their state synchronously according to some local rule (see [13] for example); asynchrony adds more realism to these models [1, 11]. In terms of a CA application, the main attraction for employing maxmin-$\omega$ is that it is asynchronous yet deterministic. Moreover, these local interactions of maxmin-$\omega$ provide a simpler and intuitive mechanism for asynchrony, mimicking the dynamics of similar models whose applications include neuronal networks [7] and virus transmission [12]. Taking these points together, maxmin-$\omega$ looks like a new member of the class of threshold models that have their roots in epidemic spreading [2].

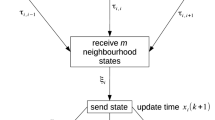
Consider a one-dimensional CA lattice, where the neighbourhood $\mathcal {N}_i$ of cell i of radius r is the set $\{i-r,\ldots ,i-1,i,i+1,\ldots ,i+r\}$, as introduced in [13]. Maxmin-$\omega$ views the CA lattice as a network, whose nodes play the role of cells. Thus, a cell state is updated at the end of a cycle. The processes that constitute such a cycle are as follows. First, the neighbourhood nodes $\mathcal {N}_i$ complete their $k^\text {th}$ cycle and then transmit their CA state to node i; the transmission of such a state from node j to i takes transmission time $\tau _{ij}(k)$. Node i waits for a fraction $\omega$ of the arriving states before processing its new CA state, which takes processing time $\xi _i(k+1)$. Once this is complete, the node updates its CA state and simultaneously transmits this state to downstream nodes, where the cycles are reiterated.

We denote the time of state change of node i by $x_i(k+1)$, whilst the CA state of node i in the same cycle is denoted $s_i(k+1)$. Thus, the $(k + 1)^\text {th}$ update time of node i is given by the following recurrence relation.

$$\begin{aligned} x_i(k+1) = x_{(\omega )}(k)+\xi _i(k+1) \end{aligned}$$

(1)

where $x_{(\omega )}(k)$ represents the $k^\text {th}$ time of arrival of the $\omega ^\text {th}$ input from the neighbourhood of i, which we define as the last of the fraction $\omega$ of inputs arriving at i; if k is clear from context, we denote this $x_{(\omega )}$ for short. If there are n nodes in the neighbourhood of i, then $x_{(\omega )}$ practically represents the time of arrival of the $m^\text {th}$ input where $m = \lceil \omega n\rceil$.

For our study, we employ an additive CA rule. We first consider an alphabet of CA states taking size Z, namely $\varSigma =\{0,1,2,\ldots ,Z-1\}$. We represent the (CA) state of the system at cycle $k\in \mathbb {N}$ by the vector $\mathbf {s}(k)= (s_1(k),s_2(k),\ldots ,s_N(k))$. Suppose a cell is contained in a neighbourhood of size $2r + 1$; then a CA rule is a function $f:\{0,1\}^{2r+1} \rightarrow \{0,1\}$ given by $s_i(k+1) = f(\mathcal {N}(s_i(k)))$, where $\mathcal {N}(s_i(k))$ denotes the CA states of $\mathcal {N}_i$ in cycle k. Further, consider

$$\begin{aligned} \mathcal {A}_i(k) = \{j\in \mathcal {N}_i:x_j(k)+\tau _{ij} \le x_{(\omega )}(k)\} \end{aligned}$$

(2)

which is the set of all nodes whose CA states arrive before or at the same time as the $\omega ^\text {th}$ input at node i. We call $\mathcal {A}_i(k)$ the set of affecting nodes of i. Thus, we focus on the following CA rule

$$\begin{aligned} s_i(k+1) = \sum _{j\in \mathcal {A}_i} s_j(k) \mod Z. \end{aligned}$$

(3)

Simply put, the CA state of each cell will be the sum of the fastest arriving states at that cell.

We exhibited the impact of maxmin-$\omega$ on CA with a binary alphabet in [9], i.e., $\varSigma = \{0,1\}$. In this paper, we demonstrate the difference in effect for an extended alphabet, i.e., $|\varSigma |>2$. In particular, we ask the question: what is the effect of maxmin-$\omega$ on the complexity of cellular automata?

2 Cellular Automata with General Alphabet

2.1 Cellular Automaton Pattern Complexity

To classify our cellular automata in space-time, we use the entropy measures of Marr and Hütt in [6]. The Shannon entropy S relies on the density $p(s_j)$ of the CA state $s_j\in \varSigma$ in the time series of the evolving CA states of each cell. Thus, the Shannon entropy of cell i is defined as

$$\begin{aligned} S_i = -\sum _{j=1}^{|\varSigma |} p(s_j)\log _2 p(s_j). \end{aligned}$$

(4)

The quantity we require is the Shannon entropy of the overall CA space-time pattern, defined as the average of $S_i$ over the N cells in the lattice: $S = (1/N)\sum _{i=1}^{N}S_i$.

The word entropy W depends on the occurrence of blocks of constant states of length l (l-words) in the time series of a cell, independent of the state comprising them. Thus, if p(l) is the density of an l-word along the time series of a cell i, then

$$\begin{aligned} W_i = -\sum _{l=1}^{T} p(l)\log _2 p(l) \end{aligned}$$

(5)

where T is the length of the time series. The word entropy of the entire CA pattern is then defined as the average of $W_i$ over the N cells: $W = (1/N)\sum _{i=1}^{N}W_i$.

For the additive CA rule (3) that we consider, each state is equally likely throughout the evolution of the CA [3]. Then we have that $p(s_j)=1/Z$, giving

$$\begin{aligned} S_i = - \sum _{j=1}^{Z}\frac{1}{Z} \log Z = \log Z. \end{aligned}$$

(6)

Taking the average of this quantity over N cells gives $S = \log Z$. The Shannon entropy is therefore expected to increase logarithmically with the size of alphabet.

As for the word entropy W, it is reliant on the state in a time series of a cell being unchanged over some fixed length l of time. Let $s_j^{(t)}$ denote the state of cell j at time $t\in \mathbb {R}$. Thus, an l-word satisfies the following.

$$\begin{aligned} s_j^{(t)} = s_j^{(t+1)} = \cdots = s_j^{(t+l-1)} \end{aligned}$$

(7)

where $s_j^{(t-1)}\ne s_j^{(t)}$ and $s_j^{(t)}\ne s_j^{(t+l)}$. Since all CA states are equally likely, $p\left( s_j^{(t)}\right) = 1/Z$ for all t. The probability of the next state being the same is $P\left( s_j^{(t)}=s_j^{(t+1)}\right) =1/Z$, whilst the probability of the next state being different is $P\left( s_j^{(t)}\ne s_j^{(t+1)}\right) =(Z-1)/Z$. Then the probability p(l) of observing an l-word is $P\left( s_j^{(t-1)}\ne s_j^{(t)} = s_j^{(t+1)} = \cdots = s_j^{(t+l-1)} \ne s_j^{(t+l)}\right)$, calculated as

$$\begin{aligned} \frac{Z-1}{Z}\times \underbrace{\frac{1}{Z}\times \cdots \times \frac{1}{Z}}_{l \text { times}}\times \frac{Z-1}{Z} = \frac{(Z-1)^2}{Z^{l+2}}. \end{aligned}$$

(8)

The inset of Fig. 1 plots p(l) as a function of Z and l; 1-words in particular are expected to be most frequent. Substituting p(l) into (5) gives $W_i$; taking the average over all cells gives $W=W_i$ here. Figure 1 plots W as a function of $|\varSigma |$. The word entropy is, thus, expected to decrease as the alphabet size increases.

Fig. 1.

Word entropy (5) as a function of alphabet size Z, for $Z\le 10$. Inset, left: p(l) against word length l for alphabet sizes 2 to 5. Inset, right: p(l) as a function of alphabet size for $l=1,\ldots ,8$, where a small l gives a higher curve

3 Cellular Automata as a Function of $\omega$

We now look at the impact of $\omega$ on the complexity of additive CA space-time output. We first introduce the concept of a reduced network.

Definition 1

In cycle k, the reduced network is the set of affecting nodes $\mathcal {A}_i(k)$ of all nodes, together with the edges that connect affecting nodes $j\in \mathcal {A}_i(k)$ to their affected node i.

For each counter k, we can draw up a reduced network. In [8], we show that this sequence of reduced networks asymptotically settles onto a fixed set of reduced networks. Formally, let us denote by $\mathcal {G}^r(k)$ the reduced network in cycle k. Then we obtain the sequence $\mathcal {G}^r(0),\mathcal {G}^r(1),\mathcal {G}^r(2),\ldots$ of reduced networks such that, for some $k\ge 0$, there exists $g\in \mathbb {N}$ such that $\mathcal {G}^r(k+g)=\mathcal {G}^r(k)$. The set $\mathcal {O}=\{\mathcal {G}^r(k),\mathcal {G}^r(k+1),\cdots ,\mathcal {G}^r(k+g)\}$ is called a periodic orbit of reduced networks. This set is dependent on the initial set of update times $\mathbf {x}(0)=(x_1(0),x_2(0),\ldots ,x_N(0))$ of the maxmin-$\omega$ system [8]. Figure 2 shows an example of such a sequence of reduced networks that enter a periodic orbit of size two; here the original network is a size 3 fully connected regular network (with neighbourhood size 3), whilst the system takes $\omega =2/3$.

Fig. 2.

Sequence of reduced networks of a maxmin-2/3 system where $N=3$. Larger arrows indicate the transitions between successive iterations of the maxmin-2/3 system

Pertinently, this means that, as $k\rightarrow \infty$, the maxmin-$\omega$ system can be replaced by a reduced system (with an underlying reduced network) with $\omega =1$. This is intuitive - since only the affecting nodes affect the future state of a node i, it is equivalent to node i accepting all (such that $\omega = 1$) inputs from $\mathcal {A}_i(k)$.

It follows that $|\mathcal {A}_i(k)|\approx m$, where $m=\lceil \omega n\rceil$. This implies that the neighbourhood size of each node in $\mathcal {G}^r(k)$ should be approximately m. In fact, due to the simultaneous arrival of some affecting nodes, $|\mathcal {A}_i(k)|\ge m$ [8]. Nevertheless, it is instructive to assume the average neighbourhood size of each node in a reduced network to be m (for example, see Fig. 2).

For further illustration, it is sufficient to take $g=1$. Asymptotically then, we need only consider one underlying network; from here onwards, we shall take all mentions of “reduced network” to refer to this asymptotic reduced network, denoted $\mathcal {G}^r$. Thus, when m is small, the neighbourhood size of each node in $\mathcal {G}^r$ is small. This implies that some CA states – namely the fastest arriving ones – are favoured over other states. Consequently, the cellular automaton state space is narrower, giving fewer state possibilities and therefore a smaller Shannon entropy. Assuming that those CA states that appear with non-zero probability are equiprobable (due to the CA being additive), we can use (6) to say that, the Shannon entropy increases with the number of states. Thus, we obtain the following lemma.

Lemma 1

The Shannon entropy of an additive CA pattern resulting from the maxmin-$\omega$ system is likely to increase with $\omega$.

We note that certain probability distributions of cell states actually correspond to a decrease in Shannon entropy with $\omega$, e.g., if $p(s_1)$ is extremely large relative to other $p(s_j)$. However, this is contradictory to the property of additivity, which says that each CA state is approximately equiprobable. Thus, we assume that such extreme skewed probability distributions are rare so that Lemma 1 is almost always satisfied.

We move onto the analysis of word entropy as a function of $\omega$. For $\omega$ small, the reduced network will have small neighbourhood size. Using the same arguments as earlier, the fastest CA states will prevail, giving few state possibilities. This is equivalent to having a small alphabet such that a range of word lengths are likely to be observed (see the inset of Fig. 1). For larger $\omega$, the reduced network will have a larger neighbourhood size such that more CA states are prevalent; the likelihood of observing l-words is therefore decreasing with $\omega$ (again, see Fig. 1, inset). Thus, we expect word entropy to decrease with $\omega$.

4 Experimental Results

We now run the maxmin-$\omega$ system and implement the additive cellular automaton rule (3). The underlying network is regular, equivalent to the one-dimensional CA lattice, and we take network size $N=11$, where cells N and 1 are connected. We record the asymptotic values of Shannon and word entropies, along with the asymptotic quantities that summarise the update times of the maxmin-$\omega$ system itself. For this purpose, we require the following definitions.

Define the function $\mathcal {M}$ as the mapping $\mathcal {M}:\mathbb {R}^N\rightarrow \mathbb {R}^N$ whose components $\mathcal {M}_i$ are of the form of Eq. (1). We represent a system of N such equations by the following.

$$\begin{aligned} \mathbf {x}(k+1) = \mathcal {M}(\mathbf {x}(k)) \end{aligned}$$

(9)

for $k\ge 0$, where $\mathbf {x}(k)=(x_1(k),x_2(k),\ldots ,x_N(k))$. Denote by $\mathcal {M}^p(\mathbf {x})$ the action of applying $\mathcal {M}$ to a vector $\mathbf {x}\in \mathbb {R}^N$ a total of p times, i.e., $\mathcal {M}^p(\mathbf {x})=\underbrace{ \mathcal {M}(\mathcal {M}(\cdots (\mathcal {M} }_{p\,{\text {times}}} (\mathbf {x}))\cdots ))$.

Definition 2

If it exists, the cycletime vector of $\mathcal {M}$ is $\chi (\mathcal {M})$ and is defined as $\lim _{k\rightarrow \infty }(\mathcal {M}^k(\mathbf {x})/k)$.

Definition 3

For some $k\ge 0$, consider the set of vectors

$$\begin{aligned} \mathbf {x}(k),\mathbf {x}(k+1),\mathbf {x}(k+2),\ldots \in \mathbb {R}^N \end{aligned}$$

where $\mathbf {x}(n)=\mathcal {M}^n(\mathbf {x}(0))$ for all $n\ge 0$. The set $x_i(k),x_i(k+1),x_i(k+2),\ldots$ is called a periodic regime of $i\in \mathbb {N}$ if there exists $\mu _i\in \mathbb {R}$ and a finite number $\rho _i,\in \mathbb {N}$ such that $x_i(k+\rho _i)=\mu _i+x_i(k)$. The period of the regime is $\rho _i$ and $\chi _i=\mu _i/\rho _i$ is the cycletime of i. The smallest k for which the periodic regime exists is called the transient time.

Under our initial conditions, $K_i$ will be finite (see [4], Theorem 12.7) and so, maxmin-$\omega$ always yields a periodic regime with the following system-wide quantities.

$$ K=\max _i\{K_i\}, \quad \rho ={\text {LCM}}_{i}(\rho _i), \quad \chi = (1/N)\sum _{i=1}^{N}\chi _i. $$

From now on, we take $\xi _i(k)$ and $\tau _i(k)$ to be independent of k, denoted $\xi _i$ and $\tau _i$, respectively. Our experiments can be described by the following steps.

• 1. Choose $\xi _i,\tau _i\in \mathbb {Z}$ both from the uniform distribution (with equal probability) taking largest value 5.

• 2. Choose an initial timing vector, $\mathbf {x}(0)=(0,\ldots ,0)$, and an initial CA state $\mathbf {s}(0)$ uniformly (with equal probability) from the alphabet $\varSigma =\{0,\ldots ,Z-1\}$.

• 3. Iterate the maxmin-$\omega$ system 100 times for each $\omega$ value from 0.05 to 1, in steps of 0.05 (so there are 20 maxmin-$\omega$ systems to run).

• 4. For each maxmin-$\omega$ system, record the period $\rho$ and cycletime $\chi$, as well as the Shannon and word entropies.

• 5. Repeat above three steps 50 times to obtain, for each maxmin-$\omega$ system above, 50 independent periods and cycletimes, and Shannon and word entropies.

• 6. For each maxmin-$\omega$ system, record the mean of the 50 periods, cycletimes, Shannon and word obtained.

Fig. 3.

Mean cycletime, period and transient time as a function of $\omega$ for a regular network of size 11 with neighbourhood size $n=9$. Each curve represents each of the alphabet sizes 2 to 10. These graphs are typical for all other sizes $n=3,5,7,11$

Fig. 4.

Shannon S and word entropy W for a regular size 11 network with neighbourhood sizes $n=9$ and 11 (results for $n=3,5,7$ similar to $n=9$). (a) Mean S and mean W versus $\omega$. Each curve represents each alphabet size $Z= 2$ to 10. (b) Mean S and mean W versus Z. Each curve represents each $\omega \in \{0.05,0.1,\ldots ,1\}$. Black: $\omega =1$, blue: $0.1\le \omega \le 0.95$, red: $\omega =0.05$.

We vary the neighbourhood radius such that neighbourhood sizes explored are $n=3,5,7,9$, and 11. We also vary the alphabet size such that, for each n, the algorithm is run for alphabet sizes $|\varSigma |=2,3,\ldots ,10$. Figures 3 and 4 summarise the mean results.

For all neighbourhood sizes except for $n=11$, the Shannon entropy is an increasing value with $\omega$ (see Fig. 4(a)), in agreement with our analytical predictions. The word entropy behaves differently, however; it is increasing for most alphabet sizes, with a sharp decrease near $\omega =1$. On the other hand, Fig. 4(b) agrees with our analytical predictions when alphabet size is approximately greater than or equal to 8; that is, W is a decreasing function of $\omega$ for a large alphabet size.

The logarithmic trend (6) of S with alphabet size is most apparent - this is attained when all CA states are equiprobable, and it is maximal, supported by the black Shannon entropy curve in Fig. 4(b), which is the $\omega =1$ case. As expected, the word entropy is decreasing with alphabet size, although the case $\omega =0.05$ is increasing (see red line in Fig. 4(b)).

Fig. 5.

Frequency of $\omega ^*$ and $Z^*$ values that yield the most complex CA patterns. Left: Frequency of $\omega ^*$ values. Right: Frequency of $Z^*$ values. We present results for neighbourhood sizes $n=9$ and $n=11$ as they show the most variation

The exception seems to be the case $n=11$. Here, S is not increasing with $\omega$, instead following a bell-like curve, taking maximal value at approximately $\omega =0.5$. This Shannon entropy is minimal when $\omega =1$ (see black/lowest curve in Fig. 4(b)), in extreme contrast to the logarithmic maximal trend for other neighbourhood sizes.

We end this section by combining the Shannon and word entropy results into one (S, W)-plane. Thus, for each n, consider a fixed alphabet size. This gives a value $(\text {mean }S,\text {mean }W)$ for each $\omega$ value. To find which of these produces the ‘most complex’ point, we take the following simple distance from the origin, for $\omega \in (0,1]$.

$$\begin{aligned} d_{\omega }= \sqrt{\bar{S}^2 + \bar{W}^2} \end{aligned}$$

(10)

where $\bar{S}=\text {mean }S$ and $\bar{W}=\text {mean }W$. Then, we are interested in $\omega ^*=\arg \max _{\omega } d_{\omega }$, i.e., the $\omega$ values that maximise $d_{\omega }$. Often there exist more than one such $\omega$. For example, for $n=3$, $\omega ^*=\{0.75,0.8,0.85,0.9,1\}$ for all alphabet sizes. In such cases, we take the mean of this list of $\omega ^*$ values.

Thus, for each alphabet size, we have one $\omega ^*$ value. Performing this calculation for all alphabet sizes up to 10, we produce histograms indicating where such $\omega ^*$ values congregate; these are shown in Fig. 5. A similar calculation finds, for a fixed $\omega$ value, the alphabet size that produces the ‘most complex’ (S, W) point; we denote this alphabet size $Z^*$, also depicted in Fig. 5.

5 Discussion

We have demonstrated the effect of maxmin-$\omega$ dynamics on an additive cellular automaton in two orthogonal ways: asynchrony was imposed via maxmin-$\omega$ and, secondly, the alphabet of state possibilities was extended.

We previously noted some correspondence in complexity between timing and CA pattern when the alphabet was binary [8, 9]. Here, we have shown that an larger alphabet generates additional facets to the story of complexity. Thus, we claim that the essence of the maxmin-$\omega$ system is best captured by a CA with a larger number of states than two. Whilst complexity does not follow simple bell-like curves, the (S, W)-plane offers some support to the argument that the most complex patterns occur when $\omega \approx 0.5$ (see Fig. 5).

It must be mentioned that the entropic measure of complexity employed in this paper is just one of various probabilistic measures that are in use. The measures that immediately seem relevant to our work are the LMC complexity [5] and the Rényi entropy [10]. An in-depth exploration is saved for a future study, suffice it to say that calculation of such measures is straightforward.

Let us briefly discuss the LMC complexity C. For our model, we construct two of these measures: (i) $C_S = SD_S$, where $D_S = \varSigma _{j=1}^Z \left( p(s_j) - 1/Z \right) ^2$ is a measure of ‘disequilibrium’; (ii) $C_W = WD_W$, where $D_W$ is a measure of disequilibrium, given by $D_W = \varSigma _{l=1}^T \left( p(l) - 1/T \right) ^2$. The values 1/Z and 1/T respectively denote the probability of observing a CA state and an l-word if all states and all words are equiprobable. Since our additive rules imply $p(s_j) = 1/Z$ for all j, we have $D_S = 0$ so that $C_S=0$. To calculate $C_W$ we substitute (8) in $D_W$ to obtain a decreasing $C_W$ with alphabet size. Thus, both $C_S$ and $C_W$ tend to behave like ideal gases, where a variety of CA patterns are observed.

The LMC complexity as a function of $\omega$ is more interesting. We predict that, for small $\omega$, since only a few cell states prevail (the fastest ones), then the overall behaviour is akin to a crystal - predictably periodic; as $\omega$ increases, more CA states become admissable, giving a wider probability distribution, though each non-zero probability is equal. Thus, $D_S$ is decreasing with $\omega$ and, since S is increasing with $\omega$, we have an intriguing situation to that of Fig. 1 of [5], with $C_S$ maximising for some value of $\omega$ between 0 and 1, and disappearing when $\omega =0$ and 1. Since p(l) is expected to decrease with $\omega$, we have $D_W\rightarrow 0$ as $\omega$ increases. Therefore, $C_W\rightarrow 0$ as $\omega \rightarrow 1$.

In all cases, although the additive rule is considered to be in Wolfram classes I and II [14], this CA is shown to produce a variety of space-time patterns, depending on $\omega$, and particularly when the alphabet is enlarged; thus, all four Wolfram classes may be exhibited simply by controlling $\omega$ and $|\varSigma |$.