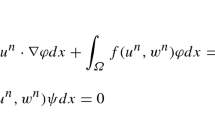Abstract
Reduced-order modeling techniques enable a remarkable speed up in the solution of the parametrized electromechanical model for heart dynamics. Being able to rapidly approximate the solution of this problem allows to investigate the impact of significant model parameters querying the parameter-to-solution map in a very inexpensive way. The construction of reduced-order approximations for cardiac electromechanics faces several challenges from both modeling and computational viewpoints, because of the multiscale nature of the problem, the need of coupling different physics, and the nonlinearities involved. Our approach relies on the reduced basis method for parametrized PDEs. This technique performs a Galerkin projection onto low-dimensional spaces built from a set of snapshots of the high-fidelity problem by the Proper Orthogonal Decomposition technique. Snapshots are obtained for different values of the parameters and computed, e.g., by the finite element method. Then, suitable hyper-reduction techniques, in particular the Discrete Empirical Interpolation Method and its matrix version, are called into play to efficiently handle nonlinear and parameter-dependent terms. In this work we show how a fast and reliable approximation of both the electrical and the mechanical model can be achieved by developing two separate reduced order models where the interaction of the cardiac electrophysiology system with the contractile muscle tissue, as well as the sub-cellular activation-contraction mechanism, are included. Open challenges and possible perspectives are finally outlined.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
1 Introduction
Cardiac electromechanics refers to a model for the description of the coupling of the electrophysiology model, which describes the propagation of the signal triggering the heart contraction, and the mechanical model, which describes the contraction and relaxation of the muscle tissue, including the sub-cellular activation-contraction mechanism. Solving such a coupled problem is crucial to investigate how clinically relevant processes affect different features of the heart beat [70].
Cardiac electromechanics is a challenging problem from both a mathematical and a numerical viewpoint, because of the coupling of different physical problems which take place at different spatial and temporal scales. Indeed, a model for the cardiac electrophysiology has to describe on one hand the sub cellular activity (1–100 μm) which gives rise to the cellular depolarization, on the other hand the spreading of the electrical signal through the whole myocardium (1–10 cm). The modeling of these processes yields a two-way coupled problem involving a PDE with a nonlinear reaction term and a system of nonlinear ODEs. To correctly track the propagation of the action potential, in the form of wave-front solutions, fine computational grids are needed, thus yielding large-scale algebraic problems to be solved. Moreover, the description of the mechanics of the cardiac tissue requires complex constitutive laws, characterized by an exponential strain energy function and the presence of muscular fibers and sheets, resulting in a complex highly nonlinear model. This turns into the need of assembling involved Jacobian matrices when relying, e.g., on the Newton method for the solution of nonlinear systems of equations. Furthermore, the heart muscle contracts after being electrically activated without the need of an external load, and this active behavior of the cardiac cells has to be properly taken into account when coupling the electrical and the mechanical models. To describe these processes different works have proposed more and more accurate electromechanical models [29, 31, 36, 53, 74, 80], very often yielding overwhelming computational costs.
Computational complexity is even more exacerbated if one is interested in going beyond a single, direct simulation. Indeed, when simulating cardiovascular problems, several input data affect the problem under investigation, often varying within a broad range and possibly affected by uncertainty. Addressing the impact of input variations on outputs of clinical interest is thus of paramount importance in order to (1) obtain reliable results, (2) calibrate the numerical solver and/or (3) personalize the mathematical model. In fact, model parameters have to be specifically tuned to fit subject-specific clinical data in order to take into account inter-patient variability. To correctly calibrate cardiac models and estimate the unknown input parameters, such as muscular fibers orientation or parameters affecting the signal propagation, several numerical simulations have to be carried out, thus calling for multiple queries of the parameter-to-solution map in fast and accurate ways. Beyond parameter estimation, this requirement also arises when dealing with sensitivity analysis, control and optimization, and uncertainty quantification, noteworthy classes of problems whose importance in cardiovascular modeling is growing faster and faster.
The need of solving these problems efficiently calls for the development of efficient and accurate reduced order modeling (ROM) techniques in electromechanics. These techniques are designed to provide accurate and reliable solutions to PDEs depending on several parameters at a greatly reduced computational cost. In particular, the reduced basis (RB) method replaces the original large-scale numerical problem (or high-fidelity approximation) originated by applying, e.g., a finite element (FE) method, with a reduced problem of substantially smaller dimension; this latter is generated through a projection of the high-fidelity problem upon a low-dimensional subspace, spanned by a set of high-fidelity solutions corresponding to suitably chosen parameters [41, 68].
In this work we show how to solve both the electrophysiology and the mechanical problems, when these depend on a set of parameters, in the framework of RB methods, also taking into account active mechanics triggered by the cellular depolarization. Because of the nonlinear nature of these problems, computational efficiency is obtained by combining a general-purpose technique to generate the low-dimensional subspace, such as proper orthogonal decomposition, and suitable hyper-reduction techniques allowing to assemble the algebraic structures required by the ROM independently of the high-fidelity arrays. This is required, e.g., when dealing with Newton iterations while solving cardiac mechanics—for which the global Jacobian matrix would have to be entirely reassembled at each Newton step—as well as time stepping in cardiac electrophysiology, for which nonlinear terms have to be evaluated at each time step, also involving the contribution from the cell model. Among recent applications of ROM techniques to problems related with the cardiovascular system, we also mention haemodynamics, for the sake of simulating blood dynamics in different flow conditions [25, 26, 54] or geometrical configurations [7, 8], also in view of the optimal design of prosthetic devices [47, 50] or parameter identification [48, 70]. Cardiac electrophysiology has also been tackled in the last decade [15, 20, 30, 35, 88], however by performing reduction only with respect to the time independent variable, thus avoiding the main difficulties related with the efficient handling of parameter-dependent problems. Recent results for parametrized problems in cardiac electrophysiology, also in view of the efficient solution of uncertainty quantification problems, can be found in [59]. Instead, regarding cardiac mechanics, this subject has only been addressed in a recent paper by the authors [14] and in [13], where also first results about one-way and two-ways coupled electromechanical problems have been obtained. The reduction of coupled problems, however, is still matter of investigation and therefore are not included in this paper.
The structure of this paper is as follows. After a brief recall (Sect. 2) on the mathematical modeling of cardiac electromechanics, we describe the high-fidelity FE approximation we start from (Sect. 3). We then introduce the key tools of the proposed ROM technique (Sect. 4): the Galerkin-POD method and suitable hyper-reduction strategies. Then, we show how to combine them to derive a ROM for both cardiac electrophysiology (Sect. 5) and mechanics (Sect. 6), independently. Numerical results dealing with patient-specific left ventricle configurations in the systolic phase are then shown (Sect. 7), and finally open critical issues and future perspectives are outlined (Sect. 8).
2 Mathematical Models
In this section we present an overview of the electromechanics mathematical models. We consider the minimal Bueno-Orovio model for describing the cellular behavior, the monodomain model for cardiac electrophysiology, and the hyperelastic Holzapfel-Ogden model for the passive ventricular mechanics, adopting an active-strain formulation to take into account active mechanics. This latter requires a dynamical system for the variable which describes fiber shortening as a function of calcium concentration (and then electrical activation).
2.1 Cardiac Electrophysiology
A mathematical model for cardiac electrophysiology has to include processes arising at different scale, ranging from subcellular activity, which originates the cellular depolarisation to the spreading of the signal in the whole myocardium. To model the whole heart, several works have considered continuous models, where the myocardium is approximated as a syncytium, that is a domain where the intra and extracellular spaces coexist at each point [31, 44, 61, 76]. These continuous models describe the spreading of the signal in the heart tissue and are usually coupled to a ionic model which describes the evolution of ion concentrations and ionic currents inside the cells. In this section we first introduce a general framework for the ionic models, focusing on the Bueno-Orovio model [17], and we show how to couple it to the bidomain and monodomain models, widely adopted continuous tissue models.
2.1.1 Cell Models
Cell models describe the evolution of the transmembrane potential across the cell membrane of a single cardiomyocyte. Several ionic models have been proposed, most of which are based on the well-studied Hodgkin-Huxley model [42]; see e.g. [58] for a review. They are all based on the assumption that the electrical properties of the cell membrane can be modeled as an electrical circuit, which connects in parallel a resistor and a capacitance: the latter describes the cell membrane which separates the intra and the extra cellular space, while the former models the ionic channels and pumps regulating ionic fluxes through the membrane. The conservation of currents across the cell membrane can be expressed through the relation
where v is the transmembrane potential, C m the membrane capacitance, I app an external applied current density and I ion the sum of the current densities through the membrane, that can be written using the general Hodgkin-Huxley formalism introduced in [42] as
Here w is a vector of gating variables taking values in [0, 1] that represent the portion of open channels on the membrane, whereas c is a vector describing the concentration of ionic species within the cell. We denote by g k(c) and v k(c) the conductance and the Nernst equilibrium potential associated to the k-th ion, and by p jk the number of sub-units composing each ionic channel, so that the ion k can flow through a ionic channel if all the sub-units forming the channel are opened. Thus, \(\prod _{j=1}^q {w_j^{p_{jk}}}\) represents the probability that the ions k flow through the cellular membrane. The term I 0(v, w, c) represents possible time independent ionic fluxes. The dynamic of a single cell can thus be described in general by a ionic model under the form:
where we denote by Ω 0 the computational domain, here representing the cell. The first set of ODEs is related to the evolution of the gating variables while the second set characterizes the evolution of the ionic concentrations during the cardiac cycle. The number of equations, the functions s and r and the overall complexity depend on the considered model. In this work, we focus on the so-called minimal model introduced by Bueno-Orovio in [17], developed to reproduce physiological action potential morphologies, at moderate computational costs.
The minimal model is a four variables model, able to reproduce experimental measures characteristics of human ventricular transmembrane potential. It can be expressed as:
where the three currents I fi, I si and I so represent the fast inward, the overall slow outward and the slow inward currents, respectively. In particular, we have:
where H(⋅) is the Heaviside function. The model parameters, provided in [17], allow to reproduce the action potential morphologies and the dynamics of more complex models, such as the Ten Tusscher model or the O’Hara and Rudy model [72]. The evolution of the transmembrane potential v and the gating variables w 1, w 2 and w 3 obtained with the considered parameters are reported in Fig. 1. In particular, we observe that the variable v correctly reproduces the action potential shape characteristic of the ventricular cardiomyocytes. We notice that the variable v is dimensionless and it can be rescaled to dimensions of mV using the equations v mv = 87.5v − 84.
Note that this model does not provide specific informations about intracellular calcium concentration. However, the variable w 3 can be assumed to be responsible of calcium dynamics, as it shows a phenomenological behavior which is really similar to the one of the calcium ions in the cardiac cells [72]. In what follows, we refer to w 3 as the calcium concentration c and denote by w = (w 1, w 2, c).
2.1.2 Tissue Models
To describe the propagation of the activation front in the cardiac muscle, we rely on a tissue model able to characterize the evolution of the transmembrane potential. This latter plays indeed a crucial role in the description of the heart contraction. In particular, the bidomain and the monodomain models have been widely used to study the cardiac electrophysiology (see e.g. [24, 66] and reference therein). These models arise from a homogenization process applied to the cardiac tissue and simulate the propagation of the electrical signal through the myocardium; a complete derivation of the two models can be found in [28].
The bidomain model, first proposed in [83], represents the cardiac tissue as a syncytium composed of intracellular and extracellular domains coexisting at every point of the tissue. Each domain is thus considered as a continuum, rather than a group of discrete cells connected with each other. Denoting by v e and v i the extracellular and the intracellular potential, respectively, and by v = v i − v e the transmembrane potential, the bidomain model can be expressed as:
where the Neumann boundary conditions express the condition that the cardiac tissue is electrically insulated. Here, C m is the membrane capacitance, I ion is the sum of the density currents through the membrane and I app is an external applied density current. The domain Ω 0 now represents a portion of myocardium; in the case of the left ventricle, its boundary ∂Ω 0 = Γ endo ∪ Γ epi ∪ Γ base is made by the endocardium, the epicardium and the base, respectively. The conductivity tensors \(D_i\in \mathbb {R}^3\) and \(D_e\in \mathbb {R}^3\) model the anisotropy of the cardiac tissue, characterized by a higher conductivity in the fiber direction, and can be expressed as:
where \(\sigma _f^{i,e}\), \(\sigma _s^{i,e}\) and \(\sigma _n^{i,e}\) are the electrical conductivities in the intracellular and extracellular domains. Here, f 0 denotes the fibers direction, s 0 the sheets direction and n 0 is orthogonal to both f 0 and s 0.
The bidomain model is currently the most complete mathematical model for describing the electrical signal propagation in the heart. However, it is computationally demanding, since to capture the rapid dynamics of the cellular reactions high resolutions in space and time is required. For this reason, a common approach in the literature is to reduce the bidomain equations to simpler tissue models. In particular, the monodomain model can be obtained by assuming that the intra and extracellular domains have equal anisotropy ratios, \({\sigma _f^{i}}/{\sigma _f^{e}}= {\sigma _s^{i}}/{\sigma _s^{e}}= {\sigma _n^{i}}/{\sigma _n^{e}}\). The monodomain model is not suitable for the description of pathological situations, such as, cardiac arrhythmias or fibrillation, since in these situations the extracellular domain influence the transmembrane potential and the ionic currents. However, it provides an accurate description of the cardiac tissue in physiological situations [27, 66], at reduced computational costs. From now on, we adopt the monodomain model as we are only interested, for the time being, to capture the relevant phenomena for describing the electromechanical coupling in healthy conditions.
The monodomain model reads as follows:
where \(\mathbf {D}\in \mathbb {R}^3\) is the conductivity tensor. In particular, we assume that
where we denote by σ f, σ s and σ n the electrical conductivities in the direction f 0, s 0 and n 0, respectively.
2.2 Cardiac Mechanics
The description of cardiac mechanics involves both a passive and an active contribution; besides the hyper-elastic behavior of the tissue, the active contraction of the muscular fibers has to be included in the force balance when modeling the systolic part of the cardiac cycle.
We consider a reference configuration Ω 0 and an actual configuration Ω at the current time t. We denote by X the position vector in Ω 0 and by x the position vector in Ω. We can now introduce the body deformation as the map φ : Ω 0 → Ω from the reference to the actual configuration, such that x = φ(X) for any X ∈ Ω 0, x ∈ Ω. The deformation gradient tensor F is defined as
By denoting u : Ω 0 → Ω, u(X) = φ(X) −X the displacement field, the deformation gradient tensor can be written as F = I + ∇u. We also denote by J = det(F) the determinant of F and by C = F T F the left Cauchy-Green strain tensor.
2.2.1 Passive Mechanics
We first provide a description of the passive ventricular mechanics, by recalling the hyperelastic model proposed by Holzapfel and Ogden in [43]. Cardiac deformations can be modeled by considering the myocardium as orthotropic, hyperelastic, and incompressible with passive properties characterized by means of an exponential strain energy function.
The equations of motion for the cardiac tissue express the balance of linear momentum in material coordinates, which reads as
where ρ 0 is the tissue density and b 0 are the body forces. Here, P p is the first (passive) Piola(-Kirchhoff) tensor, which is related to the surface tractions t 0 through the relation t 0 = P p n, where n is the normal to the boundary of the reference domain. As usual in cardiac mechanics literature (see e.g. [29, 37, 72]), inertial forces can be neglected, since they are about two orders of magnitude smaller than other terms [86], thus obtaining the quasi-static problem
We impose Neumann boundary conditions on the endocardium (Γ N = Γ endo) to model the effect of blood pressure,Footnote 1 and Robin boundary conditions on the epicardium and on the base (Γ R = Γ epi ∪ Γ base); the boundaries are reported for a patient-specific left ventricle geometry in Fig. 4. We also neglect the body forces b 0 because their contribution is negligible [72]. In conclusion, the cardiac deformation u solves:
The myocardium is considered as an hyperelastic material: there exists a strain energy function \(\mathscr {W}: \varOmega _0 \rightarrow \mathbb {R}\) related to the Piola tensor through the relation
The description of the cardiac muscle mechanics faces a number of difficulties. Indeed, the myocardium is non-homogeneous and it is composed by several layers; moreover, fibers have different orientation in each layer and rotate across the heart wall, featuring a complex mechanical characterization. To model this complex behavior we consider the orthotropic model proposed by Holzapfel and Ogden in [43], characterized by a simple invariant-based formulation. This model hinges upon the idea that for an orthotropic, incompressible material the strain energy density function can be written as
where f 0, s 0 are the two (fibers and sheets respectively) preferred directions and \(\mathscr {I}_1\), \(\mathscr {I}_{4,{\mathbf {f}}_0}\), \(\mathscr {I}_{4,{\mathbf {s}}_0}\), \(\mathscr {I}_{8,{\mathbf {f}}_0{\mathbf {s}}_0}\) are invariants of the right Cauchy-Green strain tensor,
respectively. In particular, we have
The coefficients of the Holzapfel-Ogden constitutive law are taken from [33] and are reported in Table 1.
In order to describe myocardium deformations, we consider a quasi-incompressible formulation [39, 77], which offers several advantages with respect to a full incompressible one, from both a modeling and a numerical viewpoint. Indeed, taking into account limited volumetric changes is possible according to experimental evidence since the volume of cardiac tissue can vary until 7% during systolic contraction [6]. Moreover, a quasi-incompressible formulation leads to a simpler numerical problem with respect to a full incompressible one [65]. The adopted formulation can be obtained by introducing a multiplicative decomposition F = F iso F vol of the deformation gradient tensor, where we impose det(F iso) = 1 and det(F vol) = J. This formulation leads to an additive decomposition of the isotropic part \(\mathscr {W}_1\) of the strain energy function, which reads as
where κ > 0 denotes the Bulk modulus, which measures the material resistance to a uniform compression.
2.2.2 Active Mechanics
The cardiomyocytes of the heart muscle contract after being electrically activated, without the need of an external load. This behavior can be modeled by including the active contraction of the muscular fibers in the force balance (9); however, this is a challenging task because muscular contraction occurring at the macroscale is caused by release of energy at the microscale, inside each cardiomyocyte. Different approaches have been investigated in order to obtain accurate mathematical description of the active mechanics; the most popular ones are the active stress [37, 52, 53, 62, 78] and the active strain approaches; see [4, 73] for numerical comparisons. Both strategies allow to couple electrophysiology and mechanics, defining a modified first Piola-Kirchhoff tensor P which involves a passive component describing the stress required to obtain a given deformation of the passive myocardium, and an active component denoting the tension generated by the depolarization of the propagating electrical signal that provides the internal active forces responsible for the contraction. Thus, Eq. (9) becomes
This leads to a coupled electromechanical problem, where the electrical solution affects cardiac deformations. Here we focus on the active strain approach [3, 23, 51, 81], which is based on a multiplicative decomposition of the deformation gradient tensor, under the form
F e describes the elastic deformation of the myocardium and F a(t) is the anelastic deformation due to the fibers contraction. The active strain decomposition is based on the idea that fibers inside the muscle contract and shorten; the deformation F a can thus be seen as a prescribed distortion of the microstructure, whereas the deformation at the macroscale F e is needed to ensure compatibility of F.
In particular, the anelastic deformation takes the form
where n 0 is a vector normal to f 0 and s 0; γ f, γ s and γ n are time-dependent coefficients describing the cell shortening respectively in the f 0, s 0 and n 0 directions. The fibers shortening γ f can be computed from the following evolution law
where c(t) is the calcium concentration. We remark that the anelastic deformation F a depends on the calcium concentration through the coefficients γ f, γ s and γ n. Here, \(f_A(c(t)) = \alpha (c(t)-c_0)^2R_{FL} (\mathscr {I}_{4,f})\), where we assume α = −2.5 [72], and R FL is the sarcomere force-length relationship of the cardiac cells given by
here, l 0 represents the initial length of a single contractile unit (sarcomere) and we assume l 0 = 1.95 μm, whereas the coefficients c n and d n are parameters of a truncated Fourier series fitted to match the experimental length-force relations reported in [79]; see [75] for further details. Moreover, \(\chi _{[SL_{min},SL_{max}]}(\cdot )\) is the characteristic function of the interval [SL min, SL max], which represent the minimum and maximum sarcomere length, respectively; here we assume SL min = 0.87 μm SL max = 1.33 μm [72]. Here c 0 represents the calcium concentration at the end of the diastolic phase.
The other two coefficients γ s and γ n can be directly derived from the expression of γ f, relying on an orthotropic activation model, as
The parameter κ f allows to correctly describe the thickening occurring during myocardial contraction in the sheets direction. In the mechanical equations, the Piola tensor takes the following form
leading to the following full mechanical problem, where we highlight the dependence on γ f(t):
We point out that in the active strain approach the solution of the mechanical problem depends on the calcium concentration c, rather than on the transmembrane potential. However, we need to compute the solution of the full electrical problem in order to characterize the mechanical displacement, since c is coupled to the transmembrane potential v, e.g., in the monodomain model (5).
A schematic representation of the model describing the electromechanical coupling is reported in Fig. 2.
2.3 Parameters of Interest
ROM techniques allow to efficiently solve the problems introduced so far in different scenarios in order assess the effect of clinically relevant parameters on their solutions by taking into account a possible inter-patient variability. We denote by \(\boldsymbol {\mu } \in \mathscr {P} \subset \mathbb {R}^p\) the set of p selected parameters.
In particular, we are interested in analyzing how the electrical conductivities—σ f, σ s and σ n introduced in (5)—and the fibers orientation f 0 affect heart contraction. Electrical conductivities significantly influence the propagation of the electrical signal and, consequently, the displacement of the cardiac muscle; fibers orientation highly varies among subjects and can have a crucial impact on the correct torsion and shortening of the ventricle. We will restrict our attention to these parameters in this work; note that fibers’ orientation affects both the electrophysiology and the mechanics since it directly enters in the monodomain Eq. (5) as well as in the constitutive law (11). Instead, electrical conductivities affects primarily the monodomain equation through the conductivity tensor D, and only indirectly the myocardium displacement. Additional parameters of interest are, for instance, the (isotropic) coefficient a(μ) introduced in (11), related to the stiffness of the cardiac muscle, as well as the Bulk modulus κ defined in (12), related to the material incompressibility; more can be found in [13, 14].
Regarding electrophysiology, we thus have D = D(μ) and the parametrized electrical model reads as:
If D is μ-dependent, also the variables v and w will depend on parameters. Since the activation equation depends on the solution of the electrical problem, we also have γ f = γ f(μ), so that (14) reads as
As for the mechanical problem, we have u = u(μ), either if we consider parameters directly affecting mechanics or parameters which directly enter only in the electrophysiology, so that (13) modifies as:
In this work, we neglect the influence of the blood in the ventricular chamber, thus taking g = 0—that is, p endo(t) = 0, by assuming that no information on the blood inside the ventricle are available. Note that the problem is not trivial: indeed, even if external loads are zero, stress (and then deformation) originates because of the presence of a term depending on the fiber shortening γ f.
3 Full-Order Model: Finite Element Method
Before addressing the reduction of the electrophysiology and the mechanical problems, we sketch their finite element (FE) approximation [31, 38, 82, 84], which the reduced order model is built on, and plays the role of full-order model (FOM). For the sake of notation the dependence on the parameter vector μ is understood in this section.
3.1 Electrical Model
After deriving the weak formulation of problem (16), we introduce the discretization \(\mathscr {T}_{ep}\) of the domain Ω 0 and the finite dimensional spaces Z h and Q h with dim(Z h) = N z < ∞ and dim(Q h) = N q < ∞, respectively, for the approximation of the potential v and the ionic variables \(\mathbf {w} \in \mathbb {R}^d\), d = 3. We denote by \( \{ \varphi _i \}_{i=1}^{N_z}\), φ i ∈ Z h and \( \{ \psi _i \}_{i=1}^{N_q}\), ψ i ∈ Q h, their FE bases, so that the approximated potential v h and ionic variables w h can be expressed under the form
here ψ i d are the basis functions of the space \(Q_h^d\) and the operator ∘ is the element-wise vector product. We denote the components of \({\mathbf {w}}_i \in \mathbb {R}^3\), i = 1, …, N q, as w1,i, w2,i, ci, respectively. The FE approximation of the monodomain model (5) turns into the following nonlinear system of algebraic equation
by defining the bilinear form a and the functional I as
respectively, with
Here we restrict ourselves to the case of linear (P1) finite elements, so that \(N_z=N_q=N_h^e\). We denote by \(\mathbf {V}=(\mathrm {v}_1,\dots ,\mathrm {v}_{N_h^e})^T\), W = (W 1, W 2, C), where \({\mathbf {W}}_1=(\mathrm {w}_{1,1},\dots ,\mathrm {w}_{1,N_h^e})^T\), \({\mathbf {W}}_2=(\mathrm {w}_{2,1},\dots ,\mathrm {w}_{2,N_h^e})^T\) and \(\mathbf {C}=(\mathrm {c}_{1},\dots ,\mathrm {c}_{N_h^e})^T\). Moreover, M ij = (φ j, φ i), \({\mathbf {M}}_{q,ij}^d=(\boldsymbol {\psi }_j, \boldsymbol {\psi }_i)\) and K ij = a(φ j, φ i) denote the mass matrices and the stiffness matrix associated to problem (19), respectively. To treat the nonlinear term I, we rely on the so-called ionic current interpolation (ICI) method, which introduces a linear interpolation of the ionic currents,
and makes the assembling of the ionic currents term straightforward, only requiring a matrix-vector multiplication, \(\mathbf {I}(\mathbf {V},\mathbf {W}) = \mathbf {M} \tilde {\mathbf {I}}(\mathbf {V},\mathbf {W})\), where \(\tilde {\mathbf {I}}(\mathbf {V},\mathbf {W})=( I(v_1,{\mathbf {w}}_1), \dots , I(v_{N_h^e}, {\mathbf {w}}_{N_h^e}))^T\). A further enhancement of this procedure can be obtained by considering a lumped version of the ICI strategy (L-ICI) where the ionic currents are interpolated nodally or, equivalently, the mass matrix arising in the ICI method is lumped, thus yielding \(\mathbf {I}(\mathbf {V},\mathbf {W}) = {\mathbf {M}}_L \tilde {\mathbf {I}}(\mathbf {V},\mathbf {W})\). We remark that a possible alternative to the ICI method is the so-called state variable interpolation (SVI) method, in which the transmembrane potential and the variables of the ionic model are computed on the quadrature points and then used to evaluate the ionic current in the monodomain equation. The SVI method turns out to be more accurate than the ICI, since it does not approximate the nonlinear term with piecewise linear functions. However, the ICI method represents a reasonable trade-off between accuracy and computational cost; a detailed comparison between the two approaches can be found in [63]. Moreover, the ICI method better fits with the matrix formulation of the hyper-reduction techniques we have exploited, thus making the coupling between the monodomain equation and the ionic model more efficient when dealing with the reduced order model for electrophysiology. We also point out that when using coarse meshes, the L-ICI method underestimates the propagation velocity of the electrical signal. However, this problem can be solved by artificially increasing the electrical conductivities σ f, σ s and σ n in the L-ICI method, as done in [72].
The nonlinear function s appearing in the ionic model is approximated as
so that \(\mathbf {S}(\mathbf {V},\mathbf {W})= {\mathbf {M}}_q^d \tilde {\mathbf {S}}(\mathbf {V},\mathbf {W})\), where \(\tilde {\mathbf {S}}(\mathbf {V},\mathbf {W})=(\mathbf {s}(v_1,{\mathbf {w}}_1), \dots , \mathbf {s}(v_{N_h^e},{\mathbf {w}}_{N_h^e}))^T\). Since the ionic variables can be computed at each node independently, the second equation of (19) yields to a system of \(N_h^e\) uncoupled ODEs, \(\dot {\mathbf {W}}- \tilde {\mathbf {S}}(\mathbf {V},\mathbf {W})=0\).
The spatial FE discretization of (19) thus leads to the following system:
Let us now introduce a time discretization of (22), denoting by Δt e = T∕n t the time step, with t n = nΔt e, n = 1, …, n t; the superscript n denotes a quantity evaluated at time t n. We adopt a forward Euler scheme to solve the ODEs representing the ionic model, with a sufficiently small Δt to preserve the stability of the method. To discretize in time the monodomain equation, we rely on a semi-implicit scheme; in particular, we treat the diffusion term implicitly and the reaction term explicitly. This strategy allows us to solve, at each time step, a linear system instead of a nonlinear one, as it would have been instead required by an implicit method.
We finally assume a weak coupling between all the electrophysiology fields, that is we consider an explicit algorithm to compute the solution of (22), solving sequentially two separate problems in order to compute the ionic variables w and the potential v. In conclusion, we obtain the following system: given V 0, W 0, for n = 0, …, n t − 1 compute
where mass lumping is commonly used (note the presence of the matrix M L) to reduce possible oscillations near the wave-front [46, 67].
3.2 Activation Equation
Regarding the activation Eq. (14), we first perform a Taylor series expansion around γ f = 0 of the quantity
appearing at the right-hand side of the ODE in (14). Since \(\mathscr {F}(\mathbf {u},0) = 2 \mathscr {I}_{4,f}|{ }_{c=c_0}\), we can approximate the ODE under the form
the choice M = 5 ensures that \(||\mathscr {F}(\mathbf {u},\gamma _f) - \sum _{j=1}^M {-1^j (j+1) (j+2)\mathscr {I}_{4,f} \gamma _f^j} || <0.005\), see [72]. Similarly to the discretization of the ionic model (21), the spatial semidiscretization reads
where linear finite elements have been chosen to approximate γ f. Here \({\mathbf {G}}_f= (\gamma _{f_1}, \dots , \gamma _{f_N})^T \in \mathbb {R}^{N_h^e}\) and \(\mathbf {C}\in \mathbb {R}^{N_h^e}\) denote the vectors of degrees of freedom (dofs) related to γ f and to the calcium variable c, respectively. The fully discretized problem, obtained by adopting the forward Euler scheme for the time discretization, then reads as follows: given \({\mathbf {G}}_f^{0}\), for n = 0, …, n t − 1 compute
3.3 Mechanical Model
We now turn to the FE approximation of the mechanical subproblem (15), which is a fully nonlinear, quasi-static problem since it depends on time through the coupling with the electrical subproblem. We rely on the Newton method to solve, at a given time instant, such a nonlinear problem. Performing a Newton step at the continuous level around a generic displacement \(\hat {\mathbf {u}}(t)\) yields a weak problem under the following form to be solved: find δ u(t) such that
where
and
This problem arises after integrating (15) by parts over Ω 0 and linearizing the resulting problem; recall that F is the deformation gradient tensor defined in (7).
The FE approximation of problem (27) over a suitable triangulation \(\mathscr {T}_m\) of the domain Ω 0 can be obtained in a straightforward way; in this work, we use linear (P1) finite elements to approximate the mechanical displacement, denoting by \(N_h^m\) the dimension of the FE space for the approximated displacement. We then obtain the following algebraic form of the Newton problem: for each t n, n = 0, …, N t − 1, given U (0)(t n), for every k ≥ 1 we search δ U(t n) satisfying
until \(|| \mathbf {R} ({\mathbf {u}}^k_h(t_n))||{ }_{2}< \varepsilon \), being ε > 0 a small fixed tolerance. Here, for any \(\mathbf {U} \in \mathbb {R}^{N_h^m}\),
are the components of the Jacobian \(\mathbf {J}(\mathbf {U}) \in \mathbb {R}^{N_h^m \times N_h^m}\) and the residual \(\mathbf {R}(\mathbf {U}) \in \mathbb {R}^{N_h^m}\) evaluated at \(\mathbf {U} \in \mathbb {R}^{N_h^m}\); \(\{\boldsymbol {\varphi }_i, i=1,\ldots ,N_h^m\}\) denote the (vector) basis functions of the FE space for the displacement and \(\mathbf {U}(t) = (u_1(t),\ldots ,u_{N_h^m}(t))^T\) the vector of dofs of its high-fidelity approximation u(t)—here denoted, with a slight abuse of notation, in the same way as the displacement at the continuous level.
Algorithm 1 FOM for the (one-way) coupled electromechanical model

A segregated algorithm is finally chosen for the solution of the electromechanical problem, in which the governing equations are solved sequentially—that is, segregated from one another; see Algorithm 1. This approach is shown to be appropriate when considering a model which is independent on the fibers stretch or which depends on the stretch but not on the stretch-rate [62]. In particular:
-
we consider two different time steps for the electrical and the mechanical problem. The electrophysiology requires a significantly small time-step Δt e = T∕n t in order to correctly capture the propagation front of the electrical potential. Since the mechanical displacement is slower (of a factor ranging between 10 and 100) than the electrical signal propagation, for the mechanical model it is sufficient to consider a time step Δt m = T∕N t small enough to guarantee the convergence of the Newton method. In particular, we set them so that Δt m = DΔt e, that is, n t = DN t. Since we are discretizing the activation equation with the forward Euler method, we need to solve (26) using the time step Δt e of the electrical model to guarantee the stability of the overall numerical scheme. Therefore, D time steps for the electrical subproblem (23) and the activation Eq. (26) are evaluated between two time instants in which the mechanical subproblem is solved;
-
different meshes \(\mathscr {T}_{ep}\), \(\mathscr {T}_m\) are employed for the electrical and mechanical problems, respectively; the latter problem requires less mesh-size restrictions than the former and can thus be solved on a coarser mesh [69]. This implies the need of transferring information between the two meshes: to impose the activation in the mechanical problem we need to evaluate the solution of the electrophysiology problem on \(\mathscr {T}_m\), whereas the electromechanical feedback (which here is not considered) would require to evaluate the solution of the mechanical problem on \(\mathscr {T}_{ep}\). This inter-grid transfer is performed by means of a rescaled localized radial basis functions (RBF) interpolation technique introduced in [32]; see also [9, 72].
4 Reduced Order Modeling Techniques
The reduced basis (RB) method allows to speed up the approximation of a parameter-dependent PDE in the case multiple evaluations of its solution are required for several values of the parameter \(\boldsymbol {\mu } \in \mathscr {P}\). The basic idea of the RB method is to seek the solution of a problem in a subspace of much smaller dimension than the one, N h, of the FOM space. During the offline stage, the parameter domain is explored, and a set of high-fidelity solutions (snapshots) is computed to generate a low dimensional RB space of dimension N ≪ N h. This space can be built by means of either a greedy algorithm (if suitable a posteriori error estimators are available and can be efficiently evaluated) or, in more general situations, proper orthogonal decomposition (POD) technique; see Sect. 4.1. Then, during the online phase, for each new value of μ, the RB approximation is rapidly computed by combining (possibly few) arrays stored offline, whose complexity must no longer depend on N h.
The technique is well-established for linear PDEs (both of elliptic and parabolic type) showing an affine dependence on μ; see, e.g., [68] for an in-depth presentation of the methodology. Under the assumption of affine parametric dependence, the differential operators and data can be expressed as a linear combination of μ-independent forms (which can thus be precomputed) weighted by μ-dependent coefficients, which can be inexpensively evaluated. The RB method in its classical formulation, however, is no longer efficient when dealing with nonlinear (and/or nonaffinely parametrized) problems, unless we employ suitable hyper-reduction techniques to perform system approximation in addition to solution-space reduction; in the nonlinear case, these two operations shall be performed at the same time.
We first address the issue of solution-space reduction, which is achieved by means of the POD technique. We consider the case of a nonlinear stationary problem, a class which the mechanical subproblem fits in, for the sake of general exposition. We postpone the case of time-dependent nonlinear problems—albeit treated in a semi-implicit way, thus requiring the solution of a linear system at each time step—to Sect. 5, where we address the reduction of the monodomain equation. For the sake of exposition, we formulate everything in a purely algebraic form.
4.1 POD-Galerkin Method
Let us consider the following, abstract, nonlinear μ-dependent algebraic system
and the associated Newton method: given \({\mathbf {U}}^{(0)}(\boldsymbol {\mu }) \in \mathbb {R}^{N_h}\), for k ≥ 1, find \(\delta \mathbf {U}(\boldsymbol {\mu }) \in \mathbb {R}^{N_h}\) s.t.
and iterate until ||R(U (k)(μ);μ)||2 < ε, being ε > 0 a small, given tolerance. As before, \(\mathbf {J}(\mathbf {U}(\boldsymbol {\mu });\boldsymbol {\mu }) \in \mathbb {R}^{N_h \times N_h}\) denotes the μ-dependent Jacobian matrix (with linearization around U(μ)) and \(\mathbf {R}(\mathbf {U}(\boldsymbol {\mu });\boldsymbol {\mu }) \in \mathbb {R}^{N_h}\) the μ-dependent residual vector.
In the case of mechanical problems characterized by complex nonlinear constitutive laws, the computational burden in solving (32)1 is represented by the assembling of the Jacobian matrix, which can consume almost the entire CPU time required by each Newton step. To reduce the computational complexity of problem (32), the RB method seeks, for any \(\boldsymbol {\mu } \in \mathscr {P}\), an approximation of U (k)(μ) given by a linear combination of (possibly few) basis functions,
where \({\mathbf {u}}_N^{(k)}(\boldsymbol {\mu }) \in \mathbb {R}^N\) and \(\mathbf {Z} \in \mathbb {R}^{N_h\times N}\) is a matrix whose N ≪ N h columns contained the nodal values of the RB functions. Problem (32) is then replaced by the following: given \({\mathbf {u}}_N^{(0)}(\boldsymbol {\mu }) \in \mathbb {R}^{N}\), for k ≥ 1, find \( \delta {\mathbf {u}}_N \in \mathbb {R}^{N}\) s.t.
and iterate until \(||{\mathbf {Z}}^T \mathbf {R}( \mathbf {Z} {\mathbf {u}}_N^{(k)}(\boldsymbol {\mu });\boldsymbol {\mu })||{ }_2< \varepsilon _{RB}\), being ε RB > 0 a small, given tolerance. If (34) converges, Zu N(μ) can be regarded as an approximation of U(μ) in the RB space, with \({\mathbf {u}}_N= \lim _{k \rightarrow \infty } {\mathbf {u}}_N^{(k)} \). Problem (34)1 is obtained by requiring that the Galerkin projection over V N of the FOM residual computed on the ansatz (33) vanishes, where V N has to be intended as the space spanned by the columns of Z.
The POD technique—through the so-called method of snapshots—can be used to compute the reduced basis Z (and, as we shall see in Sect. 4.2, for the construction of both DEIM and MDEIM bases). In the case of a stationary, μ-dependent nonlinear problem, POD performs the singular value decomposition of a matrix
of snapshots of the high-fidelity problem and returns an orthonormal basis of the RB space made by the first N right singular vectors of S. Here snapshots are represented by Newton steps obtained for n s parameter vectors \(\boldsymbol {\mu }_i\in \mathscr {D}\), i = 1, …, n s, randomly sampled over \(\mathscr {P}\); more ad-hoc strategies, such as e.g. latin hypercube sampling or sparse grid, could be exploited especially for high-dimensional parameter spaces.
Hence, from the factorization S = Z ΣΛ T, where Λ = diag(σ 1, σ 2, …) is the matrix of singular values of S, the POD basis Z N of dimension N ≤ n s is obtained by collecting the first N columns of Z (i.e. the first N left singular vectors), corresponding to the first N (largest) singular values; we can set the basis dimension N as the minimum integer such that
given a suitable, small tolerance ε POD > 0. The reduced basis provided by POD is optimal, in the sense that it minimizes the sum of the squared distances between each snapshot and the corresponding projection onto the subspace. When denoting by Z the POD basis, its dimension N will be understood.
4.2 Hyper-Reduction Techniques
When using Newton iterations to solve nonlinear problems, assembling the ROM for any new parameter would require to assemble (also in the online phase) the FOM arrays first and then to project them onto the reduced space, thus calling into play high-fidelity arrays at the online stage, too. This issue is even more relevant when dealing with fully nonlinear problems, for which the global Jacobian matrix has to be entirely reassembled at each Newton step.
Hyper-reduction (or system approximation) techniques aim to recover an approximate affine structure of nonlinear terms to guarantee an efficient offline-online decomposition. The archetypical hyper-reduction technique introduced in the RB framework is the empirical interpolation method (EIM), developed in [10, 49] to approximate nonaffinely parametrized functions. Its discrete variant, the so-called Discrete EIM (DEIM), was originally proposed in [21] to efficiently deal with nonlinear problems, but has also been applied to nonaffinely parametrized linear operators. More recently, a matrix version of DEIM (MDEIM) has been developed [19, 87], and then further explored in [55] to approximate the full-order parametrized operators in a purely algebraic way.
4.2.1 DEIM for Residual Approximation
For the problem at hand, at each Newton step, DEIM [21] allows to efficiently express the residual vector as a linear combination of (possibly few) μ-independent terms so that the μ-dependent weights of this combination can be efficiently computed by solving an interpolation problem. In particular, we project the residual vector \(\mathbf {R}(\mathbf {Z} {\mathbf {u}}_N^{(k)}(\boldsymbol {\mu });\boldsymbol {\mu })\) onto a low-dimensional subspace spanned by a basis \(\boldsymbol {\varPhi }_R \in \mathbb {R}^{N_h \times m_R}\) such that, ∀k ≥ 1
where \(\boldsymbol {\theta }_R(\mathbf {Z} {\mathbf {u}}_N^{(k)}(\boldsymbol {\mu }),\boldsymbol {\mu }) \in \mathbb {R}^{m_R}\) is a coefficient vector to be determined. In particular:
Algorithm 2 DEIM algorithm (as originally proposed in [21])

-
the basis Φ R can be computed (once for all) by performing POD on a set of snapshots
$$\displaystyle \begin{aligned} {\mathbf{S}}_R = \{ \mathbf{R}(\mathbf{Z} {\mathbf{u}}_N^{(k)}(\boldsymbol{\mu}_i);\boldsymbol{\mu}_i) \quad i=1, \ldots ,n_s, k=1,\ldots \}. \end{aligned}$$To obtain the residual snapshots \(\mathbf {R}(\mathbf {Z} {\mathbf {u}}_N^{(k)}(\boldsymbol {\mu }_i);\boldsymbol {\mu }_i)\), we need to solve the reduced problem (34) for different values of μ and, at each Newton iteration, to store the computed residual vectors;
-
the coefficient vector \(\boldsymbol {\theta }_R(\mathbf {Z} {\mathbf {u}}_N^{(k)}(\boldsymbol {\mu }),\boldsymbol {\mu })\) can be evaluated for each new value of μ by imposing m R interpolation constraints on a subset \(\boldsymbol {\wp }=[\wp _1, \ldots , \wp _{m_R}]\) of entries of \(\mathbf {R}(\mathbf {Z} {\mathbf {u}}_N^{(k)}(\boldsymbol {\mu });\boldsymbol {\mu })\) (the so-called magic points, introduced in [49]), selected by the DEIM algorithm, see Algorithm 2. For ease of notation, we introduce the matrix
$$\displaystyle \begin{aligned} \mathbf{P} =[{\mathbf{e}}_{\wp_1},\cdots,{\mathbf{e}}_{\wp_{m_R}}] \in \mathbb{R}^{N_h \times m_R}, \end{aligned} $$(36)where \({\mathbf {e}}_{\wp _i}=[0,\cdots ,0,1,0,\cdots ,0]^T \in \mathbb {R}^{N_h}\) is the ℘ i-th column of the identity matrix \(I \in \mathbb {R}^{N_h \times N_h}\), for i = 1, ⋯ , m R. The coefficient vector \(\boldsymbol {\theta }_R(\mathbf {Z} {\mathbf {u}}_N^{(k)}(\boldsymbol {\mu }),\boldsymbol {\mu })\) is then obtained as the solution of
$$\displaystyle \begin{aligned} {\mathbf{P}}^T \boldsymbol{\varPhi}_R \boldsymbol{\theta}_R(\mathbf{Z} {\mathbf{u}}_N^{(k)}(\boldsymbol{\mu}),\boldsymbol{\mu}) = {\mathbf{P}}^T \mathbf{R}(\mathbf{Z} {\mathbf{u}}_N^{(k)}(\boldsymbol{\mu});\boldsymbol{\mu}); \end{aligned}$$P T Φ R and \( {\mathbf {P}}^T \mathbf {R}(\mathbf {Z} {\mathbf {u}}_N^{(k)}(\boldsymbol {\mu });\boldsymbol {\mu })\) are the restrictions of Φ R and \(\mathbf {R}(\mathbf {Z} {\mathbf {u}}_N^{(k)}(\boldsymbol {\mu });\boldsymbol {\mu })\) to the subset of indices ℘, respectively.
The approximation of the reduced residual vector in (34) can be obtained by projecting (35) onto the reduced space yielding
All the quantities appearing in (37) which do not depend on μ can be precomputed offline; in the online stage we only need to assemble \({\mathbf {P}}^T \mathbf {R}(\mathbf {Z} {\mathbf {u}}_N^{(k)}(\boldsymbol {\mu });\boldsymbol {\mu })\), which is the restriction of the residual to the subset of DEIM nodes. In the FE context, this restriction can be computed by simply integrating the residual only on the quadrature points belonging to those mesh elements which provide a non-zero contribution to the entries ℘; this set of elements is usually referred to as reduced mesh [18].
4.3 Jacobian Approximation
An affine approximation of the reduced Jacobian matrix \({\mathbf {J}}_N(\mathbf {Z} {\mathbf {u}}^{(k)}_N(\boldsymbol {\mu });\boldsymbol {\mu })\) can be obtained by relying on either the DEIM algorithm or a MDEIM alternative technique.
The classical DEIM approach to tackle nonlinear problems (see e.g. [11, 22, 45, 64]) computes the reduced Jacobian J N(Zw N(μ);μ), for any \({\mathbf {w}}_N \in \mathbb {R}^N\), as the derivative of the reduced approximated residual vector (i.e. the right-hand side of (37)),
As for the residual vector, we can precompute the μ-independent quantities offline, while online we have to assemble \({\mathbf {P}}^T \mathbf {J}(\mathbf {Z} {\mathbf {w}}_N(\boldsymbol {\mu });\boldsymbol {\mu }) \in \mathbb {R}^{m_R \times N_h}\), that is the restriction of the Jacobian matrix to the rows which correspond to the indices in ℘. Consequently, we need to assemble online, at each Newton step, a matrix of dimension m R × N h, which still depends on the dimension N h of the FE problem, which is unfeasible when m R becomes large. Note that since the reduced Jacobian matrix is obtained as the derivative of the reduced residual, DEIM yields the application of the exact Newton method (i.e. with the exact reduced Jacobian matrix) although on an approximated version of problem (34).
When a large number m R of DEIM terms is obtained, a matrix version of DEIM (MDEIM) can be employed to perform hyper-reduction of the Jacobian matrices arising in (34). The idea is to directly approximate the reduced Jacobian \({\mathbf {Z}}^T \mathbf {J}(\mathbf {Z} {\mathbf {u}}_N^{(k)}(\boldsymbol {\mu });\boldsymbol {\mu }) \mathbf {Z}\) by relying on a different basis than the one used for the residual. This yields a quasi-Newton method since the reduced Jacobian matrix is not the exact derivative of the reduced residual; nevertheless, since the μ-dependent Jacobian matrix usually varies in a significantly smaller range compared to the residual vector, few (much less than m R) terms are required.
MDEIM provides an approximation of the Jacobian matrix \(\mathbf {J}(\mathbf {Z} {\mathbf {u}}_N^{(k)}(\boldsymbol {\mu });\boldsymbol {\mu })\in \mathbb {R}^{N_h \times N_h}\) under the form
being \(\{ {\mathbf {J}}^i \in \mathbb {R}^{N_h \times N_h}\), i = 1, …, m J} a set of μ-independent matrices that can be computed once for all and \(\boldsymbol {\theta _J}(\boldsymbol {\mu })=(\theta ^1_J(\boldsymbol {\mu }),\cdots ,\theta ^{m_J}_J(\boldsymbol {\mu }))^T\) a coefficient vector. This approximation is obtained by defining \(j(\mathbf {Z} {\mathbf {u}}_N^{(k)}(\boldsymbol {\mu });\boldsymbol {\mu }) = \text{vec} (\mathbf {J}(\mathbf {Z} {\mathbf {u}}_N^{(k)}(\boldsymbol {\mu });\boldsymbol {\mu }) \in \mathbb {R}^{N_h^2}\) as the vector obtained by stacking all the columns of \(\mathbf {J}(\mathbf {Z} {\mathbf {u}}_N^{(k)}(\boldsymbol {\mu });\boldsymbol {\mu })\), and approximating \(j(\mathbf {Z} {\mathbf {u}}_N^{(k)}(\boldsymbol {\mu });\boldsymbol {\mu }) \) by its DEIM counterpart
Then, the matrices J i can be computed transforming each column \(\boldsymbol {\phi }_i \in \mathbb {R}^{N_h^2 }\) of Φ J into a matrix \({\mathbf {J}}^i \in \mathbb {R}^{N_h \times N_h}\) by reverting the vec operation, as J i = vec−1(ϕ i), so that \({\mathbf {J}}_m(\mathbf {Z} {\mathbf {u}}_N^{(k)}(\boldsymbol {\mu });\boldsymbol {\mu }) = \text{vec}^{-1} ( j_m(\mathbf {Z} {\mathbf {u}}_N^{(k)}(\boldsymbol {\mu });\boldsymbol {\mu }))\). The basis Φ J and the coefficient vector θ J(μ) are determined following the same procedure used for the residual vectors, relying on a set of snapshots S J = \(\{\mathbf {J}(\mathbf {Z} {\mathbf {u}}_N^{(k)}(\boldsymbol {\mu }_i);\boldsymbol {\mu }_i), \, i=1, \dots ,n_s, \ k=1,\ldots \}\), evaluated on the reduced solution. Finally, the reduced Jacobian matrix in (34) can be approximated as
4.3.1 Efficient Assembling on a Reduced Mesh
By using DEIM and MDEIM as above, the POD solution-space reduction is first performed, while the bases associated to the DEIM and MDEIM approximations of R and J are computed at a later time. The major drawback of this strategy is that problem (34) must be solved n s times. To avoid this, we can rely on an intermediate problem where the Jacobian matrix is replaced by its MDEIM approximation and the residual is exact: given \({\mathbf {u}}_{N,m}^{(0)} \in \mathbb {R}^N\), at each Newton step we search \(\delta {\mathbf {u}}_{N,m}^{(k)} \in \mathbb {R}^N\), k ≥ 1 satisfying
and iterate until \(||{\mathbf {Z}}^T \mathbf {R}( \mathbf {Z} {\mathbf {u}}_N^{(k)}(\boldsymbol {\mu });\boldsymbol {\mu })||{ }_2< \varepsilon _{RB} \). Solving this problem is significantly faster than solving problem (34), since J is assembled only onto the reduced mesh. Moreover, problem (41) is very fast to solve since it requires almost the same effort of the full hyper-reduced problem. The complete procedure for the ROM construction is reported in Algorithm 3.
Algorithm 3 ROM construction (stationary, nonlinear problem)

5 RB Methods for Cardiac Electrophysiology
We now apply the techniques introduced in the previous section to the electrical problem. The parametrized version of problem (23) reads: given \(\boldsymbol {\mu } \in \mathscr {D}\), V 0(μ) and W 0(μ), for each n = 0, …, n t − 1 solve
A ROM for the monodomain Eq. (42)1, exploits the POD technique for the construction of the reduced space, and on the DEIM technique to approximate the nonlinear terms. Moreover, we exploit the MDEIM technique to efficiently recover an affine decomposition for the μ-dependent stiffness matrix, and use the DEIM technique to reduce the computational cost associated to the ionic model (42)2.
We consider a vector of physical parameters \(\boldsymbol {\mu } \in \mathscr {P}\) as in Eq. (16) affecting the conductivity tensor D = D(μ) (and possibly the initial data); this yields a μ-dependent stiffness matrix \(\mathbf {K}(\boldsymbol {\mu }) \in \mathbb {R}^{N_h^e \times N_h^e}\); in the case we considered a geometrical parametrization of the domain where the problem is set, also the mass matrix M L would be μ-dependent. Moreover, for the sake of simplicity we do not consider the case of parameters affecting the ionic terms; see [59] for more about this subject.
5.1 Monodomain Equation
We rely on the POD-Galerkin method recalled in Sect. 4.1: for each value of \(\boldsymbol {\mu } \in \mathscr {P}\), we approximate the FE discretization of the potential at time t n as
where \({\mathbf {V}}_{N^e}(\boldsymbol {\mu }) \in \mathbb {R}^{N^e}\) denotes the reduced transmembrane potential and Z e denotes the matrix whose columns span the RB space for the monodomain equation. By substituting (43) in (23)1 and projecting the resulting residual onto the reduced space spanned by the columns of Z e, we obtain the following problem: given \(\boldsymbol {\mu } \in \mathscr {P}\) and \({\mathbf {V}}_{N^e}^0(\boldsymbol {\mu })\), for each n = 0, …, n t − 1 solve
Since the matrix \({\mathbf {Z}}_e^T \mathbf {K}(\boldsymbol {\mu }) {\mathbf {Z}}_e \) depends on μ, it has to be reassembled for each new value of μ; to avoid this, we replace K(μ) by an approximate affine expansion
obtained through the MDEIM technique. Here \(\{ {\mathbf {K}}^i \in \mathbb {R}^{N_h^e \times N_h^e}\), i = 1, …, m K} are a set of μ-independent matrices that can be computed once for all and \(\boldsymbol {\theta }_K(\boldsymbol {\mu })=[\theta ^1_K(\boldsymbol {\mu }),\cdots ,\theta ^{m_K}_K(\boldsymbol {\mu })] \) a vector of coefficients to be evaluated for any \(\boldsymbol {\mu } \in \mathscr {P}\). In this way, no matter which kind of μ-dependence is considered in the expression of the diffusion tensor (6), the ROM stiffness matrix can be assembled using a set of precomputed quantities; in particular, if μ also includes the maximum fibers rotation angle θ max, the vector defining the fiber direction f 0(μ) cannot be written under affine form; see [13]. We point out that K(μ) is time-independent, hence it has to be assembled only once for each value of μ; in particular, during the online stage, we can compute θ K(μ) and the corresponding approximation (45) of K(μ) when selecting a new μ, and then use the computed quantities for all time instants.
Using approximation (45), problem (44) becomes: given \(\boldsymbol {\mu } \in \mathscr {P}\) and \({\mathbf {V}}_{N^e}^0(\boldsymbol {\mu })\), for each n = 0, …, n t − 1 solve
Since the term describing the ionic current is nonlinear, we replace it by its DEIM approximation. We introduce a basis \(\boldsymbol {\varPhi }_I \in \mathbb {R}^{N_h^e\times m_I}\), and express
The basis \(\boldsymbol {\varPhi }_I \in \mathbb {R}^{N_h^e\times m_I}\) has to be precomputed during the offline phase by performing a POD on a set of snapshots \(\{ \tilde {\mathbf {I}}({\mathbf {Z}}_e{\mathbf {V}}_{N^e}^n(\boldsymbol {\mu }_i),{\mathbf {W}}^{n+1}(\boldsymbol {\mu }_i))\), i = 1, …, n s}; instead, the coefficient vector \(\boldsymbol {\theta }_I({\mathbf {V}}_{N^e}^n(\boldsymbol {\mu }),{\mathbf {W}}^{n+1}(\boldsymbol {\mu })) \in \mathbb {R}^{m_I} \) has to be computed online, by solving the interpolation problem
where \({\mathbf {P}}_I^T=[{\mathbf {e}}_{\wp _{I,1}},\cdots ,{\mathbf {e}}_{\wp _{I,m_R}}]^T \in \mathbb {R}^{N_h^e \times m_I}\) is the restriction matrix to the set of DEIM indices ℘ I defined in (36). The DEIM approximation of (47) is thus
To obtain the second term of the right hand side of (44) we can simply project (49) onto the reduced space spanned by Z e, thus getting
We point out that the matrices \({\mathbf {Z}}_e^T {\mathbf {M}}_L \boldsymbol {\varPhi _I} \in \mathbb {R}^{N^e \times m_I}\) and \({\mathbf {P}}_I^T \boldsymbol {\varPhi _I} \in \mathbb {R}^{m_I \times m_I} \) can be precomputed during the offline stage, since they are μ-independent. For the sake of system approximation, during the online stage we only need to evaluate (only once) the restriction of \(\tilde {\mathbf {I}}\) to the indices ℘ I, that is, \({\mathbf {P}}_I^T \tilde {\mathbf {I}}({\mathbf {Z}}_e{\mathbf {V}}_{N^e}^n(\boldsymbol {\mu }),{\mathbf {W}}^{n+1}(\boldsymbol {\mu })) \in \mathbb {R}^{m_I}\).
Relying on (50), instead of (44) we thus obtain the following hyper-reduced monodomain equation: given \(\boldsymbol {\mu } \in \mathscr {P}\) and \({\mathbf {V}}_{N^e}^0(\boldsymbol {\mu })\), for each n = 0, …, n t − 1 solve

The construction of the reduced basis Z e and the snapshots selection strategy will be addressed in Sect. 5.3.
5.2 The Full Electrophysiology Problem
In this section we aim at developing an efficient ROM for the full electrical problem (42), which involves a PDE (monodomain equation) and a system of ODEs (ionic model). Replacing the second equation of (42) with the ROM (51) derived in the previous section, we obtain the following problem: given \(\boldsymbol {\mu } \in \mathscr {D}\) and \({\mathbf {V}}^0_{N^e}(\boldsymbol {\mu })\) and W 0(μ), for each n = 0, …, n t − 1 solve
Since the ODEs still depend on the high-fidelity approximation of the potential V n at each time t n, n = 1, …, n t, we should in principle compute the matrix-vector product \({\mathbf {V}}^n={\mathbf {Z}}_e {\mathbf {V}}_{N^e}^n\) at each time t n to evaluate \(\tilde {\mathbf {S}}({\mathbf {V}}^n(\boldsymbol {\mu }),{\mathbf {W}}^n(\boldsymbol {\mu }))\) and solve the ionic model. To avoid this operation, we can again rely on a DEIM approximation. In fact, we can express the restriction of \(\tilde {\mathbf {I}}(\mathbf {V},\mathbf {W})\) to the subset of DEIM indices ℘ I as
In particular, we observe that in order to solve (52)2, only the restriction of the ionic variables vector W n+1(μ) to the indices ℘ I is required. Hence, (52) becomes: given \(\boldsymbol {\mu } \in \mathscr {D}\), \({\mathbf {V}}^0_{N^e}(\boldsymbol {\mu })\) and W 0(μ), for each n = 0, …, n t − 1 solve
As done in (53) for the ionic current, we write
so that, exploiting the approximation \({\mathbf {V}}^{n}(\boldsymbol {\mu }) \approx {\mathbf {Z}}_e{\mathbf {V}}^{n}_{N^e}(\boldsymbol {\mu }),\ n=0,\dots ,n_t-1\), the hyper-reduced order model for the electrical problem reads as follows: given \(\boldsymbol {\mu } \in \mathscr {D}\), \({\mathbf {V}}^0_{N^e}(\boldsymbol {\mu })\) and W 0(μ), for each n = 0, …, n t − 1 solve

Hence, instead of solving the ODEs (54)1 for each degree of freedom of \(\mathscr {T}_{ep}\), we compute their solution only at m I nodes, with \(m_I \ll N_h^e\). Indeed, both the ionic model and the monodomain equation only depend on the restriction of the potential to the indices ℘ I; in particular, by recalling that
we notice that the matrix \({\mathbf {P}}_I^T {\mathbf {Z}}_e \in \mathbb {R}^{m_I \times N^e}\) can be precomputed offline. Solving the ODEs system at each node of the mesh would have been required if the activation equation underwent a similar reduction procedure and a ROM for the coupled electromechanical problem was built; see [13] for more on this subject.
5.3 Snapshots Selection Strategy
To build Z e and Φ I we rely on a POD-POD strategy, namely we perform POD with respect to both the time and the parameter vector. In particular:
-
for each parameter value \(\boldsymbol {\mu }_1,\ldots , \boldsymbol {\mu }_{n_s}\) randomly chosen in \(\mathscr {P}\), we solve the high-fidelity problem (42) and perform a POD in time to compress the snapshots V n(μ i), n = 1, …, n t, thus obtaining a basis Z i; finally, we obtain the POD basis Z e performing a POD on the n s bases Z 1, …, \({\mathbf {Z}}_{n_t}\);
-
regarding the nonlinear term, we collect the snapshots \(\tilde {\mathbf {I}}(\mathbf {Z} {\mathbf {V}}_{N^e}^n(\boldsymbol {\mu }_i),{\mathbf {W}}^{n+1}(\boldsymbol {\mu }_i))\), n = 1, …, n t, i = 1, …, n s by solving the following problem: given \({\mathbf {V}}^0_{N^e}(\boldsymbol {\mu }_i)\) and W 0(μ i), i = 1, …, n s, for each n = 0, …, n t − 1 compute
$$\displaystyle \begin{aligned} \begin{cases} {\mathbf{W}}^{n+1}(\boldsymbol{\mu}) = {\mathbf{W}}^{n}(\boldsymbol{\mu}) + \varDelta t \tilde{\mathbf{S}}({\mathbf{V}}^n(\boldsymbol{\mu}),{\mathbf{W}}^n(\boldsymbol{\mu})) \\ \begin{aligned} \Big[ \frac{C_m}{\varDelta t} {\mathbf{Z}}^T {\mathbf{M}}_L \mathbf{Z} + \sum_{i=1}^{m_K} \theta_K^i(\boldsymbol{\mu}) {\mathbf{Z}}^T {\mathbf{K}}_i \mathbf{Z} \Big] {\mathbf{V}}_{N^e}^{n+1}(\boldsymbol{\mu})&= \frac{C_m}{\varDelta t} {\mathbf{Z}}^T{\mathbf{M}}_L\mathbf{Z} {\mathbf{V}}_{N^e}^n(\boldsymbol{\mu})\\ &+ {\mathbf{Z}}^T {\mathbf{M}}_L \tilde{\mathbf{I}}(\mathbf{Z} {\mathbf{V}}_{N^e}^n(\boldsymbol{\mu}),{\mathbf{W}}^{n+1}(\boldsymbol{\mu})) \end{aligned} \end{cases} \end{aligned} $$(56)and then perform the same POD-POD procedure with respect to time and parameters as in the previous case; see Algorithm 4.
Algorithm 4 ROM construction (electrophysiology)

Here we rely on global reduced bases; considering local bases obtained by partitioning the snapshot set either with respect to time or the parameters, or, alternatively, produced by a clustering procedure in the physical space, represents a further improvement, currently under investigation; see [59] for further details.
6 RB Methods for Cardiac Mechanics
We now show how to take advantage of the techniques presented in Sect. 4 in order to build a ROM for the mechanical problem. This latter is a time-driven problem, since its solution depends on time only through its coupling with the electrophysiology model, which is intrinsically unsteady. Relying on the RB method provides a twofold advantage, since the problem has to be solved not only for different parameters, but also at several time instants.
The parametrized version of problem (28) reads: given U (0)(t n;μ) = U(t n−1;μ), for n = 1, …, N t, N t = T∕Δt m, for k ≥ 1 solve:
until \(|| \mathbf {R}({\mathbf {U}}^{(k-1)}(t_{n}; \boldsymbol {\mu });{\mathbf {G}}_f^{l}(\boldsymbol {\mu })||{ }_{2}< \varepsilon \), where k is the index of the Newton iterations, t n denotes the time instant which the mechanical problem is computed at, and l = (n + 1)D − 1, with D = Δt m∕Δt e. Here we also have made the dependence on the (discrete representation of the) fibers shortening G f; recall that the time stepping for this latter variable follows the one of the electrical problem.
For the mechanical problem, time is instead considered as an additional parameter, although with peculiar features. Indeed, as we are not interested in solving problem (57) for generic values of t selected online, we use the same time step Δt m in both the offline and online stages; in particular, online we solve the reduced problem associated with (57) only in the time instants of the form t n = n Δt m used during the offline stage for the snapshots computation.
6.1 Jacobian Approximation by the Broyden Method
When dealing with time dependent (and/or large scale) problems, (M)DEIM might be not efficient enough to guarantee a rapid approximation of the Jacobian matrix during the online phase. In particular, the classical DEIM technique (see Sect. 4.3) provides moderate computational speed-up when dealing with nonlinear problems which require a large number of terms m R. On the other hand, MDEIM may require an overwhelming amount of CPU time and memory to store the snapshots \(\mathbf {J}({\mathbf {U}}^{(k-1)}(t_n;\boldsymbol {\mu }_i);{\mathbf {G}}_f^{l}(\boldsymbol {\mu }_i))\), and to build the basis Φ J during the offline phase. For these reasons, a possible alternative to approximate the reduced Jacobian matrix (38) is to rely on a purely algebraic technique such as the Broyden method [16], developed to effectively approximate the Jacobian matrix when its analytic form is unknown, or it is too expensive to compute. This approach has been applied for the reduction of nonlinear structural problems in [71] and further improved in [13].
This yields the following hyper-reduced order model for the mechanical problem: for each t n, n = 1, …, N t, given \({\mathbf {u}}_{N,m}^{(0)}(t_n;\boldsymbol {\mu })\), for k ≥ 1 solve:
and iterate until \(||{\mathbf {R}}_{N,m}( \mathbf {Z} {\mathbf {u}}_{N,m}^{(k)}(t_n;\boldsymbol {\mu });{\mathbf {G}}_f^l(\boldsymbol {\mu }))||{ }_2< \varepsilon _{RB}\); as in (57), here l = (n + 1)D − 1. We underline that the high-fidelity approximation of the fibers shortening variable G f is considered, that is, we do not deal in this work with the reduction of the coupled electro-mechanical problem; rather, we focus on the efficient reduction of the mechanical problem only.
At each Newton step, the Broyden approximation of the reduced Jacobian matrix is computed as
where
and
The method is based on a rank-one update of the Jacobian matrix \({\mathbf {J}}_N^B({\mathbf {u}}_{N,m}^{(k)}(t_n;\boldsymbol {\mu }))\); indeed, the second term of the right hand side of (59) is a rank one matrix since every column is a scalar multiple of \(\varDelta \bar {\mathbf {u}}_{N,m}^T \), and only require simple operations between vectors of dimension N. Therefore, at the online stage each Newton step only requires a residual assembling, since the update of the reduced Jacobian matrix and the solution of the low dimensional linear system are extremely fast. On the other hand, the initialization of the Jacobian matrix \({\mathbf {J}}_N^B({\mathbf {u}}_{N,m}^{(0)}(t_n;\boldsymbol {\mu });\gamma _f(t_n,\boldsymbol {\mu }))\) at step k = 0 represents a critical aspect of the Broyden technique. To provide a suitable approximation of the exact Jacobian matrix, we consider a finite difference approximation of the form
where e i is the i-th column of the identity matrix and \(\eta \in \mathbb {R}\) is a coefficient to be properly chosen (here we take η = 10−5). η shall be small enough to guarantee an accurate approximation of the derivatives, however an excessively small value may lead to undesired cancellation errors. Note that the initialization requires to assemble online N times the residual vector—an affordable operation if N is relatively small. Instead, if N > m R, relying on DEIM to initialize the Jacobian matrix is more convenient than the finite difference approximation. In general, problems characterized by a large dimension of the reduced space N can be efficiently reduced exploiting the MDEIM technique, provided a small number m J of terms can be selected to accurately approximate the Jacobian matrix.
We close this section by pointing out that, during the online stage, only the reduced basis Z and a DEIM basis Φ R for the residual approximation are required. To build this latter, we rely on a strategy similar to the one described in Sect. 4.3.1, introducing the following intermediate problem similar to (41): for each t n, n = 0, …, N t, given \({\mathbf {u}}_{N}^{(0)}(t_n;\boldsymbol {\mu }) \in \mathbb {R}^N\), for k ≥ 1 solve:
and iterate until \(||{\mathbf {Z}}^T \mathbf {R}( \mathbf {Z} {\mathbf {u}}_{N}^{(k)}(t_n;\boldsymbol {\mu });{\mathbf {G}}_f^l(\boldsymbol {\mu }))||{ }_2< \varepsilon _{RB}\).
Precisely, we first solve the high-fidelity problem (28) n s times to compute the reduced basis Z; then, we solve (60) to store the residual snapshots \(\mathbf {R}(\mathbf {Z} {\mathbf {u}}_{N}^{(k)}(t_n; \boldsymbol {\mu }_i))\) needed to build the DEIM basis Φ R. Problem (60)1 is an inexact Newton step, for which the Jacobian matrix \(\tilde {\mathbf {J}}_N^B\) is approximated through the Broyden technique, however relying on the projection of the high-fidelity residual onto the RB space—rather than on the reduced residual, as in (59). Solving (60) is significantly faster than solving (28) since the only operation to perform is the assembling of the high-fidelity residual.The full snapshots selection procedure is summarized in the next section (see Algorithm 5).
Algorithm 5 ROM construction (mechanics)

6.2 Local-in-Time Reduced Basis
If the μ-dependent solution of a non stationary problem significantly varies throughout the time interval [0, T], describing the whole set of solutions for \(\boldsymbol {\mu } \in \mathscr {P}\) may require a large number of RB functions and, in particular, a large number of terms m R when considering nonlinear problems where the residual vector is approximated by DEIM. To overcome this issue, we build local-in-time bases of smaller dimension, instead than a unique (larger) global basis on [0, T], thus yielding a strong reduction in terms of online computational time, still retaining the same cost during the offline stage. In particular, we split the full time interval [0, T] into n b subintervals
and we build different bases on each subinterval. In particular, we compute n b set of bases \(\{ {\mathbf {Z}}^s,\boldsymbol {\varPhi }_R^s \},\ s=1,\dots ,n_b\) (and \(\boldsymbol {\varPhi }_J^s\) if using MDEIM), and each basis associated to the s-th interval is obtained by performing the POD only on the set of snapshots related to I s = [T s−1, T s].
We remark that the mechanical problem is solved in correspondence of evenly spaced time instants \(\{t_n\}_{n=0}^{N_t}\), whereas the new partition in subintervals I s is not necessarily uniform. This means that, denoting by τ s = {t n | t n ∈ I s}, the number of elements of τ s can be different from the number of elements of τ r when s ≠ r; in particular, larger subintervals I s are taken if the solution features a small variability in time, while narrow subintervals where the solution rapidly changes. The choice of number and width of the different subintervals is not trivial and multiple options can be considered. Here, we opt for an heuristic choice of the subintervals I s, s = 1, …, n b; a more-in-depth investigation is required in this respect. More general strategies to obtain multiple, local bases have been proposed in the literature; see e.g. [5, 85] for the use of proper clustering algorithms. They require to compute and store the solution snapshots, when varying time and parameters, and then to apply a clustering algorithm in order to build different bases, one for each cluster. While guaranteeing a satisfactory accuracy, snapshots storage can be quite large. Promising results in the case of cardiac electrophysiology can be found in [59].
The local-in-time basis approach combined with a POD-POD strategy allows to avoid the storage of all snapshots. Following this approach, for each μ i, i = 1, …, n s, we perform a full time-driven simulation and we store separately the snapshots U (k)(t n;μ i) associated with the subintervals I s, s = 1, …, n b. Then, for each subinterval I s, we apply the POD algorithm to the local snapshots U (k)(t n;μ i), t n ∈ I s, obtaining the POD bases Z i, s. Once we have performed the high-fidelity simulations for all μ i and we have computed all the POD bases, we build our final bases for each subinterval I s as:
A schematic representation of the method is reported in Fig. 3. The same procedure is used also to build \(\boldsymbol {\varPhi }_R^s\) and, if required, \(\boldsymbol {\varPhi }_J^s\). In this way, different snapshots can be computed simultaneously; at the end of each simulation, we can only retain the POD bases \(\{ {\mathbf {Z}}^{i,s},\boldsymbol {\varPhi }_R^{is}, \boldsymbol {\varPhi }_J^{is} \}\), thus saving significant memory resources.
The procedure described above has to be integrated with the generation of snapshots (and bases) to approximate residual vectors and Jacobian matrices; in particular, we split in two different stages the construction of \(\{ {\mathbf {Z}}^s, \boldsymbol {\varPhi }_J^s \}\) and \(\boldsymbol {\varPhi }_R^s\). The full procedure is described in Algorithm 5 in the case either MDEIM or Broyden approximations are considered.
7 Numerical Results
We apply the strategies described in the previous sections for the reduction of an electrical and a mechanical problem, both solved on a patient-specific left ventricle geometry, by focusing on the systolic phase of the heart beat. This geometry was generated from medical images using the semi-automatic segmentation method proposed in [34]. Fibers and sheets have been computed according to the algorithm proposed in [74]; this procedure is based on the assumption that sheets are lying along the radial direction s 0 and requires the solution of a Laplace problem over the ventricular domain to compute the sheets direction.
We rely on two different computational meshes: \(\mathscr {T}_{ep}\) with 248, 216 elements and \(N_h^e=45{,}817\) dofs for the electrical problem and \(\mathscr {T}_m\) with 31, 027 elements and N h = 18, 567 dofs for the mechanics. In Fig. 4 we show the two meshes, as well as the fibers distribution computed using the algorithm proposed in [74] with maximum fibers orientation on the epicardium and endocardium of θ epi = −60∘ and θ endo = 60∘, respectively. For both problems we consider as high-fidelity full-order model (FOM) the approximation obtained with linear (P1) finite elements.
7.1 Test Case 1: Electrophysiology
In the case of the electrophysiology problem, the parameters that we consider are those representing the electrical conductivities:
-
σ f ∈ [30 kΩ −1 cm −1, 80 kΩ −1 cm −1];
-
σ s = σ n ∈ [10 kΩ −1 cm −1, 30 kΩ −1 cm −1].
in the fibers direction (σ f) and in the plane orthogonal to the former (σ s = σ n), see Eq. (6). For the time discretization of the monodomain equation and the ionic model we employ a time step Δt e = 0.02 ms. The depolarization wave is initialized on a layer in the bottom part of the endocardium; this choice is motivated by the fact that the Purkinje fibers terminations are mainly located near the apex of the ventricle.
By employing the POD-Galerkin method with DEIM/MDEIM approximations for the nonlinear ionic terms/parametrized diffusion matrix described in Sect. 5 we reduce the two-way coupled electrical problem (42), which involves a PDE (monodomain equation) and a system of ODEs (ionic model). The proposed ROM yields a speed-up of more than one order of magnitude, since it takes about 0.01 s for each time step, while the FOM takes 0.12 s. The RB solutions have been computed using N e = 217 basis functions for the solution and m I = 363 DEIM terms to approximate the ionic currents, as specified in Table 2. Provided a sufficient number of basis functions N e, m I is considered, the front propagation captured by the ROM is similar to the one obtained with the FOM. However, depending on the chosen parametrization, this achievement might be more difficult to obtain; for instance, if parameters describe local variations of tissue properties (such as, for instance, the presence of a scar) the behavior of the solution is much more involved, thus requiring a larger number of basis functions to reach a good accuracy.
A comparison between the high-fidelity and the reduced solutions is reported in Fig. 5, where we observe that the two models provide very similar results from a qualitative point of view. The average relative error between the ROM and the FOM is shown in Fig. 6 for three different values of m I and is about 5%. The error has been computed over a test set of 50 randomly chosen parameters different than the values of the training sample used to compute the snapshots.
Moreover, we report in Fig. 7 the activation maps obtained for different parameter values. The electrical signal first activates the central area of the epicardium, then it spreads towards the apex and finally reaches the base. As expected, the duration of the depolarization phase is longer if electrical conductivities are smaller. The depolarization time as a function of σ f is reported in Fig. 8.
7.2 Test Case 2: Mechanics
We now turn to the reduction of the mechanical problem, recalling that for the case at hand, the electromechanical coupling is not included in the ROM—that is, for each parameter value queried online we rely on the FOM approximation of the electrophysiology model and, in particular, of the fibers’ shortening variable.
We consider as parameters the electrical conductivities (similarly to test case 1) and the orientation of the fibers:
-
σ f ∈ [30 kΩ −1 cm −1, 80 kΩ −1 cm −1];
-
σ s = σ n ∈ [10 kΩ −1 cm −1, 30 kΩ −1 cm −1];
-
θ max ∈ [30∘, 80∘];
-
t ∈ [0, 100ms].
Time can be seen as an additional parameter, since the problem is quasi-static, and needs to be solved at different time steps. In particular, we split the [0, 100 ms], corresponding to the systolic phase of the heart beat, into n b = 4 subintervals: [0, 30 ms], [30 ms, 60 ms], [60 ms, 90 ms], [90 ms, 100 ms]. Such a partition is introduced heuristically, taking into account the fact that the solution changes very rapidly during the last part of the systole; for this reason the last interval is smaller than the others. We consider a time step Δt e = 0.02 ms for the time discretization of the electrical problem, and time instants equispaced with Δ m = 3 ms for t ∈ [0, 90) and Δ m = 0.5 ms for t ∈ [90, 100] for the mechanical problem. This latter is then solved, for different parameter values, at these time instants.
In Figs. 9 and 10 we show the displacement of the myocardium obtained with the FOM and the ROM on the whole ventricle and on a longitudinal section for two different parameters.
Employing the POD-Galerkin method with DEIM/Broyden approximations for the residual vector and the Jacobian matrix described in Sect. 6 we obtain also in the case of the mechanical problem even more promising results: the proposed ROM yields a speed-up of about 20, since the ROM takes about 20 s while the FOM requires 7 min for each solution of the mechanical problem at a single time instant, on a single-core processor. In particular, the Broyden technique turns out to be really appropriate since to efficiently reduce the cardiac mechanical problem we have to choose m R significantly bigger than N.
The proposed ROM correctly captures the high-fidelity solution, as it can be seen also from the behavior of the average relative error shown in Fig. 11; the difference between the FOM and the ROM solutions is about 2%. Numerical data associated to this test case are reported in Table 3.
We show in Fig. 12 the variation of the volume inside the ventricular cavity for different values of θ max and σ f. In particular, the cases σ f = 60, σ s = σ n = 20 (left) and θ max = 60∘, σ s = σ n = 20 (right) have been considered. The associated ejection fraction has been reported in Fig. 13, where also the ventricular shortening is shown. These analyses have been carried out by varying θ max and σ f since σ s and σ n have a moderate effect on the solution. The quantity of blood ejected by the ventricle is larger when θ max and σ f assume large values. On the contrary, shortening is higher when considering small values of θ max. This behavior appears counterintuitive since we may expect that higher shortening corresponds to higher ejection fraction. To explain this phenomenon, we report in Fig. 14 the displacement of the muscle for two different values of θ max: even if for θ max = 80∘ the shortening is smaller, the cavity is more shrunk due to a larger wall thickening.
The model is able to reproduce the wall thickening and the ventricular shortening of the heart contraction. In particular, we obtain a ventricular shortening ranging from 13% to 23%, coherent with physiological values. The ejection fraction, usually measured by an echocardiogram, varies between 50% and 55% in healthy patients.
8 Challenges and Perspectives
The proper integration of several techniques to perform both solution-space reduction (Galerkin-POD method) and system approximation (DEIM/MDEIM or, alternatively to this latter, Broyden approximation) has enabled the application of the reduced basis method for parametrized PDEs to problems arising in cardiac electromechanics. Cardiac electrophysiology and mechanics problems pose several challenges to ROM techniques, because of their complex, nonlinear, multiscale (both in space and time) nature; moreover, parameter dependence might be extremely involved, for instance when aiming at describing subject-specific clinical data and exploring inter-patient variability. On the other hand, ROM techniques provide a unique opportunity to solve relevant problems related with data-model integration, such as model calibration, uncertainty characterization and propagation, parameter identification and inverse problems, data assimilation.
All these problems are of primary importance in order to translate mathematical models into clinical care. Quantitative insights coming from the repeated solution of electrophysiology corresponding to different values of material parameter could provide better understanding of heart (mis)functionality; parameter identification has potential to improve the diagnosis of cardiovascular diseases; model calibration may be beneficial to develop therapies tailored to the subject characteristics. All these problems would be computationally unaffordable when relied only on high-fidelity techniques, aiming at considering variability of geometries, a wide number of scenarios to explore, and several parameters to deal with.
The roadmap to make ROM techniques even more efficient to tackle these challenging problems needs to address several bottlenecks. Among these, we mention those which, in our opinion, are the most relevant:
-
1.
local ROMs. Using a global reduced basis for the whole parameter set and the whole time interval can be an extremely limiting approach. For instance, if the solution shows moving fronts and this latter is highly sensible with respect to parameter variations (as it might happen in the case of cardiac electrophysiology), applying the standard ROM techniques can become unfeasible. Local-in-time bases, as shown in this paper, can partially cure this problem, however more general and robust techniques to build local ROMs are required. As shown in [59, 60], a k-means clustering in the state space of the snapshots for both the solution and the nonlinear term can be a viable strategy to overcome this bottleneck;
-
2.
time behavior. So far, POD has been applied also with respect to the time independent variable, to compress information carried by a set of solution snapshots computed at different time steps, no matter which is the time behavior characterizing the problem. In general, however, reduction of parametrized PDEs becomes much more difficult when passing from elliptic (or dissipative time-dependent) to hyperbolic problems (for instance pure transport equations). More ad-hoc strategies, able for instance to detect time invariances, or to track traveling waves, should be considered in the case of cardiac electrophysiology, because of the sharpness of the front and its extremely rapid dynamics;
-
3.
coupled and multiphysics problems. Designing efficient ROMs (either monolithic or segregated) to couple different problems, such as cardiac electrophysiology and mechanics, is still an open issue, and almost untouched in the field of cardiovascular applications; preliminary investigations on the electromechanical case can be found in [13]. In this latter work it is also shown a possible strategy to realize a fully coupled electromechanical problem by including the mechano-electrical feedback only during the online stage, and relying on different ROMs for the two subproblems; Similarly, in this work the choice of using the monodomain model is performed. Such a model is adequate in physiological conditions, however the richer—but more complicated—bidomain model is required for treating some pathological conditions. The methods described in the previous sections can also apply to the bidomain model, however entailing an extra burden from a computational standpoint, because of the presence of two fields to be computed, and the different overall nature of the PDEs system.
-
4.
multiscale problems. The multiscale nature of the electromechanical model should be properly taken into account in a ROM aiming at describing multiple behaviors at different scales. Among the mentioned open problems, this is by far the most involved one, because of the intrinsic difficulty of the models at the cellular scale. Several extensions of the RB method to multiscale problems showing highly oscillating coefficients have been considered in the last decade, however only focusing on elliptic problems [1, 2, 40, 57]. When applied to these problems, the RB method enables to speed up a large number of similar computations on the fine local mesh for each new realization of the coefficient; its application to complex nonlinear materials, however, is still completely open.
-
5.
multi-fidelity problems. In view of exploiting reduced order modeling techniques to solve uncertainty quantification problems, the use of models characterized by different fidelities is also foreseen. Following, e.g., the approach relying on multi-fidelity sampling and a Bayesian formulation proposed in [12], information from an approximate, low-fidelity model can be rigorously exploited and incorporated to perform output evaluations, estimates on their variability and, ultimately, parameter studies. In this respect, the eikonal model and a recently proposed reaction-eikonal source model [56], this latter offering the computational advantages of the eikonal model while preserving the full biophysical details of a computationally costly reaction-diffusion model, could be considered as an extremely cheap, yet detailed, low-fidelity model.
The investigation and development of reliable and efficient reduced-order modeling techniques is a very active field of numerical analysis and scientific computing; with no doubt, cardiovascular applications represent one of the most challenging and significant environments.
Notes
- 1.
More specifically, we would have g = p endo(t)n where n is the unit normal vector to the boundary, and p endo = p endo(t) is the external load applied by the fluid at the endocardium wall, which in this context is assumed to be prescribed.
References
Abdulle, A., Bai, Y.: Reduced basis finite element heterogeneous multiscale method for high-order discretizations of elliptic homogenization problems. J. Comput. Phys. 231(21), 7014–7036 (2012)
Abdulle, A., Budáč, O.: A reduced basis finite element heterogeneous multiscale method for stokes flow in porous media. Comput. Methods Appl. Mech. Eng. 307, 1–31 (2016)
Ambrosi, D., Arioli, G., Nobile, F., Quarteroni, A.: Electromechanical coupling in cardiac dynamics: the active strain approach. SIAM J. Appl. Math. 71(2), 605–621 (2011). https://doi.org/10.1137/100788379
Ambrosi, D., Pezzuto, S.: Active stress vs. active strain in mechanobiology: constitutive issues. J. Elast. 107(2), 199–212 (2012)
Amsallem, D., Zahr, M., Farhat, C.: Nonlinear model order reduction based on local reduced-order bases. Int. J. Numer. Meth. Eng. 92(10), 891–916 (2012)
Ashikaga, H., Coppola, B., Yamazaki, K., Villarreal, F., Omens, J., Covell, J.: Changes in regional myocardial volume during the cardiac cycle: implications for transmural blood flow and cardiac structure. Am. J. Physiol. Heart. Circ. Physiol. 295(2), H610–H618 (2008)
Ballarin, F., Faggiano, E., Ippolito, S., Manzoni, A., Quarteroni, A., Rozza, G., Scrofani, R.: Fast simulations of patient-specific haemodynamics of coronary artery bypass grafts based on a POD–Galerkin method and a vascular shape parametrization. J. Comput. Phys. 315, 609–628 (2016)
Ballarin, F., Faggiano, E., Manzoni, A., Quarteroni, A., Rozza, G., Ippolito, S., Antona, C., Scrofani, R.: Numerical modeling of hemodynamics scenarios of patient-specific coronary artery bypass grafts. Biomech. Model. Mechanobiol. 16(4), 1373–1399 (2017)
Balzani, D., Deparis, S., Fausten, S., Forti, D., Heinlein, A., Klawonn, A., Quarteroni, A., Rheinbach, O., Schroder, J.: Aspects of Arterial Wall Simulations: Nonlinear Anisotropic Material Models and Fluid Structure Interaction. Dekan der Fak. für Mathematik und Informatik (2014)
Barrault, M., Maday, Y., Nguyen, N., Patera, A.: An empirical interpolation method: application to efficient reduced-basis discretization of partial differential equations. C. R. Math. 339(9), 667–672 (2004)
Baumann, M.: Nonlinear model order reduction using pod/deim for optimal control of Burgers’ equation. Ph.D. thesis, TU Delft, Delft University of Technology (2013)
Biehler, J., Gee, M., Wall, W.: Towards efficient uncertainty quantification in complex and large scale biomechanical problems based on a Bayesian multi fidelity scheme. Biomech. Model. Mechanobiol. 14(3), 489–513 (2015)
Bonomi, D.: Reduced-order models for the parametrized cardiac electromechanical problem. Ph.D. thesis, Politecnico di Milano (2017)
Bonomi, D., Manzoni, A., Quarteroni, A.: A matrix DEIM technique for model reduction of nonlinear parametrized problems in cardiac mechanics. Comput. Methods Appl. Mech. Eng. 324, 300–326 (2017)
Boulakia, M., Schenone, E., Gerbeau, J.: Reduced-order modeling for cardiac electrophysiology. Application to parameter identification. Int. J. Numer. Meth. Biomed. Eng. 28(6–7), 727–744 (2012)
Broyden, C.: A class of methods for solving nonlinear simultaneous equations. Math. Comput. 19(92), 577–593 (1965)
Bueno-Orovio, A., Cherry, E., Fenton, F.: Minimal model for human ventricular action potentials in tissue. J. Theor. Biol. 253(3), 544–560 (2008). https://doi.org/10.1016/j.jtbi.2008.03.029
Carlberg, K., Farhat, C., Cortial, J., Amsallem, D.: The GNAT method for nonlinear model reduction: effective implementation and application to computational fluid dynamics and turbulent flows. J. Comput. Phys. 242, 623–647 (2013)
Carlberg, K., Tuminaro, R., Boggs, P.: Preserving Lagrangian structure in nonlinear model reduction with application to structural dynamics. SIAM J. Sci. Comput. 37(2), B153–B184 (2015)
Chapelle, D., Gariah, A., Sainte-Marie, J.: Galerkin approximation with proper orthogonal decomposition: new error estimates and illustrative examples. ESAIM: Math. Model. Numer. Anal. 46(4), 731–757 (2012)
Chaturantabut, S., Sorensen, D.: Nonlinear Model Reduction via Discrete Empirical Interpolation. SIAM J. Sci. Comput. 32(5), 2737–2764 (2010). https://doi.org/10.1137/090766498
Chaturantabut, S., Sorensen, D.: Application of POD and DEIM on dimension reduction of non-linear miscible viscous fingering in porous media. Math. Comp. Model. Dyn. 17(4), 337–353 (2011)
Cherubini, C., Filippi, S., Nardinocchi, P., Teresi, L.: An electromechanical model of cardiac tissue: constitutive issues and electrophysiological effects. Prog. Biophys. Mol. Biol. 97(2–3), 562–573 (2008)
Clayton, R., Panfilov, A.: A guide to modelling cardiac electrical activity in anatomically detailed ventricles. Prog. Biophys. Mol. Biol. 96(1), 19–43 (2008). https://doi.org/10.1016/j.pbiomolbio.2007.07.004
Colciago, C., Deparis, S., Quarteroni, A.: Comparisons between reduced order models and full 3d models for fluid–structure interaction problems in haemodynamics. J. Comput. Appl. Math. 265, 120–138 (2014)
Colciago, C.M., Deparis, S., Forti, D.: Fluid-structure interaction for vascular flows: from supercomputers to laptops. In: Frei, S., Holm, B., Richter, T., Wick, T., Yang, H. (eds.) Fluid-Structure Interaction: Modeling, Adaptive Discretisations and Solvers. Radon Series on Computational and Applied Mathematics, vol. 20. De Gruyter, Berlin (2017)
Colli Franzone, P., Pavarino, L.F., Taccardi, B.: Simulating patterns of excitation, repolarization and action potential duration with cardiac bidomain and monodomain models. Math. Biosci. 197(1), 35–66 (2005)
Colli Franzone, P., Pavarino, L.F., Scacchi, S.: Mathematical Cardiac Electrophysiology. Modeling, Simulation and Applications Series, vol. 13. Springer, Milano (2014)
Colli Franzone, P., Pavarino, L.F., Scacchi, S.: Parallel multilevel solvers for the cardiac electro-mechanical coupling. Appl. Numer. Math. 95, 140–153 (2015)
Corrado, C., Lassoued, J., Mahjoub, M., Zemzemi, N.: Stability analysis of the POD reduced order method for solving the bidomain model in cardiac electrophysiology. Math. Biosci. 272, 81–91 (2016)
Dal, H., Goktepe, S., Kaliske, M., Kuhl, E.: A fully implicit finite element method for bidomain models of cardiac electromechanics. Comput. Methods Appl. Mech. Eng. 253, 323–336 (2013)
Deparis, S., Forti, D., Quarteroni, A.: A rescaled localized radial basis function interpolation on non-cartesian and nonconforming grids. SIAM J. Sci. Comput. 36(6), A2745–A2762 (2014)
Eriksson, T., Prassl, A., Plank, G., Holzapfel, G.: Influence of myocardial fiber/sheet orientations on left ventricular mechanical contraction. Math. Mech. Solids 18, 592–606 (2013)
Fedele, M., Faggiano, E., Barbarotta, L., Cremonesi, F., Formaggia, L., Perotto, S.: Semi-automatic three-dimensional vessel segmentation using a connected component localization of the region-scalable fitting energy. In: 2015 9th International Symposium on Image and Signal Processing and Analysis (ISPA), pp. 72–77. IEEE, Piscataway, NJ (2015)
Gerbeau, J., Lombardi, D., Schenone, E.: Reduced order model in cardiac electrophysiology with approximated lax pairs. Adv. Comput. Math. 41(5), 1103–1130 (2015)
Gerbi, A., Dede’, L., Quarteroni, A.: A monolithic algorithm for the simulation of cardiac electromechanics in the human left ventricle. Tech. rep., MOX - Politecnico di Milano (2017). Report 51/2017
Göktepe, S., Kuhl, E.: Electromechanics of the heart: a unified approach to the strongly coupled excitation–contraction problem. Comput. Mech. 45(2–3), 227–243 (2010)
Heidenreich, E., Ferrero, J., Doblare, M., Rodriguez, J.: Adaptive macro finite elements for the numerical solution of monodomain equations in cardiac electrophysiology. Ann. Biomed. Eng. 38(7), 2331–2345 (2010)
Helfenstein, J., Jabareen, M., Mazza, E., Govindjee, S.: On non-physical response in models for fiber-reinforced hyperelastic materials. Int. J. Solids Struct. 47(16), 2056–2061 (2010)
Hesthaven, J.S., Zhang, S., Zhu, X.: Reduced basis multiscale finite element methods for elliptic problems. Multiscale Model. Simul. 13(1), 316–337 (2015)
Hesthaven, J., Rozza, G., Stamm, B.: Certified Reduced Basis Methods for Parametrized Partial Differential Equations. SpringerBriefs Mathematics. Springer, Cham (2016)
Hodgkin, A., Huxley, A.: A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117(4), 500–544 (1952)
Holzapfel, G., Ogden, R.: Constitutive modelling of passive myocardium: a structurally based framework for material characterization. Philos. Trans. A Math. Phys. Eng. Sci. 367(1902), 3445–3475 (2009). https://doi.org/10.1098/rsta.2009.0091
Keldermann, R., Nash, M., Panfilov, A.: Modeling cardiac mechano-electrical feedback using reaction-diffusion-mechanics systems. Physica D 238(11), 1000–1007 (2009)
Krysl, P., Lall, S., Marsden, J.: Dimensional model reduction in non-linear finite element dynamics of solids and structures. Int. J. Numer. Meth. Eng. 51(4), 479–504 (2001)
Kuzmin, D.: A Guide to Numerical Methods for Transport Equations. University Erlangen-Nuremberg, Erlangen (2010)
Lassila, T., Manzoni, A., Quarteroni, A., Rozza, G.: Boundary control and shape optimization for the robust design of bypass anastomoses under uncertainty. ESAIM-Math. Model. Numer. 47(4), 1107–1131 (2013)
Lassila, T., Manzoni, A., Quarteroni, A., Rozza, G.: A reduced computational and geometrical framework for inverse problems in haemodynamics. Int. J. Numer. Methods Biomed. Eng. 29(7), 741–776 (2013)
Maday, Y., Nguyen, N.C., Patera, A.T., Pau, G.S.H.: A general multipurpose interpolation procedure: the magic points. Commun. Pure Appl. Anal. 8(1), 383–404 (2009)
Manzoni, A., Quarteroni, A., Rozza, G.: Shape optimization for viscous flows by reduced basis methods and free-form deformation. Int. J. Numer. Meth. Fluids 70(5), 646–670 (2012)
Nardinocchi, P., Teresi, L.: On the active response of soft living tissues. J. Elast. 88(1), 27–39 (2007)
Nash, M., Hunter, P.: Computational mechanics of the heart. J. Elast. 61, 113–141 (2001). https://doi.org/10.1023/A:1011084330767
Nash, M., Panfilov, A.: Electromechanical model of excitable tissue to study reentrant cardiac arrhythmias. Prog. Biophys. Mol. Biol. 85(2–3), 501–522 (2004). https://doi.org/10.1016/j.pbiomolbio.2004.01.016
Negri, F.: Efficient reduction techniques for the simulation and optimization of parametrized systems: Analysis and applications. Ph.D. thesis, Ecole Polytechnique Fédérale de Lausanne (2016)
Negri, F., Manzoni, A., Amsallem, D.: Efficient model reduction of parametrized systems by matrix discrete empirical interpolation. J. Comput. Phys. 303, 431–454 (2015)
Neic, A., Campos, F., Prassl, A., Niederer, S., Bishop, M., Vigmond, E., Plank, G.: Efficient computation of electrograms and ECGs in human whole heart simulations using a reaction-eikonal model. J. Comput. Phys. 346, 191–211 (2017)
Nguyen, N.: A multiscale reduced-basis method for parametrized elliptic partial differential equations with multiple scales. J. Comput. Phys. 227(23), 9807–9822 (2008)
Noble, D., Garny, A., Noble, P.: How the hodgkin-huxley equations inspired the cardiac physiome project. J. Physiol. 590(11), 2613–28 (2012)
Pagani, S.: Reduced-order models for inverse problems and uncertainty quantification in cardiac electrophysiology. Ph.D. thesis, Politecnico di Milano (2017)
Pagani, S., Manzoni, A., Quarteroni, A.: Numerical approximation of parametrized problems in cardiac electrophysiology by a local reduced basis method. Comput. Methods Appl. Mech. Eng. 340, 530–558 (2018)
Pathmanathan, P., Whiteley, J.: A numerical method for cardiac mechanoelectric simulations. Ann. Biomed. Eng. 37(5), 860–873 (2009)
Pathmanathan, P., Chapman, S., Gavaghan, D., Whiteley, J.: Cardiac electromechanics: the effect of contraction model on the mathematical problem and accuracy of the numerical scheme. J. Mech. Appl. Math. 63, 375–399 (2010)
Pathmanathan, P., Mirams, G., Southern, J., Whiteley, J.: The significant effect of the choice of ionic current integration method in cardiac electro-physiological simulations. Int. J. Num. Meth. Biomed. Eng. 27(1), 1751–1770 (2011). https://doi.org/10.1002/cnm. http://onlinelibrary.wiley.com/doi/10.1002/cnm.1494/full
Peherstorfer, B., Butnaru, D., Willcox, K., Bungartz, H.: Localized discrete empirical interpolation method. SIAM J. Sci. Comput. 36(1), A168–A192 (2014)
Pezzuto, S.: Mechanics of the heart – constitutive issues and numerical experiments. Ph.D. thesis, Politecnico di Milano (2013)
Potse, M., Dubé, B., Vinet, A., Cardinal, R.: A comparison of monodomain and bidomain propagation models for the human heart. Conf. Proc. IEEE Eng. Med. Biol. Soc. 53(12), 3895–3898 (2006). https://doi.org/10.1109/IEMBS.2006.259484
Quarteroni, A., Valli, A.: Numerical Approximation of Partial Differential Equations, vol. 23. Springer Science and Business Media, Berlin (2008)
Quarteroni, A., Manzoni, A., Negri, F.: Reduced Basis Methods for Partial Differential Equations: An Introduction. Unitext, vol. 92. Springer, Cham (2016)
Quarteroni, A., Lassila, T., Rossi, S., Ruiz-Baier, R.: Integrated heart – coupling multiscale and multiphysics models for the simulation of the cardiac function. Comput. Methods Appl. Mech. Eng. 314, 345–407 (2017)
Quarteroni, A., Manzoni, A., Vergara, C.: The cardiovascular system: mathematical modeling, numerical algorithms, clinical applications. Acta Numer. 26, 365–590 (2017)
Radermacher, A., Reese, S.: POD-based model reduction with empirical interpolation applied to nonlinear elasticity. Int. J. Numer. Meth. Eng. 107(6), 477–495 (2016)
Rossi, S.: Anisotropic modeling of cardiac mechanical activation. Ph.D. thesis, Ecole Politechnique Federale de Lausanne (2014)
Rossi, S., Ruiz-Baier, R., Pavarino, L.F., Quarteroni, A.: Orthotropic active strain models for the numerical simulation of cardiac biomechanics. Int. J. Numer. Meth. Biomed. Eng. 28(6–7), 761–788 (2012)
Rossi, S., Lassila, T., Ruiz-Baier, R., Sequeira, A., Quarteroni, A.: Thermodynamically consistent orthotropic activation model capturing ventricular systolic wall thickening in cardiac electromechanics. Eur. J. Mech. A/Sol. 48 (2013). https://doi.org/10.1016/j.euromechsol.2013.10.009
Ruiz-Baier, R., Gizzi, A., Rossi, S., Cherubini, C., Laadhari, A., Filippi, S., Quarteroni, A.: Mathematical modelling of active contraction in isolated cardiomyocytes. Math. Med. Biol. 31(3), 259–283 (2014)
Sainte-Marie, J., Chapelle, D., Cimrman, R., Sorine, M.: Modeling and estimation of the cardiac electromechanical activity. Comput. Struct. 84(28), 1743–1759 (2006)
Sansour, C.: On the physical assumptions underlying the volumetric-isochoric split and the case of anisotropy. Eur. J. Mech. A/Sol. 27(1), 28–39 (2008). https://doi.org/10.1016/j.euromechsol.2007.04.001
Smith, N., Nickerson, D., Crampin, E., Hunter, P.: Multiscale computational modelling of the heart. Acta Numer. 13, 371–431 (2004). https://doi.org/10.1017/S0962492904000200
Strobeck, J., Sonnenblick, E.: Myocardial contractile properties and ventricular performance. In: The Heart and Cardiovascular System: Scientific Foundations, pp. 31–49. Raven Press, New York (1986)
Sundnes, J., Wall, S., Osnes, H., Thorvaldsen, T., McCulloch, A.: Improved discretisation and linearisation of active tension in strongly coupled cardiac electro-mechanics simulations. Comput. Meth. Biomech. Biomed. Eng. 17(6), 604–615 (2014)
Taber, L., Perucchio, R.: Modeling heart development. J. Elast. 61(1–3), 165–197 (2000)
Trayanova, N., Eason, J., Aguel, F.: Computer simulations of cardiac defibrillation: a look inside the heart. Comput. Vis. Sci. 4(4), 259–270 (2002)
Tung, L.: A bi-domain model for describing ischemic myocardial DC potentials. Ph.D. thesis, Massachusetts Institute of Technology (1978)
Wang, Y., Haynor, D., Kim, Y.: An investigation of the importance of myocardial anisotropy in finite-element modeling of the heart: methodology and application to the estimation of defibrillation efficacy. IEEE Trans. Biomed. Eng. 48(12), 1377–1389 (2001)
Washabaugh, K., Amsallem, D., Zahr, M., Farhat, C.: Nonlinear model reduction for cfd problems using local reduced-order bases. In: 42nd AIAA Fluid Dynamics Conference and Exhibit, Fluid Dynamics and Co-located Conferences, AIAA Paper, vol. 2686, pp. 1–16 (2012)
Whiteley, J., Bishop, M., Gavaghan, D.: Soft tissue modelling of cardiac fibres for use in coupled mechano-electric simulations. Bull. Math. Biol. 69(7), 2199–2225 (2007)
Wirtz, D., Sorensen, D., Haasdonk, B.: A posteriori error estimation for DEIM reduced nonlinear dynamical systems. SIAM J. Sci. Comput. 36(2), A311–A338 (2014)
Yang, H., Veneziani, A.: Efficient estimation of cardiac conductivities via pod-deim model order reduction. Appl. Numer. Math. 115, 180–199 (2017)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Manzoni, A., Bonomi, D., Quarteroni, A. (2018). Reduced Order Modeling for Cardiac Electrophysiology and Mechanics: New Methodologies, Challenges and Perspectives. In: Boffi, D., Pavarino, L., Rozza, G., Scacchi, S., Vergara, C. (eds) Mathematical and Numerical Modeling of the Cardiovascular System and Applications. SEMA SIMAI Springer Series, vol 16. Springer, Cham. https://doi.org/10.1007/978-3-319-96649-6_6
Download citation
DOI: https://doi.org/10.1007/978-3-319-96649-6_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-96648-9
Online ISBN: 978-3-319-96649-6
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)