Keywords

1 Introduction

Associative memories (AMs) are mathematical models inspired by the human brain ability to store and recall information by means of associations [1]. More specifically, they are designed for the storage of a finite set of association pairs \(\{(\mathbf x ^\xi ,\mathbf y ^\xi ), \xi =1, \cdots , p\}\), called fundamental memory set. We refer to \(\mathbf x ^1,\ldots ,\mathbf x ^p\) as the stimuli and \(\mathbf y ^1,\ldots ,\mathbf y ^p\) as the desired responses. Furthermore, an AM should exhibit some error correction capability, i.e, it should yield the desired response \(\mathbf y ^\xi \) even upon the presentation of a corrupted version \(\tilde{\mathbf{x }}^\xi \) of the stimulus \(\mathbf x ^\xi \). An AM is said autoassociative if \(\mathbf x ^\xi = \mathbf y ^\xi \) for all \(\xi =1, \cdots , p\), and heteroassociative if there is at least one \(\xi \in \{1, \cdots , p\}\) such that \(\mathbf x ^\xi \ne \mathbf y ^\xi \). Applications of AM models include diagnosis [2], emotional modeling [3], pattern classification [4,5,6,7], and image processing and analysis [8, 9].

The Hopfield neural network is one of the most widely known neural network used to implement an AM [10]. Despite its many successful applications, the Hopfield network suffers from a very low storage capacity [1]. A simple but significant improvement in storage capacity of the Hopfield network is achieved by the recurrent correlation associative memory (RCAMs) [11]. RCAMs are closely related to the dense associative memory model introduced recently by Krotov and Hopfield to establish the duality between AMs and deep learning [12, 13]. Furthermore, a particular RCAM, called exponential correlation associative memory (ECAM), is equivalent to a certain recurrent kernel associative memory proposed by Garcia and Moreno [14, 15].

Like the traditional Hopfield neural network, the original ECAM is an autoassociative memory designed for the storage and recall of bipolar vectors. Many applications of AMs, however, require either an heteroassociative memory or the storage and recall of real-valued data. A heteroassociative version of the ECAM, called exponential bidirectional associative memory (EBAM), have been proposed by Jeng et al. [16]. As to the storage and recall of real-valued vectors, Chiueh and Tsai introduced the multivalued exponential recurrent associative memory (MERAM) [17].

Recently, we introduced the class of generalized recurrent exponential fuzzy associative memories (GRE-FAMs), which have been effectively applied for pattern classification [5, 18]. Briefly, GRE-FAMs are autoassociative fuzzy memories obtained from a generalization of a fuzzy version of the MERAM. Recall that a fuzzy associative memory is a fuzzy system designed for the storage and recall of fuzzy sets [19, 20]. The generalized exponential bidirectional fuzzy associative memories (GEB-FAMs), which generalize the GRE-FAMs for the heteroassociative case, have been applied for face recognition [21]. We would like to point out, however, that the dynamic of the GEB-FAMs are not fully understood yet. In view of this remark, we mostly considered single-step versions of these two AM models.

Summarizing, on the one hand, GEB-FAMs can be viewed as a fuzzy version of the bidirectional (heteroassociative) ECAM. On the other hand, ECAM is equivalent to a certain kernel associative memory. Put together, these two remarks suggest us to interpret the single-step GEB-FAMs using (fuzzy) kernel functions and, from now on, we shall refer to them as fuzzy kernel associative memories (fuzzy KAMs). Recall that a kernel is informally defined as a similarity measure that can be thought of as a dot product on a high-dimensional feature space [22]. Disregarding formal definitions, we interpret a fuzzy similarity measure as a fuzzy kernel. Such interpretation lead us to information theoretical learning whose goal is to capture the information in the parameters of a learning machine [23]. In this paper, we propose to fine tune the parameter of a fuzzy KAM using information theoretical learning.

The paper is structured as follows. Next section presents the fuzzy kernel associative memory and some theoretical results. In this section, we also describe how information theoretical learning can be used to determine the parameter of a fuzzy KAM. An application of autoassociative and heteroassociative fuzzy KAMs for pattern classification is given in Sect. 3. Computational experiments on pattern classification are provided in Sect. 4. The paper finishes with the concluding remarks in Sect. 5.

2 Fuzzy Kernel Associative Memory

A fuzzy similarity measure, or simply similarity measure, is a function that associates to each pair of fuzzy sets a real number that expresses the degree of equality of these sets. According to De Baets and Meyer [24], a fuzzy similarity measure is a symmetric binary fuzzy relation on the family of all fuzzy sets \(\mathcal {F}(U)\). In mathematical terms, a similarity measure is a mapping \(\mathcal {S}:\mathcal {F}(U) \times \mathcal {F}(U) \rightarrow [0,1]\) such that \(\mathcal {S}(A,B)=\mathcal {S}(B,A)\) for all fuzzy sets \(A,B \in \mathcal {F}(U)\). We speak of a strong similarity measure if \(\mathcal {S}(A,B)=1\) if, and only if, \(A=B\).

Given a fuzzy similarity measure, the mapping \(\kappa :\mathcal {F}(U)\times \mathcal {F}(U)\rightarrow [0,1]\) defined by the following equation for \(\alpha >0\) is also a fuzzy similarity measure

$$\begin{aligned} \kappa (A,B)=e^{\alpha (S(A,B)-1)}. \end{aligned}$$
(2.1)

Disregarding formal definitions, we shall refer to \(\kappa \) as a fuzzy kernel.

We would like to call the reader’s attention to the dependence of the fuzzy kernel \(\kappa \) on the parameter \(\alpha \) when \(\mathcal {S}\) is a strong similarity measure. On the one hand, \(\kappa \) approximates the strict equality of fuzzy sets as \(\alpha \) increases. Precisely, we have \(\kappa (A,B)=1\) if \(A=B\) and \(\kappa (A,B)=0\) otherwise as \(\alpha \rightarrow \infty \). On the other hand, \(\kappa (A,B)=1\) for all \(A,B \in \mathcal {F}(U)\) as \(\alpha \rightarrow 0\). In other words, \(\kappa \) is unable to discriminate fuzzy sets for sufficiently small \(\alpha >0\). Hence, the parameter \(\alpha \) controls the capability of the fuzzy kernel to distinguish fuzzy sets.

Let us now introduce the fuzzy kernel associative memory (fuzzy KAM):

Definition 1

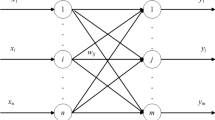
(Fuzzy KAM). Consider a fundamental memory set \(\{(A^{\xi },B^{\xi }): \xi =1, \ldots , p \} \subset \mathcal {F}(U)\times \mathcal {F}(V) \). Let \(\alpha >0\) be a real number, \(\mathcal {S}:\mathcal {F}(U)\times \mathcal {F}(U) \rightarrow [0,1]\) a similarity measure, and H a \(p\times p\) real-valued matrix. A fuzzy KAM is a mapping \(\mathcal {K}:\mathcal {F}(U)\rightarrow \mathcal {F}(V)\) defined by the following equation where \(X \in \mathcal {F}(U)\) is the input and \(Y=\mathcal {K}(X) \in \mathcal {F}(V)\) is the output:

$$\begin{aligned} Y(v) = \varphi \left( \displaystyle {\frac{\displaystyle {\sum _{\xi =1}^{p}\sum _{\mu =1}^{p}}h_{\xi \mu }\kappa (A^{\mu },X)B^{\xi }(v)}{\displaystyle {\sum _{\eta =1}^{p}\sum _{\mu =1}^{p}}h_{\eta \mu }\kappa (A^{\mu },X)}} \right) . \end{aligned}$$
(2.2)

Here, the piece-wise linear function \(\varphi (x)=\max (0, \min (1,x))\) ensures \(Y(v) \in [0,1]\), for all \(v\in V\).

Alternatively, we can write the output of a fuzzy KAM as

$$\begin{aligned} Y(v)= \varphi \left( \displaystyle {\sum _{\xi =1}^{p}w_{\xi }B^{\xi }(v)}\right) \quad \text{ where } \quad w_\xi =\frac{\displaystyle {\sum _{\mu =1}^{p}h_{\xi \mu }\kappa (A^{\mu },X)}}{\displaystyle {\sum _{\eta =1}^{p}\sum _{\mu =1}^{p}}h_{\eta \mu }\kappa (A^{\mu },X)}. \end{aligned}$$
(2.3)

In words, the output \(Y=\mathcal {K}(X)\) is given by a linear combinations of the desired responses \(B^{\xi }\)’s. Moreover, the coefficients of the linear combinations are calculated by using the parametrized fuzzy kernel \(\kappa \) given by (2.1).

As pointed out in the introduction, an autoassociative fuzzy KAM is equivalent to the single-step generalized recurrent exponential fuzzy associative memories (GRE-FAM) designed for the storage of a finite family of fuzzy sets \(\mathcal {A}=\{A^{i}, i=1, \cdots , p\} \subset \mathcal {F}(U)\) [18]. Similarly, the heteroassociative fuzzy KAM corresponds to the single-step generalized exponential bidirectional fuzzy associative memories (GEB-FAM) in the heteroassociative case [25].

The matrix H plays a very important role in the storage capacity and noise tolerance of a fuzzy KAM. The next theorem shows how to define the matrix H so that the fundamental memories are all correctly encoded in the memory.

Theorem 1

Let \(\mathcal {A}=\{(A^\xi ,B^\xi ):\xi =1, \cdots ,p\} \subset \mathcal {F}(U)\times \mathcal {F}(V)\) be the fundamental memory set, \(\mathcal {S}:\mathcal {F}(U)\times \mathcal {F}(U)\rightarrow [0,1]\) a similarity measure, \(\alpha >0\) a real number, and \(\kappa :\mathcal {F}(U)\times \mathcal {F}(U)\rightarrow [0,1]\) a fuzzy kernel defined by (2.1). If the matrix \(K=(k_{ij}) \in \mathbb {R}^{p \times p}\), whose entries are defined by

$$\begin{aligned} k_{ij}=\kappa (A^{i},A^{j}), \quad \forall i,j=1, \ldots , p, \end{aligned}$$
(2.4)

is invertible, then the fuzzy KAM obtained by considering the matrix \(H=K^{-1}\) satisfies the identity \(\mathcal {K}(A^{\xi })=B^{\xi }\) for all \(\xi =1,\ldots ,p\).

Let us briefly address the computational effort required to synthesize a fuzzy KAM based on Theorem 1. First, the fuzzy kernel \(\kappa \) is evaluated \((p^2+p)/2\) times to compute the symmetric \(p \times p\) matrix K defined by (2.4). Then, instead of determining the inverse \(H = K^{-1}\), we compute the LU factorization (or the Cholesky factorization if H is symmetric and positive definite) of K using \(\mathcal {O}(p^3)\) operations. Then, the multiplication of H by a vector is replaced by the solution of two triangular systems during the recall phase. Summarizing, \(\mathcal {O}(p^3)\) operations are performed to synthesize a fuzzy KAM.

The parameter \(\alpha \) plays an important role on the noise tolerance of a fuzzy KAM. Briefly, the higher the parameter \(\alpha \), the greater the weight of the fundamental memories most similar to the input X in the calculation of the output \(\mathcal {K}(X)\). In other words, increasing \(\alpha \) emphasizes the role of the fundamental memories most similar to the input. Thus, in some sense, the parameter \(\alpha \) controls how each fundamental memory contributes to the output of a fuzzy KAM. Formally, the next theorem states that, as \(\alpha \) tends to infinity, the output \(\mathcal {K}(X)\) converges point-wise to the arithmetic mean of the desired responses \(B^\xi \)’s whose associated stimulus \(A^\xi \)’s are the most similar to the input X.

Theorem 2

Let \(\mathcal {A}=\{(A^\xi ,B^\xi ): \xi =1, \cdots , p \} \subseteq \mathcal {F}(U)\times \mathcal {F}(V)\) be a family of fundamental memories and \(\mathcal {S}\) a strong similarity measure. Suppose that the matrix K given by (2.4) is invertible for any \(\alpha >0\). Given a fuzzy set \(X \in \mathcal {F}(U)\), define \(\varGamma \subseteq \{1,\ldots ,p\}\) as the set of the indexes of the stimulus which are the most similar to the input X in terms of \({\mathcal S}\), that is:

$$\begin{aligned} \varGamma =\{\gamma : \mathcal {S}(A^\gamma ,X) \ge \mathcal {S}(A^\xi , X), \forall \xi =1, \ldots , p\}.\end{aligned}$$
(2.5)

Then,

$$\begin{aligned} \lim _{\alpha \rightarrow \infty }Y(v)=\frac{1}{{\text {Card}}(\varGamma )}\sum _{\gamma \in \varGamma } B^{\gamma }(v), \quad \forall v \in V. \end{aligned}$$
(2.6)

where \(Y=\mathcal {K}(X)\) is the output of a fuzzy KAM. Furthermore, the weights \(w_{\xi }\) given by (2.3) satisfy the following equation for all \(\xi =1,\ldots ,p\):

$$\begin{aligned} \lim _{\alpha \rightarrow \infty } w_{\xi } = {\left\{ \begin{array}{ll} \displaystyle {\frac{1}{{\text {Card}}{\varGamma }}}, &{} \xi \in \varGamma ,\\ 0, &{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$
(2.7)

2.1 Estimating the Parameter of a Fuzzy KAM

In this section, we propose to estimate the parameter \(\alpha \) of a fuzzy KAM using information theoretical learning [23]. The basic idea is to maximize the capability of the fuzzy kernel \(\kappa \) to discriminate between two different stimulus. To this end, we use the information-theoretic descriptor of entropy.

The concept of entropy, introduced by Shannon in 1948 [26], represents a quantitative measure of uncertainty and information of a probabilistic system [27, 28]. The entropy of a n-state system is defined by the following equation where \(p_i\) denotes the probability of occurrence of the i-th state [27]:

$$\begin{aligned} E=\displaystyle {\sum _{i=1}^{n} p_i \log (1/p_i)}. \end{aligned}$$
(2.8)

The entropy given by (2.8) can be used as a measure of the amount of uncertainty of a system. Given a fundamental memory set \(\mathcal {A}=\{(A^\xi ,B^\xi ): \xi =1, \ldots , p \} \subseteq \mathcal {F}(U)\times \mathcal {F}(V)\) and a strong similarity measure \(\mathcal {S}:\mathcal {F}(U)\times \mathcal {F}(U)\rightarrow [0,1]\), we define the entropy of a fuzzy KAM \(\mathcal {K}\) by means of the equation

$$\begin{aligned} E_{\mathcal {K}}(\alpha )&= \sum _{i=1}^p \sum _{j=1}^p \kappa (A^i,A^j) \log \Big (1/\kappa (A^i,A^j)\Big ) \end{aligned}$$
(2.9)
$$\begin{aligned}&=\displaystyle {\sum _{i=1}^{p}\sum _{j=1}^{p}} - e^{\alpha (\mathcal {S}(A^{i},A^{j})-1)} \log \left( e^{\alpha (\mathcal {S}(A^{i},A^{j})-1)}\right) \end{aligned}$$
(2.10)
$$\begin{aligned}&=-\displaystyle {\sum _{i=1}^{p}\sum _{j=1}^{p}} \alpha (\mathcal {S}(A^{i},A^{j})-1)) e^{\alpha (\mathcal {S}(A^{i},A^{j})-1)}. \end{aligned}$$
(2.11)

Note that the entropy \(E_\mathcal {K}\) of a fuzzy KAM is a function of the parameter \(\alpha \). Furthermore, \(E_\mathcal {K}(\alpha )\) tend to zero if either \(\alpha \rightarrow 0\) or \(\alpha \rightarrow \infty \). Intuitively, \(E_\mathcal {K}\) quantifies the capability of the fuzzy kernel \(\kappa \) to discriminate between \(A^i\) and \(A^j\) as a function of \(\alpha \). By maximizing \(E_\mathcal {K}\), we expect to improve the noise tolerance of the fuzzy KAM. In view of this remark, we suggest to choose the parameter \(\alpha ^*\) that maximizes (2.11). Formally, we propose to define

$$\begin{aligned} \alpha ^* = \mathop {\text{ argmax }}_{\alpha > 0} E_\mathcal {K}(\alpha ).\end{aligned}$$
(2.12)

At this point, we would like to recall that Shannon derived (2.8) using classical probability theory. A fuzzy entropy that does not take into account probabilistic concepts in its definition have been provided by De Luca and Termini [29]. Although the fuzzy entropy would be more appropriate in our context, we have not observed significant improvements in our preliminary computational experiments using the fuzzy entropy compared to those obtained using the entropy of Shannon. Moreover, besides presenting lower computational cost, Shannon’s entropy showed to be more robust. Therefore, we only consider the entropy of Shannon in this paper.

3 Classifiers Based on Fuzzy KAMs

A classifier is a mapping \(\mathcal {C}:W \rightarrow \mathcal {L}\) that associates to each pattern \(w\in W\) a label \(l \in \mathcal {L}\) that represents the class which w belongs to. Classifiers are usually synthesized using a family of labeled samples, called training set. In this section, we present two approaches to define classifiers based on fuzzy KAMs. The first approach, which is inspired by sparse representation classifiers [30], is based on autoassociative fuzzy KAMs. The second approach contemplates the heteroassociative case.

3.1 The Autoassociative-Based Approach

Sparse representation classifiers [30] are based on the hypothesis that a sample Y from class i is approximately equal to a linear combination of the training data from class i. Formally, let \(\mathcal {A}_{\mathcal {L}}=\{(A^{\xi }, \ell _\xi ), \xi =1, \cdots , p\} \subset \mathcal {F}(U) \times \mathcal {L}\) be the training set, where \(A^{\xi }\) are distinct non-empty fuzzy sets on U and \(\mathcal {L}\) is a finite set of labels. If Y belongs to class i, then

$$\begin{aligned} Y(u)\approx \sum _{\xi : \ell _{\xi }=i}\alpha _\xi A^{\xi }(u), \quad \forall u \in U. \end{aligned}$$
(3.13)

Equivalently, Y can be written as:

$$\begin{aligned} Y(u)\approx \sum _{\xi =1}^{p}\alpha _\xi A^{\xi }(u), \quad \forall u \in U, \end{aligned}$$
(3.14)

where \(\alpha _\xi =0\) if \(\ell _{\xi }\ne i\). In other words, Y can be written as a sparse linear combination of the training data.

Assume we have an autoassociative fuzzy KAM \(\mathcal {K}:\mathcal {F}(U)\rightarrow \mathcal {F}(U)\) designed for the storage of the fundamental memory set \(\{\mathcal {A}^1,\ldots ,\mathcal {A}^p\}\). Given a pattern X from class i (or a noisy version \(\tilde{X}\) of X), the autoassociative fuzzy KAM is expected to produce a pattern \(\mathcal {K}(X)=Y\) that also belongs to class i. From (2.3), the output of the autoassociative fuzzy KAM satisfies

$$\begin{aligned} Y(u) = \varphi \left( \displaystyle {\sum _{\xi =1}^{p} w_{\xi }A^{\xi }(u)}\right) , \end{aligned}$$
(3.15)

where \(\varphi (x)=\max (0, \min (1,x))\). By comparing (3.14) and (3.15), except for the piece-wise linear function \(\varphi \) which can be disregarded if \(\sum _{\xi =1}^p w_\xi A^\xi (u) \in [0,1]\), we conclude that the linear combination in (3.15) should also be sparse. Therefore, the coefficients \(\alpha _\xi \) in (3.14) can be approximated by

$$\begin{aligned} \alpha _\xi = w_{\xi } \chi _i(\ell _\xi ), \quad \forall \xi =1,\ldots ,p, \end{aligned}$$
(3.16)

where \(\chi _i:\mathcal {L}\rightarrow \{0,1\}\), for \(i \in \mathcal {L}\), denotes the indicator function:

$$\begin{aligned} \chi _i(x) = {\left\{ \begin{array}{ll} 1, &{} x = i,\\ 0, &{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$
(3.17)

Observe that (3.16) implies \(\alpha _\xi =w_{\xi }\) if \(\ell _\xi =i\) and \(\alpha _\xi = 0\) otherwise. Concluding, if the input X belongs to class i, we presuppose that

$$\begin{aligned} Y(u) \approx \sum _{\xi =1}^p w_{\xi } \chi _i(\ell _\xi ) A^\xi (u), \quad \forall u \in U, \end{aligned}$$
(3.18)

In practice, however, we do not know a priori to which class the input X belongs. As a consequence, we assign to X the class \(i \in \mathcal {L}\) that minimizes the distance between Y and the linear combination \(\displaystyle {\sum _{\xi =1}^p w_{\xi } \chi _{\ell }(\ell _\xi ) A^\xi }\). Formally, we attribute to X a class label \(i \in \mathcal {L}\) such that

$$\begin{aligned} d_2 \Bigg (Y,\sum _{\xi =1}^p w_{\xi } \chi _{i}(\ell _\xi ) A^\xi \Bigg ) \le d_2\Bigg (Y, \sum _{\xi =1}^p w_{\xi } \chi _j (\ell _\xi ) A^\xi \Bigg ), \forall j \in \mathcal {L}, \end{aligned}$$
(3.19)

where \(d_2\) denotes the \(L_2\)-distance.

3.2 Heteroassociative-Based Approach

In the second approach, we define a classifier using the heteroassociative case. Precisely, we synthesize a heteroassociative fuzzy KAM designed for the storage of a fundamental memory set \(\{(A^{\xi }, B^{\xi }), \xi =1, \ldots , p\} \subset \mathcal {F}(U) \times \{0,1\}^n\), where \(n = \text{ Card }(\mathcal {L})\) denotes the number of classes, \(A^{\xi }\) represents a sample from a certain class, and \(B^{\xi } \subset \{0,1\}^n\) indicates to which class \(A^{\xi }\) belongs. In mathematical terms, the (fuzzy) set \(B^{\xi }\) associated to the stimulus \(A^\xi \) of class i is defined by:

$$\begin{aligned} B^{\xi }(v)={\left\{ \begin{array}{ll} 1, &{} \text {if } v=i \\ 0, &{} \text {if } v\ne i. \end{array}\right. } \end{aligned}$$
(3.20)

Now, given an input \(X \in \mathcal {F}(U)\), the fuzzy KAM yields a fuzzy set \(Y=\mathcal {K}(X)\). According to Eqs. (2.2) and (3.20), Y(i) is the sum of the weights \(w_{\xi }\)’s for \(\xi \) such that \(A^{\xi }\) belongs to the class i. Hence, we associate the input X to the i-th class, where i is the first index such that \(Y(i)\ge Y(j)\), for all \(j=1, \ldots , n\).

4 Computational Experiments and Results

In this section, we carry out computational experiments to evaluate the performance of the fuzzy KAM-based classifiers. Let us begin by clarifying the benchmark classification problems that we have used.

4.1 Classification Problems

Let us consider the following twenty two classification problems available at the Knowledge Extraction Based on Evolutionary Learning (KEEL) database repository as well as at the UCI Machine Learning Repository: appendicitis, cleveland, crx, ecoli, glass, heart, iris, monks, movementlibras, pima, sonar, spectfheart, vowel, wdbc, wine, satimage, texture, german, yeast, spambase, phoneme, and page-blocks [31]. We would like to point out that, due to computational limitations, we refrained to consider the classification problems: magic, pen-based, ringnorm, and twonorm. Precisely, recall that \(\mathcal {O}(p^3)\) operations are performed to synthesize a fuzzy KAM and, in these four databases, we have \(p \approx 10^4\).

Similar to previous experiments described on the literature, the experiments were conducted by using ten-fold cross validation technique. This method consists of dividing the data-set in ten parts and performing 10 tests, each one using one of the parts as a test set and the others nine parts as developing/training set. Afterward, we compute the mean of the ten accuracy values obtained in each one of the ten tests. In order to ensure a fair comparison, we used the same partitioning as in [31, 32].

Some of the data sets considered in this experiment contain both categorical and numerical features. Therefore, a pre-processing step to convert the original data into fuzzy sets was necessary. First, in order to have only numerical values, we transformed each categorical feature \(f \in \{v_1,\ldots ,v_c\}\), with \(c>1\), into a c-dimensional numerical feature \(\mathbf {n}=(n_1,n_2,\ldots ,n_c) \in \mathbb {R}^c\) as follows for all \(i=1,\ldots ,c\):

$$\begin{aligned} n_i={\left\{ \begin{array}{ll} 1, &{} f=v_i,\\ 0, &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$
(4.21)

For example, the crx data set contain nine categorical features, one of them with 14 possibilities. Such categorical feature was transformed into 14 numerical features using (4.21). At the end, an instance of the transformed crx data set contain 46 numerical features instead of 9 categorical and 6 numerical features of the original classification problem.

After all categorical features were converted into numerical values, an instance from a data set can be written as a pair \((\mathbf {x}, \ell )\), where \(\mathbf {x}=[x_1,\ldots ,x_n]^T \in \mathbb {R}^n\) is a vector of numerical features and \(\ell \in \mathcal {L}\) denotes its class label. Moreover, each feature vector \(\mathbf {x} \in \mathbb {R}^n\) can be associated with a fuzzy set \(A = [a_1,a_2,\ldots ,a_n]^T\) by means of the equation

$$\begin{aligned} a_i = \displaystyle {\frac{1}{1+e^{-(x_{i}-\mu _i)/\sigma _i}}} \in [0,1], \quad \forall i=1, \ldots , n, \end{aligned}$$
(4.22)

where \(\mu _i\) and \(\sigma _i\) represent respectively the mean and the standard deviation of ith component of all training instances. Concluding, any training set can be written as a labeled family of fuzzy sets \(\mathcal {A}_\mathcal {L}= \{(A^\xi ,\ell _\xi ):\xi =1,\ldots ,p\}\).

Besides, we have removed some repeated elements from the fundamental memories sets of the spambase and page-blocks data sets.

In our computational experiments, we considered the fuzzy KAM defined by using the Gregson similarity measure and the parameter \(\alpha ^*\) that maximizes the entropy. The Gregson similarity measure \(\mathcal {S}_G: \mathcal {F}(U)\times \mathcal {F}(U)\rightarrow [0,1]\) is given by:

$$\begin{aligned} \mathcal {S}_G(A,B)=\displaystyle {\frac{\displaystyle {\sum _{i=1}^{n}}\min (A(u_i),B(u_i))}{\displaystyle {\sum _{i=1}^{n}}\max (A(u_i),B(u_i))}}. \end{aligned}$$
(4.23)

Note that \(\mathcal {S}_G\) given by (4.23) is a strong similarity measure which can be interpreted as the quotient between the cardinality of the intersection by the cardinality of the union of A and B. Finally, we would like to point out that we studied extensively the role of a fuzzy similarity measure in GEB-FAM models applied for face recognition and the Gregson similarity measure achieved competitive results in comparison with others models from the literature [21].

Fig. 1.
figure 1

Boxplot of classification accuracies of several models of the literature in twenty two problems. The accuracy of the nine first classifiers have been extract from [32].

Full size image

Figure 1 shows the boxplot of the average accuracy produced by the autoassociative and heteroassociative fuzzy KAM-based classifiers as well as other nine models from the literature, namely: 2SLAVE [33], FH-GBML [34], SGERD [35], CBA [36], CBA2 [37], CMAR [38], CPAR [39], C4.5 [40], and FARC-HD [32]. The accuracy of the nine first classifiers have been extract from [32]. We can observe from Fig. 1 that the fuzzy KAM-based classifiers outperformed (or are at least competitive!) with the other classifiers from the literature. Let us conclude by pointing out that the outliers in the boxplot of the fuzzy KAM-based classifiers correspond to the Cleveland and Yeast classification problems.

5 Concluding Remarks

In this paper, we introduced the class of fuzzy kernel associative memories (fuzzy KAMs). Basically, a fuzzy KAM corresponds to single-step generalized exponential bidirectional fuzzy associative memories (GEB-FAMs), which have been introduced and investigated by us in the last years [5, 18, 21, 25]. Like the single-step GEB-FAMs, fuzzy KAMs can be applied in classification problems. Indeed, in this paper we reviewed two approaches for pattern classification: one using the autoassociative case and the other based on the heteroassociative case.

The main contribution of this paper is the new interpretation of the exponential of a similarity measure as a kernel function. Although we did not elaborated rigorously on the notion of a fuzzy kernel, it allowed us to apply concepts from information theoretical learning to fine tune the parameter \(\alpha \) of a fuzzy KAM. Precisely, in view of its simplicity, we proposed to determine the parameter \(\alpha ^*\) that maximizes the Shannon entropy of a fuzzy KAM.

Computational experiments with some well-know benchmark classification problems showed a superior performance, in terms of accuracy, of the fuzzy KAM-based classifiers over many other classifiers from the literature. In the future, we plan to formalize the notion of a fuzzy kernel and to investigate further the performance of the fuzzy KAM-based classifiers. We also intent to study other applications of the fuzzy KAM models.