Abstract
This work extends the study of properties related to the Atanassov’s interval-valued intuitionistic fuzzy entropy obtained as aggregation of generalized Atanassov’s intuitionistic fuzzy index, by considering the concept of conjugate fuzzy implications and their dual constructions. Many ways to define the interval entropy were compared leading to the equation proposed in this work which is more sensitive to determine the interval entropy when using different interval-valued fuzzy sets.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
- Generalized Atanassov’s intuitionistic fuzzy index
- Atanassov’s interval-valued intuitionistic fuzzy entropy
- Conjugation
- Duality
1 Introduction
By allowing the expression related to the expert uncertainty in identifying a particular membership function or even to approximate the (unknown) membership degrees, the Atanassov interval-valued intuitionistic fuzzy logic (A-IvIFL) is an increasingly popular extension of fuzzy set theory.
The Atanassov’s interval-valued intuitionistic fuzzy index (A-IvIFIx), called as hesitancy or indeterminacy degree of an element in an Atanassov-intuitionistic fuzzy set (A-IFS), provides either a measure of the lack of supporting information or a given incomplete/inconsistent proposition based on Atanassov-intuitionistic fuzzy logic (A-IFL). Thus, using intervals in \(U=[0,1]\) that approximate the unknown data related to membership degrees, we are able to model applications in which experts do not have precise knowledge.
The concept of fuzzy entropy was introduced in order to measure how far a fuzzy set (FS) is from a crisp one [14]. Since then, this concept has been adapted to the distinct extensions of FSs and with many interpretations, describing the general measure of fuzziness through the mapping between fuzzy and real systems. Analogous interpretations lead to model data of the decision-making processes which cannot be measured precisely, taking extensions of the value of entropy from a number to an interval value or even from an interval-valued intuitionistic value based on the definition of interval entropy [19].
This paper contributes with both approaches: (i) the new concept of generalized Atanassov’s intuitionistic fuzzy index (A-GIFIx) associated with a strong intuitionistic fuzzy negation \(N_I\) [2], characterized in terms of fuzzy implication operators which is described by a construction method based on the action of automorphisms; and (ii) the Atanassov’s intuitionistic fuzzy entropy (A-IFE), introduced by means of special aggregation functions of the A-GIFIx in [7].
Following the former approach, this work extends the study of the generalized Atanassov’s interval-valued intuitionistic fuzzy index (A-GIvIFIx) [10], considering the concept of conjugate and dual interval-valued fuzzy implications, mainly interested in representation method [6, 11] and providing impact on properties satisfied by the generated operations. Additionally, A-GIvIFIx associated with the standard negation together with the known Reichenbach interval-valued fuzzy implications are considered [13].
From the later approach, the Atanassov’s interval-valued intuitionistic fuzzy entropy (A-IvIFE) is studied, describing main notions for measuring fuzziness degree or uncertain information in A-IvIFL. Such entropy is able to measure how far a set defined by actions of fuzzy connectives in A-IvIFL is from one in A-IvFL or A-IFL, and therefore, from a set in FL.
Our study mainly focuses on useful information entropy measures providing another way to explore IvIFL as a model by offering application developers as method of construction of A-IvIFE from A-GIvIFIx.
Among several papers found in the literature, see [12, 19], connecting entropy measures for interval-valued intuitionistic fuzzy sets (IvIFSs) and discussing their relationships with similarity measures and inclusion measures. In [12], Jing and Min deal with the entropies of IvIFSs, proposing a \(\lambda \)-parametrized set of generalized entropy on IvIFSs and then it is proved that the new entropy is an increasing \(\lambda \)-parametrized function. In [19], a new axiomatical definition of entropy measure for A-IvIFL based on distance is proposed, which is consistent with the definition introduced in [14]. These formal studies underlying the main contribute for multi-criteria decision making problem, ranking the alternatives to study interval-valued fuzzy set models, offering application developers a method of construction of A-IvIFE from A-GIvIFIx preserving fuzziness and intuitionism based on generalized approach for an A-IvIFIx.
The preliminaries describe the basic properties of fuzzy connectives and basic concepts of A-IvIFL. The study of the A-GIvIFIx(\(N_I\)) and general results in the analysis of its properties are stated in Sect. 3. In Sect. 4, an interval version of entropy is presented based on the generalized Atanassov’s intuitionistic fuzzy index. We also consider a relationship with IvIFIx and conjugate operators. Concluding, final remarks and further work are reported.
2 Preliminaries
Main results on interval-valued fuzzy connectives and IvIFSs are reported below.
2.1 Interval-Valued Fuzzy Connectives
Let  . For each \(x\in U\), a degenerate interval [x, x] will be denoted by \(\mathbf {x}\) and the subset of all degenerate interval will be denoted by \(\mathbb {D}\). And, let \(\le _{\mathbb {U}} \, \subseteq \mathbb {U}^2\) be the Kulisch-Miranker (or product) order, such that for all \(X, Y \in \mathbb {U}\), it is given by:
. For each \(x\in U\), a degenerate interval [x, x] will be denoted by \(\mathbf {x}\) and the subset of all degenerate interval will be denoted by \(\mathbb {D}\). And, let \(\le _{\mathbb {U}} \, \subseteq \mathbb {U}^2\) be the Kulisch-Miranker (or product) order, such that for all \(X, Y \in \mathbb {U}\), it is given by:
such that \(\forall X,Y \in \mathbb {U}\),  . We also consider \(\preceq _{\mathbb {U}} \subseteq \mathbb {U}^2\) given as
. We also consider \(\preceq _{\mathbb {U}} \subseteq \mathbb {U}^2\) given as
By [5] an interval-valued aggregation (IvA)  demands the conditions:
demands the conditions:
- \(\mathbb {M}1\)::
-
\(\mathbb {M}(\mathbf {X}) = \mathbf {0} \text{ and } \mathbf {X} = (\mathbf {0}, \ldots , \mathbf {0})\); \(\mathbb {M}(\mathbf {X}) = \mathbf {1} \text{ and } \mathbf {X} = (\mathbf {1}, \ldots , \mathbf {1})\);
- \(\mathbb {M}2\)::
-
If \(\mathbf {X}=(X_1,\ldots , X_n) \le _{\mathbb {U}^n} \mathbf {Y}=(Y_1,\ldots , Y_n)\) then \(\mathbb {M}(\mathbf {X})\le _{\mathbb {U}} \mathbb {M}(\mathbf {Y})\);
- \(\mathbb {M}3\)::
-
\(\mathbb {M}({\mathbf {X}_{\sigma }}) = \mathbb {M}(X_{\sigma _1}, \ldots ,X_{\sigma _n})=\mathbb {M}(X_1,\dots , X_n)=\mathbb {M}(\mathbf {X})\).
Definition 1
[18]. An interval function \(\mathbb {N}:\mathbb {U} \rightarrow \mathbb {U}\) is an interval-valued fuzzy negation (IvFN) if, for all \(X,Y\in \mathbb {U}\), it verifies the following conditions:
- \(\mathbb {N}1\)::
-
\(\mathbb {N}([0,0])=\mathbf {1}\); e \(\mathbb {N}([1,1])=\mathbf {0}\);
- \(\mathbb {N}2a\)::
-
If \(X \ge Y\) then \(\mathbb {N}(X) \le \mathbb {N}(Y)\). \(\mathbb {N}2b\): If \(X\subseteq Y\) then \(\mathbb {N}(X)\supseteq \mathbb {N}(Y)\).
An IvFN \(\mathbb {N}\) is called strong IvFN [17] if \(\mathbb {N}\) also satisfies the involutive property:
- \(\mathbb {N}3\)::
-
\(\mathbb {N}(\mathbb {N}(X))=X\), for all \(X\in \mathbb {U}\),
The interval extension of the standard negation \(N_S(x)=1-x\) is given as:
The \(\mathbb {N}\)-dual operator of an interval-valued function \(f:\mathbb {U}^n \rightarrow \mathbb {U}\) is given as

Definition 2
[3]. A function \(\mathbb {I} (\mathbb {J}):\mathbb {U}^2\rightarrow \mathbb {U}\) is a interval fuzzy (co)implication if for all satisfies the following boundary conditions:

Additional properties can be demanded for IvFI(IvFJ):

Analogously, these properties \(\mathbb {I}_k(\mathbb {J}_k)\) can be restricted to fuzzy (co)implications by projections on \(\mathbb {D}\) and will be denoted as \(I_k(J_k)\).
Proposition 1
[8, Prop 21], A fuzzy (co)implication \(I(J):U^2\rightarrow U\) satisfies I1 (J1) and I2 (J2) iff the interval fuzzy (co)implication \(\mathbb {I}\)(\(\mathbb {J}\)) is given as
Example 1
The interval-valued extension of the Reichenbach (co)implication  (
( ) can be expressed as follows:
) can be expressed as follows:


2.2 Interval-Valued Atanassov’s Intuitionistic Fuzzy Sets
Based on [1] and later on [11], we briefly report main concepts and properties on interval-valued Atanassov’s intuitionistic fuzzy sets (IvIFSs shortly).
An A-IvIFS \(\mathbb {A}_I\) in a non-empty universe \(\chi \) is expressed as

and the set of all IvIFSs is denoted by \(\mathcal {A}_I\). Thus, an intuitionistic fuzzy truth value of an element in \(\mathbb {A}_I\) is given by a pair of intervals \((M_{A_I}(x),N_{A_I}(x))\), and

denotes the set of all Atanassov’s interval-valued intuitionistic fuzzy degreesFootnote 1 such that \((\tilde{\mathbb {U}}, \le _{\tilde{\mathbb {U}}})\) and \((\tilde{\mathbb {U}}, \preceq _{\tilde{\mathbb {U}}})\) are partial ordered sets given as
- \(\mathbb {R}_I\)1::
-
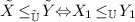 and
and  ;
; - \(\mathbb {R}_I\)2::
-
\(\tilde{X} \preceq _{\tilde{\mathbb {U}}} \tilde{Y} \Rightarrow X_1 \le _{\mathbb {U}} Y_1 \, \text{ and } \, X_2 \le _{\mathbb {U}} Y_2\), for all
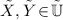 ;
;
with  and
and  as the least and greatest elements on \(\tilde{\mathbb {U}}\), respectively. Additionally, an interval-valued Atanassov’s intuitionistic fuzzy degree has two projections \(l_{\mathbb {I_{I}}},r_{\mathbb {I_{I}}}:\tilde{\mathbb {U}} \rightarrow \mathbb {U}\), defined by \(l_{\mathbb {I_I}}(\tilde{X})=X_1\) and \(r_{\mathbb {I_I}}(\tilde{X})=X_2\). When \(X_1+X_2=\mathbf {1}\) then \(A_I\) is restricted to the set \(\mathcal {A}\) of all interval-valued fuzzy sets. Moreover, the function
as the least and greatest elements on \(\tilde{\mathbb {U}}\), respectively. Additionally, an interval-valued Atanassov’s intuitionistic fuzzy degree has two projections \(l_{\mathbb {I_{I}}},r_{\mathbb {I_{I}}}:\tilde{\mathbb {U}} \rightarrow \mathbb {U}\), defined by \(l_{\mathbb {I_I}}(\tilde{X})=X_1\) and \(r_{\mathbb {I_I}}(\tilde{X})=X_2\). When \(X_1+X_2=\mathbf {1}\) then \(A_I\) is restricted to the set \(\mathcal {A}\) of all interval-valued fuzzy sets. Moreover, the function  , called an interval-valued Atanassov’s intuitionistic fuzzy index (A-IvIFIx shortly), related to an IvIFS \(A_I\), is given as
, called an interval-valued Atanassov’s intuitionistic fuzzy index (A-IvIFIx shortly), related to an IvIFS \(A_I\), is given as
An IvIFIx models not only the uncertainty degree but also the hesitancy/indeterminance degree of each x in \(A_I\). The difference between \(A_I\) and \(B_I\) is given by:

According with [18], an interval-valued Atanassov’s intuitionistic fuzzy negation (IvIFN) \(\mathbb {N}_{I}:\tilde{\mathbb {U}} \rightarrow \tilde{\mathbb {U}}\) satisfies, for all  , the following properties:
, the following properties:
- \(\mathbb {N}_I\)1::
-
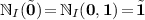 and
and 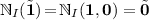 ;
; - \(\mathbb {N}_I\)2::
-
If
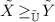 then
then 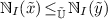 .
.
Moreover, \(\mathbb {N}_{I}\) is a strong IvIFN if it also verifies the involutive property:
- \(\mathbb {N}_I3\)::
-
\(\mathbb {N}_{I}(\mathbb {N}_{I}(\tilde{X}))=\tilde{X}\), \(\forall \tilde{X} \in \tilde{\mathbb {U}}\).
Consider \(\mathbb {N}_{I}\) as IvIFN and \(\mathbb {F}_I: \tilde{\mathbb {U}}^{n} \rightarrow \tilde{\mathbb {U}}\). By [18], the \(\mathbb {N}_{I}\)-dual interval-valued Atanassov’s intuitionistic function of \(\tilde{f}\), denoted by \({\mathbb {F}_I}_{\mathbb {N}_{I}}: \tilde{\mathbb {U}}^{n} \rightarrow \tilde{\mathbb {U}}\), is given by:
When \(\tilde{\mathbb {N}}_{I}\) is a strong IvIFN, \(\tilde{f}\) is a self-dual interval-valued intuitionistic function. And, by [18], taking a strong IvFN \(\mathbb {N}:\mathbb {U} \rightarrow \mathbb {U}\), a IvIFN \(\mathbb {N_S}_I:\tilde{\mathbb {U}} \rightarrow \tilde{\mathbb {U}}\) such that
is a strong IvIFN generated by the IvFNs \(\mathbb {N}\) and \(\mathbb {N}_S\). By [6]), a strong IvIFN is also a representable IvIFN. Additionally, if \(\mathbb {N}=\mathbb {N}_S\), Eq. (10) can be reduced to \(\mathbb {N_S}_I(\tilde{X}) = (X_2,X_1)\). Moreover, the complement of A-IvIFS \(A_I\) is defined by

An interval-valued Atanassov’s intuitionistic automorphism (A-IvIA) is a bijection increasing operator \(\varPhi : \tilde{\mathbb {U}} \rightarrow \tilde{\mathbb {U}}\). For all \(\tilde{X},\tilde{Y} \in \tilde{\mathbb {U}}\), the following hold:
- \(\mathbb {A}_I1\)::
-
\(\varPhi (\tilde{\mathbf {1}})= \tilde{\mathbf {1}}\) and \(\varPhi (\tilde{\mathbf {0}})=\tilde{\mathbf {0}}\);
- \(\mathbb {A}_I2\)::
-
\(\varPhi \circ \varPhi ^{-1}(\tilde{X})= \tilde{X}\);
- \(\mathbb {A}_I3\)::
-
\(\tilde{X} \le _{\tilde{\mathbb {U}}} \tilde{Y}\) iff \(\varPhi (\tilde{X}) \le _{\tilde{\mathbb {U}}} \varPhi (\tilde{Y})\).
In the set of all A-IvIAs (\(Aut(\tilde{\mathbb {U}})\)), the conjugate function of \(f_I: \tilde{\mathbb {U}}^n\rightarrow \tilde{\mathbb {U}}\) is a function \(f_I^{\varPhi } :\tilde{\mathbb {U}}^n \rightarrow \tilde{\mathbb {U}}\), defined as follows
Reporting main results in [9, Theorem 17], let \(\phi : \mathbb {U} \rightarrow \mathbb {U}\) be an interval-valued automorphism, \(\phi \in Aut(\mathbb {U})\). Then, a \(\phi \)-representability of \(\varPhi \) is given by
Moreover, if \(\phi \in Aut(U)\), for all \(\tilde{X} \in \tilde{\mathbb {U}}\), a \(\phi _U\)-representability of \(\varPhi \) is given by
Thus, if an IvIA is \(\phi \)-representable, it is also a \(\phi _U\)-representable automorphism [18].
3 Interval Extension of the Generalized Atanassov’s Intuitionistic Fuzzy Index
Definition 3
Let \(\mathbb {N}\) be a strong IvFN. A function  is called a generalized interval-valued intuitionistic fuzzy index \((A-GIvIFIx(\mathbb {N}))\) if, for all \(X_1, X_2, Y_1, Y_2 \in \mathbb {U}\), it holds that:
is called a generalized interval-valued intuitionistic fuzzy index \((A-GIvIFIx(\mathbb {N}))\) if, for all \(X_1, X_2, Y_1, Y_2 \in \mathbb {U}\), it holds that:
- \(\varPi 1\)::
-
\(\varPi (X_1, X_2) = \mathbf {1}\) iff \(X_1 = X_2 = \mathbf {0}\);
- \(\varPi 2\)::
-
\(\varPi (X_1, X_2) = \mathbf {0}\) iff \(X_1 + X_2 = \mathbf {1}\);
- \(\varPi 3\)::
-
If \((Y_1, Y_2) \preceq _{\tilde{\mathbb {U}}} (X_1, X_2)\) then \(\varPi (X_1, X_2) \le _{\mathbb {U}} \varPi (Y_1, Y_2)\);
- \(\varPi 4\)::
-
\(\varPi (X_1, X_2) = \varPi (\mathbb {N_S}_I(X_1, X_2))\) when \(\mathbb {N_S}_{I}\) is given by Eq.(10).
3.1 Relationship with Interval-Valued Fuzzy Connnectivess
In the following, Theorem 1 extends main results in [2].
Theorem 1
Let  be a (co)implicator verifying \(\mathbb {I}1\)(\(\mathbb {J}2\)),\(\mathbb {I}4\)(\(\mathbb {J}4\)),\(\mathbb {I}5\)(\(\mathbb {J}5\)) and \(\mathbb {I}6\)(\(\mathbb {J}6\)) and
be a (co)implicator verifying \(\mathbb {I}1\)(\(\mathbb {J}2\)),\(\mathbb {I}4\)(\(\mathbb {J}4\)),\(\mathbb {I}5\)(\(\mathbb {J}5\)) and \(\mathbb {I}6\)(\(\mathbb {J}6\)) and  be an involutive IvFN. A function
be an involutive IvFN. A function  is A-GIvIFIx(\(\mathbb {N}\)) iff it can be given as
is A-GIvIFIx(\(\mathbb {N}\)) iff it can be given as
Proof
Equation(15b) is proved below. Analogously, it can be done to Eq.(15a).
(\(\Rightarrow \)) Consider that \(\mathbb {J}:\mathbb {U}^2 \rightarrow \mathbb {U}\) verifies \(\mathbb {J}2\), \(\mathbb {J}4\), \(\mathbb {J}5\) and \(\mathbb {J}6\), it holds that:

(\(\Leftarrow \)) Considering the function \(\mathbb {J}: \mathbb {U}^2 \rightarrow \mathbb {U}\) given as \(\mathbb {J}(X_1,X_2)= \mathbf {1}\), if \(X_1 > X_2\); and \(\mathbb {J}(X_1,X_2)= \varPi _{\mathbb {N},\mathbb {J}}(X_2,\mathbb {N}_S(\mathbb {N}(X_1)))\), otherwise. The following holds:
Therefore, Theorem 1 holds.
The \(\varPhi \)-representability and \(\mathbb {N}\)-dual IvIFIx constructions are discussed below.
Proposition 2
Let \(\mathbb {I}_{\mathbb {N}}\)(\(\mathbb {J}_{\mathbb {N}})\) be the \(\mathbb {N}\)-dual operator of a (co)implication \(\mathbb {I}(\mathbb {J})\). The following holds:
Proof
\(\varPi _{\mathbb {N},\mathbb {I}_{\mathbb {N}}} (\tilde{\mathbb {X}}) = \mathbb {I}_{\mathbb {N}}(\mathbb {N}(\mathbb {N}_S(X_2)), \mathbb {N}(X_1)) =\mathbb {N}(\mathbb {I} (\mathbb {N}_S(X_2) , X_1)) = \varPi _{\mathbb {N, I}} (\tilde{\mathbb {X}})\), \(\forall \tilde{\mathbb {X}} \in \tilde{\mathbb {U}}\).
Corollary 1
When \(\mathbb {N}=\mathbb {N}_S\), Eq.(15) in Theorem 1 is given as
Proposition 3
Let \(\mathbb {N}\) be an N-representable IvFN and \(\pi _{N,I}:\tilde{U} \rightarrow U\) be A-IFIx(N). If \(\mathbb {I}, \mathbb {J}\) are representable (co)implications given by Eq.(3), a function \(\varPi _{\mathbb {N}, \mathbb {I}} : \tilde{\mathbb {U}} \rightarrow \mathbb {U}\) given by Eq.(17) can be expressed as

Proof
We proof Eq.(18a), the other one can be analogously done. By taking \((X_1,X_2)\in \tilde{\mathbb {U}}\), \(X_1 = [\underline{X}_1, \overline{X}_1], X_2 = [\underline{X}_2, \overline{X}_2]\) then \( X_1+X_2= [\underline{X}_1 + \underline{X}_2, \overline{X}_1 + \overline{X}_2] \le \mathbf {1}\), meaning that \(\overline{X}_1 + \overline{X}_2 \le 1\) and \(\underline{X}_1 + \underline{X}_2 \le 1\). Then, we have the result  . Concluding, \(\varPi _{\mathbb {N}, \mathbb {I}}(\tilde{X}) =[\varPi _{N,I}(\overline{X}_2, \overline{X}_1), \varPi _{N,I}(\underline{X}_2, \underline{X}_1)]\). So, Proposition 3 holds.
. Concluding, \(\varPi _{\mathbb {N}, \mathbb {I}}(\tilde{X}) =[\varPi _{N,I}(\overline{X}_2, \overline{X}_1), \varPi _{N,I}(\underline{X}_2, \underline{X}_1)]\). So, Proposition 3 holds.
Example 2
Consider \(\mathbb {I_{RC}}\) and related \(\mathbb {N_S}\)-dual construction \(\varPi _{\mathbb {N_S}, \mathbb {J_{RC}}}\). By preserving the conditions of Proposition 3, Eq.(18) can be expressed as

3.2 Relationship with Interval-Valued Automorphisms
Proposition 4
Let  be the \(\phi \)-conjugate of a strong IvFN \(\mathbb {N}: \mathbb {U} \rightarrow \mathbb {U}\) and \(\phi :\mathbb {U} \rightarrow \mathbb {U}\) be a \(\phi \)-representable IvA given by Eq.(14). When \(\varPhi :\tilde{\mathbb {U}} \rightarrow \tilde{\mathbb {U}}\) is a \(\varPhi \)-representable IvIFa given by Eq.(13), a function \({\varPi }^{\varPhi } : \tilde{\mathbb {U}} \rightarrow \mathbb {U}\) given by
be the \(\phi \)-conjugate of a strong IvFN \(\mathbb {N}: \mathbb {U} \rightarrow \mathbb {U}\) and \(\phi :\mathbb {U} \rightarrow \mathbb {U}\) be a \(\phi \)-representable IvA given by Eq.(14). When \(\varPhi :\tilde{\mathbb {U}} \rightarrow \tilde{\mathbb {U}}\) is a \(\varPhi \)-representable IvIFa given by Eq.(13), a function \({\varPi }^{\varPhi } : \tilde{\mathbb {U}} \rightarrow \mathbb {U}\) given by
is a \(A-GIvIFIx(\mathbb {N}_I)\) whenever \(\varPi : \tilde{\mathbb {U}} \rightarrow \mathbb {U}\) is also a \(A-GIvIFIx(\mathbb {N}_I)\).
Proof
Let \(\phi :\tilde{\mathbb {U}} \rightarrow \mathbb {U}\) be a \(\phi \)-representable A-IvA and \(\varPi : \tilde{\mathbb {U}} \rightarrow \mathbb {U}\) be a \(A-GIvIFIx(N_I)\). It holds that:

Let \(\mathbb {N}_I\) be a strong IvIFN given by Eq.(10) and \(\mathbb {N}_{I}^{\varPhi }\) its \(\varPhi -\)conjugate function.

The new results follow from Proposition 4 and Theorem 1.
Corollary 2
In conditions of Proposition 4 and also considering \(\phi \)-representable IvA given by Eq.(14), we can express Eq.(18) as follows:
Corollary 3
Let \(\varPhi \) be a \(\phi \)-representable automorphism in \(Aut(\tilde{\mathbb {U}})\) and \(\mathbb {I} (\mathbb {J}): \tilde{\mathbb {U}}^2 \rightarrow \tilde{\mathbb {U}}\) be the corresponding \(\phi \)-conjugate operator related to a (co)implication \(\mathbb {I} (\mathbb {J}): \mathbb {U}^2 \rightarrow \mathbb {U}\), verifying the conditions of Theorem 1. And, let \(\mathbb {N}^{\varPhi }\) be a strong \(\phi \)-conjugate IvFN negation. A function \(\varPi _{\mathbb {N,I}^{\phi }} (\varPi _{\mathbb {N,J}^{\phi }}) : \tilde{\mathbb {U}} \rightarrow \mathbb {U}\) given by
is an \(A-IvGIFIx(N)\) whenever \(\varPi _{\mathbb {N}, \mathbb {I}} (\varPi _{\mathbb {N}, \mathbb {J}}): \tilde{\mathbb {U}} \rightarrow \mathbb {U}\) is also a \(A-GIvIFIx(\mathbb {N})\).
Example 3
Consider \(\mathbb {I_{RC}}\) and related \(\varPhi \)-conjugate construction \(\varPi ^{\varPhi }_{\mathbb {N_S}, \mathbb {J_{RC}}}\) given by Eq.(18). For a \(\phi \)-representable IvIA, taking \(\phi (X)=X^n\) and n as an integer non-negative integer, we have the following:

4 Interval-Valued Intuitionistic Fuzzy Entropy
This section generalizes results from [7, Definition 2] also discussing properties related to the Atanassov’s interval-valued intuitionistic fuzzy entropy (A-IvIFE) which are obtained by action of an interval-valued aggregation of A-GIvIFIx.
Definition 4
An interval-valued function \(\mathbb {E}: \mathcal {A}_I \rightarrow \mathbb {U}\) is called an A-IvIFE if \(\mathbb {E}\) verifies the following properties:
-
\(\mathbb {E}2\): \(\mathbb {E}(A_I) = \mathbf {0} \Leftrightarrow A_I \in \mathcal {A}\);
-
\(\mathbb {E}2\): \(\mathbb {E}(A_I) = \mathbf {1} \Leftrightarrow M_{A_I}(x) = N_{A_I}(x) = \mathbf {0}\), \(\forall x\in \chi \);
-
\(\mathbb {E}3\): \(\mathbb {E}(A_I) = \mathbb {E}({A_I}_{c})\);
-
\(\mathbb {E}4\): If \(A_I \preceq _{\tilde{\mathbb {U}}} B_I\) then \(\mathbb {E}(A_I)\ge _{\mathbb {U}} \mathbb {E}(B_I)\), \(\forall A_I, B_I \in \mathcal {A}_I\).
Now, main properties of A-IvIFE obtained by A-GIvIFI are studied [15].
Theorem 2
Consider \(\chi = \{x_1, \ldots , x_n\}\). Let \(\mathbb {M}: \mathbb {U}^n \rightarrow \mathbb {U}\) be an automorphism, \(\mathbb {N}\) be a strong IvFN and \(\varPi \in Aut(\tilde{U})\). A function \(\mathbb {E}: \mathcal {A}_I \rightarrow \mathbb {U}\) given by
is an A-IvIFE in the sense of Definition 4.
Proof
Let \({A_I}_c\) be the complement of \(A_I\) given by Eq.(11). For all \(x_i \in \chi \) and \(A_I, B_I \in \mathcal {A}_I\), we have that:
- \(\mathbb {E}1:\) :
-
\(\mathbb {E}(A_I)=\mathbf {0} \Leftrightarrow \mathbb {M}_{i=1}^n \varPi (A_I(x_i))=\mathbf {0}\). By \(\mathbb {M}1\), \(\mathbb {E}(A_I)=\mathbf {0} \Leftrightarrow M_{A_I}(x_i)+ N_{A_I}(x_i)=\mathbf {1}\), \(\forall x_i \in \chi \). Then, by \(\varPi 2\), \(\mathbb {E}(A_I)=\mathbf {0} \Leftrightarrow A_I \in \mathcal {A}\).
- \(\mathbb {E}2:\) :
-
\(\mathbb {E}(A_I)=\mathbf {1} \Leftrightarrow \mathbb {M}_{i=1}^n \varPi (A_I(x_i))=\mathbf {1}\). By \(\mathbb {M}1\), \(\mathbb {E}(A_I)=\mathbf {1} \Leftrightarrow M_{A_I}(x_i)+ N_{A_I}(x_i)=\mathbf {0}\), meaning that \(M_{A_I}(x_i)=N_{A_I}(x_i)=\mathbf {0}\).
- \(\mathbb {E}3:\) :
-
\(\mathbb {E}(A_I)_c= \mathbb {M}_{i=1}^n \varPi ({A_I}_c(x_i)) = \varPi (\mathbb {N}_I(X_1, X_2))\). By \(\varPi 3\), the following holds \(\mathbb {E}(A_I)_c =\varPi (X_1, X_2)\). Concluding, \(\mathbb {E}(A_I)_c = \mathbb {E}(A_I)\).
- \(\mathbb {E}4:\) :
-
If \(A_I \preceq _{\tilde{\mathbb {U}}} B_I\) then \(A_I(x_i) \preceq _{\tilde{\mathbb {U}}} B_I(x_i)\). Based on \(\varPi 3\), it holds that \(\varPi (B_I(x_i)) \le _{\mathbb {U}} \varPi (A_I(x_i))\). By \(\mathbb {M}3\), we obtain that \(\mathbb {M}_{i=1}^n \varPi (B_I(x_i)) \le _{\mathbb {U}}\mathbb {M}_{i=1}^n \varPi (B_I(x_i))\). As conclusion, \(\mathbb {E}(A_I)\ge _{\mathbb {U}} \mathbb {E}(B_I)\).
Therefore, Theorem 2 is verified.
Proposition 5
Consider \(\chi = \{x_1, \ldots , x_n\}\). Let \(\mathbb {M}: \mathbb {U}^n \rightarrow \mathbb {U}\) be an IvA, \(\mathbb {N}\) be a strong IvFN and  is A-GIvIFIx(\(\mathbb {N}\)) given by Eq.(15). Then, for all \(x_i \in \chi \), an A-IvIFE \(\mathbb {E}: \mathcal {A}_I \rightarrow \mathbb {U}\) can be given by
is A-GIvIFIx(\(\mathbb {N}\)) given by Eq.(15). Then, for all \(x_i \in \chi \), an A-IvIFE \(\mathbb {E}: \mathcal {A}_I \rightarrow \mathbb {U}\) can be given by

Proof
Straightforward Theorems 1 and 2.
Corollary 4
Consider \(\mathbb {N}= \mathbb {N}_S\), A-GIvIFIx (\(\mathbb {N}_S\)) \(\varPi _{\mathbb {N, I}}\) given by Eq.(15). Then, by taking \(A_I(x_i)= (M_{A_I}(x_i), N_{A_I}(x_i)) = (X_{1i},X_{2i})\) for all \(x_i \in \chi \), an A-IvIFE \(\mathbb {E}: \mathcal {A}_I \rightarrow \mathbb {U}\) which is given in Eq.(23) can be expressed as

Proof
Straightforward Proposition 5 and Theorem 1.
Example 4
By taking the arithmetic mean as an aggregation operator, \(\mathbb {I_{RC}}\) in Eq.(4) and related IvIFIx given in Eq.(18). Let \(A_I\) be an IvIFS defined by pairs \((X_{1i},X_{2i}) \in \tilde{\mathbb {U}}\), for all \(x_i \in \chi \), an IvIFE as \(\mathbb {E}_{\varPi _{\mathbb {N}_S, \mathbb {I}_{RB}}}(X_{1i},X_{2i})= \frac{1}{n}\sum _{i=1}^n \mathbb {N}_S(\mathbb {I}_{RB} (\mathbb {N}_S(X_{2i}), X_{1i})\) can be given as follows:

4.1 Relationship with Intuitionistic Index and Conjugate Operators
Conjugation operator and duality properties related to generalized Atanassov’s Intuitionistic Fuzzy Index are reported from [10].
Proposition 6
Consider \(\chi = \{x_1, \ldots , x_n\}\) and \(\varPhi \in Aut(\tilde{\mathbb {U}})\) a \(\phi \)-representable A-IvIFA given by Eq.(13). When \(\varPi \) is \(A-GIvIFIx(\mathbb {N})\), an A-IvIFE is a function \(\mathbb {E}^{\varPhi }: \mathcal {A}_I \rightarrow \mathbb {U}\) defined by
Proof
Based on Eqs.(12) and (13), the following holds:
Figure 1 summarizes the main results related to the classes of A-GIvIFIx(\(\mathbb {N}\)) and A-IvIFE denoted by \(\mathcal {C}(\varPi )\) and \(\mathcal {C}(\mathbb {E})\), respectively. This A-IvIFE is obtained not only from generalized IvIFIx [4] but also from dual and conjugate operators.
Proposition 7
Let \(\varPhi \) be a \(\phi \)-representable automorphism in \(Aut(\tilde{\mathbb {U}})\) and \(\mathbb {I} (\mathbb {J}): \tilde{\mathbb {U}}^2 \rightarrow \tilde{\mathbb {U}}\) be the corresponding \(\phi \)-conjugate operator related to a (co)implication \(\mathbb {I} (\mathbb {J}): \mathbb {U}^2 \rightarrow \mathbb {U}\), verifying the conditions of Theorem 1. Additionally, let \(\mathbb {N}^{\varPhi }\) be a strong \(\phi \)-conjugate IvFN negation and \(\mathbb {M}: \mathbb {U}^n \rightarrow \mathbb {U}\) be an aggregation function. Then, for \(A \in \mathcal {A}\), the functions \(\mathbb {E}_{\mathbb {N,I}}, \mathbb {E}^{\varPhi }_{\mathbb {N,I}} (\mathbb {E}_{\mathbb {N,I}}, \mathbb {E}^{\varPhi }_{\mathbb {N,I}}): \mathcal {\mathbb {A}} \rightarrow \mathbb {U}\) given by
express an interval-valued Atanassov’s intuitionistic fuzzy entropy.
Proof
Straightforward from Proposition 6.
Example 5
By Eqs.(28) and (26), an IvIFE expression is obtained as follows:

4.2 Preserving Fuzzyness and Intuitionism Based on IvIFE
Based on [12], assuming that \(\chi = \{u\}\), \(A_1 = \{(u, [0.1, 0.2], [0.3, 0.4])\}\) and \(A_2 =\{(u, [0.2, 0.3], [0.4, 0.5])\}\) in order to calcule the entropies by equations below


Thus, \(\mathbb {E}(A_1)\) and \(\mathbb (E(A_2))\) contains the difference between the membership and non-membership degrees related to the hesitancy degree. However, despite the differences, the same value for related IvIFEs are matched, making impossible to distinguish the fuzziness and intuitionism of these two cases. Intuitively, it is easy to observe that \(A_1\) is more fuzzy than \(A_2\), meaning that \(\pi _{A_1} \ge \pi _{A_2}\). However, this cannot be seen by using the above Eqs.(33) and (34). So, a more sensitive definition of IvIFE is introduced in order to deal with this problem.
In our proposed methodology, we calculate the related IvIFEs by using Eqs.(26) and (32) together with corresponding IvIFIx given by Eqs.(18) and (22). See these results presented in 1st and 2nd columns of Table 1 when the inputs are given as \(A_1\) and \(A_2\). Since \(\chi \) is singleton IvIFS, the resulting hesitant degree and corresponding entropy measure coincide. Additionally, it is possible to naturally preserve properties of related interval entropy, meaning that IvIFE is an order preserving index, by including IFE. Moreover, taking \(A_3=[0.2, 0.2],[0.3, 0.3]\) and \(A_4 =[0.3, 0.3], [0.4, 0.4]\) as inputs, the entropy values obtained with the degenerate intervals related to membership and non-membership degrees are included in the interval entropy obtained with non-degenerated interval-valued inputs. See these results in the 3rd and 4th columns of Table 1.
5 Conclusion
The generalized concept of the Atanassov’s interval-valued intuitionistic fuzzy index was studied by dual and conjugate construction methods. We also extend the study of Atanassov’s intuitionistic fuzzy entropy based on such two constructors. Further work considers the extension of such study related to properties verified by the \(A-GIvIFIx(N)\) and \(A-IvIFE\) and also the use of admissible linear orders to compare the results of the interval entropy, since, in some cases, the values of interval entropy cannot be compared using the Moore’s method.
Notes
- 1.
We assume the componentwise addition on \(\mathbb {U}\), see [16].
References
Atanassov, K., Gargov, G.: Elements of intuitionistic fuzzy logic. Fuzzy Sets Syst. 95(1), 39–52 (1998)
Barrenechea, E., Bustince, H., Pagola, M., Fernàndez, J., Sanz, J.: Generalized Atanassov’s intuitionistic fuzzy index: construction method. In: Proceedings of IFSA EUSFLAT Conference, Lisbon, Portugal, pp. 20–24 (2009)
Bedregal, B., Santiago, R., Dimuro, G., Reiser, R.: Interval valued R-implications and automorphisms. In: Pre-Proceedings of the 2nd Workshop on Logical and Semantic Frameworks, with Applications, pp. 82–97 (2007)
Bustince, H., Burillo, P., Soria, F.: Automorphisms, negations and implication operators. Fuzzy Sets Syst. 134, 209–229 (2003)
Bustince, H., Montero, J., Barrenechea, E., Pagola, M.: Semiautoduality in a restricted family of aggregation operators. Fuzzy Sets Syst. 158, 1360–1377 (2007)
Bustince, H., Barrenechea, E., Pagola, M.: Generation of interval-valued fuzzy and Atanassov’s intuitionistic fuzzy connectives from fuzzy connectives and from \(K-\)alpha operators: laws for conjunctions and disjunctions, amplitude. Intell. Syst. 23, 680–714 (2008)
Bustince, H., Barrenechea, E., Pagola, M., Fernandez, J., Guerra, C., Couto, P., Melo-Pinto, P.: Generalized Atanassov’s intuitionistic fuzzy index: construction of Atanassov’s fuzzy entropy from fuzzy implication operators. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 19, 51–69 (2011)
Baczyński, M., Jayaram, B.: On the characterization of (S, N)-implications. Fuzzy Sets Syst. 158, 1713–1727 (2007)
Costa, C., Bedregal, B., Dória Neto, A.: Relating De Morgan triples with Atanassov’s intuitionistic De Morgan triples via automorphisms. Int. J. Approx. Reason. 52, 473–487 (2011)
Costa, L., Matzenauer, M., Zanottelli, R., Nascimento, M., Finger, A., Reiser, R., Yamin, A., Pilla, M.: Analysing fuzzy entropy via generalized Atanassov’s intuitionistic fuzzy indexes. Mathw. Soft Comput. 42, 22–31 (2017)
Cornelis, G., Deschrijver, G., Kerre, E.: Implications in intuitionistic fuzzy and interval-valued fuzzy set theory: construction, classification and application. Int. J. Approx. Reason. 35, 55–95 (2004)
Jing, L., Min, S.: Some entropy measures of interval-valued intuitionistic fuzzy sets and their applications. Adv. Model. Optim. 15, 211–221 (2013)
Lin, L., Xia, Z.: Intuitionistic fuzzy implication operators: expressions and properties. J. Appl. Math. Comput. 22, 325–338 (2006)
Luca, A., Termini, S.: A definition of nonprobabilistic entropy in the setting of fuzzy sets theory. Inf. Control 20, 301–312 (1972)
Miguel, L., Santos, H., Sesma-Sara, M., Bedregal, B., Jurio, A., Bustince, H.: Type-2 fuzzy entropy sets. IEEE Trans. Fuzzy Syst. 25, 993–1005 (2017)
Moore, E.: Interval arithmetic and automatic error analysis in digital computing. Stanford University (1962)
Reiser, R.H.S., Dimuro, G.P., Bedregal, B.C., Santiago, R.H.N.: Interval valued QL-implications. In: Leivant, D., de Queiroz, R. (eds.) WoLLIC 2007. LNCS, vol. 4576, pp. 307–321. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-73445-1_22
Reiser, R., Bedregal, B.: Correlation in interval-valued Atanassov’s intuitionistic fuzzy sets - conjugate and negation operators. Int. J. Uncertain. Fuzziness Knowl.Based Syst. 25, 787–820 (2017)
Zhang, Q., Xing, H., Liu, F., Ye, J., Tang, P.: Some new entropy measures for interval-valued intuitionistic fuzzy sets based on distances and their relationships with similarity and inclusion measures. Inf. Sci. 283, 55–69 (2014)
Acknowledgment
Work supported by the Brazilian funding agencies CAPES, MCTI/CNPQ, Universal (448766/2014-0), PQ (310106/2016-8), CNPq/PRONEX/FAPERGS and PqG 02/2017.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Costa, L., Matzenauer, M., Yamin, A., Reiser, R., Bedregal, B. (2018). Interval Version of Generalized Atanassov’s Intuitionistic Fuzzy Index. In: Barreto, G., Coelho, R. (eds) Fuzzy Information Processing. NAFIPS 2018. Communications in Computer and Information Science, vol 831. Springer, Cham. https://doi.org/10.1007/978-3-319-95312-0_19
Download citation
DOI: https://doi.org/10.1007/978-3-319-95312-0_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-95311-3
Online ISBN: 978-3-319-95312-0
eBook Packages: Computer ScienceComputer Science (R0)




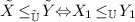 and
and  ;
;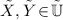 ;
;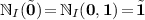 and
and 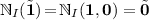 ;
;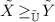 then
then 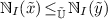 .
.