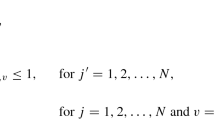Online Interval Scheduling to Maximize Total Satisfaction

Abstract

The interval scheduling problem is one variant of the scheduling problem. In this paper, we propose a novel variant of the interval scheduling problem, whose definition is as follows: given jobs are specified by their release times, deadlines and profits. An algorithm must start a job at its release time on one of m identical machines, and continue processing until its deadline on the machine to complete the job. All the jobs must be completed and the algorithm can obtain the profit of a completed job as a user’s satisfaction. It is possible to process more than one job at a time on one machine. The profit of a job is distributed uniformly between its release time and deadline, that is its interval, and the profit gained from a subinterval of a job decreases in reverse proportion to the number of jobs whose intervals intersect with the subinterval on the same machine. The objective of our variant is to maximize the total profit of completed jobs.

This formulation is naturally motivated by best-effort requests and responses to them, which appear in many situations. In best-effort requests and responses, the total amount of available resources for users is always invariant and the resources are equally shared with every user. We study online algorithms for this problem. Specifically, we show that for the case where the profits of jobs are arbitrary, there does not exist an algorithm whose competitive ratio is bounded. Then, we consider the case in which the profit of each job is equal to its length, that is, the time interval between its release time and deadline. For this case, we prove that for $m = 2$ and $m \ge 3$, the competitive ratios of a greedy algorithm are at most 4 / 3 and at most 3, respectively. Also, for each $m \ge 2$, we show a lower bound on the competitive ratio of any deterministic algorithm.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The interval scheduling problem is one of the variants of the scheduling problem, which has been widely studied. One of the most basic definitions is as follows: We have $m \ge 1$ identical machines and jobs are given. A job is characterized by the release time, deadline and weight (or value). To complete a job, we must start to process it at its release time on a machine of the m machines, and continue processing it until its deadline on that machine. That is, the processing time (or length) of the job is the time interval between its release time and deadline. The number of jobs which can be processed on one machine at a time is at most one. The objective of an algorithm is to maximize the total weight of completed jobs. There are many applications of the interval scheduling problem, such as bandwidth allocation and vehicle assignment (see e.g., [13, 14]). Many variants of this problem have been proposed and extensively studied. Furthermore, research on online settings has also been considered. In an online variant of the interval scheduling problem, a job arrives at its release time and an online algorithm must decide whether it processes the job before the next job arrives. The performance of online algorithms is evaluated using competitive analysis [3, 19]. For any input, if the total weight gained by an optimal offline algorithm is at most c times that gained by an online algorithm, the online algorithm is c-competitive.

In this paper, we introduce a novel variant of the interval scheduling problem. In many existing variants of the interval scheduling problem, jobs (or users) require resources for an algorithm, and the algorithm assigns the required resources of a machine to the job. Thus, the number of jobs assigned to one machine at a time is subject to the maximum amount of resources of the machine. The amount is generally one; that is, at most one job can be processed at a time on one machine in most variants. Therefore, we can regard such existing variants as formulating resource reservation requests by users, who designate the amount of resources they want to use in advance and the responses to them. However, it is not always possible for users to designate the amount of resources they want when they issue requests. Additionally, there are not necessarily sufficient resources of a machine to meet users’ requests. Thus, we focus on a best-effort method to manage situations, which is often considered paired with resource reservation methods. In this method, the amount of resources of a machine is always invariant and the resources are equally shared by users who want to use the resources at the same time. Then, we formulate best-effort requests and responses to them as a variant of the interval scheduling problem. Specifically, we remove the capacity constraints from machines in our variant, which makes it possible to assign jobs unlimitedly on one machine at a time. To the best of our knowledge, this is the first such formulation of the interval scheduling problem. Consider a given job as a user’s request. If a machine processes the request using sufficient resources, the user is sufficiently satisfied with the result obtained from the process. Conversely, if there are not sufficient resources to process the request, the user is less satisfied with the result than usual. Then, the objective of our variant is to maximize the total satisfaction gained by users. Bandwidth allocation in networks is one of the most suitable examples for best-effort requests and responses. In this example, the total bandwidth which may be supplied to users on the same communication link is fixed in advance, and all users share the bandwidth. Hence, the fewer users which use the communication link at a time, the greater the bandwidth which each one can use, which means that the effective speed of the communication link is higher for the users. Conversely, the more people there are using link simultaneously, the lower the effective speed for each user. As a result, if the bandwidth for a user is high, then the user’s satisfaction is high. Otherwise, it is low. Best-effort requests and responses such as bandwidth allocation could happen in many cases, for example, the use of facilities, such as swimming pools and gyms, passenger trains without reservations, and buffet style meals. Therefore, we have sufficient incentives to study our variant.

Our Results. In this paper, we propose and analyze a novel variant of the interval scheduling problem. We study online algorithms for this problem. Specifically, in the case where the profits of jobs are arbitrary; that is, the profits are not relevant to the lengths of jobs, we show that the competitive ratio of any deterministic algorithm is unbounded. Then, we introduce the profits of jobs are equal to their lengths, which is a more natural case, called the uniform profit case. In this case, the total amount of time during which at least one job is scheduled on a machine is equal to the total amount of the satisfaction gained on the machine. That is, the objective of this case can be regarded as maximizing the working hours of all the machines. We analyze the performance of a greedy algorithm GR in this case. Since GR is a significant algorithm from a practical point of view, it is worthwhile to evaluate its performance. When $m = 2$ and $m \ge 3$, we show that the competitive ratios of GR are at most 4 / 3 and at most 3, respectively. When $m = 2$, we prove that a lower bound on the competitive ratio of GR is 4 / 3. That is, for $m = 2$, our analysis of GR is tight. Also, we show lower bounds of any deterministic online algorithms for each $m \ge 2$, which are summarized in Tables 1 and 2 in Sect. 5.

Table 1. Our results

Related Results. Much research on the interval scheduling problem has been conducted. Arkin and Silverberg [1] and Bouzina and Emmons [4] provided polynomial time algorithms to solve the interval scheduling problem.

There is also much research on online interval scheduling problems. If an online algorithm aborts a job J which was placed on a machine, then we say that the algorithm preempts J. In the case in which preemption is allowed, Faigle and Nawijn [9] designed a 1-competitive algorithm to maximize the number of completed jobs. This algorithm was independently discovered by Carlisle and Lloyd [6] but used only for the offline setting. Moreover, for the variant in which the objective is to maximize the total weight of completed jobs, Woeginger [20] showed that no any competitive deterministic algorithm exists (even) for $m=1$. Canetti and Irani [5] provided a randomized online algorithm whose competitive ratio is $O(\log \varDelta )$ and proved that a lower bound on the competitive ratio of any randomized algorithm is $\varOmega ( \sqrt{ \log \varDelta /\log \log \varDelta } )$, where $\varDelta$ is the ratio of the longest length to the shortest length. This result indicates that the competitive ratio of an online algorithm may become worse depending on a given input even if it is supported by randomization. Additionally, the setting in which the jobs are unit length has been extensively studied. For the one machine setting, Woeginger [20] designed a deterministic algorithm whose competitive ratio is at most 4 and showed that this is the best possible ratio. There has also been much work regarding randomized algorithms (e.g. [8, 10,11,12, 16, 18]). When $m=1$, the current best upper and lower bounds on the competitive ratios of randomized algorithms are 2 by Fung et al. [12] and $1 + \ln 2 \ge 1.693$ by Epstein and Levin [8], respectively. For $m \ge 2$, Fung et al. [11] proved that, if m is even, an upper bound is 2, and otherwise $2 + 2/(2m-1)$. However, for $m = 2$, the current best lower bound is 2 by Fung et al. [10]. When each $m \ge 3$, Fung et al. [11] indicated that we can obtain a lower bound of $1 + \ln 2 \ge 1.693$ in a similar manner to the lower bound of Epstein and Levin [8]. If preemption is not allowed, Lipton and Tomkins [15] proposed a randomized algorithm whose competitive ratio is $O((\log \varDelta )^{1+\epsilon })$ and proved that a lower bound of any randomized algorithms is $\varOmega (\log \varDelta )$.

For a job given in the interval scheduling problem, its length is equal to the length of the time between its release time and deadline. On the other hand, a variant in which the job length is generalized has also been studied. Specifically, a parameter slack $\varepsilon > 0$ is introduced, whose value is known to an algorithm in advance, and the length of a job is at most x times as long as the length of the time between its release time and deadline, in which $x = 1/(1 + \varepsilon )$. In this variant, preemption is allowed and to complete a job, an algorithm must process it during its length by its deadline after its release time. For several m, optimal online algorithms were designed [2, 7, 17], whose competitive ratios are $1 + 1/\varepsilon$.

2 Model Description

We have $m (\ge 2)$ identical machines. A list consisting of $n (\ge 1)$ jobs is provided as an input. A job J is specified by a triplet (r, d, v), where r(J) is the release time of J, d(J) is the deadline of J, and v(J) is the profit of J. An algorithm ALG must place each job onto one of the m machines. It is possible to place more than one job at a time on one machine. The profit of a job is distributed uniformly between its release time and deadline, that is its interval, and the profit gained from a subinterval of a job decreases in reverse proportion to the number of jobs whose intervals intersect with the subinterval on the same machine. Specifically, the profit from the subinterval is defined as follows: For an algorithm ALG, if the numbers of jobs placed at any two points in an interval $(x, y) (x < y)$ are equal on ALG’s $a (\in [1, m])$th machine and (x, y) does not contain any endpoint of the interval of a job placed on the machine after processing of the input, then we call the interval a P-interval on ALG’s ath machine. Also, let $k_{ALG}(a, x, y)$ denote the number of the jobs. If an algorithm ALG places a job J onto the ath machine, then we define $m_{ALG}(J) = a$. For an algorithm ALG and a job J, suppose that the interval (r(J), d(J)) consists of $b (\ge 1)$ P-intervals $(x_{i}, x_{i+1}) (i = 1, \ldots , b-1)$ on ALG’s $m_{ALG}(J)$th machine such that $r(J) = x_1< x_2< \cdots < x_b = d(J)$. Then, we define the satisfaction (profit) which is yielded from $[x_{i}, x_{i+1}]$ of J and ALG gains as

$$ V_{ALG}(J, i) = \frac{ x_{i+1} - x_{i} }{ d(J) - r(J) } \frac{ v(J) }{ k_{ALG}(m_{ALG}(J), x_{i}, x_{i+1}) }. $$

We define the satisfaction (profit) of J gained by ALG as

$$ V_{ALG}(J) = \sum _{ i = 1 }^{ b-1 } V_{ALG}(J, i). $$

The profit of ALG for an input $\sigma$ is defined as

$$ V_{ALG}(\sigma ) = \sum _{ J \in \mathcal{L} } V_{ALG}(J), $$

where $\mathcal{L}$ is a list consisting of the n given jobs. The objective is to maximize the total satisfaction of the n jobs.

In this paper, we consider an online variant of this problem. Specifically, n jobs are given one by one. The jobs are not necessarily given in order of release time. An online algorithm must place a given job to a machine before the next job is given. Once a job is placed on a machine, it cannot be removed later. That is, preemption is not allowed. The total number n of given jobs is not known to the online algorithm, and it does not require this information until after all the jobs arrive. We say that the competitive ratio of an online algorithm A is at most c or A is c-competitive if, for any input, the profit gained by an offline optimal algorithm OPT is at most c times the profit gained by A.

3 General Profit Case

Due to page limitations, we omit almost all of the proofs in this paper. The full version of this paper is available at https://arxiv.org/abs/1805.05436.

In this section, we consider the case in which the profits of jobs are arbitrary. First, we consider the case $m=2$ for better understanding of any $m \ge 3$.

Theorem 1

When $m = 2$, there does not exist any deterministic online algorithm whose competitive ratio is bounded.

Theorem 2

For any m, there does not exist a competitive deterministic algorithm.

4 Upper Bounds for Uniform Profit Case

In this section, we consider the uniform profit case, that is, the case in which the profit of a job is equal to its length. In this case, the total amount of time during which at least one job is scheduled on a machine is equal to the total amount of the satisfaction gained on the machine. That is, the objective of this case can be regarded as maximizing the working hours of all the machines.

4.1 Preliminaries

After the end of the input, we need to evaluate the profit from each job by OPT using the profits yielded from intervals of jobs scheduled by GR to analyze the performance of GR. Then, we classify intervals (or points) in a job J by GR or OPT into the following four categories depending on the behaviors of GR and OPT for J.

For any two intervals $I = [t_{1}, t_{2}]$ and $I' = [t'_{1}, t'_{2}]$, we say that I intersects with $I'$ if $t'_{1} < t_{2}$ and $t_{1} < t'_{2}$. For any job J, we call the interval [r(J), d(J) ] the interval of J. If an algorithm ALG places two jobs onto the same machine and they intersect, then we say that they overlap. For any interval $I = [t, t']$, we call the value of $t' - t$ the length of I, written as |I|.

We give the definition of a greedy algorithm GR and analyze its performance in this section. GR places a given job J onto the machine on which GR gains the largest profit from J. The tie-breaking rule selects the minimum indexed machine.

For ease of analyzing, we introduce the following idea. Suppose that two jobs $J_1$ and $J_2$ are placed onto the same machine, and they overlap in an interval I. Also, suppose that $J_1$ is the first job placed in I on the machine. Then, pretend that the profits from I of $J_{1}$ and $J_{2}$ are |I| and zero, respectively. That is, we pretend that a job which is placed chronologically first in an interval on a machine monopolizes the machine power in the interval. Note that in the uniform profit case, the total profit gained from an interval of jobs placed on a machine depends not on how large the number of the jobs in the interval is but on whether there exists at least one job placed in the interval. That is why this assumption does not affect the profit of any algorithm.

4.2 Overview of Analysis

To evaluate the performance of GR, that is, its competitive ratio, we bound the profit of OPT at the end of the input using that of GR. Then, we classify intervals of jobs placed by either GR or OPT into four categories.

For any job J and any interval $I \subseteq [ r(J), d(J) ]$, if the profit gained from I of J by GR is zero and that by OPT is |I|, then we call I of J an OPT extra interval of J (denoted as an oe-interval, for short). Also, if the profit gained from I of J by OPT is zero and that by GR is |I|, then we call I of J a GR extra interval of J (a ge-interval, for short). If the profits gained from I of J by GR and OPT are both |I|, we call I of J a common interval of J (a c-interval, for short). For ease of presentation, we call an interval which is a c-interval or a ge-interval a profit interval (a p-interval, for short). If the profits gained from I of J by GR and OPT are both zero, we call I of J a non-profit interval of J (an n-interval, for short). Further, we call a point in an oe-interval (a ge-interval, a c-interval, and a p-interval, respectively) of J an oe-fraction (a ge-fraction, a c-fraction, and a p-fraction, respectively) of J.

We evaluate the competitive ratio of GR by “assigning” p-fractions (i.e., p-intervals) to all oe-fractions (i.e., oe-intervals) according to a routine, which is defined later. This “assignment” is realized by some functions. Let $V_{oe}(\sigma )$ be the total length of oe-intervals to which c-intervals are assigned. Let $V_{oe'}(\sigma )$ be the total length of oe-intervals to which ge-intervals are assigned. Also, let $V_{c}(\sigma )$ be the total length of c-intervals and $V_{ge}(\sigma )$ be the total length of ge-intervals. Then, we have by definition,

$$\begin{aligned} V_{GR}(\sigma ) = V_{c}(\sigma ) + V_{ge}(\sigma ) \end{aligned}$$

(1)

and

$$\begin{aligned} V_{OPT}(\sigma ) = V_{c}(\sigma ) + V_{oe}(\sigma ) + V_{oe'}(\sigma ). \end{aligned}$$

(2)

We will show the following three properties of the assignments by the routine:

1. :

Each oe-fraction is assigned a p-fraction,

2. :

a c-fraction of a job given to GR is assigned at most twice, and

3. :

a ge-fraction is assigned at most three times.

To show these, we will construct sequentially three functions $M_{1},M_{2}$ and $M_{3}$ from oe-intervals to p-intervals satisfying the following properties: Initially, for any oe-fraction f and any $i \in \{ 1, 2, 3 \}$, $M_{i}(f) = \varnothing$. At the end of the input, for any oe-fraction f, $M_{1}(f) \cup M_{2}(f) \cup M_{3}(f) \ne \varnothing$. There exists a p-fraction $f'$ such that $M_{1}(f) = f'$ if $M_{1}(f) \ne \varnothing$. There exists a ge-fraction $f'$ such that $M_{2}(f) = f'$ if $M_{2}(f) \ne \varnothing$. There exists a p-fraction $f'$ such that $M_{3}(f) = f'$ if $M_{3}(f) \ne \varnothing$. For any oe-fractions f and $f'(\ne f)$ and any $i \in \{ 1, 2, 3 \}$, $M_{i}(f) \cap M_{i}(f') = \varnothing$. Then, we have by these functions,

$$\begin{aligned} V_{oe}(\sigma ) \le 2 V_{c}(\sigma ) \end{aligned}$$

(3)

and

$$\begin{aligned} V_{oe'}(\sigma ) \le 3 V_{ge}(\sigma ). \end{aligned}$$

(4)

By Eq. (2), we have

$$\begin{aligned} V_{OPT}(\sigma )= & {} V_{c}(\sigma ) + V_{oe}(\sigma ) + V_{oe'}(\sigma ) \\\le & {} V_{c}(\sigma ) + 2 V_{c}(\sigma ) + 3 V_{ge}(\sigma ) \qquad \text {(by Eqs. (3) and (4))}\\= & {} 3 (V_{c}(\sigma ) + V_{ge}(\sigma )) = 3 V_{GR}(\sigma ), \qquad \text {(by Eq. (1))} \\ \end{aligned}$$

which leads to the following theorem:

Theorem 3

For any $m \ge 2$, the competitive ratio of GR is at most three.

4.3 Analysis of GR

For any job J and any point $t \in [ r(J), d(J) ]$, let E(J, t) denote the total length of oe-intervals of J in the interval [r(J), t]. For any job J, any job $J'$ given before J, any interval $[ t_{1}, t_{2} ]$ and any $a (\in [1, m])$, let $P_{a}(J, J', t_{1}, t_{2})$ denote the total length of p-intervals of GR’s jobs placed on the ath machine which are in $[ t_{1}, t_{2} ]$ immediately after J is placed and are not intersecting with any n-interval of $J'$. For any $a (\in [1, m])$, any job J, any job $J'$ given before J, and any point $t \in [ r(J'), d(J') ]$, define $h_{a}(J, J', t) = t'$ in which $t'$ is the point such that $P_{a}( J, J', r(J'), t' ) = E(J', t)$ and $t' \in [ r(J'), d(J') ]$ immediately after J is placed onto the machine. ($t'$ exists by Lemma 1, which is shown later.) For any $i \in \{ 1, 2, 3 \}$ and any p-fraction $f'$, define $M^{-1}_{i}(f') = \{ f \mid M_{i}(f) = f' \}$. We say that a c-fraction $f'$ such that $M_{1}^{-1}(f') = \varnothing$ is 1-assignable. We say that a ge-fraction $f'$ such that $M_{2}^{-1}(f') = \varnothing$ is 2-assignable. We say that a ge-fraction $f'$ such that $M_{2}^{-1}(f') \ne \varnothing$ and $M_{1}^{-1}(f') = \varnothing$ is 1-assignable. If a p-fraction is 1-assignable or 2-assignable, we say that it is assignable. Now we give the definition of the routine mentioned in the previous section.

In the following, we first show the existence of $t_{a}$ in Case 2.2. Next, we show that there exists $p_{a}$ in Case 2.2. That is, we prove that the routine can assign a p-fraction to each oe-fraction.

Lemma 1

For any $a (\in [1, m])$, any job J, any job $J'$ which is given before J, and any point $t \in [ r(J'), d(J') ]$, there exists the point $t'$ such that $h_{a}(J, J', t) = t'$ and $t' \in [ r(J'), d(J') ]$ immediately after J is placed.

Lemma 2

Case 2.2 is executable. That is, when Case 2.2 is executed for an oe-fraction f, f can be assigned a p-fraction $f_{a}$ such that $M^{-1}_{3}(f_{a}) = \varnothing$ immediately before executing Case 2.2.

4.4 Upper Bound for $m = 2$

When $m = 2$, we also evaluate the competitive ratio of GR by assigning p-fractions to all oe-fractions. In this case, we obtain a better upper bound on the competitive ratio of GR than one for general m by implementing more detailed assignments. If the routine assigns one ge-fraction to one oe-fraction, we say that the routine ge-assigns the ge-fraction to the oe-fraction. Also, if the routine assigns three p-fractions to one oe-fraction, we say that the routine 3p-assigns each of the p-fractions to the oe-fraction. We will show the following three properties by the assignments according to the routine defined later:

1. :

Each oe-fraction is ge-assigned or 3p-assigned,

2. :

a c-fraction of a job given to GR is 3p-assigned at most once, and

3. :

a ge-fraction is ge-assigned at most once and is 3p-assigned at most once.

We will show them by sequentially constructing two functions $N_{1}$ and $N_{2}$ from oe-intervals to p-intervals satisfying the following properties: Initially, for any oe-fraction f and any $i \in \{ 1, 2 \}$, $N_{i}(f) = \varnothing$. At the end of the input, for any oe-fraction f, $N_{1}(f) \cup N_{2}(f) \ne \varnothing$. There exist three distinct p-fractions $f_{1}, f_{2}$ and $f_{3}$ such that $N_{1}(f) = \{ f_{1}, f_{2}, f_{3} \}$ if $N_{1}(f) \ne \varnothing$. There exists a ge-fraction $f'$ such that $N_{2}(f) = f'$ if $N_{2}(f) \ne \varnothing$. For any oe-fractions f and $f'(\ne f)$ and any $i \in \{ 1, 2 \}$, $N_{i}(f) \cap N_{i}(f') = \varnothing$. Let $V_{\overline{oe}}(\sigma )$ denote the total length of oe-intervals to which the routine 3p-assigns, and let $V_{\overline{oe'}}(\sigma )$ denote the total length of oe-intervals to which the routine ge-assigns. Thus,

$$ V_{\overline{oe}}(\sigma ) \le V_{GR}(\sigma ) / 3 $$

and

$$ V_{\overline{oe'}}(\sigma ) \le V_{ge}(\sigma ). $$

Then, using these inequalities, we have

$$\begin{aligned} V_{OPT}(\sigma )= & {} V_{c}(\sigma ) + V_{\overline{oe}}(\sigma ) + V_{\overline{oe'}}(\sigma ) \\\le & {} V_{c}(\sigma ) + V_{GR}(\sigma ) / 3 + V_{ge}(\sigma ) = \frac{4}{3} V_{GR}(\sigma ). \end{aligned}$$

Therefore, we have the following theorem:

Theorem 4

When $m = 2$, the competitive ratio of GR is at most 4 / 3.

For any $i \in \{ 1, 2 \}$ and any p-fraction $f'$, define $N^{-1}_{i}(f') = \{ f \mid N_{i}(f) = f' \}$. We say that a p-fraction $f'$ is 1-assignable if $N_{1}^{-1}(f') = \varnothing$. Also, we say that a ge-fraction $f'$ is 2-assignable if $N_{2}^{-1}(f') = \varnothing$. Now we give the definition of the routine to construct the above two functions.

Lemma 3

Case 2.2 is executable. That is, when Case 2.2 is executed for an oe-fraction f, f can be assigned 3 p-fractions (i.e., 3p-assigned) each of which is 1-assignable immediately before executing Case 2.2.

We show that our analysis of GR for $m = 2$ is tight in the following theorem.

Theorem 5

When $m = 2$, for any $\varepsilon > 0$, the competitive ratio of GR is at least $4/3 - \varepsilon$.

5 Lower Bounds for Uniform Profit Case

In this section, we show lower bounds on the competitive ratios of online algorithms for the uniform profit case. For better understanding, we first consider the case of $m=2$.

Theorem 6

When $m = 2$, the competitive ratio of any deterministic online algorithm is at least $(10 - \sqrt{2}) / 7 \ge 1.226$.

Proof

Consider an online algorithm ON. The first given job is $J_1$ such that $r(J_1) = 0$ and $d(J_1) = 1$. The second job is $J_2$ such that $r(J_2) = 1+x$ and $d(J_2) = 2+x$. Note that x is set later. Without loss of generality, we may assume that both ON and OPT place $J_1$ onto the first machine.

In the following, we use two inputs. First, we consider the case where ON places $J_1$ and $J_2$ on two different machines. That is, suppose that ON places $J_{2}$ on the second machine. Then, the third job $J_3$ such that $r(J_3) = 0$ and $d(J_3) = 2 + x$ is given, and no further job arrives. We call this input $\sigma _1$. If ON places $J_3$ onto the first machine, we have $V_{ON}(\sigma _1) = 2 + x + 1 = 3 + x$. ON also gains the same profit if ON places $J_3$ onto the second machine. On the other hand, the machine onto which OPT places both $J_1$ and $J_2$ is different from that onto which $J_3$ is placed. Thus, $V_{OPT}(\sigma _1) = 2 + 2 + x = 4 + x$. By the above argument,

$$\begin{aligned} \frac{ V_{OPT}(\sigma _1) }{ V_{ON}(\sigma _1) } = \frac{ 4 + x }{ 3 + x }. \end{aligned}$$

(5)

Second, we consider the case where ON places $J_1$ and $J_2$ onto the first machine. The third job $J'_1$ such that $r(J'_1) = 1 - y$ and $d(J'_1) = 1 + x$ and the fourth job $J'_2$ such that $r(J'_2) = 1$ and $d(J'_2) = 1 + x + y$ are given, where y is fixed later. No further job is given; we call this input $\sigma _2$. We first consider the case where ON places $J'_1$ and $J'_2$ on different machines. If $J'_1$ is placed onto the first machine, on which $J_1$ and $J_2$ are placed,

$$\begin{aligned} V_{ON}(\sigma _2) = 1 + x + 1 + x + y = 2 + 2x + y. \end{aligned}$$

(6)

ON gains the same profit if $J'_2$ is placed onto the first machine. Next, we consider the case in which ON places $J'_1$ and $J'_2$ onto the machine. If the machine is the second one, then it is clear that ON gains larger profits than it does in the other case. Hence,

$$\begin{aligned} V_{ON}(\sigma _2) = 2 + x + 2y. \end{aligned}$$

(7)

Now, set $y = x$ and we have $V_{ON}(\sigma _2) = 2 + 3x$ by Eqs. (6) and (7). On the other hand, OPT places both $J_1$ and $J'_2$ onto the first machine and both $J_2$ and $J'_1$ onto the second machine. Thus, $V_{OPT}(\sigma _2) = 2 (1 + x + y) = 2 + 4x$. By the above argument,

$$\begin{aligned} \frac{ V_{OPT}(\sigma _2) }{ V_{ON}(\sigma _2) } = \frac{ 2 + 4x }{ 2 + 3x }. \end{aligned}$$

(8)

Therefore, by Eqs. (5) and (8),

$$ \frac{ V_{OPT}(\sigma ) }{ V_{ON}(\sigma ) } \ge \min \left\{ \frac{ 4 + x }{ 3 + x }, \frac{ 2 + 4x }{ 2 + 3x } \right\} = \frac{ 4 + \sqrt{2} }{ 3 + \sqrt{2} } = \frac{ 10 - \sqrt{2} }{ 7 }, $$

where we choose $x = \sqrt{2}$.

The following theorem provides lower bounds for $m \ge 3$ by generalizing the input used to prove Theorem 6.

Theorem 7

The competitive ratio of any deterministic algorithm is at least 1.101. It is better for fixed m and then refer to Table 2 for details.

Table 2. Lower bounds for each $m(\ge 3)$.