6.1 Introduction

Partial differential eigenvalue problems arise in a wide variety of applications, for example the vibration of elastic bodies (structural vibration) or multi-group diffusion in nuclear reactors [58]. Finite element analysis of these differential eigenvalue problems leads to the matrix eigenvalue problem with the entries of the matrices which are usually approximated by numerical integration. The effect of these numerical integration methods on the eigenvalue and eigenfunction errors has been investigated in the literature; see for example Fix [29], Strang and Fix [58], and others [8,9,10]. Sharp and optimal estimates of the numerical eigenfunctions and eigenvalues of finite element analysis are established in [8, 9].

Hughes et al. [41] unified the analysis of the spectrum properties of the eigenvalue problem with the dispersion analysis for wave propagation problems. They established a duality principle between them: any numerical scheme that reduces the dispersion error of the wave propagation problems reduces the eigenvalue errors of the different eigenvalues problems and vice versa. Moreover, they share the same convergence property in the sense of convergence rates [15, 43, 54]. In this work, we focus on developing quadrature rules to optimize the dispersion errors and then apply these rules to the approximation of differential eigenvalue problems.

The dispersion analysis of the finite element method and spectral element method has been studied extensively; see for example Thomson and Pinsky[59, 60], Ihlenburg and Babuska [44], Ainsworth [1,2,3], and many others [23, 28, 35,36,37,38, 45, 46, 63]. Thomson and Pinsky studied the dispersive effects of using the Legendre, spectral, and Fourier local approximation basis functions for finite element methods when applied to the Helmholtz equation [59]. The choice of the basis functions has a negligible effect on the dispersion errors. Nevertheless, the continuity of the basis functions has a significant impact. Hughes et al. [41] showed that high continuities (up to C p−1 for p-th order isogeometric elements) on the basis functions result in dramatically smaller dispersion errors than that of finite elements.

Ainsworth [1] and [2] established that the optimal convergence rate, which is of order 2p, of the dispersion error for the p-th order standard finite elements and spectral elements, respectively. The work was complete as they established the analysis for arbitrary polynomial order. The dispersive properties of these methods have been studied in detail and the most effective scheme was conjectured to be a mixed one of these two [3, 49, 56]. Ainsworth and Wajid beautifully established the optimal blending of these two methods for arbitrary polynomial order in 2010 in [3]. The blending was shown to provide two orders of extra accuracy (superconvergence) in the dispersion error, which includes the fourth order superconvergence result obtained by a modified integration rule for linear finite elements in [35]. Also, this blending scheme is equivalent to the use of nonstandard quadrature rules and therefore it can be efficiently implemented by replacing the standard Gaussian quadrature by a nonstandard rule [3].

This blending idea can be extended to isogeometric analysis (IGA), a numerical method that bridges the gap between computer aided design (CAD) and finite element analysis (FEA). We refer to [13, 19, 21, 40] for its initial development and to [20, 26, 33, 34, 41,42,43, 47, 48, 50] for its applications. The feature that distinguishes isogeometric elements from finite and spectral elements is the fact that the basis functions have up to p − 1 continuous derivatives across element boundaries, where p is the order of the underlying polynomial. The publications [4, 19, 20, 41,42,43, 55] show that highly continuous isogeometric analysis delivers more robustness and better accuracy per degree of freedom than standard finite elements. Nevertheless, a detailed analysis of the solution cost reveals that IGA is more expensive to solve on a per degree of freedom basis than the lower continuous counterparts, such as finite element analysis [16,17,18, 52]. To exploit the reduction in cost, a set of solution strategies which control the continuity of the basis functions to deliver optimal solution costs were proposed [31, 32].

The dispersion analysis of isogeometric elements is studied in [41, 43, 54], presenting significant advantages over finite elements. Hughes et al. [41] showed that the dispersion error of the isogeometric analysis with high continuity (up to C p−1 for p-th order basis function) on the basis functions is smaller than that of the lower continuity finite element counterparts. Dedè et al. [24] study the dispersion analysis of the isogeometric elements for the two-dimensional harmonic plane waves in an isotropic and homogeneous elastic medium. The anisotropic curves are represented using NURBS-based IGA and the errors associated with the compressional and shear wave velocities for different directions of the wave vector are modeled. Recently, the dispersion error minimization for isogeometric analysis has been performed numerically in Puzyrev et al. [54] and analytically in Calo et al. [15].

In this work, we seek blending quadrature rules for isogeometric element to minimize the dispersion error of the scheme and hence increase its accuracy and robustness. We focus on the dispersion analysis of isogeometric elements and apply the blending ideas introduced by [3] for finite and spectral elements to isogeometric elements by using a modified inner product. The new blending schemes reduce the errors in the approximation of the eigenvalues (and, in some cases, the eigenfunctions). Using the optimal blending, convergence rates of the dispersion error is increased by two additional orders. To analyze the errors, we characterize the errors in the eigenvalues and the eigenfunctions for all the modes. The total “error budget” of the numerical method consists of the errors arising from the approximation of eigenvalues and eigenfunctions. When the stiffness and mass terms are fully integrated, for each eigenvalue, the sum of the eigenvalue error and the square of the eigenfunction error in the L 2-norm scaled by the exact eigenvalue equals the square of the error in the energy norm. Once one of these terms are not fully integrated, this is not true any more. To account for the error of the approximated/modified inner product, we generalize Strang’s Pythagorean eigenvalue theorem to include the effect of inexact integration.

The outline of the remainder of this chapter is as follows. We first describe the model problem in Sect. 6.2. In Sect. 6.3, we present a generalization of the Pythagorean eigenvalue error theorem that accounts for the error of the modified inner products. In Sect. 6.4, we describe the optimal blending of finite and spectral elements and present an optimal blending scheme for isogeometric analysis. In Sect. 6.5, we develop a two-point quadrature rule for periodic boundaries. Numerical examples for one-dimensional and two-dimensional problems are given in Sect. 6.6. Finally, Sect. 6.7 summarizes our findings and describes future research directions.

6.2 Problem Setting

We begin with the differential eigenvalue problem

$$\displaystyle \begin{aligned} \begin{aligned} - \varDelta u & = \lambda u \quad \text{in} \quad \varOmega, \\ u & = 0 \quad \text{on} \quad \partial \varOmega, \end{aligned} \end{aligned} $$
(6.1)

where Δ = ∇2 is the Laplacian and \(\varOmega \subset \mathbb {R}^d, d=1,2,3\) is a bounded open domain with Lipschitz boundary. This eigenvalue problem has a countable infinite set of eigenvalues \({\lambda _j} \in {\mathbb {R}}\)

$$\displaystyle \begin{aligned} 0 < {\lambda _1} \le {\lambda _2} \le \cdots \le {\lambda _j} \le \cdots \end{aligned} $$
(6.2)

and an associated set of orthonormal eigenfunctions u j

$$\displaystyle \begin{aligned} ({u_j},{u_k}) = \int_{\varOmega} {{u_j}(x){u_k}} (x) \ \text{d} x = {\delta _{jk}}, \end{aligned} $$
(6.3)

where δ jk is the Kronecker delta which is equal to 1 when i = j and 0 otherwise (see for example [58]). The normalized eigenfunctions form an L 2-orthonormal basis. Moreover, using integration by parts and (6.1), they are orthogonal also in the energy inner product

$$\displaystyle \begin{aligned} (\nabla {u_j}, \nabla {u_k}) = (-\varDelta {u_j}, {u_k}) = ({\lambda _j}{u_j},{u_k}) = {\lambda _j} ({u_j},{u_k}) = {\lambda _j}{\delta _{jk}}. \end{aligned} $$
(6.4)

Let V  be the solution space, a subspace of the Hilbert space \({{H^1_0}(\varOmega )}\). The standard weak form for the eigenvalue problem: Find all eigenvalues \({\lambda _j} \in {\mathbb {R}}\) and eigenfunctions u j ∈ V  such that,

$$\displaystyle \begin{aligned} a({u_j}, w) = {\lambda _j}({u_j}, w), \quad \forall \ w \in V \end{aligned} $$
(6.5)

where

$$\displaystyle \begin{aligned} a(w,v) = \int_{\varOmega} \nabla w \cdot \nabla v \ \text{d}x, \end{aligned} $$
(6.6)

and (⋅, ⋅) is the L 2 inner product. These two inner products are associated with the following energy and L 2 norms

$$\displaystyle \begin{aligned} \left\| w \right\|{}_E = \sqrt{a(w,w)}, \quad \left\| w \right\| = \sqrt{(w,w)}. \end{aligned} $$
(6.7)

The Galerkin-type formulation of the eigenvalue problem (6.1) is the discrete form of (6.5): Seek \(\lambda _j^h \in {\mathbb {R}}\) and \(u_j^h \in V^h \subset V\) such that

$$\displaystyle \begin{aligned} a(u_j^h, {w^h}) = \lambda _j^h(u_j^h, {w^h}), \quad \forall \ {w^h} \in {V^h}, \end{aligned} $$
(6.8)

which results in the generalized matrix eigenvalue problem

$$\displaystyle \begin{aligned} \mathbf{K} \ {\mathbf{u}}^h = \lambda ^h \mathbf{M} \ {\mathbf{u}}^h, \end{aligned} $$
(6.9)

where K is referred as the stiffness matrix, M is referred as the mass matrix, and (λ h, u h) are the unknown eigenpairs.

We described the differential eigenvalue problem and its Galerkin discretization above. For dispersion analysis, we study the classical wave propagation equation

$$\displaystyle \begin{aligned} - \varDelta u + \frac{1}{c^2} \frac{\partial^2 u}{\partial^2 t} = 0, \end{aligned} $$
(6.10)

where c is the wave propagation speed. We abuse the notation of unknown u here. Assuming time-harmonic solutions of the form u(x, t) = e −iωt u(x) for a given temporal frequency ω, the wave equation reduces to the well-known Helmholtz equation

$$\displaystyle \begin{aligned} - \varDelta u - k^2 u = 0 , \end{aligned} $$
(6.11)

where the wavenumber k = ω∕c represents the ratio of the angular frequency ω to the wave propagation speed c. The wavelength is equal to 2π∕k. The discretization of (6.11) leads to the following linear equation system

$$\displaystyle \begin{aligned} \left( \mathbf{K} - k^2 \mathbf{M} \right) {\mathbf{u}}^h = 0. \end{aligned} $$
(6.12)

The equivalence between (6.1) and (6.11) or (6.9) and (6.12) is established by setting λ or λ h = k 2. Based on this equivalence, a duality principle between the spectrum analysis of the differential eigenvalue problem and the dispersion analysis of the wave propagation is established in [41]. In practice, the wavenumber is approximated and we denote it as k h. In general, k h ≠ k. Then the solution of (6.12) is a linear combination of plane waves with numerical wavenumbers k h. Hence the discrete and exact waves have different wavelengths. The goal of the dispersion analysis is to quantify this difference and define this difference as the dispersion error of a specific numerical method. That is, dispersion analysis seeks to quantify how well the discrete wavenumber k h approximates the continuous/exact k. Finally, in the view of unified analysis in [41], this dispersion error describes the errors of the approximated eigenvalues to the exact ones for (6.8) or (6.9).

6.3 Pythagorean Eigenvalue Error Theorem and Its Generalization

The theorem was first described in Strang and Fix [58] and was referred as the Pythagorean eigenvalue error theorem in Hughes [43]. In this section, we revisit this theorem in detail and generalize it.

6.3.1 The Theorem

Following Strang and Fix [58], the Rayleigh-Ritz idea for the steady-state equation ( is a differential operator) was extended to the differential eigenvalue problem. The idea leads to the finite element approximation of the eigenvalue problem. Equation (6.5) resembles the variational formulation for the steady-state equation. Hence, one expects the approximated eigenfunction errors are of the same convergence rates as those in steady-state problems. Definitely, the a priori error estimation of the eigenfunction will depend on the index j (as in j-th eigenvalue) and the accuracy will deteriorate as j increases. In fact, the errors of the approximated eigenvalues also increase and hence deteriorate the accuracy as j increases [7, 41, 58].

The a priori error analysis for the approximation of eigenfunctions and eigenvalues has a prominent connection. The motivation to derive the Pythagorean eigenvalue error theorem as stated below (see also Lemma 6.3 in [58]) is to elucidate the relation the between the eigenvalue and eigenvector errors to the total approximation error.

Theorem 6.1

For each discrete mode, with the normalization ∥u j∥ = 1 and \( \| u_j^h \| = 1\) , we have

$$\displaystyle \begin{aligned} \| u_j - u_j^h \|{}_E^2 = \lambda_j \| u_j - u_j^h \|{}^2+ \lambda_j^h - \lambda_j. \end{aligned} $$
(6.13)

By the Minmax Principle (discovered by Poincaré, Courant, and Fischer; referred by Strang and Fix), all finite element approximated eigenvalues bound the exact ones from above, that is

$$\displaystyle \begin{aligned} \lambda _j^h \ge \lambda _j \ \ \ \forall \ j . \end{aligned} $$
(6.14)

This allows us to write (6.13) in the conventional Pythagorean theorem formulation

$$\displaystyle \begin{aligned} \| u_j - u_j^h \|{}_E^2 = \Big( \sqrt{\lambda_j} \| u_j - u_j^h \| \Big)^2+ \Big( \sqrt{\lambda_j^h - \lambda_j} \Big)^2. \end{aligned} $$
(6.15)

This theorem was established with a simple proof in [58]. Alternatively, we present here

$$\displaystyle \begin{aligned} \begin{aligned} \| u_j - u_j^h \|{}_E^2 & = a(u_j - u_j^h, u_j - u_j^h) \\ & = a(u_j, u_j) - 2 a(u_j, u_j^h) + a(u_j^h, u_j^h) \\ & = \lambda_j (u_j, u_j) - 2 \lambda_j (u_j, u_j^h) + \lambda_j^h (u_j^h, u_j^h) \\ & = \lambda_j \big( (u_j, u_j) - 2 (u_j, u_j^h) + (u_j^h, u_j^h) \big) + \lambda_j^h - \lambda_j \\ & = \lambda_j \| u_j - u_j^h \|{}^2+ \lambda_j^h - \lambda_j. \end{aligned} \end{aligned} $$
(6.16)

This theorem tells that for each discrete mode, the square of the error in the energy norm consists of the eigenvalue error and the product of the eigenvalue and the square of the eigenfunction error in the L 2-norm. We can rewrite (6.13) as

$$\displaystyle \begin{aligned} \frac{{\lambda _j^h - {\lambda _j}}}{{{\lambda _j}}} + { \| {u_j^h - {u_j}} \|{}^2} = \frac{{\| {u_j^h - {u_j}} \|{}_E^2}}{{{\lambda _j}}}, \end{aligned} $$
(6.17)

which implies

$$\displaystyle \begin{aligned} \lambda _j^h - {\lambda _j} \le \| {u_j^h - {u_j}} \|{}_E^2, \end{aligned} $$
(6.18)
$$\displaystyle \begin{aligned} {\| {u_j^h - {u_j}} \|{}^2} \le \frac{{ \| {u_j^h - {u_j}} \|{}_E^2}}{{{\lambda _j}}}. \end{aligned} $$
(6.19)

This tells further the relation among the eigenvalue errors, eigenfunction error in L 2 norm, and eigenfunction error in energy norm. Once error estimation for eigenfunction error in energy norm is established, the other two are obvious. Also, the inequality (6.19) does not hold for methods that do not approximate all eigenvalues from above (that is violating (6.14)), for example, the spectral element method [2]. In general, the spectral element method is realized by using the Gauss-Legendre-Lobatto nodes to define the interpolation nodes for Lagrange basis functions in each element. This quadrature rule induces an error in the approximation of the inner products, but preserves the optimal order of convergence of the scheme. In fact, these errors in the inner product allow the numerical scheme to approximate eigenvalues from below. If the discrete method does not fully reproduce the inner products associated with the stiffness and mass matrices or these inner products are approximated using numerical integration, this theorem needs to be extended to account for the errors introduced by the approximations of the inner products.

6.3.2 The Quadrature

Now to derive the generalized Pythagorean eigenvalue error theorem, we first introduce the numerical integration with quadratures. The entries of the stiffness and mass matrices K and M in (6.9) are given by the inner products

$$\displaystyle \begin{aligned} {\mathbf{M}}_{i j} = \int_\varOmega \phi_i(x) \phi_j(x) \ \text{d}x, \end{aligned} $$
(6.20)
$$\displaystyle \begin{aligned} {\mathbf{K}}_{i j} = \int_\varOmega \nabla\phi_i(x) \cdot \nabla \phi_j(x) \ \text{d}x, \end{aligned} $$
(6.21)

where ϕ i(x) are the piecewise polynomial basis functions. Here, we consider basis functions for finite elements, spectral elements, and isogeometric analysis. M and K are symmetric positive definite matrices. Moreover, in the 1D matrices have 2p + 1 diagonal entries.

In practice, the integrals in (6.20) and (6.21) are evaluated numerically, that is, approximated by quadrature rules. Now we give a brief description of the quadrature rules for approximating the inner products (6.20) and (6.21). On a reference element \(\hat K\), an (n + 1)-point quadrature rule for a function f(x) is of the form

$$\displaystyle \begin{aligned} \int_{\hat K} \hat f(\hat{\boldsymbol{x}}) \ \text{d} \hat{\boldsymbol{x}} = \sum_{l=0}^{n} \hat{\varpi}_l \hat f (\hat{n_l}) + \hat{E}_{n+1}, \end{aligned} $$
(6.22)

where \(\hat {\varpi }_l\) are the weights, \(\hat {n_l}\) are the nodes, and \(\hat {E}_{n+1}\) is the error of the quadrature rule. For each element K, there is an invertible affine map σ such that \(K = \sigma (\hat K)\), which leads to the correspondence between the functions on K and \(\hat K\). Let J K be the corresponding Jacobian of the mapping. Then (6.22) induces a quadrature rule over the element K given by

$$\displaystyle \begin{aligned} \int_{K} f(\boldsymbol{x}) \ \text{d} \boldsymbol{x} \approx \sum_{l=0}^{n} \varpi_{l,K} f (n_{l,K}) + E_{n+1}, \end{aligned} $$
(6.23)

where \(\varpi _{l,K} = \text{det}(J_K) \hat \varpi _l\) and \(n_{l,K} = \sigma (\hat n_l)\).

The quadrature rule is exact for a given function f(x) when the remainder E n+1 is exactly zero. For example, the standard (n + 1)-point Gauss-Legendre (GL or Gauss) quadrature is exact for the linear space of polynomials of degree at most 2n + 1 (see, for example, [12, 57]).

The classical Galerkin finite element analysis typically employs the Gauss quadrature with p + 1 (where p is the polynomial order) quadrature points per parametric direction that fully integrates every term in the bilinear forms defined by the weak form. A quadrature rule is optimal if the function is evaluated with the minimal number of nodes (for example, Gauss quadrature with n + 1 evaluations is optimal for polynomials of order 2n + 1 in one dimension).

Element-level integrals may be approximated using other quadrature rules, for example the Gauss-Lobatto-Legendre (GLL or Lobatto) quadrature rule that is used in the spectral element method (SEM). The Lobatto quadrature evaluated at n + 1 nodes is accurate for polynomials up to degree 2n + 1. However, selecting a rule with p + 1 evaluations for a polynomial of order p and collocating the Lagrange nodes with the quadrature positions renders the mass matrix diagonal in 1D, 2D and 3D for arbitrary geometrical mappings. This resulting diagonal mass matrix is a more relevant result than the reduction in the accuracy of the calculation. Particularly, given that this property preserves the optimal convergence order for these higher-order schemes. Lastly, the spectral elements possess a superior phase accuracy when compared with the standard finite elements of the same polynomial order [2].

Isogeometric analysis based on NURBS (Non-Uniform Rational B-Splines) has been described in a number of papers (e.g. [13, 19, 20, 41]). Isogeometric analysis employs piecewise polynomial curves composed of linear combinations of B-spline basis functions. B-spline curves of polynomial order p may have up to p − 1 continuous derivatives across element boundaries. Three different refinement mechanisms are commonly used in isogeometric analysis, namely the h-, p- and k-refinement, as detailed in [20]. We refer the reader to [53] for the definition of common concepts of isogeometric analysis such as knot vectors, B-spline functions, and NURBS.

The derivation of optimal quadrature rules for NURBS-based isogeometric analysis with spaces of high polynomial degree and high continuity has attracted significant attention in recent years [5, 6, 11, 12, 14, 39, 42]. The efficiency of Galerkin-type numerical methods for partial differential equations depends on the formation and assembly procedures, which, in turn, largely depend on the efficiency of the quadrature rule employed. Integral evaluations based on full Gauss quadrature are known to be efficient for standard C 0 finite element methods, but inefficient for isogeometric analysis that uses higher-order continuous spline basis functions [51].

Hughes et al. [42] studied the effect of reduced Gauss integration on the finite element and isogeometric analysis eigenvalue problems. By using p Gauss points (i.e., underintegrating using one point less), one modifies the mass matrix only (in 1D). By using less than p Gauss points (i.e., underintegrating using several points less), both mass and stiffness matrices are underintegrated. Large underintegration errors may lead to the loss of stability since the stiffness matrix becomes singular. As shown in [42], this kind of underintegration led to the results that were worse than the fully integrated ones and the highest frequency errors diverged as the mesh was refined. However, as we show in the next sections, using properly designed alternative quadratures may lead to more accurate results.

The assembly of the elemental matrices into the global stiffness and mass matrices is done in a similar way for all Galerkin methods we analyze in this chapter. Similarly, the convergence rate for all Galerkin schemes we analyze is the same. However, the heterogeneity of the high-order finite element (C 0 elements, i.e., SEM and FEA) basis functions leads to a branching of the discrete spectrum and a fast degradation of the accuracy for higher frequencies. In fact, the degraded frequencies in 1D are about half of all frequencies, while in 3D this proportion reduces to about seven eighths. On uniform meshes, B-spline basis functions of the highest p − 1 continuity, on the contrary, are homogeneous and do not exhibit such branching patterns other than the outliers that correspond to the basis functions with support on the boundaries of the domain.

6.3.3 The Generalization

Now we consider the generalization. Applying quadrature rules to (6.8), we have the approximated form

$$\displaystyle \begin{aligned} a_h(\tilde u_j^h, w^h) = \tilde\lambda_j^h (\tilde u_j^h, w^h)_h \quad \forall \ w_h \in V^h, \end{aligned} $$
(6.24)

where

(6.25)

and

(6.26)

where \(\{\varpi _{l,K}^{(1)}, n_{l,K}^{(1)} \}\) and \(\{\varpi _{l,K}^{(2)}, n_{l,K}^{(2)} \}\) specify two (possibly different) quadrature rules. This leads to the matrix eigenvalue problem

$$\displaystyle \begin{aligned} {\mathbf{K}}^h \tilde{\mathbf{u}}^h = \tilde \lambda^h {\mathbf{M}}^h \tilde{\mathbf{u}}^h, \end{aligned} $$
(6.27)

where the superscripts on K and M and the tildes specify the effect of the quadratures.

Remark 6.1

For multidimensional problems on tensor product grids, the stiffness and mass matrices can be expressed as Kronecker products of 1D matrices [30]. For example, in the 2D case, the components of K and M can be represented as fourth-order tensors using the definitions of the matrices and the basis functions for the 1D case [22, 30]

$$\displaystyle \begin{aligned} \mathbf{M} _{i j k l} = \mathbf{M} ^{1D} _{i k} \mathbf{M} ^{1D} _{j l}, \end{aligned} $$
(6.28)
$$\displaystyle \begin{aligned} \mathbf{K} _{i j k l} = \mathbf{K} ^{1D} _{i k} \mathbf{M} ^{1D} _{j l} + \mathbf{K} ^{1D} _{j l} \mathbf{M} ^{1D} _{i k}, \end{aligned} $$
(6.29)

where \(\mathbf {M} ^{1D} _{i j}\) and \(\mathbf {K} ^{1D} _{i j}\) are the mass and stiffness matrices of the 1D problem as given by (6.20) and (6.21). We refer the reader to [22] for the description of the summation rules.

To understand the errors of the approximations of eigenvalues and eigenfunctions when quadratures are applied, we measure the errors they induce in the inner products. The following theorem generalizes the Pythagorean eigenvalue error theorem to account for these modified inner products [54].

Theorem 6.2

For each discrete mode, with the normalization ∥u j∥ = 1 and \(( \widetilde u_j^h, \widetilde u_j^h)_h = 1\) , we have

$$\displaystyle \begin{aligned} \| u_j - \widetilde u_j^h \|{}_E^2 = \widetilde \lambda_j^h - \lambda_j + \lambda_j \| u_j - \widetilde u_j^h \|{}^2 + \| \widetilde u^h_j \|{}_E^2 - \| \widetilde u^h_j \|{}_{E,h}^2 + \lambda_j \Big( 1 - \| \widetilde u^h_j \|{}^2 \Big), \end{aligned} $$
(6.30)

where ∥⋅∥E,h is the energy norm evaluated by a quadrature rule.

Proof

By definition and linearity of the bilinear forms, we have

$$\displaystyle \begin{aligned} \begin{aligned} \| u_j - \widetilde u_j^h \|{}_E^2 & = a(u_j - \widetilde u_j^h, u_j - \widetilde u_j^h) = a(u_j, u_j ) - 2 a(u_j, \widetilde u_j^h) + a(\widetilde u_j^h, \widetilde u_j^h). \end{aligned} \end{aligned} $$
(6.31)

From (6.5), we have

$$\displaystyle \begin{aligned} \begin{aligned} a({u_j},{u_j}) & = \lambda _j ({u_j},{u_j}), \\ a({u_j},\widetilde u_j^h ) & = \lambda _j ({u_j}, \widetilde u_j^h). \end{aligned} \end{aligned}$$

Thus, adding and subtracting a term \(\lambda _j (\tilde u_j^h, \tilde u_j^h)\), (6.31) is rewritten as

$$\displaystyle \begin{aligned} \begin{aligned} \| u_j - \widetilde u_j^h \|{}_E^2 & = \lambda_j (u_j, u_j ) - 2 \lambda_j (u_j, \widetilde u_j^h) + \lambda_j (\tilde u_j^h, \tilde u_j^h) - \lambda_j (\tilde u_j^h, \tilde u_j^h) + a(\widetilde u_j^h, \widetilde u_j^h) \\ & = \lambda_j \Big( (u_j, u_j ) - 2 (u_j, \widetilde u_j^h) + (\tilde u_j^h, \tilde u_j^h) \Big) - \lambda_j \| \widetilde u^h_j \|{}^2 + \| \widetilde u^h_j \|{}_E^2 \\ & = \lambda_j \| u_j - \tilde u_j^h \|{}^2 - \lambda_j \| \widetilde u^h_j \|{}^2 + \| \widetilde u^h_j \|{}_E^2. \end{aligned} \end{aligned}$$

From (6.24) and the definition of the modified energy norm ∥⋅∥E,h, we have

$$\displaystyle \begin{aligned} \| \widetilde u^h_j \|{}_{E,h}^2 = a_h(\tilde u_j^h, \tilde u_j^h) = \tilde\lambda_j^h (\tilde u_j^h, \tilde u_j^h)_h. \end{aligned}$$

Noting that \(( \widetilde u_j^h, \widetilde u_j^h)_h = 1\), we have

$$\displaystyle \begin{aligned} \widetilde \lambda_j^h - \lambda_j = \Big( \widetilde \lambda_j^h - \lambda_j \Big) ( \widetilde u_j^h, \widetilde u_j^h)_h = \| \widetilde u^h_j \|{}_{E,h}^2 - \lambda_j. \end{aligned}$$

Thus, adding and subtracting a term \(\widetilde \lambda _j^h - \lambda _j \) gives

$$\displaystyle \begin{aligned} \begin{aligned} \| u_j - \widetilde u_j^h \|{}_E^2 & = \lambda_j \| u_j - \tilde u_j^h \|{}^2 - \lambda_j \| \widetilde u^h_j \|{}^2 + \| \widetilde u^h_j \|{}_E^2 + \Big( \widetilde \lambda_j^h - \lambda_j \Big) - \Big( \| \widetilde u^h_j \|{}_{E,h}^2 - \lambda_j\Big) \\ & = \widetilde \lambda_j^h - \lambda_j + \lambda_j \| u_j - \widetilde u_j^h \|{}^2 + \| \widetilde u^h_j \|{}_E^2 - \| \widetilde u^h_j \|{}_{E,h}^2 + \lambda_j \Big( 1 - \| \widetilde u^h_j \|{}^2 \Big), \end{aligned} \end{aligned}$$

which completes the proof.

The equation in (6.30) can be rewritten as

$$\displaystyle \begin{aligned} \frac{ \| u_j - \widetilde u_j^h \|{}_E^2 } {\lambda_j} = \frac{ \widetilde \lambda_j^h - \lambda_j } {\lambda_j} + \| u_j - \widetilde u_j^h \|{}^2 +\frac{ \| \widetilde u^h_j \|{}_E^2 - \| \widetilde u^h_j \|{}_{E,h}^2 } {\lambda_j} + \Big( 1 - \| \widetilde u^h_j \|{}^2 \Big), \end{aligned}$$

in which the first term on the right-hand side is the relative error of the approximated eigenvalue, the second term represent the error of eigenfunction in L 2 norm, the third term shows the eigenvalue-scaled error due to the modification of the inner product associated with the stiffness, and the last term shows the error due to the modification of the inner product associated with the mass.

The left-hand side and the first two terms on the right-hand side resemble the Pythagorean eigenvalue error theorem, while the extra two terms reveal the effect of numerical integration of the inner products associated with the stiffness and the mass. In the cases when these inner products are integrated exactly, these two extra terms are zeros. Consequently, Theorem 6.2 reduces to the standard Pythagorean eigenvalue error theorem.

6.4 Optimal Blending for Finite Elements and Isogeometric Analysis

Several authors (e.g. [3, 27, 56]) studied the blended spectral-finite element method that uses nonstandard quadrature rules to achieve an improvement of two orders of accuracy compared with the fully integrated schemes. This method is based on blending the full Gauss quadrature, which exactly integrates the bilinear forms to produce the mass and stiffness matrices, with the Lobatto quadrature, which underintegrates them. This methodology exploits the fact that the fully integrated finite elements exhibit phase lead when compared with the exact solutions, while the underintegrated with Lobatto quadrature methods, such as, spectral elements have phase lag.

Ainsworth and Wajid [3] chose the blending parameter to maximize the order of accuracy in the phase error. They showed that the optimal choice for the blending parameter is given by weighting the spectral element and the finite element methods in the ratio \(\frac {p}{p+1}\). As mentioned above, this optimally blended scheme improves by two orders the convergence rate of the blended method when compared against the finite or spectral element methods that were the ingredients used in the blending. The blended scheme can be realized in practice without assembling the mass matrices for either of the schemes, but instead by replacing the standard Gaussian quadrature rule by an alternative rule, as Ainsworth and Wajid clearly explained in [3]. Thus, no additional computational cost is required by the blended scheme although the ability to generate a diagonal mass matrix by the underintegrated spectral method is lost.

To show how an improvement in the convergence rate is achieved, consider, for example, the approximate eigenfrequencies written as a series in Λ = ωh for the linear finite and spectral elements, respectively [3]

$$\displaystyle \begin{aligned} \omega^h _ {FE} h = \varLambda - \frac{\varLambda^3}{24} + O(\varLambda^5), \end{aligned} $$
(6.32)
$$\displaystyle \begin{aligned} \omega^h _ {SE} h = \varLambda + \frac{\varLambda^3}{24} + O(\varLambda^5). \end{aligned} $$
(6.33)

When these two schemes are blended using a blending parameter τ, the approximate eigenfrequencies become

$$\displaystyle \begin{aligned} \omega^h _ {BL} h = \varLambda + \frac{\varLambda^3}{24}(2 \tau - 1) + O(\varLambda^5). \end{aligned} $$
(6.34)

For τ = 0 and τ = 1, the above expression reduces to the ones obtained by the finite element and spectral element schemes, respectively. The choice of τ = 1∕2 allows the middle term of (6.34) to vanish and adds two additional orders of accuracy to the phase approximation when compared with the standard schemes. Similarly, by making the optimal choice of blending parameter \(\tau = \frac {p}{(p+1)}\) in high-order schemes, they removed the leading order term from the error expansion.

The numerical examples in Sect. 6.6 show that a similar blending can be applied to the isogeometric mass and stiffness matrices to reduce the eigenvalue error. For C 1 quadratic elements, the approximate eigenfrequencies are

$$\displaystyle \begin{aligned} \omega^h _ {GL} h = \varLambda - \frac{1}{5!}\frac{\varLambda^5}{12} + O(\varLambda^7), \end{aligned} $$
(6.35)
$$\displaystyle \begin{aligned} \omega^h _ {GLL} h = \varLambda + \frac{1}{5!}\frac{\varLambda^5}{24} + O(\varLambda^7). \end{aligned} $$
(6.36)

Similarly, blending these two rules utilizing a parameter τ gives

$$\displaystyle \begin{aligned} \omega^h _ {BL} h = \varLambda + \frac{3\tau - 2}{5! \cdot 24}\varLambda^5 + O(\varLambda^7). \end{aligned} $$
(6.37)

Thus the optimal ratio of the Lobatto and Gauss quadratures is 2 : 1 (τ = 2∕3) similar to the optimally blended spectral-finite element scheme. For C 2 cubic elements, we determine that a non-convex blending with τ = 5∕2 allows us to remove the leading error term and thus achieve two additional orders of accuracy.

Remark 6.2

In general, for C 0 elements such as the finite elements and spectral elements, the optimal blending is [3]: \(\tau = \frac {p}{(p+1)}\) for arbitrary p. This is, however, not true for isogeometric C k elements, where 1 ≤ k ≤ p − 1 and p ≥ 3. Finding the optimal blending parameter for p ≥ 3 with k > 0 remains an open question. For p ≤ 7 with k = p − 1 and the discussion on its generalization, we refer the reader to [15].

Equations (6.32)–(6.36) show that the absolute errors in the eigenfrequencies converge with the rates of \(O\left ( \varLambda ^{2p+1} \right )\) and \(O\left ( \varLambda ^{2p+3} \right ) \) for the standard and optimal schemes, respectively. If we consider the relative eigenfrequency errors, from Eqs. (6.35) and (6.36), these take the form

$$\displaystyle \begin{aligned} \frac{\omega^h h}{\varLambda} = 1 \pm \frac{\varLambda^4}{\alpha} + \cdots , \end{aligned} $$
(6.38)

that is, the convergence rate for frequencies computed using IGA approximations is \(O\left ( \varLambda ^{2p} \right ) \) as shown in [19, 55]. The optimal blending in IGA leads to a \(O\left ( \varLambda ^{2p+2} \right ) \) convergence rate for the relative eigenfrequencies. This superconvergence result is similar to the one achieved by the optimally-blending of the spectral and finite element methods of [3].

Remark 6.3

Wang et al. [61, 62] constructed super-convergent isogeometric finite elements for dispersion by blending two alternative quadrature methods. They used full Gauss and a method which reduces the bandwidth of the mass and stiffness method. Although the construction is different, algebraically the resulting algebraic system is identical for uniform meshes.

6.5 Two-Point Rules for C 1 Quadratic Isogeometric Analysis

The optimally-blended rules presented above first introduce an auxiliary parameter for combining two different standard quadrature rules. Then the parameter is determined by eliminating the highest order term in the error expansion. We can achieve a similar result by designing a nonstandard quadrature rule here.

For C 1 quadratic isogeometric analysis, the blending requires evaluations of the function at two sets of quadrature nodes on each element, which is not computationally efficient. In this section, we present a two-point rule which eliminates the leading order term in the error expansion hence results in an equivalent but computationally efficient scheme for the C 1 quadratic isogeometric elements.

We consider uniform meshes with periodic boundary conditions for the eigenvalue problem in 1D. In the reference interval [−1, 1], the two point rules are listed in Table 6.1.

Table 6.1 Two-point rules in the reference interval [−1, 1] for C 1 quadratic isogeometric analysis
Full size table

These two-point rules share some sense of symmetry and lead to the same matrix eigenvalue problem. On uniform meshes with periodic boundary conditions, all these rules give the same dispersion errors.

In a periodic boundary domain discretized with a uniform mesh, we show numerically that these two-point rules lead to the same set of eigenvalues and eigenfunctions as these obtained by the optimally-blended schemes. In fact, they result in the same stiffness and mass matrices. The two-point rules fail when we use a boundary condition other than periodic, for example, Dirichlet or Neumann conditions. This happens since the two-point rule does not integrate the stiffness terms exactly near the boundary elements where the derivatives of the B-splines basis functions do not vanish; see Fig. 6.1. We will understand and address this shortcoming in future work.

Fig. 6.1
figure 1

Isogeometric C 1 quadratic B-spline basis functions and their derivatives. (a) Basis functions. (b) Derivatives of basis functions

Full size image

For multidimensional cases, we assume that a tensor product grid is placed on the domain Ω. Then generalize these two-point rules to be 2d-point rules for d-dimensional problems by simple tensor construction. We conclude that these two-point rules developed above remain valid for higher dimensional problems. More details are referred to [15, 25].

6.6 Numerical Examples

In this section, we present numerical examples of the one- and two-dimensional problems described in Sect. 6.2 to show how the use of optimal quadratures reduce the approximation errors in isogeometric analysis.

The 1D elliptic eigenvalue problem has the following exact eigenvalues and their corresponding eigenfunctions

$$\displaystyle \begin{aligned} {{\lambda _j} = {j^2}{\pi ^2},\ \ \ {u_j} = \sqrt 2 \sin (j\pi x),} \end{aligned} $$
(6.39)

for j = 1, 2, …. The approximate eigenvalues \(\lambda _j^h\) are sorted in ascending order and are compared to the corresponding exact eigenvalues λ j. The total number of degrees of freedom (discrete modes) is N = 1000.

Figure 6.2 compares the approximation errors of C 1 quadratic isogeometric elements using the standard Gaussian quadrature and the optimal rule. We show the relative eigenvalue errors \(\frac {\mu _l^h - {\lambda _l}}{\lambda _l}\), the L 2-norm eigenfunction errors \(\left \| {{u_l} - v_l^h} \right \|{ }_0^2\) and the relative energy-norm errors \(\frac {\left \| {{u_l} - v_l^h} \right \|{ }_E^2}{\lambda _l}\). This format of error representation clearly illustrates the budget of the generalized Pythagorean eigenvalue theorem. The error in the L 2 norm \(1 - \left \| {v_l^h} \right \|{ }_0^2\) is shown only in the case when it is not zero.

Fig. 6.2
figure 2

Approximation errors for C 1 quadratic isogeometric elements with standard Gauss quadrature rule (left) and optimal blending (right)

Full size image

In Fig. 6.2, the use of the optimal quadrature leads to more accurate results. Surprisingly, not only the eigenvalues, but also the eigenfunctions of the problem are better approximated in this particular case. The optimal ratio of blending of the Lobatto and Gauss quadrature rules in this case is 2:1, which is the same to the ratio proposed by Ainsworth and Wajid (2010) for the finite element case.

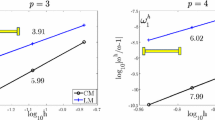
Figure 6.3 shows the dispersion errors in the eigenvalue approximation with C 1 quadratic isogeometric elements. The size of the meshes used in these simulations increases from 10 to 2560 elements. These results confirm two extra orders of convergence in the eigenvalue errors.

Fig. 6.3
figure 3

Convergence of the errors in the eigenvalue approximation using C 1 quadratic isogeometric elements with standard and optimal quadratures. The fifth (left) and tenth (right) eigenvalues are shown

Full size image

To study the behavior of discrete eigenfunctions from different parts of the spectrum, in Fig. 6.4 we compare the discrete and analytical eigenfunctions for C 1 quadratic elements. We show the 200th and the 400th eigenfunctions, where the error is low, and the 600th and the 800th eigenfunctions, for which the approximation is worse. As expected, both the fully- and under-integrated methods provide similar eigenfunctions. There is no loss of accuracy in eigenfunction approximation due to the use of the non-standard optimal quadrature rules.

Fig. 6.4
figure 4

Discrete 200th (top left), 400th (top right), 600th (bottom left) and 800th (bottom right) eigenfunctions for C 1 quadratic elements. The discrete eigenfunctions resulting from the optimal (red squares) and the standard scheme (blue line) are compared with the analytical eigenfunctions (black line). The total number of discrete modes is 1000

Full size image

We also note that for practical applications, one may look for a scheme that reduces errors in the desired intervals of wavenumber (frequency) for a given mesh size. Such blending schemes are also possible and (though not being optimal, i.e. not delivering superconvergence) they are superior in the eigenvalue approximation compared to the optimal blending in certain ranges of wavenumber that are of practical interest in wave propagation problems. We refer the reader to [54] for further details.

Next, we continue our study with the dispersion properties of the two-dimensional eigenvalue problem on tensor product meshes. Optimal quadratures for multidimensional problems are formed by tensor product of the one dimensional case. The exact eigenvalues and eigenfunctions of the 2D eigenvalue problem are given by

$$\displaystyle \begin{aligned} {{\lambda _{kl}} = {(k^2+l^2)}{\pi ^2},\ \ \ {u_{kl}} = 2 \sin (k\pi x) \sin (l\pi y),} \end{aligned} $$
(6.40)

for k, l = 1, 2, …. Again, the approximate eigenvalues \(\lambda _{kl}^h\) are sorted in ascending order.

Figure 6.5 compares the eigenvalue errors of the standard Gauss using C 1 quadratic elements with the optimal scheme (τ = 2∕3). The latter has significantly better approximation properties.

Fig. 6.5
figure 5

Approximation errors for C 1 quadratic isogeometric elements with standard Gauss (left) and optimal quadrature rule (right). Color represents the absolute value of the relative error

Full size image

These results demonstrate that the use of optimal quadratures in isogeometric analysis significantly improves the accuracy of the discrete approximations when compared to the fully-integrated Gauss-based method.

Figure 6.6 compares the eigenvalue errors for C 2 cubic isogeometric elements. Again, the optimal scheme has significantly better approximation properties than the standard method. The scale and representation format are different from those of Fig. 6.5.

Fig. 6.6
figure 6

Approximation errors for C 2 cubic isogeometric elements with standard Gauss (left) and optimal quadrature rule (right). Color represents the absolute value of the relative error

Full size image

Figure 6.7 compares the dispersion errors of the standard Gauss fully-integrated method with the optimally-blended scheme and the two-point rule described in the previous section. In this example, we use periodic knots at the boundaries of the domain. As can be seen from Fig. 6.7, the two-point rule leads to the same results as those obtained by the optimally-blended scheme. At the same time, this rule is computationally cheaper than the three-point Gauss rule or any blended scheme.

Fig. 6.7
figure 7

Approximation errors for C 1 quadratic isogeometric elements with standard Gauss, the optimal quadrature rule, and the two-point

Full size image

6.7 Conclusions and Future Outlook

To understand the dispersion properties of isogeometric analysis and to improve them, we generalize the Pythagorean eigenvalue error theorem to account for the effects of the modified inner products on the resulting weak forms. We show that the blended quadrature rules reduce the phase error of the numerical method for the eigenvalue problems.

The proposed optimally-blended scheme further improves the superior spectral accuracy of isogeometric analysis. We achieve two extra orders of convergence in the eigenvalues by applying these blended rules. We present and test two-point rules which reduce the number of quadrature nodes and the computational cost, and at the same time, produce the same eigenvalues and eigenfunctions. We believe that one can extend the method to arbitrary high-order C p−1 isogeometric elements by identifying suitable quadrature rules. Nevertheless, for higher-order polynomial approximations the only known optimal quadratures are the result of blending a Gauss rule and a Lobatto quadrature rule. The search for this class of quadratures that result in super-convergent dispersion properties and use fewer quadrature points will be the subject of our future work.

Another future direction is the study on the non-uniform meshes and non-constant coefficient wave propagation problems. The study with variable continuity is also of interest. We will study the impact of the variable continuities of the basis functions on the dispersion properties of the numerical methods and how the dispersion can be minimized by designing goal-oriented quadrature rules.