Computing with Multisets: A Survey on Reaction Automata Theory

Abstract

In Natural Computing research [18], as mathematical modeling tools of biochemical reactions, Ehrenfeucht and Rozenberg introduced a formal model called reaction systems [6] for investigating the functioning of the living cell, where two basic components (reactants and inhibitors) play a key role as a regulation mechanism in controlling interactions.

F. Okubo—The work of T.Yokomori was in part supported by JSPS KAKENHI, Grant-in-Aid for Scientific Research (C) JP17K00021, and by Waseda University grant for Special Research Project: 2017K-121. The work of F. Okubo was in part supported by JSPS KAKENHI Grant Number JP16K16008.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In Natural Computing research [18], as mathematical modeling tools of biochemical reactions, Ehrenfeucht and Rozenberg introduced a formal model called reaction systems [6] for investigating the functioning of the living cell, where two basic components (reactants and inhibitors) play a key role as a regulation mechanism in controlling interactions.

Inspired by the notion of reaction systems, reaction automata (RAs) have been first introduced in [10] as computing devices for accepting string languages. The notion of RAs is an extension of reaction systems in that RAs employ reactions which are defined by triples (consisting of reactants, inhibitors and products), however they entail dealing with multisets for reactants and products (rather than usual sets as reaction systems do). Thus, RAs are computing models based on multiset rewriting that accept string languages. Another feature that distinguishes RAs from reaction systems is that a reaction automaton receives its input by feeding one symbol of an input string at each step of the computation. In this respect, RAs have the taste similar to P automata, P systems with accepting configurations, in which the idea of taking input sequences of multisets into the systems from the environment was introduced (e.g., [5]).

This survey paper is primarily based on the research works on RAs achieved in [9,10,11,12, 15] in which various classes of RAs are considered in four types of computation process: with/without $\lambda$-input modes in rule application of the maximally parallel manner and the sequential manner.

In what follows, we make a quick survey of the results presented in this paper. The first result in the series of papers was that RAs are computationally Turing universal [10]. In the paper, space-bounded complexity classes of RAs was also introduced, and in the follow-up paper [11], it eventually turned out that exponential-bounded RAs can exactly characterize the class of context-sensitive languages. Further characterization result of the class of recursively enumerable languages was developed by using the class of linear-bounded RAs together with homomorphisms. The paper [11] also considered some of the closure properties of language classes defined by linear-bounded RAs, showing that the class forms an AFL, while the issue of the computing powers of RAs with $\lambda$-input mode in sequential manner was taken up in [9] and investigated to prove that they have again the Turing universal computability. Further investigations was made to a simpler variant of RAs called Chemical reaction automata (CRAs), and it was proved that CRAs with $\lambda$-input mode in parallel manner have the Turing universal computability, while their computing powers coincide with the class of Petri net languages when working in sequential manner. In [15], several subclasses of CRAs was introduced and their computing powers was studied. We leave more details of the results to later sections.

The rest of this section is devoted to a brief preliminary. We assume that the reader is familiar with the basic notions of reaction systems as well as of formal language theory. For unexplained details in the theory of reaction systems and in formal language theory, refer to, e.g., [6, 7], respectively.

We use the basic notations and definitions concerning multisets that follow [4]. A multiset over an alphabet V is a mapping $\mu : V \rightarrow \mathbf {N}$, where $\mathbf {N}$ is the set of non-negative integers, and for each $a \in V$, $\mu (a)$ represents the number of occurrences of a in the multiset $\mu$. The set of all multisets over V is denoted by $V^{\#}$, including the empty multiset denoted by $\mu _{\lambda }$, where $\mu _{\lambda }(a) = 0$ for all $a \in V$. A multiset $\mu$ over V can be represented by any permutation of the string $x = a^{\mu (a_1)}_1 \cdots a^{\mu (a_n)}_n$, where $V=\{a_1,a_2,\cdots ,a_n\}$. (Note that for each $a \in V$, $a^{0}$ is an empty string $\lambda$.) In this sense, a multiset $\mu$ is often identified with its string representation $x_{\mu }$ or any permutation of $x_{\mu }$. A usual set $U (\subseteq V)$ is regarded as a multiset $\mu _U$ such that $\mu _U(a) = 1$ if a is in U and $\mu _U(a) = 0$ otherwise. In particular, for each symbol $a \in V$, a multiset $\mu _{\{ a \}}$ is often denoted by a itself.

2 Reaction Automata

Inspired by the works of reaction systems (initiated by [6]), the notion of reaction automata has been introduced in [10] by extending sets in each reaction (of a reaction system) to multisets. Here, we start by recalling basic notions concerning reaction automata.

Definition 1

For a set S, a reaction in S is a 3-tuple $\mathbf{a} = (R_\mathbf{a}, I_\mathbf{a}, P_\mathbf{a})$ of finite multisets such that $R_\mathbf{a}, P_\mathbf{a} \in S^\#$, $I_\mathbf{a} \subseteq S$ and $R_\mathbf{a} \cap I_\mathbf{a} = \emptyset$. The multisets $R_\mathbf{a}$ and $P_\mathbf{a}$ are called the reactant of $\mathbf{a}$ and the product of $\mathbf{a}$, respectively, while the set $I_\mathbf{a}$ is called the inhibitor of $\mathbf{a}$.

These notations are extended to a multiset of reactions as follows: For a set of reactions A and a multiset $\alpha$ over A (i.e., $\alpha \in A^{\#}$),

$$ R_{\alpha } = \sum _{\mathbf{a}\in A} R_\mathbf{a}^{\alpha (\mathbf{a})}, \, \, I_{\alpha } = \bigcup _{ \mathbf{a} \subseteq \alpha } I_\mathbf{a}, \, P_{\alpha } = \sum _{\mathbf{a}\in A} P_\mathbf{a}^{\alpha (\mathbf{a})}, $$

Notes. (1). A is often identified with its label set and is used as an alphabet.

(2). The symbol $\sum _{\mathbf{a}\in A}$ denotes the sum of multisets.

In the existing works on reaction automata, two ways of applying reactions have been considered: the sequential manner and the maximally parallel manner. The former manner was adopted in [10, 11], while the literatures [9, 12, 15] studied the latter as well.

Definition 2

Let A be a set of reactions in S and $\alpha \in A^\#$ be a multiset of reactions over A. Then, for a finite multiset $T \in S^\#$, we say that

• (1) $\alpha$ is enabled by T if $R_\alpha \subseteq T$ and $I_\alpha \cap T = \emptyset$.

• (2) $\alpha$ is enabled by T in sequential manner if $\alpha$ is enabled by T with $|\alpha |=1$.

• (3) $\alpha$ is enabled by T in maximally parallel manner if there is no $\beta \in A^\#$ such that $\alpha \subset \beta$, and $\alpha$ and $\beta$ are enabled by T.

• (4) By $En^{sq}_{A}(T)$ and $En^{mp}_{A}(T)$, we denote the sets of all multisets of reactions $\alpha \in A^\#$ which are enabled by T in sequential manner and in maximally parallel manner, respectively.

• (5) The results of A on T, denoted by $Res^{X}_{A}(T)$ with $X \in \{ sq,mp \}$, is defined as follows:

$$ Res^X_{A}(T) = \{ T - R_{\alpha } + P_{\alpha } \, | \, \alpha \in En^X_A(T) \}. $$

We note that $Res^X_{A}(T)= \{ T \}$ if $En^X_A(T)=\emptyset$. Thus, if no multiset of reactions $\alpha \in A^{\#}$ is enabled by T, then T remains unchanged.

Definition 3

A reaction automaton (RA) $\mathcal {A}$ is a 5-tuple $\mathcal {A} = (S, \varSigma , A, D_0, f)$, where

• S is a finite set, called the background set of $\mathcal {A}$,

• $\varSigma (\subseteq S)$ is called the input alphabet of $\mathcal {A}$,

• A is a finite set of reactions in S,

• $D_0 \in S^\#$ is an initial multiset,

• $f \in S$ is a special symbol which indicates the final state.

Unlike the reaction system, a reaction automaton takes its input symbol from the environment into the current multiset (or state) representing current configuration, from time to time during the computing process. This idea was already considered and realized in the P automata theory (e.g., [5]).

Definition 4

Let $\mathcal {A} = (S, \varSigma , A, D_0, f)$ be an RA, $w = a_1 \cdots a_n \in \varSigma ^*$ and $X \in \{ sq,mp \}$. An interactive process in $\mathcal {A}$ with input w in X manner is an infinite sequence $\pi = D_0, \ldots , D_i, \ldots$, where

$$\begin{aligned} \left\{ \begin{array}{ll} D_{i+1} \in Res^X_A(a_{i+1}+D_i) &{} \hbox {(for}\,\, 0\le i \le n-1), \,\,\hbox {and} \\ D_{i+1} \in Res^X_A(D_i) &{} \hbox {(for all}\,\, i\ge n). \end{array} \right. \end{aligned}$$

In order to represent an interactive process $\pi$, we also use the “arrow notation” for $\pi$ : $D_0 \rightarrow ^{a_1} D_1 \rightarrow ^{a_2} D_2 \rightarrow ^{a_3} \cdots \rightarrow ^{a_{n-1}} D_{n-1} \rightarrow ^{a_{n}} D_{n} \rightarrow D_{n+1} \rightarrow \cdots$. By $IP_X(\mathcal {A}, w)$ we denote the set of all interactive processes in $\mathcal {A}$ with input w in X manner. If for an input string $w = a_1 \cdots a_n$, it is allowed that $a_i = \lambda$ for some $1 \le i \le n$, then an interactive process is said to be with $\lambda$-input mode. By $IP^{\lambda }_X(\mathcal {A}, w)$ we denote the set of all interactive processes in $\mathcal {A}$ with $\lambda$-input mode in X manner for the input w ([11]).

For an interactive process $\pi$ in $\mathcal {A}$ with input w, if $En^X_A(D_m) = \emptyset$ for some $m \ge |w|$, then we have that $Res_A^X(D_m)= \{ D_m \}$ and $D_m =D_{m+1}= \cdots$. In this case, considering the smallest m, we say that $\pi$ converges on $D_m$ (at the m-th step). If an interactive process $\pi$ converges on $D_m$, then $D_m$ is called the converging state of $\pi$ and the successive multisets $D_{m+1}, D_{m+2}, \ldots$ are omitted.

Definition 5

Let $\mathcal {A} = (S, \varSigma , A, D_0, f)$ be an RA and $X\in \{ sq ,mp \}$. The languages accepted by $\mathcal {A}$ are defined as follows:

$$\begin{aligned} L_X(\mathcal {A}) = \{ w \in \varSigma ^* \, |&\, \hbox { there exists}\,\, \pi \in IP_X(\mathcal {A}, w) \,\,\hbox {such that}\,\, \pi \,\, \hbox {converges on}\,\, D_m \\&\, \ \hbox {for some}\,\, m\ge |w|\,\, \hbox {and}\,\, f\,\, \hbox {is included in}\,\, D_m \} \\ L^{\lambda }_X(\mathcal {A})\! =\! \{ w \in \varSigma ^* \, |&\, \hbox { there exists}\,\, \pi \in IP^{\lambda }_X(\mathcal {A}, w)\,\, \hbox {satisfying the same as}\,L_X(\mathcal {A})\}. \end{aligned}$$

Example 1

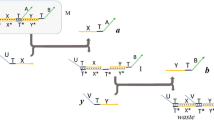
Let us consider a reaction automaton $\mathcal {A} = (\big \{ p_0, p_1,a, b, a', f \big \}, \{a,b \}, \{ \mathbf{a}_0, \mathbf{a}_1, \mathbf{a}_2, \mathbf{a}_3, \mathbf{a}_4 \}, p_0, f)$, where $\mathbf{a}_0 = ( p_0, aba', f ),\ \,\mathbf{a}_1 = ( p_0 a, b, p_0 a' ), \mathbf{a}_2 = ( p_0 a' b, \emptyset , p_1 ), \mathbf{a}_3 = ( p_1 a' b, a, p_1 ), \, \mathbf{a}_4 = ( p_1, aba', f )$. Figure 1 illustrates the whole view of possible interactive processes in $\mathcal {A}$ with inputs $a^n b^n$ for $n \ge 0$. Let $w = aaabbb \in \varSigma ^*$ be the input string and consider an interactive process $\pi$ in sequential manner such that

$$\begin{aligned} \pi : p_0 \rightarrow ^a p_0 a' \rightarrow ^a p_0 a'^2 \rightarrow ^a p_0 a'^3 \rightarrow ^b p_1 a'^2 \rightarrow ^b p_1 a' \rightarrow ^b p_1 \rightarrow f. \end{aligned}$$

It is easily seen that $\pi \in IP_{sq}(\mathcal {A}, w)$ and $w \in L_{sq}(\mathcal {A})$. Further, we see that $L_{sq}(\mathcal {A}) = \{ a^n b^n \, | \, n \ge 0 \}$ which is a context-free language.

We remark that this interactive process can be also performed by $\mathcal {A}$ in maximally parallel manner, i.e. $\pi \in IP_{mp}(\mathcal {A}, w)$. In fact, it holds that $L_{mp}(\mathcal {A}) = \{ a^n b^n \, | \, n \ge 0 \}$.

Fig. 1.

An illustration of interactive processes for accepting the language $L=\{ a^n b^n \, | \, n \ge 0 \}$ in terms of the reaction automaton $\mathcal {A}$.

3 Main Results on RAs

This section presents some results on reaction automata (RAs) that have been established in an earlier stage. In what follows, a language accepted by an RA is often referred to as an RA language.

3.1 Computing Powers of RAs and Their Subclasses

It has been proven that the accepting power of reaction automata with both manners of applying reactions coincides with that of Turing machines.

Theorem 1

([9, 10]). The followings hold :

• (1) Every recursively enumerable language is accepted by a reaction automaton in maximally parallel manner.

• (2) Every recursively enumerable language is accepted by a reaction automaton in sequential manner with $\lambda$-input mode.

• (3) There exists a recursively enumerable language which cannot be accepted by any reaction automaton in sequential manner.

The proofs are based on two facts: (i) every recursively enumerable language is accepted by a restricted two-stack machine (Theorem 8.13 in [7]) and (ii) one can devise an injective function to encode strings into multisets. The result (2) is in marked contrast to (3), which clarifies the computing power of $\lambda$-input mode in sequential manner.

The space complexity issues of reaction automata (RAs) have been considered. By restricting the volume of each multiset that is produced in an interactive process by RA, some subclasses of RAs were introduced and investigated on relations between classes of languages accepted by those subclasses of RAs and language classes in the Chomsky hierarchy.

Let $\mathcal {A}$ be an RA and $X \in \{sq, mp\}$. Motivated by the notion of a workspace for a phrase-structure grammar, we define the counterpart of RA as follows: For $w\in L_X(\mathcal {A})$ with $n=|w|$, the workspace of $\mathcal {A}$ for w is defined as:

$$ WS(w,\mathcal {A}) ={\mathrm{min}_{\pi } } \{\mathrm{max}_i \{|D_i|\mid \,\,D_i\,\, \hbox {appears in}\,\, \pi \}, \pi \in IP_{X}(\mathcal {A},w)\ \}. $$

Definition 6

Let f be a function defined on $\mathbf {N}$ and $X\in \{ sq,mp \}$.

• (1) An RA $\mathcal {A}$ is f(n)-bounded if for any $w\in L_X(\mathcal {A})$ with $n=|w|$, $WS(w,\mathcal {A})\le f(n)$.

• (2) If a function f(n) is a constant k (linear, exponential), then $\mathcal {A}$ is termed constant-bounded (resp. linear-bounded, exponential-bounded).

• (3) The class of languages accepted by constant-bounded RAs (linear-bounded, exponential-bounded, arbitrary RAs) in X manner is denoted by $\mathcal{C}o\mathcal{RA}_X$ (resp. $\mathcal {LRA}_X$, $\mathcal {ERA}_X$, $\mathcal {RA}_X$).

• (4) The class of languages accepted by constant-bounded RAs (linear-bounded, exponential-bounded, arbitrary RAs) with $\lambda$-input mode in X manner is denoted by $\mathcal{C}o\mathcal{RA}^{\lambda }_X$ (resp. $\mathcal {LRA}^{\lambda }_X$, $\mathcal {ERA}^{\lambda }_X$, $\mathcal {RA}^{\lambda }_X$).

In order to explore and make clearer inclusion relations among language classes (considered so far), it is necessary to find a family of languages (or at least a particular language) with certain properties which plays a role of witness to distinguish one class from the other. The following lemma is useful for the purpose.

Lemma 1

([9]). Let $\varSigma$ be an alphabet with $|\varSigma | \ge 2$ and $h: \varSigma ^* \rightarrow \varSigma ^*$ be an injection, and consider $L_h=\{ wh(w) \, | \, w \in \varSigma ^* \}$. Then, $L_h$ is not in $\mathcal {RA}_{sq}$.

Let us denote by $\mathcal {REG}$ ($\mathcal {CF, CS, RE}$) the class of regular (resp. context-free, context-sensitive, recursively enumerable) languages.

Theorem 2

([9, 10]). The following inclusions hold :

• (1). $\mathcal {REG}=\mathcal{C}o\mathcal{RA}_{mp} \subset \mathcal {LRA}_{mp} \subset \mathcal {ERA}_{mp} \subseteq \mathcal {RA}_{mp} = \mathcal {RE}$

• (2). $\mathcal {REG}=\mathcal{C}o\mathcal{RA}_{sq} \subset \mathcal {LRA}_{sq} \subset \mathcal {RA}_{sq} \subset \mathcal {RA}^{\lambda }_{sq} = \mathcal {RE}$.

• (3). $\mathcal {ERA}^{\lambda }_{sq}= \mathcal {ERA}_{mp}= \mathcal {CS}$.

• (4). $\mathcal {CF}$, $\mathcal {LRA}_{mp}$ and $\mathcal {RA}_{sq}$ are incomparable.

Thus, new characterizations of the classes $\mathcal {REG}, \mathcal {CS}$ and $\mathcal {RE}$ have been established in terms of the subclasses of RA languages $\mathcal{C}o\mathcal{RA}_{mp}, \mathcal {ERA}_{mp}, \mathcal {RA}_{mp}$, respectively. As seen later, however, the class $\mathcal {CF}$ has been proved incomparable to any known class of languages defined by RAs so far, exhibiting a unique position within the RA language hierarchy.

3.2 Some Other Characterizations of RA Language Classes

One of the primary issues in the formal language theory is to investigate the closure properties of a language class under various language operations. When featuring the classes $\mathcal {LRA}_{mp}$ and $\mathcal {LRA}^{\lambda }_{mp}$, the following has been proven.

Theorem 3

([10, 11])

• (1).   $\mathcal {LRA}_{mp}$ is closed under union, intersection, concatenation, derivative, $\lambda$-free morphisms, $\lambda$-free gsm-mappings and shuffle, while not closed under complementation, quotient by regular languages, morphisms or gsm-mappings.

• (2). $\mathcal {LRA}^{\lambda }_{mp}$ is closed under union, intersection, concatenation, Kleene $+$, Kleene $*$, derivative, $\lambda$-free morphisms, inverse morphisms, $\lambda$-free gsm-mappings and shuffle.

We remark that in order to prove some of the negative closure properties of $\mathcal {LRA}_{mp}$, the following lemma is of crucial importance.

Lemma 2

([10]). For an alphabet $\varSigma$ with $|\varSigma | \ge 2$, let $h:\varSigma ^* \rightarrow \varSigma ^*$ be an injection such that for any $w \in \varSigma ^*$, |h(w)| is bounded by a polynomial of |w|. Then, the language $L_h=\{ wh(w) \, | \, w \in \varSigma ^* \}$ is not in $\mathcal {LRA}_{mp}$.

Further characterization results of $\mathcal {RE}$ have been developed by using $\mathcal {LRA}_{mp}$ and $\mathcal {RA}_{sq}$together with homomorphisms and regular languages.

Theorem 4

([9, 11])

• (1). For any recursively enumerable language L, there exists an LRA $\mathcal {A}$ such that $L = h(L_{mp}(\mathcal {A}))$ for some projection h.

• (2). For any recursively enumerable language L, there exists an LRA $\mathcal {A}$ such that (or $L_{mp}(\mathcal {A}) / R$) for some regular language R.

• (3). For any recursively enumerable language L, there exists an RA $\mathcal {A}$ such that $L = h(L_{sq}(\mathcal {A}))$ for some projection h.

4 Chemical Reaction Automata

As a simple and modified version of a reaction automaton, a chemical reaction automaton (CRA) has been introduced and investigated [12]. Rather lately, this computing model CRA turned out to be important, because it can provide an online computational model for a molecular programming language called Chemical reaction networks (CRNs [19]). It is known that CRNs involve wet implementations by a molecular reaction primitive called DNA strand displacement (DSD) systems.

Specifically, a CRA is a 5-tuple $(S, \varSigma , A, D_0, F)$, where each reaction in A is of the form $(R, \emptyset , P)$ (each reaction in CRA has no inhibitor), and F is a finite set of final multisets. For convenience, each reaction in A is denoted by $R\rightarrow P$. In an interactive process of CRA, if $En^X_A(D) = \emptyset$, $Res^X_A(D)$ is undefined. A language accepted by a CRA $\mathcal {A} = (S, \varSigma , A, D_0, F)$ is defined by

$$ L_{X}^{\lambda }(\mathcal {A}) = \{ w \in \varSigma ^*_{\lambda } \, | \, \pi : D_0\rightarrow ^{a_1} D_1\rightarrow ^{a_2} \cdots \rightarrow ^{a_n} D \in IP^{\lambda }_{X}(A, w), \, D \in F \}. $$

Remarks: The acceptance condition of CRA computation is slightly different from that of RA computation. A CRA accepts an input string if the final multiset coincides with an element of F, while an RA accepts an input string if the final multiset includes a particular symbol f. This difference is significant to obtain the results in our paper.

4.1 The Computation Power of CRAs

It has been shown that CRAs working in maximally parallel manner are computationally Turing universal. Our proof requires the fact that (i) a two-counter machine is equivalent to a Turing machine as a language accepting device [7] as well as the result that (ii) for any k-counter machine, there effectively exists an equivalent CRA. From (i) and (ii), the following is derived:

Theorem 5

([12]). The computational power of CRAs with $\lambda$-input mode in maximally parallel manner is equivalent to that of Turing machines.

A naive question now arises: Concerning the computing power of CRAs whether or not there exists a real gap between working in maximally parallel manner and in sequential manner. This question is solved as a corollary of the next theorem.

Theorem 6

([12]). A language L is generated by a Petri net system if and only if L is accepted by a CRA with $\lambda$-input mode in sequential manner.

Note that among several types of Petri net languages, here we mean a language of $L^{\lambda }$-type in [17]. Since the class of Petri net languages is strictly included in the class of context-sensitive languages and is incomparable to the class of context-free languages [17], it turns out that the computational power of CRAs with $\lambda$-input mode in sequential manner is less powerful than that of CRAs with $\lambda$-input mode in maximally parallel manner.

4.2 Determinism and Reversibility in CRAs

In this section we introduce the notions of determinism and reversibility into CRAs, and investigate the computational powers of those classes of CRAs in comparison with the language classes of Chomsky hierarchy.

The computing power of reversible CRAs involves the physical realization of molecular programming of chemical reaction networks with DNA strand displacement system implementation [19], and therefore, it is of great significance to elucidate the computing capabilities of both deterministic and reversible CRAs from the theoretical viewpoint of molecular computing.

Unlike the determinism of conventional computation models such as pushdown automata, since a reactant is not divided into “input” part and “memory (multiset)” part, the determinism of CRAs cannot be decided only by a form of transition rules. This comes from the property of multiset memory, that is, from the current configuration alone, a CRA cannot identify a reactant of the next reaction to be applied. Therefore, the determinism of CRA has to be defined so as to exclude any branching computation, regardless of a non-empty input or empty input.

A CRA is said to be deterministic if for every input symbol $a \in \varSigma$ and every reachable configuration, the resultant multiset after a reaction is unique. Similar to the definition of deterministic pushdown automata, this condition is extended to the case of $\lambda$-input mode.

It is not trivial, only from their definitions, to recognize the difference of computing powers of the determinism between realtime CRA and CRA with $\lambda$-input mode, where “realtime” means “no $\lambda$ input is allowed”. The following result might be rather unexpected in some sense.

Lemma 3

([15]). If a language L is accepted by a DCRA with $\lambda$-input mode, then L is also accepted by a realtime DCRA.

Note that by our definition of DCRA, without receiving an input symbol, no configuration of a DCRA with $\lambda$-input mode can have an enabled reaction, while this is not the case for a realtime DCRA. In order to make a reaction, a realtime DCRA always requires an input symbol, even if its configuration has an enabled reaction with no input symbol.

Information preserving computations (forward and backward deterministic computations) are very important and are considered as “reversibility” in many existing research papers (e.g., [2, 3]). However, in order to understand their properties in more details, we want to take a position to think of them apart(i.e., separate into forward and backward determinisms). Thus, in our view the “reversibility” simply means that the previous configuration of computation can be uniquely determined (backward determinism).

A CRA is said to be reversible if for every input symbol $a \in \varSigma$ and every reachable configuration D, the set of configurations which directly reaches D with a is a singleton. For the case of $\lambda$-input mode, this condition is extended to the case of $\lambda$-input mode in a natural manner.

The following lemma holds true for a deterministic and reversible CRA (abbrev. DRCRA).

Lemma 4

([15]). If a language L is accepted by a DRCRA with $\lambda$-input mode, then L is also accepted by a realtime DRCRA.

By $\mathcal {CRA}_{sq}$, $\mathcal {CRA}^{\lambda }_{sq}$, $\mathcal {DCRA}_{sq}$, $\mathcal {DCRA}^{\lambda }_{sq}$, $\mathcal {RCRA}_{sq}$, $\mathcal {RCRA}^{\lambda }_{sq}$, $\mathcal {DRCRA}_{sq}$, and $\mathcal {DRCRA}^{\lambda }_{sq}$, we denote the classes of languages accepted by realtime CRAs, CRAs with $\lambda$-input mode, realtime DCRAs, DCRAs with $\lambda$-input mode, realtime RCRAs, RCRAs with $\lambda$-input mode, realtime deterministic and reversible CRAs (DRCRAs), DRCRAs with $\lambda$-input mode, respectively.

Remarks: Due to the space limitation, most of the details on the results of DCRAs and RCRAs are omitted and the reader is advised to refer to [15]. Instead, Fig. 2 summarizes the inclusion relations among various classes of CRA languages discussed in this paper, where $\mathcal{PN}$ is the class of Petri net languages of $L^{\lambda }$-type [17] and $rev\mathcal{REG}$ is the class of zero-reversible regular languages [1].

Fig. 2.

Inclusion relations among a variety of RA language classes at large.

Last but not least, it should be noted the following:

• (1). Another type of “finite automata with multiset memory (FAMMs)” was proposed and investigated in [14] which employs a rule application mode similar to (but different from) that of RAs, and with FAMM framework a new characterization of Chomsky hierarchy was established.

• (2). The reader is kindly advised to refer to another survey paper on reaction automata theory [13] for more details on the results and discussion left out in this paper because of the space limit.

5 Future Research Topics

Many subjects remain to be investigated along the research direction suggested by reaction automata.

• Inclusion relations and Computing powers:

  • Further refinements of the hierarchy of RA language classes and CRA language classes are strongly encouraged to clarify the inclusion relations in Fig. 2.

  • It is of great importance to explore the relationships between subclasses of $\mathcal {RA}$ and others defined by computing devices based on the multiset rewriting, such as a variety of P-systems and their variants (e.g., P automata and dP automata [5, 16]).

  • It is also intriguing to clarify the relationships between subclasses of CRAs studied here and others defined by reversible computing models such as reversible pushdown automata [8].

  • It remains open whether or not deterministic CRAs (with/without $\lambda$-input mode) in maximally parallel manner are Turing universal.

• Complexity issues: There remain open time complexity issues to be studied in the hierarchies of $\mathcal {RA}$ and $\mathcal {CRA}$ classes. For example, no efforts have been made yet for investigating the time complexity of any class from the hierarchies.

• Decision problems: One may be encouraged to study a variety of the decision problems on subclasses within $\mathcal {RA}$ hierarchy. For example, it is an interesting question to explore the equivalence problem for the class $\mathcal {LRA}$ or the classes of deterministic/reversible CRAs.

• Other issues: It would also be useful to develop methods for simulating a variety of chemical reactions in the real world application, by the use of the framework based on reaction automata. For that purpose, investigating stochastic models based on RAs has to be conducted, and such stochastic versions of RAs may provide useful simulation tools for analyzing any natural phenomena modeled by RAs.

Finally, considering the natural correspondence to (or analogy of) classic theory of automata, we conclude this survey with our firm belief that Reaction Automata are computational devices which deserve much further research efforts.