1 Introduction

The choice of coarse spaces play an important role in the design of fast and robust Schwarz methods for problems of multiscale nature. Standard methods with standard coarse spaces have often difficulties to solve such problems, and even fail to converge due to computing in the finite precision arithmetic. The purpose of this paper is to propose a robust coarse space, adaptively enriched, for solving second order elliptic problems in three dimensions with highly varying coefficients, using the standard finite element for the discretization and the overlapping additive Schwarz method as the preconditioner. The coefficient may have discontinuities both inside and across subdomains. The convergence of the proposed method, as presented in the paper, is independent of the distribution of the coefficient, as well as the jumps in the coefficients, when the coarse space is chosen large enough. For similar works on domain decomposition methods addressing such problems, we refer to [7, 17] and the references therein.

Additive Schwarz methods for solving elliptic problems discretized by the finite element, which was proposed over 30 years ago, have been studied extensively over the past decades, see [16, 18] for an overview. It is known in general that if the coefficients are discontinuous across subdomains but are varying moderately with in each subdomain, then the standard coarse spaces are enough to generate additive Schwarz methods which are robust with respect to those jumps, cf. e.g. [16, 18]. This is however not true in the case when the coefficients may be highly varying and discontinuous almost everywhere, the fact which has in recent years drawn several researchers’ attraction, cf. e.g. [2,3,4,5,6,7,8,9,10,11,12,13,14,15, 17].

In the present work, we extend some of the ideas presented in those papers, and propose to construct a coarse space based on the vertices of the subdomains and a twofold enrichment of the coarse space, which is done through solving two specially designed lower dimensional eigenvalue problems, one on each face common to two neighboring subdomains and one on each interior edge of the subdomains, and chosing the first few eigenfunctions corresponding to the bad eigenmodes. The analysis show that the condition number bound of the resulting system depends only on the threshold used to choose the bad eigenvalues.

The remainder of the paper is organized as follows: in Sect. 2 we introduce our differential problem, and its finite element discretization. In Sect. 3 a classical overlapping Additive Schwarz method is presented. Section 4 is devoted to the construction of our adaptive coarse space and Sect. 5 gives the theoretical bound for the condition number of the resulting system.

2 Discrete Problem

We consider the following elliptic boundary value problem: Find \(u^*\in H^1_0(\varOmega )\)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \int_\varOmega\alpha(x)\nabla u^*\nabla v \: dx&\displaystyle =&\displaystyle \int_\varOmega f v \:d x, \qquad \forall v\in H^1_0(\varOmega), \end{array} \end{aligned} $$
(1)

where α(x) ≥ α 0 > 0 is the coefficient, Ω is a polyhedral domain in \(\mathbb {R}^3\) and f ∈ L 2(Ω). Let \(\mathcal {T}_h\) be the quasi-uniform triangulation of Ω consisting of closed tetrahedra such that \(\bar {\varOmega }=\bigcup _{K\in \mathcal {T}_h}K\). Let h K denote the diameter of K, and \(h=\max _{K\in \mathcal {T}_h} h_K\) the mesh parameter for the triangulation.

We will further assume that α is piecewise constant on T h without any loss of generality. We assume that there exists a coarse nonoverlapping partitioning of Ω into open connected Lipschitz polytopes Ω i, called structures, such that \( \overline {\varOmega }=\bigcup _{i=1}^N \overline {\varOmega }_i\, \) and they are aligned with the fine triangulation, in other words a fine triangle of \(\mathcal {T}_h\) can be contained in only one of the coarse substructures. For the simplicity of presentation, we further assume that these substructures form a coarse triangulation of the domain which is shape regular in the sense of [1].

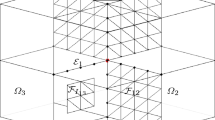
Let \(\mathcal {F}_{i j}\) denote the open face common to subdomains Ω i and Ω j, and let \(\mathcal {E}\) denote an open edge of a substructure, not in ∂Ω. We denote with Ω h, ∂Ω h, Ω ih, ∂Ω ih, \(\mathcal {F}_{i j,h}\), and \(\mathcal {E}_h\), the sets of vertices of the elements of \(\mathcal {T}_h\), corresponding to Ω, ∂Ω, Ω i, ∂Ω i, \(\mathcal {F}_{i j}\), and \(\mathcal {E}\), respectively

Let S h be the standard linear conforming finite element space defined on the triangulation \(\mathcal {T}_h\),

$$\displaystyle \begin{aligned}S_h=S_h(\varOmega):=\{u\in C(\overline{\varOmega})\cap H^1_0(\varOmega): \ v_{|K}\in P_1, \ K \in \mathcal{T}_h\}. \end{aligned}$$

The finite element approximation \(u_h^*\) of (1) is then defined as the solution to the following problem: Find \(u_h^*\in S_h\) such that

$$\displaystyle \begin{aligned} a(u_h^*,v)=\left(f,v\right),\quad \forall v\in S_h. \end{aligned} $$
(2)

Note that α can be scaled without influencing the solution, hence we can easily assume that α(x) ≥ 1. As \(\nabla u_h^*\) is piecewise constant over the fine elements, we can further assume that α is piecewise constants over the elements of \(\mathcal {T}_h\), since \( \int _K \alpha \nabla u \nabla v\: d x = (\nabla u)_{|K}(\nabla v)_{|K} \int _K \alpha (x) \: d x. \)

Since each subdomain inherits a local triangulation \(\mathcal {T}_h(\varOmega _k)\) from \(\mathcal {T}_h(\varOmega )\), two local subspaces can be defined as the following,

$$\displaystyle \begin{aligned}S_h(\varOmega_i):=\{u_{|\overline{\varOmega}_i}: u \in S_h\} \ \ \mbox{and} \ \ S_{h,0}(\varOmega_i):=S_h(\varOmega_i)\cap H^1_0(\varOmega_i), \end{aligned}$$

along with a local projection operator \(\mathcal {P}_i:S_h\rightarrow S_{h,0}(\varOmega _i)\) as the following, find \(\mathcal {P}_i u\in S_{h,0}(\varOmega _i)\) such that

$$\displaystyle \begin{aligned}a_i(\mathcal{P}_i u,v)=a_i(u,v), \quad \forall v\in S_{h,0}(\varOmega_i), \end{aligned}$$

where \(a_i(u,v):=a_{|\varOmega _i}(u,v)=\int _{\varOmega _i} \alpha (x)\nabla u \nabla v \: d x \).

The discrete harmonic part of u ∈ S h(Ω i) is defined as \(\mathcal {H}_iu:=u-\mathcal {P}_i u\), or equivalently as \(\mathcal {H}_iu\in S_h(\varOmega _i)\) which satisfies the following,

$$\displaystyle \begin{aligned} \left\{ \begin{array}{lcc} a_i(\mathcal{H}_iu,v)=0, & & \forall v\in S_{h,0}(\varOmega_i),\\ \mathcal{H}_iu(s)=u(s), & & \forall s\in \partial\varOmega_{ih}. \end{array} \right. \end{aligned} $$
(3)

We say that a function u ∈ S h is discrete harmonic if it is discrete harmonic in each subdomain, i.e. \(u_{|\varOmega _i}=\mathcal {H}_i u_{|\varOmega _i} \ \forall i\).

3 Additive Schwarz Method

In this section, we present the overlapping additive Schwarz method for the discrete problem (2). We refer to [16, 18] for a more general discussion of the method.

3.1 Decomposition of S h

The space S h is decomposed into the local subspaces {V i}i, and the global coarse space V 0, as follows.

$$\displaystyle \begin{aligned} V_i=\{u\in S_h: \ v(x)=0 \ \ \forall x\in\varOmega_h\setminus\overline{\varOmega}_i\}, \quad i=1,\ldots,N, \end{aligned}$$

where u ∈ V i can take nonzero values at the nodes that are in Ω i and on ∂Ω i only, giving {V i}i as subspaces with minimal overlap. The global coarse space V 0 is defined in Sect. 4. For i = 0, …, N, the projection like operators T i: S h → V i are defined as

$$\displaystyle \begin{aligned} a(T_iu,v)=a(u,v),\quad \forall v\in V_i. \end{aligned} $$
(4)

Now, introducing the additive Schwarz operator as \( T:=T_0+\sum _{i=1}^NT_i,\) the original problem (2) can be replaced with the following equivalent problem: Find \(u_h^*\) such that

$$\displaystyle \begin{aligned} T u_h^*=g, \end{aligned} $$
(5)

where \(g=\sum _{i=0}^Ng_i\) and g i = T iu. Note that g i may be computed without knowing the solution \(u_h^*\) of (2): \( \; a(g_i,v)=\left (f,v \right ) \) for all v ∈ V i.

4 Adaptive Vertex Coarse Space

We introduce our adaptive vertex based coarse space in this section. Each edge \(\mathcal {E}\) inherits a 1D triangulation \(\mathcal {T}_h(\mathcal {E})\) from \(\mathcal { T}_h\). For each edge \(\mathcal {E}_h\), let \(S_h(\mathcal {E})\) be the space of traces of functions of S h on the edge, that is the space of continuous piecewise linear functions on \(\mathcal {T}_h(\mathcal {E})\), let \(S_{h,0}(\mathcal {E})=S_h(\mathcal {E})\cap H^1_0(\mathcal {E})\) be its subspace with compact support, and let the edge bilinear form \(a_{\mathcal {E}}(u,v): S_{h,0}(\mathcal {E}) \times S_{h,0}(\mathcal {E}) \rightarrow \mathbb {R}\) be defined as

$$\displaystyle \begin{aligned} a_{\mathcal{E}}(u,v) =\sum_{e\in \mathcal{T}_h(\mathcal{E})} \int_e \overline{\alpha}_e u'v' \: d s, \end{aligned} $$
(6)

where \(\overline {\alpha }_e=\max _{e\subset \partial K} \alpha _K\) is the maximum value of the coefficient over the tetrahedra sharing the fine edge \(e \in \mathcal { T}_h(\mathcal {E})\). Here u′, v′ are the weak derivatives of \(u,v\in S_{h,0}(\mathcal {E})\). The definition of the form \(a_{\mathcal {E}}(u,v)\), in particular the definition of \(\overline {\alpha }\), is introduced in a way which enables us to estimate this form from above by the sum of energy norms over all subdomains which share this edge.

4.1 Vertex Based Interpolation Operator

We introduce the vertex interpolation operator I V : S h(Ω) → S h(Ω) as follows. For u ∈ S h(Ω)

  • I Vu(x) = u(x) where x is a crosspoint (a subdomain vertex inside Ω),

  • I Vu on each edge \(\mathcal {E}\) satisfies, cf. (6):

    $$\displaystyle \begin{aligned} a_{\mathcal{E}}(I_V u,v)=0, \quad \forall v\in S_{h,0}(\mathcal{E}). \end{aligned} $$
    (7)

  • I Vu(x) = 0 at all \(x\in \mathcal {F}_{i j,h}\) for each face \(\mathcal {F}_{i j}\),

  • I Vu is discrete harmonic in the sense as described in Sect. 2.

Note that I Vu is uniquely determined by the values of u at the crosspoints, as (7) uniquely determines I Vu at the edge interior nodes, I Vu is equal to zero at all face interior nodes, and then extended as discrete harmonic to the subdomain interior nodes, cf. (3). The auxiliary coarse space \(\hat {V}_0\) is then defined as the image of this interpolation operator I V, that is \( \hat {V}_0:=Im(I_V)=I_V S_h. \) The coarse space V 0 is the algebraic sum of \(\hat {V}_0\) and a sequence of small subspaces built with functions that are extensions of certain eigenfunctions of the two particular classes of eigenvalue problems presented below.

4.2 Eigenvalue Problems

We start by introducing the two classes of local eigenvalue problems, one on the subdomain edges or the edge interfaces, and one on the subdomain faces or the face interfaces.

4.2.1 Eigenvalue Problem on Edge Interface

Find the eigen pairs \((\lambda _j^{\mathcal {E}},\psi _j^{\mathcal {E}})\in \mathbb {R}_+ \times S_{h,0}(\mathcal {E})\)

$$\displaystyle \begin{aligned} a_{\mathcal{E}}(\psi_j^{\mathcal{E}},v)=\lambda_j^{\mathcal{E}} b_{\mathcal{E}}(\psi_j^{\mathcal{E}},v), \qquad \forall v\in S_{h,0}(\mathcal{E}), \end{aligned} $$
(8)

where \(a_{\mathcal {E}}(u,v)\) is as defined in (6), and

$$\displaystyle \begin{aligned} b_{\mathcal{E}}(u,v)=h^{-4}\int_{G_{\mathcal{E}}} \alpha \hat{u}\:\hat{v} \:dx, \end{aligned} $$
(9)

and \(G_{\mathcal {E}}\) is a 3D layer around and along the edge \(\mathcal {E}\), defined as the sum of all fine tetrahedra of \(\mathcal {T}_h\) those touching \(\mathcal {E}\) by a fine edge or a vertex, and \(\hat {u},\hat {v}\in S_h\) are the discrete zero extensions of \(u,v\in S_{h,0}(\mathcal {E})\). The scaling in the form \(b_{\mathcal {E}}(u,v)\), and in the form b kl(u, v) in (11) below, comes from an inverse inequality and the lines of the proof of Theorem 1, which will be provided in a full version of this paper published elsewhere. The functions \(\psi _j^{\mathcal {E}}\) are extended inside as follows, taking zero values at the nodal points of all remaining edges and faces, and then extending further inside as discrete harmonic in the sense as described in Sect. 2. The extension is denoted by the same symbol. Writing the eigenvalues in the increasing order, i.e. \(0<\lambda _1^{\mathcal {E}}\leq \lambda _2^{\mathcal {E}}\leq \ldots \lambda _{M_{\mathcal {E}}}^{\mathcal {E}}\) for \(M_{\mathcal {E}}=\mathrm {dim}(S_{h,0} (\mathcal {E}))\), we define the local edge spectral component of the coarse space as follows. Let \( V_{\mathcal {E}}= \text{Span}(\psi _j^{\mathcal {E}})_{j=1}^{n_{\mathcal {E}}}, \) where \(n_{\mathcal {E}}\leq M_{\mathcal {E}}\) is the number of eigenfunctions \(\psi _j^{\mathcal {E}}\), whose eigenvalues \(\lambda _j^{\mathcal {E}}\) are less then a given threshold prescribed for each subdomain by the user.

4.2.2 Eigenvalue Problem on Face Interface

Each face \(\mathcal {F}_{k l}\) inherits a 2D triangulation consisting of triangles \(\mathcal {T}_h(\mathcal {F}_{k l})\), and a local face finite element space \(S_h(\mathcal {F}_{k l})\) being the space of traces of S h onto \(\mathcal {F}_{k l}\), and \(S_{h,0}(\mathcal {F}_{k l})=S_h(\mathcal {F}_{k l})\cap H^1_0(\mathcal {F}_{k l})\). We introduce \(\mathcal {\overline {F}}_{I,i j}\) as the sum of closed triangles of \(\mathcal {T}_h(\mathcal {F}_{k l})\) such that all their nodes are not in \(\partial \mathcal {F}_{k l}\).

The face eigenvalue problem is then to find the eigen pairs \((\lambda _j^{k l},\psi _j^{k l})\in \mathbb {R}_+ \times S_{h,0}(\mathcal {F}_{k l})\) such that

$$\displaystyle \begin{aligned} a_{k l}(\psi_j^{k l},v)=\lambda_j^{\mathcal{F}_{k l}} b_{k l}(\psi_j^{k l},v), \qquad \forall v\in S_{h,0}(\mathcal{F}_{k l}), \end{aligned} $$
(10)

where

$$\displaystyle \begin{aligned} a_{k l}(u,v)= \sum_{\tau\subset \mathcal{F}_{I,k l}} \int_\tau \underline\alpha_\tau \nabla u(x) \nabla v(x), \quad b_{k l}(u,v)=h^{-3}\int_{G_{\mathcal{F}_{k l}}} \alpha \hat{u}\:\hat{v} \:dx, {} \end{aligned} $$
(11)

and \( \underline \alpha _\tau =\max _{\tau \subset \partial K} \alpha _K\) is the maximum value of the coefficient over the tetrahedra sharing the fine face \(\tau \in \mathcal { T}_h(F_{I,kl})\), \(G_{\mathcal {F}_{k l}}\) is a 3D layer of tetrahedra around and along the face \(\mathcal {F}_{k l}\), defined as sum of all fine tetrahedra of T h those touching \(\mathcal {F}_{k l}\) by a fine face, a fine edge or a vertex, and \(\hat {u},\hat {v}\in S_h\) are the discrete zero extensions of \(u,v\in S_{h,0}(\mathcal {F}_{k l})\). The functions \(\psi _j^{k l}\) are extended inside as follows, taking zero values at the nodal points of all remaining faces and edges, and then extending further inside as discrete harmonic in the same sense as in Sect. 2. The extension is denoted by the same symbol.

Again, by writing the eigenvalues in the increasing order as \(0\leq \lambda _1^{k l}\leq \lambda _2^{k l}\leq \ldots \lambda _{M_{k l}}^{k l}\) for \(M_{k l}=\mathrm {dim}(S_{h,0} (\mathcal {F}_{k l}))\), we can define the local face spectral component of the coarse space as follows. Let \( V_{k l}= \text{Span}(\psi _j^{k l})_{j=1}^{n_{k l}}, \) where n kl ≤ M kl is the number of eigenfunctions \(\psi _j^{k l}\) whose eigenvalues \(\lambda _j^{k l}\) are less than a given threshold provided by an user.

Finally, The coarse space V 0, after the enrichment takes the following form:

$$\displaystyle \begin{aligned} V_0=\hat{V}_0 + \sum_{\mathcal{F}_{k l}\subset \varGamma} V_{k l} + \sum_{\mathcal{E}\subset \varGamma} V_{\mathcal{E}}. \end{aligned} $$
(12)

Note that \(\hat {V}_0=I_V S_h\), as defined in Sect. 4.1.

Remark 1

The bilinear forms \(b_{\mathcal {E}}(u,v)\), cf. (9), and b kl(u, v), cf. (11), can be defined in other ways. For instance, we can consider larger layers \(G_{\mathcal {E}}\) or \(G_{\mathcal {F}_{k l}}\), or even consider nonzero extensions of \(u \in S_{h,0}(\mathcal {E})\) and \(u \in S_{h,0}(\mathcal {F}_{k l})\), but with minimal energy. We can also take the bilinear forms to be equal to the restrictions of the scaled original energy form to their respective layers or to the whole substructures, that is following the ideas of [10,11,12]. In all cases, we will have similar estimates as in Theorem 1 in the next section.

5 Condition Number

Following the abstract Schwarz framework, cf. [16, 18], and the classical theory of eigenvalue problems, we can show the following theoretical bound on the condition number for the preconditioned system of our method.

Theorem 1

For all u ∈ S h, the following holds,

$$\displaystyle \begin{aligned} \begin{array}{rcl} c\left(1+ \max_{\mathcal{E}} \frac{1}{\lambda_{n_{\mathcal{E}}+1}}+ \max_{\mathcal{F}_{k l}} \frac{1}{\lambda_{n_{k l}+1}} \right)a(u,u)\leq a(Tu,u)&\displaystyle \leq&\displaystyle C \: a(u,u), \end{array} \end{aligned} $$

where C, c are positive constants independent of the coefficient α, the mesh parameter h and the sudomain size H.