Abstract
This paper develops an asynchronous cryptographic protocol for outsourcing arbitrary stateful computation among multiple clients to an untrusted server, while guaranteeing integrity of the data. The clients communicate only with the server and merely store a short authenticator to ensure that the server does not cheat. Our contribution is two-fold. First, we extend the recent hash&prove scheme of Fiore et al. (CCS 2016) to stateful computations that support arbitrary updates by the untrusted server, in a way that can be verified by the clients. We use this scheme to generically instantiate authenticated data types. Second, we describe a protocol for multi-client verifiable computation based on an authenticated data type, and prove that it achieves a computational version of fork linearizability. This is the strongest guarantee that can be achieved in the setting where clients do not communicate directly; it ensures correctness and consistency of outputs seen by the clients individually.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Cloud computing
- Authenticated data types
- Verifiable computation
- Byzantine emulation
- Fork linearizability
1 Introduction
Cloud services are nowadays widely used for outsourcing data and computation because of their competitive pricing and immediate availability. They also allow for online collaboration by having multiple clients operate on the same data; such online services exist for, e.g., shared file storage, standard office applications, or software solutions for specific domains. For authenticity, confidentiality, and integrity of the data, however, the clients have to fully trust the cloud providers, which can access and modify the raw data without the clients’ consent or notice.
The scenario we are concerned with in this paper involves multiple clients that mutually trust each other and collaborate through an untrusted server. A practical example is a group of co-workers using a shared calendar or editing a text document hosted on a cloud server. The protocol emulates multi-client access to an abstract data type \(F\). Given an operation \( o \) and a current state \( s \), the protocol computes \(( s ', r ) \leftarrow F( s , o )\) to generate an updated state \( s '\) and an output \( r \). The role of a client \(C_{ v }\) is to invoke operation \( o \) and obtain response \( r \); the purpose of the server is to store the state of \(F\) and to perform the computation. As an example, let \(F\) be defined for a set of elements where \( o \) can be adding or deleting an element to the set. The state of the functionality will consist of the entire set. The protocol requires that all clients have public keys for digital signatures. Clients communicate only with the server; no direct communication between the clients occurs. Our protocol guarantees the integrity of responses and ensures fork linearizability, in the scenario where the server is untrusted and may be acting maliciously.
Related Work. The described problem has received considerable attention from the viewpoint of distributed systems, starting with protocols for securing untrusted storage [33]. Without communication among clients, the server may always perform a forking attack and omit the effects of operations by some clients in the communication with other clients. Clients cannot detect this attack unless they exchange information about the protocol progress or rely on synchronized clocks; the best achievable consistency guarantee has been called fork linearizability by Mazières and Shasha [33] and has been investigated before [11, 13, 30] and applied to actual systems [8, 12, 13, 28, 44]. Early works [13, 28] focused on simple read/write accesses to a storage service. More recent protocols such as BST [44] and COP [12] allow for emulating arbitrary data types, but require that the entire state be stored and the operations be computed on the client. ACOP [12] and VICOS [8] describe at a high level how to outsource both the state and the computation in a generic way, but neither work provides a cryptographic security proof.
The purpose of an authenticated data type (ADT; often also referred to as authenticated data structure) is to outsource storage of data, and the computation on it, to a server, while guaranteeing the integrity of the data. In a nutshell, while the server stores the data, the client holds a small authenticator (sometimes called digest) that relates to it. Operations on the data are performed by the server, and for each operation the server computes an integrity proof relative to the authenticator. ADTs originated as a generalization of Merkle trees [34], but instantiations of ADTs for various data types have been developed. There exist schemes for such diverse types as sets [14, 40], dictionaries [2, 24, 36], range trees [31], graphs [25], skip lists [23, 24], B-trees [35], or hash tables [39].
Non-interactive verifiable computation has been introduced as a concept to outsource computational tasks to untrusted workers [20]; schemes that achieve this for arbitrary functionalities exist [16, 20, 21, 41] and are closely related to SNARKs (e.g., [6]). These works have the disadvantage, however, that the client verifying the proof needs to process the complete input to the computation as well. This can be avoided by having the client first hash its input and then outsource it storing only the hash locally. The subsequent verifiable computation protocol must then ensure not only the correctness of the computation but also that the input used matches the pre-image of the stored hash (which increases the concrete overhead), an approach that has been adopted in several works [9, 16, 17, 43]. In this work, we build on the latest in this line of works, the hash&prove scheme of Fiore et al. [17], by a mechanism that allows for stateful computation in which an untrusted party can update the state in a verifiable manner, and that can handle multiple clients. An alternative approach for verifiable computation focuses on specific computation tasks (restricted in generality, but often more efficient), such as polynomial evaluation [4, 7], database queries [37, 45], or matrix multiplication [18].
All these works target a setting where a single client interacts with the server, they do not support multiple clients collaborating on outsourced data. The only existing approaches that capture multi-client verifiable computation are by Choi et al. [15] and Gordon et al. [26]; yet, they only support stateless computations where all clients send their inputs to the server once, the latter evaluates a function on the joint data and returns the output. Another recent related work provides multi-key homomorphic authenticators for circuits of (bounded) polynomial depth [19]. Our work differs in that it allows stateful computation on data that is permanently outsourced to the server and updated through computations initiated by the clients. López-Alt et al. [29] address a complementary goal: they achieve privacy, but do not target consistency in terms of linearizability of a stateful multi-client computation. Also, their protocol requires a round of direct communication between the clients, which we rule out.
Contributions. Our first contribution is a new and general definition of a two-party ADT, where the server manages the state of the computation, performs updates and queries; the client invokes operations and receives results from the server. This significantly deviates from standard three-party ADT s (e.g. [40, 42]) that differentiate between a data owner, the untrusted server, and client(s). The owner needs to store the entire data to perform updates and publish the new authenticator in a trusted manner, while the client(s) may only issue read-only queries to the server. Our definition allows the untrusted server to perform updates such that the resulting authenticator can be verified for its correctness, eliminating the need to have a trusted party store the entire data. The definition also generalizes existing two-party ADTs [22, 38], as we discuss in Sect. 3.
We then provide a general-purpose instantiation of an ADT, based on verifiable computation from the work of Fiore et al. [17]. Our instantiation captures arbitrary stateful deterministic computation, and the client stores only a short authenticator which consists of two elements in a bilinear group.
We also devise computational security definitions that model the distributed-systems concepts of linearizability and fork linearizability [33] via cryptographic games. This allows us to prove the security of our protocol in a computational model by reducing from the security of digital signatures and ADTs—all previous work on fork linearizability idealized the cryptographic schemes.
Finally, we describe a “lock-step” protocol to satisfy the computational fork linearizability notion, adapted from previous work [13, 33]. The protocol guarantees fork-linearizable multi-client access to a data type. It is based on our definition of ADTs; if instantiated with our ADT construction, it is an asynchronous protocol for outsourcing any stateful (deterministic) computation with shared access in a multi-client setting.
2 Preliminaries
We use the standard notation for the sets of natural numbers \(\mathbb {N}\), integers \(\mathbb {Z}\), and integers \(\mathbb {Z}_p\) modulo a number \(p \in \mathbb {N}\). We let \(\epsilon \) denote the empty string. If Z is a string then |Z| denotes its length, and \(\circ \) is an operation to concatenate two strings. We consider lists of items, where \([\ ]\) denotes the empty list, L[i] means accessing the \(i\)-th element of the list L, and \(L \leftarrow L \circ x\) means storing a new element x in L by appending it to the end of the list. If \(\mathcal {X}\) is a finite set, we let  denote picking an element of \(\mathcal {X}\) uniformly at random and assigning it to x. Algorithms may be randomized unless otherwise indicated. If A is an algorithm, we let \(y \leftarrow A(x_1,\ldots ;r)\) denote running A with uniform random coins r on inputs \(x_1,\ldots \) and assigning the output to y. We use
denote picking an element of \(\mathcal {X}\) uniformly at random and assigning it to x. Algorithms may be randomized unless otherwise indicated. If A is an algorithm, we let \(y \leftarrow A(x_1,\ldots ;r)\) denote running A with uniform random coins r on inputs \(x_1,\ldots \) and assigning the output to y. We use  as shorthand for \(y \leftarrow A(x_1,\ldots ;r)\). For an algorithm that returns pairs of values, \((y, \_) \leftarrow A(x)\) means that the second parameter of the output is ignored; this generalizes to arbitrary-length tuples. The security parameter of cryptographic schemes is denoted by \(\lambda \).
as shorthand for \(y \leftarrow A(x_1,\ldots ;r)\). For an algorithm that returns pairs of values, \((y, \_) \leftarrow A(x)\) means that the second parameter of the output is ignored; this generalizes to arbitrary-length tuples. The security parameter of cryptographic schemes is denoted by \(\lambda \).
We formalize cryptographic security properties via games, following in particular the syntax of Bellare and Rogaway [5]. By \(\Pr [\mathbf {G}]\) we denote the probability that the execution of game \(\mathbf {G}\) returns \( \textsc {True} \). We target concrete-security definitions, specifying the security of a primitive or protocol directly in terms of the adversary advantage of winning a game. Asymptotic security follows immediately from our statements. In games, integer variables, set, list and string variables, and boolean variables are assumed initialized, respectively, to \(0, \emptyset , []\) and \(\epsilon \), and \( \textsc {False} \).
System Model. The security definition for our protocol is based on well-established notions from the distributed-systems literature. In order to make cryptographic security statements and not resort to modeling all cryptography as ideal, we provide a computational definition that captures the same intuition.
Recall that our goal is to enable multiple clients \(C_{1}, \dots , C_{ u }\), with \( u \in \mathbb {N}\), to evaluate an abstract deterministic data type \(F: ( s , o ) \mapsto ( s ', r )\), where \( s , s ' \in S\) describe the global state of \(F, o \in O\) is an input of a client, and \( r \in A\) is the corresponding output or response. Each client may exchange messages with a server over an asynchronous network channel. The clients can provide inputs to \(F\) in an arbitrary order. Each execution defines a history \(\sigma \), which is a sequence of input events \((C_{ v }, o )\) and output events \((C_{ v }, r )\); for simplicity, we assume \(O\cap A= \emptyset \). An operation directly corresponds to an input/output event pair and vice versa, and an operation is complete in a history \(\sigma \) if \(\sigma \) contains an output event matching the input event.
In a sequential history, the output event of each operation directly follows the corresponding input event. Moreover, an operation \( o \) precedes an operation \( o '\) in a history \(\sigma \) if the output event of \( o \) occurs before the input event of \( o '\) in \(\sigma \). Another history \(\sigma '\) preserves the (real-time) order of \(\sigma \) if all operations of \(\sigma '\) occur in \(\sigma \) as well and their precedence relation in \(\sigma \) is also satisfied in \(\sigma '\). The goal of a protocol is to emulate \(F\). The clients only observe their own input and output events. The security of a protocol is defined in terms of how close the histories it produces are to histories produced through invocations of an ideal shared \(F\).
Linearizability. A history \(\sigma \) is linearizable with respect to a type \(F\) [27] if and only if there exists a sequential permutation \(\pi (\sigma )\) of \(\sigma \) such that
-
\(\pi (\sigma )\) preserves the (real-time) order of \(\sigma \); and
-
the operations of \(\pi (\sigma )\) satisfy the sequential specification of \(F\).
Satisfying the sequential specification of \(F\) means that if \(F\) starts in a specified initial state \( s _0\), and all operations are performed sequentially as determined by \(\pi (\sigma ) = o _1, o _2, \dots \), then with \(( s _ j , r _ j ) \leftarrow F( s _{ j -1}, o _ j )\), the output event corresponding to \( o _ j \) contains output \( r _ j \).
Linearizability is a strong guarantee as it specifies that the history \(\sigma \) could have been observed by interacting with the ideal \(F\), by only (possibly) exchanging the order of operations which were active concurrently. Unfortunately, as described in the introduction, linearizability cannot be achieved in the setting we are interested in.
Fork Linearizability. A history \(\sigma \) is called fork-linearizable with respect to a type \(F\) [13, 33] if and only if, for each client \(C_{ v }\), there exists a subsequence \(\sigma _ v \) of \(\sigma \) consisting only of complete operations and a sequential permutation \(\pi _ v (\sigma _ v )\) of \(\sigma _ v \) such that:
-
All complete operations in \(\sigma \) occurring at client \(C_{ v }\) are in \(\sigma _ v \), and
-
\(\pi _ v (\sigma _ v )\) preserves the real-time order of \(\sigma _ v \), and
-
the operations of \(\pi _ v (\sigma _ v )\) satisfy the sequential specification of \(F\), and
-
for every \( o \in \pi _ v (\sigma _ v ) \cap \pi _{ v '}(\sigma _{ v '})\), the sequence of events preceding \( o \) in \(\pi _ v (\sigma _ v )\) is the same as the sequence of events that precede \( o \) in \(\pi _{ v '}(\sigma _{ v '})\).
Fork linearizability is weaker than linearizability in that it requires consistency with \(F\) only with respect to permutations of sub-sequences of the history. This models the weaker guarantee that is achieved relative to a dishonest server that partitions the set of clients and creates independent forks of the computation in each partition. Intuitively, fork linearizability formalizes that this partitioning attack is the only possible attack; the partitions will remain split forever, and the executions within the partitions are linearizable. Fork linearizability is the strongest achievable guarantee in the setting we consider [33].
Abortable Services. When operations of \(F\) cannot be served immediately, a protocol may decide to either block or abort. Aborting and giving the client a chance to retry the operation at his own rate often has advantages compared to blocking, which might delay an application in unexpected ways. As in previous work that permitted aborts [1, 8, 12, 30], we allow operations to abort and augment \(F\) to an abortable type \(F'\) accordingly. \(F'\) is defined over the same set of states \(S\) and operations \(O\) as \(F\), but returns a tuple defined over \(S\) and \(A\cup \{ \textsc {busy} \}\). \(F'\) may return the same output as \(F\), but \(F'\) may also return \( \textsc {busy} \) and leave the state unchanged, denoting that a client is not able to execute F. Hence, \(F'\) is a non-deterministic relation and satisfies \(F'( s , o ) = \{ ( s , \textsc {busy} ), F( s , o ) \} \; .\)
Verifiable Computation. A verifiable computation scheme \( \textsc {VC} \) specifies the following. A key-generation algorithm \( \textsc {VC} . \textsc {keygen} \) that takes as input security parameter \(\lambda \) and relation \(R \subset U \times W\) and produces a pair  of evaluation key \( ek \) and verification key \( vk \). An algorithm \( \textsc {VC} . \textsc {prove} \) that takes as input evaluation key \( ek , u \in U\), and witness \(w \in W\) such that \((u,w) \in R\), and returns a proof
of evaluation key \( ek \) and verification key \( vk \). An algorithm \( \textsc {VC} . \textsc {prove} \) that takes as input evaluation key \( ek , u \in U\), and witness \(w \in W\) such that \((u,w) \in R\), and returns a proof  . As a concrete example, in the case of a circuit-based SNARK [16, 41] the witness w consists of the assignments of the internal wires of the circuit. An algorithm \( \textsc {VC} . \textsc {verify} \) that takes as input the verification key \( vk \), input u, and proof \(\xi \), and returns a Boolean \( \textsc {True} / \textsc {False} \leftarrow \textsc {VC} . \textsc {verify} ( vk , u, \xi )\) that signifies whether \(\xi \) is valid.
. As a concrete example, in the case of a circuit-based SNARK [16, 41] the witness w consists of the assignments of the internal wires of the circuit. An algorithm \( \textsc {VC} . \textsc {verify} \) that takes as input the verification key \( vk \), input u, and proof \(\xi \), and returns a Boolean \( \textsc {True} / \textsc {False} \leftarrow \textsc {VC} . \textsc {verify} ( vk , u, \xi )\) that signifies whether \(\xi \) is valid.
The correctness error of \( \textsc {VC} \) is the probability that the verification of an honestly computed proof for a correct statement returns \( \textsc {False} \). The soundness error is the advantage of a malicious prover to produce an accepting proof of a false statement. Both quantities must be small for a scheme to be useful.
The verifiable computation schemes we use in this work have a special property referred to as offline-online verification, and which is defined when the set U can be written as \(U = X \times V\). In particular, for those schemes there exist algorithms \( \textsc {VC} . \textsc {offline} \) and \( \textsc {VC} . \textsc {online} \) such that
Hash&prove Schemes. We again consider the relation \(R \subseteq U \times W\). A hash&prove scheme \( \textsc {HP} \) then allows to prove statements of the type \(\exists w \in W: R(u,w)\) for a given \(u \in U\); one crucial property of hash&prove schemes is that one can produce a short proof of the statement (using the witness w), such that the verification does not require the element \(u \in U\) but only a short representation of it.
In more detail, a multi-relation hash&prove scheme as defined by Fiore et al. [17] consists of five algorithms:
-
\( \textsc {HP} . \textsc {setup} \) takes as input security parameter \(\lambda \) and produces public parameters
 .
. -
\( \textsc {HP} . \textsc {hash} \) takes as input public parameters \( pp \) and a value \(x \in X\) and produces a hash \( h _x \leftarrow \textsc {HP} . \textsc {hash} ( pp , x)\).
-
\( \textsc {HP} . \textsc {keygen} \) takes as input public parameters \( pp \) and a relation R and outputs a key pair
 of evaluation key and verification key.
of evaluation key and verification key. -
\( \textsc {HP} . \textsc {prove} \) takes as input evaluation key \( ek _R\), values \((x,v) \in X \times V\) and witness \(w \in W\) such that \(((x,v), w) \in R\), and produces a proof
 .
. -
Finally, \( \textsc {HP} . \textsc {verify} \) takes as input verification key \( vk _R\), hash \( h _x\), value v, and proof \(\pi \) and outputs a Boolean denoting whether it accepts the proof, written \( \textsc {True} / \textsc {False} \leftarrow \textsc {HP} . \textsc {verify} ( vk _R, h _x,v,\pi )\).
An extractable hash&prove scheme has an additional (deterministic) algorithm \( \textsc {HP} . \textsc {check} \) that takes as input \( pp \) and a hash \( h \) and outputs \( \textsc {True} / \textsc {False} \leftarrow \textsc {HP} . \textsc {check} ( pp , h )\), a Boolean that signifies whether the hash is well-formed (i.e., there is a pre-image).
Correctness of \( \textsc {HP} \) is defined by requiring that the honest evaluation of the above algorithms leads to \( \textsc {HP} . \textsc {verify} \) accepting. A hash&prove scheme has two soundness properties, soundness and hash-soundness. At a high level, both soundness games require an adversary to produce a proof for a false statement that will be accepted by \( \textsc {HP} . \textsc {verify} \). Adversary \(\mathcal {A}\) is given public parameters \( pp \), evaluation key \( ek \), and verification key \( vk \). To break soundness, \(\mathcal {A}\) has to produce a proof for a statement (x, v) that is wrong according to relation R, but the proof is accepted by \( \textsc {HP} . \textsc {verify} \) for \( h _x \leftarrow \textsc {HP} . \textsc {hash} ( pp , x)\) computed honestly.
The purpose of hash soundness is to capture the scenario where \( \textsc {HP} \) supports arguments on untrusted, opaque hashes provided by the adversary. For this, the \( \textsc {HP} . \textsc {hash} \) algorithm must be extractable. The hash-soundness game operates almost as the soundness game, but instead of x, the adversary provides a hash \( h \). The adversary wins if the hash \( h \) cannot be opened consistently (by the extractor \(\mathcal {E}\)) to satisfy the relation; for further explanation, we point the readers to [17, Appendix A.1], but we stress that the extraction is needed in our context.
Finally, we define the collision advantage of adversary \(\mathcal {A}\) as

Hash&Prove for Multi-exponentiation. We recall the hash&prove scheme for multi-exponentiation introduced as \(\mathsf {XP}_\mathcal {E}\) in [17], but keep the details light since we do not use properties other than those already used there. The scheme, which we call \( \textsc {MXP} \) here, uses asymmetric bilinear prime-order groups \(\mathcal {G}_\lambda = (e, \mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T ,p, g_1, g_2)\), with an admissible bilinear map \(e: \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T\), generators \(g_1\in \mathbb {G}1\) and \(g_2\in \mathbb {G}_2\), and group order p. The main aspect we need to know about \( \textsc {MXP} \) is that, it works for inputs of the form \(x = (x_1, \dots , x_n) \in \mathbb {Z}_p^n\) and admissible relations of \( \textsc {MXP} \) are described by a vector \((G_1, \dots , G_n) \in \mathbb {G}_1^n\). The proved relation is the following: \(\prod _{i=1}^n G_i^{x_i} = c_x\) for a given \(c_x\). \( \textsc {MXP} \) uses a hash of the input \(x = (x_1, \dots , x_n) \in \mathbb {Z}_p^n\) to prove correctness across different admissible relations. The hash function is described by a vector \((H_1, \dots , H_n) \in \mathbb {G}_1^n\). For an input \(x = (x_1, \dots , x_n) \in \mathbb {Z}_p^n\), the hash is computed as \(h_x = \prod _{i=1}^n H_i^{x_i}\). In a nutshell, this will be used for proving that \(h_x\) and \(c_x\) encode the same vector x, with respect to a different basis.
Fiore et al. [17] prove \( \textsc {MXP} \) adaptively hash-sound under the Strong External DDH and the Bilinear n-Knowledge of Exponent assumptions. They then combine \( \textsc {MXP} \) with schemes for online-offline verifiable computation that use an encoding of the form \(\prod _{i=1}^n G_i^{x_i} = c_x\) as its intermediate representation, to obtain a hash&prove scheme that works for arbitrary (stateless) computations. We describe their construction in more detail in Sect. 4, before explaining our scheme that follows the same idea but extends to stateful computations.
3 Authenticated Data Types
Authenticated data types, which originated as an abstraction and generalization of Merkle trees [34], associate with a (potentially large) state of the data type a short authenticator (or digest) that is useful for verification of the integrity of operations on the state. In more detail, an abstract data type is described by a state space \(S\) with a function \(F: S\times O\rightarrow S\times A\) as before. F takes as input a state \( s \in S\) of the data type and an operation \( o \in O\) and returns a new state \( s '\) and the response \( r \in A\). The data type also specifies the initial state \( s _0 \in S\).
Here, we present a definition for what is known in the literature as a “two-party” authenticated data type (ADT) [38]. The interaction is between a client, i.e., a party that owns \(F\) and wants to outsource it, and an untrusted server that undertakes storing the state of this outsourced data type and responding to subsequent operations issued. The client, having access only to a succinct authenticator and the secret key of the scheme, wishes to be able to efficiently test that requested operations have been performed honestly by the server (see [38] for a more detailed comparison of variants of ADT modes of operation). An authenticated data type \( \textsc {ADT} \) for \(F\) consists of the following algorithms:
-
 : This algorithm sets up the secret key and the public key for the ADT scheme, for security parameter \(\lambda \). It also outputs an initial amended state \( ad \) and a succinct authenticator \( a \). We implicitly assume from now on that the public key \( pk \) is part of the secret key \( sk \) as well as the server state \( ad \). We also assume that the actual initial state \( s _0\) and authenticator \( a \) are part of \( ad \).
: This algorithm sets up the secret key and the public key for the ADT scheme, for security parameter \(\lambda \). It also outputs an initial amended state \( ad \) and a succinct authenticator \( a \). We implicitly assume from now on that the public key \( pk \) is part of the secret key \( sk \) as well as the server state \( ad \). We also assume that the actual initial state \( s _0\) and authenticator \( a \) are part of \( ad \). -
 : This algorithm takes an operation \( o \), applies it on the current version of \( ad \), and provides a correctness proof \(\pi \), from which a response \( r \) can be extracted.
: This algorithm takes an operation \( o \), applies it on the current version of \( ad \), and provides a correctness proof \(\pi \), from which a response \( r \) can be extracted. -
 : The algorithm takes the current authenticator \( a \), an operation o, and a proof \(\pi \), verifies the proof with respect to the authenticator and the operation, outputting local output \( r \), the updated authenticator \( a '\), and an additional authentication token \(t\).
: The algorithm takes the current authenticator \( a \), an operation o, and a proof \(\pi \), verifies the proof with respect to the authenticator and the operation, outputting local output \( r \), the updated authenticator \( a '\), and an additional authentication token \(t\). -
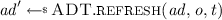 : The algorithm updates the amended state from \( ad \) to \( ad '\), using operation \( o \) and authentication token \(t\) provided by the client.
: The algorithm updates the amended state from \( ad \) to \( ad '\), using operation \( o \) and authentication token \(t\) provided by the client.
An ADT has to satisfy two conditions, correctness and soundness. Correctness formalizes that if the ADT is used faithfully, then the outputs received by the client are according to the abstract data type \(F\).
Definition 1
(Correctness). Let \( s _0\) be the initial state of data type \(F\) and \( o _1, \dots , o _ m \) be a sequence of operations. The ADT scheme \( \textsc {ADT} \) is correct if in the following computation, the assertions are always satisfied.

The second requirement for the ADT, soundness, states that a dishonest server cannot cheat. The game \(\mathbf {G}_{ \textsc {ADT} }^\mathrm {sound}\) described in Fig. 1 formalizes that it must be infeasible for the adversary (a misbehaving server) to produce a proof that makes a client accept a wrong response of an operation. The variable \( forged \) tracks whether the adversary has been successful. The list \(L[\ ]\) is used to store valid pairs of state and authenticator of the ADT, and is consequently initialized with \(( s _0, a )\) of a newly initialized ADT in position 0. The adversary \(\mathcal {A}\) is initialized with \(( ad , a )\) and can repeatedly query the verify oracle in the game by specifying an operation \( o \), the index \( pos \in \mathbb {N}\) of a state on which \( o \) shall be executed, and a proof \(\pi \). The challenger obtains state \( s \) and authenticator \( a \) of the \( pos \)-th state from the list \(L[\ ]\). The challenger (a) checks whether \( \textsc {ADT} . \textsc {verify} \) accepts the proof \(\pi \), and (b) computes the new state \( s '\) and the output \( r '\) using the correct \(F\) and state \( s \), and sets \( forged \) if the proof verified but the output \( r \) generated by \( \textsc {ADT} . \textsc {verify} \) does not match the “ideal” output \( r '\).
This game formulation ensures the outputs provided to the clients are always correct according to \(F\) and the sequence of operations performed, but also allows the adversary to “fork” and compute different operations based on the same state. This is necessary for proving the security of the protocol described in Sect. 6. Unlike for the output \( r \), the game does not formalize an explicit correctness condition for \( ad '\) to properly represent the state \( s '\) of \(F\) as updated by \( o '\); this is only modeled through the outputs generated during subsequent operations. Indeed, in the two-party model, the internal state of the server cannot be observed, and only the correctness of the responses provided to clients matters.
Definition 2
(Soundness). Let \(F\) be an abstract data type and \( \textsc {ADT} \) an ADT for \(F\). Let \(\mathcal {A}\) be an adversary. The soundness advantage of \(\mathcal {A}\) against \( \textsc {ADT} \) is defined as \(\mathrm {Adv}^{ \textsc {sound} }_{ \textsc {ADT} }\left( \mathcal {A}\right) \ := \ \Pr \left[ \mathbf {G}_{ \textsc {ADT} }^\mathrm {sound} \right] \).
To exclude trivial schemes in which the server always sends the complete state to the clients, we explicitly require that the authenticator of the clients must be succinct. More concretely, we require that the size of the authenticator is independent of the size of the state.
Definition 3
(Succinctness). Let \(F\) be an abstract data type and \( \textsc {ADT} \) an ADT with security parameter \(\lambda \) for \(F\). Then \( \textsc {ADT} \) is succinct if the bit-length of the authenticator \( a \) is always in \(\mathcal {O}(\lambda )\).
Very few existing works seek to define a two-party authenticated data structure [22, 38], since most of the literature focuses on a three-party model where the third party is a trusted data manager that permanently stores the data and is the sole entity capable of issuing updates.
The definition of [38] differs from ours as it only supports a limited class of functionalities. It requires the update issuer to appropriately modify \( ad \) himself and provide the new version to the server and, as such, this definition can only work for structures where the part of the \( ad \) that is modified after an update is “small” (e.g., for a binary hash tree, only a logarithmic number of nodes are modified). The definition of [22] supports general functionalities however, unlike ours, it cannot naturally support randomized ADT schemes as it requires the client to be able to check the validity of the new authenticator \( a '\) after an update; in case a scheme is randomized, it is not clear whether this check can be performed. In our soundness game from Fig. 1, the adversary can only win by providing a bad local output r (which, by default, is empty in the case of updates) and not with a bad authenticator, which makes it possible to handle randomized constructions. We note that our construction from Sect. 4 does not exploit this, as it is deterministic.
4 A General-Purpose Instantiation of ADT
This section contains one main technical contribution of this work, namely a general-purpose instantiation of ADT s defined in Sect. 3. Our scheme builds on the work of Fiore et al. [17], which defined hash&prove schemes in which a server proves the correctness of a computation (relative to a state) to a client that only knows a hash value of the state. The main aspect missing from [17] is the capability for an untrusted server to update the state and produce a new (verifiable) hash. The hash of an updated state can be computed incrementally as described in [17, Sect. 4.4].
Before we start describing our scheme, we recall some details of the hash&prove scheme of Fiore et al. [17]. Their scheme allows to verifiably compute a function \(f: Z \rightarrow V\) on an untrusted server, where the verification by the client does not require \(z \in Z\) but only a hash \(h_z\) of it. In accordance with the verifiable computation schemes for proving correctness of the computation, they set \(U = Z \times V\) and consider a relation \(R_f \subseteq U \times W\) such that for a pair \((z,v) \in U\) there is a witness \(w\in W\) with \(((z,v),w) \in R_f\) if and only if \(f(z) = v\). In other words, proving \(\exists w: ((z,v),w) \in R_f\) implies that \(f(z) = v\). The format of the witness w depends on the specific verifiable computation scheme in use, e.g., it may be the assignments to the wires of the circuit computing f(z).
Fiore et al. proceed via an offline-online verifiable computation scheme \( \textsc {VC} \) and a hash-extractable hash&prove scheme for multi-exponentiations \( \textsc {MXP} \). Recall that \( \textsc {MXP} \) uses a hash function that is described by a vector \( pp = (H_1, \dots , H_n) \in \mathbb {G}_1^n\) and computed as \(h_z \leftarrow \textsc {MXP} . \textsc {hash} ( pp , z) = \prod _{i=1}^n H_i^{z_i}\) for \(z = (z_1, \dots , z_n) \in \mathbb {Z}_p^n\). The hash \(h_z\), which is known to the client, is computed via \( \textsc {MXP} . \textsc {hash} ( pp , \cdot )\). The offline-online property of the scheme \( \textsc {VC} \) states that
Fiore et al. further assume that \( \textsc {VC} \) uses an intermediate representation of the form \( \textsc {VC} . \textsc {offline} ( vk , z) = c_z = \prod _{i=1}^n G_i^{z_i}\), where the group elements \(G_1,\dots ,G_n\) are included in the verification key \( vk \). This means, in a nutshell, that \( \textsc {MXP} \) can be used to prove that, for a given z, the hashes \(c_z\) and \(h_z\) encode the same z.
In the complete scheme, the server computes  , using the scheme-dependent witness w referred to above, and the evaluation key \( ek \) for the function f. It also computes \(c_z = \textsc {VC} . \textsc {offline} ( vk , z)\) and sends \(\xi \) and \(c_z\) to the client. The server proves to the client via \( \textsc {MXP} \) that \(c_z\) contains the same value z as the hash \( h _z\) known to the client. The client concludes by verifying the proof via \( \textsc {VC} . \textsc {online} \) with input \(c_z\).
, using the scheme-dependent witness w referred to above, and the evaluation key \( ek \) for the function f. It also computes \(c_z = \textsc {VC} . \textsc {offline} ( vk , z)\) and sends \(\xi \) and \(c_z\) to the client. The server proves to the client via \( \textsc {MXP} \) that \(c_z\) contains the same value z as the hash \( h _z\) known to the client. The client concludes by verifying the proof via \( \textsc {VC} . \textsc {online} \) with input \(c_z\).
Building the New Hash&Prove Scheme. Our goal is to model stateful computations of the type \(F(s, o ) = (s', r )\), using the syntax of the hash&prove scheme. Recall that the syntax of [17] does not handle stateful computations with state updates explicitly. On a high-level, our approach can be seen as computing a stateful F verifiably by first computing \((s', \_) \leftarrow F(s, o )\) without verification (where \(\_\) means that the second component of the output is ignored) and then verifiably computing \(\tilde{F}((s,s'), o ) \mapsto ( d ,r)\) defined via \((\bar{s}, r ) \leftarrow F(s, o ); d \leftarrow \bar{s} \mathrel {\overset{\scriptscriptstyle ?}{=}}s'\). In this approach, the client has to check the proof of the verifiable computation and that \( d = \textsc {True} \). Putting the output state \(s'\) into the input of the verifiable computation of \(\tilde{F}\) has the advantage that we already know how to handle hashes there: via a hash&proof scheme similar to the one of [17]. In the following, we describe our scheme more technically. It can be seen as a variant of [17] with two hashed inputs x and y.
In [17], the output of \( \textsc {VC} . \textsc {offline} ( vk , z)\) is a single value \(c_z\) that is then related to the hash \( h _z\) known to the client via \( \textsc {MXP} \). As we have two individual hashes \( h _x\) and \( h _y\) for the components x and y, respectively, we modify the construction of [17]. For \(z \in X \times Y\) with \(X = Y = \mathbb {Z}_p^n\), we modify \( \textsc {VC} . \textsc {offline} ( vk , z)\) to compute \(c_x \leftarrow \prod _{i=1}^n G_i^{x_i}\) and \(c_y \leftarrow \prod _{i=1}^n G_{n+i}^{y_i}\) for elements \(G_1, \dots , G_{2n}\) that are specified in \( vk \), and prove consistency of \(c_x\) with \( h _x\) and of \(c_y\) with \( h _y\), again using \( \textsc {MXP} \). (Note that this is \(c_z = c_x c_y\).) As argued by [17], many existing VC/SNARK constructions can be written in this way.
Summarizing the above, the main modifications over [17] are (i) that we transform a stateful \(F\) into a stateless \(\tilde{F}\), (ii) that \( \textsc {VC} . \textsc {online} \) obtains two elements \(c_x\) and \(c_y\) from \( \textsc {VC} . \textsc {offline} \), and (iii) that the output bit \( d \) has to be checked. Our stateful hash&prove system \( \textsc {SHP} \) for \(\tilde{F}\) is specified formally in Fig. 2. We formally prove that \( \textsc {SHP} \) is hash sound (analogously to [17, Corollary 4.1]) in the full version [10].
Building a General-Purpose ADT Using Our HP. The scheme \( \textsc {SHP} \) constructed above lends itself well to building a general-purpose ADT. Note that verifiable computation schemes explicitly construct the witness w required for the correctness proof; in fact, the computation of \(F\) can also be used to produce a witness w for the correctness according to \(\tilde{F}\), which is immediate for VC schemes that actually model \(F\) as a circuit [21, 41].
The general-purpose ADT \( \textsc {GA} \), which is more formally described in Fig. 3, works as follows. Algorithm \( \textsc {GA} . \textsc {init} _{}\) generates public parameters \( pp \) and a key pair \(( ek , vk )\) for \( \textsc {SHP} \), and then computes the authenticator \(( a , \_) \leftarrow \textsc {SHP} . \textsc {hash} ( pp , ( s _0, \epsilon ))\) for the initial state \( s _0\) of \(F\). Algorithm \( \textsc {GA} . \textsc {exec} _{}\) computes the new state \( s '\) via \(F\) and authenticator \(( a ', \_) \leftarrow \textsc {SHP} . \textsc {hash} ( pp , ( s ', \epsilon ))\), and generates a correctness proof \(\xi \) for the computation of \(\tilde{F}\) via \( \textsc {SHP} . \textsc {prove} \). We note that we explicitly write out the empty string \(\epsilon \), and ignore the second output component, in algorithm \(( a , \_) \leftarrow \textsc {SHP} . \textsc {hash} ( pp , ( s _0, \epsilon ))\) to be consistent with the hash&prove scheme syntax. We can safely ignore this argument at the implementation level. Algorithm \( \textsc {GA} . \textsc {verify} _{}\) checks the proof \(\xi \) via \( \textsc {SHP} . \textsc {verify} \) and also checks the bit \( d \) output by \(\tilde{F}\) to ensure that the authenticator \( a '\) is correct. Algorithm \( \textsc {GA} . \textsc {refresh} _{}\) simply updates the server state—recomputing \( s '\) and \( a '\) can be spared by caching the values from \( \textsc {GA} . \textsc {exec} _{}\). Instantiating \( \textsc {GA} \) with the schemes of [17] leads to a succinct ADT. We defer the soundness proof to the full version [10].
5 Computational Fork-Linearizable Byzantine Emulation
The application we target in this paper is verifiable multiple-client computation of an ADT \(F\) with an untrusted server for coordination. As the clients may not be online simultaneously, we do not assume any direct communication among them. The goal of the protocol is to emulate an abstract data type \(F: ( s , o ) \mapsto ( s ', r )\). As the server may be malicious, this setting is referred to as Byzantine emulation in the literature [13].
A Byzantine emulation protocol \( \textsc {BEP} \) specifies the following: A setup algorithm \( \textsc {BEP} . \textsc {setup} \) takes as parameter the number \(u\in \mathbb {N}\) of clients and outputs, for each client \( v \in \mathbb {N}\), key information \( clk _ v \), server key information \( svk \), and public key information \( pks \). (The variable \( pks \) models information that is considered public, such as the clients’ public keys.) A client algorithm \( \textsc {BEP} . \textsc {invoke} \) takes as input an operation \( o \in \left\{ 0,1\right\} ^*\), secret information \( clk \in \left\{ 0,1\right\} ^*\), public keys \( pks \in \left\{ 0,1\right\} ^*\) and state \(S_{} \in \left\{ 0,1\right\} ^*\), and outputs a message \(m\in \left\{ 0,1\right\} ^*\) and a new state \(S_{}' \in \left\{ 0,1\right\} ^*\). A client algorithm \( \textsc {BEP} . \textsc {receive} \) takes as input a message \(m\in \left\{ 0,1\right\} ^*\), and \( clk , pks \), and \(S_{}\) as above, and outputs a value \( r \in \left\{ 0,1\right\} ^* \cup \{ \textsc {abort} , \textsc {busy} \}\), a message \(m' \in \left\{ 0,1\right\} ^* \cup \{\bot \}\), and a new state \(S_{}' \in \left\{ 0,1\right\} ^*\). The return value \( \textsc {abort} \) means that the operation has been aborted because of an error or inconsistency of the system, whereas \( \textsc {busy} \) means that the server is busy executing a different operation and the client shall repeat the invocation later. A server algorithm \( \textsc {BEP} . \textsc {process} \) takes as input a message \(m\in \left\{ 0,1\right\} ^*\), purported sender \( v \in \mathbb {N}\), secret information \( svk \in \left\{ 0,1\right\} ^*\), public keys \( pks \in \left\{ 0,1\right\} ^*\)and state \(S_\textsf {s}\in \left\{ 0,1\right\} ^*\), and outputs a message \(m' \in \left\{ 0,1\right\} ^*\), intended receiver \( v '\in \mathbb {N}\), and updated state \(S_\textsf {s}' \in \left\{ 0,1\right\} ^*\).
We then define the security game \(\mathbf {G}_{ \textsc {BEP} , u ,\mathrm {P}}^\mathrm {emu}\) described in Fig. 4. Initially, the game calls \( \textsc {BEP} . \textsc {setup} \) to generate the necessary keys; the setup phase modeled here allows the clients to generate and distribute keys among them. This allows for modeling, for instance, a public-key infrastructure, or just a MAC key that is shared among all clients. (Note that we consider all clients as honest.) The adversary \(\mathcal {A}\), which models the network as well as the malicious server, is executed with input \( pks \)—the public keys of the scheme—and has access to four oracles. Oracle \(\textsc {invoke}( v , o )\) models the invocation of operation \( o \) at client \(C_{ v }\), updates the state \(S_{ v }\), and appends the input event \((C_{ v }, o )\) to the history \(\sigma \). The oracle returns a message \(m\) directed at the server. Oracle \(\textsc {receive}( v , m)\) delivers the message \(m\) to \(C_{ v }\), updates the state \(S_{ v }\), and outputs a response \( r \) and a message \(m'\). If \( r \ne \bot \), the most recently invoked operation of \(C_{ v }\) completes and the output event \((C_{ v }, r )\) is appended to \(\sigma \). If \(m' \ne \bot \), then \(m'\) is a further message directed at the server. Oracle \(\textsc {corrupt}\) returns the server state \(S_\textsf {s}\), and oracle \(\textsc {process}( v ,m)\) corresponds to delivering message \(m\) to the server as being sent by \(C_{ v }\). This updates the server state \(S_\textsf {s}\), and may return a message \(m'\) to be given to \(C_{ v }\). The game returns the result of predicate \(\mathrm {P}\) on the history \(\sigma \), which is initially empty and extended through calls of the types \(\textsc {invoke}( v , o )\) and \(\textsc {receive}( v , m)\). We define two classes of adversaries: full and benign, that we use in the security definition.
Full Adversaries: A full adversary \(\mathcal {A}_{\textsc {full}}\) invokes oracles in an arbitrary order. The only restriction is that, for each \( v \in [1, u ]\), after \(\mathcal {A}_{\textsc {full}}\) has invoked an operation of \(C_{ v }\) (with \(\textsc {invoke}( v ,\cdot )\)), then \(\mathcal {A}_{\textsc {full}}\) must not invoke another operation of \(C_{ v }\) until after the operation completes (when \(\textsc {receive}( v , \cdot )\) returns \(r \ne \bot \)). This condition means that a single client does not run concurrent operations and is often called well-formedness.
Benign Adversaries: A benign adversary \(\mathcal {A}_{\textsc {ben}}\) is restricted like \(\mathcal {A}_{\textsc {full}}\). Additionally, it makes no query to the \(\textsc {corrupt}\) oracle and delivers exactly the messages generated by the protocol; the order of messages belonging to different client operations can be modified as long as the server is allowed to finish each operation before starting the next one.
The protocol must satisfy two conditions, which are made formal in Definition 4. The first condition models the security against malicious servers, and uses the concept of fork linearizability as defined in Sect. 2. In more detail, we use a predicate \(\mathrm {fork}_{F'}\) that determines whether the history \(\sigma \) is fork linearizable with respect to the abortable type \(F'\), and the advantage of adversary \(\mathcal {A}_{\textsc {full}}\) is defined as the probability of producing a history that is not fork-linearizable. The second condition formalizes linearizability with respect to benign adversaries \(\mathcal {A}_{\textsc {ben}}\) and is defined using a predicate \(\mathrm {lin}_{F'} \wedge \mathrm {live}_{F'}\) that formalizes both linearizability and liveness.
Definition 4
Let \( \textsc {BEP} \) be a protocol and \(F\) an abstract data type. The FLBE-advantage of \(\mathcal {A}_{\textsc {full}}\) w.r.t. \( \textsc {BEP} \) and \(F\) is defined as the probability of winning the game \(\mathbf {G}_{ \textsc {BEP} , u ,\mathrm {fork}_{F'}}^\mathrm {emu}\), where \(\mathrm {fork}_{F'}\) denotes the predicate that formalizes fork linearizability with respect to \(F'\). The linearizability advantage of \(\mathcal {A}_{\textsc {ben}}\) is defined as the probability of winning the game \(\mathbf {G}_{ \textsc {BEP} , u ,\mathrm {lin}_{F}\wedge \mathrm {live}_{F}}^\mathrm {emu}\), using the predicate \(\mathrm {lin}_{F}\) that formalizes linearizability with respect to \(F\), and \(\mathrm {live}_{F}\) that formalizes that no operations abort.
The predicates \(\mathrm {fork}_{F'}\) and \(\mathrm {lin}_{F}\) are easily made formal following the descriptions in Sect. 2. The predicate \(\mathrm {live}_{F}\) simply formalizes that for every operation \( o \in \sigma \) there is a corresponding output event.
6 A Lock-Step Protocol for Emulating Shared Data Types
We describe a lock-step protocol that uses an ADT to give multiple clients access to a data type \(F\), and achieves fork linearizability via vector clocks [13, 32, 33] in a setting where the server may be malicious. By lock-step we mean that while the server processes the request of one client, all other clients will be blocked. We prove the security of the scheme based on the unforgeability of the underlying signature scheme and the soundness of the underlying ADT.
The lock-step protocol \( \textsc {LS} \), which is specified formally in Fig. 5, has a setup phase in which the keys of the ADT and one signature key pair per client are generated and distributed. Each client has access to the verification keys of all other clients; this is in practice achieved by means of a PKI. The processing then works as follows. A client \(C_{ v }\) initiates an operation \( o \) by calling \( \textsc {LS} . \textsc {invoke} \), which generates a submit message with \( o \) for the server. When this message is delivered to the server, then it generates a reply message for the client. The client performs local computation, generates a commit message for the server, finally completes the operation by returning the output \( r \).
Authenticated data types ensure the validity of each individual operation invoked by a client. After the client submits operation \( o \), the server executes \( o \) via \( \textsc {ADT} . \textsc {exec} \) and returns the proof \(\pi \) together with the previous authenticator in reply. The client verifies the server’s computation against the previous authenticator, computes the output and the new authenticator via \( \textsc {ADT} . \textsc {verify} \), and sends them to the server in commit. Finally, the new authenticator and the authentication token of the ADT are sent to the server, which updates the state via \( \textsc {ADT} . \textsc {refresh} \).
Digital signatures are used to authenticate the information that synchronizes the protocol state among the clients. After computing a new authenticator \( a '\) via \( \textsc {ADT} . \textsc {verify} \), a client signs \( a '\) and sends it back to the server in commit. When the next client initiates an operation \( o \), the reply message from the server contains the authenticator \( a '\) together with the signature. Checking the validity of this signature ensures that all operations are performed on a valid (though possibly outdated) state.
Vector clocks represent causal dependencies among events occurring in different parts of a network [3]. For clients \(C_{1}, \dots , C_{ u }\), a logical clock is described by a vector \(V \in \mathbb {N}^ u \), where the \( v \)-th component \(V[ v ]\) contains the logical time of \(C_{ v }\). In our protocol, clients increase their local logical with each operation they perform; the vector clock therefore ensures a partial order on the operations. Each client ensures that all operations it observes are totally ordered by updating its vector clock accordingly, and signing and communicating it together with the authenticator. Together with the above mechanism, this ensures that the only attack that is feasible for a server is partitioning the client set and forking the execution.
We prove in the full version [10] that the protocol achieves fork linearizability if the signature scheme and the ADT are secure. On a high level, we first perform game hops in which we idealize the guarantees of the signature scheme and the ADT used by protocol \( \textsc {LS} \). We then show that the history \(\sigma \) produced with idealized cryptography is fork-linearizable.
Theorem 1
The protocol described above emulates the abortable type \(F'\) on a Byzantine server with fork linearizability. Furthermore, if the server is correct, then all histories of the protocol are linearizable w.r.t. \(F\).
References
Aguilera, M.K., Frölund, S., Hadzilacos, V., Horn, S.L., Toueg, S.: Abortable and query-abortable objects and their efficient implementation. In: ACM PODC, pp. 23–32 (2007)
Anagnostopoulos, A., Goodrich, M.T., Tamassia, R.: Persistent authenticated dictionaries and their applications. In: Davida, G.I., Frankel, Y. (eds.) ISC 2001. LNCS, vol. 2200, pp. 379–393. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45439-X_26
Attiya, H., Welch, J.: Distributed Computing: Fundamentals, Simulations and Advanced Topics, 2nd edn. Wiley, Hoboken (2004)
Backes, M., Fiore, D., Reischuk, R.M.: Verifiable delegation of computation on outsourced data. In: ACM CCS, pp. 863–874 (2013)
Bellare, M., Rogaway, P.: The security of triple encryption and a framework for code-based game-playing proofs. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 409–426. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_25
Ben-Sasson, E., Chiesa, A., Genkin, D., Tromer, E., Virza, M.: SNARKs for C: verifying program executions succinctly and in zero knowledge. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 90–108. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_6
Benabbas, S., Gennaro, R., Vahlis, Y.: Verifiable delegation of computation over large datasets. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 111–131. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_7
Brandenburger, M., Cachin, C., Knežević, N.: Don’t trust the cloud, verify: integrity and consistency for cloud object stores. ACM TOPS 20(3), 8:1–8:30 (2017)
Braun, B., Feldman, A.J., Ren, Z., Setty, S.T.V., Blumberg, A.J., Walfish, M.: Verifying computations with state. In: SOSP, pp. 341–357. ACM (2013)
Cachin, C., Ghosh, E., Papadopoulos, D., Tackmann, B.: Stateful multi-client verifiable computation. Cryptology ePrint Archive, Report 2017/901 (2017)
Cachin, C., Keidar, I., Shraer, A.: Fork sequential consistency is blocking. Inf. Process. Lett. 109(7), 360–364 (2009)
Cachin, C., Ohrimenko, O.: Verifying the consistency of remote untrusted services with commutative operations. In: Aguilera, M.K., Querzoni, L., Shapiro, M. (eds.) OPODIS 2014. LNCS, vol. 8878, pp. 1–16. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-14472-6_1
Cachin, C., Shelat, A., Shraer, A.: Efficient fork-linearizable access to untrusted shared memory. In: ACM PODC, pp. 129–138. ACM (2007)
Canetti, R., Paneth, O., Papadopoulos, D., Triandopoulos, N.: Verifiable set operations over outsourced databases. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 113–130. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54631-0_7
Choi, S.G., Katz, J., Kumaresan, R., Cid, C.: Multi-client non-interactive verifiable computation. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 499–518. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_28
Costello, C., Fournet, C., Howell, J., Kohlweiss, M., Kreuter, B., Naehrig, M., Parno, B., Zahur, S.: Geppetto: versatile verifiable computation. In: IEEE S&P. IEEE (2015)
Fiore, D., Fournet, C., Ghosh, E., Kohlweiss, M., Ohrimenko, O., Parno, B.: Hash first, argue later: adaptive verifiable computations on outsourced data. In: ACM CCS, pp. 1304–1316. ACM (2016)
Fiore, D., Gennaro, R.: Publicly verifiable delegation of large polynomials and matrix computations, with applications. In: ACM CCS, pp. 501–512 (2012)
Fiore, D., Mitrokotsa, A., Nizzardo, L., Pagnin, E.: Multi-key homomorphic authenticators. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 499–530. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_17
Gennaro, R., Gentry, C., Parno, B.: Non-interactive verifiable computing: outsourcing computation to untrusted workers. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 465–482. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_25
Gennaro, R., Gentry, C., Parno, B., Raykova, M.: Quadratic span programs and succinct NIZKs without PCPs. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 626–645. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_37
Ghosh, E., Goodrich, M.T., Ohrimenko, O., Tamassia, R.: Verifiable zero-knowledge order queries and updates for fully dynamic lists and trees. In: Zikas, V., De Prisco, R. (eds.) SCN 2016. LNCS, vol. 9841, pp. 216–236. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-44618-9_12
Goodrich, M.T., Papamanthou, C., Tamassia, R.: On the cost of persistence and authentication in skip lists. In: Demetrescu, C. (ed.) WEA 2007. LNCS, vol. 4525, pp. 94–107. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-72845-0_8
Goodrich, M.T., Tamassia, R., Schwerin, A.: Implementation of an authenticated dictionary with skip lists and commutative hashing. In: DISCEX (2001)
Goodrich, M.T., Tamassia, R., Triandopoulos, N.: Efficient authenticated data structures for graph connectivity and geometric search problems. Algorithmica 60(3), 505–552 (2011)
Gordon, S.D., Katz, J., Liu, F.-H., Shi, E., Zhou, H.-S.: Multi-client verifiable computation with stronger security guarantees. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 144–168. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_6
Herlihy, M.P., Wing, J.M.: Linearizability: a correctness condition for concurrent objects. ACM Trans. Program. Lang. Syst. 12(3), 463–492 (1990)
Li, J., Krohn, M., Mazières, D., Shasha, D.: Secure untrusted data repository (SUNDR). In: USENIX, p. 9. USENIX Association (2004)
López-Alt, A., Tromer, E., Vaikuntanathan, V.: On-the-fly multiparty computation on the cloud via multikey fully homomorphic encryption. In: STOC (2012)
Majuntke, M., Dobre, D., Serafini, M., Suri, N.: Abortable fork-linearizable storage. In: Abdelzaher, T., Raynal, M., Santoro, N. (eds.) OPODIS 2009. LNCS, vol. 5923, pp. 255–269. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10877-8_21
Martel, C., Nuckolls, G., Devanbu, P., Gertz, M., Kwong, A., Stubblebine, S.G.: A general model for authenticated data structures. Algorithmica 39, 21–41 (2004)
Mattern, F.: Virtual time and global states of distributed systems. In: Cosnard, M. (ed.) Proceedings of the Workshop on Parallel and Distributed Algorithms, pp. 215–226 (1988)
Mazières, D., Shasha, D.: Building secure file systems out of Byzantine storage. In: ACM PODC, pp. 108–117. ACM (2002)
Merkle, R.C.: A certified digital signature. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 218–238. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_21
Mykletun, E., Narasimha, M., Tsudik, G.: Authentication and integrity in outsourced databases. TOS 2(2), 107–138 (2006)
Naor, M., Nissim, K.: Certificate revocation and certificate update. IEEE J. Sel. Areas Commun. 18(4), 561–570 (2000)
Papadopoulos, D., Papadopoulos, S., Triandopoulos, N.: Taking authenticated range queries to arbitrary dimensions. In: ACM CCS, pp. 819–830 (2014)
Papamanthou, C.: Cryptography for efficiency: new directions in authenticated data structures. Ph.D. thesis, Brown University (2011)
Papamanthou, C., Tamassia, R., Triandopoulos, N.: Authenticated hash tables. In: ACM CCS. pp. 437–448. ACM (2008)
Papamanthou, C., Tamassia, R., Triandopoulos, N.: Optimal verification of operations on dynamic sets. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 91–110. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_6
Parno, B., Howell, J., Gentry, C., Raykova, M.: Pinocchio: nearly practical verifiable computation. In: 2013 IEEE Symposium on Security and Privacy (SP) (2013)
Tamassia, R.: Authenticated data structures. In: Di Battista, G., Zwick, U. (eds.) ESA 2003. LNCS, vol. 2832, pp. 2–5. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-39658-1_2
Wahby, R.S., Setty, S.T.V., Ren, Z., Blumberg, A.J., Walfish, M.: Efficient RAM and control flow in verifiable outsourced computation. In: NDSS (2015)
Williams, P., Sion, R., Shasha, D.: The blind stone tablet: outsourcing durability to untrusted parties. In: NDSS (2009)
Zhang, Y., Katz, J., Papamanthou, C.: IntegriDB: verifiable SQL for outsourced databases. In: ACM CCS, pp. 1480–1491 (2015)
Acknowledgments
This work has been supported in part by the European Commission through the Horizon 2020 Framework Programme (H2020-ICT-2014-1) under grant agreements 644371 WITDOM and 644579 ESCUDO-CLOUD and in part by the Swiss State Secretariat for Education, Research and Innovation (SERI) under contracts 15.0098 and 15.0087. The work by Esha Ghosh was supported in part by NSF grant CNS-1525044.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Cachin, C., Ghosh, E., Papadopoulos, D., Tackmann, B. (2018). Stateful Multi-client Verifiable Computation. In: Preneel, B., Vercauteren, F. (eds) Applied Cryptography and Network Security. ACNS 2018. Lecture Notes in Computer Science(), vol 10892. Springer, Cham. https://doi.org/10.1007/978-3-319-93387-0_33
Download citation
DOI: https://doi.org/10.1007/978-3-319-93387-0_33
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-93386-3
Online ISBN: 978-3-319-93387-0
eBook Packages: Computer ScienceComputer Science (R0)





 .
. of evaluation key and verification key.
of evaluation key and verification key. .
. : This algorithm sets up the secret key and the public key for the ADT scheme, for security parameter
: This algorithm sets up the secret key and the public key for the ADT scheme, for security parameter  : This algorithm takes an operation
: This algorithm takes an operation  : The algorithm takes the current authenticator
: The algorithm takes the current authenticator 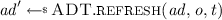 : The algorithm updates the amended state from
: The algorithm updates the amended state from 



