Local Graph Clustering by Multi-network Random Walk with Restart

Abstract

Searching local graph clusters is an important problem in big network analysis. Given a query node in a graph, local clustering aims at finding a subgraph around the query node, which consists of nodes highly relevant to the query node. Existing local clustering methods are based on single networks that contain limited information. In contrast, the real data are always comprehensive and can be represented better by multiple connected networks (multi-network). To take the advantage of heterogeneity of multi-network and improve the clustering accuracy, we advance a strategy for local graph clustering based on Multi-network Random Walk with Restart (MRWR), which discovers local clusters on a target network in association with additional networks. For the proposed local clustering method, we develop a localized approximate algorithm (AMRWR) on solid theoretical basis to speed up the searching process. To the best of our knowledge, this is the first elaboration of local clustering on a target network by integrating multiple networks. Empirical evaluations show that the proposed method improves clustering accuracy by more than 10% on average with competently short running time, compared with the alternative state-of-the-art graph clustering approaches.

1 Introduction

Networks (or graphs) are natural representations of real-world relationships. Network clustering is a fundamental problem and is the basis of many applications such as online recommendation, medical diagnosis, social networks and biological networks analysis [1,2,3,4]. The clustering of a network aims to find groups of nodes that are closely related to each other. Unlike global clustering which retrieves all clusters from a network, local clustering focuses on the subgraph within neighborhood of the query node and is less demanding in computation [5]. With the increasing size of networks, recently local clustering has attracted lots of research interest [6,7,8,9].

Fig. 1.

An example of the Disease-Symptom network. Black nodes are symptoms. Green nodes are lung diseases. Yellow nodes and orange nodes are of tuberculosis and osteomyelitis, respectively. (Color figure online)

Local clustering takes a cohesive group of nodes as the target cluster. The cohesiveness is either evaluated by goodness metrics such as conductance and density [6], or the proximity between nodes according to the network topology [10]. While existing local clustering approaches are based on single networks, cohesiveness of single network does not always reveal the real clustering structure, since the single network is often noisy and incomplete. On the contrary, complete information is usually available through multiple connected networks.

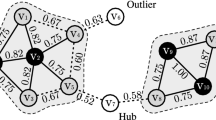
For example, Fig. 1 is a corner of a disease network and an associated symptom network. Because of the incompleteness of the disease network, the lung disease cluster is divided into subgroups with relatively sparse connections in-between. When querying a lung disease from one subgroup, the lung diseases in other groups are hard to be enclosed into the desired local cluster due to the sparse inter-group connections. However, if the symptom network is taken into account, the symptom nodes serve as bridges between lung diseases groups, which integrate the lung diseases into a whole cluster. Moreover, the symptom nodes help to distinguish the lung diseases from tuberculosis and osteomyelitis, since the lung diseases share lots of common symptoms while the tuberculosis and osteomyelitis nodes are left aside.

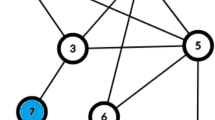
Figure 2 provides another example of 16 scholars from research areas of data mining, database and information retrieval. In the coauthor network, the data mining researchers are isolated into two groups. Associating the authors to their top-3 most published conferences, it is clear that the data mining researchers are linked with each other by various conferences while the authors considered as database or information retrieval researchers are linked to conferences of their specialized domains. For example, among all the authors only Xiaofei He frequently publishes papers in SIGIR. A similar case concerns Flip Korn and H. Jagadish et al., who are intensively relevant to database conferences such as SIGMOD, VLDB and ICDE.

Fig. 2.

An example of the Author-Conference network. Blue nodes are data mining researchers. Green nodes are researchers more relevant to information retrieval and red nodes are researchers closer to the database area. (Color figure online)

In this paper, we propose a local clustering method which integrates multiple networks. The method targets on a specific network and uses other networks to improve the clustering accuracy. To use the links from various networks, we introduce a Multi-network Random Walk with Restart (MRWR) model, which allows the random surfer goes into different networks with differentiated cross-network transition probabilities. Our theoretical analysis shows that MRWR can measure nodes proximity across multiple networks by capturing the multi-network heterogeneity.

As in the local clustering task, only proximity of nodes close to the query node is necessary, we propose a localized approximate MRWR (AMRWR) algorithm for the multi-network node-proximity calculation based on solid theoretical basis. By the AMRWR algorithm, running time of the proposed method is limited and the method is scalable to large networks. To the best of our knowledge, the proposed method is the first local clustering approach that considers multiple networks. The effectiveness and efficiency are validated by both theoretical and empirical studies in the following sections.

2 Related Work

As all current multi-network clustering approaches are global clustering [1, 2, 11,12,13,14,15], our method is more relevant to single network local clustering [6,7,8,9, 16].

Single network local clustering methods can be classified into three categories: local search [5, 17], dense subgraph [6, 8, 16] and node proximity based methods [7, 9, 10]. Conventional local search algorithms examine nodes around query node to improve a goodness function [6] by greedy or combinatorial optimization methods [5, 17]. The searching efficiency of such approaches is limited [7]. The dense subgraph methods try to find a dense subgraph around the query node, which can be a k-core [8], k-truss [18], k-plex [19], etc. The limitation of these methods is that many relevant nodes are not in a dense subgraph and may not be enclosed into the local clusters. Recently random walk and node proximity based methods are successful in local community detection [7, 9]. These approaches rank nodes with respect to the query node and cut a part of nodes with high ranking scores as the local community. All these methods are created for single networks and ignore the heterogeneity of multi-networks.

3 Problem Definitions

In this paper, the multi-network or N-network $\mathcal {G}$ consists of N interconnected single networks. The $i^\text {th}$ single network is represented by the weighted graph $G^{(i)} = (V^{(i)}, E^{(i)})$ with adjacency matrix $\mathbf {A}^{(i)} \in \mathbb {R}_+^{n_i \times n_i}$, where $n_i = |V^{(i)}|$, and each entry $\mathbf {A}^{(i)}_{xy}$ of matrix $\mathbf {A}^{(i)}$ is the weight of edge between node $V^{(i)}_x$ and node $V^{(i)}_y$ in network $G^{(i)}$. In this multi-network model, the connection between single networks $G^{(i)}$ and $G^{(j)}$ is represented by bipartite graph $G^{(ij)} = (V^{(i)}, V^{(j)}, E^{(ij)})$ with adjacency matrix $\mathbf {C}^{(ij)} \in \mathbb {R}_+^{n_i \times n_j}$, where $n_i = |V^{(i)}|$ and $n_j = |V^{(j)}|$. The entry $\mathbf {C}^{(ij)}_{xy}$ is the weight of link between node $V^{(i)}_x$ and $V^{(j)}_y$.

In this work, we focus on the clustering of a specific network, while other networks provide extra information to improve the clustering accuracy. Without loss of generality, we assume the clustering targets on the network $G^{(1)}$ with node set $V^{(1)}$. Given a query node $q \in V^{(1)}$, the goal of local clustering on multi-network $\mathcal {G}$ is to find a local cluster $S \subseteq V^{(1)}$ such that $q \in S$. The nodes in S should be cohesive not only through $G^{(1)}$, but also through other networks connected with $G^{(1)}$.

In the following section, we will discuss the cross-graph cohesiveness measure and the consequent local clustering method. We adopt the widely used random-walk-based proximity score as the cohesiveness criterion since it has been shown to be most effective in capturing local clustering structures [9, 10].

4 Methods

Random-walk-based approaches such as Random Walk with Restart (a.k.a. Personalized PageRank) are commonly used to evaluate the node proximity in the single network  [20, 21]. Compared with other methods, random walk takes advantage of local neighborhood structure of the network and thus has higher performance [7]. In this work, we generalize the single-network random walk to multi-network and propose local clustering methods based on the multi-network random walk.

4.1 Random Walk on Single Network

In Random Walk with Restart (RWR), a random surfer starts from the query node q, and randomly walks to a neighbor node according to the edge weights. At each time point $(t+1)$, the surfer goes on with probability $\alpha$ or returns to the query node q with probability $(1-\alpha )$. The proximity score of node p with respect to node q is defined as the converged probability that the surfer visits node p [21]:

$$\begin{aligned} \mathbf {r}^{(t+1)} = \alpha \cdot \mathbf {r}^{(t)} \cdot \mathbf {P} + (1-\alpha ) \cdot \mathbf {s}, \end{aligned}$$

(1)

where $\mathbf {s}$ is the row vector of the initial distribution with $q^{\text {th}}$ entry as 1 and all other entries 0, and $\mathbf {r}$ is the row vector whose $p^{\text {th}}$ entry is the visiting probability of node p. $\mathbf {P}$ is the row-stochastic transition matrix with entries $\mathbf {P}_{xy} = \frac{\mathbf {A}_{xy}}{\sum _y \mathbf {A}_{xy}}$.

An alternative perspective of Random Walk with Restart is the walk-view [10]. Repeatedly insert the right-hand side of Eq. (1) into $\mathbf {r}$, then

$$\begin{aligned} \begin{aligned} \mathbf {r}&= (1-\alpha )\sum _{k=0}^\infty \alpha ^k \mathbf {sP}^k \end{aligned} \end{aligned}$$

(2)

Since $\mathbf {P}^k$ contains probabilities of all possible length-k walks on the graph, Eq. (2) can be interpreted as that the converged vector $\mathbf {r}$ contains accumulated probabilities of all possible walks for q to each node. As the probabilities of length-k walks are discounted by factor $\alpha ^k$, the proximity is large when there are many short walks between a certain node and the query node.

4.2 Random Walk on Multi-network

The single-network RWR has no knowledge of the heterogeneity of networks, where we can not control the surfer’s behavior towards different networks. In this paper, we propose a Multi-network Random Walk with Restart (MRWR) model, in which the surfer knows the environments and chooses different transition probabilities to distinct networks.

Fig. 3.

Cross-network transition probabilities of random walk on single network and multi-network that contains two networks $G^{(1)}$ and $G^{(2)}$. $\beta ^{(ij)}$ is the transition probability between network $G^{(i)}$ and $G^{(j)}$.

In single-network random walk, the random surfer stays in the network with probability $\beta =1$ (Fig. 3a). However, for a multi-network with N networks, there are $N \times N$ different transition probability $\beta$. Figure 3b gives an example of 2-network, where $\beta ^{(11)}$ is the chance of the random surfer staying in $G^{(1)}$, $\beta ^{(12)}$ is the chance that the random surfer goes from $G^{(1)}$ to $G^{(2)}$, etc. All these transition probabilities form a matrix $\mathbf {B} = \begin{bmatrix} \beta ^{(11)}&\dots&\beta ^{(1N)}\\ \vdots&\ddots&\vdots \\ \beta ^{(N1)}&\dots&\beta ^{(NN)} \end{bmatrix}.$

The matrix $\mathbf {B}$ is also row-stochastic since the sum of probabilities to all networks must be 1. The cross-network decision of random surfer is made by these probabilities. There exist two kinds of MRWR with special matrix $\mathbf {B}$: every row is identical (rank-1), or the matrix is symmetric. We name these two special MRWR as Biased MRWR and Symmetric MRWR, respectively. In Biased MRWR, the random surfer is likely to walk into the networks with large entry value in $\mathbf {B}$ at any time. In Symmetric MRWR, however, the surfer walks between an arbitrary pair of network $G^{(i)}$ and $G^{(j)}$ back and forth with equal probabilities, as $\beta ^{(ij)} = \beta ^{(ji)}$. In this work we focus on the Biased MRWR since we bias the target network.

Comparing with single-network random walk, we may formulate the walk-view of multi-network by the following equation.

$$\begin{aligned} \begin{aligned} \mathbf {r}&= \sum _\sigma (1-\alpha )\alpha ^k \beta _\sigma \mathbf {s} \mathbf {P}_{\sigma } = \sum _\sigma (1-\alpha )\alpha ^k \prod _{i=1}^{k}\beta ^{(\sigma _i\sigma _{i+1})} \mathbf {s} \prod _{i=1}^{k} \mathbf {P}^{(\sigma _i \sigma _{i+1})}\\&= \sum _\sigma (1-\alpha )\alpha ^k \mathbf {s} \prod _{i=1}^{k} \beta ^{(\sigma _i\sigma _{i+1})} \mathbf {P}^{(\sigma _i \sigma _{i+1})}, \end{aligned} \end{aligned}$$

(3)

where $\sigma = \langle \sigma _1, \sigma _2, \dots \sigma _{k+1} \rangle$ is an arbitrary walk with length $k\ge 0$, whose $i^{\text {th}}$ node is in network $G^{(\sigma _i)}$, $1 \le \sigma _i \le N$. Similar with single-network RWR, $\alpha$ acts as the discount factor for length of walks. $\mathbf {P}_\sigma = \prod _{i=1}^k \mathbf {P}^{(\sigma _i\sigma _{i+1})}$ is the transition matrix of walk $\sigma$, and $\beta _\sigma = \prod _{i=1}^k \beta ^{(\sigma _i \sigma _{i+1})}$ is the heterogeneous discount factor of walk $\sigma$. For the transition matrix on multi-network, $\mathbf {P}^{(ij)}_{xy} = \frac{\mathbf {A}^{(i)}_{xy}}{\sum _y \mathbf {A}^{(i)}_{xy}}$ if $i = j$, otherwise $\mathbf {P}^{(ij)}_{xy} = \frac{\mathbf {C}^{(ij)}_{xy}}{\sum _y \mathbf {C}^{(ij)}_{xy}}$.

4.3 Localized Algorithm for MRWR

Due to the nature of local clustering, only proximity of nodes close to the query node is important. The exact RWR vector is not necessary and a localized approximation vector is enough in practice. In this section, we propose an Approximate MRWR calculation method (AMRWR), motivated by the approximate Personalized PageRank (APPR) algorithm [10]. The APPR algorithm simulates $\varepsilon$-approximation of the RWR score vector by a slightly different starting vector $\mathbf {s}'$, where $\mathbf {s}_x - \mathbf {s}'_x \le \varepsilon d(x)$ for every node x, $\varepsilon$ is the pair-wise error bound and d(x) is the degree of node x. Instead of calculating RWR score directly, APPR uses a local network diffusion strategy where values of the initial vector $\mathbf {s}$ diffuse towards both the target score vector $\mathbf {p}$ and itself through the network. Once each entry x of $\mathbf {s}$ is less than $\varepsilon d(x)$, the target vector $\mathbf {p}$ is the approximation of RWR score $\mathbf {r}$.

Our method is different with APPR for the following aspects. First, instead of getting approximated RWR/PPR score on unweighted graph, we extend the calculation to weighted graph. Second, the original APPR is not aware of different networks during the diffuse operations. We solve this problem by pushing different values from vector $\mathbf {s}$ to nodes of different networks, according to the cross-network transition matrix $\mathbf {B}$. Moreover, at each diffuse step, we push as much value as possible from the initial vector to reduce the running time.

The overall MRWR algorithm is demonstrated in Algorithm 1. In the algorithm, Line 2 to 3 are the initialization steps. The while loop from Line 5 to 12 process multi-network diffusion. Finally Line 13 and 14 output the RWR score of nodes in $G^{(1)}$. Here we prove the correctness of Algorithm 1 by Lemma 1 and Theorem 1. All the proofs in this paper can be found in the full version [22].

Lemma 1

The multi-network diffuse operations in Algorithm 1 construct an $\varepsilon$-approximate RWR vector from initial vector $\mathbf {s}$ through graph

$$ \widetilde{\mathbf {P}} = \begin{bmatrix} \beta ^{(11)}\mathbf {P}^{(11)}&\dots&\beta ^{(1N)}\mathbf {P}^{(1N)}\\ \vdots&\ddots&\vdots \\ \beta ^{(N1)}\mathbf {P}^{(N1)}&\dots&\beta ^{(NN)}\mathbf {P}^{(NN)} \end{bmatrix}. $$

Proof

See Sect. A.1 in the full version [22].

Theorem 1

(Effectiveness of the AMRWR Algorithm). The Algorithm 1 generates an $\varepsilon$-approximate vector for MRWR scores $\mathbf {r}$ in Eq. (3).

Proof

See Sect. A.2 in the full version [22].

Theorem 2

(Time Complexity of AMRWR). The local diffusion process in Algorithm 1 runs in $O(\frac{1}{\varepsilon (1-\alpha )})$ time.

Proof

See Sect. A.3 in the full version [22].

After calculating the proximity score of each node with respect to the query node, the clusters can be generated in two ways, the cut process (MRWR-cut) or the sweep process (MRWR-cond). Specifically, MRWR-cut chooses the top-k nodes with largest proximity scores as the target local cluster, while MRWR-cond sorts the node by the proximity score in descending order, and then scans from the top node to get a cluster with minimal conductance.

5 Experiment

We perform extensive experiments to evaluate the effectiveness and efficiency of the proposed method on a variety of real networks and synthetic graphs. The experiments are performed on a PC with 16GB memory, Intel Core i7-6700 CPU at 3.40 GHz frequency, and the Windows 10 operating system. The core functions are implemented by C++.

5.1 Datasets and Baseline Methods

We have 6 multi-networks from 3 real data sources for our experiments.

Disease-Symptom Networks [1]. This dataset contains a disease similarity network with 9,721 diseases and a symptom similarity network with 5,093 symptoms. In this dataset, there are two sets of clustering ground truth for the disease network: level-1 and level-2, where the clusters in level-1 are larger than those of level-2. We use both sets of ground truth, and denote the experiments by DS1 and DS2, accordingly.

Gene-Disease Networks [23]. The gene network represents the functional relationship between 8,503 genes. The disease network is a phenotype similarity network with 5,080 diseases. By flipping these two networks, we have two multi-networks: the Disease-Gene network (DG) and the Gene-Disease network (GD).

Author-Conference Networks [24]. The dataset comprises 20,111 authors and 20 conferences from 4 research areas. Since we have labels of both authors and conferences, we use this dataset as two multi-networks: the Author-Conference network (AC) and the Conference-Author network (CA).

We compare our approaches with six state-of-the-art methods, including densest subgraph methods Query-biased Densest Connected Subgraph (QDC) [6] and k-core clustering [8]; attributed graph clustering methods Attributed Community Query (ACQ) [25] and Focused clustering (FOC) [26]; node proximity measures Random Walk with Restart (RWR) [7] and Heat Kernel Diffusion (HKD) [9]. To be fair, all the baseline methods run on multi-networks and are tuned to their best performances. For attributed network clustering method, nodes of additional network are taken as the attributes of node in the target network. All results are averaged on 10,000 queries if not specifically stated.

5.2 Effectiveness Evaluation

To evaluate effectiveness of the selected methods, we use precision and F1-score as metrics of clustering accuracy. Given the cluster node set U and the ground truth node set V, the F1-score integrates both precision and recall, and is defined as $F(U, V) = 2 \cdot \frac{p \times r}{p + r}$, where $p = \frac{|U \cap V|}{|U|}$ is the precision and $r = \frac{|U \cap V|}{|V|}$ is the recall. The experiments are deployed on real networks. For each multi-network, we randomly pick up query nodes from the labeled ground truth. The $\beta$ of biased cross-network transition matrix $\mathbf {B} = \begin{bmatrix} \beta&1-\beta \\ \beta&1-\beta \end{bmatrix}$ is 0.6 by default, and the forward probability $\alpha$ is 0.99. We set $\beta >0.5$ as we emphasize the target network more than the additional network. Expected cluster sizes of both MRWR-cut and RWR are set to be the average cluster size of ground truth. For sensitivity of parameter $\beta$ please see section B.1 in the full version [22].

Fig. 4.

Improvement of MRWR precision, from clustering on single target network, to the multi-network clustering.

Firstly we evaluate the precision improvement of MRWR on the multi-network, comparing with MRWR on the target network only. In Fig. 4 we can see that the precision increases on every dataset, for both MRWR-cut and MRWR-cnd. The biggest performance gain is achieved by the Conference-Author (CA) network, meaning that the conference network is very noisy and much information is from the additional network. Actually the conference network is a full graph simply created by cosine similarity of keyword vectors, as shown partially in Fig. 2. The precision increment of MRWR-cnd is more obvious for most datasets (Fig. 4b). It is worth reporting that, on multi-networks, the cluster size of MRWR-cnd is 33% less than on the single networks and is closer to the ground truth cluster size. In other words, the clusters generated by MRWR-cnd on multi-network are more dense and reasonable than their single-network counterparts.

Table 1. Accuracy comparison of all selected methods on real multi-networks.

For the accuracy of selected approaches, we use F1-score as it is fair in comparing performance of different methods. Table 1 shows that our methods are overall the best on all networks. For networks DS2 and GD, MRWR-cnd is better than MRWR-cut. For all other networks, MRWR-cut has the best performance. ACQ hits the timeout on network CA and has no result in the table. The MRWR methods are balanced between precision and recall than the baselines. For example, ACQ and FOC have high precision but very low recall, as the methods can hardly enclose more nodes other than the query node due to the sparse links to the additional networks. QDC tends to detect small dense clusters, which decreases its performance on large cluster structures. On the contrary, k-core clustering inclines to a large number of nodes unrelated to the query node. Consequently, its recall is high but the precision is quite low, which also results in low F1-score.

5.3 Efficiency Evaluation

Figure 5 illustrates the average running time of all selected algorithms. For all datasets, the speed of our method outperforms all other approaches except k-core. On the DG and GD networks, MRWR is faster by 1 to 3 orders of magnitude in comparison with other algorithms except for the k-core clustering. Though k-core method is fast in clustering, its accuracy is not competent with other approaches (Table 1). The FOC takes long running time because its global searching strategy. ACQ reaches timeout on the AC network, so we omit its running time in the figure. We also measure the efficiency of MRWR on large synthetic datasets and report the result in section B.2 in the full version [22]. It shows that MRWR runs within seconds on networks with millions of nodes.

Fig. 5.

Average running time of a single query in milli-seconds, comparing all methods on all networks.

6 Conclusion

In this paper, we have introduced a local graph clustering method on multi-networks. The clustering is based on the node proximity measurement by multi-network random walk. Compared with the single network local clustering algorithms, our method takes advantage of both additional network connection and the local network structure. Empirical studies show that our method is both accurate and fast in comparison with alternative approaches. The future work is to make the random walk on multi-network more smart by learning the network heterogeneity online.