Leveraging Label Category Relationships in Multi-class Crowdsourcing

Abstract

Current quality control methods for crowdsourcing largely account for variations in worker responses to items by interactions between item difficulty and worker expertise. Few have taken into account the semantic relationships that can exist between the response label categories. When the number of the label categories is large, these relationships are naturally indicative of how crowd-workers respond to items, with expert workers tending to respond with more semantically related categories to the categories of true labels, and with difficult items tending to see greater spread in the responded labels. Based on these observations, we propose a new statistical model which contains a latent real-valued matrix for capturing the relatedness of response categories alongside variables for worker expertise, item difficulty and item true labels. The model can be easily extended to incorporate prior knowledge about the semantic relationships between response labels in the form of a hierarchy over them. Experiments show that compared with numerous state-of-the-art baselines, our model (both with and without the prior knowledge) yields superior true label prediction performance on four new crowdsourcing datasets featuring large sets of label categories.

1 Introduction

Crowdsourcing is a process in which a human intelligence task is solved collectively by a large number of online workers who get paid to independently solve parts of the task that commonly overlap. In recent years, the process has been used by machine learning communities to cheaply collect large quantities of labelled training data, thanks to the development of online service providers, such as Amazon Mechanical Turk¹ and CrowdFlower². While crowdsourcing has shown cost-effectiveness and scalability, it also produces noisy and biased labelled data as its online workforce is much less accurate than in-house experts. Furthermore, many crowdsourcing tasks in practice involve large numbers of unlabelled items under limited budgets, which often results in small numbers of responses collected for each item. Aggregating such small numbers of (oftentimes conflicting) labels using majority vote to infer the true label of each item can be unreliable.

To overcome the above issue, labels must be aggregated in such a way that the influence of “high-quality” responses should outweigh that of those “low-quality” responses for better estimating the true labels. This process is generally known as the Quality Control for Crowdsourcing (QCC). The QCC methods, largely based on statistical modeling, consider expertise of workers to govern the quality of labels they provide to items with greater expertise indicating higher quality of the labels [1,2,3,4]. Furthermore, some of the QCC methods also consider difficulty of items which counteracts worker expertise to undermine the quality of the labels [5,6,7,8,9]. All these methods have achieved overall superior performance over the majority vote. However, assuming individual crowdsourcing tasks contain small numbers of uncorrelated label categories, these methods inevitably ignores the impact of the relationships between response label categories on the quality of workers’ responses to items. In practice, it is not unusual that crowdsourcing tasks can involve labeling data across label categories correlated to one another in terms of large structural semantic relationships. A typical example is the classification of objects in images for building the database of ImageNet³ whose large number of label categories are related through the semantic relationships specified by WordNet⁴. Other examples include the classification of Webpages for the Open Directory Project, called “DMOZ”⁵, and for DBpedia⁶, whose large numbers of categories are connected through semantic relationships maintained by respective online volunteer communities. This paper focuses on leveraging semantic relationships between label categories for improving QCC performance in crowdsourcing problems especially involving highly multi-class labels. The semantic relationships are inherent in such problems and the conventional inference about them is based on human knowledge and reasoning which features prominently in crowdsourcing. Conversely, knowing the semantic relationships should contribute to accurate inference about how responses are formed in highly mult-class crowdsourcing.

When semantic relationships between categories exist in crowdsourcing, crowd-workers with greater expertise tend to respond to the same item with categories more related to the true label for the item. Moreover, the difficult items tend to see more variety in the responses (more distinct categories present) than simpler items. To be more specific, consider a simple measure of relatedness between two label categories k and $k'$ shown below:

$$\begin{aligned} \text {Relatedness}(k,k') = \frac{1}{|\text {shortest}\_\text {path}(k,k')|+1} \end{aligned}$$

(1)

where $|\text {shortest}\_\text {path}(\varvec{\cdot },\varvec{\cdot })|$ is the length of the shortest path between any pair of categories in some known semantic structure (e.g. a graph). Using this relatedness measure, Fig. 1 shows the relationship between the relatedness of the response category to the true label, and three summary statistics (namely the maximum, mean and minimum values) for the response accuracy of workers and the item difficulty (in terms of response error). The crowdsourcing task involved in this case is identifying breeds of dogs in images from ImageNet [10]. Every coloured “violin” area in each sub-figure of Fig. 1 represents the distribution of a particular summary statistics about either the response accuracy of workers or the response errors on items given the true labels. The medians of the areas with the same colours (i.e. the same summary statistics across different relatedness scores) are connected by straight lines in each sub-figure. We observe from Fig. 1 that:

• According to Fig. 1a, more related categories (with higher relatedness scores) to item true labels tend to be chosen more often as responses by workers with higher response accuracy;

• According to Fig. 1b, less related categories (with lower relatedness scores) to item true labels tend to be given more often as responses to more difficult items (i.e. ones with larger response errors in Fig. 1b).

Fig. 1.

(a) Worker response accuracy versus category relatedness. (b) Item difficulty (in terms of response error) versus category relatedness. (Color figure online)

In this paper, we leverage the above observed relationship between category relatedness and worker accuracy/item difficulty for improving the quality control of crowdsourced labels. This is done by encoding the correlations between categories into the conditional probability of a worker giving a label to an item given its true label. Such an encoding can help refine the estimation about the correctness of crowdsourced labels (which is modeled using those conditional probabilities in most QCC methods). The encoding is based on a latent symmetric relatedness matrix where each off-diagonal entry is a real-valued score representing how related categories are to one another. In this case, each category (as a true label/correct response) is associated with a continuous scale accommodating the latent relatedness scores of all the other categories as possible worker responses. We also model expertise of workers and difficulty of items on the same scale.

According to Fig. 1a, a worker with greater expertise and a category more related to the true label should have the estimated values for their respective variables reside further down the positive infinite end of the scale once learned from response data. Likewise from Fig. 1b, an item with greater difficulty and a less related category should have the estimated values situated towards the opposite end of the scale. The interactions between these variables on the scale are captured and transformed into the aforementioned conditional probabilities through an ordered logit model where the difference between item difficulty and worker expertise serves as the response-specific slope, and the off-diagonal terms in the same row of the latent relatedness matrix (corresponding to a latent true label) serve as the intercepts specific to different categories other than the true label. The off-diagonal terms in the matrix share a Normal prior, which can make use of prior knowledge (trees extracted from Wordnet and DMOZ) to better calibrate the estimates for the terms. The contributions of this paper are:

• A novel statistical model that leverages correlations/relationships between label categories for improving quality control of crowdsourced labels.

• The proposed model directly infers the latent relationships between label categories from crowdsourced labels.

• A priori knowledge of relationships between labels (in terms of a semantic hierarchy over concepts) is elegantly incorporated into the proposed model by modifying the prior over the latent relatedness variables.

2 Related Work

Two papers have considered leveraging relationships between label categories [11, 12] for improving quality control of crowdsourced labels. In [12], a model called SEEK was proposed in which the conditional probability of any possible response category a worker can give to an item given its true label category is output from a soft-max function. The function takes in the observed relatedness scores of all the response categories to the true label of the item along with the difficulty of the item and the expertise of the worker. Inside the function, the difference between the difficulty and the expertise is multiplied by the relatedness score of every response category before the results are normalized to form the corresponding conditional probabilities. Since the difference value is the same for all response categories, the conditional probabilities are thus only proportional to the relatedness scores. The larger a score is, the higher the conditional probability of the corresponding response given the true label. In comparison, our model allows the conditional probabilities to be proportional to the joint interaction between the difference and the relatedness scores. In [12], each relatedness score between a pair of categories can vary from 0 to 1. It is 1 when the two categories are the same. It is between 0 and 1 only when one of the categories is a hypernym of the other. Otherwise, the score is always 0. Clearly, this way of pre-computing the relatedness scores between categories constrains the quality control performance of SEEK in crowdsourcing tasks where most of the categories are not hypernyms. In [11], a model called DASM is proposed which share the same idea as SEEK except that the relatedness scores are pre-computed as the inverse of the Euclidean distances between categories in terms of their observed features. Both of these models rely on the availability of the external knowledge about the category relatedness, while our model is able to infer such relatedness directly from responses.

Fig. 2.

The DELRA model with and without encoding observed knowledge matrix $\varvec{X}$ specifying relationships between categories are shown in Fig. 2a and b.

3 Problem Formulation and Proposed Model

Given a large but finite set of categories $\mathcal {K}$ and a set of items $\mathcal {J}$, a set of workers $\mathcal {I}$ have provided a set of responses $\mathcal {R}$ to $\mathcal {J}$. An item $j \in \mathcal {J}$ has one unknown true label $l_j = k$, where $l_j \in \mathcal {L}$, the set of corresponding true labels of individual items in $\mathcal {J}$, and k is a particular category in $\mathcal {K}$. For the set of categories $\mathcal {K}$, there exists a tree structure organizing them in terms of their semantic relationships. The relationships are quantified into an observed real-valued relatedness matrix $\varvec{X} \in \mathbbm {R}^{|\mathcal {K}|\times |\mathcal {K}|}$. Each off-diagonal entry $x_{kk'}$ expresses how related a category $k'$ (as a response to an item) is to another category k as the true label of that item. It is calculated by Eq. (1). Based on these inputs, our model should output a corresponding set of prediction $\hat{\mathcal {L}}$ for the latent item true labels $\mathcal {L}$ such that the overall difference between the former and the latter sets across their corresponding elements is as small as possible.

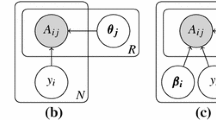
In this paper, we propose the Difficulty-Expertise-Label-Relationship-Aware (DELRA) model, characterized by a latent relatedness matrix $\varvec{S} \in \mathbbm {R}^{|\mathcal {K}|\times |\mathcal {K}|}$. The matrix specifies how related a category $k'$ (as a response to an item) is to another category k (as the true label of that item) in crowdsourcing. We assume $\varvec{S}$ is symmetric so that $s_{kk'} = s_{k'k}$ where $s_{kk'}, s_{k'k} \in \varvec{S}$. This assumption is reasonable as if crowd-workers perceive category $k'$ to be related to category k overall to a certain degree, they should also perceive the relatedness of category k to category $k'$ to the same degree. Based on the assumption, the DELRA model is shown in Fig. 2a, and has the following generative process:

• 1. Draw true label category proportions $\varvec{\theta } \sim \text {Dir}(\varvec{\gamma })$;

• 2. For each pair of categories (k,$k'$) where $k \ne k'$:

  • (a) if $k' > k$ then draw relatedness $s_{kk'} \sim \mathcal {N}(\mu _s, \sigma ^2_s)$; else $s_{kk'} \leftarrow s_{k'k}$⁷;

• 3. For each item $i \in \mathcal {J}$:

  • (a) Draw its true label $l_j \sim \text {Cat}(\varvec{\theta })$;

  • (b) Draw its difficulty $d_j \sim \mathcal {N}(\mu _d, \sigma _d)$;

• 4. For each worker $i \in \mathcal {I}$:

  • (a) Draw her expertise $e_i \sim \mathcal {N}(\mu _e, \sigma ^2_e)$;

• 5. For each worker-item pair (i, j):

  • (a) Draw response $r_{ij} \sim \text {Cat}(\varvec{\pi }_{ijl_j})$ where $\varvec{\pi }_{ijl_j}$ is a $|\mathcal {K}|$-dimensional vector with each element $\pi _{ijl_jk} = P(r_{ij} = k | l_j)$ specified as the difference between consecutive sigmoid functions as follows:

    $$\begin{aligned} \pi _{ijl_jk} = \delta _{ijl_jk} - \max _{k':\delta <\delta _{ijl_jk}}\delta _{ijl_jk'} \quad \text {where}\,\, \delta _{ijl_jl_j}= 1, \delta _{ijl_j0} = 0 \end{aligned}$$

    (2)

    Here $\delta _{ijl_j k}$ is a sigmoid function relating the odds of observing response $r_{ij}=k$ given true label $l_j$ to a linear combination of the relatedness score $s_{l_jk}$, the worker expertise $e_i$ and the question difficulty $d_j$:

    $$\begin{aligned} \delta _{ijl_jk} = \frac{1}{1 + \exp (-(s_{l_jk} - e_i + d_j))} \end{aligned}$$

    (3)

Apart from inferring the relatedness matrix $\varvec{S}$ from responses, our model also allows for the encoding of useful prior knowledge about the entries in each row of the matrix corresponding to a particular category as true labels for items to help calibrate the inference. As shown in Fig. 2b, the Normal prior $\mathcal {N}(\mu _s, \sigma ^2_s)$ in Fig. 2a shared by all the entries in the matrix is now replaced by individual priors centered on the product results between a global coefficient $\beta$ and the observed relatedness matrix $\varvec{X}$ after it is log-transformed followed by standardization, added with Normally distributed noise following $\mathcal {N}(0, \sigma ^2_s)$. Correspondingly, step 2(a) of the above generative process of the DELRA model is now changed to:

• 2. For each pair of categories (k,$k'$) where $k \ne k'$:

  • (a) if $k' > k$ then draw $s_{kk'} \sim \mathcal {N}(\beta x_{kk'}, \sigma ^2_s)$; else $s_{kk'} \leftarrow s_{k'k}$;

The global term $\beta \sim \mathcal {N}(\mu _{\beta },\sigma ^2_{\beta })$. The term $x_{kk'}$ goes through the transformation:

$$\begin{aligned} x_{kk'} \leftarrow \frac{\text {log}(x_{kk'}) - \hat{\mu }_{\text {log}(\varvec{X})}}{\hat{\sigma }_{\text {log}(\varvec{X})}} \end{aligned}$$

(4)

where $\hat{\mu }_{\text {log}(\varvec{X})}$ and $\hat{\sigma }_{\text {log}(\varvec{X})}$ are respectively the sample mean and the sample standard deviation of the logarithm of all the original terms in $\varvec{X}$. The reason behind the logarithm operation is that the outputs from the relatedness function specified by Eq. (1) are very skewed and we do not want such skewness to impact the estimation of the relatedness matrix. The reason behind the standardization operation is that every log-transformed $x_{kk'}$ is negative, thus having a negative mean. We want to adjust them to be centered on zero with scale one to allow for easier setups of priors for other model parameters. After the transformation by Eq. (4), the prior mean $\beta x_{kk'}$ for the relatedness score $s_{kk'}$ suggests how the relatedness between categories according to the semantic knowledge tree tends to correlate with their latent relatedness in crowdsourcing a priori.

4 Parameter Estimation

In this section, we describe how the model parameters are estimated. More specifically, in each iteration of the estimation, we alternate between the Collapsed Gibbs sampling for inferring the true labels of items $\mathcal {L}$ given the current estimates of the other model parameters including the worker expertise $e_i$, the item difficulty $d_j$ and the relatedness matrix $\varvec{S}$, and the LBFGS-B till its convergence for updating these parameters given the current assignment of $\mathcal {L}$.

Collapsed Gibbs Sampling for $\varvec{\mathcal {L}}$: At this stage, we obtain posterior samples for item true labels $\mathcal {L}$ given the current estimates of all the other parameters. The conditional probabilities of true label $l_j$ of item j is obtained by marginalizing out the multinomial probability vector $\varvec{\theta }$, which ends up being:

$$\begin{aligned} P(l_j=k|\mathcal {L}_{\lnot j}, \mathcal {R}_{j}, \{e_i\}_{i\in \mathcal {I}_j}, d_j, \varvec{s}_k, \varvec{\gamma }) \propto \frac{N_{\lnot jk} + \gamma _k}{\sum \limits _{z \in \mathcal {K}}(N_{\lnot jz}+\gamma _{z})} \prod \limits _{i \in \mathcal {I}_j}\pi _{ijkr_{ij}} \end{aligned}$$

(5)

where $\mathcal {I}_j$ is the set of workers who responded item j with a set of responses $\mathcal {R}_{j}$, $\mathcal {L}_{\lnot j}$ is the set of current true label assignments to all the items except j, and $N_{\lnot jk}$ is the number of items except j whose true labels are now inferred as k.

Gradient Descent for Other Parameters: The conditional probability distributions of the other model parameters including $e_i, d_j, \text {and}~S$ are hard to compute analytically due to the presence of the sigmoid function. Instead, we run the LBFGS-B till its convergence on the following objective function Q:

$$ \begin{aligned}&Q=-\log \big (p(\varvec{e}, \varvec{d}, \varvec{S} | \mathcal {R}, \mathcal {L}, \mu _{\{e,d,s\}}, \sigma ^2_{\{e,d,s\}})\big )= -\sum \limits _{j \in \mathcal {J}}\sum \limits _{i \in \mathcal {I}_j}\log (\pi _{ijl_jr_{ij}}) \nonumber \\&\qquad +\frac{1}{2}\bigg [\sum \limits _{i \in \mathcal {I}}\frac{(e_i - \mu _e)^2}{\sigma ^2_e}+\sum \limits _{j \in \mathcal {J}}\frac{(d_j - \mu _d)^2}{\sigma ^2_d}+\sum \limits _{k \in \mathcal {K}}\sum \limits _{k' \in \mathcal {K} \& k' > k}\frac{(s_{kk'} - \mu _s)^2}{\sigma ^2_s}\bigg ] \end{aligned}$$

(6)

The gradient with respect to the label-relatedness term $s_{lk}$ is computed as:

$$\begin{aligned} \frac{\partial Q}{\partial s_{lk}} = -\sum \limits _{j \in \mathcal {J}}\sum \limits _{i \in \mathcal {I}_j}\frac{\partial \log (\pi _{ijl_jr_{ij}})}{\partial s_{lk}} + \frac{s_{lk}}{\sigma ^2_s} \end{aligned}$$

(7)

where for the true label $l=l_j$ and observed response $k=r_{ij}$ we have:

$$\begin{aligned} \frac{\partial \log (\pi _{ijl_jr_{ij}})}{\partial s_{lk}} = \frac{\delta _{ijl_jk}(1-\delta _{ijl_jk})}{\pi _{ijl_jr_{ij}}} \end{aligned}$$

(8)

And for other responses $k\ne r_{ij}$ we have:

(9)

Note that we also impose symmetry on the label relatedness terms $s_{kk'} = s_{k'k}$. The gradients with respect to $e_i$ and $d_j$ are similarly easy to derive and thus omitted due to space limitations.

When observed matrix $\varvec{X}$ is introduced into the model, the coefficient $\beta$ is updated by maximum a posteriori estimation for a linear regression over $\varvec{X}$.

5 Experiments and Results

Datasets: We have collected four new crowdsourcing datasets from CrowdFlower for our experiments. Table 1 summarizes these datasets.

• Dog breed identification (Dog). The images and the set of categories used in this task originate from the Stanford Dog dataset [10]. There are 120 breeds of dogs involved in the task with 10 images for each dog breed randomly sampled from the Stanford dataset. We collected 5 labels for each image about the breed crowd-workers think appearing in that image. The 120 dog breeds are organized under the subtree “Dog” of the WordNet.

• Bird species identification (Bird). The categories involved are species of birds from the Caltech-UCSD Birds 200 dataset [13]. Originally, there are 200 bird species in this dataset, only 72 of which are present in the WordNet. As a result, we have only used these categories for the experiments and randomly sampled 10 images for each of them from the Caltech-UCSD dataset. Since this task is quite difficult, we collect on average 8 labels for each of the images.

• Classification of Webpages about string instruments (Instrument). This task asks for judgements about the sub-directories under which Webpages about string instruments should be put. All the sub-directories share one root directory “Arts/Music/Instruments/String Instruments” from DMOZ. We have collected 5 judgements for each of the 1,323 Webpages across the 193 sub-directories corresponding to different aspects of string instruments.

• Classification of Webpages about movies (Movie). The judgements collected are about the sub-directories from DMOZ under which Webpages about movies should be put. All the sub-directories involved share the root directory “Arts/Movies”. We have collected 5 judgements for each of the 737 Webpages across the 148 sub-directories about different aspects of movies.

Table 1. Dataset summary. The headers correspond to the notations introduced in Sect. 3.

Table 2. The accuracy of different models on inferring the true labels of the items across the four datasets.

5.1 True Label Prediction

To verify the capability of our model on predicting item true labels, we compare it with the following state-of-the-art crowdsourcing quality control methods.

• Generative model of Labels, Abilities, & Difficulties (GLAD) [5]. This model endows every crowd-worker and every item respectively with a latent variable about the worker’s expertise and a variable about the item’s difficulty. The expertise variable is divided by the difficulty variable to account for the probability of the label given by the worker to the item being correct.

• Multi-dimensional Wisdom of Crowds (MdWC) [9]. This model extends the concept of GLAD that worker expertise interacts with item difficulty by making the interaction factorized over latent variable vectors respectively about workers and items. It also adds another variable for each worker to account for their individual biases in choosing label categories.

• Dawid-Skene (DS) [1]. Unlike GLAD and MdWc which estimate the marginal correctness probability of a label, this model estimates the conditional probability of every label with which a worker can respond given each true label.

• Minimax entropy (Minimax) [8]. The same conditional probabilities are estimated in this model. In this case, the total entropy of the conditional probabilities over all the categories as the responses to the items given their true labels is optimized according to the minimax principle with constraints.

• Participant-Mine voting (PM) [4]. The accuracy of each worker and the true label of each item are inferred together using HITS [14] algorithm. An item is treated as a Webpage as in HITS with the total accuracy of the workers responding it as its authority level and the total difference between the true label estimate of the item and its received worker labels as its hub level.

Apart from these baselines, we also compare our model with the Majority Vote (MV), and the original SEEK model discussed in Sect. 2. Moreover, we have also changed the external knowledge matrix input to the SEEK model to be the matrix $\varvec{X}$ input to the DELRA model (called DELRA+$\varvec{X}$) with each entry transformed by Eq. (4) in both cases. We call this model SEEK+$\varvec{X}$ and use it as another baseline. Likewise, we adapt the DASM model by calculating the distance between any pair of label categories using our distance definition specified in Eq. (1) rather than theirs as we do not have any observed feature about label categories. To measure the performance of our model and all the baselines, we use the true label prediction accuracy, defined as $\frac{1}{|\mathcal {J}|}\sum _{j \in \mathcal {J}}\mathbbm {1}\{l_j=\hat{l}_j\}$.

Table 2 shows the results of the true label prediction of both DELRA and all the baselines. We can see that with and without the knowledge matrix $\varvec{X}$ incorporated, the DELRA model respectively outperforms all the baselines by at least 0.6% and 0.3% over the Dog dataset, 0.8% and 0.22% over the Bird dataset, 1.1% and 0.36% over the Instrument dataset and 0.9% and 0.25% over the Movie dataset. Especially, SEEK+$\varvec{X}$ has the exact same knowledge matrix input as DELRA+$\varvec{X}$, but has yielded lower performance even compared to the DELRA model without incorporating $\varvec{X}$. This suggests that not only our model is able to better leverage the external knowledge about semantic relationships between label categories, but also it is a better model in explaining how responses are generated from the interactions among the expertise of workers, the difficulty of items and the relationships between label categories in crowdsourcing.

5.2 True Label Prediction Under Response Sparsity

We now proceed to investigating how DELRA performs under various degrees of sparsity in crowdsourced responses. To do this, we randomly sample different proportions (i.e. between 10% and 50%) of the responses from each of the datasets and average the performance over 10 runs for each model (on each proportion). Figure 3a–d show the results of the true label prediction of all the models under varying degrees of response sparsity across the four datasets. The DELRA model incorporating the knowledge matrix $\varvec{X}$ clearly beats all the baselines with convincing margins across 10% to 50% of the total responses from each dataset. Moreover, even without access to the external knowledge $\varvec{X}$, DELRA still performs closely to the performance of SEEK+$\varvec{X}$ and outperform the other baselines when the sampling proportion is greater than 10%. When the sampling proportion is only 10%, DELRA without $\varvec{X}$ seems to suffer from the response sparsity as any other baseline that has not leveraged $\varvec{X}$.

Fig. 3.

The accuracy of different models on inferring the true labels of the items from 10% to 50% of the total responses across the four datasets. Note that x-axis and y-axis in each figure are respectively the sampling proportions of responses and the average true label prediction accuracy over 10 runs.

5.3 Consistency of Learned Relatedness Between Categories

In this experiment, we evaluate how consistent the estimates of the relatedness between categories from DELRA without $\varvec{X}$ are with the relatedness scores in $\varvec{X}$ pre-computed using Eq. (1) followed by the transformation in Eq. (4). More specifically, for each label category, we calculate the Pearson correlation coefficients between the Top-N most related category rank of the other label categories in terms of the estimates of their relatedness to the category, and the Top-N rank of the same set of categories in terms of their pre-computed transformed relatedness scores for that category. We set N to be 2, 3, 5, 10 and 15 to obtain the respective average Pearson correlation coefficients across all the label categories. We also implement two supervised baselines (in terms of knowing true labels) for obtaining the Top$-N$ rank of the most related categories:

• Top-N rank by frequency - asymmetric. For each label category, the relatedness of the other label categories to it is their frequencies as the responses to the items with the label category as their true labels.

• Top-N rank by frequency - symmetric. For each label category, the relatedness of the other label categories to it is their frequencies as either the responses to the items with that label category as their true labels, or the true labels of the items which receive that label category as the responses.

Figure 4a–d show how the Top-N most related category ranks by both the DELRA model without $\varvec{X}$ and the two baselines are correlated with the Top-N ranks by the ground-truth relatedness scores calculated by Eq. (1). Showing overall higher average correlation with the ground-truth relatedness scores across the four datasets, our model clearly yields more consistent category relatedness estimates than the two baselines even though it is unsupervised. We conjecture this is attributed to the ability of our model in distinguishing responses of different quality by accounting for the interaction between worker expertise and item difficulty, while the baselines treat all the responses as the same in their quality.

Fig. 4.

Average Pearson correlation coefficients between the Top-N most related category rank yielded by different methods, and the ground-truth Top-N rank yielded by the pre-computed related scores based on Eq. (1). Note that x-axis and y-axis in each figure are N and average correlation, respectively.

6 Conclusion

We propose DELRA, a quality control framework for crowdsourcing that leverages the semantic relationships between label categories. It features a latent real-valued matrix that captures the relatedness between response categories alongside variables for worker expertise, item difficulty and item true labels. DELRA encodes the joint interaction among these variables to refine estimation of conditional probabilities of responses given true labels. This leads DELRA to outperform numerous state-of-the-art quality control methods in terms of true label prediction. Moreover, DELRA allows for elegant encoding of a priori knowledge regarding the relationships between categories for calibrating the estimation of the latent relatedness matrix. This leads to its further improvements in the prediction. Finally, the relatedness matrix learned solely from response data by DELRA shows convincing consistency with the relatedness matrix pre-computed from the external semantic relationships between the categories.