Anomaly Detection Technique Robust to Units and Scales of Measurement

Abstract

Existing anomaly detection methods are sensitive to units and scales of measurement. Their performances vary significantly if feature values are measured in different units or scales. In many data mining applications, units and scales of feature values may not be known. This paper introduces a new anomaly detection technique using unsupervised stochastic forest, called ‘usfAD’, which is robust to units and scales of measurement. Empirical results show that it produces more consistent results than five state-of-the-art anomaly detection techniques across a wide range of synthetic and benchmark datasets.

1 Introduction

The data mining task of anomaly detection is to detect unusual data instances which do not conform to normal or expected data automatically. The unusual data are called anomalies or outliers. Anomaly detection has many applications such as detecting fraudulent transactions in banking and intrusion detection in computer networks. The task of automatic detection of anomalies has been solved using supervised, unsupervised or semi-supervised learning [1].

In supervised techniques, a classification model is learned to classify test data as either anomaly or normal. They require labelled training data from both normal and anomaly classes. Obtaining labelled training data from anomaly class is challenging in many applications [1]. Unsupervised techniques do not require labelled training data and rank test data based on their anomaly scores directly. They assume that most of the test data are normal and anomalies are few. They may perform poorly when the assumption does not hold [1]. Semi-supervised techniques learn a model representing normal data from labelled normal training data only and rank test data based on their compliance to the model. Majority of data in anomaly detection problems are normal, and thus labelled normal training data can be obtained easily in many applications [1]. This paper focuses on the semi-supervised anomaly detection task.

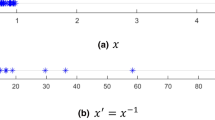
Most existing unsupervised and semi-supervised anomaly detection techniques assume that anomalies are few and different, i.e., anomalies have feature values that are very different from those of normal instances and lie in low density regions [1,2,3,4,5,6]. This assumption may not be always true in data mining applications where the units and scales of measurement of feature values are often not known. An anomalous instance may appear to be a normal instance when feature values are measured in different scales. For example, the instance represented by red dot in Fig. 1(a) is clearly an anomaly but it looks like a normal point if the data are measured as $x'=1/x$ (represented by red dot in Fig. 1(b)). Many existing anomaly detection methods fail to detect the anomaly in Fig. 1(b). In other words, their performances vary significantly if feature values are measured in different units or scales, i.e., they are sensitive to units and scales of measurement.

Fig. 1.

An example of data represented in two scales. The data point represented by red dot in case (a) is clearly appeared to be an anomaly whereas the corresponding point in case (b) is more like a normal data.

In real-world applications, feature values can be measured in different units and/or scales. For example, fuel efficiency of vehicles can be measured in km/litre or litre/km and annual income of individuals can be measured in an integer scale like $x=100000$ or using a logarithmic scale of base 10 like $x'=5$. Unfortunately, units and scales of feature values are often not provided when data are given for anomaly detection where only magnitudes of feature values are available. Many existing anomaly detection methods may perform poorly if feature values are not measured in appropriate units or scales for the task.

Recently, the impact of units and scales of feature values in the context of pairwise similarity measurement of data has been studied [7, 8]. Fernando and Webb (2017) introduced a scale invariant similarity measure using a variant of unsupervised random forest called ‘Unsupervised Stochastic Forest’ (USF) [7]. Each tree in USF partitions the space into regions using a small subsamples of data and the partition is robust to units and scales of feature values.

In this paper, we introduce an anomaly detection technique robust to units and scales of measurement using USF, called ‘usfAD’. In each tree, the space is partitioned using a small subsamples of labelled normal training data. Then in each node of trees, normal and anomaly regions are defined based on the labelled normal training data falling in the node. In the testing phase, anomaly score of a test instance is computed in each tree based on the depth of the first node where the test instance lies in the anomaly region. The overall anomaly score is computed by aggregating anomaly scores over a collection of trees. Our empirical results over a wide range of synthetic and benchmark datasets show that it is robust to units and scales of feature values and it produces more consistent results in comparison to five state-of-the-art anomaly detection techniques.

The rest of the paper is organised as follows. Preliminaries and previous work related to this paper are discussed in Sect. 2. The proposed semi-supervised anomaly detection technique of ‘usfAD’ is discussed in Sect. 3 followed by the empirical evaluation in Sect. 4 and concluding remarks in the last Section.

2 Preliminaries and Related Work

We assume that data are represented by vectors in an M-dimensional real domain (${\mathbb R}^M$) where each dimension represents a feature of data. Each data instance $\mathbf{x}$ is an M-dimensional vector $\langle x_{1},x_{2},\cdots ,x_{M}\rangle$ where each component $x_i\in \mathbb R$ represents its value of the $i^{th}$ feature. Let D be a collection of N training data of normal instances and Q be a collection of n test instances which is a mixture of normal and anomalous data. The task in semi-supervised anomaly detection is to learn an anomaly detection model from D and rank instances in Q based on their anomaly scores.

Popular nearest neighbour (NN) based methods [2, 9, 10] rank a test instance $\mathbf{x}\in Q$ based on its kNNs in D. Being very different from normal data, anomalies are expected to have larger distances to their kNNs than normal instances. Local Outlier Factor (LOF) [2] is the most widely used kNN-based anomaly detection method. It does not require any training. Test instances are ranked based on the ratio of their local reachability distance (lrd) to the average lrd of their kNNs in D. The lrd of an instance is estimated using the distance to its $k^{th}$ NN. Euclidean distance is a common choice of distance measure.

Another distance or similarity based anomaly detection technique is One-Class Support Vector Machine (SVM) [3]. It learns a model of normal data based on pairwise similarities of training instances using kernel tricks [11]. It requires a kernel function to compute pairwise similarities of instances. Gaussian kernel is a common choice of kernel function that uses Euclidean distance. Test instances are ranked based on their deviation from the model of normal data.

Both NN-based and SVM-based methods can be computationally expensive when training data size $N=|D|$ is large. Though the time complexity of NN search can be reduced to $O(\log N)$ from O(NM) by using indexing schemes such as k:d-trees [12], their effectiveness degrades as the number of dimensions increases and become useless in high dimensional spaces. Recently, Sugiyama and Borgwardt (2013) introduced a simpler and efficient NN-based anomaly detector called Sp [5] where test instances are ranked based on their distances to their nearest neighbours (1NN) in a small random subsamples of training data, $\mathcal{D}\subset D$, $|\mathcal{D}|=\psi \ll N$. They have shown that Sp with $\psi$ as small as 25 performs better than or competitive to LOF but runs several orders of magnitude faster.

Liu et al. (2008) introduced an efficient anomaly detector using unsupervised random forest called Isolation Forest (iforest) [4] which does not use distance measure. It constructs an ensemble of random trees where each tree is constructed from a small subsamples of training data ($\mathcal{D}\subset D$). It attempts to isolate instances in $\mathcal{D}$ through recursive axis-parallel random split of feature space in each tree. Because anomalies are few and different, they are expected to have shorter average path lengths than those of normal instances over a collection of trees.

Another efficient anomaly detection method which does not require distance measure is based on histograms [6, 13]. It discretises feature values in each dimension into a fixed number of equal-width bins and frequency of training data in each bin is recorded. Being few and different, anomalies are expected to fall in bins with small frequencies in many dimensions. Aryal et al. (2016) introduced a simple histogram-based anomaly detection method called Simple Probabilistic Anomaly Detector (SPAD) [6] which is more robust to skewed training data because bin width in each dimension depends on the data variance in that dimension.

All these existing methods discussed above rely on the assumption that anomalies have feature values significantly different from normal instances. As discussed in Sect. 1 (Fig. 1), this may not be always true because the distribution of feature values depends on the units and scales of measurement. Existing methods may not perform well if feature values are not measured in appropriate scales so that this assumption holds. Therefore, existing methods are sensitive to units and scales of measurement.

Very recently, the impact of units and scales of measurement of feature values in distance-based pairwise similarity measurement of data has been studied [7, 8]. When feature values are measured in different units or scales, the ordering of feature values is either preserved or reversed. Exploiting this characteristic, Fernando and Webb (2017) introduced a non-distance based similarity measure which is robust to units and scales of measurement. The similarity of two instances is defined as the number of shared leaves in a collection of t trees called Unsupervised Stochastic Forest (USF) [7]. Each tree is constructed from a small subsamples of data, $\mathcal{D}\subset D$ where $|\mathcal{D}|=2^h$ and h is a user-defined parameter that determines the height of trees. At each internal node in a tree, subsamples are partitioned into two equal subsets by splitting at the median of values in a randomly chosen attribute. Because of the median split, the similarity measure is robust to units and scales of measurement.

In the next section, we combine the ideas of USF and iforest to introduce a new effective and efficient anomaly detection method which is robust to units and scales of measurement.

3 New Method Robust to Units and Scales of Measurement

iforest [4] attempts to isolate instances in data subsamples using random splits resulting in unbalanced binary trees. Anomalies are expected to fall in leaves with shorter pathlengths in many trees. However, the implementation of iforest is sensitive to units and scales of feature values. At each internal node of a tree, the space is partitioned by selecting a random split between the range of sample values in a randomly selected dimension. The probability of having a split between two consecutive points is proportional to their distance which is sensitive to units and scales of measurement.

USF [7] isolates instances in data subsamples using median splits resulting in balanced binary trees. The median split makes it robust to units and scales of measurement. However, the concept of pathlength can not be used to detect anomalies because all leaves are at the same height.

We propose the following extensions to USF so that pathlengths in trees can be used as a measure to rank test instances to detect anomalies. Once a balanced binary tree is constructed from $\mathcal{D}\subset D$, the entire training data D are passed through the tree to define normal and anomaly regions in each node. In each internal node, the normal range is defined by the minimum and maximum of feature values of the normal training data falling in the node in the dimension j selected to partition the space. In each leaf node, the normal range is defined by the bounding hyper-rectangle covered by the training data falling in the leaf node i.e., minimum and maximum values of training data in all M dimensions. Regions outside of the normal range is considered as anomaly regions in each node. The number of training data falling in each leaf is also recorded.

While a test instance $\mathbf{x}$ is traversing $i^{th}$ tree during testing, first we check whether it lies within the defined normal range at each node. We traverse further down the tree only if it is within the range, otherwise we terminate and return the pathlength of the node where it lies outside of the normal range as the anomaly score of $\mathbf{x}$ in $i^{th}$ tree (let’s say $p_i(\mathbf{x})$). If $\mathbf{x}$ traverses to a leaf and lies in the normal region, the anomaly score is defined as the pathlength augmented by the training data mass in the leaf (let’s say m) as $p_i(\mathbf{x}) = h+\log _2 m$. The second term is the height of a binary search tree constructed from m data instances and $p_i(\mathbf{x})$ will the be the total height if the leaf node was allowed to grow further until all instances are isolated. This augmentation is important to differentiate leaf nodes with high data mass from those with low data mass because their anomaly scores should be different. Similar adjustment was done in iforest [4].

Algorithms to construct a tree from $\mathcal{D}$ (a random subsamples of D of size $2^h$), updating ranges and data mass using D and computing score of a test instance $\mathbf{x}$ are provided in Algorithms 1, 2 and 3, respectively.

The overall anomaly score of $\mathbf{x}$ is estimated by aggregating pathlengths over t trees, $score(\mathbf{x})=\frac{1}{t}\sum _{i=1}^t p_i(\mathbf{x})$. Anomalies will have smaller score than normal instances. We call the proposed unsupervised stochastic forest based anomaly detection method ‘usfAD’. It is based on the same idea of isolating anomaly regions from normal regions as used in iforest [4] but using different mechanism of isolation.

As distance is not involved and trees are construct using median splits, usfAD is robust to units and scales of measurement. Even though the size of ranges can be changed with the change in units or scales of measurement, the ordering of values is either preserved (e.g., logarithmic scale) or reversed (e.g., inverse). If a point u lies in the range [x, y] in one scale, the corresponding point $u'$ is expected to lie in the corresponding range [$x'$, $y'$] in another scale. Because of the split at the mid point of two values in the middle (median in the case of even data), there will be small variations in the definition of regions in different scales resulting in small differences in the anomaly detection accuracy.

Figure 2 shows the contour plots of anomaly scores of every point in a two-dimensional space using iforest ($t=100, \psi =256$) and usfAD ($t=100, h=5$) in a dataset in two scales: x and $x'=1/x$. It shows that though iforest can detect the anomaly in the original space (Fig. 2(b)), it fails to detect the same anomaly after inverse transformation (Fig. 2(e)). But usfAD has no problem detecting the anomaly in both scales (see Figs. 2(c) and (f)).

Fig. 2.

Anomaly contours of iforest and usfAD in a two-dimensional dataset in two different scales. Note that data are normalised to be in the unit range of [0, 1] in each dimension in all contour plots. The darker the colour, the higher the chances of being anomaly. Note that the anomaly point represented by the red dot is not considered as a part of training data D or $D'$ which includes only the normal instances represented by blue asterisks. (Color figure online)

In the training phase, usfAD requires to create t trees and update normal data range in each tree using the entire training data. It’s training runtime complexity is $O(Nth + \psi M)$. Note that $\psi =2^h$. It needs $O(t\psi M)$ space to store t trees and normal range for all M dimensions in each leaf node. In the testing phase, the runtime complexity of ranking n test instances is $O(n(th + M))$. Because testing time is independent of training data size N, it runs faster than LOF and SVM in datasets with large N. It runs slower than iforest due to the overhead to check range in each node from the root to a leaf in each tree.

4 Empirical Evaluation

In this section, we present the results of experiments conducted to evaluate the performance of usfAD against five state-of-the-art anomaly detectors: LOF, one-class SVM, iforest, Sp and SPAD. We used synthetic and benchmark datasets in our experiments. All experiments were conducted in semi-supervised setting where half of the normal instances in a dataset were used as labelled training data and the remaining other half of normal data and anomalies are considered as test data as done in [14]. Anomaly detection model was learned from the training data and tested on the test data. Area under the ROC curve (AUC) was used as the performance evaluation measure. For random methods: iforest, Sp and usfAD, each experiment was repeated 10 times and reported the average AUC. A significance test was conducted using the confidence interval based on the two standard errors over 10 runs. The same training and test sets of a dataset were used for all experiments with the dataset. Feature values are normalised to be in the unit range of [0, 1] in each dimension.

Fig. 3.

Two-dimensional synthetic datasets. Each dataset contains 2000 normal instances represented by blue asterisks and 12 anomalies represented by red dots. (Color figure online)

We used the implementation of LOF and SVM included in the Scikit-learn machine learning library [15]. Other methods and experimental setups were also implemented in Python using the Scikit-learn library. All the experiments were conducted in a Linux machine with 2.27 GHz processor and 8 GB memory. Parameters in algorithms were set to suggested values by respective authors: $k=\lfloor \sqrt{N}\rfloor$ in LOF; subsample size $\psi =25$ in Sp; number of bins $b=\lfloor \log _2N\rfloor +1$ in SPAD; and $t=100$ and $\psi =256$ in iforest. We used the default settings of SVM. For usfAD, default values of $h=5$ and $t=100$ were used.

4.1 Synthetic Datasets

We used six two-dimensional datasets as shown in Fig. 3 to evaluate the robustness of anomaly detection algorithms with different scales of measurement. We used four order preserving and order reversing transformations of data using square, square root, logarithm and inverse, where each feature value x was transformed as $x^2$ and $\sqrt{x}$, $\log x$ and $\frac{1}{x}$, respectively. Because $\frac{1}{x}$ and $\log x$ are not defined for $x=0$, all transformations were applied on $\hat{x}=c(x+\delta )$ where $\delta =0.0001$ and $c=100$. Note that the original feature values in both dimensions were normalised to the unit range of [0, 1] before applying the transformations to ensure the same effect of $\delta$ and c in both dimensions. Once the feature values were transformed, they were renormalised to be in the unit range again. We used exactly the same procedure of transformation as employed by [7].

Fig. 4.

AUC of contending methods in the six synthetic datasets with order preserving and order reversing transformations of data.

AUC of all contending measures in six synthetic datasets with and without transformations are presented in Fig. 4. It shows that usfAD produced best or equivalent to the best results in all cases. It produces similar results in all datasets with the original feature values and all four transformations. This results show that it is robust to units and scales of measurement.

All five existing measures were sensitive to transformations of data. Among them, LOF is the least sensitive. It could be because of the use of relative $k^{th}$NN distance of $\mathbf{x}$ to its kNNs’ $k^{th}$NN distances which captures the contrast in the locality well even though overall variance of data is changed due to transformations. Its performance also dropped with inverse and logarithmic transformations in Waves and Corners. Other four contenders failed to detect all anomalies correctly even in the original scale in four datasets. It is interesting to note that some existing methods produced better results with a transformation than in the original space, e.g., SVM produced best results with the inverse transformation in Gaussians and Spiral.

Table 1. Benchmark datasets

4.2 Benchmark Datasets

We used 15 benchmark datasets from UCI machine learning data repository [16], many of which were used in the iforest and SPAD papers. The properties of datasets are provided in Table 1. Data in each dimension were normalised to be in the unit range of [0, 1]. To demonstrate the robustness of usfAD to scales of measurement, we also evaluated the performance of contending measures in benchmark datasets with the inverse transformation ($x'=1/x$) which was done as discussed in Sect. 4.1.

The AUC of all contenders in the 15 benchmark datasets is provided in Table 2. In the original scale, usfAD produced best or equivalent to the best result in seven datasets followed by LOF in five, iforest in four, SPAD and SVM in three each and Sp in one dataset only. usfAD produced significantly better AUC than the closest contender in Musk2 (ID 10) - AUC of 0.908 by usfAD vs that of 0.700 by LOF. The average results in the last row show that usfAD produced more consistent results than existing methods across different datasets.

Table 2. Anomaly detection performance (AUC) in benchmark datasets in the given original scale (x) and inverse transformation ($x'=1/x$). First column is the dataset ID from Table 1. The average AUC over the 15 datasets is provided in the last row. Best or equivalent to the best results based on the two standard errors confidence interval of random methods over 10 runs in each scale are underlined.

With the inverse transformation, the performance of all existing methods dropped in many cases. usfAD produced best or equivalent to the best result in 10 datasets followed by SPAD in four, iforest and LOF in two each, and Sp in one dataset only. SVM did not produce best or equivalent to the best result in any dataset. It is interesting to note that some existing methods produced better results with the inverse transformation than in the original space, e.g., LOF, SPAD and Sp in Miniboone (ID 7); iforest, Sp and SVM in Musk2 (ID 10) etc.

In terms of runtime, usfAD was one order of magnitude faster than LOF and SVM in large and/or high dimensional datasets. For example, to complete one run of experiment in Miniboone, usfAD took 440 s whereas LOF and SVM took 2308 s and 1187 s, respectively. However, it was up to one order of magnitude slower than Sp, SPAD and iforest. In Miniboone, Sp took 22 s, SPAD took 43 s and iforest took 83 s.

5 Concluding Remarks

Existing anomaly detection methods largely rely on spatial distances of data to identify anomalous instances. They may fail to detect anomalies which are masked due to the use of inappropriate units or scales of measurement. In many data mining applications, units and scales of feature values are often not provided where only magnitudes of feature values are given. Thus, an anomaly detection method which is robust to units and scales of measurement is preferred. In this paper, we introduce one such technique using unsupervised stochastic forest. Our empirical results in synthetic and benchmark datasets suggest that the proposed method is robust to units and scales of measurement and it’s performance is either better or competitive to existing methods. It produces more consistent and stable results across a wide rage of data with different order preserving and order reversing transformations.