Normal Modes of Chaotic Vibrations and Transient Normal Modes in Nonlinear Systems

Abstract

Nonlinear normal modes of forced chaotic vibrations can be found in models which are obtained by discretization of some elastic systems that have lost stability under external compressive force. Transient nonlinear normal modes, which exist only for some specific values of the system energy, appear in nonlinear dissipative systems in vicinity of external or internal resonance. These dissipative systems under resonance conditions are analyzed by transformation to reduced systems stated with respect to the parameter which characterizes the system energy, the arctangent of the amplitudes ratio and the phase difference.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Concept of nonlinear normal modes (NNMs), first proposed by Kauderer and Rosenberg [1, 2], is an important step of investigation of the nonlinear systems behavior. Principal fundamentals of the NNMs theory and different applications of the theory are presented in [3,4,5].

The NNMs concept can be used not only for periodic vibrations. In particular, the NNMs having smooth trajectories in configuration space and chaotic in time behavior can be found in some non-conservative systems. Such vibration modes are observed in post-buckling dynamics of elastic systems that have lost stability under external compressive force.

In vicinity of the internal resonance the transfer of energy from unstable NNMs to stable ones is noted. This phenomenon is discussed in various publications. A description of the energy transfer was presented in the pioneering publication [6], where it was showed that in spring pendulum a transfer of angular oscillation mode to vertical oscillation one, and back, takes place near the fundamental frequencies ratio of 2:1. The transfer of energy caused by internal resonance was also investigated in [7,8,9]. Some principal results in problems of the energy transfer are summarized in the book [10]. The book [11] is devoted to complex behavior of autonomous and non-autonomous nonlinear systems under the internal resonance conditions. Here an interaction of nonlinear vibration modes in neighborhood of external and internal resonances in nonlinear dissipative systems is analyzed by the multiple scales method [12] and a transformation to so-called reduced system. The reduced system is written with respect to some variable which characterizes the system energy, arctangent of ratio of amplitudes and difference of phases. Earlier the reduced system was used for conservative systems in [13, 14] and for dissipative systems in [15]. The new phenomenon in analysis of transient of the dissipative system near resonance is an appearance of so-called transient nonlinear normal vibration modes (TNNMs) [15] which are realized only for some levels of the systems energy that is, for some specific values of time, corresponding to these energy levels. It is important that near these values of time motions of the dissipative systems are close to the modes, that is the TNNMs are attractive.

An appearance of TNNMs in the system with a limited power-supply (or non-ideal system) having nonlinear absorber and in the spring-pendulum system (oscillator-rotator) is considered. The systems with a limited power-supply are characterized by interaction of source of energy and elastic sub-system which is under action of the source. The most important effect observed in such systems is the Sommerfeld effect [16], when the stable resonance regime with large amplitudes is appeared in the elastic sub-system. Resonance dynamics of such systems was first described by V.O. Kononenko [17]. Then investigations on the subject were continued in numerous publications, in particular, in [18,19,20]. Some surveys on studies of the non-ideal systems dynamics are made in [12, 21]. Transfer of energy from some unstable mode to other stable one, that is the so-called “saturation phenomenon”, in such systems under the internal resonance condition, is described in [22]. Reduction of the vibration amplitudes in the non-ideal systems coupled with different type nonlinear absorbers and dampers, is studied in [23, 24]. Forced synchronic regimes of the oscillator-rotator system are analyzed in [25]. Free stationary and non-stationary regimes, as well localization of energy in such system are considered in [26].

The paper is organized as follow. Forced NNMs in models which are obtained by discretization of some elastic systems are examined in Sect. 2. These NNMs with chaotic in time behavior, are obtained in post-buckling dynamics of such systems. In Sect. 3, external resonances on the first fundamental frequency and both external and internal resonances in the dissipative system with a limited power supply coupled with nonlinear absorber are considered. Resonance behavior in the dissipative spring-pendulum system for a case of simultaneous external and internal resonances is considered in Sect. 4. Modes of coupled vibrations and localized modes, including TNNMs are obtained; their influence to transient process in these systems is shown.

2 Forced Nonlinear Normal Modes of Chaotic Vibrations

Consider the following system that can be obtained by discretization of equations of nonlinear dynamics of some elastic systems:

$$ \begin{aligned} & \ddot{y}_{1} + \delta \dot{y}_{1} - \alpha y_{1} + \beta y_{1}^{3} + cy_{1} y_{2}^{2} = f\,\cos \omega t, \\ & \ddot{y}_{2} + \delta \dot{y}_{2\,} + ay_{2} + by_{2}^{3} + cy_{2\,} y_{1}^{2} = 0, \\ \end{aligned} $$

(1)

where $y_{1} \left( t \right)$ and $y_{2} \left( t \right)$ are unknown functions; $\delta$ is the coefficient determining friction; all coefficients are positive, excepting the coefficient $\alpha$ which can have any sign. In the case $\alpha > 0$ the Eq. (1) describe post-critical dynamics of the corresponding elastic systems.

The system (1) can be obtained, in particular, in the following problems: the beam bending vibrations within framework of the Kirchhoff beam theory and the dynamics of cylindrical shells described by the Donnell equations can be considered. Then a discretization by the Bubnov–Galerkin procedure is used. If displacements of the nonlinear elastic system are approximated by a single harmonic of the Fourier series expansion for spatial coordinates, a system having a single degree of freedom is obtained. Behavior of the model described by the non-autonomous Duffing equation was examined in numerous publications. Chaotic motions begin when the force amplitudes are slowly increased [27]. If two harmonics of the Fourier series for spatial coordinates are used, one obtains a set of two second order ODEs, coupled in nonlinear terms only. Two NNMs, which are determined by smooth trajectories in the system configuration place, exist here. One of these modes can be chaotic in time in some domain of the system parameters. Boundaries of the domain are determined as some combination of the external amplitude and parameters of nonlinearity and dissipation. The energy transfer from some vibration mode to another one is possible. Thus one can formulate a problem of the stability of periodic or chaotic vibration mode in the higher-dimensional spaces. The orbital stability of trajectories of the regular or chaotic modes is determined by the numerical-analytical approach which is based on the known Lyapunov definition of stability [28].

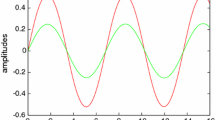
In Figs. 1 and 2 phase places of the variables $y_{1} \left( t \right)$ and $y_{2} \left( t \right)$ show orbital stability/instability of the NNM trajectory $y_{2} = 0$ for some parameters of the system (1). The variable $y_{2}$ is considered here as variation of the NNM trajectory in orthogonal direction. Note that these results are obtained for the problem of the post-buckling nonlinear beam dynamics.

Fig. 1

The unstable mode of regular vibrations

Fig. 2

The stable mode of chaotic vibrations

3 Transient Nonlinear Normal Modes in Dissipative System with a Limited Power-Supply Coupled with Nonlinear Absorber

One considers the resonance behavior of the dissipative non-ideal system which contains the nonlinear absorber with cubic type nonlinearity. Model under consideration is shown in Fig. 3. The motor $D$ acts to the elastic sub-system by the crank shaft. The nonlinear oscillator is attached to the elastic sub-system of the mass M.

Fig. 3

System with a limited power-supply coupled with non-linear absorber

Equations describing motion of the system are the following:

$$ \begin{array}{*{20}l} {I\ddot{\varphi } = \varepsilon (L(\dot{\varphi }) - H(\dot{\varphi }) + c_{1} r(x - r\,\sin \varphi )\cos \varphi ),} \hfill \\ {M\ddot{x} + \varepsilon \eta \dot{x} + cx + c_{2} (x - y) + \gamma (x - y)^{3} = \varepsilon c_{1} r\,\sin \varphi ,} \hfill \\ {\varepsilon m\ddot{y} + \varepsilon \eta \dot{y} - c_{2} (x - y) - \gamma (x - y)^{3} = 0.} \hfill \\ \end{array} $$

(2)

Here the following notation is used: $M$ is a mass of the elastic sub-system; $r$ is a radius of the crank shaft; coefficients $c = c_{0} + c_{1}$ and $c_{2}$ characterize stiffness of springs in the system; $m$ is a mass of the nonlinear absorber; $I$ is a moment of inertia of rotating masses; $H(\dot{\varphi }) = d\dot{\varphi }$ is the moment of resistance to rotation; $L = a + b\dot{\varphi }$ is a driving moment of the motor. The small parameter ε characterizes a smallness of mass of absorber with respect to the mass of elastic sub-system, of dissipation in the system and of the vibration components in variability in time of the angle ${\upvarphi }$ velocity with respect to the constant component of the velocity.

Equations of motion (2) are transformed and presented of the next form:

$$ \begin{array}{*{20}l} {\ddot{\varphi } = \varepsilon (\bar{A} + \dot{\varphi } + \bar{C}x\,\cos \varphi - \bar{D}\,\sin 2\varphi ),} \hfill \\ {\ddot{x} + \omega_{x}^{2} x - qy + 2\varepsilon \eta_{x} \dot{x} + \varepsilon \gamma_{x} (x - y)^{3} = \varepsilon k\,\sin \varphi ,} \hfill \\ {\ddot{y} + \omega_{y}^{2} y - \omega_{y}^{2} x + 2\varepsilon \eta_{y} \dot{y} - \varepsilon \gamma_{y} (x - y)^{3} = 0,} \hfill \\ \end{array} $$

(3)

where $\bar{A} = \frac{a}{I}$, $\bar{B} = \frac{b - d}{I}$, $\bar{C} = \frac{{c_{1} r}}{I}$, $\bar{D} = \frac{{c_{1} r^{2} }}{2I}$, $\omega_{x}^{2} = \frac{{c + c_{2} }}{M}$, $2\eta_{x} = \frac{\eta }{M}$, $\gamma_{x}^{{}} = \frac{\gamma }{M}$, $q = \frac{{c_{2} }}{M}$, $k = \frac{{c_{1} r}}{M}$, $\omega_{y}^{2} = \frac{{c_{2} }}{m}$, $2\eta_{y} = \frac{\eta }{m}$, $\gamma_{y}^{{}} = \frac{\gamma }{m}$.

One transforms the system (3) to principal coordinates, solving corresponding eigenvalue problem of the linearized system. Fundamental frequencies and coordinates of eigenvectors $\chi_{1,2} = (\alpha_{1,2} ,\beta_{1,2} )$ are the following:

$$ \omega_{{_{1,2} }}^{2} = \frac{{(\omega_{x}^{2} + \omega_{y}^{2} ) \mp \sqrt {(\omega_{x}^{2} - \omega_{y}^{2} )^{2} + 4\omega_{y}^{2} q} }}{2}, $$

(4)

$$ \alpha_{1,2} = 1,\beta_{1,2} = \frac{{2\omega_{y}^{2} }}{{(\omega_{y}^{2} - \omega_{x}^{2} ) \pm \sqrt {(\omega_{x}^{2} - \omega_{y}^{2} )^{2} + 4\omega_{y}^{2} q} }}. $$

(5)

In the principal coordinates the system under consideration can be written of the form:

$$ \begin{array}{*{20}l} {\ddot{\varphi } = \varepsilon (\bar{A} + \bar{B}\dot{\varphi } + \bar{C}(z_{1} + z_{2} )\cos \varphi - \bar{D}\,\sin 2\varphi ),} \hfill \\ {\ddot{z}_{1} + \omega_{1}^{2} z_{1} = \frac{{\varepsilon \beta_{2} }}{{\beta_{2} - \beta_{1} }}( - 2\eta_{x} (\dot{z}_{1} + \dot{z}_{2} ) - \gamma_{x} (z_{1} + z_{2} - \beta_{1} z_{1} - \beta_{2} z_{2} )^{3} + k\,\sin \varphi )} \hfill \\ { - \frac{\varepsilon }{{\beta_{2} - \beta_{1} }}( - 2\eta_{y} (\beta_{1} \dot{z}_{1} + \beta_{2} \dot{z}_{2} ) + \gamma_{y} (z_{1} + z_{2} - \beta_{1} z_{1} - \beta_{2} z_{2} )^{3} ),} \hfill \\ {\ddot{z}_{2} + \omega_{2}^{2} z_{2} = \frac{\varepsilon }{{\beta_{2} - \beta_{1} }}( - 2\eta_{y} (\beta_{1} \dot{z}_{1} + \beta_{2} \dot{z}_{2} ) + \gamma_{y} (z_{1} + z_{2} - \beta_{1} z_{1} - \beta_{2} z_{2} )^{3} )} \hfill \\ { - \frac{{\varepsilon \beta_{1} }}{{\beta_{2} - \beta_{1} }}( - 2\eta_{x} (\dot{z}_{1} + \dot{z}_{2} ) - \gamma_{x} (z_{1} + z_{2} - \beta_{1} z_{1} - \beta_{2} z_{2} )^{3} + k\,\sin \varphi ).} \hfill \\ \end{array} $$

(6)

To analyze the external resonance on the fundamental frequency corresponding to the coordinate $z_{1}$, one introduces the detuning parameter Δ by the relation $\Omega ^{2} = \omega_{1}^{2} + \varepsilon \Delta$. The multiple scale method [12] is used here. So, the following scales of time as new independent variables are introduced: $T_{0} = t; T_{1} = \varepsilon t,$ etc. All generalized coordinates of the system (6) are presented as functions of these variables. The next standard transformations are used:

$$ \frac{d}{d\tau } = \frac{\partial }{{\partial T_{0} }} + \varepsilon \frac{\partial }{{\partial T_{1} }} + \cdots ,\frac{{d^{2} }}{{d\tau^{2} }} = \frac{{\partial^{2} }}{{\partial T_{0}^{2} }} + 2\varepsilon \frac{{\partial^{2} }}{{\partial T_{1} \partial T_{0} }} + \cdots $$

(7)

The variables $\varphi$, $z_{1}$ and $z_{2}$ are presented also as power series by the small parameter. Saving only the zero and first approximations by the small parameter, $\varphi = \varphi_{0} + \varepsilon \varphi_{1}$, $z_{1} = z_{10} + \varepsilon z_{11}$, $z_{2} = z_{20} + \varepsilon z_{21}$, one obtains the following PDE systems:

$$ \frac{{\partial^{2} \varphi_{0} }}{{\partial T_{0}^{2} }} = 0,\quad \frac{{\partial^{2} z_{10} }}{{\partial T_{0}^{2} }} +\Omega ^{2} z_{10} = 0,\quad \frac{{\partial^{2} z_{20} }}{{\partial T_{0}^{2} }} + \omega_{2}^{2} z_{20} = 0, $$

(8)

$$ \begin{array}{*{20}l} {\frac{{\partial^{2} \varphi_{1} }}{{\partial T_{0}^{2} }} = - 2\frac{{\partial^{2} \varphi_{0} }}{{\partial T_{0} \partial T_{1} }} + \bar{A} + \bar{B}\left( {\frac{{\partial \varphi_{0} }}{{\partial T_{0} }}} \right) + \bar{C}(z_{10} + z_{20} )\cos \varphi_{0} - \bar{D}\,\sin 2\varphi_{0} ,} \hfill \\ {\frac{{\partial^{2} z_{11} }}{{\partial T_{0}^{2} }} +\Omega ^{2} z_{11} = - 2\frac{{\partial^{2} z_{10} }}{{\partial T_{0} \partial T_{1} }} + \Delta z_{10} + \frac{1}{{\beta_{2} - \beta_{1} }}\left[ {\beta_{2} \left( { - 2\eta_{x} \frac{{\partial (z_{10} + z_{20} )}}{{\partial T_{0} }} - \gamma_{x} } \right.(z_{10} + z_{20} } \right.} \hfill \\ {\left. {\left. { - \beta_{1} z_{10} - \beta_{2} z_{20} )^{3} + k\,\sin \varphi_{0} } \right) + 2\eta_{y} \frac{{\partial (\beta_{1} z_{10} + \beta_{2} z_{20} )}}{{\partial T_{0} }} - \gamma_{y} (z_{10} + z_{20} - \beta_{1} z_{10} - \beta_{2} z_{20} )^{3} } \right],} \hfill \\ {\frac{{\partial^{2} z_{20} }}{{\partial T_{0}^{2} }} + \omega_{2}^{2} z_{20} = - 2\frac{{\partial^{2} z_{20} }}{{\partial T_{0} \partial T_{1} }} + \frac{1}{{\beta_{2} - \beta_{1} }}\left[ { - 2\eta_{y} \frac{{\partial (\beta_{1} z_{10} + \beta_{2} z_{20} )}}{{\partial T_{0} }} + \gamma_{y} (z_{10} + z_{20} } \right.} \hfill \\ { - \beta_{1} z_{10} - \beta_{2} z_{20} )^{3} - \left. {\beta_{1} \left( { - 2\eta_{x} \frac{{\partial (z_{10} + z_{20} )}}{{\partial T_{0} }} - \gamma_{x} (z_{10} + z_{20} - \beta_{1} z_{10} - \beta_{2} z_{20} )^{3} + k\,\sin \varphi_{0} } \right)} \right].} \hfill \\ \end{array} $$

(9)

Solution of the Eq. (8) is presented as

$$ \varphi_{0} =\Omega t,z_{10} = C_{1} e^{{i\Omega T_{0} }} + \bar{C}_{1} e^{{ - i\Omega T_{0} }} ,z_{20} = C_{2} e^{{i\omega_{2} T_{0} }} + \bar{C}_{2} e^{{ - i\omega_{2} T_{0} }} , $$

(10)

where $\Omega$ is the constant by the time scale $T_{0}$, but this is a function by the scale $T_{1}$.

Introducing relations (10) to the system (9), it is possible to write the following conditions of the secular terms elimination:

$$ \begin{aligned} \frac{{\partial\Omega }}{{\partial T_{1} }} & = \frac{1}{2}(\bar{A} + \bar{B}\Omega ) + \frac{1}{4}\bar{C}(C_{1} + \bar{C}_{1} ), \\ & \quad - 2i\Omega \frac{{\partial C_{1} }}{{\partial T_{1} }} + (\Delta + iL\Omega )C_{1} + 2C_{1} (\Omega T_{0} - i)\frac{{\partial\Omega }}{{\partial T_{1} }} - MC_{1}^{2} \bar{C}_{1} - PC_{1} C_{2} \bar{C}_{2} - iN = 0, \\ & \quad - 2i\omega_{2} \frac{{\partial C_{2} }}{{\partial T_{1} }} + iSC_{2} + RC_{2}^{2} \bar{C}_{2} + TC_{2} C_{1} \bar{C}_{1} = 0, \\ \end{aligned} $$

(11)

where $L = \frac{2}{{\beta_{2} - \beta_{1} }}(\beta_{1} \eta_{y} - \beta_{2} \eta_{x} )$, $P = \frac{{6(1 - \beta_{1} )(1 - \beta_{2} )^{2} }}{{\beta_{2} - \beta_{1} }}(\beta_{2} \gamma_{x} + \gamma_{y} )$, $N = \frac{{k\beta_{2} }}{{2(\beta_{2} - \beta_{1} )}}$, $M = \frac{{3(1 - \beta_{1} )^{3} }}{{\beta_{2} - \beta_{1} }}(\beta_{2} \gamma_{x} + \gamma_{y} )$, $S = \frac{{2\omega_{2} }}{{\beta_{2} - \beta_{1} }}(\beta_{1} \eta_{x} - \beta_{2} \eta_{y} )$, $T = \frac{{6(1 - \beta_{2} )(1 - \beta_{1} )^{2} }}{{\beta_{2} - \beta_{1} }}(\beta_{1} \gamma_{x} + \gamma_{y} )$, $R = \frac{{3(1 - \beta_{2} )^{3} }}{{\beta_{2} - \beta_{1} }}(\beta_{1} \gamma_{x} + \gamma_{y} ).$

By the change of variables, $C_{1} = a_{1} e^{{ib_{1} }}$, $C_{2} = a_{2} e^{{ib_{2} }}$ one has from the system (11) the following equations with respect to amplitudes and phases of the unknown solutions in the resonance domain, and the equation with respect to the variables $\Omega$:

$$ \begin{aligned} \frac{{\partial\Omega }}{{\partial T_{1} }} & = \frac{1}{2}(\bar{A} + \bar{B}\Omega + \bar{C}a_{1} \cos b_{1} ), \\ \frac{{\partial a_{1} }}{{\partial T_{1} }} & = \frac{L}{2}a_{1} - \frac{{a_{1} }}{\Omega }\frac{{\partial\Omega }}{{\partial T_{1} }} - \frac{N}{{2\Omega }}\cos b_{1} , \\ \frac{{\partial b_{1} }}{{\partial T_{1} }} & = - \frac{\Delta }{{2\Omega }} + \frac{M}{{2\Omega }}a_{1}^{2} + \frac{P}{{2\Omega }}a_{2}^{2} + T_{0} \frac{{\partial\Omega }}{{\partial T_{1} }} + \frac{N}{{2\Omega a_{1} }}\sin b{}_{1}, \\ \frac{{\partial a_{2} }}{{\partial T_{1} }} & = \frac{S}{{2\omega_{2} }}a_{2} , \\ \frac{{\partial b_{2} }}{{\partial T_{1} }} & = - \frac{R}{{2\omega_{2} }}a_{2}^{2} - \frac{T}{{2\omega_{2} }}a_{1}^{2} . \\ \end{aligned} $$

(12)

Note that the first equation of the system (12) corresponds to unsteady regime when the variable $\Omega$ changes in time. If $\Omega = const$, one obtains the well-known relation [17, 19, 20] connecting the rotor constant and amplitude of the elastic vibration as $L(\Omega ) - H(\Omega ) - 0,5\Omega \eta A_{1}^{2} = 0$, where $A_{1} = 2a_{1}$ is the vibration amplitude, and $\eta$ is a coefficient of dissipation. Here the unsteady behavior of the non-ideal system under consideration is investigated. The change of variables, $a_{1} = K\,\sin \psi$, $a_{2} = K\,\cos \psi$, is introduced, and the following reduced system [13,14,15] is obtained:

$$ \begin{aligned} \frac{{\partial\Omega }}{{\partial T_{1} }} & = \frac{1}{2}(\bar{A} + \bar{B}\Omega + \bar{C}K\,\sin \psi \,\cos b_{1} ), \\ \frac{\partial K}{{\partial T_{1} }} & = \frac{{L\Omega - \bar{A} - \bar{B}\Omega }}{{2\Omega }}K\,\sin^{2} \psi + \frac{S}{{2\omega_{2} }}K\,\cos^{2} \psi - \left( {\frac{{\bar{C}}}{{2\Omega }}K^{2} \sin^{2} \psi + \frac{N}{{2\Omega }}} \right)\cos b_{1} \sin \psi , \\ \frac{\partial \psi }{{\partial T_{1} }} & = \left( {\frac{{L\Omega - \bar{A} - \bar{B}\Omega }}{{2\Omega }} - \frac{S}{{2\omega_{2} }}} \right)\sin \psi \,\cos \psi - \left( {\frac{{\bar{C}}}{{2\Omega }}K\,\sin^{2} \psi + \frac{N}{{2\Omega K}}} \right)\cos \psi \,\cos b_{1} , \\ \frac{{\partial b_{1} }}{{\partial T_{1} }} & = - \frac{{\Delta +\Omega T_{0} (\bar{A} + \bar{B}\Omega )}}{{2\Omega }} - \frac{{T_{0} \bar{C}}}{2}K\,\sin \psi \,\cos b_{1} + \frac{M}{{2\Omega }}K^{2} \sin^{2} \psi + \frac{P}{{2\Omega }}K^{2} \cos^{2} \psi + \frac{N}{{2\Omega K\,\sin \psi }}\sin b{}_{1}, \\ \frac{{\partial b_{2} }}{{\partial T_{1} }} & = - \frac{R}{{2\omega_{2} }}K^{2} \cos^{2} \psi - \frac{T}{{2\omega_{2} }}K^{2} \sin^{2} \psi , \\ \end{aligned} $$

(13)

where the variable parameter $K$ characterizes the reduced system energy; $\psi$ is an arctangent of ratio of amplitudes. Equation with respect to difference of phases, $\varphi = b_{1} - b_{2}$ can be written as

$$ \begin{aligned} \frac{\partial \varphi }{{\partial T_{1} }} & = - \frac{{\Delta +\Omega T_{0} (\bar{A} + \bar{B}\Omega )}}{{2\Omega }} - \frac{{T_{0} \bar{C}}}{2}K\,\sin \psi \,\cos b_{1} + \frac{M}{{2\Omega }}K^{2} \sin^{2} \psi + \frac{P}{{2\Omega }}K^{2} \cos^{2} \psi \\ & \quad + \frac{N}{{2\Omega K\,\sin \psi }}\sin b{}_{1} + \frac{R}{{2\omega_{2} }}K^{2} \cos^{2} \psi + \frac{T}{{2\omega_{2} }}K^{2} \sin^{2} \psi . \\ \end{aligned} $$

(14)

One analyzes the equilibriums in the Eqs. (13), (14). The relation $\sin \psi = 0$ corresponds to energy localization on the coordinate $z_{2}$, and the relation $\cos \psi = 0$ corresponds to energy localization on the coordinate $z_{1}$.

Under the relation $\sin \psi = 0$ a condition of existence of the equilibrium in the third equation of the system (13) gives us the equation $\cos b_{1} = 0$. This equilibrium corresponds to the following relation for the energy: $\frac{\partial K}{{\partial T_{1} }} = \frac{S}{{2\omega_{2} }}K$. Taking into account that the parameter $S$ is negative for any system parameters, we can conclude that the energy of this equilibrium position decreases; so, the localized vibrations are unstable. If $\cos \psi = 0$, the third equation of the system (13) is an identity. So, this equilibrium position of the reduced system is situated at the straight line $\psi = \frac{\pi }{2}$. In this case a conclusion about change of energy and stability of the equilibrium position can be made by analysis of trajectories in the place (φ, ψ).

For a case when both $\sin \psi \ne 0$ and $\cos \psi \ne 0$, an existence of the equilibrium position of the third equation of the system (13) is possible if $\cos b_{1} = \frac{{(L\Omega - \bar{A} - \bar{B}\Omega - S\Omega /\omega_{2} )K\,\sin \psi }}{{N + \bar{C}K^{2} \sin^{2} \psi }}$. One has from here the inequality $\left| {\frac{{(L\Omega - \bar{A} - \bar{B}\Omega - S\Omega /\omega_{2} )K\,\sin \psi }}{{N + \bar{C}K^{2} \sin^{2} \psi }}} \right| \le 1$. On the other hand, the function $\sin \psi$ can be found from the equation

$$ \bar{C}K^{2} \cos b_{1} \sin^{2} \psi - (L\Omega - \bar{A} - \bar{B}\Omega - S\Omega /\omega_{2} )K\,\sin \psi + N\,\cos b_{1} = 0, $$

that is, $\sin \psi = \frac{{(L\Omega - \bar{A} - \bar{B}\Omega - S\Omega /\omega_{2} ) \pm \sqrt {(L - \bar{A} - \bar{B}\Omega - S\Omega /\omega_{2} )^{2} - 4\bar{C}N\,\cos b_{1}^{2} } }}{{2\bar{C}K\,\cos b_{1} }}$.

One has from here an inequality, $\left| {\frac{{(L\Omega - \bar{A} - \bar{B}\Omega - S\Omega /\omega_{2} ) \pm \sqrt {(L - \bar{A} - \bar{B}\Omega - S\Omega /\omega_{2} )^{2} - 4\bar{C}N\,\cos b_{1}^{2} } }}{{2\bar{C}K\,\cos b_{1} }}} \right| \le 1$, and a condition of the discriminant positiveness as $(L\Omega - \bar{A} - \bar{B}\Omega - S\Omega /\omega_{2} )^{2} - 4\bar{C}N\,\cos b_{1}^{2} \ge 0$.

We can see from the Eq. (13) that in this case $\psi$ and $\varphi$ are functions of $K$, so, this equilibrium position is not stationary. This position corresponds to vibrations which are equivalent to NNMs of coupled vibrations of the conservative sub-system of the system (6). This mode of coupled vibrations is realized only for some specific value of time, corresponding to conditions presented above, so, it can be called as transient nonlinear vibration mode (TNNM). It is interesting that near this value of time motions of the system are close to the mode, that is, the TNNM is attractive.

The system (13) is integrated by the Runge–Kutta method; initial conditions take values on the interval $0 \le \psi (0) \le \pi /2$, and the following system parameters are chosen: $K(0) = 0.1$, $c_{0} = 1$ Ν/m, $c_{1} = 1$ Ν/m, $c_{2} = 0.2$ Ν/m, $M = 1$ kg, $m = 0.05$ kg, $\beta = 0.05$, $\gamma = 0.3$ Ν/m, $r = 0.05$ m, $\bar{A} = 0.115$, $\bar{B} = - 0.08$, $\bar{C} = 0.01$ and $\Delta (0) = - 0.5$. A dependence $\varphi (\psi )$ is shown in Fig. 4 where trajectories do not remain near the straight line $\psi = 0$, and tend in time to the line $\psi = \frac{\pi }{2}$, that is, localized on $z_{1}$ vibrations are stable near resonance, and localized on $z_{2}$ vibrations lose stability. Some trajectories approach the equilibrium position corresponding to the TNNM of coupled vibrations, and remain near this state while one exists. When the time increases the coupled vibrations disappear, and motions of the system tend to the stable localized mode.

Fig. 4

Dependence $\varphi (\psi )$ for the external resonance on the first fundamental frequency

The transfer from the localization on $z_{1}$ to the stable vibration mode of localization on $z_{2}$ is shown in Fig. 5. We can see that for some values of time trajectories in Fig. 5 are close to two TNNMs of the coupled vibrations which appear here.

Fig. 5

Dependences $z_{2}$ $(z_{1} )$ for the external resonance on the first fundamental frequency

Similar results can be obtained for a case of external resonance on the second fundamental frequency. For a case of both external and internal resonances after the transformation to reduced system and analysis of the system the following conclusions can be made (corresponding relations are not presented here): two localized vibration modes are TNNMs existing only for some values of time when the specific values of energy are reached. Any time only coupled vibrations exist in the system. The reduced system is integrated by the Runge–Kutta method. Initial conditions are changed on the interval 0 ≤ ψ(0) ≤ π/2, and the next system parameters are chosen: $K(0) = 0.1$, $c_{0} = 0.1$ Ν/m, $c_{1} = 0.14$ Ν/m, $c_{2} = 0.01$ Ν/m, $M = 1$ kg, $m = 0.1$ kg, $\beta = 0.2$, $\gamma = 1.5$ Ν/m, $r = 2.1$ m, $\bar{A} = 0.02$, $\bar{B} = - 0.009$, $\bar{C} = 0.005$ and $\Delta (0) = 0.04$. Dependence $\varphi (\psi )$ is shown in Fig. 6 where we can see two equilibrium positions corresponding to coupled vibrations of the elastic subsystem and absorber. TNNMs correspond to ψ = 0 and π/2. All trajectories pass from the equilibrium position at the top of the figure to the equilibrium position in the bottom of the figure, the last one corresponds to the stable mode of coupled vibrations. The obtained results are confirmed by direct numerical simulation of the initial nonlinear system.

Fig. 6

Dependence $\varphi (\psi )$ for the both external and internal resonances

4 Transient Nonlinear Normal Modes in Dissipative Spring-Pendulum System Under Resonance Conditions

The spring-pendulum system with small dissipation under external periodic excitation is considered (Fig. 7).

Fig. 7

Spring-pendulum system

Equations of motion of the system are the following:

$$ \begin{aligned} & \ddot{u} + \omega_{u}^{2} x + \varepsilon \eta_{u} \dot{u} - \mu (\ddot{\theta }\sin \theta + \dot{\theta }^{2} \cos \theta ) = \varepsilon^{2} f\,\cos \tau , \\ & \ddot{\theta } + \varepsilon \eta_{\theta } \dot{\theta } + p^{2} \sin \theta - \ddot{u}\,\sin \theta = 0, \\ \end{aligned} $$

(15)

where $u = \frac{y}{R}$, $\tau =\Omega t$, $\omega = \sqrt {\frac{k}{M + m}}$, $p^{2} = \frac{g}{R\varOmega }$, $\mu = m/(m + M)$, $\omega_{u}^{2} = 1/\varOmega^{2}$, $f = \frac{{F_{0} }}{{(M + m)R\omega^{2} \varOmega^{2} }}$, $\eta {}_{u} = \frac{{\beta_{u} }}{(M + m)\varOmega }$, $\eta_{\theta } = \frac{{\beta_{\theta } }}{m\varOmega }$; $\beta_{u}$ and $\beta_{\theta }$ are coefficients of dissipation; ε is the small parameter.

There are two Kauderer–Rosenberg NNMs in the system (15) without dissipation and external excitation: the localized $u -$ mode of vertical vibrations $(u = u(\tau ),\theta = 0)$ and the non-localized mode, when vibration amplitudes for vertical and angle coordinates are comparable. When dissipation exists, vibration modes are not the Kauderer–Rosenberg NNMs, because they are not periodic.

To consider motions of the system under consideration in the vicinity of both external and internal resonances one introduces to equations of motion (15) two detuning parameters $\varDelta_{1}$ and $\varDelta_{2}$ by two relations. First relation, $\omega_{u}^{2} = 1 + \varepsilon \varDelta_{1}$ corresponds to the vicinity of external resonance, and the second one, $p^{2} = 0.25 \,+\, \varepsilon \Delta_{2}$ corresponds to the vicinity of the main parametrical resonance of the system (15). Using these resonance relations and expansions in power series for sinθ and cosθ, one has the following equations of the first and second approximations by the small parameter ε:

$$ \begin{aligned} & \frac{{\partial^{2} u_{0} }}{{\partial T_{0}^{2} }} + u_{0} = 0, \\ & \frac{{\partial^{2} \theta_{0} }}{{\partial T_{0}^{2} }} + \frac{1}{4}\theta_{0} = 0, \\ \end{aligned} $$

(16)

$$ \begin{aligned} \frac{{\partial^{2} u_{1} }}{{\partial T_{0}^{2} }} + u_{1} & = - \Delta_{1} u_{0} - 2\frac{{\partial^{2} u_{0} }}{{\partial T_{1} \partial T_{0} }} + \mu \left( {\frac{{\partial^{2} \theta_{0} }}{{\partial T_{0}^{2} }}} \right)\theta_{0} + \mu \left( {\frac{{\partial \theta_{0} }}{{\partial T_{0} }}} \right)^{2} - \eta_{u} \frac{{\partial u_{0} }}{{\partial T_{0} }} + \frac{f}{2}(e^{{iT_{0} }} + e^{{ - iT_{0} }} ), \\ \frac{{\partial^{2} \theta_{1} }}{{\partial T_{0}^{2} }} + \theta_{1} & = - \Delta_{2} \theta_{0} - 2\frac{{\partial^{2} \theta_{0} }}{{\partial T_{1} \partial T_{0} }} + \left( {\frac{{\partial^{2} u_{0} }}{{\partial T_{0}^{2} }}} \right)\theta_{0} - \eta_{\theta } \frac{{\partial \theta_{0} }}{{\partial T_{0} }}. \\ \end{aligned} $$

(17)

Solution of the system (16),

$$ \begin{aligned} u_{0} & = C_{u} (T_{1} )e^{{iT_{0} }} + \bar{C}_{u} (T_{1} )e^{{ - iT_{0} }} , \\ \theta_{0} & = C_{\theta } (T_{1} )e^{{\frac{1}{2}iT_{0} }} + \bar{C}_{\theta } (T_{1} )e^{{ - \frac{1}{2}iT_{0} }} , \\ \end{aligned} $$

(18)

is substituted to Eq. (17). Then secular terms are eliminated; as a result, one has the following nonlinear equations:

$$ \begin{aligned} & 2i\frac{{\partial C_{u} }}{{\partial T_{1} }} + \frac{\mu }{2}C_{\theta }^{2} + C_{u} \Delta_{1} + i\eta_{u} C_{u} - \frac{f}{2} = 0, \\ & i\frac{{\partial C_{\theta } }}{{\partial T_{1} }} + C_{u} \bar{C}_{\theta } + C_{\theta } \Delta_{2} + \frac{1}{2}i\eta_{\theta } C_{\theta } = 0. \\ \end{aligned} $$

(19)

Change of variables, $C_{u} = a_{u} e^{{i\beta_{u} }}$, $C_{\theta } = a_{\theta } e^{{i\beta_{\theta } }}$ gives the system of modulation equations written with respect to amplitudes $a_{u}$, $a_{\theta }$ and phases $\beta {}_{u}$, $\beta {}_{\theta }$. Next change of variables, $a_{u} = \frac{\sqrt \mu }{2}K\,\cos \psi$, $a_{\theta } = K\,\sin \psi$, gives the reduced system, written with respect to the energy K, the arctangent of the amplitudes ratio $\psi$ and the phases $\beta {}_{u}$, $\beta {}_{\theta }$:

$$ \begin{aligned} K^{{\prime }} & = - K\left( {\frac{{\eta_{u} }}{2}\cos^{2} \psi + \frac{{\eta_{\theta } }}{2}\sin^{2} \psi } \right) - \frac{f}{2\sqrt \mu }\sin \beta_{u} \cos \psi , \\ \psi^{{\prime }} & = \sin \psi \left. {\left( {\frac{\sqrt \mu }{2}K\,\sin (2\beta_{\theta } - \beta_{u} )} \right. + \frac{{\eta_{u} - \eta_{\theta } }}{2}\cos \psi + \frac{f}{2\sqrt \mu K}\sin \beta_{u} } \right), \\ \beta_{u}^{{\prime }} & = \frac{{\Delta_{1} }}{2} + \frac{\sqrt \mu }{2}\frac{{K\,\sin^{2} \psi }}{\cos \psi }\cos (2\beta_{\theta } - \beta_{u} ) - \frac{f}{2\sqrt \mu K\,\cos \psi }\cos \beta_{u} , \\ \beta_{\theta }^{{\prime }} & = \Delta_{2} + \frac{\sqrt \mu }{2}K\,\cos \psi \,\cos (2\beta_{\theta } - \beta_{u} ). \\ \end{aligned} $$

(20)

Equilibrium positions for the second equation of the system (20) are considered. Condition $\sin \psi \equiv 0$ corresponds to the localized mode of the spring vibrations. This mode exists for all values of the energy $K$; it is described by the straight line $\psi = 0$ in the plane $(\psi ,\varphi )$. For the case, when both $\cos \psi \ne 0$, and $\sin \psi \ne 0$, it is possible to observe mode of coupled vibrations of the system (15). Condition of the mode existence can be obtained from the second equation of the reduced system (20) as $\cos \psi = \frac{\sqrt \mu }{{\eta_{\theta } - \eta_{u} }}K\,\sin (2\beta_{\theta } - \beta_{u} ) + \frac{f}{{2\sqrt \mu K(\eta_{\theta } - \eta_{u} )}}\sin \beta_{u}$. This condition corresponds to two modes of coupled vibrations. The further examination shows that one of them is stable and another one is the transient mode of coupled vibrations.

To construct trajectories in the place $(\psi ,\varphi )$ the system (20) is integrated numerically, when the initial value of arctangent of the amplitudes ratio changes on the interval $0 \le \psi (0) \le \frac{\pi }{2}$, $K(0) = 0.5$ and system parameters are the following: $\eta_{u} = 0.3$, $\eta_{\theta } = 0.2$, $\mu = 0.4$, $\Delta_{1} = 0.2$, $\Delta_{2} = 0.1$, $f = 0.35$. Trajectories in the place $(\psi ,\varphi )$ for the case of simultaneous external and internal resonances are shown in Fig. 8. Each trajectory has a loop near some quasi-equilibrium state of the reduced system. This state moves in the space $(\psi ,\varphi )$ and corresponds to TNNM of coupled vibrations existing only for specific values of the system energy, that is, the TNNM exist in some moments of time corresponding to these energy levels. This transient mode is attractive and other motions are close to this TNNM near the mentioned moment of time. We can see in the Fig. 8, that later, when the TNNM disappears, trajectories in the plane $(\psi ,\varphi )$ approach the equilibrium position which corresponds to the stable mode of coupled vibrations. Note that this equilibrium position is closer to the straight line $\psi = \frac{\pi }{2}$, which corresponds to localized on pendulum vibrations, than to the straight line $\psi = 0$, which corresponds to localized vibrations of spring. We can see that the mode of the localized vibrations of spring is not stable.

Fig. 8

Trajectories in the place $(\psi ,\varphi )$

To illustrate behavior of the spring-pendulum system in vicinity of the resonance the initial system is integrated numerically on the interval $\tau \in [0,\,5000]$ for the following initial values $a_{u} (0) = 0.05$, $a_{\theta } (0) = 0.01$, $\beta_{u} (0) = 0.1$, $\beta_{\theta } (0) = 0.2$ and system parameters $\eta_{u} = 0.3$, $\eta_{\theta } = 0.2$, $f = 0.35$, $\Delta_{1} = 0.2$, $\Delta_{2} = 0.1$. The first approximation of the solution can be written as $u_{0} = 2a{}_{u}\cos (\tau + \beta_{u} )$, $\theta_{0} = 2a{}_{\theta }\cos (\frac{1}{2}\tau + \beta_{\theta } )$. Trajectories in the system configuration plane are shown in Fig. 9 for the following intervals of time: $\tau \in [0,\,100]$ (Fig. 8a), $\tau \in [4800,\,5000]$ (Fig. 8b) and $\tau \in [0,\,5000]$ (Fig. 8c). Here the transient nonlinear normal mode of coupled vibrations appears. At the beginning of the process motions of the system are close to this TNNM which is determined by parabolic trajectory (Fig. 8a). Then, due to instability of this mode, motions of the system tend to the stable mode of coupled vibrations. Trajectory of this stable mode can be observed in Fig. 8b where vibrations for large values of time are shown. The stable mode is close to the localized mode of the pendulum vibrations, and this fact can be used in the problem of vibration absorption. Namely, it is possible to guarantee the energy transfer from vibrations of spring to vibrations of pendulum, where the vibration energy can be dissipated. It is clear that the numerical simulation fully confirms results obtained by analysis of the reduced system.

Fig. 9

Trajectories $u(\theta )$ in configuration space for $t \in [0,\,100]$ (a); $t \in [4800,\,5000]$ (b); $t \in [0,\,5000]$ (c)

5 Conclusion

The NNMs which are different from the NNMs proposed by Kauderer–Rosenberg are obtained in some non-conservative systems. Namely, NNMs having smooth trajectories in configuration space and chaotic in time behavior can be found in analysis of some of elastic systems. It seems that this is typical situation in post-buckling dynamics of shells, arches etc.

Resonance dynamics of the dissipative limited power-supply system with a nonlinear vibration absorber and the dissipative spring-pendulum system is investigated by the multiple-scale method and transformation to the reduced system. In the non-ideal system, in the case of external resonance on the first fundamental frequency, except the localized vibration modes, the TNNM of coupled vibrations appears. This mode exists only for some value of energy, that is, for a single moment of time. This mode is attractive near the mentioned moment of time. In the case of simultaneous external and internal resonances two modes of coupled vibrations appear; one of them is unstable, and motions of the system come close to the stable NNMs of the coupled vibrations. Two localized modes are TNNMs in this case. Existence of the localized modes depends on the energy levels and the system parameters; they are attractive near moments of their existence. For the dissipative spring-pendulum system in the case of simultaneous external and internal resonances the mode of coupled vibrations is stable, and the localized mode loses stability. The TNNM also exists here for some level of the system energy. Reliability of obtained analytical results is verified by numerical simulation. We can conclude that such transient normal modes essentially affects to transient process of the nonlinear dissipative system.