6.1 Introduction

The study of size-dependent properties of matter is a fascinating subject, because it challenges our physical and chemical intuition, which is mostly based on the behavior of the bulk material. What is found both experimentally is that properties of materials are strongly size-dependent. Thus, when particle size is in the nanoscale, optical, electric, chemical, and magnetic properties change as a function of the size of the particle. Such a dependence can be justified in terms of quantum models because the distribution of energy levels and the geometry of a system are determined by the solution to Schrödinger equation, which in turn governs the electronic structure and the interatomic distances, key quantities in determining the properties of a material.

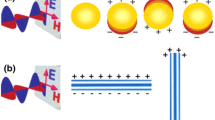
In this tutorial, we will mostly be interested in how the optical response of molecules is affected by their interactions with nanoparticles . In the first part, we will consider the case of plasmonic materials, e.g., gold and silver, which exhibit localized surface plasmons (LSP). The simplest way to describe plasmons is to consider them as excitations of an electron gas, which in this context is represented by the conduction electrons of the metal. LSP are non-propagating excitations of the conduction electrons of metallic nanostructures coupled to an external electromagnetic field. This response is resonant in nature as a function of the frequency of the field, which translates into an induced polarizability that exhibits a maximum, known as a localized plasmon resonance (PR). As a consequence, the radiation absorption intensity exhibits a maximum at the plasmon resonance, which is also correlated with the phenomenon of field amplification both inside and in the near-field zone outside the nanoparticle. This field enhancement is responsible for a variety of optical responses, e.g., fluorescence and Raman of molecules either chemically bonded or nonbonded to the metal nanoparticle. In the specific case of surface-enhanced Raman spectroscopy , the field enhancement factor of the molecular response can reach 12 orders of magnitude. This is a key element in the design of plasmonic sensors.

In the second part of this tutorial, we will consider the optical response of molecules chemically attached to the surface of a metal oxide, e.g., TiO2. These materials are bulk semiconductors with a band gap that prevents the formation of plasmons, which requires the presence of delocalized conduction electrons, at least in their ground state. As a consequence, the field enhancement mechanism is absent in these nanoparticles, However, processes of interfacial charge transfer determine the appearance of chemically induced enhancement in the SERS response and a strong quenching of fluorescence in molecules attached to the nanoparticle, which are essential for the design of molecular senses using non-plasmonic materials.

6.2 Nanosensors

Very efficient sensors can be developed by using the properties of matter at the nanoscale. Several such sensors have been developed by taking advantage of changes in the melting point, fluorescence, electrical conductivity, magnetic permeability, and chemical reactivity, as well as the large surface to volume ratio of nanoparticles. These properties of nanomaterials can be used in generating a signal when analyte molecules interact with the nanoparticle, which acts as a functional unit in a sensing device.

The basic schematics for the design of a sensor are displayed in Fig. 6.1.

Fig. 6.1
figure 1

Schematic of a nanosensor

Full size image

6.3 PR-based Sensors

Since field amplification occurs both inside and in the near-field zone outside the plasmonic nanoparticles, their use as sensors is possible even in the absence of chemical bond between the molecular analyte and the NP. But, before analyzing the changes in the plasmonic response of a NP due to the presence of a molecular analyte, which is our main objective here, it is important to have a basic description of the optical response of a plasmonic NP to an external electromagnetic field. In what follows we follow closely the treatment in S. A. Maier’s book, Plasmonics: Fundamentals and Applications. Springer 2007.

6.3.1 Dielectric Function and Conductivity

The first step to describe the optical response of a material is to establish a connection between the dielectric function and the conductivity. We start by recalling Maxwell’s equation, which governs the electromagnetic response and field propagation. We write these fundamental equations in the following form:

$$ \bigtriangledown .\mathbf{D}={\rho}_{\mathrm{ext}} $$
(6.1a)
$$ \bigtriangledown .\mathbf{B}=0 $$
(6.1b)
$$ \bigtriangledown \times \mathbf{E}=-\frac{\mathit{\partial}\mathbf{B}}{\mathit{\partial}\mathbf{t}} $$
(6.1c)
$$ \bigtriangledown \times \mathbf{H}={\mathbf{J}}_{\mathrm{ext}}+\frac{\mathit{\partial}\mathbf{D}}{\mathit{\partial t}} $$
(6.1d)

where D, B, E, and H are the dielectric displacement, the magnetic induction, the electric field, and the magnetic field. These equations link the four macroscopic fields, with the external charge, ρext, and the current density Jext. This form of writing Maxwell’s equations is convenient for the description of optical response, because the charge and the current density are divided as sums of internal and external contributions, that is, ρtot = ρext + ρ, and Jtot = Jext + J. In this description, the external components drive the system, while the internal set responds to the external stimuli.

The two auxiliary fields, D and H, are defined by

$$ \mathbf{D}={\varepsilon}_o\mathbf{E}+\mathbf{P} $$
(6.2a)
$$ \mathbf{H}=\frac{1}{\mu_o}\mathbf{B}-\mathbf{M} $$
(6.2b)

where P is the polarization, M is the magnetization, and εo and μo are the electric permittivity and magnetic permeability of vacuum, respectively.

For linear, isotropic, and nonmagnetic media , one can introduce the constitutive relations

$$ \mathbf{D}={\varepsilon}_o\varepsilon \mathbf{E} $$
(6.3a)
$$ \mathbf{B}={\mu}_o\mu \mathbf{B} $$
(6.3b)

In these equations ε is the dielectric constant, and μ is the relative permeability. The linear relationship between D and E is equivalent to the equation used in describing the optical response of a material under the influence of an external electric field

$$ \mathbf{P}={\varepsilon}_o\chi \mathbf{E} $$
(6.4)

where χ is the dielectric susceptibility. Inserting (6.4) and (6.2a) into (6.3a) yields the important equation ε = 1 + χ.

In the linear response regime, another important relationship between the internal current density and the electric field can be established, by introducing the conductivity σ.

$$ \mathbf{J}=\sigma \mathbf{E} $$
(6.5)

To describe the optical response of metals, one needs to generalize Eqs. (6.3a) and (6.5) to take into account the non-locality in time and space. This leads to considering the general equations

$$ \mathbf{D}\left(\mathbf{r},t\right)={\varepsilon}_o\int {dt}^{\hbox{'}}{dr}^{\hbox{'}}\varepsilon \left(\mathbf{r}-{\mathbf{r}}^{\hbox{'}},t-{t}^{\hbox{'}}\right)E\left({\mathbf{r}}^{\hbox{'}},{t}^{\hbox{'}}\right) $$
(6.6a)
$$ \mathbf{J}\left(\mathbf{r},t\right)={\varepsilon}_o\int {dt}^{\hbox{'}}{dr}^{\hbox{'}}\sigma \left(\mathbf{r}-{\mathbf{r}}^{\hbox{'}},t-{t}^{\hbox{'}}\right)E\left({\mathbf{r}}^{\hbox{'}},{t}^{\hbox{'}}\right) $$
(6.6b)

taking the Fourier transform of these two fields

$$ \mathbf{D}\left(\mathbf{k},\omega \right)=\int dtd\mathbf{r}{e}^{i\left(\mathbf{k}.\mathbf{r}-\omega t\right)}\mathbf{D}\left(\mathbf{r},t\right) $$
(6.7a)
$$ \mathbf{J}\left(\mathbf{k},\omega \right)=\int dtd\mathbf{r}{e}^{i\left(\mathbf{k}.\mathbf{r}-\omega t\right)}\mathbf{J}\left(\mathbf{r},t\right) $$
(6.7b)

Using Eqs. (6.7a) and (6.7b) together with Eqs. (6.2a) and (6.2b), it is possible to derive a fundamental relationship between the dielectric function and the conductivity.

$$ \varepsilon \left(\mathbf{k},\omega \right)=1+\frac{i\sigma \left(\mathbf{k},\omega \right)}{\varepsilon_0\omega } $$
(6.8)

6.3.1.1 Drude Model for a Free Electron Gas

The simplest model for a metal consists of treating conduction electrons as a classical “gas” of free electrons with density n. The electrons in this plasma oscillate in response to the field, and their motion is damped due to collisions occurring with a characteristic collision frequency γ = 1/τ, where τ is the relaxation time of the free electron gas.

The Newton equation of motion for an electron of the plasma under the influence of an external field E is then

$$ m\ddot{\mathbf{x}}+ m\gamma \dot{\mathbf{x}}=-e\mathbf{E} $$
(6.9)

The displaced electrons contribute to the macroscopic polarization

$$ \mathbf{P}=- ne\mathbf{x} $$
(6.10)

Assuming a simple field of the form E(t) = Eoe−iωt, and solving Eq. (6.9), it can be calculated to be

$$ \mathbf{P}=-\frac{ne^2}{m\left({\omega}^2+ i\gamma \omega \right)}\mathbf{E} $$
(6.11)

Inserting this equation into Eq. ((6.2a), we obtain

$$ \mathbf{D}={\varepsilon}_o\left(1-\frac{\omega_p^2}{m\left({\omega}^2+ i\gamma \omega \right)}\right)\mathbf{E} $$
(6.12)

where \( {\omega}_p^2=\frac{ne^2}{\varepsilon_om} \) is the plasma frequency of the electron gas. The frequency-dependent complex dielectric function of the electron gas is then

$$ \varepsilon \left(\omega \right)=1-\frac{\omega_p^2}{\omega^2+ i\gamma \omega} $$
(6.13)

6.3.1.2 Mie Theory

A semiclassical description of the response of a metal NP to an electromagnetic field is given by Mie theory , which is an appropriate level of description of many applications where the details of the quantum description are not required. We use here the metallic nanoparticle boundary element method (MNPBEM) toolbox version of Mie model.

6.3.1.2.1 Quasistatic Approximation

The primary aim of the MNPBEM toolbox is solving Maxwell’s equations using boundary conditions of the particles’ surface in order to calculate the stimulated electromagnetic fields.

A quasistatic approximation can be implemented when the particles are much smaller than the wavelength of the external electromagnetic field.

The electrostatic potential is solved for while maintaining full frequency-dependent dielectric functions when considering boundary conditions by solving the Poisson-Laplace equation. This is an unbounded, homogenous point surface solution of the Poisson equation including electrostatic Green function:

∇ 2 G r r ′ =−4πδ r − r ′
(6.14)
$$ G\left(\boldsymbol{r}-{\boldsymbol{r}}^{\prime}\right)=\frac{1}{\left|\boldsymbol{r}-{\boldsymbol{r}}^{\prime}\right|} $$
(6.15)

where G represents the Green function from the Coulomb equation and r represents the distance from the center of mass.

In this case we have an inhomogeneous dielectric environment , so the boundaries are split between the gold nanoparticle and the surrounding medium.

$$ \phi \left(\boldsymbol{r}\right)={\phi}_{ext}\left(\boldsymbol{r}\right)+{\oint}_{V_i}G\left(\boldsymbol{r},\boldsymbol{s}\right)\rho \left(\boldsymbol{s}\right) da $$
(6.16)

ϕ and ϕext represent the electrostatic potential and the external electrostatic potential, respectively. ρ(s) is the surface charge distribution located at the particle boundary, ρ(s) is the surface charge distribution located at the boundary, ∂Vi. \( \frac{\partial }{\partial n} \) denotes the derivative along the direction of the outer surface normal, and ε1 and ε2 are the dielectric functions of the particles and the medium that it sits, respectively.

$$ \Lambda \rho \left(\boldsymbol{s}\right)+\oint \frac{\partial G\left(\boldsymbol{s},{\boldsymbol{s}}^{\prime}\right)}{\partial n}\rho \left(\boldsymbol{s}\right)d{a}^{\prime }=-\frac{\partial {\phi}_{\mathrm{ext}}\left(\boldsymbol{s}\right)}{\partial n},\Lambda =2\pi \frac{\varepsilon_2+{\varepsilon}_1}{\varepsilon_2-{\varepsilon}_1} $$
(6.17)

This is used to elucidate the surface charge distribution ρ.

Λ is governed by the dielectric functions in- and outside the particle boundaries. ε1 and ε2 represent the two dielectric functions, the first represents inside of the gold nanoparticle and the second the medium, water, in which the particle sits.

$$ \Lambda {\rho}_i+{\sum}_j{\left(\frac{\partial G}{\partial n}\right)}_{ij}\rho =-{\left(\frac{\partial {\phi}_{\mathrm{ext}}}{\partial n}\right)}_i $$
(6.18)

ρ represents surface charges which can be elucidated by simple matrix inversion. The surface derivative \( {\left(\frac{\partial G}{\partial n}\right)}_{ij} \) of the Green function connects surface element i and j, and the surface derivative \( {\left(\frac{\partial G}{\partial n}\right)}_{ij} \) of the external potential.

6.3.1.2.2 Full Maxwell’s Equations

6.3.1.3 Helmholtz Equation and Green Function

∇ 2 + k i 2 G i r r ′ =−4πδ r − r ′ , G i r r ′ = e ik i r − r ′ r − r ′
(6.19)

\( {k}_i=\sqrt{\varepsilon_i}k \) is the wavenumber in the medium.

\( k=\frac{\omega }{c} \) is the wavenumber in a vacuum and c is the speed of light.

The magnetic permeability μ is set to one throughout.

6.3.1.4 For an Inhomogeneous Dielectric Environment

$$ \phi \left(\boldsymbol{r}\right)={\phi}_{ext}\left(\boldsymbol{r}\right)+{\oint}_{V_i}{G}_i\left(\boldsymbol{r},\boldsymbol{s}\right){\sigma}_i\left(\boldsymbol{s}\right) da $$
(6.20)
$$ \boldsymbol{A}\left(\boldsymbol{r}\right)={\boldsymbol{A}}_{ext}\left(\boldsymbol{r}\right)+{\oint}_{V_i}{G}_i\left(\boldsymbol{r},\boldsymbol{s}\right){\boldsymbol{h}}_i\left(\boldsymbol{s}\right) da $$
(6.21)

This fulfills the Helmholtz equations everywhere except at the particle boundaries. σi and hi are surface charge and current distributions, and φext and Aext are the scalar and vector potentials characterizing the external perturbation . The scalar and vector potentials are additionally related through the Lorentz gauge condition ∇ ⋅ A = ikεϕ.

6.3.1.4.1 Dielectric Environment

This defines that the particle is closed by the following summation rule.

$$ {\oint}_{\partial {V}_i}\frac{\partial G\left(\boldsymbol{s},{\boldsymbol{s}}^{\prime}\right)}{\partial n}d{a}^{\prime }=2\pi, {\sum}_j{\left(\frac{\partial G}{\partial n}\right)}_{ij}=2\pi $$
(6.22)

An oscillating dipole d is assumed to be located in the vicinity of a metallic nanosphere, and the corresponding equations in Mie theory need to be adjusted to calculate the resulting electric field.

$$ \boldsymbol{E}\left(\boldsymbol{r}\right)={k}^2\boldsymbol{G}\left(\boldsymbol{r},{\boldsymbol{r}}^{\prime };\omega \right).\boldsymbol{d} $$
(6.23)
$$ \boldsymbol{k}=\frac{\omega }{c} $$
(6.24)

The resulting physical description can be used to model changes in the plasmonic response with a metal NP due to both the presence of a dipole that represents a discrete structure mimicking a molecule and a solvent characterized by a dielectric constant.

6.3.2 A Showcase: Using PR to Diagnose Infectious Diseases

The design of new nanosensors for biomedical applications requires a concerted theory-experiment to optimize both the fabrication conditions and the interpretation of the measurements within a relatively simple conceptual framework [1,2,3]. As mentioned in the introduction, the general strategy for the design of nanosensors based on photonic materials such as the noble metals involves using the plasmonic resonance as basic optical signal, whose intensity, shift, and splitting characterize the response of the system [4,5,6]. Changes in the plasmonic response are due to combination of chemical and physical factors, e.g., molecule-nanoparticle charge transfer, or changes in the dielectric constant of the medium associated with the coating of the nanoparticle with the chemical species involved in the detection process [5, 7,8,9,10,11]. For biomedical applications, the coating agent is frequently one of the two members of the antigen-antibody pair involved in the immune response [3, 12, 13].

In this section, we describe the main results of our investigation about the interaction between bovine serum albumin (BSA) and gold colloids using ultraviolet (UV) and visible light absorption spectroscopy measurements to determine the surface coverage and binding activity [4,5,6, 13, 14]. The binding of BSA to the ubiquitous citrate-coated gold nanoparticles (AuNP) suggests an electrostatic interaction mechanism [11, 13, 15]. Surface coverage on the colloids is based on the concentration of BSA [10]. The measurements of the surface plasmon resonance (SPR) show that BSA and citrate-coated AuNP achieve stabilization and surface coverage at or above the isoelectric point (~4.7) and that the optical response of the system corresponds to a change in intensity only of the SPR [4,5,6, 8, 10]. The data supports a non-covalent and non-spontaneous binding mechanism of gold colloids and shows a maximum surface coverage that is dependent on concentration [10, 13].

Our hypothesis is that AuNP flip surface charges of the antibodies and bind non-covalently due to electrostatic and hydrophobic interactions [8, 10, 13, 16]. This causes the SPR intensity to decrease because of the monolayer coating disrupting the signal [13, 17, 18]. To achieve this non-covalent binding mechanism, the pH of the buffer used for conjugation to the gold nanoparticles must have a negative net charge [2, 8]. Usually this means that the pH is above the isoelectric point (pI) of the protein or antibody and for BSA this value is ~4.7, so the buffer must be above a pH of 5 [2, 8, 10, 11, 13, 15]. The ubiquitous citrate coating of the AuNPs in dH2O ensures that the net charge remains negative.

The results indicate that a simple theoretical framework, based on Mie theory, can explain the most important experimental trends. The key feature is that the optical response depends on choosing a dielectric constant, which in turn is determined by the conditions of electrostatic equilibrium [5, 8]. The MNPBEM toolbox is a flexible software that can simulate metallic nanoparticles, specifically gold nanoparticles using boundary element method [19]. The toolbox will set up homogeneous, isotropic dielectric functions with strict boundaries, which will then be used to calculate and solve Maxwell’s equations and compare to Mie theory. By writing, manipulating, and altering the coded data within the toolkit, a very reasonable representation of the experimental system can be achieved.

6.4 Experimental Results

6.4.1 Methods

6.4.1.1 Conjugation of AuNP and BSA

Three standard bovine serum albumin (BSA – 1 mg/ml stock solution) solutions were prepared and diluted with concentrations ranging from 1 mg/ml to 1 μg/ml. This was done by adding 10 mg BSA to 10 ml of dH2O to a 15 ml centrifuge tube. Similarly, a second and third dilution was done by adding 9 ml of dH2O to 15 ml centrifuge tubes and adding 1 ml of the 1 mg/ml BSA solution and 0.1 mg/ml BSA solution, respectively, for total volumes of 10 ml. Gold nanoparticles from Ted Pella , Inc. were aliquoted in 2 ml Eppendorf tubes with 1 ml of 20 nm AuNP containing 7 × 1010 particles/ml and 60 nm AuNP containing 2.6 × 1010 particles/ml in 0.1 M phosphate buffer (pH = 7). With 0.2 ml PCR tubes, 6 concentrations of BSA and the AuNP with phosphate buffer were prepared ranging from 0.024 mg/ml to 0.2 mg/ml. The tubes incubated at 37 ° C for 10 min. Each concentration was measured in triplicate using a UV-visible light spectrophotometer.

6.4.1.2 UV-Vis Spectroscopy and Light Scattering

The samples were measured using Ocean Optics USB4000 UV-Vis spectrometer between 400 and 800 nm using SpectraSuite Software for control and data acquisition. A quartz cuvette of 1 mm path length was used to acquire every sample. A deuterium-halogen light source was used to collect the UV-Vis spectra. The data collection was collected at 1 s integration time , and 5 spectra were averaged for each sample. The drift in spectral recordings was accounted for by normalizing the measurements in Plot2 scientific 2D plotting program. Any Mie theory calculations for light extinction were made with the Mie theory calculator from the nanocomposix website (http://nanocomposix.com/pages/tools).

6.4.1.3 Plots and Experimental Results

The experimental results followed the predicted hypothesis that asserted as concentration increases the SPR intensity decreases. Figure 6.2 shows the 60 nm AuNP with BSA concentrations ranging from 0.024 mg/ml to 0.2 mg/ml. Not shown here, the 20 nm AuNP with BSA also yielded very similar results along with the 50% by volume glycerol/water as the solvent.

Fig. 6.2
figure 2

Absorbance spectroscopy for 60 nm AuNP with phosphate buffer in a water solvent and BSA concentrations ranging from 0.024 mg/ml to 0.2 mg/ml

Full size image

Figure 6.3 is the first derivative of the absorbance spectroscopy plot from Fig. 6.2. This plot reduces noise in the spectrophotometry caused by scattering and characterizes the rate change of the absorbance with respect to the wavelength [6, 20]. Additionally, λmax of the absorbance band also passes through zero at the same wavelength [6]. This correlates to the minimum and maximum of the spectra being inflection points in that absorbance band [6].

Fig. 6.3
figure 3

First derivative of the absorbance spectroscopy for 60 nm AuNP with phosphate buffer in a water solvent and BSA concentrations ranging from 0.024 mg/ml to 0.2 mg/ml

Full size image

To further analyze this correlation, λmax was taken against the concentration of BSA and 60 nm AuNP as shown in Fig. 6.4. The intensity of the SPR decreases as the concentration of BSA increases, and the intensity drop plateaus once the AuNP are coated. The application of these results, as previously mentioned, can be applied to biosensing technologies that take advantage of these properties for drug delivery, amplification of immunosensors, and rapid ELISAs [21,22,23].

Fig. 6.4
figure 4

λmax (intensity) versus BSA concentration with 60 nm AuNP

Full size image
6.4.1.3.1 Computational Model

The computational component models the plasmonic response of gold nanoparticles of 60 nm and 20 nm diameter in a water solution and again in a water-glycerol solution. These are the control experiments to assess the plasmonic response of the gold colloids without the interactions of the BSA. The experimental results reveal that the peak plasmonic response wavelengths for the 60 nm and 20 nm gold nanoparticles are 534 nm and 523 nm, respectively. As increasing concentrations of BSA are implemented and then increased, a depression and spreading of this peak wavelength is observed.

The MNPBEM toolbox is a flexible software that is able to simulate metallic nanoparticles, specifically gold nanoparticles using boundary element method. The toolbox will set up homogeneous and isotropic dielectric functions with strict boundaries, which will then be used to calculate and solve Maxwell’s equations and compare to MIE theory. By writing, manipulating, and altering the coded data within the toolkit, an accurate representation of the experimental system can be modelled.

The simulation consists of the following steps: first the dielectric functions of the particle and the solution in which the particle sits are defined. The particles, surface features, and boundaries are then outlined. Subsequently, the code specifies the nature of the plane wave excitation; this information is used to input into the BEM solver equations for which auxiliary surface charges are computed which produces a graph of total decay rate vs. plasmon excitation wavelength.

6.4.1.3.1.1 Description of Results and Techniques Used to Obtain Results

The BEMMNP toolkit uses boundary element method which defines systems with strict borders and well-defined dielectric functions [19]. The system that is outlined is for a 60 nm gold nanoparticle embedded in water solution.

Figure 6.5, “initialization,” describes a single sphere embedded in a homogeneous dielectric environment. The water dielectric environment is described using its refractive index, 1.33. The gold nanoparticle is expressed through dielectric functions whose values are tabulated on file for specific photon energies and performs a spline interpolation. The diameter and the surface vertices of the gold nanoparticle are then outlined by use of the polar coordinates pi and theta. Lastly the code specifies that the particle boundary is closed.

Fig. 6.5
figure 5

Initialization code for resonance response of gold nanoparticle when embedded in water

Full size image

Figure 6.6 sets up an oscillating dipole along the z axis where the energies are defined by the wavelength of the dipole. We test from 400 nm to 900 nm as this wavelength range corresponds to the UV-visible spectrum of light (Fig. 6.7).

Fig. 6.6
figure 6

Dipole oscillator code for resonance response of gold nanoparticle when embedded in water

Full size image
Fig. 6.7
figure 7

BEM simulation code for resonance response of gold nanoparticle when embedded in water

Full size image

The BEM solvers use the particle boundaries and Maxwell’s equation to solve for the surface charges and currents. This results in the total and radiative decay of the plasmonic response in the gold nanoparticles to be calculated. The final plots are then coded for but are omitted from this report (Fig. 6.8).

Fig. 6.8
figure 8

Mie theory comparison code for resonance response of gold nanoparticle when embedded in water

Full size image

Finally, the MNPBEM toolkit allows the setup of an identical system in which it solves for the total radiative decay over energy, for comparison, by Mie theory [19]. Mie theory is a solution to Maxwell’s equations which accurately describe the scattering of an electromagnetic plane wave by a sphere, for example, a gold nanoparticle.

Figure 6.9 represents the plasmonic response of a 60 nm gold nanoparticle embedded in water and is the output of the code. The maximum decay rate occurs at 530 nm and at a total decay rate of 68. The plot of the 20 nm gold nanoparticle has a very similar aesthetic, with a much greater decay rate and marginally lower maximum wavelength peak. Current results also show that as the BSA antibody is introduced the maximum peak shifts to higher wavelengths (lower energies) and that the total decay rate reduces.

Fig. 6.9
figure 9

Total decay rate vs. wavelength resonance response of a 60 nm gold nanoparticle when embedded in water

Full size image

6.5 SERS-Based Sensors in Molecule-Metal Oxide Hybrids

Hybrid nanosystems formed by a molecule (M) and a nanoparticle (NP) that is either a bulk-phase metal (MNP) or a semiconductor (SCNP) are of fundamental importance in sensors , photonics, catalysis , and photovoltaics devices [24,25,26,27,28,29,30,31,32,33,34,35], just to mention a few areas of current interest. An important reference for our work is single-molecule SERS in M-MNP systems a technique that was developed a few years ago [36,37,38,39]. The fundamental physics of the enhancement is related to a Raman transition in the presence of a giant dipole field that arises as of plasmon resonance mediated increase of the local electromagnetic field and an increase in the polarizability. The combined effect can be very substantial, more than 6 orders of magnitude, and has made SM-SERS an extremely sensitive molecular analysis and sensing technique.

Hybrid M-SCNP are of great importance for the design of photovoltaic devices [32], e.g., DSSC (dye-sensitized solar cells) [40, 41], artificial photosynthesis [42,43,44,45], photocatalysts [46, 47], and biomolecular sensors [24,25,26,27,28]. A critical and largely unresolved issue in this field is the understanding of the charge transfer (CT) interfacial properties and the dynamics of exciton separation and recombination [48,49,50,51,52,53]. As opposed to the case in M-MNP hybrids, the specific details of the chemical bond between the molecule and the NP are of paramount importance in controlling interfacial CT. This makes the study of these systems a complex problem in electronic structure because of the importance of many-body effects, the influence of electron correlation, and the difficulties involved in a full geometry optimization. In addition, any realistic treatment must include dynamical aspects in a time-dependent picture because of the different time scales involved in CT and exciton dynamics and an appropriate description of excited states that could be very relevant for all the processes mentioned above.

The inclusion of one or more electronic excited states, in addition to the ground state, has considerable methodological and practical implications. An accurate description of both fluorescence and Raman spectra depends on an appropriate characterization of the states involved in the process.

6.5.1 A Unified Description of Scattering and Fluorescence Processes in M-MNP Hybrids

A model that has strongly influenced our thinking for this proposal was the one introduced in references [54, 55] for a system consisting of two metal NPs of radius R and a molecule, represented by a dipole at distances d1and d2 from the NPs, that is schematically presented in Fig. 1 (taken from Ref. [54]). The model considers two molecular electronic states which are approximated by two displaced harmonic oscillator potential energy curves corresponding to the ground (g) and excited (e) states. The inclusion of three vibrational states per harmonic oscillator for each harmonic potential completes the description of the quantum state manifold for this problem.

figure a

For the free molecule, the absorption and Raman cross sections can be calculated using first-order perturbation theory to be

$$ {\sigma}_A={p}_o^2\frac{\Omega_L}{c{\varepsilon}_o}\sum \limits_n\frac{\mathrm{h}{\Gamma}_{\mathrm{tot}}f\left(0,n\right)f\left(0,n\right)}{{\left(\mathrm{h}{\Omega}_L-n\mathrm{h}\omega -\mathrm{h}{\Omega}_{ge}\right)}^2+{\mathrm{h}}^2{\Gamma}_{tot}^2} $$
(6.25)
$$ {\sigma}_R={p}_o^4\frac{{\omega^{\prime}}^3{\Omega}_L}{6{\pi \varepsilon}_o^2{c}^4}{\left|\sum \limits_n\frac{\mathrm{h}{\Gamma}_{\mathrm{tot}}f\left(0,n\right)f\left(0,n\right)}{{\left(\mathrm{h}{\Omega}_L-n\mathrm{h}\omega -\mathrm{h}{\Omega}_{ge}\right)}^2+{\mathrm{h}}^2{\Gamma}_{tot}^2}\right|}^2 $$
(6.26)

In the presence of the metal NPs, the two processes are interconnected via the time evolution of the effective dipole moment. The calculation of the total scattering cross section involving Raman and Rayleigh scattering and fluorescence can be computed in the following way. The emitted light intensity at position ro is proportional to the field correlation function.

$$ {I}_{em}\left({\mathbf{r}}_o,t\right)=2{\varepsilon}_oc\left\langle {E}_{\theta}^{\left(-\right)}\left({\mathbf{r}}_o,t\right){E}_{\theta}^{\left(+\right)}\left({\mathbf{r}}_o,t\right)\right\rangle $$
(6.27)

Equation (6.27) can be transformed to the frequency domain using the Wiener-Khintchine to obtain the total power spectrum as

$$ {I}_{em}\left({\mathbf{r}}_o,\omega \right)=\frac{1}{\pi}\operatorname{Re}\underset{0}{\overset{\infty }{\int }} d\tau 2{\varepsilon}_oc\left\langle {E}_{\theta}^{\left(-\right)}\left({\mathbf{r}}_o,0\right){E}_{\theta}^{\left(+\right)}\left({\mathbf{r}}_o,\tau \right)\right\rangle {e}^{i\omega t} $$
(6.28)

The model assumes that the electric fields are caused by the electric dipole moment p(t) of the molecule which generates the radiated electric field \( \overrightarrow{E}=\theta {pe}^{i\left( kr-\omega t\right)}{\omega}^2\sin \theta /\left(4{\pi \varepsilon}_o{c}^2r\right) \). The double-differential scattering and fluorescence cross section is then obtained as

$$ \frac{d^2\sigma }{d\Omega d\left(\mathrm{h}\omega \right)}=\frac{\omega^4{\sin}^2\theta }{I_{i n}8{\pi}^3{c}^3{\varepsilon}_o\mathrm{h}}\operatorname{Re}\underset{0}{\overset{\infty }{\int }} d\tau {e}^{i\omega \tau}\left\langle {p}^{\left(-\right)}(0){p}^{\left(+\right)}\left(\tau \right)\right\rangle $$
(6.29)

The next step in the calculation is to compute the dipole time-correlation function in Eq. (6.29), which in turns requires solving Liouville equation for the molecular density matrix. The total Hamiltonian for the system is written as

$$ H={H}_{\mathrm{mol}}+{H}^{\prime }+{H}_{\mathrm{fluc}}+{H}_{\mathrm{env}}, $$
(6.30)

where Hmol, H′, Hfluc, and Henv are the molecular Hamiltonian , the molecule-field interaction, the molecule interaction with field vacuum fluctuations, and the interaction with any other material environment, respectively. Liouville equation can then be written as

$$ i\frac{d\rho}{d t}=\frac{1}{\mathrm{h}}\left[{H}_{\mathrm{mol}}+{H}^{\prime },\rho \right]+{L}_{tr}\rho +{L}_{ph}\rho $$
(6.31)

The first term in (6.31) describes the contribution from the molecular Hamiltonian and the interaction H′. The relaxation superoperators Ltr describe the damping of the density matrix as a result of transitions caused by Hfluc that cause the spontaneous emission of photons and Lph describe relaxation and dephasing caused by the material environment, i.e., the coupling to the NPs. The explicit description of the relaxation superoperators in Reference [55] is achieved through the introduction of two sets of parameters Γkj and γph representing the total decay rate from state k to state j and the dephasing rate, respectively. These parameters enter into Liouville equation in the following way:

$$ {L}_{tr}\rho =-\sum \limits_{kj}\frac{i{\Gamma}_{kj}}{2}\left[{\sigma}_{jk}{\sigma}_{kj}\rho +{\rho \sigma}_{jk}{\sigma}_{kj}-2{\sigma}_{kj}{\rho \sigma}_{jk}\right] $$
(6.32)
$$ {L}_{ph}{\rho}_{jk}=-i{\gamma}_{ph}{\rho}_{kj} $$
(6.33)

with σkj denoting a matrix with the only nonzero element “kj” equal to 1.

In general, a solution of the density matrix is not sufficient to calculate the dipole time-correlation function in (6.29); however, use of the Onsager-Lax quantum regression theorem, which hinges on the validity of the Markovian approximation, permits to calculate a two-time correlation function from a single-time correlation function, thereby providing all the necessary quantities to compute the absorption and scattering cross section (6.29).

6.5.2 Density Matrix Treatment of Combined Instantaneous and Delayed Dissipation

A second background ingredient that constitutes important guidance in our approach to this proposal is the work of Micha and coworkers [56,57,58,59,60,61] where a density matrix approach is used to simultaneously include relaxation, damping and dephasing processes that occur in different time scales, something that in their terminology is called instantaneous and delayed dissipation. This model assumes a separation of the entire system in a primary region that is described using a reduced density matrix (RDM) and a secondary region representing the environment. Fast dissipation is described by a Lindblad term associated with electronic transitions induced in the primary region by its interaction with the secondary one. The delayed dissipation is given by a time integral with a memory term derived from the time correlation of atomic displacements in the medium. The separation into instantaneous and delayed dissipation is based on the different time scales of electronic and vibrational transitions. The model has been successfully applied to a number of physically relevant situations involving the dynamics of electronically excited adsorbates on solid surfaces, a system where a realistic description of the chemical bond between the molecule and the surface is important, a situation reminiscent of the subject of our proposal.

The model is involved, but the basic equations can be understood using a simplified version of the quantum theory of relaxation. The total Hamiltonian for the system and the environment can be written in the usual way:

$$ H={H}_S+{H}_R+V $$
(6.34)

where (S) and (R) correspond to the primary and secondary region, respectively. Assuming that the interaction is switched at time t = 0 and that prior to this S and R are uncorrelated, Liouville Eq. (6.31) can be written in the interaction picture as

$$ {\dot{\rho}}_I(t)=-\left(i/\mathrm{h}\right)\left[{V}_I(t),{\rho}_I(0)\right]-{\left(1/\mathrm{h}\right)}^2\underset{0}{\overset{t}{\int }}{dt}^{\hbox{'}}\left[{V}_I(t),\left[{V}_I\left({t}^{\hbox{'}}\right),{\rho}_I\left({t}^{\hbox{'}}\right)\right]\right] $$
(6.35)

The RDM describing the system of interest S is the partial trace of the full density matrix with respect to the reservoir

$$ {\rho}_{SI}(t)={tr}_R{\rho}_I(t), $$
(6.36)

and its evolution equation can be found directly from ((6.35) as

$$ {\dot{\rho}}_{SI}(t)=-\left(i/\mathrm{h}\right){tr}_R\left[{V}_I(t),{\rho}_I(0)\right]-{\left(1/\mathrm{h}\right)}^2\underset{0}{\overset{t}{\int }}{dt}^{\hbox{'}}{tr}_R\left[{V}_I(t),\left[{V}_I\left({t}^{\hbox{'}}\right),{\rho}_I\left({t}^{\hbox{'}}\right)\right]\right] $$
(6.37)

Two keys assumptions are commonly made to simplify Eq. (6.37):

(i) The reservoir is considered to be in thermal equilibrium at all times, that is,

$$ {\displaystyle \begin{array}{l}{\rho}_I(t)={\rho}_{SI}(t){\rho}_R(0)\\ {}{\rho}_R(0)=\exp \left(-{H}_R/ kT\right)/Z\end{array}} $$
(6.38)

with Z the partition function.

(ii) The Markov approximation whereby memory effects are neglected. This amounts to making the replacement ρSI(t') → ρSI(t) in the integral in Eq. (6.35).

With these two approximations that introduce irreversibility into the dynamics of the system, the equation for the RDM is

$$ {\dot{\rho}}_{SI}(t)=-\left(i/\mathrm{h}\right){tr}_R\left[{V}_I(t),{\rho}_S(0){\rho}_R(0)\right]-{\left(1/\mathrm{h}\right)}^2\underset{0}{\overset{t}{\int }}{dt}^{\hbox{'}}{tr}_R\left[{V}_I(t),\left[{V}_I\left({t}^{\hbox{'}}\right),{\rho}_{SI}(t){\rho}_R(0)\right]\right] $$
(6.39)

The last step is making the connection between the general equations of quantum relaxation and Micha et al.’s work which is to make an assumption about the specific form of the interaction V. This is assumed to be of the form

$$ {V}_I(t)=\sum \limits_i{F}_i(t){Q}_i $$
(6.40)

where Fi(t) and Qi(t) are reservoir- and system-only operators, respectively. Using the Markov approximation for the reservoir and including all the approximations mentioned so far, one can write Eq. (6.39) in such a way that all the information on the reservoir is contained in the time-correlation functions of the reservoirs:

$$ i\mathrm{h}\frac{d{\rho}_{SI}}{dt}=-\frac{i}{\mathrm{h}}\sum \limits_{ij}\underset{0}{\overset{\infty }{\int }}{dt}^{\hbox{'}\hbox{'}}\left\{\begin{array}{l}\left[{Q}_i(t),{Q}_j\left(t-{t}^{\hbox{'}\hbox{'}}\right){\rho}_{SI}(t)\right]\left\langle {F}_i\left({t}^{\hbox{'}\hbox{'}}\right){F}_j\right\rangle -\\ {}\left[{Q}_i(t),{\rho}_{SI}(t){Q}_j\left(t-{t}^{\hbox{'}\hbox{'}}\right)\right]\times \left\langle {F}_i{F}_j\left({t}^{\hbox{'}\hbox{'}}\right)\right\rangle \end{array}\right\} $$
(6.41)

This can be written in a much more compact way by defining laxation superoperator R such that

$$ i\mathrm{h}\frac{d{\rho}_{SI}}{dt}=R{\rho}_{SI} $$
(6.42)

whose matrix components are directly related to the parameters Γlk and γph and in Eqs. (6.32) and (6.33). Computing these parameters requires some explicit assumptions about the reservoir dynamics that must be tested for each specific system.

6.6 Conclusions and Final Remarks

We have described in this tutorial some of the basic physics underlying the design of molecular sensors using NPs with different electronic properties. In one case, plasmonic sensors are based on the optical response leading to changes on the plasmon resonance. In the other, the sensor is based on a molecular property, Raman spectrum, that is strongly enhanced due to interfacial charge transfer between the molecule and the NP. We presented very recent experimental results using plasmonic sensors that can be understood using a Mie theory-based model for the plasmonic response.