Abstract
We extend the notion of natural extension, that gives the least committal extension of a given assessment, from the theory of sets of desirable gambles to that of choice functions. We give an expression of this natural extension and characterise its existence by means of a property called avoiding complete rejection. We prove that our notion reduces indeed to the standard one in the case of choice functions determined by binary comparisons, and that these are not general enough to determine all coherent choice function. Finally, we investigate the compatibility of the notion of natural extension with the structural assessment of indifference between a set of options.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Since the publication of the seminal works in [1, 2], coherent choice functions have been used widely as a model of the rational behaviour of an individual or a group. In particular, [3] established an axiomatisation of coherent choice functions, generalising the axioms in [4] to allow for incomparability.
In previous works [5, 6], we have investigated some of the properties of coherent choice functions, their connection with the models considered earlier by Seidenfeld et al. [3] and also those particular coherent choice functions that are related to the optimality criteria of maximality and E-admissibility. In all those cases we took for granted that the choice function is given on the full class of option sets, and that it is coherent. However, it is somewhat unrealistic to assume that the subject always specifies an entire choice function: this means that he would have to specify for every option set which are the options he chooses, and this in a manner that is coherent in the sense that we shall discuss later on. Rather, a subject will typically specify a choice function only partially, by specifying the rejection of some options from some option sets. We call this partial specification of a choice function his assessment. Such an assessment can consist of an arbitrary amount of rejection statements; we do not rule out here the possibility that the subject’s assessment consists of an uncountable collection of rejection statements.
The question we shall tackle in this paper is the following: given such an assessment, what is the implied choice between other option sets, using only the consequences of coherence?
To answer this question, after giving some preliminary notions in Sect. 2, we shall define in Sect. 3 the natural extension, when it exists, as the least committal coherent choice function that ‘extends’ a given assessment. In Sect. 4 we shall show that our notion is compatible with the eponymous notion established in the theory of sets of desirable gambles, that correspond to choice functions determined by binary comparisons. Then in Sect. 5 we use our work to show (i) that a coherent choice function may not be determined as the infima of a family of binary choice functions; and (ii) that the notion of natural extension can also be made compatible with a structural assessment of indifference. Finally, some additional comments are given in Sect. 6. Due to the space constraints, proofs have been omitted.
2 Preliminary Concepts
Consider a real vector space  provided with the vector addition \(+\) and scalar multiplication. We denote its additive identity by 0. Elements of
provided with the vector addition \(+\) and scalar multiplication. We denote its additive identity by 0. Elements of  are intended as abstract representation of options between which a subject can express his preferences, by specifying choice functions. We therefore call
are intended as abstract representation of options between which a subject can express his preferences, by specifying choice functions. We therefore call  also the option space. We denote by
also the option space. We denote by  the set of all non-empty finite subsets of
the set of all non-empty finite subsets of  , a strict subset of the power set
, a strict subset of the power set  of
of  . Elements
. Elements  of
of  are the option sets amongst which a subject can choose his preferred options. When it is clear what option space
are the option sets amongst which a subject can choose his preferred options. When it is clear what option space  we are considering, we will also use the simpler notation \(\mathcal {Q}\), and use \(\mathcal {Q}_0\) to denote those option sets that include 0. We will assume throughout that
we are considering, we will also use the simpler notation \(\mathcal {Q}\), and use \(\mathcal {Q}_0\) to denote those option sets that include 0. We will assume throughout that  is ordered by a vector ordering
is ordered by a vector ordering  . We will associate with it the strict partial order
. We will associate with it the strict partial order  , as follows:
, as follows:  , for all
, for all  and
and  in
in  . For notational convenience, we let
. For notational convenience, we let  ,
,  , and
, and  .
.
Definition 1
A choice function  on an option space
on an option space  is a map
is a map

The idea underlying this simple definition is that a choice function  selects the set
selects the set  of ‘best’ options in the option set
of ‘best’ options in the option set  . Our definition resembles the one commonly used in the literature [3, 7, 8], except perhaps for an also not entirely unusual restriction to finite option sets [9,10,11].
. Our definition resembles the one commonly used in the literature [3, 7, 8], except perhaps for an also not entirely unusual restriction to finite option sets [9,10,11].
Equivalently to a choice function  , we may consider its associated rejection function
, we may consider its associated rejection function  , defined by
, defined by  for all
for all  in \(\mathcal {Q}\). It returns the options
in \(\mathcal {Q}\). It returns the options  that are rejected—not selected—by
that are rejected—not selected—by  . We collect all the rejection functions in the set \(\mathbf {R}\). For technical reasons, we shall focus on rejection functions in this paper. Moreover, we shall restrict our attention to those rejection functions that satisfy a number of rationality requirements; they are called coherent. For brevity, we will commonly refer to choice functions and rejection functions as choice models, in order to distinguish them from models of desirability (see Sect. 4).
. We collect all the rejection functions in the set \(\mathbf {R}\). For technical reasons, we shall focus on rejection functions in this paper. Moreover, we shall restrict our attention to those rejection functions that satisfy a number of rationality requirements; they are called coherent. For brevity, we will commonly refer to choice functions and rejection functions as choice models, in order to distinguish them from models of desirability (see Sect. 4).
Definition 2
(Coherent rejection function). We call a rejection function  on
on  coherent if for all
coherent if for all  ,
,  and
and  in \(\mathcal {Q}\), all
in \(\mathcal {Q}\), all  and
and  in
in  , and all \(\lambda \) in \(\mathbb {R}_{>0}\):
, and all \(\lambda \) in \(\mathbb {R}_{>0}\):
- \(\mathrm {R1.}\) :
-
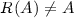 ;
; - \(\mathrm {R2.}\) :
-
if
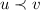 then
then  ;
; - \(\mathrm {R3.}\) :
-
- \(\mathrm {a.}\) :
-
if
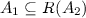 and
and  then
then 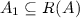 ;
; - \(\mathrm {b.}\) :
-
if
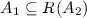 and
and  then
then 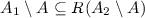 ;
;
- \(\mathrm {R4.}\) :
-
- \(\mathrm {a.}\) :
-
if
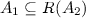 then
then 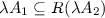 ;
; - \(\mathrm {b.}\) :
-
if
 then
then 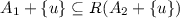 .
.
We collect all coherent rejection functions on  in the set
in the set  , often simply denoted as \(\overline{\mathbf {R}}\) when it is clear from the context which vector space we are using.
, often simply denoted as \(\overline{\mathbf {R}}\) when it is clear from the context which vector space we are using.
These axioms constitute a subset of the ones introduced by Seidenfeld et al. [3], duly translated from horse lotteries to our abstract options, which are more general as shown in earlier work of ours [5, Sect. 3]. In this respect, our notion of coherence is less restrictive than theirs. On the other hand, our Axiom R2 is more restrictive than the corresponding one in [3]. This is necessary in order to link coherent choice functions and coherent sets of desirable gambles (see [5, Sect. 4]).
In order to be able to use choice models for conservative reasoning, as we will do, we provide them with a partial order  having the interpretation of ‘being at most as informative as’. For any
having the interpretation of ‘being at most as informative as’. For any  and
and  in \(\mathbf {R}\), we let
in \(\mathbf {R}\), we let  . For any collection
. For any collection  of rejection functions, the infimum
of rejection functions, the infimum  is the rejection function given by
is the rejection function given by  for every
for every  in \(\mathcal {Q}\).
in \(\mathcal {Q}\).
3 Natural Extension of Rejection Functions
We consider now a rejection function that is defined on some subset of the class \(\mathcal {Q}\) of all option sets, and investigate under which conditions it is possible to extend it to a rejection function on \(\mathcal {Q}\) that satisfies the coherence axioms. Taking into account Axiom R4b, we can assume without loss of generality that our assessment is made in terms of option sets that reject the option 0.
To be more specific, we assume that an assessment \(\mathcal {B}\) is a subset of \(\mathcal {Q}_0\). It consists of an arbitrary collection of option sets that include 0. Its interpretation is that 0 should be rejected from every option set  in \(\mathcal {B}\). We are looking for the least informative coherent rejection function
in \(\mathcal {B}\). We are looking for the least informative coherent rejection function  that extends the assessment \(\mathcal {B}\), by which we mean that
that extends the assessment \(\mathcal {B}\), by which we mean that  for all
for all  in \(\mathcal {B}\).Footnote 1
in \(\mathcal {B}\).Footnote 1
Definition 3
(Natural extension). Given any assessment \(\mathcal {B}\subseteq \mathcal {Q}_0\), the natural extension of \(\mathcal {B}\) is the rejection function

where we let \(\inf \emptyset \) be equal to  , the identity rejection function that maps every option set to itself.
, the identity rejection function that maps every option set to itself.
We can equivalently define the natural extension as a choice function instead of a rejection function, but that turns out to be notationally more involved, which is why we have decided to use rejection functions in this paper.
The above definition is not very useful for practical inference purposes: it does not provide an explicit expression for  . To try and remedy this, consider the special rejection function
. To try and remedy this, consider the special rejection function  based on the assessment \(\mathcal {B}\), defined as:
based on the assessment \(\mathcal {B}\), defined as:

for all  in \(\mathcal {Q}\). From here on, we let \(\preccurlyeq \) be the ordering on \(\mathcal {Q}\) defined by
in \(\mathcal {Q}\). From here on, we let \(\preccurlyeq \) be the ordering on \(\mathcal {Q}\) defined by  .
.
Proposition 1
Consider \(\mathcal {B}\subseteq \mathcal {Q}_0\). Then  is the least informative rejection function that satisfies Axioms R2–R4 and extends \(\mathcal {B}\).
is the least informative rejection function that satisfies Axioms R2–R4 and extends \(\mathcal {B}\).
After inspection of the rationality Axioms R1–R4, we see that all axioms but the first are productive, in the sense that application of these axioms allow us to identify new rejected options within, possibly, new option sets. Axiom R1 however is a destructive one: it indicates how far our rejections can go, and where the inferences should stop. Indeed, it requires that, within a given option set  , not every element of
, not every element of  should be rejected. In other words, it requires that, for any given option set, we should choose at least one of its elements. Therefore we need to be careful and avoid assessments that lead to a violation of Axiom R1, or to a complete rejection of some option set.
should be rejected. In other words, it requires that, for any given option set, we should choose at least one of its elements. Therefore we need to be careful and avoid assessments that lead to a violation of Axiom R1, or to a complete rejection of some option set.
Definition 4
(Avoiding complete rejection). Given any assessment \(\mathcal {B}\subseteq \mathcal {Q}_0\), we say that \(\mathcal {B}\) avoids complete rejection when  satisfies Axiom R1.
satisfies Axiom R1.
To see that this notion is not trivial, consider the following example:
Example 1
As an example of an assessment that does not avoid complete rejection, consider  for an arbitrary
for an arbitrary  in
in  . By Proposition 1,
. By Proposition 1,  extends \(\mathcal {B}\) (so
extends \(\mathcal {B}\) (so  and
and  ) and satisfies Axioms R2–R4. By Axiom R4b, from
) and satisfies Axioms R2–R4. By Axiom R4b, from  we infer that
we infer that  . Using that
. Using that  , we infer that
, we infer that  , contradicting Axiom R1. Therefore \(\mathcal {B}\) does not avoid complete rejection. \(\lozenge \)
, contradicting Axiom R1. Therefore \(\mathcal {B}\) does not avoid complete rejection. \(\lozenge \)
Theorem 1
Consider any assessment \(\mathcal {B}\subseteq \mathcal {Q}_0\). Then the following statements are equivalent:
- \(\mathrm {(i)}\) :
-
\(\mathcal {B}\) avoids complete rejection;
- \(\mathrm {(ii)}\) :
-
There is a coherent extension of \(\mathcal {B}\):
 ;
; - \(\mathrm {(iii)}\) :
-
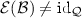 ;
; - \(\mathrm {(iv)}\) :
-
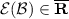 ;
; - \(\mathrm {(v)}\) :
-
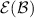 is the least informative rejection function that is coherent and extends \(\mathcal {B}\).
is the least informative rejection function that is coherent and extends \(\mathcal {B}\).
When any of these equivalent statements hold, then  .
.
4 Connection with Desirability
Let us compare our discussion of natural extension with the case of binary preferences and desirability. A desirability assessment  is usually (see for instance Sect. 1.2 of Ref. [12], and also Ref. [13]) a set of options that the agent finds desirable—strictly prefers to the zero option. As we did for choice functions, we pay special attention to coherent sets of desirable options. The following is an immediate generalisation of existing coherence definitions [12, 13] from gambles to abstract options.
is usually (see for instance Sect. 1.2 of Ref. [12], and also Ref. [13]) a set of options that the agent finds desirable—strictly prefers to the zero option. As we did for choice functions, we pay special attention to coherent sets of desirable options. The following is an immediate generalisation of existing coherence definitions [12, 13] from gambles to abstract options.
Definition 5
(Coherent set of desirable options). We call a set of desirable options  coherent if for all
coherent if for all  and
and  in
in  and \(\lambda \) in \(\mathbb {R}_{>0}\):
and \(\lambda \) in \(\mathbb {R}_{>0}\):
- \(\mathrm {D1.}\) :
-
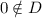 ;
; - \(\mathrm {D2.}\) :
-
if
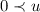 then
then 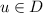 ;
; - \(\mathrm {D3.}\) :
-
if
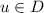 then
then 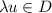 ;
; - \(\mathrm {D4.}\) :
-
if
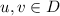 then
then 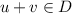 .
.
We collect all coherent sets of desirable options in the set  , often simply denoted as \(\overline{\mathbf {D}}\) when it is clear from the context which vector space we are using.
, often simply denoted as \(\overline{\mathbf {D}}\) when it is clear from the context which vector space we are using.
Any coherent set of desirable options  gives rise to a coherent rejection function
gives rise to a coherent rejection function  given by
given by  for all
for all  in \(\mathcal {Q}\).
in \(\mathcal {Q}\).
Of course, any desirability assessment  can be transformed into an assessment for rejection functions: we simply assess that 0 is rejected in the binary choice between 0 and
can be transformed into an assessment for rejection functions: we simply assess that 0 is rejected in the binary choice between 0 and  , for every option
, for every option  in
in  . The assessment based on
. The assessment based on  is therefore given by
is therefore given by  ; clearly
; clearly  and
and  are in a one-to-one correspondence: given an assessment
are in a one-to-one correspondence: given an assessment  that consists of an arbitrary family of binary option sets, we retrieve
that consists of an arbitrary family of binary option sets, we retrieve  as
as  .
.
Given any desirability assessment  and any set of desirable options
and any set of desirable options  , we say that
, we say that  extends
extends  if
if  . Our next proposition expresses this in terms of rejection functions.
. Our next proposition expresses this in terms of rejection functions.
Proposition 2
Consider any desirability assessment  and any set of desirable options
and any set of desirable options  . Then
. Then  extends
extends  if and only if
if and only if  extends
extends  .
.
For desirability, Axioms D2–D4 are the productive ones, while the only destructive axiom is Axiom D1. The property for desirability that corresponds to avoiding complete rejection for choice models is avoiding non-positivity, commonly formulated as (see for instance Ref. [13, Definition 1])

for the desirability assessment  . Here, \(\mathrm {posi}\) stands for ‘positive hull’, and is defined by
. Here, \(\mathrm {posi}\) stands for ‘positive hull’, and is defined by

Theorem 1 is the equivalent for choice models of the natural extension theorem for desirability. Let us state this natural extension theorem for desirability.
Theorem 2
[13, Theorem 1]. Consider any desirability assessment  , and define its natural extension as
, and define its natural extension as

where we let  . Then the following statements are equivalent:
. Then the following statements are equivalent:
- \(\mathrm {(i)}\) :
-
 avoids non-positivity;
avoids non-positivity; - \(\mathrm {(ii)}\) :
-
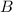 is included in some coherent set of desirable options;
is included in some coherent set of desirable options; - \(\mathrm {(iii)}\) :
-
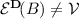 ;
; - \(\mathrm {(iv)}\) :
-
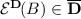 ;
; - \(\mathrm {(v)}\) :
-
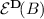 is the least informative set of desirable options that is coherent and includes
is the least informative set of desirable options that is coherent and includes 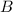 .
.
When any of these equivalent statements hold,  .
.
Our next result tells us that the procedure of natural extension we have established for rejection functions is an extension of the procedure of natural extension for coherent sets of desirable gambles considered above.
Theorem 3
Consider any desirability assessment  . Then
. Then  avoids non-positivity if and only if
avoids non-positivity if and only if  avoids complete rejection, and if this is the case, then
avoids complete rejection, and if this is the case, then  .
.
To summarise these statements, consider the commuting diagram in Fig. 1, where we have used the maps

Start with a desirability assessment  that avoids non-positivity. Taking the natural extension for desirability commutes with taking the corresponding assessment (for choice models), then the natural extension, and eventually going back to the set of desirable options corresponding to this natural extension. Furthermore, taking the natural extension of the corresponding assessment (for choice models) commutes with taking the natural extension for desirability, and then going to the corresponding rejection function.
that avoids non-positivity. Taking the natural extension for desirability commutes with taking the corresponding assessment (for choice models), then the natural extension, and eventually going back to the set of desirable options corresponding to this natural extension. Furthermore, taking the natural extension of the corresponding assessment (for choice models) commutes with taking the natural extension for desirability, and then going to the corresponding rejection function.
5 Examples
5.1 Choice Functions That Are No Infima of Binary Choice Functions
Many important choice functions are infima of purely binary choice models: consider, for instance, the E-admissible or M-admissible choice functions [6]. It is an important question whether all coherent choice functions are infima of purely binary choice functions; if this question answered positively, this would immediately imply a representation theorem. If this question is answered in the negative, choice functions would constitute a theory that is more general than sets of desirable gambles in two ways: not only because it allows for more than binary choice, also because it is capable of expressing preferences that can never be retrieved as an infimum of purely binary preferences.
Below we will answer this question in the negative: we will define a special rejection function  , based some particular assessment \(\mathcal {B}\subseteq \mathcal {Q}_0\), and prove that it is no infimum of purely binary rejection functions.
, based some particular assessment \(\mathcal {B}\subseteq \mathcal {Q}_0\), and prove that it is no infimum of purely binary rejection functions.
Example 2
We will work with the special vector space of gambles  on a binary possibility space
on a binary possibility space  , ordered by the standard point-wise ordering \(\le \): for any f, g in \(\mathcal {L}\), we let
, ordered by the standard point-wise ordering \(\le \): for any f, g in \(\mathcal {L}\), we let  .
.
We consider a single assessment  , where
, where  consists of a gamble and one scaled variant of it, together with 0: the assessment we consider is
consists of a gamble and one scaled variant of it, together with 0: the assessment we consider is  with
with  a gamble and \(\lambda \) an element of \(\mathbb {R}_{>0}\) and different from 1. We assume that
a gamble and \(\lambda \) an element of \(\mathbb {R}_{>0}\) and different from 1. We assume that  , and that \(\lambda >1\). The idea is that
, and that \(\lambda >1\). The idea is that  consists of 0 and two gambles that lie on the same line through 0, and on the same side of that line; see Fig. 2 for an illustration of the assessment.
consists of 0 and two gambles that lie on the same line through 0, and on the same side of that line; see Fig. 2 for an illustration of the assessment.
Note that this assessment indeed avoids complete rejection: for instance, the coherent set of desirable options  satisfies
satisfies  . Therefore,
. Therefore,  is a coherent rejection function. To prove that
is a coherent rejection function. To prove that  is no infimum of purely binary rejection functions, we first show the intermediate result that
is no infimum of purely binary rejection functions, we first show the intermediate result that  , where
, where  . To prove this, assume ex absurdo that
. To prove this, assume ex absurdo that  , and infer using Eq. (1.1) that then there would be some
, and infer using Eq. (1.1) that then there would be some  in \(\mathcal {Q}\) such that
in \(\mathcal {Q}\) such that

At this point, remark already that  : indeed, if ex absurdo
: indeed, if ex absurdo  , then
, then  , so we need only consider
, so we need only consider  . Infer that
. Infer that  and
and  , leading to a contradiction. Therefore,
, leading to a contradiction. Therefore,  .
.
Without loss of generality, we let  where n belongs to \(\mathbb {N}\) and
where n belongs to \(\mathbb {N}\) and  to \(\mathcal {L}\), so
to \(\mathcal {L}\), so  .
.
It then follows that  .
.
Let us prove as an intermediate result that  . To see this, since
. To see this, since  , infer that
, infer that  , and assume ex absurdo that
, and assume ex absurdo that  . Let
. Let  be an element of
be an element of  , then
, then  , so
, so  is undominated in
is undominated in  whence
whence  for all \(\mu \) in \(\mathbb {R}_{>0}\). Note that, since
for all \(\mu \) in \(\mathbb {R}_{>0}\). Note that, since  belongs to
belongs to  , also
, also  belongs to
belongs to  for every \(\mu \) in \(\mathbb {R}_{>0}\). Therefore, since an element of
for every \(\mu \) in \(\mathbb {R}_{>0}\). Therefore, since an element of  can never be dominated by an element of
can never be dominated by an element of  , also
, also  for all \(\mu \) in \(\mathbb {R}_{>0}\). We deduce that also
for all \(\mu \) in \(\mathbb {R}_{>0}\). We deduce that also  for all \(\mu \) in \(\mathbb {R}_{>0}\). Since
for all \(\mu \) in \(\mathbb {R}_{>0}\). Since  belongs to
belongs to  , also
, also  , a contradiction. So we have that
, a contradiction. So we have that  , and therefore, again because an element of
, and therefore, again because an element of  can never be dominated by an element of
can never be dominated by an element of  , also
, also  .
.
Now we go back to Eq. (1.4), and consider first  . Then
. Then  or
or  . Since
. Since  , in particular
, in particular  , so the only possibility left is
, so the only possibility left is  , or, in other words,
, or, in other words,  for some \(\mu \) in \(\mathbb {R}_{>0}\). There are three possibilities: if (i) \(\mu =1\), then
for some \(\mu \) in \(\mathbb {R}_{>0}\). There are three possibilities: if (i) \(\mu =1\), then  —and therefore, since
—and therefore, since  , necessarily
, necessarily  —for some i in
—for some i in  ; if (ii) \(\mu =\frac{1}{\lambda }\) then
; if (ii) \(\mu =\frac{1}{\lambda }\) then  —and therefore, since
—and therefore, since  , necessarily
, necessarily  —for some j in
—for some j in  ; and finally, if (iii)
; and finally, if (iii)  , then
, then  and
and  —and therefore, since
—and therefore, since  , necessarily
, necessarily  and
and  —for some k and \(\ell \) in
—for some k and \(\ell \) in  . These are illustrated in Fig. 3.
. These are illustrated in Fig. 3.
In any case, we find that  . Without loss of generality, let
. Without loss of generality, let  be the unique gamble in
be the unique gamble in  with highest value in \(\mathrm {T}\):
with highest value in \(\mathrm {T}\):  . Then, since
. Then, since  , by Eq. (1.4) we have that
, by Eq. (1.4) we have that  or
or  . Since
. Since  and
and  , we find in particular
, we find in particular  , whence
, whence  . Therefore necessarily
. Therefore necessarily  for some \(\mu \) in \(\mathbb {R}_{>0}\). Note that both
for some \(\mu \) in \(\mathbb {R}_{>0}\). Note that both  and
and  belong to
belong to  , and have a value in \(\mathrm {T}\) that is strictly higher than
, and have a value in \(\mathrm {T}\) that is strictly higher than  . But at least one of
. But at least one of  or
or  is not equal to
is not equal to  , and therefore an element of
, and therefore an element of  , a contradiction with the fact that
, a contradiction with the fact that  . Therefore indeed
. Therefore indeed  .
.
So we have found a rejection function  such that
such that  but
but  . However, any rejection function
. However, any rejection function  that is defined by means of a coherent set of desirable options
that is defined by means of a coherent set of desirable options  satisfies that
satisfies that

and Eq. (1.5) is preserved when taking infima of rejection functions. As a consequence,  is no infimum of purely binary rejection functions. \(\lozenge \)
is no infimum of purely binary rejection functions. \(\lozenge \)
5.2 Natural Extension and Indifference
Next we investigate if it is possible to obtain an extension of a given assessment that takes into account not only the implications of coherence, as we did with the natural extension, but also some assessments of indifference between a set of options. To see how this comes about, note that, in addition to a subject’s set of desirable options  —the options he strictly prefers to the zero option—we can also consider the options that he considers to be equivalent to the zero option. We call these options indifferent. A set of indifferent options
—the options he strictly prefers to the zero option—we can also consider the options that he considers to be equivalent to the zero option. We call these options indifferent. A set of indifferent options  is simply a subset of
is simply a subset of  , but as before with desirable options, we pay special attention to coherent sets of indifferent options.
, but as before with desirable options, we pay special attention to coherent sets of indifferent options.
Definition 6
A set of indifferent options  is called coherent if for all
is called coherent if for all  in
in  and \(\lambda \) in \(\mathbb {R}\):
and \(\lambda \) in \(\mathbb {R}\):
- \(\mathrm {I}_{1}.\) :
-
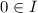 ;
; - \(\mathrm {I}_{2}.\) :
-
if
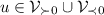 then
then 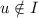 ;
; - \(\mathrm {I}_{3}.\) :
-
if
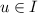 then
then  ;
; - \(\mathrm {I}_{4}.\) :
-
if
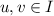 then
then 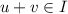 .
.
Taken together, Axioms I3 and I4 are equivalent to  , and due to Axiom I1,
, and due to Axiom I1,  is non-empty and therefore a linear subspace of
is non-empty and therefore a linear subspace of  .
.
The interaction between indifferent and desirable options is subject to rationality criteria as well: they should be compatible with one another.
Definition 7
Given a set of desirable options  and a coherent set of indifferent options
and a coherent set of indifferent options  , we call
, we call  compatible with
compatible with  if
if  .
.
We collect all options that are indifferent to an option  into the equivalence class
into the equivalence class  . We also denote
. We also denote  as
as  . Of course,
. Of course,  is a linear subspace, and the classes
is a linear subspace, and the classes  are affine subspaces of
are affine subspaces of  . The set of all these equivalence classes is the quotient space
. The set of all these equivalence classes is the quotient space  . This quotient space is a vector space under the vector addition and the scalar multiplication.
. This quotient space is a vector space under the vector addition and the scalar multiplication.  is the additive identity of
is the additive identity of  .
.
Definition 8
We call a rejection function  on
on  compatible with a coherent set of indifferent options
compatible with a coherent set of indifferent options  if there is some representing rejection function
if there is some representing rejection function  on
on  such that
such that  for all
for all  in
in  .
.
We refer to an earlier paper [6] of ours for a study of the compatibility of the structural assessment of coherence with the theory of coherent rejection functions, and to [14, 15] for other works on this topic.
The natural extension under indifference, if it is coherent, is the least informative coherent rejection function that extends the assessment  and is compatible with the set of indifferent options
and is compatible with the set of indifferent options  .
.
Definition 9
Given any assessment  and any coherent set of indifferent options
and any coherent set of indifferent options  , the natural extension of \(\mathcal {B}\) under
, the natural extension of \(\mathcal {B}\) under  is the rejection function
is the rejection function

where, as usual, we let  , the identity rejection function that maps every option set to itself.
, the identity rejection function that maps every option set to itself.
To help link this definition with a more constructive and explicit expression, consider the special rejection function  , defined by:
, defined by:

where we let  , being—loosely speaking—the assessment \(\mathcal {B}\) expressed in the quotient space
, being—loosely speaking—the assessment \(\mathcal {B}\) expressed in the quotient space  . Recall that
. Recall that  , as defined in Eq. (1.1), is relative to a given but otherwise arbitrary vector space
, as defined in Eq. (1.1), is relative to a given but otherwise arbitrary vector space  . Our special rejection function
. Our special rejection function  uses the version
uses the version  on
on  instead of
instead of  .
.
The following is the counterpart of Proposition 1 under indifference:
Proposition 3
Consider any assessment  and any coherent set of indifferent options
and any coherent set of indifferent options  . Then
. Then  is the least informative rejection function that satisfies Axioms R2–R4, extends \(\mathcal {B}\), and is compatible with
is the least informative rejection function that satisfies Axioms R2–R4, extends \(\mathcal {B}\), and is compatible with  .
.
Recall from our results on the (normal) natural extension from Sect. 3 that not every assessment is extendible to a coherent rejection function: this is only the case if the assessment avoids complete rejection. Here too, when we deal with the natural extension under indifference, something similar occurs.
Definition 10
(Avoiding complete rejection under indifference). Given any assessment  and any coherent set of indifferent options
and any coherent set of indifferent options  , we say that \(\mathcal {B}\) avoids complete rejection under
, we say that \(\mathcal {B}\) avoids complete rejection under  when
when  satisfies Axiom R1.
satisfies Axiom R1.
However, and perhaps surprisingly, avoiding complete rejection under indifference is sufficient for avoiding complete rejection:
Proposition 4
Consider any assessment  and any coherent set if indifferent options
and any coherent set if indifferent options  . Then \(\mathcal {B}\) avoids complete rejection under
. Then \(\mathcal {B}\) avoids complete rejection under  if and only if
if and only if  avoids complete rejection, and both those equivalent conditions imply that \(\mathcal {B}\) avoids complete rejection.
avoids complete rejection, and both those equivalent conditions imply that \(\mathcal {B}\) avoids complete rejection.
This allows us to formulate a counterpart to Theorem 1 for natural extension under indifference:
Theorem 4
Consider any assessment \(\mathcal {B}\subseteq \mathcal {Q}_0\) and any coherent set of indifferent options  . Then the following statements are equivalent:
. Then the following statements are equivalent:
- \(\mathrm {(i)}\) :
-
\(\mathcal {B}\) avoids complete rejection under
 ;
; - \(\mathrm {(ii)}\) :
-
There is some
 in
in 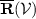 that extends \(\mathcal {B}\) that is compatible with
that extends \(\mathcal {B}\) that is compatible with 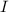 , meaning that
, meaning that  and
and 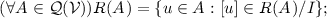
- \(\mathrm {(iii)}\) :
-
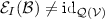 ;
; - \(\mathrm {(iv)}\) :
-
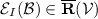 ;
; - \(\mathrm {(v)}\) :
-
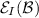 is the least informative rejection function that is coherent, extends \(\mathcal {B}\), and is compatible with
is the least informative rejection function that is coherent, extends \(\mathcal {B}\), and is compatible with 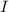 .
.
When any of these equivalent statements hold, then  .
.
6 Conclusions
In this paper, we have investigated the natural extension of choice functions, found an expression for it, and characterised the assessments that have coherent extensions. We made the connection with binary choice, and showed how the well-known natural extension for desirability follows from our natural extension.
As future lines of research, we would like to study the compatibility of the notion of natural extension with other structural assessments; in this respect, we have already investigated the compatibility with a notion of irrelevance when modelling multivariate choice functions. It is an open problem to study whether something similar can be made with respect to the exchangeable choice functions we have considered in [16].
Notes
- 1.
This is not an extension of a rejection function defined on a smaller domain \(\mathcal {B}\) to a bigger domain \(\mathcal {Q}_0\). Rather, it is the extension of an assessment, where we do not necessarily know all the rejected options in every option set
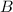 in \(\mathcal {B}\) (except for 0).
in \(\mathcal {B}\) (except for 0).
References
Arrow, K.: Social Choice and Individual Values. Yale University Press (1951)
Uzawa, H.: Note on preference and axioms of choice. Ann. Inst. Stat. Math. 8, 35–40 (1956)
Seidenfeld, T., Schervish, M.J., Kadane, J.B.: Coherent choice functions under uncertainty. Synthese 172(1), 157–176 (2010)
Rubin, H.: A weak system of axioms for “rational” behavior and the nonseparability of utility from prior. Stat. Risk Model. 5(1–2), 47–58 (1987)
Van Camp, A., Miranda, E., de Cooman, G.: Lexicographic choice functions. Int. J. Approx. Reason. 92, 97–119 (2018)
Van Camp, A., de Cooman, G., Miranda, E., Quaeghebeur, E.: Coherent choice functions, desirability and indifference. Fuzzy Sets Syst. 341(C), 1–36 (2018). https://doi.org/10.1016/j.fss.2017.05.019
Aizerman, M.A.: New problems in the general choice theory. Soc. Choice Welfare 2, 235–282 (1985)
Sen, A.: Social choice theory: a re-examination. Econometrica 45, 53–89 (1977)
He, J.: A generalized unification theorem for choice theoretic foundations: avoiding the necessity of pairs and triplets. Economics Discussion Paper 2012–23, Kiel Institute for the World Economy (2012)
Schwartz, T.: Rationality and the myth of the maximum. Noûs 6(2), 97–117 (1972)
Sen, A.: Choice functions and revealed preference. Rev. Econ. Stud. 38(3), 307–317 (1971)
Quaeghebeur, E.: Desirability. In: Augustin, T., Coolen, F.P.A., de Cooman, G., Troffaes, M.C.M. (eds.) Introduction to Imprecise Probabilities, pp. 1–27. Wiley, Hoboken (2014)
de Cooman, G., Quaeghebeur, E.: Exchangeability and sets of desirable gambles. Int. J. Approx. Reason. 53(3), 363–395 (2012). Precisely imprecise: a collection of papers dedicated to Henry E. Kyburg, Jr
Bradley, S.: How to choose among choice functions. In: Augustin, T., Doria, S., Miranda, E., Quaeghebeur, E. (eds.) Proceedings of ISIPTA 2015, pp. 57–66. Aracne (2015)
Seidenfeld, T.: Decision without independence and without ordering: what is the difference? Econ. Philos. 4, 267–290 (1988)
Van Camp, A., de Cooman, G.: Exchangeable choice functions. In: Antonucci, A., Corani, G., Couso, I., Destercke, S. (eds.) Proceedings of ISIPTA 2017. Proceedings of Machine Learning Research, vol. 62, pp. 346–357 (2017)
Acknowledgements
The research in this paper has been supported by project TIN2014-59543-P.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Van Camp, A., Miranda, E., de Cooman, G. (2018). Natural Extension of Choice Functions. In: Medina, J., et al. Information Processing and Management of Uncertainty in Knowledge-Based Systems. Theory and Foundations. IPMU 2018. Communications in Computer and Information Science, vol 854. Springer, Cham. https://doi.org/10.1007/978-3-319-91476-3_17
Download citation
DOI: https://doi.org/10.1007/978-3-319-91476-3_17
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-91475-6
Online ISBN: 978-3-319-91476-3
eBook Packages: Computer ScienceComputer Science (R0)





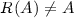 ;
;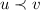 then
then  ;
;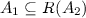 and
and  then
then 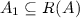 ;
;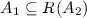 and
and  then
then 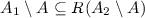 ;
;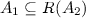 then
then 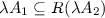 ;
; then
then 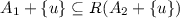 .
. ;
;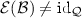 ;
;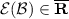 ;
;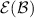 is the least informative rejection function that is coherent and extends
is the least informative rejection function that is coherent and extends 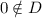 ;
;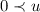 then
then 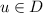 ;
;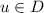 then
then 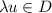 ;
;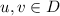 then
then 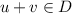 .
. avoids non-positivity;
avoids non-positivity;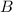 is included in some coherent set of desirable options;
is included in some coherent set of desirable options;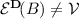 ;
;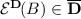 ;
;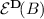 is the least informative set of desirable options that is coherent and includes
is the least informative set of desirable options that is coherent and includes 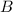 .
.


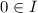 ;
;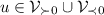 then
then 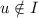 ;
;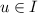 then
then  ;
;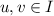 then
then 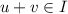 .
. ;
; in
in 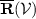 that extends
that extends 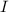 , meaning that
, meaning that  and
and 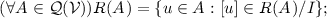
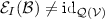 ;
;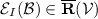 ;
;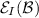 is the least informative rejection function that is coherent, extends
is the least informative rejection function that is coherent, extends 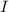 .
. in
in