Keywords

1 Introduction

Energy harvesting from the parametric pendulum is a topic of growing interest for scientists and engineers [1,2,3,4], due to the high kinetic energy available in its rotational motion. The basic idea of the devices consists of a pendulum with a vertical motion induced by an ambient energy source. If stable rotations of the pendulum can be reached, a generator attached to the axis of rotation could extract electrical energy. Being the parametric pendulum a problem of escape from a potential well [5], rotations are required because they represent the most energetic motion [6]. Although conceptually simple, this technology is still at a laboratory stage mostly due to the complex nonlinear dynamics of the system. Two sources of ambient vibrations are mainly considered as external excitation: vibrating machines and the motion of the sea waves. In both cases, rotations are possible only in some forcing scenarios. But while sea waves present a stochastic behavior, machine vibrations are generally of harmonic nature, with a consequent high degree of predictability. This is an important feature in the design of suitable pendulum harvesters because the physical dimensions of the system can be defined in terms of the forcing parameters. The goal of the design always is to improve the ability of reaching rotational motion.

In this work, reciprocating motion is regarded as external excitation. This motion is interesting because it can be found in a wide range of industrial machines, including engines and pumps, where a crank-rod system is used. Reciprocating motion is similar to sinusoidal, which is the classical excitation in literature, but slightly more complex [7]. The study of differences and similarities among these two excitations is interesting since many experimental devices aimed to the study of the classic parametric pendulum employ a crank-rod mechanism due to its simplicity [2, 8, 9].

The article is organized as follows. After this introduction, the governing equation of the system under study is presented. The central part of the paper is devoted to the exploration of rotatory dynamics of the pendular system, including an overview of rotating responses, a parametric study and an integrity analysis of the basins of rotations. Finally, the main conclusions of the study are summarized and discussed.

2 The Parametric Pendulum Under Reciprocating Excitation

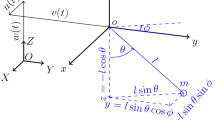
The governing differential equation of the parametrically excited pendulum of Fig. 1 can be set up by using Lagrange’s equation for single-DOF non conservative systems, and its derivation can be easily followed in any classic book of nonlinear dynamics [5, 10]. It is a second-order ordinary differential equation given by

Fig. 1
figure 1

The parametric pendulum excited by a reciprocating motion in vertical direction

Full size image
$$ ml^{2} \frac{{d^{2} \theta }}{{d\tau^{2} }} + c\frac{d\theta }{d\tau } + ml\left( {\frac{{d^{2} y}}{{d\tau^{2} }} + g} \right)\,\sin \theta = 0 $$
(1)

where m is the mass of the pendulum bob, l the distance between the center of gravity and the pendulum axis, c the viscous damping coefficient, τ the time, g the acceleration of gravity, y the vertical displacement of the pendulum system, and θ is the angle positively measured anticlockwise from the hanging position. A reciprocating motion provided by a crank-rod system [7] constitutes the imposed motion y to the pendulum device. This is shown in Fig. 1. The connecting joint between rod and crank rotates at a constant frequency \( \Omega \), following a circumferential trajectory. Thus, the displacement of that joint projected horizontally or vertically is sinusoidal in time. However, the angle between the rod and the vertical direction is continuously changing during the cycle of motion. Therefore the linear motion of the upper end of the rod is more complex than a simple sine function. Such excitation gives to the pendulum system the following displacement

$$ y = r\left( {1 - \cos\Omega \tau } \right) + L\left( {1 - \sqrt {1 - \lambda^{2} \sin^{2}\Omega \tau } } \right) $$
(2)

where r is the crank radius, L is the length of the rod and the crank-rod ratio is \( \lambda \) = r/L.

Now, introducing (2) into (1), a non-dimensional equation is obtained as

$$ \ddot{\theta } + \beta \dot{\theta } + \left( {R\,\cos \omega t + \lambda^{3} R\frac{{\Lambda _{3} }}{{\Lambda _{1}^{3} }} + \lambda R\frac{{\Lambda _{2} }}{{\Lambda _{1} }} + 1} \right)\,\sin \theta = 0 $$
(3)

where the following definitions have been made

$$ \begin{array}{*{20}c} {\omega_{0} = \sqrt {\frac{g}{l}} ,\quad t = \omega_{0} \tau ,\quad \beta = \frac{c}{{ml^{2} \omega_{0} }},\quad \omega = \frac{\Omega }{{\omega_{0} }},\quad R = \frac{{r\omega^{2} }}{l},} \\ {\Lambda _{1} = \sqrt {1 - \lambda^{2} \sin^{2} \omega t} ,\quad\Lambda _{2} = \cos^{2} \omega t - \sin^{2} \omega t,\quad\Lambda _{3} = \cos^{2} \omega t \cdot \sin^{2} \omega t} \\ \end{array} $$
(4)

The superimposed dot in (3) means derivation with respect to dimensionless time t. The magnitudes R, ω and β are non-dimensional parameters associated to the forcing amplitude, forcing frequency and damping, respectively. Depending on \( \lambda \), R, ω and β, and initial conditions \( \theta_{0} \) and \( \dot{\theta }_{0} \), different steady states of the system can be obtained [11]. These responses include: rest position, oscillations, rotations and chaos.

3 Exploring Rotating Attractors

3.1 Overview

The dynamics of rotating attractors is explored, for different configurations of the parametric pendulum under reciprocating excitation. Equation (3) is solved numerically by employing a dimensionless simulation time of ts = 2500, with the purpose of ensure steady state responses. Control spaces, bifurcation diagrams and basins of attraction are constructed, based on extensive numerical simulations, considering different settings of the control parameters \( \lambda \), R, ω and β. To avoid transients, the first td = 2300 are discarded in the construction of all the diagrams.

Steady state rotations are classified in four categories [12]: pure rotations, oscillating rotations, straddling rotations and large amplitude rotations. Pure rotations have a very significant attribute: the angular velocity always keeps the same sign (\( \dot{\theta } > 0 \) or \( \dot{\theta } < 0 \)). This ensures no change in the direction of rotation, implying no oscillatory motion of any kind. Pure rotations exist in conjugate pairs: clockwise and anticlockwise [13]. A pure rotation is highly energetic, being the desired motion for energy harvesting purposes. In this article, pure rotations are regarded as synonymous of rotations, while the other categories are considered merely as oscillations.

For a given set (R, ω), the coexistence of periodic and chaotic solutions is possible, evidencing the nonlinear nature of the system. This coexistence depends on initial conditions. As an example, the control space R-ω of Fig. 2 shows all the possible steady states. This map is constructed as follows: for each fixed pair (R, ω), several simulations are performed employing different initial conditions, which produces different dynamical patterns; the topology of all these patterns is computed to give the color classification of the corresponding point (R, ω) in the control space. It can be seen that, for low excitation amplitudes, the rest position is the commonest solution. As R increases, oscillations, rotations and tumbling chaos appear. Rotations are the dominant type of stable solutions in the main resonance zone (ω = 2), but for most of the scenarios they coexist with other responses. Besides, there is a wide range of the control space where rotations are not possible, irrespective of the initial conditions.

Fig. 2
figure 2

Control space R-ω showing the physical responses of a system with \( \lambda \) = 0.126 and β = 0.1. Rotn=1 means “pure rotations of period 1” while Rotn=2+ means “pure rotations of period 2 or higher”

Full size image

3.2 Influence of the Crank/Rod Ratio λ

In Fig. 3, control spaces R-ω are presented for different values of \( \lambda \), with fixed damping of β = 0.1.

Fig. 3
figure 3

Control space R-ω for the purely rotating attractors (clockwise and anticlockwise) with β = 0.1 and: a \( \lambda \) = 0 (classic parametric pendulum); b \( \lambda \) = 0.126; c \( \lambda \) = 0.185; d \( \lambda \) = 0.356. (): period-1 rotations; (): period-2 or higher rotations; (): coexisting period-1 and period-2 or higher rotations

Full size image

Figure 3a corresponds to the classic parametric pendulum (sinusoidal forcing), which can be recovered from (3) by setting \( \lambda \) = 0. For low \( \lambda \) (say \( \lambda \) ≾ 0.3, Fig. 3b, c), the bifurcational behavior is topologically similar to the classic system. For higher \( \lambda \) (Fig. 3d), an additional rotation zone appears due to the significance of \( \lambda \)-terms in (3). These additional rotating attractors are studied by means of the bifurcation diagrams of Fig. 4. Figure 4a, b are constructed by fixing ω in the control space of Fig. 3d and plotting Poincaré points of the steady state response (a sampling time 2 π/ω is employed). In Fig. 4a, the main resonance (ω = 2) is studied. Up to R ≈ 1.31, the system is topologically similar to the classic parametric pendulum (see [11] for an equivalent bifurcation diagram with \( \lambda \) = 0): two period-1 symmetric rotations appear at a saddle-node bifurcation (R ≈ 0.42), then undergo a period-doubling cascade (R ≈ 1.07) and vanish at a crisis scenario (R ≈ 1.31). Then, after a narrow strip of tumbling chaos, a period-6 oscillation (actually a large amplitude rotation) appears as the only stable solution for a relatively broad range of R, until it also vanishes in a crisis. At R ≈ 1.58 tumbling chaos take place. The additional rotating attractors appear at R ≈ 2.31, maintaining as solutions of the physical system up to R = 3.5 and above. Two minor period-3 rotating attractors are born at R ≈ 2.89, but they soon vanish in a crisis at R ≈ 2.9, after a rapid period-doubling cascade. Rotations and tumbling chaos coexists with the inverted pendulum solution from R ≈ 3.35 on. Bifurcation diagram of Fig. 4b shows the three pairs of rotating attractors which can be obtained for sufficiently high values of \( \lambda \) and β = 0.1. Attractors appearing at R ≈ 0.36 and R ≈ 2.44 exist in the classic parametric pendulum, while attractors at R ≈ 1.88 are exclusive of the reciprocating excitation. Figure 4c is associated to the control space of Fig. 3b, i.e. a low-\( \lambda \) scenario. As expected, additional rotation zones cannot be found in such situation, with a bifurcational behavior similar to the classic parametric pendulum.

Fig. 4
figure 4

Bifurcation diagram of the non-dimensional angular velocity for β = 0.1 and: a ω = 2, \( \lambda \) = 0.356; b ω = 1.45, \( \lambda \) = 0.356; c ω = 1.82, \( \lambda \) = 0.126; d R = 2.7, ω = 2. (): clockwise rotations, (): anticlockwise rotations, (): rest, (): oscillations, (): tumbling chaos

Full size image

Figure 3c shows a bifurcation diagram of \( \lambda \), obtained by fixing R, ω and β in such a way to ensure the existence of the additional rotational attractors for a high value of \( \lambda \) (say \( \lambda \) = 0.356 as in Fig. 3d). As expected from Fig. 3a–c, there are not stable rotating solutions for low \( \lambda \), but as \( \lambda \) is increased rotations appear at a saddle-node bifurcation (\( \lambda \) ≈ 0.303). Now, considering \( \lambda \) = 0.4 as an upper practical limit of mechanical systems, results of Fig. 4d seem to indicate that an almost extreme value of \( \lambda \) is needed to ensure the existence of those additional rotating attractors. This is correct for β = 0.1, but not for lower amounts of damping, as shown in the next subsection.

3.3 Influence of the Damping Parameter β

The previous study was conducted assuming a fixed damping of β = 0.1. Besides speeding numerical integration, this choice allows us to compare our results with those in many other works of literature [6, 11,12,13,14]. But it has been demonstrated [6] that damping must be of β < 0.1 to ensure a viable energy extraction. Thus, a scenario with lower damping must be studied.

For \( \lambda \) = 0, it is known that a change in damping moves the control space R-ω downwards or upwards, by decreasing or increasing β respectively [8, 12,13,14,15] In fact, it has been pointed [8] that an increase of the excitation amplitude (R in our system) is equivalent to a decrease of β and vice versa. A more complex damping behavior was found for reciprocating excitation. This is evidenced in Fig. 5. Control space of Fig. 5a can be compared with that of Fig. 3b, since for both cases \( \lambda \) = 0.126 but with different β. From this comparison it is clear that with a decrement of β, an additional rotation zone appears, just as happened when the parameter \( \lambda \) was increased (Fig. 3a–d). The bifurcation diagram of Fig. 5b shows that as β decreases with fixed R, ω and \( \lambda \), a pair of rotational attractors arise at a saddle node bifurcation (β ≈ 0.118). This saddle node is the same of Fig. 4b but projected on the β-\( \dot{\theta } \) plane instead of the \( \lambda \)-\( \dot{\theta } \) plane. An imaginary motion picture of the bifurcation diagram in Fig. 5b as \( \lambda \) decreases should show the saddle node moving left, until the rotating attractors completely vanish when \( \lambda \) = 0, leaving behind only tumbling chaos. In conclusion, with an adequate (not necessarily extremely high) value of the crank-rod ratio \( \lambda \), the additional rotating attractors exist for a range of β where energy extraction is feasible [6].

Fig. 5
figure 5

a Control space R-ω for the purely rotating attractors (clockwise and anticlockwise) with \( \lambda \) = 0.126, β = 0.027. (): period-1 rotations; (): period-2 or higher rotations; (): coexisting period-1 and period-2 or higher rotations. b Bifurcation diagram of the non-dimensional angular velocity for R = 2.7, ω = 2, \( \lambda \) = 0.356. (): clockwise rotations, (): anticlockwise rotations, (): rest, (): oscillations, (): tumbling chaos

Full size image

Finally, Fig. 5b suggests that the rotational response at low β deserves some attention. For β = 0.01, most of the rotations has period-1 (some period-4 motions are observed). However, steady states can be preceded by long periods of transient tumbling chaos [16]. In such cases, a very large simulation is required to avoid the transient. Figure 6 shows an example where a non-dimensional time of td = 10,000 must be discarded to obtain a steady period-1 rotation. This phenomenon explains the “blurred” rotating attractor of Fig. 5b and also the intermittencies of Figs. 3d and 5a.

Fig. 6
figure 6

Phase portraits and Poincaré sampling for R = 2.7, ω = 2, \( \lambda \) = 0.356 and β = 0.01. Initial conditions θ = 2 and \( \dot{\theta } \) = –1.88. Simulation time ts = 45,000. a Discarded time td = 7500, transient tumbling chaos is present. b Discarded time td = 10,000, transient tumbling chaos is avoided and period-1 rotation is obtained. (): pendulum response, (): Poincaré points

Full size image

3.4 Robustness and Probability of Rotations

After establishing the parameter settings where rotations are possible, the dynamics of the basins of attraction must be studied. This is necessary to know how difficult it is to achieve a steady state rotation, and how predictable could be this motion.

The dynamics of the basins of rotation is followed, as R increases. Figure 7 shows basins of attraction associated to the bifurcation diagram of Fig. 4a. The birth of rotations at a saddle node bifurcation (R ≈ 0.425) is observed and, as R increases, the basin of rotations grows (Fig. 7a, b). After the homoclinic tangency [5], the basin boundary initiates its fractalization: fractal fingers sweep across the basin of oscillations, leading to the erosion of the entire basin (Fig. 7c–e). At R = 1.3 (Fig. 7f) the basin of rotations is almost fully eroded; there is a high final state sensitivity: small variations of the initial conditions modifies the attractor ultimately chosen [5]; rotating chaos is present [8, 13], but it is about to be replaced by tumbling chaos. At R ≈ 1.32 there is a crisis and then, for a broad range of R, tumbling chaos is the only stable attractor. At R ≈ 2.22 a new basin of rotations appears inside the chaotic basin (Fig. 7g). This basin evolves until it fractalizes from R ≈ 2.75 on. At R = 3, both the basin of rotations and tumbling chaos are eroded. Rotations are of period-1 and they evidence long chaotic transients, as discussed in the previous subsection.

Fig. 7
figure 7

Basin sequence for ω = 2, \( \lambda \) = 0.356, β = 0.1 and: a R = 0.45, born of period-1 rotations; b R = 0.6, basin of rotations grows; c R = 0.65, fractal erosion starts; d R = 0.75 and e R = 1, progress of erosion; f R = 1.3, basins of oscillations and rotations almost vanish; g R = 2.22, born of period-3 rotations; h R = 2.7, basin of rotations grows; i R = 3, new erosion. (): clockwise rotations, (): anticlockwise rotations, (): oscillations, (): tumbling chaos

Full size image

A visual inspection of Fig. 7 allows qualitative observations on the interaction among attractors. But with a view on energy harvesting, a quantitative evaluation of the robustness is required. For this purpose, the integrity factor (IF) is considered, which is defined in 2D as the normalized radius of the largest circle entirely belonging to a basin [17]. As rotations are studied regardless of its period, the IF can be thought as a measure of sensitivity of rotations to initial conditions: with a high IF (IF → 1), a small variation of the initial conditions also produces a steady rotation; meanwhile, with a low IF (IF → 0), the opposite happens. Besides, since initial conditions usually cannot be accurately determined in practice, it is important to know what happens given an unknown initial state. Thus PRot is defined as the probability of occurrence of rotations, for random initial conditions into a given range. Being IF and PRot two normalized magnitudes, they can be compared directly.

Results of the robustness/probabilistic analysis are presented in Fig. 8. Up to fractalization (R ≈ 0.65, see Fig. 7c), PRot and IF give increasing values since rotations are confined into their basin. The peak of robustness is at R ≈ 0.6 (IF = 0.129). As erosion evolves, the IF decays as the final state sensitivity increases, but PRot keeps growing since more initial conditions give rotations (Fig. 7d, e). At R = 1.2 the basin of oscillations is almost fully eroded and there is not possible in practice to predict the direction of rotations. PRot reaches a maximum: PRot = 0.66. Right before the crisis (R ≈ 1.32), rotations vanish and PRot fall dramatically. At the crisis, a few initial conditions produce rotations: IF = 0 and PRot ≈ 0. Similar behavior is observed for the rotational attractors at R ≈ 2.22, which are exclusive of reciprocating excitation. The peak probability is PRot = 0.71 (R = 3.5), as 71% of the initial conditions produce rotations.

Fig. 8
figure 8

Integrity and probabilistic analysis of rotations as R is increased, for ω = 2, \( \lambda \) = 0.356 and β = 0.1. (): probability of rotations, PRot; (): integrity factor, IF

Full size image

It is interesting to note that for some settings of the parameters it could be PRot = 1. This means that all initial states produce rotations. Actually, Fig. 9 has a “red zone” where all the responses are rotational with period-1. Due to the erosion of the basin, final state sensitivity is high; but the choice is reduced to clockwise or anticlockwise rotations, thus only direction of motion is unpredictable.

Fig. 9
figure 9

Probability of period-1 rotations given random initial conditions (\( \lambda \) = 0.356)

Full size image

4 Conclusions

The dynamics of the parametric pendulum with a reciprocating excitation was addressed with a view on energy harvesting. A rich dynamic behavior is elucidated, with substantial differences with respect to the classic sinusoidal forcing. Crank/rod ratio and viscous damping are crucial for rotational dynamics of the system: with a sufficiently high crank/rod ratio and/or a sufficiently low damping, new rotating attractors appear which are impossible with a sinusoidal excitation. These attractors exist for ranges of damping where energy extraction is feasible, more that more excitation scenarios allow rotational motion, increasing the possibilities for energy extraction.

The structural stability of the attractors and probabilities of obtaining rotations with unknown initial conditions were studied. It is shown that both robustness and probability of rotations grow until fractal erosion of the phase portrait starts. After this, robustness decays due to fractal erosion, but probability keeps growing since more initial conditions produce rotations. This means that rotations are easy to obtain but direction of rotation is difficult to predict due to a high final state sensitivity. The first is good for energy harvesting purposes, while the second should not lead to great difficulties in practical applications: rotations are desired, regardless of their direction.

A main conclusion of this work is that rotations are reachable and predictable with an adequate configuration of forcing and damping parameters. These parameters are closely related to the design of a suitable pendulum harvester. As excitation source is commonly known, damping depends only on the pendulum system and must be measured. Of course, a low friction is desired in energy harvesting applications.