1 Introduction

The first experimental study of a shock wave reflection off a concave double wedge was performed by Ginzburg and Markov [1]. The experimental investigation of this phenomenon was continued by Syshchikova and Krassovskaya [2]. The experiments were carried out in the reflection parameters domain where both regular and Mach reflection are possible (dual-solution domain). It was shown that when a planar shock wave reflects off the concave double wedge, the Mach reflection configuration is observed, while the reflection off a single wedge is regular. Ben-Dor et al. [3] performed detailed experimental and analytical study of the reflection of a shock wave from concave and convex double wedges. The seven domains of different reflection processes were determined. It was found that the transition wedge angle between regular and Mach reflection depends on the angle difference between the first and the second wedges. Moreover, Ben-Dor et al. [4] showed experimentally that the final reflection which develops on the second surface asymptotically approaches the configuration which would have been obtained had the incident shock wave reflected off a straight wedge having an angle equal to the angle of the second wedge. The numerical simulation of the reflection of a planar shock wave off a concave double wedge was made by A. Bagabir et al. [5]. Unfortunately, the interpretation of the numerical results is not quite correct.

An extensive experimental study of a shock wave reflection over concave cylindrical surface was performed by Takayama and Sasaki [6]. In recent years, the investigation on a shock wave reflection over concave cylindrical and elliptical walls was reinitiated [7,8,9,10]. In general case (reflecting wall is 1/4 of a circle), reflection process follows the following sequence of events: von Neumann reflection (vNR) → Mach reflection (MR) → regular reflection (RR). Here we omit from consideration an inverse Mach reflection and transitioned regular reflection as variations of MR and RR. Of particular interest is the transition from Mach to regular reflection. It was found that the transition angle is significantly larger than that found in the case for a straight wedge at the same Mach number or the transition point predicted by the von Neumann’s theory.

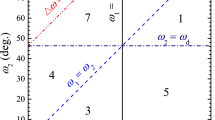
The simplest model for studying how reflection configuration evolves from one type to another is a double wedge. The schematic illustration of a shock wave reflection over a concave double wedge is shown in Fig. 1. Here β 1 and β 2 are the angles of the first and second surfaces, and Δβ = β 2 – β 1 is the inclination of the second surface with respect to the first surface. An initial incident shock wave I reflects from the first wall as a Mach reflection (MR). Then the Mach stem M 1 of this configuration reflects from the second surface. In this study of interest is a case when the Mach stem M 1 reflects from the second surface also as a MR. Eventually collision of two three-shock configuration occurs. New three-shock structure results from the collision. The objective of the study is to elucidate how this new configuration will develop with the passage of time. The results of experimental and numerical study of the interaction of a planar shock wave with a concave double wedge are given.

Fig. 1
figure 1

Scheme of a shock wave reflection over a concave double wedge

Full size image

2 Investigation Methods

The experiments have been carried out on the shock tube with rectangular cross section 50 × 150 mm2 in carbon dioxide. The flow field images have been obtained with the use of a shadow method.

Numerical simulation has been performed with the help of a code [11], which is based on an explicit quasi-monotonous scheme of Godunov with high order of approximation. The use of unstructured grids with the dynamical adaptation to the inhomogeneities of flows allows getting detailed information about the evolution of complex shock wave structures.

3 Results and Discussion

Figure 2 shows the boundaries and domains of existence of different reflection types in the (ζ, β) plane for gas with γ = 1.29. Here ζ, β, and γ are the density ratio across an incident shock wave, an angle of a wedge, and a gas-specific heat ratio, respectively. The value ζ is related to a Mach number of an incident shock wave M s through

$$ {M}_{\mathrm{S}}^2=\left(n-1\right)\zeta /\left(n-\zeta \right), $$

where n = (γ + 1)/(γ – 1) is the limiting value of the density ratio across the shock front.

Fig. 2
figure 2

Boundaries and domains of existence of different reflection types

Full size image

The elementary two-shock and three-shock theories predict the following boundaries. Boundary E divides the (ζ, β) plane into subdomains of regular reflection (above line E) and irregular (not necessarily Mach) reflection (under line E). Boundaries B and C divide the solution domain into three subdomains, which are distinct from each other in directivity of the shocks of three-shock configuration. Above line B the configurations contain two incoming shocks propagating in the opposite directions and one outgoing shock. Between lines B and C, the configurations contain one incoming and two outgoing shocks. That is, the domain above line B can be considered as the domain of the irregular opposite collision of two shock waves. And still, this domain is usually considered as a domain of an inverse Mach reflection. It should be noted that there are two dual-solution domains. In the domain limited by curves B and E, both regular and Mach reflections are possible; in the domain above line B, both regular reflection and irregular collision of two shocks (or inverse Mach reflection) are possible. The dual-solution domains are of particular interest.

In the present paper, the reflection of a shock wave with the Mach number M s = 3.2 is investigated. The parameters of the wedges we used in experiments and calculations are listed in Table 1.

Table 1 Parameters of the double wedges
Full size table

The given initial values M s and β 2 are in the dual solution domain where both regular and Mach reflections are possible. The reflection of the shock wave over the single wedge with β = 50° is regular (Fig. 3). The result of the experimental study for var.1 is shown in Fig. 4. Dynamics of the shock wave configurations in motion of the incident shock wave along the second surface of the double wedge is given as sequence of the shadow images. At given initial conditions, the reflection of an incident shock wave off the first surface is an MR, and the reflection of the Mach stem off the second surface results in a double Mach reflection (DMR). Interaction of the MR and the DMR leads to formation of new shock wave configuration with the additional shock wave systems (Fig. 4a). Figure 4b–d demonstrates the dynamics of the flow structure on the second surface of the double wedge. Unfortunately, it is not clear what interactions lead to the formation of the additional shock wave configurations. The attention should be paid to the combination of the shear layers shown in Fig. 5. This appears to be the case when four shear layers meet. One can see that the shear layers have not the intersection point. Instead of common point, the peculiarity as the “ʅ-shape” shear layer occurs.

Fig. 3
figure 3

Reflection of a shock wave over a single wedge

Full size image
Fig. 4
figure 4

Experimental results for var.1

Full size image
Fig. 5
figure 5

Enlarged fragment of Fig. 4d

Full size image
Fig. 6
figure 6

Numerical results for var.2

Full size image

To elucidate the process of the formation of a final shock wave reflection configuration, we performed calculations for the variants 1–4. For var.2, the numerical density contours are presented in Fig. 6. At the given conditions, an incident shock wave reflects off the first wedge as a transitional Mach reflection (TMR). The Mach stem of this pattern reflects off the second wedge also as a TMR (Fig. 6a). The kinks k 1and k 2 are clearly seen for both patterns. In Fig. 6b the flow image shows the moment when the reflected wave of the second TMR approaches the slipstream of the first TMR. The next image (Fig. 6c) corresponds to the moment when the reflected shock wave of the second TMR has interacted with the slipstream of the first TMR, but the triple points of the reflection patterns (T 1, T 2) do not merge yet (Fig. 6c). The complex flow picture arises after the collision of the triple points of the TMRs (Fig. 6d). New three-shock configuration with the triple point T is formed. We suggest that the tree-shock configuration is the result of the collision of the initial incident shock wave and the Mach stem of the second TMR. The interaction of reflected waves of the TMRs results in additional three-shock configuration with the triple point T*. Note that the shock wave between the points T and T* is curved. An attention should also be paid to multiple arrangement of the slipstreams: a slipstream emanating from the triple point T, a slipstream resulting from the reflection of an incident shock off the first wedge, and a slipstream resulting from the reflection of the Mach stem of the first TMR from the second wedge. The development of the final three-shock configuration in time is presented in Fig. 6e, f. The behavior of the three-shock configuration is identical as for a shock wave reflection off a single wedge. The height of the Mach stem is increased during the time.

Figure 7 shows the data of numerical simulation for vars.3 (Fig. 7a, c, e) and 4 (Fig. 7b, d, f). For both cases the incident shock reflects from the first surface of the double wedge as a double Mach reflection (DMR), and the Mach stem of this pattern reflects from the second surface also as a DMR (Fig. 7a, b). After merging of the triple points for both variants, the three-shock configurations with the additional structures in the disturbed regions are formed (Fig. 7c, d). As calculations show, for var.4, the size of the Mach stem of the three-shock pattern increases in time, and one expects that the three-shock configuration will asymptotically approach the pseudo-steady Mach reflection over 60°wedge (Fig. 7e). For the double wedge with the angles of the second wedge equal to 62°, the triple point moves toward the second surface, and the transitioned regular reflection pattern TRR is formed (Fig. 7f). Comparing the numerical data for two variants, it is possible to suggest that the MR→RR transition may occur at the reflection over the double wedge with the angles 30°and 61°.

Fig. 7
figure 7

Numerical results for vars.3 and 4

Full size image

The trajectories of the triple points T of the final three-shock configuration with respect to the second wedge surface are given in Fig. 8. (x’, y’) frame origin is attached to the tip of the second surface. The point A is the starting point of the reflection of the first Mach stem over the second wedge. The straight lines AB are the trajectories of the second triple points produced by reflection of the Mach stems over the second wedges. The point B corresponds to the moment of the formation of the final three-shock configuration. The curves BC are the region of unsteady transitional process. Further, the triple point trajectories become straights (lines CD). This clearly points at the self-similar development of the final three-shock configurations. The lines CD for vars. 1–3 (Fig. 8a–c) indicate that the three-shock patterns asymptotically approach to the pseudo-steady Mach reflection. For var. 4 (Fig. 8d), the three-shock configuration terminates, and a regular reflection forms. The data of the experimental and numerical investigation show that the reflection type formed on the first surface of a concave double wedge evolves into the reflection type on the second surface by means of complex unsteady interactions between shock waves.

Fig. 8
figure 8

Trajectories of the triple points T

Full size image

4 Conclusion

The reflection of a planar shock wave over a concave double wedge is considered both experimentally and numerically. The reflection on the first wedge provides the initial condition for the reflection on the second wedge. The process of the formation of the shock configuration on the second surface contains truly unsteady stage. The data obtained show that the final Mach configuration moves first toward the second surface and then the height of the Mach stem begins to increase. It is shown that the Mach reflection is formed in the dual-solution domain where regular and Mach reflection can exist. A regular reflection is formed in the dual solution domain where regular reflection and inverse Mach reflection can exist.

The work has been supported by RFBR grant № 15-01-04635.