1 Introduction

The general theory of elastic dielectrics dates back to [1], and has been further developed in, e.g., [2,3,4] and [5]. Elastic dielectrics belong to the class of so-called smart or intelligent materials, which are often used as structurally integrated materials to put structures into practice, which exhibit both, sensing and actuating authority. Such structures are denoted as smart structures. Prominent examples are piezoelectric materials, but also electro-active polymers. Concerning the latter we refer to, e.g., [6] or [7]. Due to the large deformations in electro-active polymers, nonlinear and electro-mechanically coupled formulations are required, in which two types of coupling are typically accounted for: coupling by means of electrostatic forces and constitutive coupling through coupling effects like electrostriction, see, e.g., [6]. For three-dimensional Eulerian and Lagrangian formulations, we refer to [8] and [9].

A practically important sub-class of electro-active polymers are dielectric elastomers, for which the constitutive coupling is often assumed negligible, and the actuation is then caused solely by the electrostatic forces. Practical applications of such dielectric elastomer actuation devices can be found, e.g., in [10,11,12] and [13]. In general problems of dielectric elastomer actuators numerical methods, such as the Finite Element method, are applied implementing solid elements for general three-dimensional problems [9, 14, 15] or solid shell elements to account for the typical thinness of the dielectric elastomer actuators, as developed in [16].

In our own previous work, see [17], we proposed a strategy for the modeling of thin dielectric elastomer plates, in which the plate was considered as a material surface with mechanical and electrical degrees of freedom, and the specific constitutive relations were obtained from the three-dimensional ones by the assumption of a plane stress and an a-priori assumption concerning the distribution of the strain through the thickness of the plate. Numerical integration was applied to compute the structural two-dimensional constitutive relations. In elasticity such an approach has been successfully used for elastic plates and shells [18, 19] and [20], and extended to the electro-mechanically coupled problem of piezoelectric plates and shells in [21] and [22].

In this paper we directly postulate the form of the two-dimensional augmented free energy for the structural plate problem, from which structural two-dimensional constitutive relations follow as a consequence from an extension of the principle of virtual work to the electro-mechanically coupled problem. We compute results with the proposed direct approach and compare them to validated results reported in [17].

2 Nonlinear Dielectric Elastomer Plates as Material Surfaces

In this section we briefly summarize the governing equations of thin plates modeled as material surfaces with mechanical and electrical degrees of freedom. For details concerning these equations we refer the reader to [17] and [22]. In particular, we consider the plate as a two-dimensional continuum of “needles” with five mechanical degrees of freedom, three translations δ r, and two rotations δ k, in which the variation of the unit normal vector k lies in the tangential plane. This resembles the notion of a single director attached to each particle of the plate, introduced in [23]. Concerning the electrical degrees of freedom, we use only the dominant one—the electric potential difference V .

2.1 Strain Measures

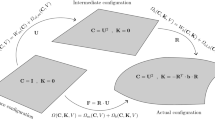
The material surface is plane in the reference configuration, and it is denoted as reference surface. In the deformed or actual configuration the deformed material surface is denoted as actual surface. The first metric tensor of the reference surface A = I plays the role of the two-dimensional identity tensor. The second metric tensor is zero for the plane reference surface, B = 0. For the actual surface the first and second metric tensors are a and b. The reference configuration and the actual configuration of the material surface are related to each other by means of a deformation gradient tensor F = (∇r)T with the position vector r of points of the actual surface and the differential operator ∇ of the reference surface. With the aid of the deformation gradient tensor, we introduce two tensor valued Green strain measures for the material surface, which are defined as the difference between the two metric tensors in the two configurations; yet, with the proper transformation by means of F applied to the metric tensors of the actual surface a and b. These two strain measures are

$$\displaystyle \begin{aligned} \boldsymbol{\varepsilon} = \frac{1}{2} \left({\mathbf{F}}^T \cdot \mathbf{a} \cdot \mathbf{F} - \mathbf{I} \right) \;,\quad \boldsymbol{\kappa} = - {\mathbf{F}}^T \cdot \mathbf{b} \cdot \mathbf{F}, {} \end{aligned} $$
(1)

with the right-Cauchy Green tensor C of the material surface as C = F T ⋅a ⋅F = F T ⋅F. Both strain measures remain constant, if and only if the motion of the material surface is a rigid body motion, see [24] for a discussion.

2.2 Principle of Virtual Work

We introduce a generalized principle of virtual work as

$$\displaystyle \begin{aligned} \int_{A}{ \delta (\eta_0 \varOmega) dA} + \int_{A}{ \sigma \delta V dA} + \delta A^{e} = 0, {} \end{aligned} $$
(2)

with the mass η 0 per unit undeformed area. Integration is done over the domain A of the reference surface. η 0Ω is the plate augmented free energy per unit area in the reference configuration, δA e is the virtual work of external forces and moments, which through boundary forces and moments involves mechanical and electrical sources, and the second integral accounts for the external electric charge σ per unit reference area with δV  being the variation of the electric potential. It has been shown before, see [17], that the augmented free energy of the plate has the form η 0Ω = η 0Ω(ε, κ, V ), such that its variation reads

$$\displaystyle \begin{aligned} \delta (\eta_0 \varOmega) = \eta_0 \frac{\partial \varOmega}{\partial \boldsymbol{\varepsilon}} \cdot \cdot \, \delta \boldsymbol{\varepsilon} + \eta_0 \frac{\partial \varOmega}{\partial \boldsymbol{\kappa}} \cdot \cdot \, \delta \boldsymbol{\kappa} + \eta_0 \frac{\partial \varOmega}{\partial V} \delta V. {} \end{aligned} $$
(3)

Moreover, stress measures τ and μ as well as the internal charge q per unit reference area are obtained through the constitutive relations

$$\displaystyle \begin{aligned} \boldsymbol{\tau} = \eta_0 \frac{\partial \varOmega}{\partial \boldsymbol{\varepsilon}} = 2 \eta_0 \frac{\partial \varOmega}{\partial \mathbf{C}} \, , \; \boldsymbol{\mu} = \eta_0 \frac{\partial \varOmega}{\partial \boldsymbol{\kappa}} \, , \; q = - \eta_0 \frac{\partial \varOmega}{\partial V}, {} \end{aligned} $$
(4)

and the variation becomes δ(η 0Ω) = τ ⋅⋅ δ ε + μ ⋅⋅ δ κ − qδV .

With the extended principle of virtual work at hand, we can derive the governing equations or use the principle as a starting point for a numerical solution. In any case, it remains to derive the specific form for the plate augmented free energy η 0Ω(ε, κ, V ).

2.3 Augmented Free Energy

First, we study a single layer dielectric elastomer plate with the thickness h. The material is assumed to exhibit a neo-Hookean behavior and to be incompressible. Moreover, we consider the thickness center surface as the material surface. In analogy to the three-dimensional case, we decompose the structural augmented free energy into a purely mechanical part η 0Ω mech and an electrical part η 0Ω elec. The mechanical part is further additively composed of a membrane part and a bending part, \(\varOmega ^{mech} = \varOmega ^{mech}_{m}+\varOmega ^{mech}_{b}\). With the right Cauchy–Green tensor C of the material surface, we introduce the membrane part of the mechanical contribution to the structural augmented free energy in analogy to a plane stress augmented free energy for an incompressible neo-Hookean material as

$$\displaystyle \begin{aligned} \eta_0 \varOmega^{mech}_m = \frac{1}{2} \frac{A}{4} \left( \text{tr} \mathbf{C} + (\text{det} \mathbf{C})^{-1} - 3 \right), \end{aligned} $$
(5)

with the extensional stiffness A = Y h(1 − ν 2)−1 known from linear plate theory. In the latter incompressibility is accounted for by means of ν = 0.5 and Young’s modulus becomes Y = 3μ; then, A = 4μh holds. Next, we introduce the bending part \(\varOmega ^{mech}_{b}\) of the structural augmented free energy in analogy to the bending energy of an isotropic incompressible Kirchhoff plate as

$$\displaystyle \begin{aligned} \eta \varOmega^{mech}_b = \frac{1}{2} \tilde{D} \left( \frac{1}{2} (\text{tr} \tilde{\boldsymbol{\kappa}})^2 + \frac{1}{2} \tilde{\boldsymbol{\kappa}} \cdot \cdot \, \tilde{\boldsymbol{\kappa}} \right), \end{aligned} $$
(6)

in which all entities are referred to the actual configuration. J = detF is the area change from the undeformed to the deformed configuration, η = J −1η 0 is the mass per unit area in the deformed configuration, \(\tilde {\boldsymbol {\kappa }} = - \mathbf {b} = {\mathbf {F}}^{-T} \cdot \boldsymbol {\kappa } \cdot {\mathbf {F}}^{-1}\) is the negative second metric tensor of the actual surface, and the thickness change is accounted for in the definition of a plate stiffness \(\tilde {D} = J^{-3} D\). D = Y h 3∕12(1 − ν 2)−1 is the classical plate stiffness, which for an incompressible material with ν = 0.5 is D = μh 3∕3. Therefore, we have

$$\displaystyle \begin{aligned} \eta_0 \varOmega^{mech}_b = \frac{1}{2} (\text{det} \mathbf{C})^{-1} D \left( (\text{tr} \tilde{\boldsymbol{\kappa}})^2 - \text{det} \tilde{\boldsymbol{\kappa}} \right) \end{aligned} $$
(7)

for the bending part of the augmented free energy. Concerning the electrical contribution to the augmented free energy we write \(2 \eta \varOmega ^{elec} = - \tilde {c} V^2\), with the voltage V  and the capacity \(\tilde {c}\) per unit deformed area, which is related to the capacity per unit undeformed area c by \(\tilde {c} = J c\). Therefore, we have

$$\displaystyle \begin{aligned} \eta_0 \varOmega^{elec} = - \frac{1}{2} c V^2 (\text{det} \mathbf{C}). \end{aligned} $$
(8)

We summarize our result. In the nonlinear case we have the augmented free energy of a single layer incompressible dielectric elastomer plate

$$\displaystyle \begin{aligned} \eta_0 \varOmega (\mathbf{C}, \tilde{\boldsymbol{\kappa}}, V^2) &= \frac{1}{2} \frac{A}{4} \left( \text{tr} \mathbf{C} + (\text{det} \mathbf{C})^{-1} - 3 \right)\\ & \quad + \frac{1}{2} (\text{det} \mathbf{C})^{-1} D \left( (\text{tr} \tilde{\boldsymbol{\kappa}})^2 - \text{det} \tilde{\boldsymbol{\kappa}} \right) - \frac{1}{2} c V^2 (\text{det} \mathbf{C}), \end{aligned} $$
(9)

in which C = 2ε + I holds. Moreover, we note the identities \(\text{tr} \tilde {\boldsymbol {\kappa }} = \text{tr} ({\mathbf {C}}^{-1} \cdot \boldsymbol {\kappa })\) and \(\text{det} \tilde {\boldsymbol {\kappa }} = \text{det} ({\mathbf {C}}^{-1} \cdot \boldsymbol {\kappa })\), from which we conclude that Ω = Ω(ε, κ, V ) is true.

Change of Material Surface

Our formulation holds only for a single layer dielectric elastomer plate, for which the physical thickness center surface is taken as the material surface. Using a different physical surface as the material surface, we must extend the form of the augmented free energy accordingly. Owing to the thinness of the plate, we assume the curvature tensor κ to be invariant under such a change of the material surface. In contrast, the right Cauchy–Green tensor C is not invariant, but transforms according to C →C + 2λ mκ, in which λ m is a geometry parameter accounting for the change of the material surface. Moreover, λ m is of the same order of smallness as the plate thickness h. We start the derivation with the membrane energy \(\eta _0 \varOmega ^{mech}_m = \eta _0 \varOmega ^{mech}_m(\mathbf {C})\) by replacing C with C + 2λ mκ and conducting a formal expansion with respect to λ m up to terms of order \(\lambda _m^3\). This results into

$$\displaystyle \begin{aligned} \eta_0 \varOmega^{mech}_m &\approx \frac{1}{2} \frac{A}{4} \left( \text{tr} \mathbf{C} + (\text{det} \mathbf{C})^{-1} - 3 \right) + \frac{1}{2} \frac{A}{2} \lambda_m \left( \text{tr} \boldsymbol{\kappa} - (\text{det} \mathbf{C})^{-1} \text{tr} \tilde{\boldsymbol{\kappa}} \right)\\ &\quad + \frac{1}{2} A \lambda_m^2 (\text{det} \mathbf{C})^{-1} \left( (\text{tr} \tilde{\boldsymbol{\kappa}})^2 - \text{det} \tilde{\boldsymbol{\kappa}} \right)\\ &\quad + \frac{1}{2} 2 A \lambda_m^3 (\text{det} \mathbf{C})^{-2} \text{tr} \tilde{\boldsymbol{\kappa}} \left( 2 \text{det} \boldsymbol{\kappa} - \text{det} \mathbf{C} ( \text{tr} \tilde{\boldsymbol{\kappa}} )^2 \right) . \end{aligned} $$
(10)

Likewise, we treat the electrical part of the energy and find the exact result

$$\displaystyle \begin{aligned} \eta_0 \varOmega^{elec} = - \frac{1}{2} c V^2 \left( \text{det} \mathbf{C} \left( 1 + 2 \lambda_m \text{tr} \tilde{\boldsymbol{\kappa}} \right) + 4 \lambda_m^2 \text{det} \boldsymbol{\kappa} \right).\end{aligned} $$
(11)

Concerning the bending energy we note that it is proportional to h 3 rather than the membrane energy, which is only proportional to h. Therefore, the order of smallness of the bending energy is already \(\lambda _m^2\) and it is sufficient to have a formal expansion with respect to λ m up to terms of order λ m; hence,

$$\displaystyle \begin{aligned} \eta_0 \varOmega^{mech}_b &\approx \frac{1}{2} (\text{det} \mathbf{C})^{-1} D \left( (\text{tr} \tilde{\boldsymbol{\kappa}})^2 - \text{det} \tilde{\boldsymbol{\kappa}} \right)\\ &\quad + \frac{1}{2} 6 D \lambda_m (\text{det} \mathbf{C})^{-2} \text{tr} \tilde{\boldsymbol{\kappa}} \left( 2 \text{det} \boldsymbol{\kappa} - \text{det} \mathbf{C} ( \text{tr} \tilde{\boldsymbol{\kappa}} )^2 \right).\end{aligned} $$
(12)

In conclusion, we write the augmented free energy for the single layer dielectric elastomer plate as

$$\displaystyle \begin{aligned} \eta_0 \varOmega &= \frac{1}{2} \frac{A}{4} \left( \text{tr} \mathbf{C} + (\text{det} \mathbf{C})^{-1} - 3 \right) + \frac{1}{2} \frac{A}{2} \lambda_m \left( \text{tr} \boldsymbol{\kappa} - (\text{det} \mathbf{C})^{-1} \text{tr} \tilde{\boldsymbol{\kappa}} \right)\\ &\quad + \frac{1}{2} \left(D + A \lambda_m^2 \right) (\text{det} \mathbf{C})^{-1} \left( (\text{tr} \tilde{\boldsymbol{\kappa}})^2 - \text{det} \tilde{\boldsymbol{\kappa}} \right)\\ &\quad + \frac{1}{2} 2 \left( A \lambda_m^2 + 3 D \right) \lambda_m (\text{det} \mathbf{C})^{-2} \text{tr} \tilde{\boldsymbol{\kappa}} \left( 2 \text{det} \boldsymbol{\kappa} - \text{det} \mathbf{C} ( \text{tr} \tilde{\boldsymbol{\kappa}} )^2 \right)\\ &\quad - \frac{1}{2} c V^2 \left( \text{det} \mathbf{C} \left( 1 + 2 \lambda_m \text{tr} \tilde{\boldsymbol{\kappa}} \right) + 4 \lambda_m^2 \text{det} \boldsymbol{\kappa} \right), \end{aligned} $$
(13)

in which A and D are stiffnesses referring to the center surface of the plate, whereas λ m characterizes the distance of the material surface from this center surface. However, we are not so much interested in the derivation of these parameters, but rather in the functional dependency of the different terms of the augmented free energy on the strain measures. To identify the material parameters as well as the sources of actuation we will linearize our formulation and compare the result to the well-known linear theory.

Small Strain Regime

Finally, we linearize the augmented free energy in the small strain regime, in which we have C = I + 2λ ε with λ as a formal small parameter; also κ is formally replaced by λ κ. Concerning the voltage V  we assume its square to be of order λ. Then, an expansion in the vicinity of λ = 0 finds the principal term λ 1 of the augmented free energy to be independent from any deformation measure. Therefore, the leading order term for the plate theory is of order λ 2 and it reads

$$\displaystyle \begin{aligned} \eta_0 \varOmega^{lin} &= \frac{1}{2} \left( A \left( (\text{tr} \boldsymbol{\varepsilon})^2 - \text{det} \boldsymbol{\varepsilon} \right) - 2 c V^2 \text{tr} \boldsymbol{\varepsilon} \right) + \frac{1}{2} A \lambda_m \left( \text{tr} \boldsymbol{\varepsilon} \text{tr} \boldsymbol{\kappa} + \boldsymbol{\varepsilon} \cdot \cdot \, \boldsymbol{\kappa} \right)\\ &\quad + \frac{1}{2} \left( \left(D + A \lambda_m^2 \right) \left( (\text{tr} \boldsymbol{\kappa})^2 - \text{det} \boldsymbol{\kappa} \right) - 2 c \lambda_m V^2 \text{tr} \boldsymbol{\kappa} \right). \end{aligned} $$
(14)

On the other hand, the linear theory of thin plates with eigenstrains is well studied, see [25]; for the case of an isotropic incompressible material obeying Hooke’s law using any other surface than the neutral surface as a reference surface we have

$$\displaystyle \begin{aligned} \eta_0 \varOmega^{Hooke} &= \frac{1}{2} \left( \bar{A} \left( (\text{tr} \boldsymbol{\varepsilon})^2 - \text{det} \boldsymbol{\varepsilon} \right) - 2 \tau^* \text{tr} \boldsymbol{\varepsilon} \right) + \frac{1}{2} \bar{B} \left( \text{tr} \boldsymbol{\varepsilon} \text{tr} \boldsymbol{\kappa} + \boldsymbol{\varepsilon} \cdot \cdot \, \boldsymbol{\kappa} \right)\\ &\quad + \frac{1}{2} \left( \bar{D} \left( (\text{tr} \boldsymbol{\kappa})^2 - \text{det} \boldsymbol{\kappa} \right) - 2 \mu^* \text{tr} \boldsymbol{\kappa} \right), {} \end{aligned} $$
(15)

in which the actuation enters classically by means of so-called Eigenspannungsquellen τ ∗ and μ ∗ = Z mτ ∗, provided the corresponding source is constant through the thickness. Z m is the thickness position of the neutral surface, which is in the thickness center of the plate. The extensional stiffness \(\bar {A}\), the coupling stiffness \(\bar {B}\), and the bending stiffness \(\bar {D}\) as well as the Eigenspannungsquellen are defined as

$$\displaystyle \begin{aligned} (\bar{A}, \bar{B}, \bar{D}) &= 4 \mu \int_{Z_o}^{Z_o+h}{(1,Z,Z^2) dZ},\\ (\tau^* , \mu^*) &= \int_{Z_o}^{Z_o+h}{\varepsilon_0 \varepsilon_r \left( \frac{V}{h} \right)^2 (1,Z) dZ} ,\\ Z_m &= \frac{1}{h}\int_{Z_o}^{Z_o+h}{Z dZ}. \end{aligned} $$
(16)

Z o is the thickness coordinate of the upper side of the plate and ε 0 and ε r are the permittivity in vacuum and the relative permittivity. This specific type of actuation is due to Coulomb forces. Comparing the linearized version of the nonlinear theory to the linear theory we identify the material parameters and the actuation of the nonlinear theory, and eventually write the augmented free energy as

$$\displaystyle \begin{aligned} \eta_0 \varOmega &= \frac{1}{2} \frac{\bar{A}}{4} \left( \text{tr} \mathbf{C} + (\text{det} \mathbf{C})^{-1} - 3 \right) + \frac{1}{2} \frac{\bar{B}}{2} \left( \text{tr} \boldsymbol{\kappa} - (\text{det} \mathbf{C})^{-1} \text{tr} \tilde{\boldsymbol{\kappa}} \right)\\ &\quad + \frac{1}{2} \bar{D} (\text{det} \mathbf{C})^{-1} \left( (\text{tr} \tilde{\boldsymbol{\kappa}})^2 - \text{det} \tilde{\boldsymbol{\kappa}} \right) + \frac{1}{2} 2 \bar{K} (\text{det} \mathbf{C})^{-2} \text{tr} \tilde{\boldsymbol{\kappa}} \left( 2 \text{det} \boldsymbol{\kappa} - \text{det} \mathbf{C} ( \text{tr} \tilde{\boldsymbol{\kappa}} )^2 \right)\\ &\quad - \frac{1}{2} \tau^* \left( \text{det} \mathbf{C} \left( 1 + 2 Z_m \text{tr} \tilde{\boldsymbol{\kappa}} \right) + 4 Z_m^2 \text{det} \boldsymbol{\kappa} \right). {} \end{aligned} $$
(17)

with τ ∗ = cV 2 and ch = ε 0ε r. By analogy, we identify the corresponding higher order coupling stiffness \(\bar {K}\) as

$$\displaystyle \begin{aligned} \bar{K} = 4 \mu \int_{Z_o}^{Z_o+h}{Z^3 dZ}. \end{aligned} $$
(18)

This completes the discussion of the augmented free energy. Having this energy at hand we can easily study layered plates as well, because the choice of the material surface as any physical surface is possible.

3 Validation

As a simple example, we are studying a rectangular plate with dimension a × b × h = 100 mm × 50 mm × 1 mm made of two perfectly connected layers; the material parameters are ε r = 4.7 and μ = 20, 698 Pa. An electrode at the connecting interface is grounded and a voltage can be applied at the two outer electrodes. In particular, the voltage is applied at the lower electrode and the upper one is grounded as well; this configuration will result into a bending actuator. The plate is fully clamped at x = 0 and free at the other edges. As no external forces are applied and the voltage is prescribed, the principle of virtual work reduces to a stationarity principle,

$$\displaystyle \begin{aligned} \delta \varSigma = 0 \quad \text{with} \; \varSigma = \int_{A}{ \eta_0 \varOmega (\boldsymbol{\varepsilon},\boldsymbol{\kappa},V) dA}. {} \end{aligned} $$
(19)

As we are mainly interested in verifying the proposed form of the augmented free energy, we compute solutions with a simple Ritz approximation within the framework of the von-Karman and Tsien theory, see [26], rather than for the fully geometric nonlinear theory. Therefore, the strain measures ε and κ are approximated as

$$\displaystyle \begin{aligned} \boldsymbol{\varepsilon} = \frac{1}{2} \left( \nabla {\mathbf{u}}^S + \nabla w \nabla w \right) \;,\quad \boldsymbol{\kappa} = - \nabla \nabla w, {} \end{aligned} $$
(20)

in which w is the plate deflection and u the in-plane displacement vector; ∇u S denotes the symmetric part of the displacement gradient tensor. For the Ritz-Ansatz we set

$$\displaystyle \begin{aligned} u(x,y) = \sum_{i=1}^5 {x^i u_i} \; , \quad v(x,y) = 0 \;,\quad w(x,y) = \sum_{i=1}^5 {x^{i+1} w_i} . {} \end{aligned} $$
(21)

We increase the voltage in the bottom layer starting with V = 0 V up to V = 2000 V and show results for the non-dimensional end point deflection w∕h and the non-dimensional end point axial position x∕h in the center of the free end in the top row of Fig. 1. Results are presented for four different physical surfaces used as the material surface—the bottom and the top surface of the plate, the center surface of the plate, which represents the neutral plane, with \(\bar {B} = 0\) and \(\bar {K} = 0\), and the center surface of the actuated bottom layer, which is the neutral plane of the bottom layer. One can see that the deflection and the axial positions are close to each other independent from the choice of the material surface. These results verify the proper modeling concerning the choice of the material surface; yet, they still need to be validated against other results. This is done in the two plots in the bottom row of Fig. 1. Here, neutral plane refers to the present theory using the center surface as the material surface and bottom—no correction to the present theory using the bottom surface as the material surface, but setting \(\bar {K} = 0\). Clearly, one can see the significance of the material parameter \(\bar {K}\), if the material surface is not the neutral plane of the plate. Gauss refers to the result computed with the same Ritz-Ansatz within the von-Karman and Tsien approximation, but with the augmented free energy as

$$\displaystyle \begin{aligned} \varrho_0 \varOmega_3 = \frac{1}{2} \mu \left( \text{tr} {\mathbf{C}}_3 + (\text{det} {\mathbf{C}}_3)^{-1} - 3 \right) - \frac{1}{2} \varepsilon_0 \varepsilon_r \det{{\mathbf{C}}_3} \left( \frac{V}{h / 2} \right)^2, \end{aligned} $$
(22)

with C 3 = 2(ε + Z κ) + I. A numerical integration through the thickness then finds the plate augmented free energy. This type of modeling is already well tested against results from the literature in [17] using finite elements within the geometrically exact formulation. As the present results—neutral plane—coincide very well with the ones using the numerical integration—Gauss—we conclude that the plate augmented free energy, as given in Eq. (17), is a proper formulation.

Fig. 1
figure 1

Non-dimensional end point deflection w∕h and the non-dimensional end point axial position x∕h for different physical surfaces

Full size image

4 Conclusions

In this paper we primarily focused on postulating a specific form for the two-dimensional augmented free energy of a thin plate made of layers of incompressible dielectric elastomers. The particular case of a neo-Hookean material was considered. The resulting novel formulation was validated against results based on a-priori assumptions imposed on the state of stress and the distribution of the strain through the thickness of the plate, which are already well tested. A very good agreement was obtained.