Abstract
Some voting systems are reliant on external authentication services. Others use cryptography to implement their own. We combine digital signatures and non-interactive proofs to derive a generic construction for voting systems with their own authentication mechanisms, from systems that rely on external authentication services. We prove that our construction produces systems satisfying ballot secrecy and election verifiability, assuming the underlying voting system does. Moreover, we observe that works based on similar ideas provide neither ballot secrecy nor election verifiability. Finally, we demonstrate applicability of our results by applying our construction to the Helios voting system.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
1 Introduction
An election is a decision-making procedure to choose representatives [17, 22, 30]. Choices should be made freely by voters with equal influence, and this must be ensured by voting systems [24, 25, 42]. Some voting systems rely on external authentication services to ensure choices are made by voters. E.g., Helios [2, 26] supports authentication via Facebook, Google and Yahoo using OAuth.Footnote 1 Other voting systems use cryptography to implement their own authentication mechanisms. E.g., the voting system by Juels et al. uses a combination of encrypted nonces and plaintext equality tests for authentication [20]. We combine digital signatures and non-interactive proofs to derive a construction for voting systems with their own authentication mechanisms from systems that rely on external service providers. Our construction produces voting systems which require less trust, since systems built upon cryptography are typically preferable to systems trusting external service providers.
Many voting systems rely on art, rather than science, to ensure that choices are made freely by voters with equal influence. Such systems build upon creativity and skill, rather than scientific foundations, and are typically broken in ways that compromise free choice, e.g., [16, 39, 43, 44], or permit adversaries to unduly influence the outcome, e.g., [10, 19]. By contrast, we prove that our construction produces voting systems that satisfy rigorous and precise security definitions of ballot secrecy and election verifiability that capture voters voting freely with equal influence.Footnote 2
We demonstrate applicability of our construction by deriving voting systems with their own authentication mechanisms from Helios. Moreover, we compare those systems to Helios-C [13], a variant of Helios for two-candidate elections in which ballots are digitally signed. Our comparison reveals some subtle distinctions and we show that Helios-C does not satisfy our security definition, whereas our construction produces voting systems that do.
Structure. Section 2 recalls election scheme syntax. Section 3 presents our construction. Section 4 proves that our construction produces systems satisfying ballot secrecy. Section 5 proves that election verifiability is also satisfied. Section 6 demonstrates the application of our construction to the Helios voting system and compares the resulting systems to Helios-C. We conclude in Sect. 7. The appendices recall security definitions for voting systems and present proofs. Definitions of cryptographic primitives and associated security definitions are deferred to an accompanying technical report [28].
2 Election Scheme Syntax
We recall syntax by Smyth et al. [36] for a class of voting systems that consist of the following four steps. First, a tallierFootnote 3 generates a key pair and (optionally) a registrar generates credentials for voters. Secondly, each voter constructs and casts a ballot for their vote. These ballots are recorded on a bulletin board. Thirdly, the tallier tallies the recorded ballots and announces an outcome, i.e., a distribution of votes. Finally, voters and other interested parties check that the outcome corresponds to votes expressed in recorded ballots.
Definition 1
(Election scheme [36]). An election scheme with external authentication is a tuple of efficient algorithms \((\mathsf {Setup}, \mathsf {Vote}, \mathsf {Tally}, \mathsf {Verify})\) and an election scheme with internal authentication is a tuple of efficient algorithms \((\mathsf {Setup}, \mathsf {Register}, \mathsf {Vote}, \mathsf {Tally}, \mathsf {Verify})\), such that:Footnote 4
-
\(\mathsf {Setup}\), denoted \(( pk , sk , mb , mc ) \leftarrow \mathsf {Setup}(\kappa )\), is run by the tallier. \(\mathsf {Setup}\) takes a security parameter
 as input and outputs a key pair \( pk , sk \), a maximum number of ballots \( mb \), and a maximum number of candidates \( mc \).
as input and outputs a key pair \( pk , sk \), a maximum number of ballots \( mb \), and a maximum number of candidates \( mc \). -
\(\mathsf {Register}\), denoted
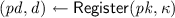 , is run by the registrar. It takes as input the public key \( pk \) of the tallier and a security parameter \(\kappa \), and it outputs a credential pair \(( pd , d )\), where \( pd \) is a public credential and \( d \) is a private credential.
, is run by the registrar. It takes as input the public key \( pk \) of the tallier and a security parameter \(\kappa \), and it outputs a credential pair \(( pd , d )\), where \( pd \) is a public credential and \( d \) is a private credential. -
\(\mathsf {Vote}\), denoted \(b\leftarrow \mathsf {Vote}(\langle d \rangle , pk , nc ,v,\kappa )\), is run by voters. \(\mathsf {Vote}\) takes as input a private credential \( d \) (optional), a public key \( pk \), some number of candidates \( nc \), a voter’s vote v, and a security parameter \(\kappa \). The vote should be selected from a sequence \(1,\dots , nc \) of candidates. \(\mathsf {Vote}\) outputs a ballot b or error symbol \(\perp \).
-
\(\mathsf {Tally}\), denoted \((\mathbf{v}, pf )\leftarrow \mathsf {Tally}( sk , nc , \mathfrak {bb},\langle L\rangle ,\kappa )\), is run by the tallier. \(\mathsf {Tally}\) takes as input a private key \( sk \), some number of candidates \( nc \), a bulletin board \(\mathfrak {bb}\), an electoral roll \(L\) (optional), and a security parameter \(\kappa \), where \(\mathfrak {bb}\) is a set. It outputs an election outcome \(\mathbf{v}\) and a non-interactive proof \( pf \) that the outcome is correct. An election outcome is a vector \(\mathbf{v}\) of length \( nc \) such that \(\mathbf{v}[v]\) indicates the number of votes for candidate v.
-
\(\mathsf {Verify}\), denoted \(s \leftarrow \mathsf {Verify}( pk , nc , \mathfrak {bb},\langle L\rangle , \mathbf{v}, pf , \kappa )\), is run to audit an election. It takes as input a public key \( pk \), some number of candidates \( nc \), a bulletin board \(\mathfrak {bb}\), an electoral roll \(L\) (optional), an election outcome \(\mathbf{v}\), a proof \( pf \), and a security parameter \(\kappa \). It outputs a bit s, which is 1 if the election verifies successfully and 0 otherwise.
Election schemes with internal authentication must always use optional inputs, whereas election schemes with external authentication must not. Both schemes must satisfy correctness: there exists a negligible function \(\mathsf {negl}\), such that for all security parameters \(\kappa \), integers \( nb \) and \( nc \), and votes \(v_1, \dots , {}v_{ nb } \in \{1, \dots , nc \}\), it holds that if \(\mathbf{v}\) is a vector of length \( nc \) whose components are all 0, then

where algorithm \(\mathsf {Register}\) is only applied for election scheme with internal authentication and optional inputs are only used for election scheme with internal authentication.
3 Our Construction
Election schemes with internal authentication can be derived from schemes with external authentication using a digital signature scheme and a non-interactive proof system: Each voter publishes a ballot constructed using the underlying scheme with external authentication, along with a signature on that ballot and a proof that they constructed both the ballot and the signature. Signatures and proofs are used to ensure that each tallied vote was cast by an authorised voter.
Our construction is formal described in Definition 3. It is parameterised by an election scheme with external authentication, a digital signature scheme, and a non-interactive proof system, derived from an underlying sigma protocol and a hash function, using the Fiat-Shamir transformation.Footnote 5 Hence, we denote election schemes derived using our construction as  , where the underlying election scheme, signature scheme, sigma protocol and hash function are \(\varGamma \), \(\varOmega \), \(\varSigma \) and \(\mathcal H\), respectively. To ensure our construction produces election schemes with internal authentication, the non-interactive proof system must be defined for a suitable relation, and we define such a relation as follows.
, where the underlying election scheme, signature scheme, sigma protocol and hash function are \(\varGamma \), \(\varOmega \), \(\varSigma \) and \(\mathcal H\), respectively. To ensure our construction produces election schemes with internal authentication, the non-interactive proof system must be defined for a suitable relation, and we define such a relation as follows.
Definition 2
Given an election scheme with external authentication \(\varGamma = (\mathsf {Setup}, \mathsf {Vote}, \mathsf {Tally}, \mathsf {Verify})\) and a digital signature scheme \(\varOmega = (\mathsf {Gen}_\varOmega , \mathsf {Sign}_\varOmega , \mathsf {Verify}_\varOmega )\), we define binary relation \(R(\varGamma ,\varOmega )\) over vectors of length 6 and vectors of length 4 such that \((( pk , b, \sigma , nc , \kappa ), (v, r, d , r')) \in R(\varGamma ,\varOmega ) \Leftrightarrow b = \mathsf {Vote}( pk , nc , v, \kappa ;r) \wedge \sigma = \mathsf {Sign}_\varOmega ( d , b; r')\).
Definition 3
(Construction). Suppose \(\varGamma = (\mathsf {Setup}_\varGamma , \mathsf {Vote}_\varGamma , \mathsf {Tally}_\varGamma , \mathsf {Verify}_\varGamma )\) is an election scheme with external authentication, \(\varOmega = (\mathsf {Gen}_\varOmega , \mathsf {Sign}_\varOmega , \mathsf {Verify}_\varOmega )\) is a digital signature scheme, \(\varSigma \) is a sigma protocol for a binary relation \(R(\varGamma ,\varOmega )\), and \(\mathcal H\) is a hash function. Let \(\mathsf {FS}(\varSigma ,\mathcal H) = (\mathsf {Prove}_\varSigma , \mathsf {Verify}_\varSigma )\). We define  such that:
such that:
-
\(\mathsf {Setup}(\kappa )\) computes \(( pk , sk , mb , mc ) \leftarrow \mathsf {Setup}_\varGamma ({}\kappa )\) and outputs \(( pk , sk , mb , mc )\).
-
 computes \(( pd , d )\leftarrow \mathsf {Gen}_\varOmega (\kappa )\) and outputs \(( pd ,( pd , d ))\).
computes \(( pd , d )\leftarrow \mathsf {Gen}_\varOmega (\kappa )\) and outputs \(( pd ,( pd , d ))\). -
\(\mathsf {Vote}( d ', pk , nc ,v,\kappa )\) parses \( d '\) as \(( pd , d )\) and outputs \(\perp \) if parsing fails, selects coins r and \(r'\) uniformly at random, computes

and outputs \(( pd ,b,\sigma ,\tau )\).
-
\(\mathsf {Tally}( sk , nc , \mathfrak {bb},L,\kappa )\) computes \((\mathbf{v}, pf ) \leftarrow \mathsf {Tally}_\varGamma ( sk , \mathsf {auth}(\mathfrak {bb},L),{} nc , {}\kappa )\) and outputs \((\mathbf{v}, pf )\).
-
\(\mathsf {Verify}( pk , nc , \mathfrak {bb},L, \mathbf{v}, pf , \kappa )\) computes \(s \leftarrow \mathsf {Verify}_\varGamma ( pk , \mathsf {auth}(\mathfrak {bb},L), nc , \mathbf{v}, pf , \kappa )\) and outputs s.
Set \(\mathsf {auth}(\mathfrak {bb},L) = \{b \mid ( pd , b, \sigma , \tau )\in \mathfrak {bb}\wedge \mathsf {Verify}_\varOmega ( pd , b, \sigma ) = 1 \wedge \mathsf {Verify}_\varSigma (( pk , b, nc , \kappa ), \tau , \kappa ) = 1 \wedge pd \in L\wedge ( pd , b', \sigma ', \tau ')\not \in \mathfrak {bb}\setminus \{( pd , b, \sigma , \tau )\} \wedge \mathsf {Verify}_\varOmega ( pd , b', \sigma ') = 1 \}\).
Our construction uses function \(\mathsf {auth}\) to ensure tallied ballots are authorised and to discard ballots submitted under the same credential (i.e., if there is more than one ballot submitted with a private credential, then all ballots submitted under that credential are discarded). Since election schemes with internal authentication must satisfy correctness, the underlying digital signature scheme must ensure that key pairs are distinct. Hence, correctness of our construction depends on security of the underlying digital signature scheme, albeit in a tedious manner. Since we exploit strong unforgeability of the signature scheme for results in the following sections, we assume the same property here (to ensure key pairs are distinct). Weaker conditions could be used for generality.
Lemma 1
Let \(\varGamma \) be an election scheme with external authentication, \(\varOmega \) be a digital signature scheme, \(\varSigma \) be a sigma protocol for relation \(R(\varGamma ,\varOmega )\), and \(\mathcal H\) be a random oracle. Suppose \(\varOmega \) satisfies strong unforgeability. We have  is an election scheme with internal authentication.
is an election scheme with internal authentication.
The proof of Lemma 1 appears in our companion technical report [28].
4 Our Construction Ensures Ballot Secrecy
We adopt the definition of ballot secrecy for election schemes with external authentication (\(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Ext}\)) by Smyth [32]. That definition appears to be the most suitable in the literature, because it detects the largest class of attacks [32, Sect. 7]. In particular, it detects attacks that arise when the adversary controls the bulletin board or the communications channel, whereas other definitions, e.g., [5,6,7,8, 11, 12, 35], fail to detect such attacks. A definition of ballot secrecy for election schemes with internal authentication (\(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Int}\)) can be derived from Smyth’s definition by a natural, straightforward extension that takes credentials into account. Both definitions are presented in Appendix A. The definition of ballot secrecy we recall challenges an adversary, who has access to the election outcome, to distinguish between ballots.
We can prove that our construction ensures ballot secrecy (a formal proof of Theorem 2 appears in Appendix A), assuming the underlying election scheme satisfies ballot secrecy and the underlying sigma protocol satisfies special soundness and special honest verifier zero-knowledge.
Theorem 2
Let \(\varGamma \) be an election scheme with external authentication, \(\varOmega \) be a digital signature scheme, \(\varSigma \) be a sigma protocol for relation \(R(\varGamma ,\varOmega )\), and \(\mathcal H\) be a random oracle. Suppose \(\varGamma \) satisfies \(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Ext}\), \(\varSigma \) satisfies special soundness and special honest verifier zero-knowledge, and \(\varOmega \) satisfies strong unforgeability. Election scheme with internal authentication  satisfies \(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Int}\).
satisfies \(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Int}\).
Proof sketch
Ballot secrecy of election scheme  follows from secrecy of the underlying scheme \(\varGamma \), because signatures and non-interactive zero-knowledge proofs do not leak information. (Special soundness and special honest verifier zero-knowledge ensure proof system \(\mathsf {FS}(\varSigma ,\mathcal H)\) is zero-knowledge [7].) \(\square \)
follows from secrecy of the underlying scheme \(\varGamma \), because signatures and non-interactive zero-knowledge proofs do not leak information. (Special soundness and special honest verifier zero-knowledge ensure proof system \(\mathsf {FS}(\varSigma ,\mathcal H)\) is zero-knowledge [7].) \(\square \)
We demonstrate applicability of Theorem 2 using a construction for election schemes from asymmetric encryption.Footnote 6
Definition 4
(\(\mathsf {Enc2Vote}\) [29]). Given a perfectly correct asymmetric encryption scheme \(\varPi = (\mathsf {Gen}, \mathsf {Enc},\mathsf {Dec})\) satisfying \(\mathsf {IND}\textsf {-}\mathsf {CPA}\), election scheme with external authentication \(\mathsf {Enc2Vote}(\varPi )\) is defined as follows:
-
\(\mathsf {Setup}(\kappa )\) computes \(( pk , sk )\leftarrow \mathsf {Gen}(\kappa )\) and outputs \(( pk , sk , \textit{poly}(\kappa ), |\mathfrak m|)\).
-
\(\mathsf {Vote}( pk , nc ,v,\kappa )\) computes \(b\leftarrow \mathsf {Enc}( pk ,v)\) and outputs b if \(1\le v \le nc \le |\mathfrak m|\) and \(\perp \) otherwise.
-
\(\mathsf {Tally}( sk , nc , \mathfrak {bb}, \kappa )\) initialises vector \(\mathbf{v}\) of length \( nc \), computes for \(b\in \mathfrak {bb}\) do \(v\leftarrow \mathsf {Dec}( sk ,b);\) if \(1\le v\le nc \) then \(\mathbf{v}[v] \leftarrow \mathbf{v}[v]+1\), and outputs \((\mathbf{v},\epsilon )\).
-
\(\mathsf {Verify}( pk , nc , \mathfrak {bb}, \mathbf{v}, pf , \kappa )\) outputs 1.
Algorithm \(\mathsf {Setup}\) requires \(\textit{poly}\) to be a polynomial function, algorithms \(\mathsf {Setup}\) and \(\mathsf {Vote}\) require \(\mathfrak m = \{1,\dots ,|\mathfrak m|\}\) to be the encryption scheme’s plaintext space, and algorithm \(\mathsf {Tally}\) requires \(\epsilon \) to be a constant symbol.
Intuitively, given a non-malleable asymmetric encryption scheme \(\varPi \),Footnote 7 \(\mathsf {Enc2Vote}(\varPi )\) derives ballot secrecy from \(\varPi \) until tallying and tallying maintains ballot secrecy by returning only the number of votes for each candidate.
Proposition 3
([29, 32]). Let \(\varPi \) be an encryption scheme with perfect correctness. If \(\varPi \) satisfies \(\textsf {IND}{\text {-}}\textsf {PA0}\), then election scheme with external authentication \(\mathsf {Enc2Vote}(\varPi )\) satisfies \(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Ext}\).
Hence, by Theorem 2, we have the following result.
Corollary 4
Let \(\varPi \) be an asymmetric encryption scheme with perfect correctness, \(\varOmega \) be a digital signature scheme, \(\varSigma \) be a sigma protocol for relation \(R(\mathsf {Enc2Vote}(\varPi ),\varOmega )\), and \(\mathcal H\) be a random oracle. Suppose \(\varPi \) satisfies \(\textsf {IND}{\text {-}}\textsf {PA0}\), \(\varSigma \) satisfies special soundness and special honest verifier zero-knowledge, and \(\varOmega \) satisfies strong unforgeability. Election scheme with internal authentication  satisfies \(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Int}\).
satisfies \(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Int}\).
Clearly election scheme \(\mathsf {Enc2Vote}\) does not satisfy universal verifiability, because it will accept any election outcome.
5 Our Construction Ensures Election Verifiability
We adopt definitions of individual (\(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Ext}\)) and universal (\(\mathsf {Exp}\text {-}\mathsf {UV}\text {-}\mathsf {Ext}\)) verifiability for election schemes with external authentication from Smyth et al. [36]. We also adopt their definitions of individual (\(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Int}\)), universal (\(\mathsf {Exp}\text {-}\mathsf {UV}\text {-}\mathsf {Int}\)) and eligibility (\(\mathsf {Exp}\text {-}\mathsf {EV}\text {-}\mathsf {Int}\)) verifiability for schemes with internal authentication. Those definitions seem to be the most suitable in the literature, because they detect the largest class of attacks. In particular, they detect collusion and biasing attacks [36, Sect. 7], whereas other definitions, e.g., [13, 20, 21], fail to detect such attacks. The definitions are presented in Appendix B.
The definitions by Smyth, Frink, and Clarkson et al. work as follows: Individual verifiability challenges the adversary to generate a collision from algorithm \(\mathsf {Vote}\). Universal verifiability challenges the adversary to concoct a scenario in which either: \(\mathsf {Verify}\) accepts, but the election outcome is not correct, or \(\mathsf {Tally}\) produces an election outcome that \(\mathsf {Verify}\) rejects. Hence, universal verifiability requires algorithm \(\mathsf {Verify}\) to accept if and only if the election outcome is correct. Finally, eligibility verifiability challenges an adversary, which can corrupt voters, to generate a valid ballot under a non-corrupt voter’s private credential.
We can prove that our construction ensures election verifiability. Individual and eligibility verifiability of  follow from security of the underlying signature scheme, and universal verifiability follows from universal verifiability of the underlying election scheme \(\varGamma \).
follow from security of the underlying signature scheme, and universal verifiability follows from universal verifiability of the underlying election scheme \(\varGamma \).
Theorem 5
Let \(\varGamma \) be an election scheme with external authentication, \(\varOmega \) be a digital signature scheme, \(\varSigma \) be a sigma protocol for relation \(R(\varGamma ,\varOmega )\), and \(\mathcal H\) be a random oracle. Suppose \(\varOmega \) satisfies strong unforgeability, \(\varSigma \) satisfies special soundness and special honest verifier zero-knowledge, and \(\varGamma \) satisfies \(\mathsf {Exp}\text {-}\mathsf {UV}\text {-}\mathsf {Ext}\). Election scheme with internal authentication  satisfies \(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Int}\), \(\mathsf {Exp}\text {-}\mathsf {EV}\text {-}\mathsf {Int}\), and \(\mathsf {Exp}\text {-}\mathsf {UV}\text {-}\mathsf {Int}\).
satisfies \(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Int}\), \(\mathsf {Exp}\text {-}\mathsf {EV}\text {-}\mathsf {Int}\), and \(\mathsf {Exp}\text {-}\mathsf {UV}\text {-}\mathsf {Int}\).
Proof sketch
Individual verifiability is satisfied because voters can check that their signatures appear on the bulletin board. Universal verifiability is satisfied because the underlying voting scheme does, and the properties of \(\varOmega \) and \(\varSigma \) ensure only authorised ballots are tallied. And eligibility verifiability is satisfied because anyone can check that signatures belong to registered voters. \(\square \)
A formal proof of Theorem 5 follows immediately from our proofs of individual, universal and eligibility verifiability, which we defer to Appendix B (Lemmata 10–12).
We demonstrate applicability of our results for election schemes from nonces.
Definition 5
(\(\mathsf {Nonce}\) [36]). Election scheme with external authentication \(\mathsf {Nonce}\) is defined as follows:
-
\(\mathsf {Setup}(\kappa )\) outputs \(({\perp },{\perp },p_1(\kappa ),p_2(\kappa ))\), where \(p_1\) and \(p_2\) may be any polynomial functions.
-
\(\mathsf {Vote}( pk , nc ,v,\kappa )\) selects a nonce r uniformly at random from \(\mathbb Z_{2^\kappa }\) and outputs (r, v).
-
\(\mathsf {Tally}( sk , nc , \mathfrak {bb},\kappa )\) computes a vector \(\mathbf{v}\) of length \( nc \), such that \(\mathbf{v}\) is a tally of the votes on \(\mathfrak {bb}\) for which the nonce is in \(\mathbb Z_{2^\kappa }\), and outputs \((\mathbf{v},{\perp })\).
-
\(\mathsf {Verify}( pk ,\mathfrak {bb}, nc ,\mathbf{v}, pf ,\kappa )\) outputs 1 if \((\mathbf{v}, pf ) = \mathsf {Tally}({\perp }, nc , \mathfrak {bb},\kappa )\), and 0 otherwise.
Intuitively, election scheme \(\mathsf {Nonce}\) ensures verifiability because voters can use their nonce to check that their ballot is recorded (individual verifiability) and anyone can recompute the election outcome to check that it corresponds to votes expressed in recorded ballots (universal verifiability).
Proposition 6
([36]). Election scheme with external authentication \(\mathsf {Nonce}\) satisfies \(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Ext}\) and \(\mathsf {Exp}\text {-}\mathsf {UV}\text {-}\mathsf {Ext}\).
Hence, by Theorem 5, we have the following result.
Corollary 7
Let \(\varOmega \) be a digital signature scheme, \(\varSigma \) be a sigma protocol for relation \(R(\mathsf {Nonce},\varOmega )\), and \(\mathcal H\) be a random oracle. Suppose \(\varOmega \) satisfies strong unforgeability and \(\varSigma \) satisfies special soundness and special honest verifier zero-knowledge. Election scheme with internal authentication  satisfies \(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Int}\), \(\mathsf {Exp}\text {-}\mathsf {UV}\text {-}\mathsf {Int}\), and \(\mathsf {Exp}\text {-}\mathsf {EV}\text {-}\mathsf {Int}\).
satisfies \(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Int}\), \(\mathsf {Exp}\text {-}\mathsf {UV}\text {-}\mathsf {Int}\), and \(\mathsf {Exp}\text {-}\mathsf {EV}\text {-}\mathsf {Int}\).
Clearly election scheme Nonce does not satisfy ballot secrecy.
6 Case Study: A Secret, Verifiable Election Scheme with Internal Authentication
Helios is an open-source, web-based electronic voting system which has been used in binding elections. The International Association of Cryptologic Research has used Helios annually since 2010 to elect board members [4, 18], the ACM used Helios for their 2014 general election [40], the Catholic University of Louvain used Helios to elect the university president in 2009 [2], and Princeton University has used Helios since 2009 to elect student governments. Informally, Helios can be modelled as the following election scheme with external authentication:
-
\(\mathsf {Setup}\) generates a key pair for an asymmetric homomorphic encryption scheme, proves correct key generation in zero-knowledge, and outputs the public key coupled with the proof.
-
\(\mathsf {Vote}\) encrypts the vote, proves correct ciphertext construction and that the vote is selected from the sequence of candidates (both in zero-knowledge), and outputs the ciphertext coupled with the proof.
-
\(\mathsf {Tally}\) proceeds as follows. First, any ballots on the bulletin board for which proofs do not hold are discarded. Secondly, the ciphertexts in the remaining ballots are homomorphically combined, the homomorphic combination is decrypted to reveal the election outcome, and correctness of decryption is proved in zero-knowledge. Finally, the election outcome and proof of correct decryption are output.
-
\(\mathsf {Verify}\) recomputes the homomorphic combination, checks the proofs, and outputs 1 if these checks succeed and 0 otherwise.
The original scheme [2] is known to be vulnerable to attacks against ballot secrecy and verifiability,Footnote 8 and defences against those attacks have been proposed [7, 15, 32, 35]. We adopt the formal definition of a Helios variant by Smyth et al. [36], which adopts non-malleable ballots [32, 37] and uses the Fiat–Shamir transformation with statements in hashes [7] to defend against those attacks. Henceforth, we write Helios’16 to refer to that formalisation.
Using our construction we derive an election scheme with internal authentication from Helios’16 and prove privacy and verifiability using our results.
Theorem 8
Let \(\varOmega \) be a digital signature scheme, \(\varSigma \) be a sigma protocol for relation \(R(\text {Helios'16},\varOmega )\), and \(\mathcal H\) be a random oracle. Suppose \(\varOmega \) satisfies strong unforgeability and \(\varSigma \) satisfies special soundness and special honest verifier zero-knowledge. Election scheme with internal authentication  satisfies \(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Int}\), \(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Int}\), \(\mathsf {Exp}\text {-}\mathsf {UV}\text {-}\mathsf {Int}\), and \(\mathsf {Exp}\text {-}\mathsf {EV}\text {-}\mathsf {Int}\).
satisfies \(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Int}\), \(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Int}\), \(\mathsf {Exp}\text {-}\mathsf {UV}\text {-}\mathsf {Int}\), and \(\mathsf {Exp}\text {-}\mathsf {EV}\text {-}\mathsf {Int}\).
Proof
Helios’16 satisfies \(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Ext}\), \(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Ext}\), and \(\mathsf {Exp}\text {-}\mathsf {UV}\text {-}\mathsf {Ext}\) [32, 36], \(\mathsf {FS}(\varSigma ,\mathcal H)\) satisfies zero-knowledge [7], and we conclude by Theorems 2 and 5. \(\square \)
Comparison with Helios-C. Schemes derived from Helios using our construction are similar to Helios-C [13, 14]. Indeed, they use ballots that include a Helios ballot and a signature on that Helios ballot. The schemes derived by our construction also include proofs of correct construction, unlike Helios-C. We will see that this distinction is crucial to ensure ballot secrecy.
Cortier et al. [13, Sect. 5] analysed Helios-C using the definition of ballot secrecy by Bernhard et al. [7]. That definition assumes “ballots are recorded-as-cast, i.e., cast ballots are preserved with integrity through the ballot collection process” [32, Sect. 7]. Unfortunately, ballot secrecy is not satisfied without this assumption, because Helios-C uses malleable ballots.
Remark 9
Helios-C does not satisfy \(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Int}\).
Proof sketch
An adversary can observe and block a voter’s ballot,Footnote 9 extract the underlying Helios ballot, sign that ballot, and post the ballot and signature on the bulletin board. The adversary can then exploit the relation between ballots to recover the voter’s vote from the election outcome. (Cf. [15].) \(\square \)
 ballots extend non-malleable Helios’16 ballots with a signature and a proof demonstrating construction of both the embedded Helios’16 ballot and signature, thus,
ballots extend non-malleable Helios’16 ballots with a signature and a proof demonstrating construction of both the embedded Helios’16 ballot and signature, thus,  uses non-malleable ballots, so it is not similarly effected.
uses non-malleable ballots, so it is not similarly effected.
Beyond secrecy, Smyth et al. [36] have shown that Helios-C does not satisfy \(\mathsf {Exp}\text {-}\mathsf {UV}\text {-}\mathsf {Int}\). Hence, we improve upon Helios-C by satisfying \(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Ext}\) and \(\mathsf {Exp}\text {-}\mathsf {UV}\text {-}\mathsf {Int}\).
Our results can also be applied to the variant of Helios that applies a mixnet to encrypted votes and decrypts the mixed encrypted votes to reveal the outcome [1, 9], rather than homomorphically combining encrypted votes and decrypting the homomorphic combination to reveal the outcome. Tsoukalas et al. [41] released Zeus as a fork of Helios spliced with mixnet code to derive an implementation of that variant, and Yingtong Li released helios-server-mixnet as an extension of Zeus with threshold asymmetric encryption.Footnote 10 We could use our construction to derive an election scheme with internal authentication from the mixnet variant of Helios and use our privacy and verifiability results to prove security. Since the ideas remain the same, we do not pursue further details.
7 Conclusion
This work was initiated by a desire to eliminate trust assumptions placed upon the operators of external authentication services. Cortier et al. made progress in this direction with Helios-C, which builds upon Helios by signing ballots. We discovered that Helios-C does not satisfy ballot secrecy in the presence of an adversary that controls the bulletin board or the communication channel, and it is known that verifiability is not satisfied either. We realised that proving correct construction of both the Helios ballot and the signature suffices for non-malleability. This prompted the design of our construction and led to the accompanying security proofs that it produces voting systems satisfying ballot secrecy and verifiability. Finally, we demonstrated the applicability of our results by applying our construction to the Helios voting system. The next step would be to select a suitable sigma protocol and signature scheme to instantiate our construction concretely. And an interesting and useful direction for future work will be to consider, in general, the practical challenges of implementing our construction efficiently.
Notes
- 1.
Meyer and Smyth describe the application of OAuth in Helios [23].
- 2.
- 3.
Some voting systems permit the tallier’s role to be distributed amongst several talliers. For simplicity, we consider only a single tallier in this paper.
- 4.
Let \(A(x_1,\dots ,x_n; r)\) denote the output of probabilistic algorithm A on inputs \(x_1,\dots ,x_n\) and random coins r. Let \(A(x_1,\dots ,x_n)\) denote \(A(x_1,\dots ,x_n;r)\), where r is chosen uniformly at random. And let \(\leftarrow \) denote assignment. Moreover, let \(\langle x \rangle \) denote an optional input and \(\mathbf{v}[v]\) denote component v of vector \(\mathbf{v}\).
- 5.
Let \(\mathsf {FS}(\varSigma ,\mathcal H)\) denote the non-interactive proof system derived by application of the Fiat-Shamir transformation to sigma protocol \(\varSigma \) and hash function \(\mathcal H\).
- 6.
We omit a formal definition of asymmetric encryption for brevity.
- 7.
We adopt the formal definition of comparison based non-malleability under chosen plaintext attack, which coincides with indistinguishability under a parallel chosen-ciphertext attack (\(\textsf {IND}{\text {-}}\textsf {PA0}\)) [3]. We omit formal security definitions for brevity.
- 8.
- 9.
Ballot blocking violates the recorded-as-cast assumption used in Cortier et al.’s proof.
- 10.
Smyth [34] shows that vulnerabilities in Helios cause vulnerabilities in implementations of the mixnet variant and proves verifiability is satisfied when a fix is applied.
- 11.
Oracles may access game parameters, e.g., \( pk \).
- 12.
Function \( correct\text {-}outcome \) uses a counting quantifier [31] denoted \(\exists ^{=}\). Predicate \((\exists ^{=\ell } x : P(x))\) holds exactly when there are \(\ell \) distinct values for x such that P(x) is satisfied. Variable x is bound by the quantifier, whereas \(\ell \) is free.
References
Adida, B.: Helios: web-based open-audit voting. In: USENIX Security 2008: 17th USENIX Security Symposium, pp. 335–348. USENIX Association (2008)
Adida, B., Marneffe, O., Pereira, O., Quisquater, J.: Electing a university president using open-audit voting: analysis of real-world use of Helios. In: EVT/WOTE 2009: Electronic Voting Technology Workshop/Workshop on Trustworthy Elections. USENIX Association (2009)
Bellare, M., Sahai, A.: Non-malleable encryption: equivalence between two notions, and an indistinguishability-based characterization. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 519–536. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48405-1_33
Benaloh, J., Vaudenay, S., Quisquater, J.: Final report of IACR electronic voting committee. International Association for Cryptologic Research, September 2010. https://iacr.org/elections/eVoting/finalReportHelios_2010-09-27.html
Bernhard, D., Cortier, V., Galindo, D., Pereira, O., Warinschi, B.: SoK: a comprehensive analysis of game-based ballot privacy definitions. In: S&P 2015: 36th Security and Privacy Symposium. IEEE Computer Society (2015)
Bernhard, D., Cortier, V., Pereira, O., Smyth, B., Warinschi, B.: Adapting Helios for provable ballot privacy. In: Atluri, V., Diaz, C. (eds.) ESORICS 2011. LNCS, vol. 6879, pp. 335–354. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-23822-2_19
Bernhard, D., Pereira, O., Warinschi, B.: How not to prove yourself: pitfalls of the Fiat-Shamir heuristic and applications to Helios. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 626–643. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34961-4_38
Bernhard, D., Pereira, O., Warinschi, B.: On necessary and sufficient conditions for private Ballot submission. Cryptology ePrint Archive, Report 2012/236 (version 20120430:154117b) (2012)
Bulens, P., Giry, D., Pereira, O.: Running mixnet-based elections with Helios. In: EVT/WOTE 2011: Electronic Voting Technology Workshop/Workshop on Trustworthy Elections. USENIX Association (2011)
Bundesverfassungsgericht (Germany’s Federal Constitutional Court): Use of voting computers in 2005 Bundestag election unconstitutional. Press release 19/2009, March 2009
Cortier, V., Galindo, D., Glondu, S., Izabachene, M.: A generic construction for voting correctness at minimum cost - application to Helios. Cryptology ePrint Archive, Report 2013/177 (version 20130521:145727) (2013)
Cortier, V., Galindo, D., Glondu, S., Izabachene, M.: Distributed elgamal à la pedersen: application to Helios. In: WPES 2013: Workshop on Privacy in the Electronic Society, pp. 131–142. ACM Press (2013)
Cortier, V., Galindo, D., Glondu, S., Izabachène, M.: Election verifiability for Helios under weaker trust assumptions. In: Kutyłowski, M., Vaidya, J. (eds.) ESORICS 2014 Part II. LNCS, vol. 8713, pp. 327–344. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-11212-1_19
Cortier, V., Galindo, D., Glondu, S., Izabachène, M.: Election verifiability for Helios under weaker trust assumptions. Technical report RR-8555, INRIA (2014)
Cortier, V., Smyth, B.: Attacking and fixing Helios: an analysis of ballot secrecy. In: CSF 2011: 24th Computer Security Foundations Symposium, pp. 297–311. IEEE Computer Society (2011)
Gonggrijp, R., Hengeveld, W.J.: Studying the Nedap/Groenendaal ES3B voting computer: a computer security perspective. In: EVT 2007: Electronic Voting Technology Workshop. USENIX Association (2007)
Gumbel, A.: Steal This Vote: Dirty Elections and the Rotten History of Democracy in America. Nation Books, New York (2005)
Haber, S., Benaloh, J., Halevi, S.: The Helios e-voting demo for the IACR. International Association for Cryptologic Research, May 2010. https://iacr.org/elections/eVoting/heliosDemo.pdf
Jones, D.W., Simons, B.: Broken ballots: will your vote count? CSLI Lecture Notes, vol. 204. Stanford University, Center for the Study of Language and Information (2012)
Juels, A., Catalano, D., Jakobsson, M.: Coercion-resistant electronic elections. In: Chaum, D., Jakobsson, M., Rivest, R.L., Ryan, P.Y.A., Benaloh, J., Kutylowski, M., Adida, B. (eds.) Towards Trustworthy Elections. LNCS, vol. 6000, pp. 37–63. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-12980-3_2
Kiayias, A., Zacharias, T., Zhang, B.: End-to-end verifiable elections in the standard model. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015 Part II. LNCS, vol. 9057, pp. 468–498. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_16
Lijphart, A., Grofman, B.: Choosing an Electoral System: Issues and Alternatives. Praeger, New York (1984)
Meyer, M., Smyth, B.: An attack against the Helios election system that exploits re-voting. arXiv, Report 1612.04099 (2017)
Organization for Security and Co-operation in Europe: Document of the Copenhagen Meeting of the Conference on the Human Dimension of the CSCE (1990)
Organization of American States: American Convention on Human Rights, “Pact of San Jose, Costa Rica” (1969)
Pereira, O.: Internet voting with Helios. In: Real-World Electronic Voting: Design, Analysis and Deployment, Chap. 11. CRC Press (2016)
Quaglia, E.A., Smyth, B.: A short introduction to secrecy and verifiability for elections. arXiv, Report 1702.03168 (2017)
Quaglia, E.A., Smyth, B.: Authentication with weaker trust assumptions for voting systems (2018). https://bensmyth.com/publications/2018-voting-authentication/
Quaglia, E.A., Smyth, B.: Secret, verifiable auctions from elections. Cryptology ePrint Archive, Report 2015/1204 (2018)
Saalfeld, T.: On dogs and whips: recorded votes. In: Döring, H. (ed.) Parliaments and Majority Rule in Western Europe, Chap. 16. St. Martin’s Press (1995)
Schweikardt, N.: Arithmetic, first-order logic, and counting quantifiers. ACM Trans. Comput. Logic 6(3), 634–671 (2005)
Smyth, B.: Ballot secrecy: security definition, sufficient conditions, and analysis of Helios. Cryptology ePrint Archive, Report 2015/942 (2018)
Smyth, B.: A foundation for secret, verifiable elections (2018). https://bensmyth.com/publications/2018-secrecy-verifiability-elections-tutorial/
Smyth, B.: Verifiability of Helios mixnet. In: Voting 2018: 3rd Workshop on Advances in Secure Electronic Voting. LNCS, Springer (2018)
Smyth, B., Bernhard, D.: Ballot secrecy and ballot independence coincide. In: Crampton, J., Jajodia, S., Mayes, K. (eds.) ESORICS 2013. LNCS, vol. 8134, pp. 463–480. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40203-6_26
Smyth, B., Frink, S., Clarkson, M.R.: Election Verifiability: Cryptographic Definitions and an Analysis of Helios, Helios-C, and JCJ. Cryptology ePrint Archive, Report 2015/233 (2017)
Smyth, B., Hanatani, Y., Muratani, H.: NM-CPA secure encryption with proofs of plaintext knowledge. In: Tanaka, K., Suga, Y. (eds.) IWSEC 2015. LNCS, vol. 9241, pp. 115–134. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-22425-1_8
Smyth, B., Pironti, A.: Truncating TLS Connections to Violate Beliefs in Web Applications. In: WOOT 2013: 7th USENIX Workshop on Offensive Technologies. USENIX Association (2013). First Appeared at Black Hat USA 2013
Springall, D., Finkenauer, T., Durumeric, Z., Kitcat, J., Hursti, H., MacAlpine, M., Halderman, J.A.: Security analysis of the estonian internet voting system. In: CCS 2014: 21st ACM Conference on Computer and Communications Security, pp. 703–715. ACM Press (2014)
Staff, C.: ACM’s 2014 General Election: Please Take This Opportunity to Vote. Commun. ACM 57(5), 9–17 (2014)
Tsoukalas, G., Papadimitriou, K., Louridas, P., Tsanakas, P.: From Helios to Zeus. J. Elect. Technol. Syst. 1(1), 1–17 (2013)
United Nations: Universal Declaration of Human Rights (1948)
Wolchok, S., Wustrow, E., Halderman, J.A., Prasad, H.K., Kankipati, A., Sakhamuri, S.K., Yagati, V., Gonggrijp, R.: Security analysis of India’s electronic voting machines. In: CCS 2010: 17th ACM Conference on Computer and Communications Security, pp. 1–14. ACM Press (2010)
Wolchok, S., Wustrow, E., Isabel, D., Halderman, J.A.: Attacking the Washington, D.C. internet voting system. In: Keromytis, A.D. (ed.) FC 2012. LNCS, vol. 7397, pp. 114–128. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32946-3_10
Acknowledgements
In the context of [36], Smyth conceived the fundamental ideas of our construction for election schemes with internal authentication. In addition, Smyth discovered that Helios-C does not satisfy ballot secrecy, whilst analysing election verifiability. Smyth and his co-authors, Frink & Clarkson, decided not to publish these results. This paper builds upon those unpublished results and we are grateful to Frink and Clarkson for their part in inspiring this line of work.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Ballot Privacy: Definitions and Proofs
We recall Smyth’s definition of ballot secrecy for election schemes with external authentication (Definition 6), and present a natural, straightforward extension of that definition to capture ballot secrecy for election schemes with internal authentication (Definition 7). Our definitions both use predicate \( balanced \) such that \( balanced (\mathfrak {bb}, nc ,B)\) holds when: for all votes \(v\in \{1,\dots , nc \}\) we have \(|\{b \mid b \in \mathfrak {bb}\wedge \exists v_1 \mathrel . (b,v,v_1) \in B\}| = |\{b \mid b \in \mathfrak {bb}\wedge \exists v_0 \mathrel . (b,v_0,v) \in B\}|\). Intuitively, the definitions challenge an adversary to determine whether the left-right oracle produces ballots for “left” or “right” inputs, by giving the adversary the oracle’s outputs, as well as the election outcome and tallying proof. The definitions prevent the adversary from trivially distinguishing ballots by requiring predicate \( balanced \) to hold.
Definition 6
(\(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Ext}\) [32]). Let \(\varGamma = (\mathsf {Setup}, \mathsf {Vote}, \mathsf {Tally}, \mathsf {Verify})\) be an election scheme with external authentication, \(\mathcal {A}\) be an adversary, \(\kappa \) be a security parameter, and \(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Ext}(\varGamma ,\mathcal {A},\kappa )\) be the following game.

Oracle \(\mathcal O_{}\) is defined as follows:Footnote 11
-
\(\mathcal O_{}(v_0,v_1)\) computes if \(v_0,v_1\in \{1, \ldots , nc \}\) then
 .
.
We say \(\varGamma \) satisfies \(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Ext}\), if for all probabilistic polynomial-time adversaries \(\mathcal {A}\), there exists a negligible function \(\mathsf {negl}\), such that for all security parameters \(\kappa \), we have \(\mathsf {Succ}(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Ext}(\varGamma , \mathcal {A}, \kappa )) \le \frac{1}{2}+\mathsf {negl}(\kappa )\).
Definition 7
(\(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Int}\)). Let \(\varGamma = (\mathsf {Setup}, \mathsf {Register}, \mathsf {Vote}, \mathsf {Tally}, \mathsf {Verify})\) be an election scheme with internal authentication, \(\mathcal {A}\) be an adversary, \(\kappa \) be a security parameter, and \(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Int}(\varGamma ,\mathcal {A},\kappa )\) be the following game.

Oracle \(\mathcal O_{}\) is defined as follows:
-
\(\mathcal O_{}(i,v_0,v_1)\) computes if \(v_0,v_1\in \{1, \ldots , nc \} \wedge i\not \in R\) then
 ; and
; and -
\(\mathcal O_{}(i)\) computes if \(i\not \in R\) then
 .
.
We say \(\varGamma \) satisfies \(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Int}\), if for all probabilistic polynomial-time adversaries \(\mathcal {A}\), there exists a negligible function \(\mathsf {negl}\), such that for all security parameters \(\kappa \), we have \(\mathsf {Succ}(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Int}(\varGamma ,\mathcal {A}, \kappa )) \le \frac{1}{2}+ \mathsf {negl}(\kappa )\).
Game \(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Int}\) extends \(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Ext}\) to take credentials into account. In particular, the challenger constructs \( nv \) credentials, where \( nv \) is chosen by the adversary. These credentials are used to construct ballots and for tallying. Public and private credentials are available to the adversary. Albeit, the oracle will only reveal a private credential if it has not used it to construct a ballot. Moreover, the oracle may only use a private credential to construct a ballot if it has not revealed it nor constructed a previous ballot with it.
Proof of Theorem 2
Suppose \(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Int}\) is not satisfied by  , i.e., there exists a adversary \(\mathcal {A}\) such that for all negligible functions \(\mathsf {negl}\) there exists a security parameter \(\kappa \) and
, i.e., there exists a adversary \(\mathcal {A}\) such that for all negligible functions \(\mathsf {negl}\) there exists a security parameter \(\kappa \) and  . We construct an adversary \(\mathcal {B}\) against \(\varGamma \) from \(\mathcal {A}\).
. We construct an adversary \(\mathcal {B}\) against \(\varGamma \) from \(\mathcal {A}\).
Let \(\varGamma = (\mathsf {Setup}_\varGamma , \mathsf {Vote}_\varGamma , \mathsf {Tally}_\varGamma , \mathsf {Verify}_\varGamma )\), \(\varOmega = (\mathsf {Gen}_\varOmega , \mathsf {Sign}_\varOmega , \mathsf {Verify}_\varOmega )\), \(\mathsf {FS}(\varSigma ,\mathcal H) = (\mathsf {Prove}_\varSigma , \mathsf {Verify}_\varSigma )\) , and 
 . By [7, Theorem 1], non-interactive proof system \((\mathsf {Prove}_\varSigma , \mathsf {Verify}_\varSigma )\) satisfies zero-knowledge, i.e., there exists a simulator for \((\mathsf {Prove}_\varSigma , \mathsf {Verify}_\varSigma )\). Let \(\mathcal S\) be such a simulator. We define \(\mathcal {B}\) as follows:
. By [7, Theorem 1], non-interactive proof system \((\mathsf {Prove}_\varSigma , \mathsf {Verify}_\varSigma )\) satisfies zero-knowledge, i.e., there exists a simulator for \((\mathsf {Prove}_\varSigma , \mathsf {Verify}_\varSigma )\). Let \(\mathcal S\) be such a simulator. We define \(\mathcal {B}\) as follows:
-
\(\mathcal {B}( pk ,\kappa )\) computes \( nv \leftarrow \mathcal {A}( pk ,\kappa )\); for \(1 \le i \le nv \) do
 \( nc \leftarrow \mathcal {A}( pd _1,\dots , pd _{ nv })\) and outputs \( nc \).
\( nc \leftarrow \mathcal {A}( pd _1,\dots , pd _{ nv })\) and outputs \( nc \). -
\(\mathcal {B}()\) computes \(R\leftarrow \emptyset ; \mathfrak {bb}\leftarrow \mathcal {A}^{\mathcal O_{}}(); \mathfrak {bb}\leftarrow \mathsf {auth}(\mathfrak {bb},\{ pd _1,\dots , pd _{ nv }\})\) and outputs \(\mathfrak {bb}\), handling oracle calls from \(\mathcal {A}\) as follows. Given an oracle call \(\mathcal O_{}(i,v_0,v_1)\) such that \(v_0,v_1\in \{1, \ldots , nc \} \wedge i\not \in R\), adversary \(\mathcal {B}\) computes \(b\leftarrow \mathcal O_{}(v_0,v_1); \sigma \leftarrow \mathsf {Sign}_\varOmega ( d _i, b); \tau \leftarrow \mathcal S(( pk ,b,\sigma , nc ,\kappa ),\kappa ); R\leftarrow R \cup \{i\}\) and returns \(( pd _i,b,\sigma ,\tau )\) to \(\mathcal {A}\). Moreover, given an oracle call \(\mathcal O_{}(i)\) such that \(i\not \in R\), adversary \(\mathcal {B}\) computes \(R\leftarrow R \cup \{i\}\) and returns \( d _i\) to \(\mathcal {A}\).
-
\(\mathcal {B}(\mathbf{v}, pf )\) computes \(g\leftarrow \mathcal {A}(\mathbf{v}, pf )\) and outputs g.
We prove that \(\mathcal {B}\) wins \(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Ext}\) against \(\varGamma \).
Suppose \(( pk , sk , mb , mc )\) is an output of \(\mathsf {Setup}_\varGamma (\kappa )\) and \( nc \) is an output of \(\mathcal {B}( pk ,\kappa )\). It is trivial to see that \(\mathcal {B}( pk ,\kappa )\) simulates \(\mathcal {A}\)’s challenger to \(\mathcal {A}\). Let \(\beta \) be a bit. Suppose \(\mathfrak {bb}\) is an output of \(\mathcal {B}()\). Since \(\mathcal S\) is a simulator for \((\mathsf {Prove}_\varSigma , \mathsf {Verify}_\varSigma )\), we have \(\mathcal {B}()\) simulates \(\mathcal {A}\)’s challenger to \(\mathcal {A}\). In particular, \(\mathcal {B}()\) simulates oracle calls \(\mathcal O_{}(i,v_0,v_1)\). Indeed, adversary \(\mathcal {B}\) computes \( b\leftarrow \mathcal O_{}(v_0,v_1);\sigma \leftarrow \mathsf {Sign}_\varOmega ( d _i, b); \tau \leftarrow \mathcal S(( pk ,b,\sigma , nc ,\kappa ),\kappa ) \), which, by definition of \(\mathcal {B}\)’s oracle, is equivalent to \( b\leftarrow \mathsf {Vote}_\varGamma ( pk , nc ,v_\beta , \kappa ); \sigma \leftarrow \mathsf {Sign}_\varOmega ( d _i, b); \tau \leftarrow \mathcal S(( pk ,b,\sigma , nc ,\kappa ),\kappa ) \). And \(\mathcal {A}\)’s oracle computes \(b\leftarrow \mathsf {Vote}( d _i, pk , nc ,v_\beta , \kappa )\), i.e., \( b \leftarrow \mathsf {Vote}_\varGamma ( pk , nc , v_\beta , \kappa ;r); \sigma \leftarrow \mathsf {Sign}_\varOmega ( d _i, b; r'); \tau \leftarrow \mathsf {Prove}_\varSigma (( pk , b, \sigma , nc , \kappa ),(v_\beta ,r, d _i,r'),\kappa ) \), where r and \(r'\) are coins chosen uniformly at random. Hence, computations of b, \(\sigma \) and \(\tau \) by \(\mathcal {B}\) and \(\mathcal {A}\)’s oracle are equivalent, with overwhelming probability. Suppose \((\mathbf{v}, pf )\) is an output of \(\mathsf {Tally}_\varGamma ( sk ,\mathfrak {bb},{} nc ,{}\kappa )\) and g is an output of \(\mathcal {B}(\mathbf{v}, pf )\). We have \(\mathcal {B}(\mathbf{v}, pf )\) simulates \(\mathcal {A}\)’s challenger to \(\mathcal {A}\), because outputs of \(\mathsf {Tally}_\varGamma ( sk ',\mathsf {auth}(\mathfrak {bb}',L),{} nc ',{}\kappa ')\) and \(\mathsf {Tally}( sk ', nc ',\mathfrak {bb}',L,\kappa ')\) are indistinguishable for all \( sk '\), \(\mathfrak {bb}'\), L, \( nc '\), and \(\kappa '\). Indeed, \(\mathsf {Tally}\) computes \((\mathbf{v}', pf ') \leftarrow \mathsf {Tally}_\varGamma ( sk ', \mathsf {auth}(\mathfrak {bb}',L),{} nc ',{}\kappa ')\) and outputs \((\mathbf{v}', pf ')\). Since adversary \(\mathcal {B}\) simulates \(\mathcal {A}\)’s challenger, with overwhelming probability. It follows that \(\mathcal {B}\) determines \(\beta \) correctly with the same success as \(\mathcal {A}\) with overwhelming probability. Hence, \(\mathcal {B}\) wins \(\mathsf {Ballot}\text {-}\mathsf {Secrecy}\text {-}\mathsf {Ext}(\varGamma ,\mathcal {A}, \kappa )\), with overwhelming probability, deriving a contradiction and concluding our proof. \(\square \)
B Election Verifiability: Definitions and Proofs
1.1 B.1 Individual Verifiability
Definition 8
(\(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Ext}\) [36]). Let \(\varGamma = (\mathsf {Setup}, \mathsf {Vote}, \mathsf {Tally}, \mathsf {Verify})\) be an election scheme with external authentication, \(\mathcal {A}\) be an adversary, \(\kappa \) be a security parameter, and \(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Ext}(\varGamma , \mathcal {A}, \kappa )\) be the following game.

We say \(\varGamma \) satisfies \(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Ext}\), if for all probabilistic polynomial-time adversaries \(\mathcal {A}\), there exists a negligible function \(\mathsf {negl}\), such that for all security parameters \(\kappa \), we have \(\mathsf {Succ}(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Ext}(\varGamma , \mathcal {A}, \kappa ))\le \mathsf {negl}(\kappa )\).
Definition 9
(\(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Int}\) [36]). Let \(\varGamma = (\mathsf {Setup}, \mathsf {Register}, \mathsf {Vote}, \mathsf {Tally}, \mathsf {Verify})\) be an election scheme with external authentication, \(\mathcal {A}\) be an adversary, \(\kappa \) be a security parameter, and \(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Int}(\varPi , \mathcal {A}, \kappa )\) be the following game.

Oracle \(C\) is defined such that \(C(i)\) computes \( Crpt \leftarrow Crpt \cup \{d_i\}\) and outputs \(d_i\), where \(1\le i \le nv \).
We say \(\varGamma \) satisfies \(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Int}\), if for all probabilistic polynomial-time adversaries \(\mathcal {A}\), there exists a negligible function \(\mathsf {negl}\), such that for all security parameters \(\kappa \), we have \(\mathsf {Succ}(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Int}(\varPi , \mathcal {A}, \kappa ))\le \mathsf {negl}(\kappa )\).
Lemma 10
Let \(\varGamma = (\mathsf {Setup}, \mathsf {Register}, \mathsf {Vote}, \mathsf {Tally}, \mathsf {Verify})\) be an election scheme with external authentication, \(\varOmega = (\mathsf {Gen}, \mathsf {Sign}, \mathsf {Verify})\) be a digital signature scheme, \(\varSigma \) be a sigma protocol for relation \(R(\varGamma ,\varOmega )\), and \(\mathcal H\) be a hash function. Suppose \(\varOmega \) satisfies strong unforgeability. We have  satisfies \(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Int}\).
satisfies \(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Int}\).
Proof
Suppose  does not satisfy \(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Int}\). Hence, there exists a PPT adversary \(\mathcal {A}\), such that for all negligible functions \(\mathsf {negl}\), there exists a security parameter \(\kappa \) and
does not satisfy \(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Int}\). Hence, there exists a PPT adversary \(\mathcal {A}\), such that for all negligible functions \(\mathsf {negl}\), there exists a security parameter \(\kappa \) and  . We construct the following adversary \(\mathcal {B}\) against strong unforgeability from \(\mathcal {A}\):
. We construct the following adversary \(\mathcal {B}\) against strong unforgeability from \(\mathcal {A}\):

where \(C(i)\) outputs \( d _i\) if \(i\not =i^*\) and aborts otherwise. We prove that \(\mathcal {B}\) wins strong unforgeability against \(\varOmega \).
Since adversary \(\mathcal {B}\) chooses \(i^*\) uniformly at random and independently of adversary \(\mathcal {A}\), and since \(\mathcal {A}\) is a winning adversary, hence, does not corrupt at least two distinct credentials, we have that \(\mathcal {B}\) aborts with a probability upper-bounded by \(\frac{ nv -2}{ nv }\). Let us consider the probability that \(\mathcal {B}\) wins, when there is no abort. Suppose \(( pd , d )\) is an output of \(\mathsf {Gen}(\kappa )\), \(( pk , nv )\) is an output of \(\mathcal {A}(\kappa )\), and \(i^*\) is chosen uniformly at random from \(\{1,\dots , nv \}\). Further suppose \(( pd _i, d _i)\) is an output of  for each \(i \in \{1,\dots , nv \}\setminus \{i^*\}\). It is straightforward to see that \(\mathcal {B}\) simulates the challenger and oracle in \(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Int}\) to \(\mathcal {A}\). Suppose \(( nc , v, v', j, k)\) is an output of \(\mathcal {A}^{C}(\{ pd _1,\dots , pd _{i^*-1}, pd , pd _{i^*+1},\dots , pd _{ nv }\})\). Since \(\mathcal {A}\) is a winning adversary, outputs of \(\mathsf {Vote}( d _j, pk , nc ,v,\kappa )\) and \(\mathsf {Vote}( d _k, pk , nc ,v', \kappa )\) collide with non-negligible probability. Hence, if \(i^*=k\), then \(\mathsf {Vote}( d _j, pk , nc ,v, \kappa )\) outputs \(( pd _j, b, \sigma , \tau )\) such that \(\sigma \) is a signature on b with respect to private key \( d _{i^*}\), otherwise \((i^*=j)\), \(\mathsf {Vote}( d _k, pk , nc ,v',\kappa )\) outputs \(( pd _k,b,\sigma ,\tau )\) such that \(\sigma \) is a signature on b with respect to private key \( d _{i^*}\). Thus, \(\mathsf {Succ}(\mathsf {Exp}\text {-}\mathsf {StrongSign}(\varGamma , \mathcal {B},\kappa ))\) is at least
for each \(i \in \{1,\dots , nv \}\setminus \{i^*\}\). It is straightforward to see that \(\mathcal {B}\) simulates the challenger and oracle in \(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Int}\) to \(\mathcal {A}\). Suppose \(( nc , v, v', j, k)\) is an output of \(\mathcal {A}^{C}(\{ pd _1,\dots , pd _{i^*-1}, pd , pd _{i^*+1},\dots , pd _{ nv }\})\). Since \(\mathcal {A}\) is a winning adversary, outputs of \(\mathsf {Vote}( d _j, pk , nc ,v,\kappa )\) and \(\mathsf {Vote}( d _k, pk , nc ,v', \kappa )\) collide with non-negligible probability. Hence, if \(i^*=k\), then \(\mathsf {Vote}( d _j, pk , nc ,v, \kappa )\) outputs \(( pd _j, b, \sigma , \tau )\) such that \(\sigma \) is a signature on b with respect to private key \( d _{i^*}\), otherwise \((i^*=j)\), \(\mathsf {Vote}( d _k, pk , nc ,v',\kappa )\) outputs \(( pd _k,b,\sigma ,\tau )\) such that \(\sigma \) is a signature on b with respect to private key \( d _{i^*}\). Thus, \(\mathsf {Succ}(\mathsf {Exp}\text {-}\mathsf {StrongSign}(\varGamma , \mathcal {B},\kappa ))\) is at least  , which is non-negligible. \(\square \)
, which is non-negligible. \(\square \)
1.2 B.2 Universal Verifiability
External authentication. Algorithm \(\mathsf {Verify}\) is required to accept iff the election outcome is correct. The notion of a correct outcome is captured using function \( correct\text {-}outcome \), which is defined such that for all \( pk \), \( nc \), \(\mathfrak {bb}\), \(\kappa \), \(\ell \), and \(v \in \{1, \ldots , nc \}\), we have \( correct\text {-}outcome ( pk , nc ,\mathfrak {bb},\kappa )[v] = \ell \) iff \(\exists ^{=\ell } b\in \mathfrak {bb}\setminus \{\bot \} : \exists r : b=\mathsf {Vote}( pk , nc ,v,\kappa ; r) \),Footnote 12 and the produced vector is of length \( nc \). Hence, component v of vector \( correct\text {-}outcome ( pk , nc ,\mathfrak {bb},\kappa )\) equals \(\ell \) iff there exist \(\ell \) ballots on the bulletin board that are votes for candidate v. The function requires ballots to be interpreted for only one candidate, which can be ensured by injectivity.
The if requirement of universal verifiability is captured by Completeness, which stipulates that election outcomes produced by algorithm \(\mathsf {Tally}\) will actually be accepted by algorithm \(\mathsf {Verify}\). And the only if requirement is captured by Soundness, which challenges an adversary to concoct a scenario in which algorithm \(\mathsf {Verify}\) accepts, but the election outcome is not correct.
Definition 10
([36]). An election scheme with external authentication \((\mathsf {Setup}, \mathsf {Vote}, \mathsf {Tally}, \mathsf {Verify})\) satisfies Soundness, if the scheme satisfies Injectivity [36] and for all probabilistic polynomial-time adversaries \(\mathcal {A}\), there exists a negligible function \(\mathsf {negl}\), such that for all security parameters \(\kappa \), we have  .
.
An election scheme with external authentication satisfies \(\mathsf {Exp}\text {-}\mathsf {UV}\text {-}\mathsf {Ext}\), if Injectivity, Completeness and Soundness are satisfied, where formal definitions of Injectivity and Completeness appear in [36].
Internal authentication. Function \( correct\text {-}outcome \) is now modified to tally only authorised ballots: let function \( correct\text {-}outcome \) now be defined such that for all \( pk \), \( nc \), \(\mathfrak {bb}\), \(M\), \(\kappa \), \(\ell \), and \(v \in \{1,\ldots , nc \}\), we have \( correct\text {-}outcome ( pk , nc , \mathfrak {bb}, M, \kappa )[v] = \ell \) iff \(\exists ^{=\ell } b\in authorized ( pk , nc ,(\mathfrak {bb}\setminus \{\bot \}),M, \kappa ) \mathrel : \exists d , r : b=\mathsf {Vote}( d , pk , nc ,v,\kappa ; r)\). A ballot is authorised if it is constructed with a private credential from \(M\), and that private credential was not used to construct any other ballot on \(\mathfrak {bb}\). Let \( authorized \) be defined as follows: \( authorized ( pk , nc , \mathfrak {bb}, M, \kappa ) = \{b \mathrel {:}\; b \in \mathfrak {bb}\mathrel \wedge \exists pd , d , v, r \mathrel : b=\mathsf {Vote}( d , pk , nc ,v,\kappa ; r) \mathrel \wedge ( pd , d )\in M\mathrel \wedge \lnot \exists b',v',r' : b' \in (\mathfrak {bb}\setminus \{b\}) \mathrel \wedge b'=\mathsf {Vote}( d , pk , nc ,v',\kappa ; r')\} \).
Definition 11
([36]). An election scheme with internal authentication \((\mathsf {Setup}, \mathsf {Register}, \mathsf {Vote}, \mathsf {Tally}, \mathsf {Verify})\) satisfies Soundness, if the scheme satisfies Injectivity [36] and for all probabilistic polynomial-time adversaries \(\mathcal {A}\), there exists a negligible function \(\mathsf {negl}\), such that for all security parameters \(\kappa \), we have \(\Pr [( pk , nv ) \leftarrow \mathcal {A}(\kappa );\) for \(1 \le i \le nv \) do  ;
; 

 .
.
An election scheme with internal authentication satisfies \(\mathsf {Exp}\text {-}\mathsf {UV}\text {-}\mathsf {Int}\), if Injectivity, Completeness and Soundness are satisfied.
Lemma 11
Let \(\varGamma = (\mathsf {Setup}_\varGamma , \mathsf {Vote}_\varGamma , \mathsf {Tally}_\varGamma , \mathsf {Verify}_\varGamma )\) be an election scheme with external authentication, \(\varOmega = (\mathsf {Gen}_\varOmega , \mathsf {Sign}_\varOmega , \mathsf {Verify}_\varOmega )\) be a perfectly correct digital signature scheme, \(\varSigma \) be a sigma protocol for relation \(R(\varGamma ,\varOmega )\), and \(\mathcal H\) be a random oracle. Moreover, let \(\mathsf {FS}(\varSigma ,\mathcal H) = (\mathsf {Prove}_\varSigma , \mathsf {Verify}_\varSigma )\). Suppose \(\varGamma \) satisfies \(\mathsf {Exp}\text {-}\mathsf {UV}\text {-}\mathsf {Ext}\), \(\varOmega \) satisfies strong unforgeabilityand \(\varSigma \) satisfies perfect special soundness and special honest verifier zero-knowledge. Election scheme with internal authentication  satisfies \(\mathsf {Exp}\text {-}\mathsf {UV}\text {-}\mathsf {Int}\).
satisfies \(\mathsf {Exp}\text {-}\mathsf {UV}\text {-}\mathsf {Int}\).
Proof
We prove that  satisfies Injectivity, Completeness and Soundness: The proofs for Injectivity and Completeness are quite straightforward and can be found in our technical report [28].
satisfies Injectivity, Completeness and Soundness: The proofs for Injectivity and Completeness are quite straightforward and can be found in our technical report [28].
Soundness. We prove that  satisfies Soundness by contradiction. Suppose
satisfies Soundness by contradiction. Suppose  does not satisfy Soundness, i.e., there exists an adversary \(\mathcal {A}\) such that for all negligible functions \(\mathsf {negl}\) there exists a security parameter \(\kappa \) and the probability defined in Definition 11 is greater than \( \mathsf {negl}(\kappa )\). We use \(\mathcal {A}\) to construct an adversary \(\mathcal {B}\) that wins the Soundness game against \(\varGamma \).
does not satisfy Soundness, i.e., there exists an adversary \(\mathcal {A}\) such that for all negligible functions \(\mathsf {negl}\) there exists a security parameter \(\kappa \) and the probability defined in Definition 11 is greater than \( \mathsf {negl}(\kappa )\). We use \(\mathcal {A}\) to construct an adversary \(\mathcal {B}\) that wins the Soundness game against \(\varGamma \).

We prove that \(\mathcal {B}\) wins the Soundness game against \(\varGamma \).
Suppose \(( pk , nv )\) is an output of \(\mathcal {A}(\kappa )\) and \(( pd _1, d _1),\dots ,( pd _{ nv }, d _{ nv })\) are outputs of  . Let \(L= \{ pd _1,\dots , pd _{ nv }\}\) and \(M= \{( pd _1, d _1), \dots , ( pd _{ nv }, d _{ nv })\}\). Suppose \((\mathfrak {bb}, nc , \mathbf{v}, pf )\) is an output of \(\mathcal {A}(M)\). Further suppose \(( pk , nc , \mathsf {auth}(\mathfrak {bb},L), \mathbf{v}, pf )\) is an output of \(\mathcal {B}(\kappa )\). Since \(\mathcal {A}\) is a winning adversary, we have \(\mathsf {Verify}( pk , nc ,\mathfrak {bb},L, \mathbf{v}, pf ,\kappa ) = 1\), with non-negligible probability. By inspection of algorithm \(\mathsf {Verify}\), we have \(\mathsf {Verify}( pk , nc ,\mathfrak {bb},L, \mathbf{v}, pf ,\kappa ) = 1\) implies \(\mathsf {Verify}_\varGamma ( pk , \mathsf {auth}(\mathfrak {bb},L), nc , \mathbf{v}, pf , \kappa ) = 1\). Hence, it remains to show \(\mathbf{v}\ne correct\text {-}outcome ( pk , nc , \mathsf {auth}(\mathfrak {bb},L), \kappa )\), with probability greater than \(\mathsf {negl}(\kappa )\).
. Let \(L= \{ pd _1,\dots , pd _{ nv }\}\) and \(M= \{( pd _1, d _1), \dots , ( pd _{ nv }, d _{ nv })\}\). Suppose \((\mathfrak {bb}, nc , \mathbf{v}, pf )\) is an output of \(\mathcal {A}(M)\). Further suppose \(( pk , nc , \mathsf {auth}(\mathfrak {bb},L), \mathbf{v}, pf )\) is an output of \(\mathcal {B}(\kappa )\). Since \(\mathcal {A}\) is a winning adversary, we have \(\mathsf {Verify}( pk , nc ,\mathfrak {bb},L, \mathbf{v}, pf ,\kappa ) = 1\), with non-negligible probability. By inspection of algorithm \(\mathsf {Verify}\), we have \(\mathsf {Verify}( pk , nc ,\mathfrak {bb},L, \mathbf{v}, pf ,\kappa ) = 1\) implies \(\mathsf {Verify}_\varGamma ( pk , \mathsf {auth}(\mathfrak {bb},L), nc , \mathbf{v}, pf , \kappa ) = 1\). Hence, it remains to show \(\mathbf{v}\ne correct\text {-}outcome ( pk , nc , \mathsf {auth}(\mathfrak {bb},L), \kappa )\), with probability greater than \(\mathsf {negl}(\kappa )\).
By definition of function \( correct\text {-}outcome \), we have \(\mathbf{v}\) is a vector of length \( nc \) such that
Since \(\mathcal {A}\) is a winning adversary, it suffices to derive
Let set \(auth^* ( pk , nc ,\mathfrak {bb},M,\kappa )\!=\!\{b^*| ( pd , b^*, \sigma , \tau ) \in authorized ( pk , nc ,\mathfrak {bb},M,\kappa ) \}\). To prove (1), it suffices to show \(\mathsf {auth}(\mathfrak {bb},L)\setminus \{\perp \} = auth^* ( pk , nc ,\mathfrak {bb},M,\kappa )\setminus \{\perp \}\), since this would imply that \( correct\text {-}outcome \) is computed on sets of corresponding ballots in both the external and internal authentication setting.
-
\(auth^*( pk , nc ,\mathfrak {bb},M,\kappa )\setminus \{\perp \} \subseteq \mathsf {auth}(\mathfrak {bb},L)\setminus \{\perp \}\)
If \(b^* \in auth^*( pk , nc ,\mathfrak {bb},M,\kappa )\), then \(b^* \ne \ \perp \) and there exists \(b \in authorized ( pk , nc ,\mathfrak {bb},M,\kappa )\) such that (i) \(b \in \mathfrak {bb}\); (ii) \(\exists pd , d , v, r,r',r'' \mathrel : b = ( pd ,b^*,\sigma ,\tau )\), \(b^* = \mathsf {Vote}_\varGamma ( pk , nc ,v,\kappa ;r)\), \(\sigma = \mathsf {Sign}_\varOmega ( d ,b^*;r')\), and \(\tau = \mathsf {Prove}_\varSigma (( pk , b^*, \sigma , nc , \kappa ), (v, r, d , r'), \kappa ; r'')\), which – by correctness of \(\varOmega \) and completeness of \(\varSigma \) – implies \(\mathsf {Verify}_\varOmega ( pd , b^*, \sigma ) =1\) and \(\mathsf {Verify}_\varSigma (( pk , b^*, nc , \kappa ), \tau , \kappa ))=1\); (iii) \( ( pd , d )\in M\), which implies \( pd \in L\) by construction; and (iv) \(\lnot \exists b', v', r,r',r'' \mathrel : b' \in (\mathfrak {bb}\setminus \{b\}) \wedge b' = ( pd , b^{*'}, \sigma ', \tau ')\), \(b^{*'} = \mathsf {Vote}_\varGamma ( pk , nc ,v',\kappa ;r)\), \(\sigma ' = \mathsf {Sign}_\varOmega ( d ,b^{*'};r')\), and \(\tau ' = \mathsf {Prove}_\varSigma (( pk ,b^{*'}, \sigma ', nc ,\kappa ),(v',r, d ,r'),\kappa ; r'')\), which, by correctness of \(\varOmega \), implies \(\mathsf {Verify}_\varOmega ( pd , b^{*'}, \sigma ') =1\). It follows by (i)–(iv) that \(b^* \in auth^*( pk , nc ,\mathfrak {bb},M,\kappa )\) implies \(b^* \in \mathsf {auth}(\mathfrak {bb},L)\setminus \{\perp \}\).
-
\( \mathsf {auth}(\mathfrak {bb},L)\setminus \{\perp \} \subseteq auth^*( pk , nc ,\mathfrak {bb},M,\kappa )\setminus \{\perp \}\)
If \(b^* \in \mathsf {auth}(\mathfrak {bb},L)\setminus \{\perp \}\), then \(b^* \ne \ \perp \) such that (i) \(( pd , b^*, \sigma , \tau ) \in \mathfrak {bb}\); (ii) \(\mathsf {Verify}_\varOmega ( pd , b^*, \sigma ) =1\) and \(\mathsf {Verify}_\varSigma (( pk , b^*, nc , \kappa ), \tau , \kappa ))=1\), which – by the security of \(\varOmega \) and \(\varSigma \) – implies \(\exists pd , d , v, r,r',r'' \mathrel : \) \(b^* = \mathsf {Vote}_\varGamma ( pk , nc ,v,\kappa ;r)\), \(\sigma = \mathsf {Sign}_\varOmega ( d ,b^*;r')\), and \(\tau = \mathsf {Prove}_\varSigma (( pk ,b^*,\sigma , nc ,\kappa ), (v,r, d ,r'),\kappa ; r'')\). Indeed, suppose this is not true, i.e., such values do not exist. Then \((b^*, \sigma )\) and \((( pk , b^*, nc , \kappa ), \tau )\) could be used by adversaries to break the unforgeability property of \(\varOmega \) and the special soundness and special honest verifier zero-knowledge property of \(\varSigma \), respectively. Furthermore, we have (iii) \( pd \in L\), which implies \( ( pd , d )\in M\) by construction; and (iv) \(b' = ( pd , b^{*'}, \sigma ', \tau ') \notin (\mathfrak {bb}\setminus \{( pd , b^*, \sigma , \tau )\}) \wedge \mathsf {Verify}_\varOmega ( pd , b^{*'}, \sigma ') =1\), which implies \(\lnot \exists b', v', r,r',r'' \mathrel : b' \in (\mathfrak {bb}\setminus \{b\}) \wedge b' = ( pd , b^{*'}, \sigma ', \tau ')\), \(b^{*'} = \mathsf {Vote}_\varGamma ( pk , nc ,v',\kappa ;r)\), \(\sigma ' = \mathsf {Sign}_\varOmega ( d ,b^{*'};r')\), and \(\tau ' = \mathsf {Prove}_\varSigma (( pk , b^{*'}, \sigma ', nc , \kappa ), (v', r, d , r'), \kappa ; r'')\), as per definition of \( authorized \), concluding our proof. \(\square \)
1.3 B.3 Eligibility Verifiability
Definition 12
(Eligibility verifiability [36]). Let \(\varGamma = (\mathsf {Setup}, \mathsf {Register}, \mathsf {Vote}, \mathsf {Tally}, \mathsf {Verify})\) be an election scheme with internal authentication, \(\mathcal {A}\) be an adversary, \(\kappa \) be a security parameter, and \(\mathsf {Exp}\text {-}\mathsf {EV}\text {-}\mathsf {Int}(\varPi , \mathcal {A}, \kappa )\) be the following game.

Oracle \(C\) is the same oracle as in \(\mathsf {Exp}\text {-}\mathsf {IV}\text {-}\mathsf {Int}\), and oracle \(R\) is defined such that \(R(i,v, nc )\) computes \(b \leftarrow \mathsf {Vote}( d _i, pk , nc ,v,k); Rvld \leftarrow Rvld \cup \{b\}\) and outputs b.
We say \(\varGamma \) satisfies \(\mathsf {Exp}\text {-}\mathsf {EV}\text {-}\mathsf {Int}\), if for all probabilistic polynomial-time adversaries \(\mathcal {A}\), there exists a negligible function \(\mathsf {negl}\), such that for all security parameters \(\kappa \), we have \(\mathsf {Succ}(\mathsf {Exp}\text {-}\mathsf {EV}\text {-}\mathsf {Int}(\varPi , \mathcal {A}, \kappa ))\le \mathsf {negl}(\kappa )\).
Lemma 12
Let \(\varGamma = (\mathsf {Setup}_\varGamma , \mathsf {Vote}_\varGamma , \mathsf {Tally}_\varGamma , \mathsf {Verify}_\varGamma )\) be an election scheme with external authentication, \(\varOmega = (\mathsf {Gen}_\varOmega , \mathsf {Sign}_\varOmega , \mathsf {Verify}_\varOmega )\) be a digital signature scheme, \(\varSigma \) be a sigma protocol for relation \(R(\varGamma ,\varOmega )\), and \(\mathcal H\) be a hash function. Suppose \(\varSigma \) satisfies special soundness and special honest verifier zero-knowledge, and \(\varOmega \) satisfies strong unforgeability. Election scheme with internal authentication  satisfies \(\mathsf {Exp}\text {-}\mathsf {EV}\text {-}\mathsf {Int}\).
satisfies \(\mathsf {Exp}\text {-}\mathsf {EV}\text {-}\mathsf {Int}\).
Proof
Suppose  does not satisfy \(\mathsf {Exp}\text {-}\mathsf {EV}\text {-}\mathsf {Int}\), i.e., there exists an adversary \(\mathcal {A}\) such that for all negligible functions \(\mathsf {negl}\) there exists a security parameter \(\kappa \) and \(\mathsf {Succ}(\mathsf {Exp}\text {-}\mathsf {EV}\text {-}\mathsf {Int}(\varPi , \mathcal {A}, \kappa ))> \mathsf {negl}(\kappa )\). We construct the following adversary \(\mathcal {B}\) against the strong unforgeability of \(\varOmega \) from \(\mathcal {A}\).
does not satisfy \(\mathsf {Exp}\text {-}\mathsf {EV}\text {-}\mathsf {Int}\), i.e., there exists an adversary \(\mathcal {A}\) such that for all negligible functions \(\mathsf {negl}\) there exists a security parameter \(\kappa \) and \(\mathsf {Succ}(\mathsf {Exp}\text {-}\mathsf {EV}\text {-}\mathsf {Int}(\varPi , \mathcal {A}, \kappa ))> \mathsf {negl}(\kappa )\). We construct the following adversary \(\mathcal {B}\) against the strong unforgeability of \(\varOmega \) from \(\mathcal {A}\).

where oracle calls are handled as follows:
-
C(i) computes \( Crpt \leftarrow Crpt \cup \{ d _i \}\) and returns \( d _i\) if \(i\not =i^*\), and aborts otherwise.
-
\(R(i, v, nc )\) distinguishes two cases: If \(i=i^*\), then \(\mathcal {B}\) computes \(b \leftarrow \mathsf {Vote}_\varGamma ( pk , nc , v, \kappa ); \sigma \leftarrow \mathcal O_{}(b);\tau \leftarrow \mathcal S(( pk ,b,\sigma , nc ,\kappa ),\kappa )\), computes \( Rvld \leftarrow Rvld \cup \{ ( pd , b, \sigma , \tau )\}\), and returns \(( pd , b, \sigma , \tau )\), where \(\mathcal S\) is a simulator for \(\mathsf {FS}(\varSigma ,\mathcal H)\) that exists by [7, Theorem 1]. Otherwise, \(\mathcal {B}\) computes \(b \leftarrow \mathsf {Vote}( d _i, pk , nc , v, \kappa )\), \( Rvld \leftarrow Rvld \cup \{ b\}\) and returns b.
We prove that \(\mathcal {B}\) wins the strong unforgeability game against \(\varOmega \).
Let \(\kappa \) be a security parameter. Suppose \(( pd , d )\) is an output of \(\mathsf {Gen}(\kappa )\) and \(( pk , nv )\) is an output of \(\mathcal {A}(\kappa )\). Let \(i^*\) be an integer chosen uniformly at random from \(\{1, \ldots , nv \}\). Suppose \(( pd _i, d _i)\) is an output of \(\mathsf {Register}( pk ,\kappa )\), for each \(i \in \{1, \ldots , nv \}\setminus \{ i^* \} \). Let us consider an execution of \(\mathcal {A}(\{ pd _{1}, \dots , pd _{i^*-1}, pd , pd _{i^*+1}, \dots , pd _{ nv }\})\). Let \(( nc , v, i, b)\) be the output of \(\mathcal {A}\). By definition of algorithm \(\mathsf {Register}\), it is trivial to see that \(\mathcal {B}\) simulates \(\mathcal {A}\)’s challenger to \(\mathcal {A}\). Moreover, \(\mathcal {B}\) simulates oracle C to \(\mathcal {A}\), except when \(\mathcal {B}\) aborts. Furthermore, \(\mathcal {B}\) simulates oracle R to \(\mathcal {A}\) as well. In particular, simulator \(\mathcal S\) produces proofs that are indistinguishable from proofs constructed by non-interactive proof system \(\mathsf {FS}(\varSigma ,\mathcal H)\).
We denote by \(\textsf {Good}\) the event that \(i=i^* \). Now, let us assess \(\mathcal {B}\)’s probability not to abort, to determine the success probability of \(\mathcal {B}\). Since \(\mathcal {A}\) is not allowed to corrupt the credential it finally outputs (as \(\mathcal {A}\) is a winning adversary, \( d _{i} \notin Crpt \) must hold), a sufficient condition for \(\mathcal {B}\) not to be asked for the unknown private credential \( d _i\) is to be lucky when drawing \(i^*\leftarrow \{1, \ldots , nv \}\) at random and have event \(\textsf {Good}\) occurring.
This is the case with probability \(\Pr [\textsf {Good}] = \frac{1}{ nv }\) since the choice of \(i^*\) is completely independent of \(\mathcal {A}\)’s view. Therefore we have \( \mathsf {Succ}(\mathsf {Exp}\text {-}\mathsf {EV}\text {-}\mathsf {Int}(\varPi , \mathcal {A}, \kappa ))\le nv \cdot \textsf {Succ}(\mathsf {Exp}\text {-}\mathsf {StrongSign}(\varOmega ,\mathcal {B},k)) \). \(\square \)
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Quaglia, E.A., Smyth, B. (2018). Authentication with Weaker Trust Assumptions for Voting Systems. In: Joux, A., Nitaj, A., Rachidi, T. (eds) Progress in Cryptology – AFRICACRYPT 2018. AFRICACRYPT 2018. Lecture Notes in Computer Science(), vol 10831. Springer, Cham. https://doi.org/10.1007/978-3-319-89339-6_18
Download citation
DOI: https://doi.org/10.1007/978-3-319-89339-6_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89338-9
Online ISBN: 978-3-319-89339-6
eBook Packages: Computer ScienceComputer Science (R0)





 as input and outputs a key pair
as input and outputs a key pair 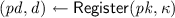 , is run by the registrar. It takes as input the public key
, is run by the registrar. It takes as input the public key  computes
computes 
 .
. ; and
; and .
.