Optimal Vehicle Suspensions: A System-Level Study of Potential Benefits and Limitations

Abstract

Fundamental ride and handling aspects of active and semi-active suspensions are presented in a systematic way starting with simple vehicle models as basic building blocks. Optimal, mostly Linear-Quadratic (H2), principles are used to gradually reveal and explore key system characteristics where each additional model Degree-of-Freedom (DoF) brings new insight into potential system benefits and limitations. The chapter concludes with practical considerations and examples including some that go beyond the more traditional ride and handling benefits.

1 Introduction

1.1 Goals/Objectives

During the past several decades there was a substantial activity in the area of automotive computer controls and related mechatronics developments. This started in the 1970s with engine controls and later included transmission and overall powertrain controls. Subsequent additions included brake and driveline controls such as four- and all-wheel drives, for example.

While there were substantial evolutionary developments in controls of longitudinal direction or X-dimension of vehicle motion, on the other hand there was relatively less activity and progress in the other two dimensions—lateral or Y and vertical or Z dimension—in terms of actual production applications. This is in particular true for the case of vertical vehicle motion control via appropriate advanced, controllable suspensions. While there were occasional major waves of agitated and at times almost frantic activity in this area in the past, currently the only advanced suspensions that saw some actual market penetration and usage are the so-called semi-active suspensions, which are essentially controllable dampers.

The main objective of these lectures is to present potential benefits and associated requirements and limitations of advanced active and semi-active suspensions. It is hoped that this will lead to additional insight and revived interest towards further developments in the above “forgotten dimension”, which may represent a major yet not fully explored and exploited opportunity. In addition to addressing the opportunities in more traditional areas of improved ride and handling the new class of advanced suspensions may be especially attractive and timely addition to overall vehicle controls in view of ever increasing interests in the areas of active safety, driver assist technologies and autonomous vehicles. The conglomerate of all those benefits may eventually lead to wide-spread production of advanced suspensions benefiting millions of customers.

1.2 Basic Definitions

Before proceeding it is necessary to define some basic notions to avoid possible misunderstandings, i.e. so that we are all on the same plane going forward through these notes. In particular, we are concerned with such notions as what sort of vehicle suspensions we are going to deal with in the sequel. The definitions are mainly based on the notion of passivity, which is closely related to energy supplied to or dissipated by the suspension unit.

Passive suspensions. They typically consist of shock absorbers and springs and as such they don’t require any external energy sources i.e. they dissipate the energy through the process of heating up the shock absorbers or dampers. They are seen on most past and contemporary vehicles in the form of Macpherson struts (seen typically as front suspension on most contemporary vehicles), multilink suspensions (seen on most luxury-type vehicles) and others.

Active suspensions. Unlike their passive counterparts, active suspensions do require external sources of energy provided through pumps and electro-motors, for example, to fully achieve their intended function. In turn they result in superior performance at the expense of higher costs, increased complexity, more demanding packaging requirements, and, in general, reduced robustness. In particular, while—as we will see later—the active suspension can result in substantial improvements in ride and handling and other benefits, their implementations also face significant challenges such as containment of the so-called “secondary ride” that is demonstrated through excitation of higher frequencies typically around and above 10–20 Hz. In terms of actual practical implementation through different energy media one distinguishes between:

• Electro-pneumatic active suspensions including Load-Leveling

• Electro-hydraulic active suspension

• Electrical active suspension

Furthermore one can distinguish between single and double acting (i.e. one- or two-sided actuation, where controlling force is acting upon one or both sides of an actuator), and between narrow and wide band actuators depending on the frequency range or “fidelity” of actuator desired force (or velocity/displacement) delivery.

Semi-Active (SA) suspensions. As their name implies, SA suspensions fall between active and passive suspensions. They are controllable, “smart” dampers or shock absorbers that require relatively very small amount of energy to modulate their damping parameter and thus perform their desired function—produce the desired force, whenever possible in view of the passivity constraint (to be discussed next). Due to small energy requirements the SA suspensions can be in practice regarded as essentially smart passive devices.

Mathematical definition of passivity. The above are more intuitive or practical definitions of passivity and related passive or active suspensions. A more precise definition of passivity follows from similar definitions used in the areas of electrical networks and mathematics (Anderson and Vongpanitlers 1973). Accordingly, an operator P is passive if there exists some constant k such that the inner product

$$ \left\langle {Pv} \mathrel{\left | {\vphantom {{Pv} v}} \right. \kern-0pt} {v} \right\rangle_{T} \ge k $$

(1)

where the inequality must hold for any final times T and all elements of v(.) from an extended inner space composed of all functions that do not “explode” i.e. have finite escape time. Associating v with velocity across actuator and Pv with corresponding force, then the above inequality reflects the energy conservation (in the case of equality) or dissipation (in the case of inequality) that is characteristic of passive suspensions consisting of a spring and/or damper or shock absorber, respectively. In this particular example the above inner product amounts to time-integration of the product of actuator force and velocity i.e. integration of power across the actuator, which is the energy dissipated or produced by the actuator. With passive suspension this energy is positive and larger or equal the amount of the initial energy contained in the actuator as represented by constant k; the inequality must hold for any final time T and velocity profile v(t).

For Linear Time-Invariant (LTI) systems the above passivity constraint with k = 0 is equivalent to a requirement that the associated transfer function matrix P(s) is Rational Positive Real (RPR) matrix. The RPR matrix P(x) must satisfy a set of conditions (Anderson and Vongpanitlers 1973) that include P(.) being analytic in the r.h.s. plane i.e. all elements of P must have poles where Re(s) ≤ 0. Thus it can be said that for any passive suspension that can be described by the LTI transfer functions the associated impedance matrix P must be a RPR matrix. This provides one way of checking if a given suspension constitutive relation can be realized via passive means or it may require an active actuator implementation.

1.3 Historical Background

There is a relatively long history of efforts in the area of active suspensions. They have been mentioned and considered already in the 1960s through theoretical studies by Bender (1967a, b), Bender et al. (1967), Karnopp and Trikha (1969), Young and Wormley (1973), Thompson (1971) and others, mostly from MIT. Since then there were numerous studies on potential benefits and limitations of active suspensions in the context of ride and to some extent handling; most of this earlier work is summarized in Sharp and Crolla (1987), Elbeheiry et al. (1995), Hrovat (1997) and more recently in Mastinu and Ploechl (2014), Tseng and Hrovat (2015).

While there was much effort and progress in terms of theoretical analysis and overall insight, the progress in actual production implementation of active suspensions was relatively slow and somewhat sporadic. To this end there was a major wave and push towards the latter during late 1980s and early 1990s. It started with the Lotus efforts aimed towards formula F1 racing. In particular, a special Lotus Esprit experimental vehicle was used through many years of research and development resulting in some very impressive media shows and demonstrations. This is also reflected in the January 21, 1987, New York Times article, with citations from different automotive media evaluators ranging from “most impressive thing I’ve ever tried” to “the greatest single advance in car engineering since the war”.

However, it should be pointed out that the most impressive demonstrations were done on special test tracks that amplified large, low frequency road undulations, which were “ideal” for exciting the dominant heave mode of body dynamics. The latter is typically around 1–2 Hz with relatively low damping ratio (Hrovat 1997). In reality, most actual roads are not of this type and ride benefits were then less dramatic.

At the time most automotive OEM’s or companies on practically all continents, but especially in Japan and the US (Akatsu et al. 1990; Goto et al. 1990; Goran et al. 1992), have been heavily involved in R&D towards realizing a practical active suspension that would robustly and reliably deliver most of ride and handling benefits at reasonable cost, weight, packaging and energy requirements. While there was considerable progress in experimental and test vehicle developments of active suspensions only a few such systems saw actual production. This was in the form of limited production series introduced during the 1990s by Nissan in the Infinity Q45a (Akatsu et al. 1990) and Toyota in the 1989 Celica (Goto et al. 1990) which were eventually discontinued. One of the main reasons for this lack of wide-spread usage is that active suspensions at the time did not deliver sufficient value: their performance as measured in terms of ride and handling improvements were not noticeable enough while at the same time their cost was prohibitively high for all but the most luxurious vehicle segments.

Subsequently, for the next two decades the active suspension efforts were mostly limited to further theoretical developments done mostly in academia and few industrial R&D institutions. In particular, the latter include long-standing internal efforts within Bose in developing their electrical active suspension, which attracted significant media attention at the time (Moran 2004). At present, there is only one significant production application of active suspensions—the so-called ABC, Active Body Control, introduced by Mercedes. This was recently further enhanced under Magic Body Control (MBC) where for the first time the use of road roughness preview ahead of the vehicle has been used based on stereo cameras (Anonymous 2017a; Streiter 2008). It is interesting that the ABC/MBC has been offered by Mercedes as standard equipment on their top line, luxury models.

Last but not necessarily least, it should be mentioned that while active suspensions did not see wide-spread in-vehicle production applications thus far, their SA counterparts did find much larger acceptance and can now be found in many vehicles under different marketing designations such as Continuously Controlled Damping (CCD), Magnetic Ride/MagneRide Control and others. While their performance was in general somewhat inferior to corresponding active suspension performance at the time, their cost, robustness, relative simplicity and lower packaging requirements and parts count all were more favorable. Thus they resulted in higher value and acceptance rates so far.

1.4 Motivation

Since the first wave of active suspension efforts dating back to 1980s and 90s did not succeed to bring a widespread production introduction of this high-tech concept it is appropriate to ask—why reconsider it now? While this is a fair question there are a number of factors that evolved during the last couple of decades that warrant re-examination of this relatively dormant field. This includes:

• Further developments and continuous progress in the areas of Control Systems and Optimization, and related Optimal Control methodologies such as Model Predictive Controls (MPC) that are becoming more and more applicable to Automotive Controls (Ulsoy et al. 2012; Rajamani 2012; Hrovat et al. 2011a, b);

• Further developments and progress in computers—both hardware and software, electronics/mechatronics, conventional (passive) suspensions, and electrical machinery;

• Ever increasing emphasis on and importance of Active Safety (van Zanten 2014);

• Recent trends in sensors and infrastructure enhancements; this includes cameras, Lidar, Vehicle to Vehicle (V2V) and Vehicle to Infrastructure (V2I) communications, various forms of mapping including 3D mapping etc. Most of these new technological developments will facilitate highly effective preview controls based on, for example, MPC optimization (Xu et al. 2016; Hrovat et al. 2012);

• Recent developments and widespread efforts in Autonomous Vehicles (AV), which could free many current drivers to do many other tasks and activities such as writing a report or playing his or her favorite computer game; all this will be much easier to accomplish having an AV with a more steady platform facilitated by a fully active suspension.

1.5 Brief Overview of Automotive Controls

As shown in the previous section, the field of automatic controls is central for many of the ongoing activities and developments that are highly relevant for the next possible wave of active suspensions. When speaking of “controls” here we are primarily focusing on computer controls, which have been prevalent in the automotive field for more than four decades by now. This implies related areas of control-oriented modeling, which uses appropriately simplified models, along with many computer-assisted control system design, analysis and simulation tools and methods such as MATLAB, for example. The latter include open- and closed-loop control algorithm design and analysis based on both classical as well as so-called “modern” or advanced controls; optimization/optimal control design; signal processing and diagnostics; system identification and estimation; Neural nets, Fuzzy logic controls, and Artificial Intelligence (AI); along with associated architecture, sensors, actuators, processes and embedded real-time software/CAE tools.

The automotive computer controls started in 1970s with the advent of microprocessors, which were first used for engine controls, in particular spark advance control that was prior to this accomplished through hardware means. Since their modest beginnings in early 1970s the computer controls then propagated to all aspects of engine and powertrain operations. This includes: Air-Fuel (A/F) ratio control; Idle Speed Control (ISC); Exhaust Gas Recirculation (EGR) control; Waste Gate (WG) control in case of boosted engines; many features of Automatic Transmission (AT) control; and others (Hrovat et al. 2011a).

In almost all those cases the previous hardware-based controls have been replaced by software. In the process the functionality and complexity of hardware solutions that evolved through decades of ingenious refinements was transferred to software, which grew more and more complex with time. However, one huge advantage of software control implementations is their inherent flexibility: it is much easier to modify computer programs then the corresponding hardware implementations.

Next, the computer or more precisely microcomputer controls propagated to many areas of chassis and overall vehicle dynamics and related functionality. This includes, in a somewhat chronometric order, the following features: ABS brake effectiveness/stopping distance control; Traction Control (TC), which can be viewed as a counterpart of ABS especially helpful when driving on slippery roads; Electronic Stability Control (ESC)—a very effective safety feature helping prevent many accidents, especially in emergency situations; Load Leveling (LL) used for vehicle posture control; Four Wheel/All Wheel Drive (4WD/AWD) drivetrain control that aims at optimizing traction on all four driven wheels, again especially relevant for driving on slippery, snow- or ice-covered roads; Continuously Controlled Damping (CCD) semi-active suspension control; Adaptive Cruise Control (ACC) sometimes also called Autonomous Cruise Control due to its ability to lock-in behind a leading vehicle and keep the related distance constant in terms of time distance between the two; Electrical Power Assist Steering (EPAS) and numerous forms of EPAS-based vehicle controls such as Active Front Steer (AFS), Four Wheel Steer (4WS), Lane Keeping Aid (LKA), Trailer Backup Assist (TBA), and, more recently various means developed to assist or fully control the parking tasks such as Fully Automated Parking Assist (FAPA) and Remote Parking Assist (RePA).

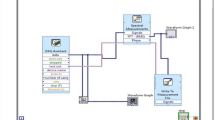
From the above somewhat lengthy list one can observe that most of the automotive computer controls developed to date have been applied—via powertrain, brake, and 4WD actuation, for example—in the longitudinal or X-direction (or dimension) of vehicle motion. This is visualized in Fig. 1, which displays various functionalities placed at their predominant axis of action. Next comes the lateral or Y-direction, which has seen significant revival of activities lately. On the other hand there is relatively little activity seen along the Z-axis or vertical motion of a vehicle where we see only the Mercedes ABC system as a sole representative of active suspension controls. As we will argue in a sequel, this “forgotten dimension” may represent a major opportunity for further expansion and application of automotive computer controls in the future.

Fig. 1

3D representation of various automotive control functionalities

1.6 LQ Optimal Control Problem

There are many ways one could design an advanced, active vehicle suspension system. Some of those can be based on different optimization methodologies. In this work we focus on one of the most popular optimization methodologies—the Linear Quadratic (LQ) optimal control techniques, which, as we will see in a sequel, is particularly revealing and well-suited for our vehicle suspension design problem.

Deterministic LQ problem statement and solution. Since most of the optimization work pursued in the present study is based on the Linear Quadratic (LQ) optimal control approach (Athans and Falb 1966; Anderson and Moore 1971; Kwakernaak and Sivan 1972; Levine 2011) we will now briefly summarize main characteristics of this by now well-established and quite popular methodology, which years back was referred to as “advanced or modern controls”. As it name implies the LQ technique involves linear vehicle or plant models and quadratic optimization or performance index. The linear models can be either time-varying or time-invariant (LTI); presently we will almost exclusively deal with the latter i.e. LTI models. In addition, we will focus on infinite-time regulator problem that, as we will see below, results in feedback controls with constant control gains. The corresponding deterministic LQ optimal control problem can be stated as minimization of the following Performance Index (PI):

$$ {\text{Minimize}}_{{{\text{w}} . {\text{r}} . {\text{t}} . {\text{u}}}} \left[ {PI = \int\limits_{0}^{\infty } {\left( {x^{T} (t)Qx(t) + u^{T} (t)Ru(t) + 2x^{T} (t)Nu(t)} \right)dt} } \right] $$

(2)

subject to LTI vehicle model dynamics

$$ \begin{aligned} \frac{dx}{dt} & = Ax + Bu + Gv_{d} \\ y & = Cx + Du \\ x(0) & = x_{0} \\ \end{aligned} $$

(3)

where the PI weighting matrices R^T= R > 0, Q^T= Q ≥ 0, y is the output variable associated with the PI of Eq. (2), and v _d is a vector of deterministic disturbances. In the present case the latter are typically modeled as unit impulses in ground velocity, which is equivalent to unit steps in ground displacement (in case of more complex ground inputs they can sometimes be captured by expanding the state-space to include the augmented states representing different ground displacement shapes).

Often the above step-like disturbance terms can be fully or partially captured by the equivalent initial condition vector, x₀. For example, in the simple case of a 1D, 1DoF optimization treated in Sect. 3.1, one can approach the underlying deterministic two-state optimization problem as the one with zero initial conditions and an impulse in ground velocity i.e. step in ground displacement. Alternatively, the same problem can be approached as the one with zero ground input (v _d  = 0) and non-zero initial conditions where the first state—the one corresponding to the rattlespace displacement—is initially set to 1 (x₁ = 1) to represent the initial compression of the suspension space that is equivalent to the above-mentioned unit step in ground displacement. Later we will discuss another equivalence—the one between the above deterministic LQ results and corresponding stochastic case. But first, let us summarize the general solution to the above optimization problem and then say few words about the important topics of the stability and robustness of the LQ-optimal solution, which is critical for any possible practical implementation of the LQ-like control strategy.

The optimal solution to the above deterministic, infinite-horizon, continuous-time LQ regulator problem is given by following feedback controller:

$$ u* = - Kx $$

(4)

where the constant feedback gain matrix K is given by

$$ K = R^{ - 1} \left( {B^{T} P + N^{T} } \right) $$

(5)

and P is obtained by solving the following Algebraic Riccati Equation (ARE)

$$ A^{T} P + PA - \left( {PB + N} \right)R^{ - 1} \left( {B^{T} P + N^{T} } \right) + Q = 0 $$

(6)

Now, for the case when N = 0, which is most often encountered here, if the pair (A, B) is stabilizable and (A, C) is observable, where Q = C^TC, then the above ARE has a unique positive-definitive solution P > 0, which results in an asymptotically stable, LQ-optimal, closed-loop system. If (A, B) is stabilizable and (A, C) is detectable, then the above ARE has a unique positive semi-definitive solution P ≥ 0, which again results in asymptotically stable, LQ-optimal, closed-loop system. When N ≠ 0 then the equivalent, more stringent stability conditions can be found in Anderson and Moore (1971).

Robustness of LQ regulator. Robustness properties of the deterministic LQ optimal regulator for the nominal or most often cited case when the cross-weighting matrix N = 0, are well known. Here under “robustness” we refer to system ability to still maintain good performance and stability despite the unavoidable errors due to model mismatch, and many other unpredictable noise factors that typically occur in practice. Assuming that all the states are available the Single-Input-Single-Output (SISO) gain margin is very generous and can range between 6 db and infinity, i.e. the nominal gain of 1 can vary from 0.5 and +∞, whereas the associated phase margin is 60°. Similar results apply for each individual control channel of the corresponding Multi-Input-Multi-Output (MIMO) case under some mild additional assumptions as elaborated by Safonov and Athans (1977).

However, as shown by Ulsoy et al. (1994), once the non-zero cross-weighting matrix N is introduced, the above impressive robustness properties of the “standard” LQ regulator don’t apply anymore and can be significantly reduced. For example, in the context of the present vehicle dynamics ride and handling optimization problem this situation arises when one augments the actuator-only secondary suspension of a quarter-car setting (see Sect. 3.2 below) with some passive counterparts such as an additional supporting spring and possibly a damper. These passive components could reduce maximum and average force and energy requirements from an active actuator. However, there could be instances when the actuator needs to provide net active power thus requiring total neutralization of the passive elements (or partial reduction of the spring stiffness) and if this action is overdone due to modeling and other errors one could see the potential for significant degradation in system performance including destabilizing effects of ending up with a net negative spring or damper effects, for example.

In addition to the above, the robustness of the LQ solution can be further eroded when not all of the system states are directly measured and available for controls (Ulsoy et al. 1994). Indeed, more often than not this is the case in practice since some state measurements are very difficult to make and some may be too costly. If the system in question is observable then these missing states can be reconstructed via different state estimation techniques, such as Luenberger observer (Levine 2011), for example. However, the additional dynamics and related dynamic delays typically result in further reduction of robustness and associated gain and phase margins. These issues are further amplified in the case when various noises are present—either in the process i.e. model dynamics and/or state or output measurements that will be discussed next.

Stochastic case—LQG controller. As described later (Sect. 2.2) most road inputs relevant for vehicle ride dynamics can be described as random, stationary stochastic processes. In this case the above deterministic LQ optimization problem transforms to an equivalent stochastic counterpart with an additional assumption that all random noises are white and of Gaussian character. The resulting optimization problem is then referred to as Linear Quadratic Gaussian (LQG) optimal control problem. In the context of present usage it can be formulated as minimization of the following Performance Index

$$ {\text{Minimize}}_{{{\text{w}} . {\text{r}} . {\text{t}} . {\text{u}}}} \left[ {PI = E\left( {x^{T} Qx + u^{T} Ru + 2x^{T} Nu} \right)} \right] $$

(7)

subject to LTI vehicle dynamics

$$ \frac{dx}{dt} = Ax + Bu + Gw_{d} $$

(8)

where the expectation operator E(.) represents steady-state mean square (co-variance matrix) values of the affected variables. Here w _d is the system disturbance in the form of aforementioned Gaussian white noise process characterized by

$$ \begin{aligned} & E\left[ {w_{d} (t)} \right] = 0 \\ & E\left[ {w_{d} (t_{1} )w_{d} (t_{2} )} \right] = 2\pi W\delta \left( {t_{1} - t_{2} } \right) \\ \end{aligned} $$

(9)

with δ(.) representing the impulse or Dirac delta function, and W being the two-sided road (vertical) velocity power spectral density, which is equal to the product of road roughness coefficient and vehicle velocity (see Sect. 2.2 below). Special care should be exercised regarding the factor 2π since some road descriptions may imply different factor. This can be traced to different definitions of the associated Fourier transforms (Weisstein 2017). In practice this means that one should be aware of the context how different psd data were obtained, especially when dealing with measured road spectra (Mastinu and Ploechl 2014).

The solution to the stochastic LQG problem is given by the same optimal feedback gain matrix K as in the corresponding deterministic LQ regulator problem. The only difference is that in the general LQG case one uses Kalman estimate of the state vector x, which amounts to a linear unbiased minimum error variance estimate obtained via Kalman-Busy optimal filtering (Sage and White 1977; Anderson and Moore 1990; Levine 2011). However, just as in the above deterministic case, the estimation with associated filter dynamics and measurement noises can significantly erode the robustness margins of the LQG controller. Indeed, as shown by Doyle (1978) even a simple two-state example can result in practically zero robustness for sufficiently large measurement noises and state weighting matrix Q. Another, more practical i.e. physical example was provided by How and Frazzoli (2010) who used an LQG controller to stabilize an inverted pendulum on a cart. It is shown that again one can encounter a situation where vanishingly small robustness margins are present around the nominally stable closed-loop system.

Calculation of performance metrics. In order to calculate different rms and mean-square values we use the following Lyapunov-like equation for the closed-loop covariance matrix X

$$ \left( {A - BK} \right)X + X\left( {A - BK} \right)^{T} = - G\Gamma G^{T} $$

(10)

where Γ corresponds to the ground velocity psd quantity 2πW. Setting Γ = 1 and solving the above equation will then result in normalized covariance matrix, where all relevant entries are normalized by 2πW, i.e. the related rms values are normalized by $\sqrt {2{\uppi }W}$ . This type of normalization will be used through most of the present chapter. Once the covariance matrix X is known one can then calculate the expected mean-square optimal control input from

$$ E\left( {u^{2} } \right) = KXK^{T} $$

(11)

Other output quantities of interest that are linear functions of states can be calculated in a similar fashion.

To summarize. The infinite time deterministic LQ problem and its stochastic LQG counterpart share the same optimal feedback control structure and associated gain matrix K. In the context of present active suspension study, there are number of equivalent or similar LQ optimization settings that lead to identical control structure and gains. First, in the case of a deterministic LQ regulator, there is equivalence between appropriately posed initial condition response problem and related step input in ground displacement (or an impulse in ground velocity). Both of those deterministic settings are equivalent to the stochastic LQG problem formulation where ground input is now represented through white-noise in velocity process. In all three optimization cases we end up with the same optimal feedback control structure with the same gain K as per the above Eq. (5).

Regarding the robustness of the LQ regulator there are two different answers depending on the structure of the problem. In the case when there are no cross-weight terms (N = 0 in PI) and when all the states are available then the LQ regulator results in a robust closed loop system with gain margin of at least 6 db and phase margin of 60°. However, this is in general not the case when N ≠ 0 and/or when some of the states have to be estimated—either via an estimator or Kalman-Busy filter. In the present case we will mostly deal with the idealized situation where N = 0 and all the states are available for controls. While this is an idealized assumption the main objective of the present study is to establish best possible performance potentials of active suspensions realizing that eventual actual implementation will result in some degradation of performance and robustness. These are important topics for further investigation along the V-diagram of Fig. 2 that should be pursued in the future once the optimal performance has been identified along with related high-level architecture, bandwidth, and other requirements.

Fig. 2

V diagram representation of system-engineering approach to advanced suspension design (MB stands for “Model Based”)

1.7 System-Level Approach

In order to investigate potential benefits and limitations of active suspensions we propose to start with a system- level (“30,000 ft” or “10,000 m”) study based on simple vehicle models and related requirements and constraints. In particular, it is proposed to start with establishing optimal ride and handling potentials based on a simple, linear one-dimensional (1D) and 2D vehicle models. This is accomplished by using appropriate optimal control tools such as the well-known optimal Linear-Quadratic (LQ) methods, to determine global best possible performance under ideal conditions and constraints.

The rationale being that if we cannot identify sufficient potential benefits within a simple setting under numerous simplifying, mostly favorable assumptions and thus less stringent constraints, there is little incentive to proceed with the study toward more detailed and complex models and optimization settings with many much more stringent constraints. The advantage of this “30,000 ft approach” is that due its simplicity it can cover large territory of potential solutions and produce a global view of the potential benefits and limitations. The key word here is “global” since many opportunities may be missed or overstated if one focuses on just one or two isolated points, as is the case with some studies.

On the other hand, depending on the outcome of the above “high-level” global study one can decide whether to proceed toward more detailed (“10,000 ft and below”) studies based on more complex, possibly non-linear models. As such this approach may be viewed as “top-down” as opposed to “bottom-up” approach where one starts with the complex and very detailed models and then gradually simplifies them toward control-oriented models and studies. Each approach has some advantages and disadvantages and may be more or less appropriate depending on a given task at hand.

The above top-down approach is particularly suitable for applying system-engineering principles (Anonymous 2017b) following the Model-based System Engineering V methodology (Anonymous 2017c) shown on Fig. 2. The entry point to the System V is at the upper left brunch of V starting with overall customer-level requirements regarding system functionality and conceptual mode of operations. Starting with overall customer requirements one can then use the above simple models and appropriate optimization tools to establish what are the best possible performance metrics and are they good enough to satisfy top level customer requirements. In addition one can then obtain the outlines of needed architecture and associated design and other engineering constraints such as desired actuator configuration and bandwidth or fidelity. Essentially, such a top-level optimization process uses modeling and related synthesis to produce results that can in turn then be used as requirements and guidance for subsequent more detailed lower-level work based on more detailed models and so on as one proceeds down the left branch of the System V. Eventually the process reverses as one progresses through the r.h.s. branch of V going through verification and validation phases starting from component tests all the way to validation of the whole system operation and performance.

At this stage, following the above systematic approach we start by specifying the high-level requirements for an advanced, high-performance vehicle suspension. They can be listed as follows:

• 1. Maintain proper vehicle posture when subject to various inertial and external forces and moments caused by braking, turning, wind gust, and other operational events and disturbances;

• 2. Provide superior ride comfort (in an optimal sense to be further elaborated in a sequel) when subject to road roughness inputs, which act as a major disturbance to a vehicle;

• 3. Secure superior road handling (in an optimal sense to be further elaborated in a sequel) and overall vehicle agility;

• 4. Avoid excessive suspension stroke to avoid hitting jounce and rebound stops (this is the so-called “rattlespace” constraint requirement);

• 5. Enable additional benefits and functionality that will facilitate enhanced active safety and introduction of new, exciting functionality leading to superior customer experience (the “wow” factor).

In practice, the first requirement is typically best addressed through feed-forward control based on more detailed (possibly non-linear) models since some of the main disturbances regarding posture control come from known sources such as engine and brakes, which are initiated by the driver and thus known in advance to some extent. From the above list we will focus on Ride and Handling requirements 2–4 for most of the subsequent sections with some comments regarding many future exciting potential benefits being discussed in the last part of the chapter.

2 Setting up the Stage

In this section we will set the stage for the LQ optimization that will be used in the subsequent section. To this end we will next discuss the appropriate, simple Performance Index (PI) reflecting the above ride and handling requirements along with pertinent constraints. Next, we will address the numerical description and construction of an appropriately simple vertical road input representing the main disturbance acting upon the system. Also, we will address what are the appropriate, simple vehicle models that should be paired with the above. Finally, we will briefly mention many of the underlying assumptions used throughout this chapter.

Note that the key words here are “appropriately simple” since for a global, comprehensive analysis at this high of a level it is imperative to deal with an appropriately simplified setting. This means that all aspects of the problem (PI, constraints, disturbances, models) are in synch as far as the level of complexity is concerned. Indeed, it would not make much sense nor it would be efficient to have a very detailed, 3D vehicle model but a simple “1D” PI or road description, and vice versa.

2.1 Performance Index and Related Constraints

Since one of the main objectives of the present work is to establish ride benefits of advanced active and semi-active suspensions, our first task will be to define an appropriate ride comfort index, which will in turn be used to define the associated optimization Performance Index (PI). This has been a subject of many investigations in the past. In its very nature this is an intrinsically subjective metric and as such may be a subject of many more studies in the future, especially as we face different modes of transportation such as autonomous driving, for example.

One of the first field-test studies to address the ride comfort metric was done in the 1970s by Smith et al. (1978). The authors used couple of different vehicles driven on 18 different roads with a total of 78 passengers. Their conclusion was that, “excellent correlation was found to exist between the subjective ride ratings and simple root mean square acceleration measurements at either the vehicle floorboard or the passenger/seat interface”. The key results of this study are reproduced in Fig. 3 where the horizontal axis represents the average or mean personal ratings and vertical axis represents rms acceleration measured for combined vertical and lateral directions. Here higher ratings represent better ride comfort. Similar results were obtained for the case limited to vertical accelerations only.

Fig. 3

Least square fit to experimental data by Smith et al. (1978) expressing Mean Personal Rating (MPR) as a function of rms acceleration

Further refinements of the rms ride comfort PI metric are possible through introduction of the vehicle or seat-track vertical jerk, which is the derivative of the vertical acceleration (Fearnsides et al. 1974). The rationale being that the addition of jerk will capture contributions from high-frequency disturbances that are typically part of Noise Vibration and Harshness (NVH) spectrum. We will use this additional jerk term when addressing some elementary ride optimization problem based on simple, 1D vehicle models.

In addition to the above simple rms-based ride metrics there were number of attempts to expand this metric in order to include frequency-dependence of human sensitivity to vibrations. This was captured by the ISO standard 2631, which also takes into account the length of human exposure to vibration (Anonymous 1972). Additional information about various ride metrics and their further enhancements—such as a comprehensive NASA metric applicable to 3D motions—can be found in Hrovat (1993), Tseng and Hrovat (2015) and references therein.

It is interesting that some of the early comparison studies (Smith 1976; Smith et al. 1978) found the simple rms metric comparable to more complex counterparts such as the above ISO standard. Since the usage of proper ride metric depends on the context of its usage and since in the present setting we focus on simple models, optimization methods (LQ), and metrics, in what follows we will exclusively use the rms ride metrics mentioned above. We remark that, if desired, it is easy to incorporate frequency-weighting into the LQ-type metric by augmenting the state-space model with appropriate filter states associated with the desired frequency shaping. Additional considerations may apply when dealing with future autonomous vehicles where ride sickness effects may be more pronounced due to lack of driving activity (Wada 2016).

At this point it is important to stress that if the ride comfort were the only objective of the optimization then the solution would be simple i.e. to keep the rms acceleration (and jerk) equal to zero for all times by making the total suspension force equal to vehicle weight for all times. This may work fine in isolated cases of driving on flat surfaces. However, the main issue with such a suspension would be that it would require unrealistically large suspension strokes or so-called “rattlespace” to negotiate hills and valleys and similar large road deviations from flat surfaces (in the extreme, one could consider airplanes as limiting case of such “air cushion” vehicles).

In practice, the available suspension stroke is limited as determined by jounce and rebound stops. Although these “bump stops” represent hard constraints they are often approximated by soft constraints in the form of rms or mean-square limitations on rattlespace. The latter are then appended to the mean-square ride comfort metric to form an overall PI that will be used for LQ or H₂ optimization based on a simplest possible 1D vehicle model to be considered in Sect. 3.1.

In addition to the above rattlespace constraint we will later introduce an additional constraint when dealing with slightly more detailed 1D or quarter-car vehicle models. The main purpose of this additional constraint will be to limit tire wheel-hop, which can be detrimental to vehicle handling as well as ride. This yet another mean-square constraint (this time on tire deflection or relative motion w.r.t. ground) will be addressed in Sect. 3.2.

2.2 Road Description

As elaborated in Hrovat (1993) there are two kinds of disturbances that affect vehicle ride and handling. One is caused by road roughness irregularities and the other by different inertial and aerodynamic forces due to braking, turning, and wind gusts, for example. In this paper we focus on road or ground input disturbances, which are the most relevant for present ride studies.

There are many ways to describe road inputs, which can be classified as shocks and vibrations. Shocks are discrete events of short duration and high magnitude, such as encountered while suddenly hitting a pothole or road bump at relatively high speed. On the other hand, vibrations are characterized by prolonged and consistent excitations that are typically encountered during long trips on highways and other roads.

When considering vibration excitation, road roughness is typically described as a stationary random process of a given displacement power spectral density, p.s.d. (Bendat and Piersol 1971). An example of measured displacement or roughness power spectral densities of various roads and terrains from Sevin and Pilkey (1971) is shown in Fig. 4.

Fig. 4

Measured power spectral densities of various terrain/road surfaces (according to Sevin and Pilkey (1971) where factor 1/2π was used when relating autocorrelation function to psd)

Comparing the actual measured traces with the straight line of negative 2:1 slope in the log-log scale one obtains the following often used approximation describing road displacement p.s.d., S(.):

$$ S\left(\Omega \right) = A/\Omega ^{n} $$

(12)

where Ω is the spatial frequency in units of “radians per length” (rad/ft in the case of Fig. 4) and n ≈ 2. The above displacement spectra imply that the corresponding vertical velocity spectrum as experienced from a moving vehicle is constant for all frequencies i.e. white noise with intensity of A * V, where V is vehicle forward velocity. The white-noise characterization of the road input conveniently matches the well-known LQG (Linear Quadratic Gaussian) optimal control setting, which presupposes the white-noise Gaussian process and measurement noises (see Sect. 1.6).

Further reinforcements about the above white character of many measured roads can be seen in Figs. 5 and 6 from Smith (1982).

Fig. 5

Comparison of best-fit road model with exponent n = 2.02 and measured Road #1 (cf. Hrovat 1997)

Fig. 6

Comparison of best-fit road model with exponent n = 1.99 and measured Road #2 (cf. Hrovat 1997)

Additional examples can be found in Hrovat (1993) and references therein where one can also find references to more elaborate and/or multi-dimensional models of road roughness such as discussed by Dodds and Robson (1973) and Rill (1983), for example.

Numerical procedure used to construct an approximate white-in-velocity Gaussian road sequence for usage in simulations is discussed in Hrovat and Margolis (1975). The procedure starts with a sequence of uniformly distributed random numbers with triangular autocorrelation function. The corresponding p.s.d. is then approximately white up to certain frequency band, which is controlled by the choice of random sequence update rate. The sequence is next passed though appropriate bandpass filter to wash out large road protrusions such as hills and valleys, on the one hand, and high frequency noise that is well beyond the underlying models bandwidth fidelity, on the other. In the final step, the sequence is ensemble averaged to produce the desired Gaussian characteristics.

2.3 Vehicle Models

In order to complete the optimization setting we now briefly introduce some of the simple vehicle models to be used in the rest of this work. We start with linear, time invariant models of lowest complexity and gradually add additional dimensions and Degrees-of-Freedom (DoF). The simplest possible model is shown in Fig. 7. It consists of only a sprung mass, M _s , and an active suspension actuator that can produce any desired force U while supporting vehicle mass M _s .

Fig. 7

Simple 1D, One Degree-of-Freedom (DoF) vehicle model

The vehicle is assumed to traverse an uneven road with constant velocity V, which creates a vertical input w(t) acting upon the lower mounting point of the active suspension actuator. The vertical velocity input w(t) is proportional to vehicle velocity V and the spatial slope of the road unevenness. It is in this context that one talks about the “moving ground” when referring to w(t). As discussed earlier for the purpose of the present study the spatial slope is approximated by a white-noise process so that w(t) is also white with p.s.d. intensity proportional to V.

Next we introduce models resulting from considering only one corner of a vehicle. These are the so-called quarter-car models—some of which are shown in Fig. 8. In addition to the sprung mass M _s , which is now appropriately proportionated to a given corner, we also have an unsprung mass, m _us , which reflects the wheel/tire subassembly with associated mass components due to steering links, knuckles etc. The unsprung mass is typically only a fraction (one-fifth or less) of the corresponding sprung mass and is suspended between the primary suspension provided by tire flexibility and secondary suspension that can be passive, active or semi-active. A point-wise tire-road contact is considered, and the tire filtering effect may be included, as needed.

Fig. 8

Various 1D, 2DoF vehicle models: with active suspension (a); with active suspension and vanishing unsprung mass (b); with passive suspension (c)

As the next logical step in model complexity, we consider the so-called half vehicle, 2D, models the simplest variant—without unsprung masses—being shown in Fig. 9. It includes vehicle (sprung mass) pitch motion represented by angle θ, and vertical or heave motion represented by vertical displacement, z, of its Center of Mass, CM.

Fig. 9

Half-car, 2D vehicle model

Finally the full 3D models are represented in Fig. 10, which shows the simplest possible 3D model consisting of vehicle heave, pitch and roll modes. Note that again the unsprung masses have been neglected for this lowest-level 3D model; they can be easily added later, as needed.

Fig. 10

Full-car, 3D vehicle model

The above 1D, 2D and 3D model variants are the ones most often used in studies dealing with system-level advanced suspension optimization and synthesis,. However, depending on the task at hand one may add some additional elements and components such as subsystems consisting of an engine/powertrain suspended on their mounts, and a driver suspended on a seat. Similar 2D, 6 DoF model has been evaluated through actual vehicle tests and the corresponding results are shown in Figs. 11 and 12. This illustrates that even a relatively simple, linear, time-invariant 2D models can provide good fidelity up to the bandwidth of 10 Hz and more. If further improvements in fidelity are desired then one may have to consider additional modeling details and degrees of freedom and possibly even augment the present lumped parameter models with flexible counterparts, as needed and appropriate. The underlying assumption is that we are dealing with linear vehicle models that are needed for the above LQ optimization approach.

Fig. 11

Measured and predicted acceleration PSD’s at CG for linear 6 DoF, 2D model per Smith and Sigman (1981)

Fig. 12

Measured and predicted unsprung mass acceleration PSD’s for linear 6 DoF, 2D model per Smith and Sigman (1981)

2.4 Assumptions

There are many implicit and explicit assumptions used throughout the course of this work. Some of them we have already enumerated in the previous sections when introducing rationale for chosen performance metrics, road disturbance representation, and different simplified vehicle models. Numerous additional assumptions can be found in Hrovat (1997) and references therein such as Hrovat (1988). They include the assumption that in what follows all state variables are available for controls; that—as indicated earlier—all external load effects will be neglected for most of the present study and assumed to be treated separately, mostly in the context of feed-forward controls; and that all actuators are assumed infinitely fast and accurate.

In addition, since one can consider suspension system to be essentially a filter for road roughness induced disturbances, this filtering or attenuation should not include (large) hills and valleys and similar low frequency ground inputs that vehicle should follow. This can be achieved through appropriate signal processing (detrending) of key signals used for control. The latter is especially relevant for so-called “skyhook” damper and spring implementations to be discussed in a sequel.

3 Optimization Results

In this section we proceed with developing optimal control results for different scenarios starting with the simplest possible 1D, 1DoF setting and gradually progressing toward 2D and 3D cases. At each step we build upon the acquired knowledge and insight, which in turn serves as a footing for the next step based on a more detailed model representation. In the process we reveal essential characteristics of each optimization setup in terms of potential ride and handling benefits, and fundamental constraints—such as different invariant points in key frequency transfer function maps imposed by a given structural constraint, for example. While focusing on best possible performance outcomes, which typically imply an active suspension solution, we will also try to put these optimal results in a proper perspective by comparing them with the corresponding passive suspension counterparts.

3.1 Simple 1D, 1DoF Case

Problem statement. Referring to Sect. 2, we can now pose the following optimal control problem for the case of a simple, 1D, 1DoF model represented in Fig. 7:

$$ {\text{Minimize}}_{{{\text{w}} . {\text{r}} . {\text{t}} . {\text{u}}}} \left[ {PI = E\left( {x_{1}^{2} + ru^{2} } \right)} \right] $$

(13)

subject to the following second-order state equations

$$ \begin{aligned} & dx_{1} /dt = x_{2} - w \\ & dx_{2} /dt = u \\ \end{aligned} $$

(14)

where as seen from Fig. 7, the states x₁ and x₂ represent suspension rattlespace and sprung mass velocity, respectively, and u is a normalized force U/M _s , which in the present case equals to sprung mass acceleration. The PI of Eq. (13) then captures the requirements for smooth ride (low u) balanced against the competing requirement for limited rattlespace (low x₁). The disturbance w when seen from a moving vehicle appears as a vertical velocity input caused by road irregularities. It is modeled according to the aforementioned zero-mean, Gaussian white-noise velocity characterization discussed in Sects. 1.6 and 2.2.

One DoF LQG problem solution—Skyhook structure. The solution to the above LQG problem follows the procedure outlined in Sect. 1.6. Since we are dealing with a simple second-order system it is now possible to obtain an entirely analytical solution to this problem. We start with the Riccati equation (6)

$$ A^{T} P + PA - \left( {PB + N} \right)R^{ - 1} \left( {B^{T} P + N^{T} } \right) + Q = 0 $$

(15)

where in the present case

$$ A = \left[ {\begin{array}{*{20}c} 0 & 1 \\ 0 & 0 \\ \end{array} } \right],\quad B = \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right],\quad N = 0,\quad Q = \left[ {\begin{array}{*{20}c} 0 & 0 \\ 1 & 0 \\ \end{array} } \right],\quad P = \left[ {\begin{array}{*{20}c} {P_{1} } & {P_{2} } \\ {P_{2} } & {P_{3} } \\ \end{array} } \right],\quad R = r $$

(16)

Substituting these expressions into the above ARE and solving for P we get

$$ P_{1} = \sqrt 2 r^{{\frac{1}{4}}} ,\quad P_{2} = \sqrt r ,\quad P_{3} = \sqrt 2 r^{{\frac{3}{4}}} $$

(17)

so that the optimal control gain matrix from Eq. (5) becomes

$$ K = \frac{1}{r}\left[ {\begin{array}{*{20}c} {P_{2} } & {P_{3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {r^{{-\frac{1}{2}}} } & {\sqrt 2 r^{{-\frac{1}{4}}} } \\ \end{array} } \right] $$

(18)

Thus the LQ-optimal feedback control u _LQ becomes

$$ u_{LQ} = -\frac{1}{{r^{1/2} }}x_{1} - \frac{\sqrt 2 }{{r^{1/4} }}x_{2} $$

(19)

Since u represents a normalized force, the optimal suspension structure amounts to a spring of normalized spring constant $r^{ {-}1/2} ,$ and a damper with normalized damping constant of $\sqrt 2 r^{ {-}1/4} .$ While the optimal spring is placed between the vehicle sprung mass and “moving” ground, the optimal damper is placed between the vehicle sprung mass and an inertial ground. For this reason the latter configuration is called “skyhook” damper. The optimal skyhook structure is shown in Fig. 13 along with the corresponding optimal performance boundary, both shown as full lines in the figure. Note that this optimal structure could be inferred even before solving the above LQ problem. This follows from the fact that the LQ optimal control amounts to a feedback control based on two states with negative signs resulting from the fact that the closed-loops system is asymptotically stable.

Fig. 13

Optimal structure and performance trade-offs for 1 DoF model with PI of Eq. 13 (solid lines) and Eq. 22 (dashed lines)

The optimal performance line in Fig. 13 has been calculated using covariance Eq. (10) of Sect. 1.6, where for the sake of efficiency of presentation both states have been normalized w.r.t. $\sqrt {2{\uppi }AV}$ so that in general traversing rougher roads and/or at higher speeds leads to larger normalized acceleration due to limited available rattlespace. Just as in the case of optimal gain calculation, it has again been possible to analytically determine all PI quantities of interest. Actual calculation steps can be found in the Appendix. The resulting optimal trade-off is given by the following equation

$$ u_{LQ,rms,norm} = \frac{3\sqrt 3 }{{8x_{1,rms,norm}^{3} }} $$

(20)

This is represented in Fig. 13 by solid straight line with a slope of −3 on the log-log scale so that each 10% increase in available rattlespace facilitates 30% decrease in rms acceleration levels. The optimal trade-off line is parameterized by the weighting factor r. As it can be seen from the above equation for normalized force u _LQ , which in the present case equals sprung mass acceleration—larger weights r result in softer suspension settings with related smaller accelerations and larger rattlespace requirements.

In terms of actual practical realization, the skyhook damper structure cannot be implemented in the configuration shown in Fig. 13 since an inertial ground is not available from a moving vehicle. Thus in the context of a simple 1D, 1DoF model under consideration, the suspension members can only be placed between sprung mass and a “moving” ground. It is then shown in Hrovat (1982) by using the definition of passivity from Sect. 1.2 that so positioned suspension actuator must be an active device in order to implement the above LQ-optimal control strategy. It is interesting to mention that one “almost” optimal all passive structure was shown in Young and Wormley (1973). It consists of a serial combination of a spring and damper all in series with the sprung mass. However, although such a structure resulted in desired transfer functions there was a pole-zero cancellation corresponding to the unstable pole at zero. This reflects the inability of such a structure to support the sprung mass weight and also it violates the asymptotic stability property of the LQ-optimal solution.

The skyhook structure has a number of advantages. Since the skyhook damper is not in direct contact with the moving ground it can be tuned to higher damping values than its more conventional counterpart placed between the moving ground and sprung mass. Indeed, typical damping ratios for the conventional passive suspension are in the range of 0.2–0.3. On the other hand from the above equations one can see that the LQ-optimal damping ratio is significantly higher and equals $\sqrt 2 /2\, \approx \,0.7.$ The latter leads to more effective containment of sprung mass oscillations especially the ones induced by frequencies around vehicle dominant heave mode of oscillations typically around 1–2 Hz. This is the area where back-to-back comparison between active and passive suspensions is typically the most impressive when performed on a specially constructed test tracks with large, low frequency undulations that can excite the above heave mode at right vehicle speeds.

Consideration of external loads. It is interesting that the above elevated damping ratio will also help in containment of load-induced dynamic disturbances due to inertia effects when braking, accelerating, turning and similar (Hrovat 1997). Here it should be reminded that, as explained earlier, load disturbances have not been explicitly considered so far. However, for completeness we briefly mention the work of Young and Wormley (1973) where the authors address simultaneous effects of both road as well as load disturbances. The load disturbances were primarily due to aerodynamic forces acting upon a proposed high-speed ground transportation vehicle. These aerodynamic forces that included wind gust and similar were modeled as a random process in the form of a low-pass filtered white noise. The authors show that large and random load forces can significantly deteriorate the LQG performance from Fig. 13 where, depending on the magnitude of these forces, there could be a significant deviation in the optimal performance line toward saturation in the direction of the lower r.h.s. of the plot. However, these load effects become significant at very high wind speeds w.r.t. vehicles that were travelling at speeds up to 300 mph, such as high-speed trains discussed by Young and Wormley (1973). Another area of relevance is racecars such as Formula 1 vehicles, which are subject to large aerodynamic loads. For most of conventional vehicles this is not the case, and besides, since vehicle speed is known, one could use feed-forward controls to counteract any mean aerodynamic loading (as well as any loading due to inertia forces caused by braking, turning etc.).

Introduction of Semi-Active (SA) control. Although as discussed before it is not possible to implement the LQ-optimal skyhook structure using more standard passive components, one can still attempt to approach the LQ-optimal performance by using semi-active dampers (Crosby and Karnopp 1973). One such strategy would be to attempt to reproduce the optimal skyhook damper force whenever possible i.e. whenever there is a passive power required by the SA damper placed between sprung mass and moving ground (in reality this will be between sprung mass and unsprung masses, as discussed in Sect. 3.2 based on quarter-car 2DoF vehicle models). At any instant when this passivity constraint is not satisfied the SA force is turned off since this is in some sense the “closest” that one could get to optimal force at that moment. While not optimal this simple strategy leads to close to optimal performance in practice.

Inclusion of jerk in PI. Although the vehicle sprung mass vertical acceleration has been generally accepted as main indicator of passenger ride comfort, some authors (Fearnsides et al. 1974) argued that in addition to acceleration one should also consider jerk—derivative of acceleration—as an additional metric when evaluating ride comfort. This case was elaborated by Hrovat and Hubbard (1981). To this end we expand the original PI of Eq. (13) by one additional term proportional to the mean-square of expected sprung mass jerk. The augmented PI is then

$$ PI_{j} = E\left[ {x_{1}^{2} + r_{1} u^{2} + r_{2} \left( {du/dt} \right)^{2} } \right] $$

(21)

This can be next aligned with the standard LQG formulation by defining the normalized force i.e. sprung mass acceleration, u, as a new state, x₃, so that the derivative of u, which is equal to sprung mass jerk, then becomes the new control u₁. The resulting LQG optimization problem can now be stated as

$$ {\text{Minimize}}_{{{\text{w}} . {\text{r}} . {\text{t}} . {\text{u}}_{ 1} }} \left[ {PI_{j} = E\left( {x_{1}^{2} + r_{1} x_{3}^{2} + r_{2} u_{1}^{2} } \right)} \right] $$

(22)

subject to the following state equations

$$ \begin{aligned} dx_{1} /dt & = x_{2} - w(t) \\ dx_{2} /dt & = u\hat{ = }x_{3} \\ dx_{3} /dt & = u_{1} \\ \end{aligned} $$

(23)

with r₁, r₂ ≥ 0, r₁ + r₂ > 0, and the white noise process w(t) specified as before.

The LQ-optimal solution to this problem is given by the following feedback control law

$$ u_{1,LQ} = -Kx(t) = -k_{1} x_{1} - k_{2} x_{2} - k_{3} x_{3} $$

(24)

where it was again possible to obtain analytical solutions for control gains k₁,k₂ and k₃ as a function of weighting parameters r₁ and r₂ (Hrovat and Hubbard 1981). Moreover, since the new control, u₁, i.e. jerk, is equal to derivative of acceleration, and the latter is in turn equal to the original control, u, one can now write the original optimal control—normalized control force as

$$ u_{LQ} = {-}K\int {x(t)dt = - k_{1} } \int {x_{1} dt} - k_{2} \int {x_{2} dt} - k_{3} x_{2} $$

(25)

The first integral term on the r.h.s. equals the integral of rattlespace, second is integral of sprung mass velocity, which is equal to sprung mass position, and the last term involves sprung mass velocity. This leads to a structure depicted through dashed lines in Fig. 13. In addition to the skyhook damper this new LQG-optimal structure includes a skyhook spring and a (possibly fast) load-leveling device acting upon the integral of suspension deflection. Both—the skyhook damper and spring—are attached to an inertial ground that is in practice not available from a moving vehicle. As implied by the assumptions in Sect. 2.4, this “inertial” ground should represent a low-pass filtered or smoothed version of the road that retains large hills, valleys and similar. In practice this can be achieved through proper signal processing such as, for example, high-pass filtering of vehicle accelerations and velocities that would detrend large, low frequency components. In addition, with current efforts on 3D road mapping, it should be possible to know some portions of the road elevation well in advance thus further facilitating a creation of an appropriate “inertial” ground.

At this stage it is of interest to see how would the jerk-optimal suspension compare w.r.t. more standard acceleration-only case. Relevant analytical calculations have been performed in Hrovat and Hubbard (1981); the results fall in-between the full and dashed lines in Fig. 13. As indicated previously, the full line corresponds to the standard 1DoF case with acceleration-only weighting. The dashed line then represents the other special case when r₁ = 0 so that in this case only the vehicle jerk has been optimized as a measure of ride comfort. For this jerk-only weighting one can analytically express the relations between optimal normalized rms rattlespace and acceleration as

$$ x_{3,rms,norm} = \frac{{\sqrt {1000} }}{{36x_{1,rms,norm}^{3} }} $$

(26)

This is plotted in the log-log scale of Fig. 13 as a dashed straight line parallel to the standard case where r₂ = 0. As it can be seen from Fig. 13 the difference in performance in terms of acceleration-rattlespace trade-off is relatively small in-between the two extreme cases. For example, for the same level of rms suspension stroke the acceleration-only optimal suspension results in up to 26% lower acceleration levels or, equivalently, the jerk-only optimal suspension results in up to 35% higher rms acceleration levels while substantially reducing the related jerk (theoretically, for the standard case of acceleration-only weighting the rms jerk tends toward infinity, which in practice may lead to very large jerk levels).

In addition to the substantial jerk reduction, there are a number of other advantages associated with jerk-optimal suspension. This includes relatively large damping ratios between 0.5 and 0.7, and the presence of integrating, load-leveling component, which can provide good load containment and posture control. As opposed to more traditional load-leveling systems that may take seconds and minutes to establish new level, the present load-leveling system can be fast, depending on the desired overall closed-loop system bandwidth. It should be pointed out that the above skyhook spring-and-damper structure, and the fact that the optimal controller includes load-leveling, imply that—just as in the standard 1DoF case—one will necessarily need an active actuator to implement the jerk-optimal strategy.

Summary. While extremely simple the above standard 1D, 1DoF case provides many useful data and insightful information about the structure and key characteristics of an optimal suspension. This includes:

• Special so-called “skyhook” damper that provides superior isolation from road-induced vibrations and shocks;

• Superior heave mode damping with relatively high damping ratio of 0.7 when compared to conventional passive suspension damping, which is typically in the range between 0.2 and 0.3;

• Better dynamic load containment with up to 2–3 times smaller sags due to, for example, sudden braking or cornering (Hrovat 1997);

• Optimal skyhook algorithm points to a practical strategy for semi-active suspension control—today SA suspensions are already widely used in the industry and “skyhook” is one of the most popular approaches for controlling the SA devices.

• As an extension of the above standard 1DoF case one can also consider including jerk as an additional metric of ride (dis)comfort. This naturally leads to concepts of skyhook spring and fast load leveling resulting in substantial jerk reduction and thus further smoothing and filtering of the ground input effects.

It should be stressed again that this simple analysis and synthesis is only the first step in system-engineering based approach to advanced vehicle suspension design. For example, reference (Evers 2010) addresses design of optimized cabin suspensions for commercial trucks by starting with LQ design for the simple, 1 DoF models discussed above. It then introduces much more detailed 4 DoF quarter car models that include engine/powertrain module suspended on engine mounts and some other additional effects. It is interesting that after detailed analysis and appropriate approximations the study concludes that for the quarter-car models under considerations the acceleration- and jerk-optimal controllers based on the simple 1 DoF models perform close to the optimal controllers based on the full eight- and nine-state models, respectively.

It could be said that in terms of the System V diagram from Fig. 2 we are at around the tip of the left branch of V. While in general many more steps still need to follow down the System V diagram, including input signal processing, actuator design, load containment, system diagnostics and similar, nevertheless the above insight serves as a solid “first base” (in the lingo of American baseball) for subsequent R&D steps. At each such step we should gain some unique insight, which will in turn point out to additional tasks and details needed to bring production-worthy advanced active suspension to life.

3.2 Quarter-Car, 2DoF Case

A natural next step when progressing from the above simplest possible 1DoF model is to include the so-called unsprung mass associated with the wheel-tire component and all the related attached masses of steering and suspension subsystems. The resulting “quarter-car” model is shown in Fig. 8. Part (a) from Fig. 8 corresponds to the active suspension model we will be dealing with next, while models from parts (b) and (c) will be used later for comparison purposes in order to put our optimization results in proper perspective.

Wheel-hop dynamics and related constraint. Introduction of unsprung mass and tire stiffness brings an additional degree-of-freedom and an additional limitation or constraint upon our system. The constraint comes from the fact that this additional dynamics may lead to wheel-hop oscillations on uneven roads which in turn may lead to some loss of vehicle handling capability. More precisely, excessive wheel hop leads to large variations in tire normal force, which then results in the net loss of average normal force due to tire nonlinearity (concavity). Net effect is some loss of tire tractive and cornering i.e. handling capability. The latter is illustrated in Fig. 14 from Asgari and Hrovat (1991) where it can be seen that there is almost a linear relation between the rms tire deflection due to wheel hop dynamics and the percent deviation from an original, straight path of a vehicle subjected to sudden crosswind disturbance. Thus, as is common in related literature, we will try to limit the undesirable wheel-hop effects by introducing an additional quadratic penalty term for tire deflection in the original performance index, Eq. (13).

Fig. 14

Percent path deviation versus change in tire deflection for simulated sudden crosswind disturbance per (Asgari and Hrovat 1991)

Problem statement. Based on the above discussion and Fig. 14, we will next define an appropriate performance index for the 2DoF quarter-car problem as

$$ {\text{Minimize}}_{{{\text{w}} . {\text{r}} . {\text{t}} . {\text{u}}}} \left[ {PI = E\left( {r_{1} x_{1}^{2} + r_{2} x_{3}^{2} + u^{2} } \right)} \right] $$

(27)

subject to the following quarter-car dynamics corresponding to Fig. 8a

$$ dx_{1} /dt = x_{2} - w $$

(28)

$$ m_{us} dx_{2} /dt = -k_{us} x_{1} + U $$

(29)

$$ dx_{3} /dt = x_{4} - x_{2} $$

(30)

$$ m_{s} dx_{4} /dt = {-}U $$

(31)

where we have introduced an additional term r₁ x ²₁ in the above PI to penalize excessive tire deflections. The rest of the symbols are self-explanatory: m _us and k _us stand for unsprung mass and (tire) stiffness, respectively; w is again the white-noise ground velocity input; U represents the active suspension actuator force, and u is normalized active force, which again equals sprung mass acceleration, u = U/m _s .

After normalizing the above set of four state equations one can end up with another set of four with only two physical parameters instead of the original three (m _s , m _us , k _us ). The two normalized parameters are ω₁ = 2πf₁= (k _us /m _us )^1/2, which is natural “wheel-hop” frequency of the unsprung mass subsystem, and ρ = m _s /m _us . The normalized control, u, is now again equal to sprung mass acceleration. The resulting LQG problem was solved using control systems CAE/CAD tools such as Matlab and its predecessor Matrixx. Again, we were interested for a global solution that will provide a comprehensive map and insight into the potential benefits and limitations of the proposed active suspension concept. This was very much facilitated by the above tools.

The optimal control solution was in the form of a linear feedback of states, where according to Sect. 2.4 we assume that all four states are known

$$ u = -\sum\limits_{i = 1}^{4} {k_{i} x_{i} } $$

(32)

With this control and using the covariance Eq. (10) we can next calculate and plot various performance metrics. The global plot of normalized rms acceleration versus normalized rms rattlespace is shown in Fig. 15, parameterized by weighting factors r₁ and r₂. The plot has been obtained for the case with f₁=10 Hz and ρ = 10. From this “tornado-like” plot it can be seen that higher values of r₁ and r₂ result in less comfortable rides. Similar comments apply to Fig. 16, which shows normalize rms acceleration versus corresponding tire deflection.

Fig. 15

Optimal normalized sprung mass acceleration versus rattlespace trade-offs for quarter-car, 2 DoF vehicle model

Fig. 16

Optimal normalized sprung mass acceleration versus tire deflection trade-offs for quarter-car, 2 DoF vehicle model

More precisely, as it can be seen from Fig. 15, higher value of rattlespace penalty, r₂, results in smaller suspension excursions but larger sprung mass accelerations i.e. less comfortable ride. Similarly, from Fig. 16 it can be seen that higher value of the tire wheel-hop deflection penalty, r₁, results in smaller tire excursions but larger sprung mass accelerations, and thus better handling but worse ride comfort. The shaded areas in Figs. 15 and 16 correspond to the areas of practical significance for the present vehicle ride optimization problem. The following example from Hrovat (1997) illustrates how could one use the above plots in early phase of an advanced suspension design.

Illustrative example. Assume that you have been given a task to perform a preliminary, system-level study of potential benefits of an advanced active suspension applied to an autonomous commuter vehicle. In order to facilitate the unhindered activities such as reading, texting, writing and similar, the proposed suspension should deliver best possible ride quality within given design constraints during a typical commute at nominal speed of V = 80 ft/s (88.5 km/h) on a road characterized by road roughness coefficient of A = 1.6 × 10⁻⁵ ft (4.9 × 10⁻⁶ m).

The design constraints are that the rms tire deflection should remain bounded within 1 in. (2.54 cm) from static equilibrium value 99.7% of time, and that the rms of suspension deflection (rattlespace) should remain bounded within 3 in. (7.62 cm) from its static value 99.7% of time. What would be the best possible i.e. the lowest rms acceleration in this case based on the above quarter-car model with f₁=10 Hz, ρ = 10, and assuming that the road input is characterized by a Gaussian distribution? How realistic is the resulting closed-loop design in terms of underlying dynamics, stability, robustness and bandwidth requirements?

We start by normalizing different constraint variables so that we can then use the global optimal plots of Figs. 15 and 16. Since for most on-road operations the tire (wheel-hop) constraint is more stringent than the rattlespace counterpart we first explore the limiting case of x₁. The Gaussian assumption and 99.7% time requirement (i.e. the well-known 3σ rule) imply that the rms tire deflection must be less than 1/3 in. or 0.85 cm. The normalized rms tire deflection for the above speed and road then must remain within

$$ x_{1,rms,norm} < 0.31\,{\text{s}}^{1/2} $$

(33)

Choosing the above as the limiting value we proceed to Fig. 16 from where we obtain the corresponding limiting i.e. smallest possible normalized rms acceleration

$$ u_{rms,norm} \, \approx \,10\,{\text{s}}^{ - 3/2} $$

(34)

Choosing u _rms,norm  = 10.9 s^−3/2 results in only 3%g rms acceleration. This particular candidate design is indicated as point A₁ in Fig. 16. Note that this level of rms acceleration is at the lowest r.h.s. end of the scale used for subjective tests in Fig. 3 thus securing highest level of ride comfort.

At this stage we need to check if the rattlespace constraint has been satisfied. To this end we enter the value of 10.9 s^−3/2 into the vertical, normalized rms acceleration axis on Fig. 15 from where, for the aforementioned design point A, we get the normalized rms rattlespace value as

$$ x_{3,rms,norm} = 0.605\,{\text{s}}^{1/2} $$

(35)

which then results in actual rms value of only 0.67 in. implying 3σ value of 2 in. (5.08 cm). This is well within the required ±3 in. constraint thus showing that the most critical constraint in the present example is on tire deflection and related road holding and handling. As indicated earlier, this is usually the case with most on-road operating situations.

For the above design A we can next determine from Fig. 15 the associated PI weights

$$ r_{1} = 1100,\quad r_{2} = 100 $$

(36)

With these values one can then obtain the optimal control gains

$$ k_{1} = 6.084,\quad k_{2} = - 0.548,\quad k_{3} = 10.0,\quad k_{4} = 4.438 $$

(37)

so that the closed loop system eigenvalues become

$$ e_{1,2} = -2.2\, \pm \,j2.26,\quad e_{3,4} = -2.75\, \pm \,j62.9 $$

(38)

Note that the first set of eigenvalues corresponds to the well-damped oscillatory mode associated with vehicle sprung mass heave or vertical vibration. It is characterized by a natural frequency of only 0.5 Hz with the damping ratio of 0.7, which by now should be well known from our previous 1DoF “skyhook” study (it will be shown later that this 0.7 ratio is also LQ-optimal for vehicle models of higher dimensions, i.e. 2D and 3D models). The relatively low natural frequency of 0.5 Hz falls significantly below most of current vehicle suspensions and is an indication of an overall “softer” suspension setting.

The second oscillatory mode corresponds to the wheel-hop dynamics. It is characterized by natural “wheel-hop” frequency of 10 Hz, and relatively small damping ratio of only 4.4%. Whether this small amount of wheel-hop damping will be sufficient will depend on the operating conditions, particular adaptive optimal control strategy used, and similar factors. For example, this may be acceptable while driving on the long straight stretches of the road where handling may be less critical. On the other hand driving on winding stretches of the road may require much higher wheel hop damping and thus an optimal control strategy that will adapt to different driving conditions, as needed. We will address this—along with some possible hardware i.e. structural modifications—in more detail in subsequent sections.

Before closing this illustrative example let us summarize how we answered the original inquiries. First, we have succeeded to quantify what is the best possible ride comfort level within given design constraints. Moreover, we have obtained some insight about the resulting closed-loop system dynamics. While stable it did display some potential issues and challenges such as robust containment of relatively low wheel-hop damping. The latter may have to be addressed through software and possibly hardware means, as we will discuss later.

Finally, a word of caution regarding bandwidth requirements of the resulting closed-loop system. On the first glance, based on the above system eigenvalues it would appear that the bandwidth requirements on the actuator force production would extend to 10 Hz and more. However, such relatively high-bandwidth systems can be challenging to implement in practice since they tend to negatively influence so-called “secondary ride” i.e. they tend to transmit high frequency road induced disturbances. This also points out to the fact that force-related bandwidth requirements are only part of the story. Indeed, even if we were required to keep the actuator force constant and equal to vehicle weight (for “bestest” possible ride with zero acceleration) i.e. if we were asked for zero force bandwidth, this task would by no means be trivial due to the fact that our actuator mounting points are subject to constant motion and road-induced disturbance. Some of these important design-related issues will be discussed later and some are beyond the scope of this system-level study at the left-top end of System V diagram of Fig. 2.

Passive suspension comparison. It can be shown (Smith and Walker 2000) that the above optimal suspension strategy requires an active device, which is to be expected based on our previous 1DoF results. At this stage it is appropriate to ask how does this active suspension (Fig. 8a) compare with a conventional passive counterpart from Fig. 8c. This is shown in Fig. 17, which focuses on the more critical constraint i.e. tire deflection versus sprung mass acceleration trade-off. For simplicity we show only the limiting curves for r₁ ≅ 0, and r₂ ≅ 0. Superimposed on the figure are traces of passive suspension performance trade-offs for heave mode natural frequencies between 1 and 1.5 Hz, and damping ratios varying between 0.02 and 1.

Fig. 17

Comparison between conventional passive suspension (point P1) and optimal active counterparts (points A1 and A) in terms of ride and handling trade-offs

From Fig. 17 it can be seen that the best passive suspension setting—in terms of present trade-offs between smooth ride and firm handling—corresponds to point P₁ with natural frequency of 1 Hz and damping ratio of 0.3. The latter is typically in the range seen on most conventional vehicles that have been optimized through many generations of iterative work primarily based on experience and intuition. In addition, it can be seen that the best active setting for the same amount of tire deflection corresponds to point A₁, which is only 11% below the passive counterpart in terms of rms acceleration. Thus if one focuses at only this narrow region (as was the case with prior investigations by some authors) then one would conclude that there is not much potential in active suspensions, especially taking into account that most likely the results of the present simplified high-level study constitute upper bounds of best possible performance.

However, one inherent advantage of active suspensions is that they can adapt to different road/driving conditions so that different control settings can be used on different stretches of the road. In other words, we could move either to the right or left of point A₁ in Fig. 17. Thus on the long straight stretches of a highway, such as exist in Nevada, for example, one could relax the settings to mimic a soft suspension with very smooth ride thus moving to the right of point A₁. This is shown as point A, which corresponds to our Illustrative Example design. Note that in this case there is a 67% reduction in rms acceleration when compared with the passive case P₁. According to Fig. 3, such as large reduction can lead to substantial improvement in subjective ride comfort ratings.

Alternatively, on winding roads one can go for much firmer suspension settings for superior road holding and handling. In this case one would move to the left of point A₁ trading improved vehicle agility for reduced ride comfort. This is not possible for passive suspensions, which cannot move much farther to the left from point P₁.

We will next extend our comparison to Frequency Transfer Functions (FTF) between the above three design cases, A₁, P₁, and A. This is shown in Figs. 18, 19 and 20 for the three PI metrics of primary interest, sprung mass acceleration, tire deflection and suspension stroke, respectively. By associating the rms values of these quantities with the area under different frequency response curves we can clearly see from Fig. 18 that design A will lead to much smaller rms acceleration. On the other hand from Figs. 19 and 20 we can also see that this design results in a large resonant peak at the tire natural frequency, which will lead to increased wheel hop. This is in accordance with our previous observation that the design A will result in relatively small wheel-hop damping. From the above FTF’s we can make the following additional observations as given in the following paragraph/subsection.

Fig. 18

Frequency response function of sprung mass acceleration versus ground input velocity for passive and active suspensions from Fig. 17

Fig. 19

Frequency response function of tire deflection versus ground input velocity for passive and active suspensions from Fig. 17

Fig. 20

Frequency response function of suspension stroke versus ground input velocity for passive and active suspensions from Fig. 17

Invariant Points (IP). Turning our attention back to Fig. 18 it can be seen that both active suspension settings A and A1, do a good job in reducing the acceleration levels around the dominant, sprung mass heave mode of oscillations in the neighborhood of 1 Hz. However, this is not the case with the second oscillatory mode around the wheel hop frequency of 10 Hz where all three transfer functions seem to pass through the same point. Indeed, it turns out that this is exactly an invariant point for our original quarter-car structure. This was first observed by Thompson (1971) and then extended by Hedrick and Butsuen (1990) to include an additional invariant point at the frequency corresponding to the case of locked secondary suspension i.e. sprung and unsprung masses vibrating in synch on a tire spring. This can be seen from the following equations where we start with the original set of four state Eqs. (28–31). Summing up second and fourth equation we get the overall momentum-like equation for the two-mass subsystem

$$ m_{s} \frac{{dx_{4} }}{dt} + m_{us} \frac{{dx_{2} }}{dt} = -k_{t} x_{1} $$

(39)

By defining (absolute) displacements of sprung and unsprung masses as x _s and x _us , and substituting $x_{us} = x_{1} + \smallint wdt$ in the above equation, the corresponding Laplace transform becomes

$$ m_{s} sX_{4} (s) + \left( {k_{t} + m_{us} s^{2} } \right)X_{1} (s) = -m_{us} sW(s) $$

(40)

Dividing the above equation by road velocity Laplace transform quantity, W(s), and defining the three transfer functions associated with the PI acceleration, rattlespace, and tire deflection metrics as

$$ G_{A} (s) = \frac{{sX_{4} (s)}}{W(s)},\quad G_{R} (s) = \frac{{X_{3} (s)}}{W(s)},\quad G_{TD} (s) = \frac{{X_{1} (s)}}{W(s)} $$

(41)

after dividing with W(s) and setting s = jω, we can rewrite the above equation as in Hedrick and Butsuen (1990)

$$ m_{s} G_{A} (j\omega ) + \left( {k_{t} - m_{us} \omega^{2} } \right)G_{TD} (j\omega ) = - m_{us} j\omega $$

(42)

From this equation we can conclude that at the wheel hop natural frequency $\omega_{1} = \sqrt {k_{t} / {m_{us}}}$ the sprung mass acceleration transfer function, G _A , has an invariant point equal to

$$ G_{A} (j\omega_{1} ) = - j\frac{{\sqrt {m_{us} k_{t} } }}{{m_{s} }} = - j\frac{{\omega_{1} }}{\rho } $$

(43)

which, for our case with ρ = 10, f₁ = 10 Hz, is equal to j 2π. The corresponding gain or magnitude of G _A is 2π or $15.97\,{\text{dB}}\,\approx\,16\,{\text{dB}}$ (cf. Fig. 18).

Using similar kind of manipulations starting with the above Eq. (39) but this time substituting x _s = x _us + x₃, we end up with the following equation

$$ -m_{s} \omega^{2} G_{R} (j\omega ) + \left[ {k_{t} - \left( {m_{s} + m_{us} } \right)\omega^{2} } \right]G_{TD} (j\omega ) = -( {m_{us} + m_{s} })j\omega $$

(44)

From this equation we see that there is now an invariant point at

$$ \omega_{2} = \sqrt {k_{t} /\left( {m_{us} + m_{s} } \right)} = \omega_{1} /\sqrt {\rho + 1} $$

(45)

where the rattlespace or suspension deflection transfer function, G _R , has the following constant value

$$ G_{R} (\omega_{2} ) = j\frac{{\left( {m_{us} + m_{s} } \right)}}{{m_{s} \omega_{2} }} = j\frac{\rho + 1}{{\rho \omega_{2} }} $$

(46)

For our case with ρ = 10, f₁ = 10 Hz, we have ω₂ = 2π3.02 and corresponding gain of G _R is 0.058 or −24.7 dB (cf. Figure 20). As mentioned previously the above invariant point frequency ω₂ corresponds to natural frequency of a combined sprung and unsprung mass oscillating on tire spring; it is typically in the range between 3 and 5 Hz.

Based on Eqs. (42) and (44) it was observed by Hedrick and Butsuen (1990) that once one of the above three transfer functions is specified the other two follow from the constraint equations. For example, choosing G _A (s) then implies that G _TD (s) follows from Eq. (42), which in turn fixes G _R via (44). A physical interpretation of the above invariance is that within the given quarter-car structure of Fig. 8a we observe that a single suspension actuator placed in-between sprung and unsprung masses is asked to perform conflicting tasks of minimizing sprung mass acceleration for improved ride comfort while at the same time providing adequate wheel hop damping and road holding. It should be pointed out that the above invariances and related limitations hold independent of the particular suspension type—passive, active or semi-active—or control strategy used, as long as the fundamental mechanical structure remains the same.

3.3 Comparison Between 1DoF and 2DoF Cases

In order to put the above results into proper perspective we next try to compare the two basic active suspension cases studied so far: the simple 1DoF configuration of Fig. 7 and the 2DoF case from Fig. 8a. To this end we overlay the 1DoF optimal trade-offs over the corresponding 2 DoF results as shown in Fig. 21. From this figure we can make two observations. From the lower right side we can see that for the most part the optimal 1 DoF case results are significantly better i.e. below the 2 DoF trade-offs. This is to be expected since the 2 DoF problem introduced one more constraint—tire deflection—that should then lead to less favorable outcome.

Fig. 21

Comparison between “basic” 1DoF and 2DoF optimization trade-offs

On the other hand from the upper left side we see that in some areas the reverse is true i.e. the 1 DoF performance appears even worse than the 2 DoF case! The reason for this apparent discrepancy is that we are not actually comparing apples to apples since on the horizontal axis we are comparing total deflection between sprung mass and ground of the 1 DoF system with the deflection between sprung and unsprung masses of a 2 DoF system. As the rattlespace constraint becomes more and more stringent i.e. as the suspension becomes more and more stiff the advantage of the 2 DoF structure becomes more pronounced due to the ameliorating effects of primary suspension i.e. due to more pronounced contribution from tire deflection.

To rectify this situation and facilitate more appropriate (apples-to-apples) comparison, we introduce a modified 1 DoF model shown in Fig. 8b. It is a limiting case of standard 2 DoF model with unsprung mass reduced to zero. The corresponding optimal trade-offs are shown in Fig. 22, where we can now see—as one would expect—that the upper left side of the plot is close to and below the corresponding 2 DoF line. At the same time the lower right side approaches and merges with the previous “standard” 1 DoF case optimal trade-offs.

Fig. 22

Comparison between 2DoF and various 1DoF optimization trade-offs

The observation that this optimal structure with vanishing unsprung mass, m _us = 0, offers superior performance w.r.t. corresponding 2 DoF counterparts is logical consequence of the fact that reduced unsprung mass for a given sprung mass, i.e. larger ρ, leads to improved performance trade-offs as shown by Hrovat (1988), for example. In the context of the present problem the new 1 DoF structure can be seen as limiting case of 2 DoF model as unsprung mass becomes smaller and smaller. Another observation from the lower right side of the plot is that for most operations where good ride is of primary concern, we see that there is a significant loss of performance associated with the 2 DoF models, which is primarily due to the additional, wheel-hop imposed constraint.

3.4 Dynamic Vibration Absorber

At this stage it would be natural to inquiry how we could recover some of the above lost performance and thus sway the optimal trade-offs in the direction of the arrow in Fig. 22. To address this inquiry we know from the Invariant Points (IP) discussion that this will not be possible within the given 2 DoF structure of Fig. 8a. Thus the answer should be pursued through structural i.e. hardware modification. One logical candidate to consider is tuned mass damper or Dynamic Absorber (DA).

As we know from the IP subsection, one of the most critical invariant points is at the wheel-hop frequency and associate pronounced resonant peak due to relatively low damping in this mode. Thus, if we could increase this damping without negatively influencing sprung mass accelerations we may achieve our goal. This leads us to the modified quarter-car configuration (3 DoF system) shown in Fig. 23 where we use a DA tuned to wheel-hop frequency to alleviate the above issue i.e. increase wheel hop damping without simultaneously increasing sprung mass acceleration. The DA mass was chosen as one tenth of the unsprung mass and corresponding DA damping ratio was chosen as 0.2.

Fig. 23

Quarter-car 2DoF vehicle model with dynamic vibration absorber (DA)

The results of this global study are shown in Figs. 24 and 25. As it can be seen, the DA effectively sways the optimal trade-offs toward the corresponding 1 DoF case, which is especially pronounced in the case of acceleration versus rattlespace trade-off in Fig. 24. This means that with the help of DA, our original smooth ride design point A with very lightly damped wheel-hop mode now transform to point A′, where based on Figs. 24 and 25 we can see that both the sprung mass acceleration and tire deflection are further reduced resulting in improved ride comfort and handling. From these figures we can conclude that further substantial improvements are possible up to the point where now rattlespace constraint becomes the limiting factor. For example, for design point A″ we see that suspension deflection requirement is the same as for the previous design case A while tire deflection and especially sprung mass acceleration are both reduced.

Fig. 24

Impact of dynamic absorber on ride versus rattlespace trade-offs (Hrovat 1997)

Fig. 25

Impact of dynamic absorber on ride versus handling/tire deflection trade-offs (Hrovat 1997)

At this stage to put all this into broader perspective and gain additional insight into DA benefits, it is appropriate to compare performance of the above designs A and A′ with design case A₁ and related passive case P₁ discussed in Sect. 3.2 (also see Fig. 17). The corresponding frequency response curves are given in Figs. 26 and 27, which show sprung mass acceleration and tire deflection gain transfer functions, respectively. From Fig. 26 we see that that for all three cases, P₁, A₁, and A, the sprung mass accelerations pass through the invariant point at the wheel-hop frequency of 10 Hz. However, for case A′, which includes a DA, we see that the invariant peak at 10 Hz has been substantially reduced (by more than 10 dB). This demonstrates that structural changes introduced by DA eliminate this important and detrimental quarter-car constraint. At the same time, from Fig. 27 it can be seen that the strong resonant peak in tire deflection at 10 Hz has been substantially reduced when compared with the soft case A′ with the potential for further reduction at the resonant peak but at the expense of more narrow notch. All those considerations can also be seen in related time responses where excessive oscillations of the soft suspension case A′ have been contained with the help of DA.

Fig. 26

Frequency response function of sprung mass acceleration versus ground input velocity for passive and active suspensions with and w/o DA

Fig. 27

Frequency response function of tire deflection versus ground input velocity for passive and active suspensions with and w/o DA

The above study demonstrates significant potential benefits of dynamic vibration absorbers. Their main drawback is added weight and more challenging packaging requirements. To date there has been only one widespread, production application of the DA concept. This was implemented in the highly popular Citroen 2CV (sub)compact vehicle that was legendary for its supreme ride, especially for such a small vehicle. According to the June 1987 Car magazine article, the 2CV ride was characterized by the following statement, “You will be enjoying the scenery on top of a chassis which, in terms of small car terms, has no peer in ride comfort.”

In closing this section we observe that we did not re-optimize the total 3 DoF system with the DA included. This would lead to further improvements at the expense of increased complexity since we would be feeding back six states instead of four. Additional refinements are possible by optimizing combined or “hybrid” system consisting of an active actuator and DA with free design parameters (DA mass, damping, stiffness). One could also contemplate an active or at least SA dynamic vibration absorber as proposed by Hrovat (1990). We will later focus on the ultimate i.e. best possible quarter car configuration in the sense of LQG-optimal performance. But first let us introduce an interesting mechanical element that shares some (but not all of) characteristics of dynamic vibration absorber.

3.5 Inerter and DA Comparison

Inerter was introduced by Smith (2002) as a mechanical device where inertia-like force is proportional to the difference of two accelerations across the device terminals shown in the insert of Fig. 28, i.e.

Fig. 28

Race-car suspension with an inerter: schematic diagram (a); equivalent quarter car schematic (b); and corresponding bond graph (c)

$$ F = M_{eff} \frac{{d\left( {v_{L} - v_{R} } \right)}}{dt} $$

(47)

where M _eff stands for the effective (linear) inertia due to reflected inertias of the inner rotational masses within the inerter of Fig. 28, and v _L and v _R stand for the corresponding left and right terminal velocities, respectively. Note that, in terms of bond graphs, the above device is a one-port with two distinct terminals. Further generalization of this interesting concept might be possible in the form of a two-port that represents inertia-coupling that is characteristic of planetary transmissions, for example (Hrovat et al. 2000).

It can be said that inerter is in part similar to the more common inertia element where inertia force is proportional to the acceleration of the inertia element or derivative of the associated momentum (Karnopp et al. 2012). Indeed, by grounding one of the two terminals we end up with a standard inertia element.

It is interesting that the (generalized) inerter elements were present for quite some time in different mechanical and hydraulic systems such as differentiators, planetary gears, engine mounts, and hydraulic suspensions, for example. This can also be seen from corresponding bond graphs where inerters can be revealed through non-trivial attachments of inertia elements to a zero junction, where the latter indicates a difference of two speeds or generalized flows (Karnopp et al. 2012; Karnopp and Rosenberg 1970; Hrovat et al. 2000). While some of them may not satisfy somewhat restrictive requirements originally postulated in Smith (2002) they are certainly very useful as demonstrated through millions of vehicles and other devices. In any case, Smith deserves credit for explicitly identifying and promoting this somewhat ubiquitous yet “hidden” structural component, and at the same time devising an interesting practical mechanical inerter device that has found significant applications in the car-racing arena.

The device is sketched in Fig. 28 in the context of a racecar application. Based on available information (Clarke 2012; Smith 2011; Scarborough 2011) the setup seems to consist of a standard mechanical spring and damper configuration augmented with a black-box device placed across the left and right side of a vehicle front suspension elements or rockers. Assuming that the black box device is an inerter without additional internal components and assuming symmetrical road inputs at the left and right side of a vehicle an equivalent quarter car representation and corresponding bond graph model are shown in Fig. 28b and c, respectively.

From the bond graph it can be seen that in this particular case the inerter is represented by an inertia element in differential causality (Karnopp et al. 2012). However, this may not always be the case. For example, inserting an additional spring in series with the current C-R-I suspension setup would remove this constraint. Based on the bond graph of Fig. 28c, it can be deduced that the sprung and unsprung masses effectively act in series with the inerter with the reflected inertia, J _eff . This can be seen directly from the bond graph due to the corresponding 0-junctions.

In reference (Smith 2002) it is shown that under certain conditions the inerter-based suspension structure can produce notch filter-like effect similar to tuned mass dampers or dynamic vibration absorbers (DA). Specifically, this was demonstrated for a single mass case where such mass has been supported by a vibration absorption-type suspension consisting of a parallel combination of inerter and spring, which were in turn placed in series with a parallel combination of another spring and a damper. The underlying assumption was that the mass is subject to the base input oscillations with strong single-component frequency content. It was then shown that by tuning the inerter-spring combination to this input frequency one could achieve complete disturbance cancellation comparable to similarly tuned DA.

According to available literature the inerter was used to improve wheel adherence to the track with Formula 1 racecars although the quantitative extent of this improvement was not given. It is interesting that a DA-type device used by a competing team was not allowed by the Formula 1 governing body although the effects were apparently similar (Clarke 2012; Scarborough 2011). It is possible that this was due to lack of full understanding of how these two devices operate in the context of car racing.

While there was strong similarity between inerter-based and DA-based vibration isolation in the case of single mass exposed to base oscillation, this similarity seems to brake down in the case of a 2DoF quarter car configuration. In particular, note from Fig. 28 that the inerter, as a one-port device, imposes equal forces on the sprung and unsprung masses so that the Invariant Point constraint at the critical wheel-hop frequency still applies (it is interesting that in the case of no system damping this IP constraint reduces to a singularity). This is fundamentally different from the DA structure of Fig. 23. Consequently it is expected that the quarter-car performance will not improve to the degree seen with the DA. Indeed, the available publications (Smith and Wang 2004; Papageorgiou and Smith 2006; Scheibe and Smith 2009) seem to confirm this, although they were based on somewhat localized studies where only one or maximally two attributes were considered at the time. Further extensions could include jerk as component of ride comfort, although this may disadvantage inerter-based suspensions due to their inherent inertia-like effects and potentially less favorable high-frequency roll-off.

3.6 Best Possible Quarter-Car Performance and Related Structure

Based on encouraging results with DA-enhanced quarter-car structure it was natural to look into different possible extensions and variations of this concept in a search toward best possible quarter-car performance. To this end reference (Hrovat 1990) investigated potential benefits of augmenting the conventional, passive tuned mass damper or DA with an additional active actuator acting in-between the DA and unsprung mass. This lead to up to 35% lower sprung mass acceleration and 26% lower tire deflection w.r.t. previously mentioned LQ optimal case A″ with passive DA—see Figs. 24 and 25. At the same time the suspension stroke or rattlespace excursions have been kept almost the same in all cases. Similar results were obtained for the configuration where only the DA-equivalent mass was kept without the accompanying spring and damper so that only an active “unsprung” actuator was used to suspend the DA-equivalent mass. However, the required active actuator energy and force were significantly higher in this case thus confirming the usefulness of a full DA structure even when augmented by an active actuator attached to the DA mass.

Observing that significant additional benefits in performance resulted from having unequal forces acting upon sprung and unsprung masses facilitated by the DA-like structure, we now pose the following optimization problem as an extension of the previous analysis. The problem setting is illustrated in Fig. 29a. This time we are considering two independent actuators—one acting upon the sprung mass and the other on the unsprung counterpart. Note that while in the previous DA-based setting we were limited how much force could the unsprung actuator impose due to limiting motion capabilities of the DA mass, this sort of constraint is not imposed now.

Fig. 29

Formulation of optimal 2DoF two-actuator problem (a), and corresponding best possible, optimal structure (b)

In addition we make use of the fact that there is a natural two time-scale separation associated with quarter-car problem, where the slow mode corresponds to the sprung mass oscillatory mode around 1–2 Hz and the fast mode corresponds to unsprung mass wheel-hop mode around 8–12 Hz. Anticipating this separation we structure the states as shown in Fig. 29a. The associated PI then has the same three components (weighted means square of sprung mass acceleration and tire and suspension deflection) as before with an additional term penalizing the unsprung force

$$ {\text{Minimize}}_{{{\text{w}} . {\text{r}} . {\text{t}} . {\text{u}}_{ 1} , {\text{u}}_{ 2} }} \left[ {PI = E\left( {u_{1}^{2} + r_{1} x_{3}^{2} + r_{2} \left( {x_{1} - x_{3} } \right)^{2} + r_{3} u_{2}^{2} } \right)} \right] $$

(48)

where u₁ is the sprung mass acceleration equal to U _s /m _s , and u₂ corresponds to normalized unsprung force, i.e. u₂= U _us /m _us . Now letting the penalty r₃ on normalized unsprung force be very small one ends up with the so-called (partially) cheap controls (Saberi and Sannuti 1987). In the process we can think of the cheap control u₂ as an essentially “structure optimizer”. Eventually letting r₃ go toward zero and transforming the cheap control problem to an equivalent singular perturbation problem we end up with the optimal structure depicted in Fig. 29b (Hrovat 1990).

Note that the structure optimizer u₂ was used to effectively eliminate the unsprung mass, which is in accordance with the established fact that reduced unsprung mass helps the overall ride and handling performance (Hrovat 1988). This was also confirmed by our previous analysis from Fig. 22 comparing the optimal 2 DoF and 1 DoF performances. In addition, the structure optimizer i.e. cheap and fast control adjusts the incremental stiffness of primary and secondary suspensions to best accommodate the respective weights r₁ and r₃, thus resulting in the best possible performance. Once the wheel hop mode has been so contained the sprung mass control u₁ can then be used to contain the slow, sprung mass mode according to the well-known 1 DoF LQ-optimal rules with skyhook damper and an overall damping ratio of 0.7.

The above “most” optimal quarter-car structure results in additional substantial benefits. An illustrative example from Hrovat (1990) shows normalized sprung mass acceleration of only 1.17 s^−3/2, with well-contained tire and suspension deflections. While it would be difficult to realize such a suspension in practice (e.g. it may require very powerful jets on each, sprung and unsprung masses) these limiting results can serve as a benchmark of best possible performance that any practical suspension realization can be compared against. It also confirms our previous results and intuition about the superiority of a simple 1 DoF structure in the context of a quarter-car vehicle models.

As a final remark in this section we mention that we could also pose the question what is the best possible passive two-port suspension setup as a counterpart to the active setting from Fig. 29a. To this end one could follow similar approach based on passive network optimization and synthesis that was elegantly done in Papageorgiou and Smith (2006) for the case of passive one-port suspension structures. It is expected that some portions of such a two-port extension would contain DA-like components. Further optimal passive extensions could include cross-coupling between left and right as well as front and rear sides of a vehicle, such as can be seen in so-called interconnecting or equalizing-type suspensions first found on Citroen 2 CV (Pevsner 1957), which was well-known for its smooth ride.

3.7 2D, Half-Car Models

Since we have pretty much exhausted various quarter-car optimization scenarios the next logical step is to consider the half-car models and related LQ optimization. We start with 2 DoF half-car model shown in Fig. 30. It includes vehicle heave and pitch modes.

Fig. 30

Half-car, 2D vehicle model with 2DoF (heave and pitch)

This is reflected in the following performance index

$$ PI = E\left[ {r_{1} \left( {d^{2} z/dt^{2} } \right)^{2} + r_{2} \left( {d^{2}\Theta /dt^{2} } \right)^{2} + r_{3} z_{f}^{2} + r_{4} z_{r}^{2} } \right] $$

(49)

where different quantities have been defined w.r.t. Fig. 30 with z _f and z _r standing for the front and rear suspension rattlespace—in the present case where we did not include the unsprung masses, this is the distance between the ground and front and rear end of the sprung mass. Note that this PI could be slightly modified to explicitly include the acceleration at a specific position such as driver’s or some (VIP) passenger’s seat, for example.

Optimization of the above PI under four state equations representing the simplest possible 2D, Half-car model has been done in Krtolica and Hrovat (1992). It is interesting that in this case it was still possible to analytically solve the LQ optimal problem. The resulting closed-loop control system was again characterized by the optimal damping ratio of 0.7 in both heave and pitch modes. The same reference establishes necessary and sufficient conditions to decouple the original two-dimensional, 2 DoF, half-car LQ optimization problem into two one-dimensional, 1 DoF, quarter-car problems; these conditions are

$$ \begin{aligned} & M_{s} \cdot l_{f} \cdot l_{r} = J_{p} \\ & r_{1} \cdot l_{f} \cdot l_{r} = r_{2} \\ \end{aligned} $$

(50)

where M _s and J _p are vehicle sprung mass and pitch moment of inertia about the center of mass, CM, and l _f and l _r are front and rear distances from CM (see Fig. 30). The first condition depends on vehicle physical parameters and is typically satisfied within 20% by most present vehicles. The second condition depends on the PI weighting parameters r₁ and r₂, which are at designer’s disposal and can often be chosen to satisfy the above constraint while at the same time leading to a reasonable design, i.e. compromise between heave and pitch aspect of ride.

Through the above decoupling one can see the connection between the previously established wealth of results for the simple 1 DoF quarter-car vehicle models and the corresponding 2 DoF, half-car case. This parallel can be extended to more complex 4 DoF, half-car models that include unsprung masses, as shown in Fig. 31.

Fig. 31

Half-car, 4DoF vehicle model (a) and, corresponding decoupled model consisting of two quarter-car, 2DoF sub-models (b)

It turns out that the same decoupling conditions apply in this case as well leading to two decoupled 2 DoF, quarter-car models shown in Fig. 31b. This again establishes the link between more complex half-car models and corresponding quarter-car counterparts for which there is an abundance of previously established results. In practice this means that a reasonable approach to an active suspension system design may start with controlling the corners enhanced with some additional, typically feed-forward action to counteract different pitch disturbance due to braking, accelerating and similar.

At this stage we note that the 2D setup of Figs. 30 and 31 facilitates preview of road ahead of certain points of a vehicle. In particular we see that front wheels could serve as sensors or previewers of road inputs ahead of rear suspension units. In general, having some advance knowledge of the future disturbances may be invaluable in some situations and highly beneficial in many.

While in case of most automobiles this kind of preview may be relatively short and of limited effectiveness, it could be much more pronounced in some other vehicles such as heavy-duty trucks (“18-wheelers”) and especially trains (Karnopp 1968). Similar applies to some more recent transportation paradigms under consideration such as vehicle platooning or convoys of trucks that is becoming more and more realistic proposition due to rapid advances in sensors, actuators and processing intelligence needed for (semi)autonomous driving. This includes preview information provided by on-board cameras, lidars, and availability of 3D road maps and V2V communication, where vehicles ahead may serve as “sensors” for following vehicles.

One of the first studies investigating potential benefits of preview was done by Bender (1967a) who started with logical simplest case of 1 DoF vehicle models. Using the Wiener-Hopf optimization approach (which is similar to—albeit more restrictive than—the hereby pursued LQG approach) the author obtained the global optimal performance maps shown in Fig. 32, where the axes are the same as in Fig. 13 with horizontal axis corresponding to normalized rattlespace (or, more precisely, to the distance between sprung mass and road) and vertical axis corresponding to normalized sprung mass acceleration. The straight line for no preview (i.e. preview time T = 0 s) corresponds to the case studied earlier—this was represented as the full line in Fig. 13.

Fig. 32

Optimal 1DoF active suspension (S) performance for different preview times, T (Bender 1967)

On the other hand the line with infinite preview (T = ∞) indicates the best possible performance under preview. Based on the analysis from Bender (1967a) the optimal infinite preview line in a log-log scale of Fig. 32 can be expressed as

$$ u_{rms,norm} = \frac{3\sqrt 3 }{{128x_{1,rms,norm}^{3} }} $$

(51)

Comparing this expression with the corresponding expression for the 1 DoF case without preview (see Eq. (20) in Sect. 3.1 and Eq. (72) in the Appendix) one can conclude that there is a substantial, 16-fold, potential for reducing the sprung mass acceleration while keeping the overall rattlespace the same. While this requires knowing all of the future, from Fig. 32 it can be seen that even knowing only 0.5 s of advanced road ahead could lead to significant benefits in the context of the present 1 DoF problem.

An extension of the above 1 DoF preview case toward the 2 DoF quarter-car counterpart was considered in Hrovat (1991a). The approach taken was to shift the time point of reference so that instead of considering a preview system one ends up with a dynamic system with delays for which there is an abundance of research results (Richard 2003; Fridman 2014). This was achieved by shifting the observer vantage point from vehicle to some distance ahead of vehicle corresponding to the magnitude of preview. Figure 33 illustrates this graphically.

Fig. 33

Conceptual representation of road preview process

The resulting carpet plots of normalized rms acceleration versus suspension rattlespace and tire deflection are shown in Figs. 34 and 35, respectively. While, as it might have been expected from previous non-preview analysis, the performance improvements are now less dramatic than for the 1 DoF case of Fig. 32, the plots still reveal opportunities for further significant improvements in both ride as well as handling aspects of vehicle performance. In particular, from Fig. 35 one can see that even a relatively short amount of preview of only 0.1 or 0.2 s can make significant difference in terms of the sprung mass acceleration versus tire deflection trade-offs, which is also a reflection of the fact that this particular trade-off is in good part associated with the fast, wheel-hop mode.

Fig. 34

Normalized acceleration versus rattlespace trade-offs for quarter-car, 2DoF vehicle model with different preview times, t_r

Fig. 35

Normalized acceleration versus tire deflection trade-offs for quarter-car, 2DoF vehicle model with different preview times, t_r

To put this short preview times in proper perspective—a preview of 0.1 s corresponds to traversing the distance of little more than one wheelbase length of Ford Fusion sedan (wheelbase distance between front and rear wheels being 2.84 m in this case) at speeds of 65 mph or 29 m/s. This indicates that one could in theory benefit from even such a short preview times or equivalent distances. However, to fully exploit such opportunities one would in practice need very fast and accurate “high-fidelity” actuators and/or some ingenious hardware design measures and innovations. Additional aspects of preview control in the context of quarter-car models, such as bandwidth requirements and frequency responses, can be found in Pilbeam and Sharp (1993), Hac (1992), Hrovat (1997) and references therein.

3.8 3D, Full-Car Models

The optimization problem treated thus far for 1D, quarter-car and 2D, half-car models can be naturally extended toward the full 3D setting. Thus, following the above example of 1D–2D extension, one would now add sprung mass roll acceleration to the PI of Sect. 3.7 in addition to rattlespace constraint for each of the four vehicle corners; the resulting PI is given below (see Fig. 10)

$$ PI = E\left[ {q_{A} z_{A}^{2} + q_{B} z_{B}^{2} + q_{C} z_{C}^{2} + q_{D} z_{D}^{2} + r_{1} \left( {d^{2} z/dt^{2} } \right)^{2} + r_{2} \left( {d^{2}\Theta /dt^{2} } \right)^{2} + r_{3} \left( {d^{2} \phi /dt^{2} } \right)^{2} } \right] $$

(52)

Some of the first studies based on the LQG approach were presented in Barak (1985), Chalasani (1986), Barak and Hrovat (1988). The approach taken by Hrovat (1991b) is based on the simplest possible 3D model where one again starts by neglecting the unsprung masses. For this particular case with some additional mild assumptions on the road roughness characterization, it was possible to obtain an analytical solution even for this 3D problem, as elaborated in Hrovat (1991b).

Based on these analytical results it was possible to make a number of observations about the optimal system characteristics. This includes the fact that all three optimal body modes have the highly desirable damping ratio of 0.7, which is an extension of similar results for 1D and 2D cases. In addition, under some mild conditions shown in Fig. 36, the original 3D problem can be decoupled into two subsystems: one being the 2D pitch and heave subsystem, and another being a special roll subsystem as depicted in Fig. 36. Furthermore, if the previously established conditions for 2D decoupling hold (see Fig. 36) then the pitch and heave subsystem can be further decoupled into two basic, 1D optimization problems.

Fig. 36

Full-car, 3D vehicle model and related simplifications

This way the original full car optimization problem has been transformed into much simpler half and quarter car optimization setting. In this manner we have established a link with the previously obtained wealth of results for 1D and 2D optimization cases. Some other approaches and results based on the full 3D model including unsprung masses can be found in Barak (1985), Chalasani (1986), for example. Further extensions of the 3D model are possible to include flexible modes (in case of long trucks and similar vehicles) and flexible guideways, such as long (suspension) bridges and similar structures (Margolis 1978; Karnopp et al. 2012).

4 Model Predictive Control (MPC) as an Extension of Preview Control

In this section, we review the usage of Model Predictive Control in suspension control where it can incorporate not only the road preview but the other dynamic considerations including constraints, mode switchings and other non-linearities. Figure 37 illustrates suspension travel limits, bumper nonlinearities, and tire road interaction nonlinearities or constraints.

Fig. 37

Dynamic mode switching, nonlinearities, and constraints

As indicated earlier (e.g. Sect. 3.1), in semi-active suspension systems, the suspension force can be modulated through a range of damping force within the associated passivity constraint. In this case the suspension force cannot track an arbitrary desired force from the unconstrained LQ optimization-derived control law. As a compromise, the semi-active control design typically follows its unconstrained active counterpart when it can, and operates along the passivity envelope when it cannot. For example, the damping force is adjusted to follow the desired suspension force derived from the optimal control law, and set to zero when a negative damping force is required. This control is therefore commonly referred to as “clipped optimal”.

The optimal control law for the semi-active system has been posed as a constrained LQ optimization and solved numerically in Hrovat et al. (1988), Tseng and Hedrick (1994), involving the iterative solution of a time-varying force constraint. A specific example in Tseng and Hedrick (1994) showed that up to a 10% advantage with respect to clipped-optimal can be achieved. However, it also found that the amount of improvement depends on driven scenarios and is usually very limited. A later work (Giorgetti et al. 2006) leveraged the explicit hybrid MPC to confirm analytically the previously obtained numerical finding that clipped optimal is not the optimal control for semi-active suspensions in general.

In practical suspension design, rebound and jounce bumpers are needed within the rattle space to ensure no metal to metal contact when the vehicle encounters a large road disturbance. Since the power and force of an actuator are limited, an optimal active suspension controller may want to take advantage of this passive nonlinearity in the vehicle. A hybrid MPC controller was discussed in Xu et al. (2016) to demonstrate the control’s potential in further enhancing overall suspension performance, given limited actuation force/power. As is well known, the power and force of a hardware actuator are limited since they are tightly correlated to the practical constraints of cost and weight.

Noting that the tire of a vehicle may briefly lose road contact when encountering a large road disturbance such as an abrupt pothole or a brick on the road, a preview-based hybrid MPC can be designed (Xu et al. 2016) to take advantage of the upcoming road profile as well as the knowledge of non-symmetric tire behavior (when leaving the ground).

In a preview-based Model Predictive Control, not only is the vehicle response in the future prediction horizon “simulated and evaluated”, but also is the road profile within the prediction horizon “measured and buffered”. Bringing the future road profile into the augmented system dynamics is a native capability within the MPC framework where the look-ahead road input at each sampling time is measured, if available, and buffered until it reaches the vehicle (See Fig. 33). As such, a road preview MPC can be developed to enhance performance (Xu et al. 2016) using the same framework of MPC without preview.

A benchmark simulation comparison for a quarter car going through a curb with the step change of 0.1 m in road height is illustrated in Fig. 38, where the overall cost function, rms tire deflection, suspension rms deflection, and sprung mass rms acceleration are listed. All the controllers (LQR, MPC, and hybrid MPC) utilized 0.1 s preview, while the LQR controller assumed linear model, the MPC controller constrained the suspension and tire deflection to within their linear and symmetric region, and the hybrid MPC accounted for more detailed representation of suspension nonlinearities and unsymmetrical tire behavior. Significant improvement can be achieved with MPC and hybrid MPC where the realistic nonlinearity can be predicted and managed to avoid hitting the suspension jounce bumper.

Fig. 38

Benchmark comparison among LQR preview, MPC, and hybrid MPC

5 Other Concepts, Features, and Related Practical Considerations

5.1 Other Concepts

As the suspension performance index often includes conflicting terms, multi-objective optimization—symbolic or numeric—has been widely used to systematically manage nonlinearities and constraints (Gobbi and Mastinu 2001; Chatillon et al. 2006; Chen et al. 2003). The solution of a multi-objective optimization finds the best trade-off among the various pre-defined control terms. This is also known as Pareto optimization used in systematic design procedures, which is in many cases similar to the global optimization approach pursued in Sect. 3.

On the other hand, there are approaches with simpler concepts that focus on emulating an ideal damping for the single element in consideration. Among them, one of the most popular approaches is the skyhook concept which is supposed to emulate a damper connected between the sprung mass and the sky or a moving cloud representing an absolute, inertial ground. The skyhook control focuses on passenger comfort with proper trade-off between suspension travel and tire force variation. An analogous concept was introduced to focus on the minimization of tire force variation. Instead of putting a damper between the sprung mass and a moving cloud (aka sky or “inertial ground”), it suggests to put a heavy duty damper between the unsprung mass and the moving ground, hence its name “ground hook” (Novak and Valasek 1996; Valasek et al. 1997). In its implementation, the suspension device located between sprung and unsprung mass emulates a damping of the unsprung mass with respect to the ground i.e. road. Its emphasis is on the prevention of road damage and minimization of tire force variations. Practical advantages for road, soil, and bridges have been supported by experimental results with a prototype truck (Valasek et al. 1998, 2003). Figure 39 illustrates the concept of sky hook, ground hook, and their combined implementation.

Fig. 39

Illustration of skyhook, groundhook, and their combination

An attempt to extend the above LQ optimization results to a nonlinear setting is presented in Karlsson et al. (2000, 2001a, b). The idea was to put additional, higher order (e.g. quartic) penalty on the rattle space, which in reality is best represented by hard constraint as opposed to soft constraint representation used in the typical LQ setting of Sect. 3. As a consequence of this increased penalty, there is more efficient utilization of rattle space, especially in case of large bumps and potholes that could otherwise result in unacceptably large impact forces.

5.2 Hydraulic Suspensions and Their Brief History

A brief history of hydraulic-based suspensions is illustrated in Fig. 40 where various version of hydraulic and related electro-hydraulic suspensions have been implemented in production vehicles, ranging from low, mid, to high bandwidth, ride height focused to vehicle roll response motivated. Note that the Kinetic Suspension Technology (Sherman 2011) is essentially a semi-active suspension system acting between different corners while Nissan Infinity Q45a (Akatsu et al. 1990) and Mercedes ABC (Merker et al. 2002) are narrow bandwidth active suspension (NBAS) systems, to be discussed in Sect. 5.6.

Fig. 40

Brief history of hydraulic suspensions

5.3 Self-leveling Feature

Various self-leveling systems have been introduced in the market including the ones illustrated in Fig. 40. Notable examples include the Hydropneumatic systems developed by Citroen (Nastasić 2002) and the Electronically-Controlled Air Suspension on Lincoln by Ford Motor Company (Chance 1984). This feature allowed these vehicles to maintain proper ride height and suspension stiffness over a wider range of vehicle loading. It adjusts the vehicle ride height, usually very slowly, in order to balance among (1) soft and comfortable ride from the softer-than-usual passive spring, (2) proper vehicle attitude/stance, and (3) increased rattle space for anticipated or unknown road disturbance ahead. This feature has been implemented in the Lincoln Mark VIII in the 90s and most recently in Tesla Motor Model S (Edmunds 2012; Korosec 2014). It enables the lowering of the vehicle at highway speeds to improve aerodynamics and therefore, better fuel economy and driving range.

5.4 Variable Suspension Damping (Semi-active Suspension) Feature

Production semi-active suspension systems are generally constructed using an adjustable damper in parallel with the secondary suspension spring. These are typically constructed from pneumatic and/or hydraulic piston/cylinder combinations with electromechanical control of an orifice. Actuator bandwidth is primarily determined by the reaction time of the controlling valve and associated pressure/force production dynamics. A modern version can be found in Lincoln’s Continuous Controlled Damping system introduced in 2006. The Lincoln system uses a suite of sensors that constantly monitor suspension motion, body movement, steering and braking inputs and adjusts the suspension in milliseconds, helping keep the car smoothly on track (See Fig. 41). Specifically, it monitors up to 46 inputs and reacts on average within 20 ms (Nicolas 2014) to reduce roll, pitch, and heave motions, while enhancing driving comfort and dynamics, and isolating the vehicle from road harshness.

Fig. 41

Illustration of Lincoln CCD mitigating pothole impact by “stiffening” the damper

Another implementation of adjustable damping is through magneto-rheological (MR) fluids. MR fluid viscosity can be changed electronically, allowing the force across the actuator to change quickly (Bodie and Hac 2000). This method benefits from faster response time, although limited fluid life may contribute to service concerns. One MR damper application is found in the 2002 Cadillac Seville STS and 2003 Chevrolet Corvette whose MR fluid system was co-developed by Delphi and Lord Corporation.

5.5 Variable Suspension Geometry/Low Power Low Bandwidth Active Suspension Feature

A variable geometry suspension adjusts the ratio of wheel movement to the deflection of the suspension spring in real-time. By changing the leverage of the passive suspension spring depending on wheel motion, it essentially controls the wheel rate or effective spring stiffness.

Various systems and hardware configurations that provide variable suspension geometry have been proposed in the literature (Venhovens and van der Knaap 1995; Sharp 1998; Watanabe and Sharp 1999; Tumova 2004) including the “Delft Active Suspension” concept that was implemented as a prototype vehicle and demonstrated experimentally.

A specific variable geometry design, the “Delft Active Suspension” (van der Knapp 1989; Venhovens et al. 1992; Evers et al. 2008), is realized with a cone mechanism and illustrated in Fig. 42. This mechanism connects the spring to the car body on one end and to a rotatable crank on the other end. The crank is joint-connected to the suspension/wheel control arm and can be rotated at the joint around the base of the imaginary cone. The cone mechanism serves two purposes; (1) the length of the spring remains the same as the crank rotates, and (2) the ratio of movement between the wheel/tire control arm and the crank changes as the crank rotates (see Fig. 42). The intent is that the power required for geometry variation and the associated force leveraging of wheel rate will be much less than for directly changing the desired force. Ideally, with the configuration, the mechanism would require very low power and low energy. In practice, however, the precise arrangement and alignment could be compromised by suspension motion and deflection, and associated always-present friction.

Fig. 42

Delft active suspension realized with a cone mechanism

5.6 Narrow Bandwidth Active Suspensions (NBAS)

Narrow bandwidth active suspensions are characterized by relatively low force-production bandwidth of up to few Hertz, which results from an architecture where the dominant compliance is placed in geometric series with the active force generator. Most of the NBAS implementations thus far have been of electro-hydraulic type. Some representative electro-hydraulic active suspension configurations are shown in Fig. 43. Starting with a general structure shown in Fig. 43a one can use the bond graph of Fig. 43b to derive an equivalent all-mechanical structure shown in Fig. 43c. In the special case when the flow source Q_B is not present one ends up with the load-leveling-like configuration shown in Fig. 43d where we assumed a very soft, possibly pneumatic or air spring compliance. Finally, if the flow source Q_A is not present then we end up with the configuration shown in Fig. 43e. This is similar to some NBAS architectures—note in particular the serial arrangement between the dominant spring and the active force generator represented by the electro-hydraulic actuator that includes the controlled flow source Q_B.

Fig. 43

Electro-hydraulic suspension configurations: a general structure; b corresponding bond graph; c equivalent mechanical system; d typical structure with Q _B ≡ 0; e typical structure with Q _A  ≡ 0 (based on Karnopp 1987)

As suggested by Hrovat (1997) the above NBAS model could be further enhanced by inclusion of inertia effects due to hydraulic line dynamics, which can be especially relevant in case of relatively long and narrow lines or tubing. This is shown in Fig. 44, where the hydraulic conduit connecting the two flow sources, Q _A and Q _B , and suspension cylinder has been modeled as an inerter element represented by a differential causality within the associated bond graph of Fig. 44. A corresponding all-mechanical configuration is also shown in that figure. At this point, it should be mentioned that more recently there were attempts to develop and commercialize the hydraulic inerter (Scarborough 2011) as an alternative to its more common mechanical inerter counterpart. This may have some advantages in terms of packaging and overall design/cost flexibility, depending on particular implementation situation.

Fig. 44

Electro-hydraulic suspension model including hydraulic inertia (inerter-like) effects, equivalent bond graph, and all-mechanical counterpart

Further extensions of the above electro-hydraulic structures are possible by including an additional compliance near the suspension cylinder. This is shown in Fig. 45a along with an associated controlled damping mechanism. In the case that the latter is of an on/off type and neglecting all active sources (i.e. setting Q _A and Q _B to zero) one ends up with a semi-passive suspension shown in Fig. 45b. This is similar to Citroen hydro-pneumatic suspension (Carbonaro 1990) where one uses the on-off valve to control the effective suspension stiffness. The bond graph for the generic configuration of Fig. 45a is shown in Fig. 45c. Note in particular, that the inerter element corresponding to fluid line inertia is now in an integral causality with corresponding increase in the number of system states. Based on this bond graph one can easily deduce the corresponding all-mechanical suspension structure shown in Fig. 45d.

Fig. 45

Electro-hydraulic suspension configurations including hydraulic inertia (inerter) effects, and additional compliance and controlled (on-off) damping: a generic structure; b Citroen-like hydro-pneumatic semi-passive equivalent with Q _A  = Q _B  = 0; c corresponding generic bond graph; d equivalent all-mechanical system

A special case of the generic configuration of a typical electro-hydraulic (semi)active suspension from Fig. 45 is shown in Fig. 46. This is one of the first production implementations of the NBAS system developed by Nissan for their Infinity Q45a luxury vehicle (Akatsu et al. 1990). Note in particular the presence of an accumulator, which effectively acts in series with the actuator thus limiting the actuator bandwidth while at the same time filtering high-frequency road-induced disturbances. This corresponds to the accumulator with stiffness k _A in Fig. 45a. While the Infinity Q45a system used pressure control valve (Fig. 46a) another alternative would be to use the flow control valve shown in Fig. 46b.

Fig. 46

Nissan infinity Q45a N-B active suspension

In late 1990s Mercedes introduced their Active Body Control—ABC advanced suspension control system illustrated in Fig. 47 (Merker et al. 2002), which is structurally similar to the NBAS architecture generalized in Fig. 45. However, there is an important practical difference. While Infinity Q45a system used an hydraulic accumulator to implement the above mentioned in-series stiffness k_A, the Mercedes ABC suspension uses a mechanical counterpart similar to the one shown in Fig. 45d. For most cases the two would be equivalent except in the case when there is significant friction or even stiction within the actuator piston/cylinder combination in which case the mechanical implementation would lead to smaller road-induced disturbances resulting in better ride comfort. Through the years Mercedes has further developed and enhanced their system, which has recently included preview of the road based on stereo cameras. This system is now marketed under Magic Body Control (MBC) on their high-end luxury vehicles (Anonymous 2017a; Streiter 2008).

Fig. 47

Mercedes ABC system (based on Merker et al. 2002)

5.7 Broad Bandwidth Active Suspensions (BBAS)

Broad bandwidth active suspensions are characterized by relatively high force-production bandwidth that may extend up to and beyond the wheel-hop frequencies. This typically implies a very fast actuation and relatively stiff in-series compliance k _A in Fig. 45. The negative aspect of the latter is that the high-frequency road-induced disturbances are more easily transmitted to the sprung mass resulting in increased NVH (Noise, Vibration and Harshness) i.e. less comfortable secondary ride. While most of the BBAS implementations thus far have been of electro-hydraulic type equipped with high-fidelity servo-valves, there is also a case to be made for all electrical actuation, especially in view of increasing emphasis on Hybrid (HEV) and Battery Electric Vehicles (BEV).

As an example of electro-hydraulic implementation, we will next consider the BBAS prototype system (Fig. 48) that was developed at Ford Research Laboratory in the early nineties and successfully demonstrated in a research vehicle. It consisted of four high-fidelity electro-hydraulic servo actuators, one at each corner, installed onto a 1989 Ford Thunderbird (Goran and Smith 1996). The concept hardware and software not only verified the potential in ride quality improvement but also identified the shortcomings of the implemented hardware structure including actual power consumption, secondary ride harshness, and actuator noise.

Fig. 48

Illustration of Ford broadband active suspension prototype

The Ford Thunderbird BBAS system was controlled through four-way servo valves, which have high precision and speed of response. In addition, the BBAS actuators were based on double-acting cylinders capable of equally fast rebound and jounce strokes. The vehicle also had one central processor operating at lower rates, and four corner-unit micro-processors for fast signal/control processing; four actuator displacement sensors and four load cells for internal (force) loop calculations; and four air springs—one at each corner placed in parallel with the BBAS actuators. The air springs serve to support and self-center the vehicle sprung mass as is typical of load leveling systems. At the same time they provide lower sprung mass natural frequency for more comfortable basic ride, which is then appropriately dynamically modified through the BBAS actuators. The system incorporated 26 various sensors, including accelerometers, pressure sensors, vehicle speed sensors and others.

The BBAS control strategy was based on coordinated individual wheel control and consisted of two hierarchical control levels (Goran et al. 1992). The outer loop level operated at a 20 ms rate. It calculated the desired corner forces for the four BBAS actuators, desired operating modes (handling or ride dominated) and checked the overall system integrity. The ride related calculations were based on quarter-car vehicle models aimed at emulating skyhook damping at each corner, which is often very close to the optimal possible ride benefit (Hrovat 2014). Different effective spring and damping rates were used depending on prevailing operating modes, i.e. ride or handling. Additional details about the system and its performance can be found in Goran et al. (1992), Goran and Smith (1996).

An example of an Electrical Active Suspension (EAS) implementation (Davis and Patil 1991) in a prototype Ford vehicle is shown in Fig. 49. An important aspect of this BBAS system development was creation of an appropriate validated model, with special emphasis on actuator model fidelity. The corresponding bond graph model is shown in Fig. 50. This model was validated using bench testing and the results—in terms of relevant frequency transfer function plots—are shown in Fig. 51. It can be seen that there is in general very good correlation between the model and test data. Once validated, this model was used in the process of this—at the time very novel—BBAS system development, which culminated in successful demonstration in a research vehicle. More recent example of an EAS system development can be seen in Moran (2004), Gysen et al. (2010), Anderson et al. 2013) indicating renewed interest in this promising concept, especially in view of increased emphasis on electric (HEV and BEV) vehicles.

Fig. 49

Ford broadband electric active suspension (EAS) prototype

Fig. 50

Bond graph of Ford EAS broadband active suspension quarter car

Fig. 51

Ford EAS actuator model validation

6 Optimization-Based Analysis of Active Suspensions for Integrated Vehicle Controls

As discussed in the previous sections, active suspension is commonly considered under the framework of vertical vehicle dynamics control primarily aimed at improvements in ride comfort. In this section, we expand upon this traditional application by introducing some recent developments based on more detailed, non-linear vehicle models and more general optimization methodology. In particular, a collocation-type control trajectory optimization method is used to analyze to which extent the application of fully active suspension (FAS) can be broaden to the tasks of vehicle handling/cornering control and braking distance reduction, as well as enhanced active safety, in general. The analysis is extended to the ride control task for the case of emphasized, discrete road disturbances such as high-magnitude bumps and potholes. The main optimal control objective is to provide a favorable trade-off of ride comfort and road holding capability, as well as a robustness against wheel damage, e.g. at the pothole trailing edge. The presentation is based on the recent papers (Čorić et al. 2016a, b, 2017), which include more details on vehicle modeling, optimization problem formulation, and optimization results and related discussions.

6.1 Vehicle Dynamics Model

The conducted optimization study is mostly based on the 10 DOF passenger vehicle dynamics model depicted in Fig. 52a, b (Hancock 2006). The model state variables include longitudinal (U), lateral (V), and heave (W) velocities, and roll (p), pitch (q), and yaw (r) rates, as well as the four state variables related to the rotational speeds ω _i of each wheel, i = 1, …, 4. For the ride control optimization task, the simple quarter-car vehicle model shown in Fig. 52c (Hrovat 1997) is mostly used. The 10 DOF model is extended by the unsprung mass dynamics (dashed lines in Fig. 52b) when verifying the basic 10 DOF model-based optimization results, or when using the full vehicle model for ride control optimization.

Fig. 52

10 DOF vehicle dynamics model (a, b) and quarter car model (c)

The variable ΔF _zi (or F _a in Fig. 52c) represents the FAS control input to be optimized along with other control inputs such as Δδ₁ = Δδ₂ (for active front steering, AFS) and T _i (for active brakes, ABS).

The tire is described by the 1994 Magic formula combined-slip model, including the relaxation length dynamics for the lateral DOF (Pacejka 2006). The longitudinal and lateral tire forces are scaled by the tire-road friction coefficient μ.

6.2 Braking Distance Reduction

The optimization objective is to find the control input vector u = [T₁,…,T₄, ∆F_z1,…, ∆F_z4], which minimizes the final longitudinal position X(t _f ) of the vehicle on the fixed time interval [0, t _f ], i.e. the cost function to be minimized is specified as

$$ J_{0} = X(t_{f} ) $$

(53)

The optimization is subject to hard constraints on the tire normal load F _zi , i = 1, …, 4, the FAS control inputs ΔF _zi , and the suspension deflection z _i , see Fig. 52b and Čorić et al. (2017):

$$ F_{zi} \ge F_{z\hbox{min} } $$

(54)

$$ -\Delta F_{z\hbox{max} } \le \Delta F_{zi} \, \le \Delta F_{z\hbox{max} } $$

(55)

$$ -d_{j} \le z_{i} - z_{0i}^{{}} \, \le d_{j} $$

(56)

In order to provide a well-damped system response, the cost function (53) is extended with additive soft constraint terms of mean-square type on the variables $\dot{\eta }_{i}$, $\dot{F}_{zi}$, $\Delta F_{zi}$, and $\Delta \dot{F}_{zi}$, where η _i denotes the tire longitudinal slip. Similarly, to ensure straight ahead motion of the vehicle during the braking maneuver in the case of split-μ scenario, the mean-square constraints are introduced for the yaw rate (r) and the lateral displacement (Y) variables, and the active front or rear steering input is added to the control vector to be optimized.

Figure 53 shows the vehicle response for a pulse-type, low-high-low transient-μ scenario, where the FAS and brake control inputs, ΔF _zi and T _i , i = 1, …, 4, are simultaneously optimized. The FAS provides a load boost on those tires that experience the high-μ condition (first front, F _zf  = F_z1+ F_z2, and then rear tires, F _zr  = F_z3+ F_z4). This results in a boost of the longitudinal deceleration –a _x , and finally in reduction of the braking distance by 5.1% (on the given, fixed time horizon).

Fig. 53

Comparative Brakes and FAS + Brakes optimization results for pulse-type transient-μ scenario

The side effects of FAS action include excitation of vehicle heave and pitch dynamics. This results in the long stroke in the heave, Z, direction (approx. ±10 cm; which is closely related to the suspension deflection constraint (56), with d _j  = 10 cm), and the corresponding heave acceleration peak of 0.69 g. The pitch angle response θ includes some more oscillatory content as the results of FAS action.

In order to produce a strong tire load boost during the high-μ period and at the same time satisfy the suspension stroke constraint, the FAS relaxes the tire load immediately before and after the high-μ interval (see F _zf and F _zr ). These tire load holes have a weaker effect on the deceleration −a _x than the load boost, because they occur during the low-μ intervals.

The analysis is extended in Čorić et al. (2017) for other μ-scenarios. The braking distance reduction is lower for the step-type, high-low transient-μ case (around 2% for the same μ levels and time horizon values) and much smaller for the constant-μ scenario (0.5%). In the latter case, the performance gain is higher (around 2%) if the ABS actuator bandwidth is lower than the FAS bandwidth. This is because the FAS can boost the tire load when the braking torque is being settled i.e. when it is close to maximum, while preparing for the boost through generating the tire load hole in the early stage of braking torque transient.

In the split-μ scenario (μ_1,3 = 1 and μ_2,4 = 0.1 in the particular case, Fig. 54), the FAS again transfers the load to the high-μ tires (the left tires in this case), and the braking distance is reduced by 2.1%. To keep the vehicle moving straight ahead, the optimized active front steering (AFS) input δ _f is such to counteract the yaw torque caused by unequal left and right braking forces. Between the high-μ tires, the load is transferred to the non-steered (left rear) tire, because it has a larger longitudinal force potential according to the friction circle (Pacejka 2006). It is important to note that the overall FAS action is such to form a warp arrangement of the four FAS forces (see the normal load, F _zi , responses in Fig. 54). In this case the total FAS force ΣΔF _zi is approximately equal to zero, thus avoiding any notable have motion, and allowing for control of tire load distribution over long steady-state intervals. Namely, the load redistribution occurs during the whole maneuver interval (Fig. 54), unlike in the transient-μ case where only a temporary load boost (preceded by load hole) was achievable due to the suspension deflection/heave stroke constraint (Fig. 53). It should also be noted that a chassis roll is induced towards the high-μ wheels.

Fig. 54

Comparative brakes and brakes + FAS optimization results for split-µ maneuver with included AFS actuator

The constant-μ scenario has been extended by imposing oscillatory behavior of the longitudinal slip (through an equality constraint), in order to mimic the ABS-inherent limit-cycle behavior. The optimized FAS action is such to increase the tire load in the wheel torque peak periods, thus resulting in a higher tire friction potential in those periods, and finally boosted deceleration. This is in accordance with the FAS + ABS control strategy proposed by Alleyne (1997).

6.3 Handling Control—Stabilization

The standardized sine-with-dwell maneuver-based test (Anonymous 2007) is used to evaluate the FAS control authority in stabilizing the vehicle. In this maneuver, a “robot” steering wheel angle (SWA) with the amplitude δ _k , the frequency of 0.7 Hz, and the dwelling period of 0.5 s, is applied to a vehicle coasting at the velocity U = 80 km/h for the tire-road friction coefficient µ = 0.9. Unlike the original test specification, where repetitive tests with a growing SWA are executed, only the worst-case scenario related to the SWA amplitude δ _k ≅ 270° is considered in optimization. In order to reflect the test requests on limiting the yaw rate response (stabilization) and maximizing the lateral displacement Y (responsiveness) during the maneuver interval [0, t _f  = 4 s], the following cost function is considered:

$$ J = \int\limits_{0}^{{t_{f} }} {(r - r_{R} )^{2} dt} - k\,\hbox{max} (Y) $$

(57)

where r _R is the target yaw rate generated by a vehicle dynamics reference model, and k is the weighting factor selected to achieve a trade-off between the two conflicting objectives. The optimization is subject to inequality constraints (54)–(56). The optimized control variables are FAS inputs ΔF _zi , i = 1, …, 4. A more detailed elaboration of the optimization problem formulation and a more detailed discussion of the optimization results are presented in Čorić et al. (2017).

Figure 55 shows the optimization results for the considered sine-with-dwell maneuver. A typical though simplified feedback-type ESC reference strategy predominantly brakes the outer front wheel (F_x1) to generate an oversteer compensation (OSC) component of the yaw torque M _z and stabilize the vehicle (Tseng et al. 1999). The OSC action is emphasized in the interval around t = 1 s in order to suppress the excursion of sideslip angle β resulting in stabilization effect, as well as around t = 2 s, but to a lower extent.

Fig. 55

Comparative FAS + ESC optimization results for sine-with-dwell maneuver, including comparison with passive vehicle and ESC-only cases

The ESC + FAS optimization results in Fig. 55 point to a significant yaw rate error reduction leading to 45% lower yaw rate root-mean-square (RMS) error, and also β-peak reduction resulting in a wider stability margin (see the performance indices given in Table 1). This is achieved by two distinct actions that can be observed in Fig. 55: (i) the total tire load boost (see ΣF _zi around t = 0.7 s and t = 1.3 s) that increases the lateral acceleration a _y over its saturation level for improved handling, and (ii) transfer of load from front to rear tires to generate OSC yaw torque (see F _zf and F _zr around t = 0.65 s and t = 1.9 s). As side effects, the former excites significant heave motion (the heave acceleration peak of 0.38 g, Table 1), while the latter causes emphasized pitch angle magnitudes (θ). The lateral displacement Y (i.e. the responsiveness) remains largely unaffected. However, the agility is notably improved in the case of integrated control (U(t _f ) is higher, t _f  = 4 s), because the ESC + FAS system uses the brakes to a lower extent than in the ESC-only case (see F_x1, …, F_x4).

Table 1 Comparative stability control performance indices for different actuator configurations and FAS control strategies (k = 0.01 in Eq. (57))

Since the optimization is inherently conducted over the full time window (full-horizon preview is available), the comparison between the optimized FAS control action and the causal ESC action (no preview) is strictly speaking unfair. To provide a more appropriate comparison between the FAS and ESC systems control authorities, the same preview-based optimization approach has been applied in the FAS-only case (ΔF _zi inputs are optimized) and active brake-only case (T _i inputs are optimized). The corresponding results given in Table 1 under the labels ‘FAS1’ and ‘Active brakes’ show that the optimized FAS and active brake systems give comparable yaw rate RMS errors. The advantages of FAS control include improved responsiveness (by 17%) and agility (by 40%), while the disadvantages are related to increased magnitudes of heave acceleration (0.5 g vs. 0.04 g) and pitch angle (3.4° vs. 2°).

In order to investigate if the ultimate FAS performance can be approached by simpler control actions based on lower number of control DOFs, the FAS control input optimization scenarios defined in the legend of Table 1 under the labels ‘FAS2’–‘FAS7’ are also considered. The main conclusions drawn from the corresponding performance indices are as follows: (1) the application of zero total FAS force constraint (FAS2; three control inputs) gives only slight reduction of control performance, with an advantage of no heave motion excitation (no total tire load boost is allowed); (2) in the cases of longitudinally symmetric force constraint and warp-related constraints (FAS4 and FAS5, respectively; two control inputs in both cases), the performance also remains high, the pitch motion excitation is avoided (no front/rear tire load transfer is allowed), but the heave acceleration is excessive; and (3) in the case of coupled warp-related constraint (FAS7; only a single control input), the performance is notably deteriorated, but it is still better than that of the ESC case, and both pitch and heave dynamics excitation is avoided. For the coupled warp-related constraint, the FAS control makes the front tire loads more distinctive from each other and the rear tire loads more balanced, thus providing an oversteer compensation action based on the convexity of the lateral force versus normal load tire curve (Pacejka 2006). At the same time, the total tire load, heave, and suspension deflection are kept approximately constant, so that the control action can be applied during steady-state turns, as well. FAS3 configuration gives comparable performance as in the case of FAS7 configuration, but it includes one control DOF more. FAS6 configuration is inferior to other configuration, because it does not allow for load boost, front/rear load transfer, and different left/right load transfers on the two axles.

6.4 Handling Control—Path Following

A path following minimization objective is used along a double lane change maneuver (DLC) to further investigate the FAS control authority, particularly under the conditions of understeer behavior (with respect to reference trajectory). The optimization problem is to find the FAS control inputs ΔF _zi (t), 0 ≤ t ≤ t _f , i =1, …, 4, which minimize the cost function

$$ J = \underbrace {{\int\limits_{0}^{{t_{f} }} {\left( {Y - Y_{R} (X)} \right)^{2} dt} }}_{{J_{0} }} + k_{1} \int\limits_{0}^{{t_{f} }} {\sum\limits_{i = 1}^{4} {(F_{zi} - F_{zi0} )^{2} dt + k_{2} } } \int\limits_{0}^{{t_{f} }} {\theta^{2} dt + k_{3} \int\limits_{0}^{{t_{f} }} {\phi^{2} dt} } + k_{4} \int\limits_{0}^{{t_{f} }} {\sum\limits_{i = 1}^{4} {\dot{\eta }_{i}^{2} dt} } $$

(58)

subject to inequality constraints similar to those given by Eqs. (54)–(56). In addition to the main, cost function term J₀, which penalizes the path following error, there are other, soft constraint-related terms penalizing the control effort, pitch and roll magnitudes, and excessive longitudinal slip excursions.

Figure 56 shows the optimization results for the worst-case DLC Maneuver 3. The reference response corresponds to the passive vehicle for μ = 1, zero driveline torque, and optimized driver steering input. The achieved vehicle path Y(X) is used as the reference path for other cases presented in the same figure, where the same driver steering input is applied, but for the reduced tire-road friction coefficient μ = 0.6 and the driveline input torque T _in  = 250 Nm. Under these conditions the passive vehicle (‘No control’ case) becomes unstable (see β). The optimized active front steering (AFS) control stabilizes the vehicle and provides an accurate path following.

Fig. 56

Comparative AFS and FAS + AFS optimization results for path following task and Maneuver 3 (μ = 0.6, T _in  = 250 Nm)

The path following RMS error is further reduced (by 30%) when the integrated AFS + FAS control is applied. Since the AFS has a large control authority over the lateral vehicle dynamics, the FAS action is focused on the effect of boosting the total tire load (ΣF _zi ) and, thus, the lateral acceleration (a _y ) capacity in the critical intervals. The FAS also provides a certain rear-to-front tire load transfer by strongly unloading the rear axle for understeer compensation (USC) around the intervals of 0.3, 1.1, and 2.6 s. The side effects of FAS action are again related to excitation of heave and pitch dynamics: the heave acceleration peak is 0.6 g while the pitch angle amplitude is relatively modest (1°).

Table 2 shows the performance indices related to FAS-only optimization results obtained for Maneuver 1 (μ = 0.6, T _in  = 0) and different sets of cost function weighting factors given in the table legend. In the unconstrained case (no hard and soft constraints, Case 1), almost ideal path following can be achieved (J₀ → 0). However, this case is unrealistic due to very high heave peaks required by the strong FAS action (43 cm from the equilibrium Z₀), i.e. due to violation of the suspension stroke limits (±10 cm). After adding the hard constraint on suspension stroke (Eq. (56); Case 2), the path following RMS error (J₀/t _f )^1/2 grows significantly, but it remains substantially lower compared to the no-control case. By adding the soft constraint on control effort (Cases 3 and 4), the FAS control amplitudes become smaller, thus reducing the FAS consumed energy $E = \int {\Delta F_{zi} v_{zi} dt}$, as well as the pitch angle, heave, and heave acceleration magnitudes. This is paid for by reduction of the path following performance, which is more emphasized in the case with higher control effort weighting factor k₁ (Case 4). When compared to the optimization results for Case 5 (considered in Fig. 56; the pitch and roll angle magnitudes are constrained), the less restrictive tuning related to Case 3 provides a significant improvement in the path following performance (30% lower RMS error). However, the control effort is increased to such extent that the tire load lower amplitudes approach the limit value set to 500 N.

Table 2 Comparative performance indices of FAS optimization results for different sets of constraints and Maneuver 1 (μ = 0.6, T _in  = 0)

Table 3 shows the path following RMS errors (m) for various single- and multi-actuator configurations, and different DLC maneuver types. Maneuver 1 is similar to the already described Maneuver 3, but the driveline torque is set to zero. Maneuver 2 is executed for the non-reduced friction coefficient (μ = 1) like in the reference case, but with a relatively high driveline torque (T _in  = 350 Nm). The results in Table 3 indicate that the FAS-only control is inferior to the AFS/ARS control, which may appear to be in contrast with the handling control results from Sect. 6.3, where the FAS was very competitive to active brake control. This is because in the considered control task a strong USC action is required, including the preview action during the initial period when the vehicle moves straight ahead (see δ _f  = δ₁ = δ₂ in the AFS case in Fig. 56). The fact that the FAS cannot generate lateral tire force in the absence of tire sideslip angle explains its inferiority compared to AFS. Nevertheless, it effectively stabilizes the vehicle and provides relatively accurate path following.

Table 3 Comparative path following RMS error values (m) for different active steering and FAS configurations and different DLC maneuver types

Table 3 further shows that the ARS is more effective than AFS, because it utilizes a driver-untapped lateral force potential of rear tires (Deur et al. 2014). The FAS action is, thus, less effective when integrated with ARS (than with AFS), and it is reduced solely to the unique ability of FAS to boost the total tire load and the lateral acceleration. This unique control authority explains why the FAS brings more significant improvement to the AFS (in the AFS + FAS configuration) than the ARS does (in the ARS + AFS = 4WS configuration).

There are several other, secondary mechanisms through which the FAS can improve the vehicle handling performance (Čorić et al. 2016b). First, for a throttle-on maneuver and the example of rear-wheel-drive vehicle, the FAS unloads the inner driven tire to increase its longitudinal slip and, thus, weaken its lateral force to provide USC. Next, as already mentioned in Sect. 6.3, the FAS can increase the left-right tire load difference on the front axle and make the tire load more balanced on the rear axle, thus generating OSC yaw torque based on the convexity feature of the tire lateral force versus load static curve. Finally, the FAS can provide the vehicle tilting effect as an USC intervention acting through the front-axle bump steer component of the toe effect.

6.5 Ride Comfort and Tire Impact Control for Bumps and Potholes

In the case of bump-type road disturbance and the quarter-car vehicle model given in Fig. 52c, the cost function is defined as (see Sect. 3.2):

$$ J = k_{11} \underbrace {{\int\limits_{0}^{{t_{f} }} {\dot{x}_{4}^{2} dt} }}_{{J_{11} }} + k_{12} \underbrace {{\int\limits_{0}^{{t_{f} }} {(x_{1} - x_{10} )^{2} dt} }}_{{J_{12} }} + k_{13} \underbrace {{\int\limits_{0}^{{t_{f} }} {(x_{3} - x_{30} )^{2} dt} }}_{{J_{13} }} + k_{14} \underbrace {{\int\limits_{0}^{{t_{f} }} {\dot{F}_{a}^{2} dt} }}_{{J_{14} }} $$

(59)

where the terms J₁₁, …, J₁₄ penalize the ride discomfort, loss of road holding/handling ability, excessive suspension stroke, and control input oscillations, respectively. The only hard constraint applied in the basic optimization case relates to the FAS actuator force limits: −2500 ≤ F _a [N] ≤ 2500.

The dashed-line blue curves in Fig. 57 represent the corresponding optimization results for the case of high-amplitude bump (10 cm), bump length of 0.1 s, and the bump preview time of 0.2 s (see z _r response). Immediately before the bump occurrence, the FAS generates a positive force F _a , which tends to lift the tire (see x₁ and F _z , and also Fig. 52c), thus reducing the strong tire-bump impact. Consequently, the sprung mass acceleration dx₄/dt is suppressed when compared to the passive vehicle, thus resulting in better ride comfort. After the wheel hop peak, occurring around t = 0.3 s (see x₁), the FAS abruptly reverses its action (F _a  < 0) to prevent the strong sprung mass (free) fall that would affect the ride comfort. However, such “bang-bang”-like FAS action excites strong oscillations of the system response, which results in residual wheel hops and related temporary losses of road holding ability (F _z  = 0). During the bump preview period (t < 0.2 s), the FAS prepares for the tire lift action at the leading bump edge by exciting the unsprung mass oscillations with a proper phase angle.

Fig. 57

Optimization results for emphasized discrete bump-type road disturbance

The solid-line red response in Fig. 57 corresponds to the case of imposing the lower-limit constraint on the tire normal load (F _z  > 1000 N), and also applying the final time conditions on the state and control variable that are equal to the corresponding initial conditions. The wheel is prevented from hopping (see x₁ and F _z responses) by generating a strong negative FAS force F _a after the bump peak (0.25 < t (s) < 0.3), which presses the wheel to the ground. However, the reactive force of the same amount F _a acts on the sprung mass (see Fig. 52), thus causing a very strong peak of the sprung mass acceleration and affecting the ride comfort. Therefore, there is an evident trade-off between the ride comfort and road holding ability. The summarized performance plot shown in Fig. 58 indicate that the cost function weighting factors can be tuned so that both ride comfort and road holding indices are notably better than in the passive vehicle case, particularly in the high-bump case.

Fig. 58

Pareto frontier-like diagram for two main performance indices ((J₁₂/ t _f )^1/2 versus (J₁₁/ t _f )^1/2 based on definition in Eq. (59)) and low (2 cm) and high (10 cm) amplitude of bump-type road disturbance

The analysis has been extended to the case of full vehicle model (Fig. 52a, b) with the unsprung mass dynamics included. It has been found that there is an additional cross-axle FAS control mechanism, which reduces variation of the total (four-corner) sprung mass/chassis force for improved ride comfort (Čorić et al. 2016a). This mechanism counteracts the anti-wheel-hop peak of suspension force on the active axle (the one exposed to the bump) by means of suspension force reduction on the inactive axle.

In the pothole case the cost function is formulated as

$$ J = \underbrace {{\int\limits_{0}^{{t_{f} }} {\left( {F_{a} (x_{2} - x_{4} )} \right)^{2} dt} }}_{{J_{31} }} + k_{32} \underbrace {{\int\limits_{0}^{{t_{f} }} {\dot{x}_{4}^{2} dt} }}_{{J_{32} }} + k_{33} \underbrace {{\left({-\left.{\hbox{min} (z_{u} )} \right|_{{\tau_{p} }}^{{\tau_{p} + T}} } \right)}}_{{J_{33} }} + k_{34} \underbrace {{\int\limits_{0}^{{t_{f} }} {F_{a}^{2} dt} }}_{{J_{34} }} $$

(60)

The main difference compared to the cost function (59) relates to two additional terms, J₃₁ and J₃₃, which penalize the FAS actuator energy consumption and the tire sensitivity to damage during the pothole interval, respectively. The hard constraints include the aforementioned actuator force limit and the state variable boundary condition.

Figure 59 shows the optimization results for the case of square-shape pothole with the depth of 0.1 m, length of 0.1 s, and the preview time of 0.2 s. Regardless of the cost function tuning, the optimal system behavior is such that the wheel hops over the pothole (see x _b ) to prevent the wheel damage on the pothole trailing edge (see x₁ and F _z immediately after t = 0.3 s). To effectively prepare for the wheel hop, the FAS first increases the (absolute value of) tire deflection x₁ immediately before the pothole (F _a  < 0). It then quickly reverses its control action (F _a  > 0) to lift the wheel near the pothole leading edge (t ≅ 0.2 s) with some significant hop-off velocity x₂. The response of FAS energy consumption E indicates that the FAS predominantly generates active force (dE/dt > 0), where the power peaks equal around 1.5 kW.

Fig. 59

Optimization results for emphasized discrete pothole-type road disturbance of square shape

The main difference between the two active control responses in Fig. 59 is that the wheel entirely hops over the pothole when the emphasis is on damage prevention (solid red curves) compared to the case when the ride comfort is emphasized (dashed blue curves). In the former case, the FAS action F _a is stronger (longer) both in the preview phase (t < 0.2 s) and during the pothole period (0.2 < t (s) < 0.3), in order to better prepare for the wheel hop and keep the wheel lifted action when hopping over. The post-pothole peak of the normal tire force F _z is not only lower in that case, but it occurs after the trailing edge, thus reducing further the possibility of wheel damage. However, the ride comfort is reduced (see dx₄/dt) due to the stronger FAS activity before and during the pothole period.

Another cost function tuning case is also considered in (Čorić et al. 2016a), where the emphasis is on energy consumption. In this case the FAS action is such that it keeps the suspension deflection x₃ approximately constant during the pothole period (and longer), i.e. no power is consumed in that case (as dx₃/dt ≅ 0 holds in that case). This results in halving the energy consumption compared to the previous two cases, but the ride comfort or wheel damage robustness is compromised.

The above results are further illustrated by the performance indices listed in Table 4 based on the definition of the cost function terms in Eq. (60), and for three characteristic sets of weighting functions. In all cases, the FAS improves the wheel damage robustness (see J₃₃), and, it also, improves the ride comfort performance (J₃₂) when compared to the passive vehicle. In Case 3, the wheel damage is avoided, while the other two cost indices are modestly high. In Case 2 the energy consumption is the lowest, but ride comfort and wheel damage robustness are inferior compared to Case 1.

Table 4 Comparative performance indices for passive vehicle and three FAS control optimization cases for pothole-type road disturbance

The case of long pothole is analyzed in (Čorić et al. 2016a), as well. In that case the optimal behavior includes the phases of (i) wheel landing and traveling over the pothole bottom, and (ii) hopping over the pothole trailing edge.

6.6 Summary

The presented control variable optimization study has pointed to the unique control authority of FAS, which relates to boosting the tire load for providing an increased tire friction potential and improved vehicle dynamics control (VDC) performance. The tire load boost can be applied under conditions of non-uniform tire friction coefficient μ (the load is increased during the high-μ interval, e.g. for improved ABS performance) or during the critical handling/cornering maneuvers (to increase the lateral acceleration over its μ-related saturation level and improve the VDC performance without affecting the agility). The VDC performance can also be enhanced by the FAS ability to generate oversteer compensation- or understeer compensation-yaw torque by transferring the load to rear or front tires, respectively. There are additional FAS control mechanisms for enhanced VDC, such as those relying on spinning a driven tire by reducing its load, balancing the left-right tire load on an axle to boost its lateral force, and increasing the steering effort through the bump steer component of the toe effect. Finally, in the case of emphasized discrete road disturbances such as high-amplitude bumps and potholes, a proper (optimal) FAS control action can improve both ride comfort and road holding performance. Moreover, in the pothole case, the wheel damage can be prevented by forcing it to hop over the pothole.

However, the FAS control action has certain side effects and limitations. The tire load boost and load transfer actions are directly associated with excitation of heave and pitch dynamics, respectively, thus affecting the driving comfort. Due to the limited suspension stroke, the FAS actions can last only for a relatively short interval, and they would, thus, not be very effective in nearly steady-state turns or transient maneuvers performed at slower rates of change. To emphasize the FAS control effect (e.g. the tire load boost) and satisfy the suspension stroke constraint, the FAS action typically includes a preparatory phase during the preview period (e.g. a tire load hole), and is usually succeeded by a similar relaxation phase. This makes the control system development more challenging, as it would require some kind of on-line optimization that is typically included within the model predictive control framework, and a preview of critical period of maneuver and/or road disturbance. Another limitation relates to the fact that the FAS cannot influence the tire lateral forces unless the tire is subject to non-zero lateral sideslip angle. This affects the effectiveness of understeer compensation, particularly when it is a part of preview control action during straight ahead driving.

There is though a FAS action that is not associated with most of the above side effects. When the tire normal loads are distributed in the warp-like arrangement, the FAS action does not excite the heave and pitch dynamics, and it can be applied during steady-state turns and braking maneuvers in a simplified (more conventional) control law formulation. However, this action has a lower control authority than the load boost and front/rear load transfer actions, thus usually resulting in limited control performance enhancement.

It is believed that the encouraging results of this study may serve as a solid basis and inspiration for future possible extensions, especially when combined with (semi)autonomous vehicles fortified by V2V, V2I, detailed 3D mapping, and similar exciting and promising future developments.

Appendix

In this appendix we establish the LQG-optimal trade-off line for the 1 DoF model of Fig. 7. We start with the covariance (Lyapunov) equation

$$ \left( {A - BK} \right)X + X\left( {A - BK} \right)^{T} = - G\Gamma G^{T} $$

(61)

where in our case G^T= [−1 0] and Γ = 1 since we are dealing with normalized covariance,

$$ X = \left[ {\begin{array}{*{20}c} {X_{1} } & {X_{3} } \\ {X_{3} } & {X_{2} } \\ \end{array} } \right] $$

(62)

where,

$$ X_{1} = \left( {X_{1,rms,norm} } \right)^{2} , {\text{ and }}X_{2} = \left( {X_{2,rms,norm} } \right)^{2} $$

(63)

Define

$$ A_{CL} = A - BK = \left[ {\begin{array}{*{20}c} 0 & 1 \\ { - k_{1} } & { - k_{2} } \\ \end{array} } \right] $$

(64)

with optimal control gains

$$ k_{1} = r^{ - 1/2} ,\quad \, k_{2}^{{}} = \sqrt 2 r^{ - 1/4} $$

(65)

then the covariance equation becomes

$$ A_{CL} X + XA_{CL}^{T} = -GG^{T} $$

(66)

or

$$ \left[ {\begin{array}{*{20}c} {2X_{3} } & {X_{2} - k_{1} X_{1} - k_{2} X_{3} } \\ {X_{2} - k_{1} X_{1} - k_{2} X_{3} } & { - 2k_{1} X_{3} - 2k_{2} X_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {-1} & 0 \\ 0 & 0 \\ \end{array} } \right] $$

(67)

Solving for X₁, X₂, and X₃,

$$ X_{1} = \frac{3}{2\sqrt 2 }r^{1/4} ,\quad X_{2} = \frac{1}{2\sqrt 2 }r^{-1/4} ,\quad \, X_{3} = -\frac{1}{2} $$

(68)

from where we get the normalized rms rattlespace

$$ x_{1,rms,norm} = \sqrt {X_{1} } = \frac{\sqrt 3 }{{\sqrt {2\sqrt 2 } }}r^{1/8} $$

(69)

The normalized rms sprung mass acceleration then follows from

$$ U = KXK^{T} = \frac{1}{2\sqrt 2 }r^{ - 3/4} $$

(70)

so that

$$ U = \frac{27}{64}X_{1}^{ - 3} $$

(71)

resulting in the normalized rms acceleration versus rattlespace equation

$$ u_{rms,norm} = \frac{3\sqrt 3 }{8}x_{1,rms,norm}^{ - 3} $$

(72)

which was used to plot the corresponding optimal trade-off line in Fig. 13.