Abstract
We present constructions of CPA-secure (leveled) homomorphic encryption from learning with errors (LWE) problem. We use the construction introduced by Gentry, Sahai and Waters ‘GSW’ (CRYPTO’13) as building blocks of our schemes. We apply their approximate eigenvector method to our scheme. In contrast to the GSW scheme we provide extensions of the (leveled) homomorphic identity-based encryption (IBE) and (leveled) homomorphic attribute-based encryption (ABE) on the multi-identity and multi-attribute settings respectively. We realize the (leveled) homomorphic property for the multi-party setting by applying tensor product and natural logarithm. Tensor product and natural logarithm allow to evaluate different ciphertexts computed under different public keys. Similar to the GSW scheme, our constructions do not need any evaluation key, which enables evaluation even without the knowledge of user’s public key.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
- Encoding
- Attribute-based Encryption (ABE)
- Learning With Errors (LWE)
- Ciphertext
- Identity-based Encryption (IBE)
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Since the proposal of public key cryptography (PKC), construction of an efficient encryption has always been interesting and challenging problem. The first efficient constructions were Boneh-Franklin identity-based encryption (IBE) [8] and Cock’s IBE [20]. The former uses pairing over elliptic curve and the later was based on quadratic residuosity. After years when lattices were found useful to design post-quantum constructions, Gentry et al. [22] proposed new possibility to design IBE from lattices. The topic of IBE has been widely studied in cryptography and various possibilities on it have been explored. Attribute-based encryption (ABE) is a special form of IBE, where identities are fine grained and replaced by particular attributes of the users. Homomorphic encryption [21] is another special encryption which has been studied parallel to ABE and serves various useful application in cryptography. In a wide review of PKC of last decade these topics namely IBE, ABE, homomorphic encryption, lattice-based encryption have gained much attentions as they cover a major section of recent research in PKC. Since the last couple of years researchers have focused to achieve mixed functionality by combining two or more properties in a single protocol. In this paper we achieve compact encryption schemes by combining functionalities of above crucial notions. Below we discuss each individual topic with their state of art.
Identity-Based Encryption. An identity-based encryption was introduced by Shamir [38] and it allows users to send encrypted messages knowing only the recipient’s identity. Practical implementations were proposed only many years later. The first IBE was given by Boneh and Franklin [8] and since then it got a lot of attention from the cryptographic community. The first construction using lattices was given by Gentry et al. [22]. Other IBE construction were presented in [1, 2, 15, 34] and proved secure in the standard model using LWE assumption. Gentry et al.’s construction [23] allows to construct a fully homomorphic identity-based encryption which is also secure under the LWE hardness problem. The shortcoming of an IBE scheme is that it cannot have a unique identifier for each person. Usually users are identified by their attributes. This leads to the next cryptographic construction, called attribute-based encryption. In a nutshell, an attribute-based encryption represents a generalization of an IBE scheme, since in an IBE scheme ciphertexts are encrypted under one attribute, the identity. In contrast, an attribute-based encryption provides a scheme where ciphertexts are associated with many attributes. In the next paragraph we give an overview of this scheme.
Attribute-Based Encryption. An attribute-based encryption (ABE) scheme that allows fine-grained access control on encrypted data, was introduced by Sahai and Waters [37]. The idea of an ABE is to associate ciphertexts and private keys with sets of descriptive attributes such that the decryption is only possible if the overlap of these two sets is sufficient. There are two flavors of an attribute-based encryption, a key-policy ABE (KP-ABE) and a ciphertext-policy ABE (CP-ABE). A key-policy ABE handles with ciphertexts which are annotated with attributes while private keys which are associated with certain access structures. The reason for these access structure is to specify which ciphertexts can be chosen to be decrypted by user. The other ABE flavor, a ciphertext-policy model was introduced by Bethencourt et al. [6] and by Cheung and Newport [17]. A work that analyzes the first expressive construction was presented by Goyal et al. [25] in the standard model. Other standard model CP-ABE constructions were provided by Waters [41] and Lewko et al. [28]. In CP-ABE scheme attribute sets are assigned to private keys, where the sender specifies an access policy such that receiver’s attribute set can comply with it. Attrapadung et al. [5] introduced an ABE scheme with constant-size ciphertexts. Goyal et al. [26] generalized those techniques from [37] and introduced a new technique where user’s key is associated with a tree-access structure and the leaves are associated with attributes. User is able to decrypt a ciphertext if the attributes associated with a ciphertext satisfy key’s access structure. This technique differs from secret-sharing schemes by the fact that any communication between different parties is forbidden. An ABE scheme which allows a group of authorities to monitor only a certain subset of attributes was developed by Chase [16]. This multi-authority ABE construction allows to corrupt any number of attribute authorities but guarantees security of encryption as long as not all required attributes can be obtained from those corrupt authorities. The first ABE construction based on lattices was introduced by Boyen [10]. Since these both discussed encryption flavours provide attractive features for security issues of cloud computing, we recall in the following paragraph the motivation of cryptographic applications in cloud computing.
Homomorphic Encryption. Our paper handles with leveled homomorphic encryption which represents a meaningful field of fully homomorphic encryption. The latter had an enormous development in recent years and became an attractive cryptographic tool due to its functionality which allows to evaluate certain computations on encrypted data sets. Gentry [21] introduced the first fully homomorphic encryption scheme based on cryptographic assumptions. His construction is based on the hardness of problems defined on ideal lattices, which are not deeply and well-studied yet. The benefit of using these ideal lattices is that they support addition and multiplication of homomorphic encryption. Other fully homomorphic encryption schemes which are not based on lattices but relied on ideals in rings were presented in [14, 39, 40]. Brakerski and Vaikuntanathan [13] presented a fully homomorphic scheme based on a well-studied assumption - called the learning with errors assumption (LWE). A comparatively simple fully homomorphic encryption scheme also based on LWE problem has been presented by Gentry et al. [23]. They presented a new technique which they called approximate eigenvector method where homomorphic addition and multiplication are provided by simple matrix addition and multiplication. In contrast to previous fully homomoprhic schemes, Gentry et al.’s construction does not require any evaluation key and evaluation can even be calculated without knowing user’s public key. This feature allowed the authors to construct the first fully homomorphic identity-based encryption.
Lattice-Based Encryption. Lattice-based cryptography developed rapidly and became a significant part of cryptographic primitives in the last few years. Cryptosystems based on the hardness of lattice problems became so powerful because of their provable security guarantees, simplicity, potential efficiency and their security against quantum attacks. This new kind of cryptography which represents a part of post-quantum cryptography, was invented by the breakthrough results of Ajtai [4] in 1996. There are so far several constructions of lattice-based primitives, such like one-way functions [31], collision resistant hash functions [4], signatures [9], public-key encryption [35, 36], encryption for threshold functions [3], identity based encryption [15, 22], lossy trapdoor functions [22]. Agrawal and Boyen [2] presented an IBE construction based on hard problems in lattices in the standard model. The construction is anonymous, which means that it is usable for searching on encrypted data because the ciphertext does not reveals the identity of the recipient. The most of these cryptographic applications [2, 3, 22, 36] are based on the presumed hardness of LWE (Learning With Errors) problem. One of the connections between lattices and LWE is given by a polynomial-time quantum algorithm that solves standard lattice problems, given access to an oracle that solves the LWE problem. There are other algorithms which run in exponential time, e.g. the Blum et al. [7], Micciancio and Voulgaris [32] algorithms are the best known algorithms for solving LWE problem which run in time \(2^{\mathcal {O}(n)}\). Most of the cryptosystems based on lattices [2, 3, 22] rely on the Learning With Errors (LWE) problem which was introduced by Regev [36]. Before we can present our contribution we recall shortly the basics of identity-based encryption and attribute-based encryption as it takes an important part of our underlying work.
Cloud computing. Cloud computing allows users to use big data storage and computation capabilities at a very low price. Since its invention, cloud computing became an important application for the recent cryptographic protocols. Storing data on a cloud system enables users to reduce purchase and maintaining cost of computing and storage tools which attracted a lot of attention from computer users. When personal and confidential data is outsourced to a cloud server there is a need to guarantee the customers that their data will not be watched by anybody. Therefore cryptographic encryption became a crucial tool in cloud security. Distributing the role and responsibility of a single party involved in a cloud application, allowed to improvements for the cloud security. The idea of distributing the power of a single party under multiple parties in a multi-party protocol has been developed by Kamara et al. [27]. López-Alt et al. [30] presented a multi-key fully homomorphic encryption from the NTRU encryption scheme that allows computation of ciphertexts under different unrelated keys. In the following paragraph we present our main contribution which encompasses the aforementioned cryptographic constructions and we suggest how to apply our construction to cloud computing.
Contribution. In contrast to the scheme in [23] which introduced a single-authority leveled homomorphic attribute-based encryption (FHABE) and single identity-based encryption (FHIBE), we present in our work two constructions employing multiple authorities in case of attribute-based encryption or multiple identities in case of identity-based encryption where a ciphertext is encrypted under different public keys. The construction in [23] is advantageous in comparison to previous fully homomorphic encryption [12] which required existence of evaluation keys to evaluate several ciphertexts. This is also an advantage of our scheme, because our evaluator can execute homomorphic operations without using any evaluation key. Our scheme presents an alternative construction of a leveled homomorphic IBE and leveled homomorphic ABE schemes employing multiple identities. In addition to the technique from [23] we recall the well-known tensor product in order to allow the homomorphic encryption which supports multiplication operations of different ciphertexts using multiple identities in case of IBE scheme and multiple authorities in case of ABE scheme. In comparison to the López-Alt et al. work [30] which provided a multi-party construction, we introduce a new technique for the addition of ciphertexts without use of evaluation keys, which makes our construction more advantageous than the scheme in [30].
Related Work. The first multi-key fully homomorphic encryption introduced by López-Alt et al. [30] relies on a non-standard assumption, called the Decisional Small Polynomial Ratio assumption and employs evaluation keys during the evaluation process. Clear and McGoldrick [18] introduced the first multi-identity and multi-key leveled FHE and multi-identity fully homomorphic IBE (FHIBE) scheme secure under the hardness of learning with errors assumption. They presented a new compiler, which converts a single-identity FHIBE scheme into a multi-identity FHIBE scheme. Their technique involves a masking system which makes the computations more difficult than in case of a single-identity FHIBE. In their later work, Clear and McGoldrick [19] presented a pure fully homomorphic attribute-based encryption scheme which is the first achievement without using indistinguishability obfuscation. However they couldn’t achieve a pure fully homomorphic multi-attribute based encryption scheme. We note that we do not claim achievement of pure fully homomorphic property, but we claim achievement of homomorphism according to the multiplication of ciphertexts using the new mathematical constructs such like tensor product and natural logarithm. The latter guarantees that the compactness property of the evaluated ciphertext keeps preserved. In contrast to the construction in [18], our work provides a simple and alternative construction of multi-identity homomorphic IBE scheme and a new construction of multi-authority leveled homomorphic ABE using the natural logarithm as an auxiliary for the homomorphic evaluation. Brakerski et al. [11] showed that a cross-evaluation of attributes is possible, such that the size of the ciphertext remains independent of attributes. Mukherjee and Wichs [33] showed how to homomorphically evaluate data which as encrypted under different public keys.
2 Preliminaries
In this section we recall learning with errors problem and the flattening technique from [23]. Other preliminaries are provided in the appendix.
Definition 1
(LWE Problem). For an integer q and error distribution \(\chi \), the goal of LWE\({}_{q,\chi }\) in n dimensions problem is to find \(\mathbf{s}\in \mathbb {Z}_q^n\) with overwhelming probability, given access to any arbitrary poly(n) number of samples from \(A_{\mathbf{s},\chi }\) for some random \(\mathbf{s}\).
In matrix form this problem looks as follows: collecting the vectors \(\mathbf{a}_i\in \mathbb {Z}_q^n\) into a matrix \(\mathbf{A}\in \mathbb {Z}_q^{n\times m}\) and the error terms \(e_i\in \mathbb {Z}\) and values \(t_i\in \mathbb {Z}_q\) as the entries of the m-dimensional vector \(\mathbf{t}\in \mathbb {Z}_q^{m}\) we obtain the input \(\mathbf{A},\ \mathbf{t}=\mathbf{A}^t{\varvec{s}}+{\varvec{e}}\mod q\).
2.1 Flattening Ciphertexts
In this paragraph we recall the technique from [23] which keeps ciphertexts strongly bounded. It was used to realize the first leveled homomorphic identity-based and leveled homomorphic attribute-based encryption as showed in [23]. Using transformations from [13], vectors can be modified without affecting dot products.
We assume two vectors \({\varvec{a}},{\varvec{b}}\in \mathbb {Z}_{q}^{k}\) and set \(l=\left\lfloor \log _2 q\right\rfloor +1\) and \(N=k\cdot l\). Let \(\mathtt {BitDecomp}({\varvec{a}})\) be the N-dimensional vector \((a_{1,0},\ldots ,a_{1,l-1},\ldots ,a_{k,0},\ldots ,a_{k,l-1})\), where \(a_{i,j}\) is the j-th bit in \(a_i\)’s binary representation. For some vector \({\varvec{a}}'=(a_{1,0},\ldots ,a_{1,l-1},\ldots ,a_{k,0},\ldots ,a_{k,l-1})\), let
be the inverse of \(\mathtt {BitDecomp}\), which is well defined. It means that even if the input is not a bit-vector, the inverse is well-defined.
Let \(\mathtt {Flatten}({\varvec{a}}')=\mathtt {BitDecomp}(\mathtt {BitDecomp}^{-1}({\varvec{a}}'))\) be a N-dimensional bit vector. For a matrix A, let \(\mathtt {BitDecomp}(A)\), \(\mathtt {BitDecomp}^{-1}(A),\mathtt {Flatten}(A)\) being applied to each row of A. Let \(\mathtt {Powerof2}({\varvec{b}})=(b_1,2b_1,\ldots ,2^{l-1}b_1,\ldots ,b_k,2b_k,\ldots ,2^{l-1}b_k)\). Observe following properties for any N-dimensional \({\varvec{a}}'\):
The leveled homomorphic encryption (LHE) scheme from [23] works as follows. For suitable parameters \(q,n,m=\mathcal {O}(n \log q)\) the LWE instance consists of a \(m\times (n+1)\) matrix A, s.t. there is a vector \(s\in \mathbb {Z}_q^{n+1}\), where the first entry is 1 and \(e=A\cdot s\) is a small error vector. We assume that A is public and s is secret. A ciphertext C encrypts \(\mu \) if \(C\cdot {\varvec{v}}=\mu {\varvec{v}}+{\varvec{e}}\), where \({\varvec{v}}\) is a N-dimensional secret key. To decrypt message \(\mu \), the i-th row \(C_{id_i}\) is extracted from C and \(x\leftarrow \left\langle C_{id_i},{\varvec{v}}\right\rangle =\mu v_i+e_i\) computed. The vector \({\varvec{v}}\) is called approximate eigenvector. Let \({\varvec{v}}=\mathtt {Powerof2}({\varvec{s}})\), which is a vector of dimension \(N=(n+1)\cdot l\) for \(l=\left\lfloor \log _2 q\right\rfloor +1\). It holds: \(\mathtt {Flatten}(C)\cdot {\varvec{v}}=C\cdot {\varvec{v}}\).
To encrypt a message \(\mu \in \mathbb {Z}_q\), a random matrix \(R\in \{0,1\}^{N\times m}\) is generated and \(C=\mathtt {Flatten}(\mu \cdot I_N+\mathtt {BitDecomp}(R\cdot A))\) computed. Note that \(\mathtt {Flatten}\) operation does not affect the product with \({\varvec{v}}\), i.e.
3 Leveled Homomorphic Multi-identity-Based Encryption
Intuition. As mentioned before, the first leveled homomorphic multi-identity-based encryption scheme was introduced by Clear and McGoldric [18]. The idea is to extend the single-identity setting to the multi-identity setting, such that each ciphertext encrypts a different message under a different identity. To enable the evaluation of different ciphertexts, we propose a new technique using the already presented mathematical tool, “tensor product” for multiplication of those ciphertexts. In this section we present the compilation of our leveled homomorphic multi-identity-based encryption (LHMIBE) from LWE-based IBE scheme, where the ciphertexts are computed on different identities and evaluation procedure calculates a function on input of these ciphertexts. We provide the syntax of our LHMIBE scheme in the following definition.
Definition 2
(LHMIBE). A leveled homomorphic multi-identity-based encryption scheme consists of the following five algorithms:
-
\(\mathtt {Setup}(1^{\lambda })\mathrm{:}\) On input the security parameter \(1^{\lambda }, \lambda \in \mathbb {N}\) output the master key pair (msk, mpk).
-
\(\mathtt {Extract}(mpk,msk,id_i)\mathrm{:}\) On input a master secret key msk and an identity \(id_i\), output \((id_i,sk_{id_i})\).
-
\(\mathtt {Encrypt}(mpk,id_i,\mu _i)\mathrm{:}\) On input mpk, an identity \(id_i\) and a message \(\mu _i\), output a ciphertext C.
-
\(\mathtt {Eval}(F,C_{id_1},\ldots ,C_{id_n})\mathrm{:}\) On input a function F, n different ciphertexts \(C_{id_i}, i\in [n]\), output \(\hat{C}\).
-
\(\mathtt {Decrypt}(\hat{C},sk_{id_1},\ldots ,sk_{id_n})\mathrm{:}\) On input n secret keys \(\{sk_{id_i}\}_{i\in [n]}\) and evaluated ciphertext \(\hat{C}\), output \(\hat{\mu }(=F(\mu _1,\ldots ,\mu _n))\).
Further, we propose a transformation from an LWE-based IBE scheme into a leveled homomorphic multi-identity-based encryption (LHMIBE) scheme, that supports homomorphic operations on ciphertexts produced for different identities. We rely on the following properties of LWE-based IBE schemes [1, 15, 22]:
-
(1)
The decryption key for identity \(id_i\) and the corresponding ciphertext for \(id_i\), are \(sk_{id_i}, C_{id_i}\in \mathbb {Z}_{q}^{n'}\). We extend the decryption key by adding 1 as the first component.
-
(2)
If \(C_{id_i}\) encrypts 0, then \(\left\langle C_{id_i},sk_{id_i}\right\rangle \) is small.
-
(3)
Encryptions of 0 are indistinguishable from uniform vectors over \(\mathbb {Z}_q\) (under LWE assumption).
We stress that the technique from [23] cannot be applied to our setting where ciphertexts can possibly be encryptions under different identities. Our construction offers an alternative evaluation technique based on tensor product and natural logarithm. The evaluation function F is a homomorphic function, allowing to compute a product of ciphertexts by summing the evaluated individual ciphertexts. To provide this functionality, we use the natural logarithm. Since the ciphertext \(C_{id_i}\) is represented as a \(N\times N\) matrix in the following paragraphs, and the secret keys are N-dimensional vectors, i.e. \(C_{id_i}\in \mathbb {Z}_{q}^{N\times N}, {\varvec{sk}}_{id_i}\in \mathbb {Z}_{q}^{N}\), the evaluation function F has the following form:
The n different decryption keys \(\{{\varvec{v}}_{id_i}\}_{i\in [n]}\) operate on the resulting ciphertext as follows:
3.1 The Scheme
Let \(\varSigma \) be a LWE-based IBE scheme with the above properties. Our transformation of \(\varSigma \) into an LHMIBE scheme proceeds as follows:
-
\(\mathtt {Setup}(1^{\lambda })\): Run the \(\mathtt {Setup}\) algorithm of \(\varSigma \) to generate (mpk, msk).
-
\(\mathtt {Extract}(mpk,msk,id_i)\mathrm{:}\) Run the extraction algorithm of \(\varSigma \) scheme to compute \(sk_{id_i}^{ibe}\in \mathbb {Z}_{q}^{m}\), which is the decryption key of IBE scheme. Then set \({\varvec{s}}_{id_i}:={\varvec{sk}}_{id_i}'=(1,sk_{id_i}^{ibe})\in \mathbb {Z}_{q}^{m+1}\). Compute the decryption key of LHMIBE scheme as \(\mathtt {Powerof2}(s_{id_i})={\varvec{v}}_{id_i}\in \mathbb {Z}_{q}^{l\cdot (m+1)}\), where \({\varvec{v}}_{id_i}=(v_{id_i,1},\ldots ,v_{id_N})\) for \(i\in \{1,\ldots ,n\}\), \(N=l(m+1)\). Output \((i,{\varvec{v}}_{id_i})\).
-
\(\mathtt {Encrypt}(mpk,id_{i},\mu _i)\mathrm{:}\) To encrypt the message \(\mu _i\in \{0,1\}\) for \(i\in [n]\), invoke \(\mathtt {Encrypt}\) of \(\varSigma \) in order to compute \(N=l\cdot (m+1)\) encryptions of 0. The resulted ciphertext is denoted by \(C_{id_i}'\). Taking \(C_{id_i}'\), compute the ciphertext of LHMIBE as follows: \(C_{id_i}=\mathtt {Flatten}\left( \mu \cdot I_N+\mathtt {BitDecomp}(C_{id_i}')\right) \).
-
\(\mathtt {Eval}(mpk,C_{id_1},\ldots ,C_{id_n},F)\mathrm{:}\) Take as input ciphertexts, \(C_{id_1},\ldots ,C_{id_n}\) and an evaluation function F. Output \(F(C_{id_1}\ldots , C_{id_n})=\log \left( \bigotimes _{i=1}^{n} C_{id_i}\right) =\hat{C}\).
-
\(\mathtt {Decrypt}(mpk,\hat{C},{\varvec{v}}_{id_1},\ldots ,{\varvec{v}}_{id_n})\mathrm{:}\) On input master public key mpk, evaluated ciphertext \(\hat{C}\) and the n secret keys \({\varvec{v}}_{id_1},\ldots ,{\varvec{v}}_{id_n}\), compute \(\log \left[ \left( \bigotimes _{i=1}^{n}C_{id_i}\right) \left( \bigotimes _{i=1}^{n}{\varvec{v}}_{id_i}\right) \right] =\log \left[ \bigotimes _{i=1}^{n}C_{id_i}{\varvec{v}}_{id_i}\right] \).
Correctness. To show the validity of decryption procedure, we observe the following computation:

Note: \({\varvec{v}}_{id_i}^{-1}:=({\varvec{v}}_{id_i,1}^{-1},\ldots ,{\varvec{v}}_{id_{i},N}^{-1})\) is defined as inverse of the components of \({\varvec{v}}_{id_i}:=({\varvec{v}}_{id_i,1},\ldots ,{\varvec{v}}_{id_{i},N})\). Furthermore holds \(C_{id_i}{\varvec{v}}_{id_i}=\left( \mu _i{\varvec{v}}_{id_i}+e_{i}\right) \).
3.2 Security Analysis
We prove in this section that the resulting LHMIBE construction is IND-ID-CPA secure according to the following Definition below. We note that an adversary obtains at most \(n-1\) secret keys. Since the security of our construction is given in the CPA model we assume an adversary having access to the extract oracle which on input an identity outputs the corresponding secret key corresponding tho that identity. We provide the limits of an adversary by not allowing her to query the extraction oracle on the same identity which was used during the encryption process. The security definition is given below:
Definition 3
(LHMIBE Indistinguishability). Let \(\mathcal {A}_{ind}\) be a probabilistic polynomial time adversary against the IND-ID-CPA security of the LHMIBE scheme, F an evaluation function and \(b\in \{0,1\}\) a bit which is associated with the following experiment \(\mathbf{Exp}_{LHMIBE,\mathcal {A}_{ind}}^{IND\text {-}ID\text {-}CPA\text {-}b}(1^{\lambda })\):
-
1.
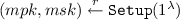 .
. -
2.
\(F,st,(id_{1}^{*},\mu _{1,0},\mu _{1,1}),\ldots ,(id_{n}^{*},\mu _{n,0},\mu _{n,1})\leftarrow \mathcal {A}_{ind}^{\mathcal {O}\mathtt {Extract}(\cdot )}(mpk,find)\).
-
3.
Compute \(\{{\varvec{v}}_{id_i}\}_{i\in [n-1]}\leftarrow \mathtt {Extract}(mpk,msk,id_i)\) and set \(S=\{(id_i,{\varvec{v}}_{id_i})\}_{i}\) with \(i\in [n]\). At the beginning of the experiment the set S is empty.
-
4.
If \((id_i,\cdot )\notin S\), run \({\varvec{v}}_{id_i}\leftarrow \mathtt {Extract}(mpk,msk,id_i)\) and add \((id_i,{\varvec{v}}_{id_i})\) to S.
-
5.
Compute \(C_{i,b}^{*}=\mathtt {Encrypt}(mpk,id_{i}^{*},\mu _{i,b})\), with different identities \(i\in [n]\).
-
6.
\(\hat{C}_{b}=\mathtt {Eval}(mpk,C_{1,b}^{*},\ldots , C_{n,b}^{*},F)\).
-
7.
\(b'\leftarrow \mathcal {A}_{ind}^{\mathcal {O}\mathtt {Extract}(\cdot )}(\hat{C}_b,\{C_{i,b}^{*}\}_{i\in [n]},st)\), where \(b'\in \{0,1\}\).
\(\mathcal {O}\mathtt {Extract}(id_i)\mathrm{:}\) On input \(id_i\) the oracle checks if \((id_i,\cdot )\) is in the list S. If so, returns \({\varvec{v}}_{id_i}\) to the adversary. Otherwise the oracle runs  and gives \({\varvec{v}}_{id_i}\) to \(\mathcal {A}\). If \(|S|>n-1\), the oracle returns \(\bot \).
and gives \({\varvec{v}}_{id_i}\) to \(\mathcal {A}\). If \(|S|>n-1\), the oracle returns \(\bot \).
\(\mathcal {A}_{ind}\) wins if \(b'=b\) meaning that \(\mathcal {A}_{ind}\) can distinguish whether \(\hat{C}_b\) was produced from \(C_{1,0},\ldots ,C_{n,0}\) or \(C_{1,1},\ldots ,C_{n,1}\) and \(\mathcal {A}_{ind}\) did not issue secret key extraction query on \(id_{i}^{*}\). The advantage of \(\mathcal {A}_{ind}\) is \(\mathbf{Adv}_{LHMIBE,\mathcal {A}_{ind}}^{IND\text {-}ID\text {-}CPA}=\):
The LHMIBE scheme is IND-ID-CPA secure if \(\mathbf{Adv}_{LHMIBE,\mathcal {A}_{ind}}^{IND\text {-}ID\text {-}CPA}\) is negligible.
Remark 1
Furthermore, our LHMIBE scheme has to fulfill the compactness property which is formulated as following: There exists a polynomial \(p(\lambda ,L,\cdot )\), such that \(|\hat{C}|\le p(\lambda ,L,\cdot )\), where L is the depth of the ciphertext. We note that this property is satisfied by our construction since \(\hat{C}\) is the result of natural logarithm on input of individual ciphertexts. W.l.o.g. for sufficiently large arguments of the natural logarithm, it is obvious that \(\log (\cdot )\le p(\cdot )\).
Theorem 1
Our LHMIBE scheme is IND-ID-CPA secure given that \((\mathbb {Z}_q,n,\chi )\)-LWE is hard.
Proof
Let \(\mathcal {A}_{ind}\) be an adversary against IND-ID-CPA security of LHMIBE scheme. We use \(\mathcal {A}_{ind}\) to construct an algorithm \(\mathcal {B}\) against the IND-ID-CPA security of the underlying \(\varSigma \) scheme which was proven secure in [23]. Thereafter we use \(\mathcal {B}\) to construct an adversary \(\mathcal {C}\) against LWE problem. The challenger \(\mathcal {B}\) sets the public parameters of \(\varSigma \) equal to (mpk, msk) of LHMIBE scheme.
Key Extract Queries: When \(\mathcal {A}_{ind}\) issues queries on \(id_i'\) where \((id_i',\cdot )\notin S\) and \(id_i'\ne id_{i}^{*}\), the algorithm \(\mathcal {B}\), which controls the set S, is invoked on that input and forwards the query to its own oracle \(\mathcal {O}\mathtt {Extract}_{\varSigma }\) of the underlying IBE scheme \(\varSigma \) which returns \(sk_{id_i}\) to \(\mathcal {B}\). Algorithm \(\mathcal {B}\) sets \({\varvec{s}}_{id_i'}=(1,sk_{id_i'})\in \mathbb {Z}_{q}^{m+1}\) and \({\varvec{v}}_{id_i'}=\mathtt {Powerof2}({\varvec{s}}_{id_i'})\in \mathbb {Z}_{q}^{l(m+1)}\) and sends \({\varvec{v}}_{id_i'}\) to \(\mathcal {A}_{ind}\). At some point \(\mathcal {A}_{ind}\) outputs \((id_{1}^{*},\mu _1),\ldots ,(id_{n}^{*},\mu _n)\) on which it wants to be challenged. If \(\mathcal {B}\) didn’t guess the identities and messages correctly then it aborts the simulation. The probability that \(\mathcal {B}\) does not abort is \(1/|\mathcal {M}|^2\), where \(\mathcal {M}\) is the message space.
Challenge Ciphertext: Algorithm \(\mathcal {B}\) computes \(C_i^{*}\leftarrow \mathtt {Encrypt}(mpk,id_{i}^{*},m_{i})\) by running the encryption algorithm of \(\varSigma \) scheme and taking as input the randomly guessed \(id_{i}^{*}\). \(\mathcal {A}_{ind}\) computes challenge ciphertext \(C_i^{*}\leftarrow \mathtt {Encrypt}(pp,id_{i}^{*},m_{i})\). \(\mathcal {A}_{ind}\) does the same for the remained \(n-2\) identities. \(\mathcal {B}\) simulates F by randomly choosing  and sends it to \(\mathcal {A}_{ind}\).
and sends it to \(\mathcal {A}_{ind}\).
Guess: Simulator \(\mathcal {B}\) issues up to \(q_E\) queries on \(id_i\) and outputs a guess \(b'\). After making additional queries \(\mathcal {A}_{ind}\) outputs a guess b. The probability that \(b'=b\) is \(\frac{1}{q_E}\). Thus the advantage that \(\mathcal {A}_{ind}\) wins the game is given by \(\mathbf{Adv}_{\mathcal {B}}\ge \frac{1}{q_E|\mathcal {M}|^2}{} \mathbf{Adv}_{\mathcal {A}_{ind}}\).
Reduction to LWE problem: Now we assume an adversary \(\mathcal {C}\) against LWE problem which simulates the outputs for adversary \(\mathcal {B}\) against \(\varSigma \) scheme. The instance of LWE problem is given as a sampling oracle \(\mathcal {O}\). This oracle can be either purely random \(\mathcal {O}_r\) or pseudo-random \(\mathcal {O}_s\) for some secret \(s\in \mathbb {Z}_q^{N},\) where \(N=l(m+1)\). \(\mathcal {C}\) queries from his sampling oracle \(\mathcal {O}\) and receives for each request i a fresh pair \(({\varvec{a}}_i,t_i)\in \mathbb {Z}_q^n\times \mathbb {Z}_q\). In the next step \(\mathcal {B}\) chooses target identity it wants to attack \(id^{*}\). The challenger \(\mathcal {C}\) simulates for \(\mathcal {B}\) the public parameters (mpk, msk) using LWE samples and sends them to \(\mathcal {B}\). When \(\mathcal {B}\) issues private key extraction queries on \(id_i\), \(\mathcal {C}\) simulates them using the samples which it received from its oracle \(\mathcal {O}\) that statistically close to uniform values. \(\mathcal {C}\) sends the simulated values to \(\mathcal {B}\).
The simulation of the challenge ciphertext proceeds in a similar manner using as input entries from the LWE instance. Finally simulator \(\mathcal {C}\) sends the ciphertext to \(\mathcal {B}\). For the simulation of the ciphertext we differ between two oracles. When the LWE oracle is given by \(\mathcal {O}_s\) (i.e. it is pseudo-random), the ciphertext is randomly distributed including some random noise vector which is distributed corresponding to the distribution \(\varPhi _{\alpha }^{m}\), which describes a certain noise distribution over \(\mathbb {Z}_q\), as showed in [36]. When \(\mathcal {O}\) is given by \(\mathcal {O}_r\) then the ciphertext is uniform and independent over \(\mathbb {Z}_{q}^{N}\), for some \(n'\). Eventually the simulated ciphertext is always uniform in \(\mathbb {Z}_q\times \mathbb {Z}_{q}^{N}\). After issuing additional queries, \(\mathcal {B}\) guesses a bit \(b'\). The LWE adversary \(\mathcal {C}\) outputs its guess as the result of the LWE challenge. Finally we follow that \(\mathcal {C}'\)s advantage in solving LWE is at least the same as \(\mathcal {B}'\)s advantage in distinguishing the ciphertext from a random value, i.e.: \(\mathbf{Adv}_{\mathcal {C}}\ge \frac{1}{q_E}{} \mathbf{Adv}_{\mathcal {B}}\). \(\square \)
4 Leveled Homomorphic Attribute-Based Encryption in Single and Multi-authority Setting
In this section we extend the definition of a single setting attribute-based encryption introduced in [23] and present a leveled homomoprhic attribute-based encryption (LHABE). We first define a LHABE scheme assuming existence of a single attribute authority, which is responsible for the generation of the secret keys corresponding to a certain string. This string can either describe an attribute set in case of a ciphertext-policy ABE scheme or the string can be related to an access policy in case of key-policy ABE scheme. We do not specify the definition for one of the mentioned flavours of ABE scheme. Instead, we provide a general definition where attributes and policy are represented by certain strings. To do so, we assume that a leveled homomorphic ABE scheme is associated to some computable relation R(x, y) for \(x\in \{0,1\}^l,y\in \{0,1\}^{l'}\) as it was showed in [23].
Gentry et al. [23] mentioned the possibility of extension of their scheme so that the evaluation algorithm operates under multiple indices \(x_1,\ldots ,x_n\). The decryption process can rely on different possibilities. The result can be decrypted using either the same secret key \(sk_y\) such that \(R(x_i,y)=1\) for all \(i\in [1,k]\) or using different secret keys \(sk_{y_1},\ldots ,sk_{y_k}\) such that \(R(x_i,y_j)=1\) for \(i,j\in [1,k]\). Our evaluation techniques based on tensor product and natural logarithm allow us to realize these extensions. We note that in first case where we have only one decryption key \(sk_y\) and different strings \(x_i\), we can provide a single authority ABE scheme whose ciphertexts are encrypted under different indices, while in second case with different secret keys \(sk_{y_j}\) we can construct the first leveled homomorphic ABE scheme employing multiple authorities, such that each secret key can be generated by a different authority. In this section we present the two extensions of [23], a leveled homomorphic single authority ABE and a leveled homomorphic multi-authority ABE (LHMABE) schemes.
4.1 Leveled Homomorphic ABE Scheme (LHABE)
In this section we introduce a leveled homomorphic ABE scheme that operates on different indices \(x_i\). Since the construction in [23] didn’t provide a concrete scheme over different indices, we resolve this drawback and instantiate in our work a construction of a LHABE scheme where distinct messages \(\mu _i\) are encrypted using another public string \(x_i\). The decryption process is possible if the decryption key which was generated on a fixed chosen string y is valid and the following relation holds: \(R(x_i,y)=1\) for all \(x_i\in \{0,1\}^l\).
Syntax. A leveled homomorphic ABE scheme consists of the following algorithms:
-
\(\mathtt {Setup}(1^{\lambda })\mathrm{:}\) On input a security parameter \(1^{\lambda }\), output (mpk, msk).
-
\(\mathtt {KeyGen}(mpk,msk,y)\mathrm{:}\) On input (mpk, msk), a string y generate \(sk_y\).
-
\(\mathtt {Encrypt}(mpk,m_i,x_i)\mathrm{:}\) On input a master public key mpk, a message \(m_i\) and a string \(x_i\), output a ciphertext \(C_i\) for \(i\in \{1,\ldots ,k\}\).
-
\(\mathtt {Eval}(mpk,F,\{x_i\}_{i\in [k]},C_1,\ldots ,C_k)\mathrm{:}\) On input mpk, an evaluation function F, set of strings \(\{x_i\}_{i\in [k]}\) and a set of k ciphertexts \(C_1,\ldots ,C_n\) homomorphically evaluate F and output \(\hat{C}\).
-
\(\mathtt {Decrypt}(mpk,\hat{C},sk_{y})\mathrm{:}\) On input master public key mpk, an evaluated ciphertext \(\hat{C}\) and the secret key \(sk_y\), decrypt the function \(\hat{C}=F(C_1,\ldots ,C_k)\) if \(R(x,y)=1\).
In the following definition we present a leveled homomorphic attribute-based encryption (LHABE) which is compiled from a secure LWE based attribute-based encryption scheme.
The Scheme. Let \(\varSigma '\) denote an LWE-based attribute-based encryption scheme. A leveled homomorphic ABE scheme consists of the following algorithms:
-
\(\mathtt {Setup}(1^{\lambda })\mathrm{:}\) On input security parameter, run \(\mathtt {Setup}\) algorithm of \(\varSigma '\) and generate authority’s public key and authority’s secret key (apk, ask).
-
\(\mathtt {Extract}(apk,ask,y)\mathrm{:}\) Run the \(\mathtt {KeyGen}\) algorithm of \(\varSigma '\) scheme to compute \(sk_{y}\in \mathbb {Z}_{q}^{m}\), which is the decryption key of that scheme embedding a string \(y\in \{0,1\}^{l}\) into the key. Set \(s:=sk_{y}'=\left( 1,sk_{y}\right) \in \mathbb {Z}_{q}^{m+1}\). It computes the decryption key of LHABE scheme as \(\mathtt {Powerof2}(s)={\varvec{v}}_y\in \mathbb {Z}_{q}^{l\cdot (m+1)}\).
-
\(\mathtt {Encrypt}(apk,x_{i},\mu _{i})\mathrm{:}\) On input authority’s public key apk, an attribute string \(x_i\), \(i\in [n]\) with \(R(x_i,y)=1\) and a message \(\mu _{i}, i\in [n]\) run \(\mathtt {Encrypt}\) of ABE scheme \(\varSigma '\) in order to compute \(N=l\cdot (m+1)\) encryptions of 0. The result is denoted by \(C_{i}'\). Taking \(C_{i}'\) compute: \(C_{i}=\mathtt {Flatten}\left( \mu \cdot I_N+\mathtt {BitDecomp}(C_{i}')\right) \).
-
\(\mathtt {Eval}(apk_i,\{x_i\}_{i\in [n]},C_{1},\ldots ,C_{n},F)\mathrm{:}\) Take as input apk, the ciphertexts, \(C_{1},\ldots ,C_{n}\) on messages \(\mu _1,\ldots ,\mu _n\) and an evaluation function F. Output: \(F(C_1,\ldots ,C_n)=\log \left( \bigotimes _{i=1}^{n} C_{i}\right) =\hat{C}\).
-
\(\mathtt {Decrypt}(mpk,\hat{C},{\varvec{v}}_y)\mathrm{:}\) On input the authorities’ secret keys \({\varvec{v}}_y\), an evaluated ciphertext F, compute \({\varvec{v}}_{y}^{-1}\) (where \({\varvec{v}}_{y}^{-1}\) is the vector consisting of inverse components of vector \({\varvec{v}}_y\). Using this inverse \({\varvec{v}}_{y}^{-1}\), compute:
It outputs a product of messages  .
.
Correctness. Since there is only one secret key v, the decryption process is given by multiplication with the secret key \({\varvec{v}}\) and then by division of this product by \({\varvec{v}}^{-1}\). Correctness of decryption can be verified in the following computations assuming that the different ciphertexts can be decrypted using the same secret key. In the end we apply the exponential function to get the decrypted plaintext:

4.2 Security Analysis of LHABE
In this paragraph we define the security of our leveled homomorphic ABE scheme and provide the proof of security. We assume an adaptive adversary who specifies the set of strings \(x_i\), \(i\in [k]\) after receiving the public key. He is allowed to issue queries to the private key extraction oracle to string y of his choice, as long as \(R(x_i,y)=0\), where \(x_i,i\in [k]\) are strings required for the encryption process, which have to be announced before the adversary obtains the public and secret keys of the authority.
Definition 4
(LHABE Indistinguishability). Let \(\mathcal {A}_{ind}\) be a probabilistic polynomial time adversary against the IND-CPA security of the leveled homomorphic ABE scheme, F an evaluation function and \(b\in \{0,1\}\) is a bit associated with the following experiment: \(\mathbf {Exp}_{LHABE,\mathcal {A}_{ind}}^{IND\text {-}CPA\text {-}b}(1^{\lambda })\):
-
1.
\(\left( apk,ask\right) \leftarrow \mathtt {Setup}(1^{\lambda })\),
-
2.
\(F,st,(x_{1}^{*},\mu _{1,0},\mu _{1,1}),\ldots ,(x_{n}^{*},\mu _{n,0},\mu _{n,1})\leftarrow \mathcal {A}_{ind}^{\mathcal {O}\mathtt {Extract}(\cdot )}(find,apk)\).
-
3.
Compute \(\{{\varvec{v}}_{y}\}_{i\in [n-1]}\leftarrow \mathtt {Extract}(apk,ask,y)\).
-
4.
Compute \(C_{i,b}^{*}=\mathtt {Encrypt}(apk,x_{i}^{*},\mu _{i,b})\), where \(i\in [n]\) are different attributes and messages. We assume that each message is encrypted under another attribute.
-
5.
\(\hat{C}_b=\mathtt {Eval}(mpk,C_{1,b}^{*},\ldots , C_{n,b}^{*},F)\).
-
6.
\(b'\leftarrow \mathcal {A}_{ind}^{\mathcal {O}\mathtt {Extract}(\cdot )}(\hat{C}_b,\{C_{i,b}^{*}\}_{i\in [n]},st)\), where \(b'\in \{0,1\}\).
\(\mathcal {O}\mathtt {Extract}(y)\mathrm{:}\) On input a string y, the oracle checks if \(R(x_{i}^{*},y)=1\). If so, it returns \(\bot \), otherwise runs  and gives \({\varvec{v}}_y\) to \(\mathcal {A}_{ind}\).
and gives \({\varvec{v}}_y\) to \(\mathcal {A}_{ind}\).
\(\mathcal {A}_{ind}\) wins if \(b'=b\), meaning that \(\mathcal {A}_{ind}\) can distinguish whether \(\hat{C}_b\) was produced from \(C_{1,0},\ldots ,C_{n,0}\) or from \(C_{1,1},\ldots ,C_{n,1}\). The advantage of \(\mathcal {A}_{ind}\) is defined as:
The leveled homomorphic ABE (LHABE) scheme is IND-CPA secure if the above defined advantage \(\mathbf{Adv}_{LHABE, \mathcal {A}_{ind}}^{IND\text {-}CPA}\) is negligible.
Remark 2
Furthermore, our LHABE scheme fulfills the compactness property which is justified analogously to the compactness property of LHMIBE scheme.
Theorem 2
Our leveled homomorphic ABE scheme is IND-CPA secure provided that \((\mathbb {Z}_q,n,\chi )\)-LWE holds.
4.3 Leveled Homomorphic Multi-authority ABE Scheme (LHMABE)
In this section we present the compilation of our leveled homomorphic multi-authority ABE scheme (LHMABE) from an LWE-based ABE scheme. We begin with the description of its syntax. Our scheme is associated to some efficient computable relation \(R(x_i,y_j),x\in \{0,1\}^{l},y\{0,1\}^{l'}\).
Definition 5
(LHMABE Scheme). A leveled homomorphic multi-authority ABE scheme consists of the following five algorithms:
-
\(\mathtt {Setup}(1^{\lambda },1^{n})\mathrm{:}\) On input a security parameter \(1^{\lambda }\) output attribute public key \(apk_i\) and attribute secret key \(ask_i\) for each authority \(j\in \{1,\ldots ,k\}\).
-
\(\mathtt {KeyGen}(apk_i,ask_i,y_i)\mathrm{:}\) On input master public and master secret key pair, a string \(y_i\in \{0,1\}^l\), the attribute authority i, generate a secret key \(sk_{y_i}\) which embeds the corresponding policy.
-
\(\mathtt {Encrypt}(\{apk_i\}_{i\in [k]},\mu _{\xi },x_i)\mathrm{:}\) On input a set of attributes represented by string \(x_i\), a set of trusted authorities and their public keys, output a ciphertext \(C_i\).
-
\(\mathtt {Eval}(apk,F,\{x_i\}_{i\in [k]},C_1,\ldots ,C_n)\mathrm{:}\) On input a function F, set of strings \(\{x_i\}_{i\in [k]}\) and a set of n ciphertexts \(C_1,\ldots ,C_n\), homomorphically evaluate F and output \(\hat{C}\).
-
\(\mathtt {Decrypt}(C,\{sk_{y_i}\}_{i\in [k]})\mathrm{:}\) On input a ciphertext C, a set of secret keys \(\{sk_{y_i}\}_{i\in [k]}\) decrypt the message if for every index i there is some index j s.t. \(R(x_i,y_j)=1\).
The main idea of our leveled homomorphic MABE (LHMABE) scheme is a compilation from an already existing LWE-based ABE scheme and an extension to the multi-authority setting. There exist only few of such systems which have been realized and proved secure under the LWE assumption. Boyen [10] introduced a key policy attribute-based functional encryption which relies on the LWE problem. Gorbunov et al. [24] constructed an ABE scheme for circuits based on LWE. Gentry et al. [23] presented the first leveled homomorphic ABE scheme using compilation from ABE schemes [26, 37].
With introduction of multiple authorities the role of the key extraction algorithm in [10, 23, 24] is distributed among a multiple number of authorities where each of them computes a secret key for the user corresponding to a string \(y_i\in \{0,1\}^{l}\). Our construction allows to encrypt different messages \(\mu _i\) using different strings \(x_i\in \{0,1\}^{l'},i\in [1,n]\) and to evaluate them to a certain ciphertext. The user is able to decrypt the evaluated value only if for each \(x_i\) there exists some j such that \(R(x_i,y_j)=1\).
The Scheme. Let \(\varSigma '\) be a LWE-based attribute-based encryption scheme. We note that the encryption of different messages can be computed using different strings \(x_i\in \{0,1\}^{l}\), but it also includes the possibility to encrypt at least two different messages \(\mu _i,\mu _j\) under the same string \(x_i\). A leveled homomorphic MABE scheme consists of the following algorithms:
-
\(\mathtt {Setup}(1^{\lambda })\mathrm{:}\) On input security parameter, generate authority’s public key and authority’s secret key \(apk_i,ask_i\) for each authority \(i\in [k]\).
-
\(\mathtt {Extract}(apk_i,ask_i,y_i)\mathrm{:}\) Run the \(\mathtt {KeyGen}\) algorithm of \(\varSigma '\) scheme to compute \(sk_{i}\in \mathbb {Z}_{q}^{m}\), which is the decryption key of that scheme embedding an access policy given by \(y_i\) into the key. Set \({\varvec{s}}_{i}:=sk_{i}=(1,sk_{i,\varSigma '})\in \mathbb {Z}_{q}^{m+1}\). We note that \(sk_{i,\varSigma '}\) is the decryption key of scheme \(\varSigma '\). Compute the decryption key of ABE scheme as \(\mathtt {Powerof2}({\varvec{s}}_{i})={\varvec{v}}_{y_i}\in \mathbb {Z}_{q}^{l\cdot (m+1)}\), for \(i\in \{1,\ldots ,n\}\).
-
\(\mathtt {Encrypt}\left( \{apk_i\}_{i\in [n]},x_{i},\mu _{i}\right) \mathrm{:}\) On input authority’s public key \(\{apk_i\}\) for all \(i\in [n]\) authorities, an attribute string \(y_i\), for \(i\in [n]\) and a message \(\mu _{i}, i\in [n]\), run \(\mathtt {Encrypt}\) of ABE scheme \(\varSigma '\) in order to compute \(N=l\cdot (m+1)\) encryptions of 0. The resulted ciphertext is denoted by \(C_{i}'\). Taking \(C_{i}'\) compute: \(C_{i}=\mathtt {Flatten}\left( \mu _i\cdot I_N+\mathtt {BitDecomp}(C_{i}')\right) \).
-
\(\mathtt {Eval}(\{apk_i\}_{i\in [n]},{\{x_i\}_{i\in [n]}} , C_{1},\ldots ,C_{n},F)\mathrm{:}\) On input the ciphertexts, \(C_{1},\ldots ,C_{n}\) on messages \(\mu _1,\ldots ,\mu _n\) and an evaluation function \(F(C_1,\ldots ,C_n)\), compute: \(F(C_{1},\ldots ,C_{n})=\log \left( \prod (C_{1}\otimes \ldots \otimes C_{n})\right) \).
-
\(\mathtt {Decrypt}(mpk,\hat{C},\{{\varvec{v}}_{y_j}\}_{i\in [n]})\mathrm{:}\) On input master public key mpk, evaluated ciphertext \(\hat{C}\) and n secret keys \({\varvec{v}}_{y_1},\ldots ,{\varvec{v}}_{y_n}\), compute
$$\log \left[ {\varvec{v}}_{y_1}^{-1}\otimes \ldots \otimes {\varvec{v}}_{y_n}^{-1}\right] +\log \left[ \bigotimes _{i=1}^{n}C_{i}\right] +\log \left[ \left( \bigotimes _{i=1}^{n}{\varvec{v}}_{y_i}\right) \right] $$and output \(\hat{\mu }\), where
 .
.
Correctness. Correctness of decryption can be verified in the following computations, assuming that the different ciphertexts can be decrypted using different secret key. In the end we apply the exponential function to get the decrypted plaintext:
4.4 Security Analysis of LHMABE
In the following definition we define the indistinguishability property of our scheme. We assume an adaptive adversary \(\mathcal {A}_{ind}\) who outputs a set of target strings \(y_{i}^{*}\) for \(i\in [n]\) after receiving the public key. Further we give \(\mathcal {A}_{ind}\) access to a key extraction oracle on input a string \(x_i\) with the restriction that there is no \(y_{j}^{*}, j\in [n]\), such that \(R(y_{j}^{*},x_i)=1\). A successful decryption is only possible if the user has all of the n decryption keys corresponding to the strings \(\{x_i\}_{i\in [n]}\) which were used during the encryption of n different messages. Without loss of generality, there can be messages which were encrypted under the same string \(y_{i}^{*}\).
Definition 6
(LHMABE Indistinguishability). Let \(\mathcal {A}_{ind}\) be a probabilistic polynomial time adversary against the IND-CPA security of the leveled homomorphic MABE scheme, F an evaluation function and \(b\in \{0,1\}\) a bit associated with the following experiment: \(\mathbf {Exp}_{LHMABE,\mathcal {A}_{ind}}^{IND\text {-}CPA\text {-}b}(1^{\lambda })\):
-
1.
\(\left( apk_i,ask_i\right) \leftarrow \mathtt {Setup}(1^{\lambda })\),
-
2.
\(F,st,(y_{1}^{*},\mu _{1,0},\mu _{1,1}),\ldots ,(y_{n}^{*},\mu _{n,0},\mu _{n,1})\leftarrow \mathcal {A}_{ind}^{\mathcal {O}\mathtt {Extract}(\cdot )}(find,apk_i)\).
-
3.
Compute \(\{{\varvec{v}}_{y_i}\}_{i\in [n-1]}\leftarrow \mathtt {Extract}(apk_i,ask_i,y_i)\) and set \(S=\{(y_i,{\varvec{v}}_{y_i})\}_{i\in [n]}\). At the beginning of the experiment the set S is empty.
-
4.
If \((y_{i}^{*},\cdot )\notin S\), run \({\varvec{v}}_{y_{i}^{*}}\leftarrow \mathtt {Extract}(apk_i,ask_i,y_{i}^{*})\), s.t. \(R(y_{i}^{*},x_i)=1\), add \((y_{i}^{*},{\varvec{v}}_{y_i})\) to S.
-
5.
Compute \(C_{i,b}^{*}=\mathtt {Encrypt}(apk_i,x_{i}^{*},\mu _{i,b})\), where \(i\in [n]\) is the index of different identities.
-
6.
\(\hat{C}_b=\mathtt {Eval}(\{apk_i\}_{i\in [n]},C_{1,b}^{*},\ldots , C_{n,b}^{*},F)\).
-
7.
\(b'\leftarrow \mathcal {A}_{ind}^{\mathcal {O}\mathtt {Extract}(\cdot )}(\hat{C}_b,\{C_{i,b}^{*}\}_{i\in [n]},st)\), where \(b'\in \{0,1\}\).
\(\mathcal {O}\mathtt {Extract}(ask_i,y_i)\mathrm{:}\) On input \((ask_i,y_i)\), the oracle checks if there is an \(y_{i}^{*}\) in the announced set of strings, such that \(R(y_{j}^{*},x_i)=1\). If so, returns \(\bot \). Otherwise it runs  and gives \({\varvec{v}}_{y_i}\) to \(\mathcal {A}_{ind}\). If \(|L|>n-1\), the oracle returns \(\bot \).
and gives \({\varvec{v}}_{y_i}\) to \(\mathcal {A}_{ind}\). If \(|L|>n-1\), the oracle returns \(\bot \).
\(\mathcal {A}_{ind}\) wins if \(b'=b\), meaning that \(\mathcal {A}_{ind}\) can distinguish whether \(\hat{C}_b\) was produced from \(C_{1,0},\ldots ,C_{n,0}\) or from \(C_{1,1},\ldots ,C_{n,1}\) and \(\mathcal {A}_{ind}\) did not issue queries on \(x_i\) with \(R(y_{j}^{*},x_i)=1\) for some \(y_{j}^{*}\in \{0,1\}^{l}\). \(\mathcal {A}_{ind}\)’s advantage is:
The LHMABE scheme is IND-CPA secure if \(\mathbf{Adv}_{LHMABE, \mathcal {A}_{ind}}\) is negligible.
Remark 3
Furthermore, our LHMABE scheme fulfills the compactness property which is justified analogously to the compactness property of LHMIBE scheme.
Theorem 3
Our leveled homomorphic MABE scheme is IND-CPA secure provided that \((\mathbb {Z}_q,n,\chi )\)-LWE holds.
Proof
Let \(\mathcal {A}_{ind}\) be an adversary against IND-CPA security of our leveled homomorphic multi-authority ABE scheme. We use \(\mathcal {A}_{ind}\) to construct an algorithm \(\mathcal {B}\) against the LWE problem.
Setup: The instance of LWE problem is given as a sampling oracle \(\mathcal {O}\). This oracle can be either purely random \(\mathcal {O}_r\) or pseudo-random \(\mathcal {O}_s\) for some secret \(s\in \mathbb {Z}_q^{N},\) where \(N=l(m+1)\) as in the scheme. In order to simulate \(\mathcal {A}_{ind}'\)s public parameters, \(\mathcal {B}\) issues N queries on samples to his sampling oracle \(\mathcal {O}\) and receives upon each request i a fresh pair \(({\varvec{a}}_i,t_i)\in \mathbb {Z}_q^n\times \mathbb {Z}_q\). The simulator \(\mathcal {B}\) computes for \(\mathcal {A}_{ind}\) the public parameters \((apk_i,ask_i)\) for each attribute authority using LWE samples and sends them to \(\mathcal {A}_{ind}\).
Key Extract Queries: When \(\mathcal {A}_{ind}\) issues private key extraction queries to its key extract oracle on input \((ask_i,y_i), i\in [n]\), simulator \(\mathcal {B}\) computes the required secret keys \(sk_{i}\) using the samplings obtained from its oracle and the simulated public key. We assume that \(\mathcal {B}\) has control over the set of strings \(\{y_{i}^{*}\}_{i\in [n]}\). If there is an \(y_j\in \{y_{i}^{*}\}_{i\in [n]}\) such that \(R(y_j,x_i)=1\), \(\mathcal {B}\) aborts the simulation. Otherwise it returns the simulated secret keys to \(\mathcal {A}_{ind}\). The outputs are statistically close to uniform values. \(\mathcal {B}\) sends the simulated values to \(\mathcal {A}_{ind}\). We assume that \(\mathcal {A}_{ind}\) issued in total \(q_E\) private key extraction queries.
Furthermore \(\mathcal {A}_{ind}\) outputs a set of target strings \(\{y_{i}^{*}\}_{i\in [n]}\) with the corresponding messages \(\mu _1,\ldots ,\mu _n\) it wants to be challenged on.
Challenge ciphertext: The simulation of the challenge ciphertext also works using as input the entries from the LWE instance, choosing N random vector pairs  for \(i\in [n]\), taking the message bits \(\mu _i\) and calculating \(C\leftarrow {\varvec{b}}_i\cdot \mu _i+{\varvec{e}}_i\). Finally the ciphertext is sent to \(\mathcal {B}\). When the LWE oracle is given by \(\mathcal {O}_s\) (i.e. it is pseudo-random), the ciphertext is randomly distributed including some random noise vector according to the noisy distribution \(\chi \). When \(\mathcal {O}\) is given by \(\mathcal {O}_r\) then the ciphertext is uniform and independent over \(\mathbb {Z}_{q}^{N}\). Eventually the simulated ciphertext is always uniform in \(\mathbb {Z}_q\times \mathbb {Z}_{q}^{N}\).
for \(i\in [n]\), taking the message bits \(\mu _i\) and calculating \(C\leftarrow {\varvec{b}}_i\cdot \mu _i+{\varvec{e}}_i\). Finally the ciphertext is sent to \(\mathcal {B}\). When the LWE oracle is given by \(\mathcal {O}_s\) (i.e. it is pseudo-random), the ciphertext is randomly distributed including some random noise vector according to the noisy distribution \(\chi \). When \(\mathcal {O}\) is given by \(\mathcal {O}_r\) then the ciphertext is uniform and independent over \(\mathbb {Z}_{q}^{N}\). Eventually the simulated ciphertext is always uniform in \(\mathbb {Z}_q\times \mathbb {Z}_{q}^{N}\).
Guess: After issuing additional queries, \(\mathcal {A}_{ind}\) guesses a bit \(b'\in \{0,1\}\). The LWE adversary \(\mathcal {B}\) outputs its guess as result of the LWE challenge. Finally we follow that \(\mathcal {B}'\)s advantage in solving LWE is at least the same as \(\mathcal {A}_{ind}'\)s advantage in distinguishing the ciphertext from a random value, i.e.: \(\mathbf{Adv}_{\mathcal {B}}\ge \frac{1}{q_E}{} \mathbf{Adv}_{\mathcal {A}_{ind}}\). \(\square \)
4.5 Application to Cloud Computing
Leveled homomorphic attribute-based encryption has significant relevance for cloud systems and their security. Attribute-based encryption allows an additional option for many applications of functional encryption in cloud computing. It enables a data owner, who outsourced her encrypted data to a cloud, to control the access to the uploaded data. A useful application to personal health records in cloud computing based on multi-authorities and multi-users attribute-based encryption presented by Li et al. [29] can profit by enabling users of the scheme to evaluate different ciphertexts on different messages without even revealing those messages. The shortcoming of Li et al.’s [29] construction is the impossibility to perform complex mathematical computations on encrypted data. Our ABE construction in multi-authority setting in Sect. 4.3 provides this attractive property. The data owner which uploads the data to a cloud server has the possibility to encrypt further several data files and compute a functional value of the resulted ciphertexts. The data user, which has the valid access formula is able to decrypt the evaluated ciphertexts and obtain a functional value of the plaintexts. Our construction allows the cloud users to take advantage of analytical cloud services. Our scheme from Sect. 3.1, where distinct ciphertexts are encrypted using distinct identities can also be applied to the cloud storage setting. In this case our construction allows a data owner to encrypt different data for a certain group of users with distinct identities, such that each user is able to decrypt an evaluated value of different plaintexts.
5 Conclusion
In this paper we presented a new construct called tensor product in combination with natural logarithm in order to enable leveled homomorphic encryption under different public keys. Using these mathematical constructions we first introduced a leveled homomorphic encryption under multiple identities. We defined the security of that scheme and provided the corresponding proof. Furthermore we presented a leveled homomorphic attribute-based encryption in two different settings. In the first setting we assumed that the evaluation function operates on ciphertext under common index x, while in the second setting the evaluation function was performed under distinct indices. We defined the security notions for both ABE schemes and proved them secure. Our constructions enable a multi-key leveled homomorphic encryption on lattices using simple mathematical computations in contrast to so far existing milti-identity FHIBE by [18] and provide efficient applications to the cloud storage setting.
References
Agrawal, S., Boneh, D., Boyen, X.: Efficient lattice (H)IBE in the standard model. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 553–572. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_28
Agrawal, S., Boyen, X.: Identity-based encryption from lattices in the standard model. http://www.cs.stanford.edu/~xb/ab09/
Agrawal, S., Boyen, X., Vaikuntanathan, V., Voulgaris, P., Wee, H.: Functional encryption for threshold functions (or fuzzy IBE) from lattices. In: Fischlin, M., Buchmann, J., Manulis, M. (eds.) PKC 2012. LNCS, vol. 7293, pp. 280–297. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-30057-8_17
Ajtai, M.: Generating hard instances of lattice problems (extended abstract). In: Proceedings of 28th Annual ACM Symposium on the Theory of Computing, pp. 99–108. ACM (1996)
Attrapadung, N., Herranz, J., Laguillaumie, F., Libert, B., de Panafieu, E., Ràfols, C.: Attribute-based encryption schemes with constant-size ciphertexts. Theoret. Comput. Sci. 422, 15–38 (2012)
Bethencourt, J., Sahai, A., Waters, B.: Ciphertext-policy attribute-based encryption. In: 2007 IEEE Symposium on Security and Privacy (S&P 2007), pp. 321–334. IEEE Computer Society (2007)
Blum, A., Kalai, A., Wasserman, H.: Noise-tolerant learning, the parity problem, and the statistical query model. In: Proceedings of 32nd Annual ACM Symposium on Theory of Computing, pp. 435–440 (2000)
Boneh, D., Franklin, M.: Identity-based encryption from the weil pairing. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 213–229. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_13
Boyen, X.: Lattice mixing and vanishing trapdoors: a framework for fully secure short signatures and more. In: Nguyen, P.Q., Pointcheval, D. (eds.) PKC 2010. LNCS, vol. 6056, pp. 499–517. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13013-7_29
Boyen, X.: Attribute-based functional encryption on lattices. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 122–142. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_8
Brakerski, Z., Cash, D., Tsabary, R., Wee, H.: Targeted homomorphic attribute-based encryption. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 330–360. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_13
Brakerski, Z., Gentry, C., Vaikuntanathan, V.: Fully homomorphic encryption without bootstrapping. In: Electronic Colloquium on Computational Complexity (ECCC), vol. 18, p. 111 (2011)
Brakerski, Z., Vaikuntanathan, V.: Efficient fully homomorphic encryption from (standard) LWE. In: IEEE 52nd Annual Symposium on Foundations of Computer Science, FOCS, 2011, pp. 97–106. IEEE Computer Society (2011)
Brakerski, Z., Vaikuntanathan, V.: Fully homomorphic encryption from ring-LWE and security for key dependent messages. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 505–524. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_29
Cash, D., Hofheinz, D., Kiltz, E., Peikert, C.: Bonsai trees, or how to delegate a lattice basis. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 523–552. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_27
Chase, M.: Multi-authority attribute based encryption. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 515–534. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_28
Cheung, L., Newport, C.C.: Provably secure ciphertext policy ABE. In: Proceedings of 2007 ACM Conference on Computer and Communications Security, CCS 2007, pp. 456–465. ACM (2007)
Clear, M., McGoldrick, C.: Multi-identity and multi-key leveled FHE from learning with errors. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 630–656. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_31
Clear, M., McGoldrick, C.: Attribute-based fully homomorphic encryption with a bounded number of inputs. In: Pointcheval, D., Nitaj, A., Rachidi, T. (eds.) AFRICACRYPT 2016. LNCS, vol. 9646, pp. 307–324. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-31517-1_16
Cocks, C.: An identity based encryption scheme based on quadratic residues. In: Honary, B. (ed.) Cryptography and Coding 2001. LNCS, vol. 2260, pp. 360–363. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45325-3_32
Gentry, C.: Fully homomorphic encryption using ideal lattices. In: Proceedings of 41st Annual ACM Symposium on Theory of Computing, STOC 2009, pp. 169–178. ACM (2009)
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: Proceedings of 40th Annual ACM Symposium on Theory of Computing, STOC 2008, pp. 197–206. ACM (2008)
Gentry, C., Sahai, A., Waters, B.: Homomorphic encryption from learning with errors: conceptually-simpler, asymptotically-faster, attribute-based. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 75–92. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_5
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Attribute-based encryption for circuits. In: Symposium on Theory of Computing Conference, STOC 2013, pp. 545–554. ACM (2013)
Goyal, V., Jain, A., Pandey, O., Sahai, A.: Bounded ciphertext policy attribute based encryption. In: Aceto, L., Damgård, I., Goldberg, L.A., Halldórsson, M.M., Ingólfsdóttir, A., Walukiewicz, I. (eds.) ICALP 2008. LNCS, vol. 5126, pp. 579–591. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-70583-3_47
Goyal, V., Pandey, O., Sahai, A., Waters, B.: Attribute-based encryption for fine-grained access control of encrypted data, pp. 89–98 (2006)
Kamara, S., Mohassel, P., Raykova, M.: Outsourcing multi-party computation. IACR Cryptology ePrint Archive, 2011:272 (2011)
Lewko, A., Okamoto, T., Sahai, A., Takashima, K., Waters, B.: Fully secure functional encryption: attribute-based encryption and (hierarchical) inner product encryption. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 62–91. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_4
Li, M., Yu, S., Ren, K., Lou, W.: Securing personal health records in cloud computing: patient-centric and fine-grained data access control in multi-owner settings. In: Jajodia, S., Zhou, J. (eds.) SecureComm 2010. LNICST, vol. 50, pp. 89–106. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-16161-2_6
López-Alt, A., Tromer, E., Vaikuntanathan, V.: On-the-fly multiparty computation on the cloud via multikey fully homomorphic encryption. In: Proceedings of 44th Symposium on Theory of Computing Conference, STOC 2012, pp. 1219–1234 (2012)
Micciancio, D.: Generalized compact knapsacks, cyclic lattices, and efficient one-way functions from worst case complexity assumptions. In: FOCS 2002, pp. 356–365 (2002)
Micciancio, D., Voulgaris, P.: A deterministic single exponential time algorithm for most lattice problems based on Voronoi cell computations. SIAM J. Comput. 42(3), 1364–1391 (2013)
Mukherjee, P., Wichs, D.: Two round multiparty computation via multi-key FHE. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 735–763. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_26
Peikert, C.: Bonsai trees (or, arboriculture in lattice-based cryptography). IACR Cryptology ePrint Archive, 2009:359 (2009)
Peikert, C.: Public-key cryptosystems from the worst-case shortest vector problem. In: Proceedings of 41st Annual ACM Symposium on Theory of Computing, STOC 2009, pp. 333–342 (2009)
Regev, O.: On lattices, learning with errors, random linear codes and cryptography. In: Proceedings of 37th Annual ACM Symposium on Theory of Computing, STOC 2005, pp. 84–93 (2005)
Sahai, A., Waters, B.: Fuzzy identity based encryption. IACR Cryptology ePrint Archive, 2004:86 (2004)
Shamir, A.: Identity-based cryptosystems and signature schemes. In: Blakley, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 47–53. Springer, Heidelberg (1985). https://doi.org/10.1007/3-540-39568-7_5
Smart, N.P., Vercauteren, F.: Fully homomorphic encryption with relatively small key and ciphertext sizes. In: Nguyen, P.Q., Pointcheval, D. (eds.) PKC 2010. LNCS, vol. 6056, pp. 420–443. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13013-7_25
van Dijk, M., Gentry, C., Halevi, S., Vaikuntanathan, V.: Fully homomorphic encryption over the integers. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 24–43. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_2
Waters, B.: Ciphertext-policy attribute-based encryption: an expressive, efficient, and provably secure realization. In: Catalano, D., Fazio, N., Gennaro, R., Nicolosi, A. (eds.) PKC 2011. LNCS, vol. 6571, pp. 53–70. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19379-8_4
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Lattices
Let \(B=\{b_1,\ldots ,b_n\}\subset \mathbb {R}^{n}\) be a basis of a lattice \(\varLambda \) which consists of n linearly independent vectors. The n-dimensional lattice \(\varLambda \) is then defined as \(\varLambda =\sum \limits _{i=1}^{n}\mathbb {Z}b_i\). The i-th minimum of a lattice \(\varLambda \), denoted by \(\lambda _i(\varLambda )\) is the smallest radius r such that \(\varLambda \) contains i linearly independent vectors of norms \(\le r\). (The norm of vector \(b_i\) is defined as \(\left\| b_i\right\| =\sqrt{\sum \limits _{j=1}^{n}c_{i,j}^2}\), where \(c_{i,j}, j\in \{1,\ldots ,n\}\) are the coefficients of vector \(b_i\). We denote by \(\lambda _1^{\infty }(\varLambda )\) the minimum distance measured in the infinity norm, which is defined as \(\left\| b_i\right\| _{\infty }:=\max (\left| c_{i,1}\right| ,\ldots ,\left| c_{i,n}\right| )\). Additionally we recall \(\left\| B\right\| =\max \left\| b_i\right\| \) and its fundamental parallelepiped is given by \(P(B)=\left\{ \sum \limits _{i=1}^{n}a_ib_i\ |\ \mathbf{a}\in \left[ 0,1\right) ^n\right\} \). The integer n is called the rank of the basis. Note that a lattice basis is not unique, since for any unimodular matrix \(A\in \mathbb {Z}^{n\times n}\) the product \(B\cdot U\) is also a basis of \(\varLambda \).
Integer Lattices. The following specific lattices contain \(q\mathbb {Z}^{m}\) as a sub-lattice for a prime q. For \(A\in \mathbb {Z}_{q}^{n\times m}\) and \(s\in \mathbb {Z}_{q}^{n}\), define:
Many lattice-based works rely on Gaussian-like distributions called Discrete Gaussians. In the following paragraph we recall the main notations of this distribution.
Discrete Gaussians. Let L be a subset of \(\mathbb {Z}^{m}\). For a vector \(c\in \mathbb {R}^m\) and a positive \(\sigma \in \mathbb {R}\), define
The discrete Gaussian distribution over L with center c and parameter \(\sigma \) is given by \(\mathcal {D}_{L,\sigma ,c}(y)=\frac{\rho _{\sigma ,c}(y)}{\rho _{\sigma ,c}(L)}, \ \forall y\in L\). The distribution \(\mathcal {D}_{L,\sigma ,c}\) is usually defined over the lattice \(L=\varLambda _{q}^{\bot }(A)\) for \(A\in \mathbb {Z}_{q}^{n\times m}\).
B Learning With Errors (LWE)
The LWE problem, first introduced by Regev [36], relies on the Gaussian error distribution \(\chi \), which is given as \(\chi =D_{\mathbb {Z},s}\) over the integers. The LWE problem assumes of access to a challenge oracle \(\mathcal {O}\), which is either a purely random sampler \(\mathcal {O}_r\) or a noisy pseudo-random sampler \(\mathcal {O}_s\), with some random secret key \(s\in \mathbb {Z}_{q}^{s}\). For positive integers n and \(q\ge 2\), a vector \({\varvec{s}}\in \mathbb {Z}_{q}^{n}\) and error term \(e\leftarrow \chi \), the LWE distribution \(A_{{\varvec{s}},\chi }\) is sampled over \(\mathbb {Z}_{q}^{n}\times \mathbb {Z}_q\). Chosen a vector \({\varvec{a}}\in \mathbb {Z}_q^n\) uniformly at random it outputs the pair \(({\varvec{a}},t=\left\langle {\varvec{a}},{\varvec{s}}\right\rangle +e\mod q)\in \mathbb {Z}_q^n\times \mathbb {Z}_q\). A more detailed description of \(\chi \) can be found in [36]. The sampling oracles work in the following way:
- \(\mathcal {O}_s\)::
-
outputs samples of the form \(({\varvec{a}},t)=({\varvec{a}},{\varvec{a}}{\varvec{s}}+e)\in \mathbb {Z}_{q}^{n}\times \mathbb {Z}_q\), where \({\varvec{s}}\in \mathbb {Z}_{q}^{n}\) is uniformly distributed value across all invocations and \(e\in \mathbb {Z}_q\) is a fresh sample from \(\chi \).
- \(\mathcal {O}_r\)::
-
outputs truly random samples from \(\mathbb {Z}_{q}^{n}\times \mathbb {Z}_q\).
C Proof of Theorem 2
Proof
Since the security of this construction relies on the hardness of LWE problem we show how to build an algorithm which can simulate the outputs for the LHABE adversary. Let \(\mathcal {A}_{ind}\) be an adversary against IND-CPA security of our leveled homomorphic ABE scheme. We use \(\mathcal {A}_{ind}\) to construct an algorithm \(\mathcal {B}\) against the LWE problem. As known from the Definition of LWE, the decision algorithm has access to a sampling oracle \(\mathcal {O}\), which can be either a pseudorandom sampler \(\mathcal {O}_s\) or a truly random sampler \(\mathcal {O}_r\). We assume a simulator \(\mathcal {B}\) which simulates the environment for LHABE adversary \(\mathcal {A}_{ind}\) in order to decide which oracle is given. \(\mathcal {B}\) queries from its oracle \(\mathcal {O}\) the LWE samples and obtains n pairs \(({\varvec{a}}_i,t_i)\in \mathbb {Z}_q^N\times \mathbb {Z}_q\), for \(N=l(m+1)\). \(\mathcal {A}_{ind}\) announces a set of strings \(\{x_i\}_{i\in k}\) it wants to be challenged on. The simulator \(\mathcal {B}\) constructs the public key using the obtained LWE instance of l pairs \(({\varvec{a}}_i,t_i)\) for \(i\in [l(m+1)]\), where the public key is represented by a \(n\times m\) matrix and a m-dimensional vector. When \(\mathcal {A}\) issues key generation queries on input apk, the LWE adversary simulates the queries using previously sampled public key apk and setting \({\varvec{s}}=(1,s_1)\in \mathbb {Z}_{q}^{l(m+1)}\), where \(apk\cdot {\varvec{s}}={\varvec{e}}\) that is small and \(s_1\in \mathbb {Z}_q^{lm}\) is also assumed to be small according to distribution \(\chi \). In order to encrypt 0, \(\mathcal {B}\) samples N times the vectors  according to \(\chi \) and outputs a ciphertext \(C\leftarrow {\varvec{b}}\cdot apk+{\varvec{e}}'\). This ciphertext is indistinguishable from random by applying a standard hybrid argument. The decryption is possible by computing a product of \(\left\langle C,{\varvec{s}}\right\rangle \) and outputting \(\mu =0\) if the result is small or \(\mu =1\) otherwise. \(\square \)
according to \(\chi \) and outputs a ciphertext \(C\leftarrow {\varvec{b}}\cdot apk+{\varvec{e}}'\). This ciphertext is indistinguishable from random by applying a standard hybrid argument. The decryption is possible by computing a product of \(\left\langle C,{\varvec{s}}\right\rangle \) and outputting \(\mu =0\) if the result is small or \(\mu =1\) otherwise. \(\square \)
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Kuchta, V., Sharma, G., Sahu, R.A., Markowitch, O. (2018). Multi-party (Leveled) Homomorphic Encryption on Identity-Based and Attribute-Based Settings. In: Kim, H., Kim, DC. (eds) Information Security and Cryptology – ICISC 2017. ICISC 2017. Lecture Notes in Computer Science(), vol 10779. Springer, Cham. https://doi.org/10.1007/978-3-319-78556-1_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-78556-1_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-78555-4
Online ISBN: 978-3-319-78556-1
eBook Packages: Computer ScienceComputer Science (R0)





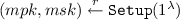 .
. .
.