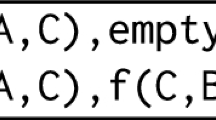Pruning Hypothesis Spaces Using Learned Domain Theories

Abstract

We present a method to prune hypothesis spaces in the context of inductive logic programming. The main strategy of our method consists in removing hypotheses that are equivalent to already considered hypotheses. The distinguishing feature of our method is that we use learned domain theories to check for equivalence, in contrast to existing approaches which only prune isomorphic hypotheses. Specifically, we use such learned domain theories to saturate hypotheses and then check if these saturations are isomorphic. While conceptually simple, we experimentally show that the resulting pruning strategy can be surprisingly effective in reducing both computation time and memory consumption when searching for long clauses, compared to approaches that only consider isomorphism.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

A key challenge for inductive logic programmming (ILP) algorithms (e.g. Progol [12]) is the fact that they typically have to search through large hypothesis spaces. Methods for pruning this search space have the potential to dramatically improve the quality of learned hypotheses and/or the runtime of the algorithms. One way of doing this is by filtering isomorphic hypotheses, which is the strategy used, for instance, in the relational pattern mining algorithm Farmr [14]. However, pruning isomorphic hypotheses is often not optimal, in the sense that it may be possible to prune hypotheses which are not isomorphic, but which are nonetheless equivalent in the considered domain. For example, the hypothesis that “if X is the father of Y then X and Y have the same last name” is equivalent to the hypothesis that “if X is male and a parent of Y then X and Y have the same last name”.

In this paper, we introduce a method which explicitly tries to prune equivalent hypotheses that are created during the hypothesis search, while still maintaining completeness¹. One important challenge is that we need a quick way of testing whether a new hypothesis is equivalent to a previously considered one. To this end, we propose a saturation method which, given a first-order-logic clause, derives a longer saturated clause that is equivalent to it modulo a domain theory. This saturation method has the important property that two clauses are equivalent, given a domain theory, whenever their saturations are isomorphic. This means that we can use saturations to detect equivalent hypotheses as follows. We compute saturations of all hypotheses as they are being constructed, as well as certain invariants² of these saturations. Then we use the invariants to compute hashes for the saturated hypotheses, which allows us to use hash tables to efficiently narrow down the set of previously constructed hypotheses against which equivalence needs to be tested. In this way, we can avoid the need to explicitly compare new hypotheses with all previously constructed ones, which would clearly be infeasible in spaces with possibly millions of hypotheses. Note that this technique crucially relies on the use of saturations, and would not be possible with e.g. just a notion of relative subsumption modulo a background theory. To avoid the need for any prior domain knowledge, our method learns the required domain theories from the training data.

We experimentally show that our method can be orders of magnitude faster than methods which merely check for isomorphism, even when taking into account the time needed for learning domain theories.

2 Preliminaries

In this section, we first give an overview of the notations and terminology from first-order logic that will be used throughout the paper, after which Sect. 2.2 describes the considered learning setting.

2.1 First-Order Logic

We consider a function-free first-order language, which is built from a finite set of constants, variables, and predicates in the usual way. A term is a variable or a constant. An atom is a formula of the form $p(t_1,...,t_n)$, where p is an n-ary predicate symbol and $t_1,...,t_n$ are terms. A literal is an atom or the negation of an atom. A clause A is a universally quantified disjunction of literals $\forall x_1...\forall x_n: \phi _1 \vee ... \vee \phi _k$, such that $x_1,..,x_n$ are the only variables occurring in the literals $\phi _1,...,\phi _k$. For the ease of presentation, we will sometimes identify a clause A with the corresponding set of literals $\{\phi _1,..., \phi _k\}$. The set of variables occurring in a clause A is written as $\textit{vars}(A)$ and the set of all terms as $\textit{terms}(A)$. For a clause A, we define the sign flipping operation as $\widetilde{A} {\mathop {=}\limits ^{def}} \bigvee _{l \in A} \tilde{l}$, where $\tilde{a}=\lnot a$ and $\tilde{\lnot a}=a$ for an atom a. In other words, the sign flipping operation simply replaces each literal by its negation.

A substitution $\theta$ is a mapping from variables to terms. For a clause A, we write $A\theta$ for the clause $\{\phi \theta \,|\, \phi \in A\}$, where $\phi \theta$ is obtained by replacing each occurrence in $\phi$ of a variable v by the corresponding term $\theta (v)$. If A and B are clauses then we say that A $\theta$-subsumes B (denoted $A \preceq _{\theta }B$) if and only if there is a substitution $\theta$ such that $A\theta \subseteq B$. If $A \preceq _\theta B$ and $B \preceq _\theta A$, we call A and B $\theta$-equivalent (denoted $A \approx _{\theta } B$). Note that the $\approx _{\theta }$ relation is indeed an equivalence relation (i.e. it is reflexive, symmetric and transitive). Clauses A and B are said to be isomorphic (denoted $A \approx _{iso} B$) if there exists an injective substitution $\theta$ such that $A\theta = B$. Finally, we say that A OI-subsumes B (denoted $A \preceq _{OI}B$ [6]) if there is an injective substitution such that $A\theta \subseteq B$. Note that A is isomorphic to B iff $A \preceq _{OI}B$ and $B \preceq _{OI}A$.

Example 1

Let us consider the following four clauses:

$$\begin{aligned} C_1&= p_1(A,B) \vee \lnot p_2(A,B) \\ C_2&= p_1(A,B) \vee \lnot p_2(A,B) \vee \lnot p_2(A,C) \\ C_3&= p_1(X,Y) \vee \lnot p_2(X,Y) \vee \lnot p_2(X,Z) \\ C_4&= p_1(A,B) \vee \lnot p_3(A,B) \end{aligned}$$

Then we can easily verify that $C_1 \approx _\theta C_2 \approx _\theta C_3$ (and thus also $C_i \preceq _{\theta }C_j$ for $i,j \in \{1,2,3\})$. We also have $C_1 \not \approx _{iso} C_2$, $C_1 \not \approx _{iso} C_3$, $C_2 \approx _{iso} C_3$, as well as $C_i \not \preceq _{\theta }C_4$ and $C_4 \not \preceq _{\theta }C_i$ for any $i \in \{1,2,3\}$. Finally we also have $C_1 \preceq _{OI}C_i$ for $i \in \{1,2,3\}$, $C_2 \preceq _{OI}C_3$ and $C_3 \preceq _{OI}C_2$.

A literal is ground if it does not contain any variables. A grounding substitution is a substitution in which each variable is mapped to a constant. Clearly, if $\theta$ is a grounding substitution, then for any literal $\phi$ it holds that $\phi \theta$ is ground. An interpretation $\omega$ is defined as a set of ground literals. A clause $A=\{\phi _1,...,\phi _n\}$ is satisfied by $\omega$, written $\omega \models A$, if for each grounding substitution $\theta$, it holds that $\{\phi _1\theta ,...,\phi _n\theta \}\cap \omega \ne \emptyset$. In particular, note that a ground literal $\phi$ is satisfied by $\omega$ if $\phi \in \omega$. The satisfaction relation $\models$ is extended to (sets of) propositional combinations of clauses in the usual way. If $\omega \models T$, for T a propositional combination of clauses, we say that $\omega$ is a model of T. If T has at least one model, we say T is satisfiable. Finally, for two (propositional combinations of) clauses A and B, we write $A\models B$ if every model of A is also a model of B. Note that if $A \preceq _\theta B$ for clauses A and B then $A \models B$, but the converse does not hold in general.

Deciding $\theta$-subsumption between two clauses is an NP-complete problem. It is closely related to constraint satisfaction problems with finite domains and tabular constraints [4], conjunctive query containment [3] and homomorphism of relational structures. The formulation of $\theta$-subsumption as a constraint satisfaction problem has been exploited in the ILP literature for the development of fast $\theta$-subsumption algorithms [8, 11]. CSP solvers can also be used to check whether two clauses are isomorphic, by using the primal CSP encoding described in [11] together with an alldifferent constraint [7] over CSP variables representing logical variables. In practice, this approach to isomorphism checking can be further optimized by pre-computing a directed hypergraph variant of Weisfeiler-Lehman coloring [22] (where terms play the role of hyper-vertices and literals the role of directed hyper-edges) and by enriching the respective clauses by unary literals with predicates representing the labels obtained by the Weisfeiler-Lehman procedure, which helps the CSP solver to reduce its search space.

2.2 Learning Setting

In this paper we will work in the classical setting of learning from interpretations [16]. In this setting, examples are interpretations and hypotheses are clausal theories (i.e. conjunctions of clauses). An example e is said to be covered by a hypothesis H if $e \models H$ (i.e. e is covered by H if it is a model of H). Given a set of positive examples $\mathcal {E}^+$ and negative examples $\mathcal {E}^-$, the training task is then to find a hypothesis H from some class of hypotheses $\mathcal {H}$ which optimizes a given scoring function (e.g. training error). For the ease of presentation, we will restrict ourselves to classes $\mathcal {H}$ of hypotheses in the form of clausal theories without constants, as constants can be emulated by unary predicates (since we do not consider functions).

The covering relation $e \models H$ can be checked using a $\theta$-subsumption solver as follows. Each hypothesis H can be written as a conjunction of clauses $H = C_1 \wedge \dots \wedge C_n$. Clearly, $e \not \models H$ if there is an i in $\{1,\dots ,n\}$ such that $e \models \lnot C_i$, which holds precisely when $C_i \preceq _{\theta }\lnot (\bigwedge e)$.

Example 2

Let us consider the following example, inspired by the Michalski’s East-West trains datasets [20]:

$$\begin{aligned} e = \{&\textit{eastBound}(\textit{car1}), \textit{hasCar}(\textit{car1}), \textit{hasLoad}(car1,load1), \textit{boxShape}(load1), \\&\lnot \textit{eastBound}(\textit{load1}), \lnot \textit{hasCar}(\textit{load1}), \lnot \textit{hasLoad}(\textit{load1},\textit{car1}), \\&\lnot \textit{hasLoad}(\textit{load1},\textit{load1}), \lnot \textit{hasLoad}(\textit{car1},\textit{car1}), {\lnot \textit{boxShape}(car1)} \} \end{aligned}$$

and two hypotheses $H_1$ and $H_2$

$$\begin{aligned} H_1&= \textit{eastBound}(C) \vee \lnot \textit{hasLoad}(C,L) \vee \lnot \textit{boxShape}(L) \\ H_2&= \lnot \textit{eastBound}(C) \vee \lnot \textit{hasLoad}(C,L) \end{aligned}$$

To check if $e \models H_i$, $i = 1,2$, using a $\theta$-subsumption solver, we construct

$$\begin{aligned} \lnot (\bigwedge e)&= \lnot \textit{eastBound}(\textit{car1}) \vee \lnot \textit{hasCar}(\textit{car1}) \vee \lnot \textit{hasLoad}(car1,load1) \\&\vee \textit{boxShape}(load1) \vee \textit{eastBound}(\textit{load1}) \vee \textit{hasCar}(\textit{load1}) \\&\vee \textit{hasLoad}(\textit{load1},\textit{car1}) \vee \textit{hasLoad}(\textit{load1},\textit{load1}) \vee \textit{hasLoad}(\textit{car1},\textit{car1})\\&{\vee \textit{boxShape}(car1)} \end{aligned}$$

It is then easy to check that $H_1 \not \preceq _{\theta }\lnot (\bigwedge e)$ and $H_2 \preceq _{\theta }\lnot (\bigwedge e)$, from which it follows that $e \models H_1$ and $e \not \models H_2$.

In practice, when using a $\theta$-subsumption solver to check $C_i \preceq _{\theta }\lnot (\bigwedge e)$, it is usually beneficial to flip the signs of all the literals, i.e. to instead check $\widetilde{C_i} \preceq _{\theta }\bigvee e$, which is clearly equivalent. This is because $\theta$-subsumption solvers often represent negative literals in interpretations implicitly to avoid excessive memory consumption³, relying on the assumption that most predicates in real-life datasets are sparse.

2.3 Theorem Proving Using SAT Solvers

The methods described in this paper will require access to an efficient theorem prover for clausal theories. Since we restrict ourselves to function-free theories without equality, we can rely on a simple theorem-proving procedure based on propositionalization, which is a consequence of the following well-known result⁴ [13].

Theorem 1 (Herbrand’s Theorem)

Let $\mathcal {L}$ be a first-order language without equality and with at least one constant symbol, and let $\mathcal {T}$ be a set of clauses. Then $\mathcal {T}$ is unsatisfiable iff there exists some finite set $\mathcal {T}_0$ of $\mathcal {L}$-ground instances of clauses from $\mathcal {T}$ that is unsatisfiable.

Here $A\theta$ is called an $\mathcal {L}$-ground instance of a clause A if $\theta$ is a grounding substitution that maps each variable occurring in A to a constant from the language $\mathcal {L}$.

In particular, to decide if $\mathcal {T} \models C$ holds, where T is a set of clauses and C is a clause (without constants and function symbols), we need to check if $\mathcal {T} \wedge \lnot C$ is unsatisfiable. Since Skolemization preserves satisfiability, this is the case iff $\mathcal {T} \wedge \lnot C_{Sk}$ is unsatisfiable, where $\lnot C_{Sk}$ is obtained from $\lnot C$ using Skolemization. Let us now consider the restriction $\mathcal {L}_{Sk}$ of the considered first-order language $\mathcal {L}$ to the constants appearing in $C_{Sk}$, or to some auxiliary constant $s_0$ if there are no constants in $C_{Sk}$. From Herbrand’s theorem, we know that $\mathcal {T} \wedge \lnot C_{Sk}$ is unsatisfiable in $\mathcal {L}_{Sk}$ iff the grounding of this formula w.r.t. the constants from $\mathcal {L}_{Sk}$ is satisfiable, which we can efficiently check using a SAT solver. Moreover, it is easy to see that $\mathcal {T} \wedge \lnot C_{Sk}$ is unsatisfiable in $\mathcal {L}_{Sk}$ iff this formula is unsatisfiable in $\mathcal {L}$ ⁵.

In practice, it is not always necessary to completely ground the formula $\mathcal {T} \wedge \lnot C_{Sk}$. It is often beneficial to use an incremental grounding strategy similar to cutting plane inference in Markov logic [19]. To check if a clausal theory $\mathcal {T}$ is satisfiable, this method proceeds as follows.  

Step 0::

start with an empty Herbrand interpretation $\mathcal {H}$ and an empty set of ground formulas $\mathcal {G}$.

Step 1::

check which groundings of the formulas in $\mathcal {T}$ are not satisfied by $\mathcal {H}$ (e.g. using a CSP solver). If there are no such groundings, the algorithm returns $\mathcal {H}$, which is a model of $\mathcal {T}$. Otherwise the groundings are added to $\mathcal {G}$.

Step 2::

use a SAT solver to find a model of $\mathcal {G}$. If $\mathcal {G}$ does not have any model then $\mathcal {T}$ is unsatisfiable and the method finishes. Otherwise replace $\mathcal {H}$ by this model and go back to Step 1.

 

3 Pruning Hypothesis Spaces Using Domain Theories

In this section we show how domain theories can be used to prune the search space of ILP systems. Let us start with two motivating examples.

Example 3

Let us consider the following two hypotheses for some target concept x:

$$\begin{aligned} H_1&= \textit{x}(A) \vee \lnot \textit{animal}(A) \vee \lnot \textit{cod}(A) \\ H_2&= \textit{x}(A) \vee \lnot \textit{fish}(A) \vee \lnot \textit{cod}(A) \end{aligned}$$

Intuitively, these two hypotheses are equivalent since every cod is a fish and every fish is an animal. Yet ILP systems would need to consider both of these hypotheses separately because $H_1$ and $H_2$ are not isomorphic, they are not $\theta$-equivalent and neither of them $\theta$-subsumes the other.

Example 4

Problems with redundant hypotheses abound in datasets of molecules, which are widespread in the ILP literature. For instance, consider the following two hypotheses:

$$\begin{aligned} H_1&= \textit{x}(A) \vee \lnot \textit{carb}(A) \vee \lnot \textit{bond}(A,B) \vee \lnot \textit{bond}(B,C) \vee \lnot \textit{hydro}(C) \\ H_2&= \textit{x}(A) \vee \lnot \textit{carb}(A) \vee \lnot \textit{bond}(A,B) \vee \lnot \textit{bond}(C,B) \vee \lnot \textit{hydro}(C) \end{aligned}$$

These two hypotheses intuitively represent the same molecular structures (a carbon and a hydrogen both connected to the same atom of unspecified type). Again, however, their equivalence cannot be detected without the domain knowledge that bonds in molecular datasets are symmetric⁶.

In the remainder of this section we will describe how background knowledge can be used to detect equivalent hypotheses. First, we introduce the notion of saturations of clauses in Sect. 3.1. Subsequently, in Sect. 3.2 we show why pruning hypotheses based on these saturations does not hurt the completeness of a refinement operator. In Sect. 3.3, we then explain how these saturations can be used to efficiently prune search spaces of ILP algorithms. In Sect. 3.4 we describe a simple method for learning domain theories from the given training data. Finally, in Sect. 3.5 we show why using relative subsumption is not sufficient.

3.1 Saturations

The main technical ingredient of the proposed method is the following notion of saturation.

Definition 1 (Saturation of a clause)

Let $\mathcal {B}$ be a clausal theory and C a clause (without constants or function symbols). If $\mathcal {B} \not \models C$, we define the saturation of C w.r.t. $\mathcal {B}$ to be the maximal clause $C'$ satisfying: (i) $\textit{vars}(C') = \textit{vars}(C)$ and (ii) $\mathcal {B} \wedge C'\theta \models C\theta$ for any injective grounding substitution $\theta$. If $\mathcal {B} \models C$, we define the saturation of C w.r.t. $\mathcal {B}$ to be $\mathbf {T}$, where $\mathbf {T}$ denotes tautology.

When $\mathcal {B}$ is clear from the context, we will simply refer to $C'$ as the saturation of C.

Definition 1 naturally leads to a straightforward procedure for computing the saturation of a given clause. Let $\mathcal {P} = \{ l_1, l_2, \dots , l_n \}$ be the set of all literals which can be constructed using variables from C and predicate symbols from $\mathcal {B}$ and C. Let $\theta$ be an arbitrary injective grounding substitution; note that we can indeed take $\theta$ to be arbitrary because $\mathcal {B}$ and C do not contain constants. If $\mathcal {B} \not \models C$, the saturation of C is given by the following clause:

$$\begin{aligned} {\bigvee \{l \in \mathcal {P} : \mathcal {B} \models \lnot l\theta \vee C\theta \} } \end{aligned}$$

(1)

This means in particular that we can straightforwardly use the SAT based theorem proving method from Sect. 2.3 to compute saturations. The fact that (1) correctly characterizes the saturation can be seen as follows. If $C'$ is the saturation of C then $\mathcal {B} \wedge C'\theta \models C\theta$ by definition, which is equivalent to $\mathcal {B} \wedge \lnot (C\theta ) \models \lnot (C'\theta )$. We have $\lnot (C'\theta ) = \bigwedge \{\tilde{l}\theta : \mathcal {B} \wedge \lnot (C\theta )\models \tilde{l}\theta \} = \bigwedge \{\tilde{l}\theta : \mathcal {B} \wedge l\theta \models C\theta \}$, and thus $C'\theta = \bigvee \{l\theta : \mathcal {B} \wedge l\theta \models C\theta \}$. Finally, since $\theta$ is injective, we have⁷ $C' = (C'\theta )\theta ^- = \bigvee \{l : \mathcal {B} \wedge l\theta \models C\theta \}$.

Example 5

Let us consider the following theory

$$\mathcal {B} = \{ \lnot \textit{friends}(X,Y) \vee \textit{friends}(Y,X) \} $$

which expresses the fact that friendship is a symmetric relation and a clause

$$C = \lnot \textit{friends}(X,Y) \vee \textit{happy}(X).$$

To find the saturation of this clause, we first need a suitable injective substitution $\theta$; let us take $\theta = \{ X \mapsto c_1, Y \mapsto c_2 \}$. Then we have

$$\begin{aligned} \mathcal {B} \cup \lnot (C\theta )&= \mathcal {B} \cup \{ \textit{friends}(c_1, c_2) \wedge \lnot \textit{happy}(c_1) \}\\&\models \textit{friends}(c_1, c_2) \wedge \textit{friends}(c_2, c_1) \wedge \lnot \textit{happy}(c_1), \end{aligned}$$

After negating the latter formula and inverting the substitution (noting that it is injective) we get the following saturation:

$$C' = \lnot \textit{friends}(X,Y) \vee \lnot \textit{friends}(Y,X) \vee \textit{happy}(X).$$

Now, let us consider another clause $D = \lnot \textit{friends}(X,Y) \vee \textit{happy}(Y)$. This clause is not isomorphic to C. However, it is easy to see that its saturation

$$D' = \lnot \textit{friends}(X,Y) \vee \lnot \textit{friends}(Y,X) \vee \textit{happy}(Y)$$

is isomorphic to the saturation $C'$ of C.

The next proposition will become important later in the paper as it will allow us to replace clauses by their saturations when learning from interpretations.

Proposition 1

If $C'$ is a saturation of C w.r.t. $\mathcal {B}$ then $\mathcal {B} \wedge C' \models C$.

Proof

We have $\mathcal {B} \wedge C' \models C$ iff $\mathcal {B} \wedge C' \wedge \lnot C$ is unsatisfiable. Skolemizing $\lnot C$, this is equivalent to $\mathcal {B} \wedge C' \wedge \lnot (C\theta _{Sk})$ being unsatisfiable, where $\theta _{Sk}$ is a substitution representing the Skolemization. As in Sect. 2.3, we find that the satisfiability of $\mathcal {B} \wedge C' \wedge \lnot (C\theta _{Sk})$ is also equivalent to the satisfiability of the grounding of $\mathcal {B} \wedge C' \wedge \lnot (C\theta _{Sk})$ w.r.t. the Skolem constants introduced by $\theta _{Sk}$. In particular, this grounding must contain the ground clause $C'\theta _{Sk}$. From the definition of saturation, we have that $\mathcal {B} \wedge C'\theta _{Sk} \wedge \lnot (C\theta _{Sk}) \models \mathbf {F}$, where $\mathbf {F}$ denotes falsity (noting that $\theta _{Sk}$ is injective). It follows that $\mathcal {B} \wedge C' \wedge \lnot C \models \mathbf {F}$, and thus also $\mathcal {B} \wedge C' \models C$.    $\square$

The next proposition shows that saturations cover the same examples as the clauses from which they were obtained, when $\mathcal {B}$ is a domain theory that is valid for all examples in the dataset.

Proposition 2

Let $\mathcal {B}$ be a clausal theory such that for all examples e from a given dataset it holds that $e \models \mathcal {B}$. Let C be a clause and let $C'$ be its saturation w.r.t. $\mathcal {B}$. Then for any example e from the dataset we have $(e \models C) \Leftrightarrow (e \models C')$.

Proof

From the characterization of saturation in (1), it straightforwardly follows that $C\models C'$, hence $e \models C$ implies $e \models C'$. Conversely, if $e\models C'$, then we have $e\models \mathcal {B} \wedge C'$, since we assumed that $e \models \mathcal {B}$. Since we furthermore know from Proposition 1 that $\mathcal {B} \wedge C' \models C$, it follows that $e\models C$.

Finally, we define positive and negative saturations, which only add positive or negative literals to clauses. Among others, this will be useful in settings where we are only learning Horn clauses.

Definition 2

A positive (resp. negative) saturation of C is defined as $C'' = C \cup \{l \in C' : l \text{ is } \text{ a } \text{ positive } \text{(resp. } \text{ negative) } \text{ literal }\}$ where $C'$ is a saturation of C.

Propositions 1 and 2 are also valid for positive or negative saturations; their proofs can be straightforwardly adapted. When computing the positive (resp. negative) saturation, we can restrict the set $\mathcal {P}$ of candidate literals to the positive (resp. negative) ones. This can speed up the computation of saturations significantly.

3.2 Searching the Space of Saturations

In this section we show how saturations can be used together with refinement operators to search the space of clauses ordered by OI-subsumption⁸. Specifically, we show that if we have a refinement operator that can completely generate some set of clauses then we can use the same refinement operator, in combination with a procedure for computing saturations, to generate the set of all saturations of the considered set of clauses. Since this set of saturations is typically smaller than the complete set of clauses (as many clauses can lead to the same saturated clauses), this is already beneficial for reducing the size of the hypothesis space. In Sect. 3.3, we show that it also allows us to very quickly prune equivalent clauses. First we give a definition of refinement operator [21].

Definition 3 (Refinement operator)

Let $\mathcal {L}$ be a first-order language. A refinement operator⁹ on the set $\mathcal {C}$ of all $\mathcal {L}$-clauses is a function $\rho : \mathcal {C} \rightarrow 2^{\mathcal {C}}$ such that for any $C \in \mathcal {C}$ and any $D \in \rho (C)$ it holds $C \preceq _{OI} D$. A refinement operator $\rho$ is complete if for any two clauses C and D such that $C \preceq _{OI} D$, a clause E isomorphic to D ($D \approx _{iso} E$) can be obtained from C by repeated application of the refinement operator (i.e. $E \in \rho (\rho (\dots \rho (C)\dots ))$).

Most works define refinement operators w.r.t. $\theta$-subsumption instead of OI-subsumption [21]. We need the restriction to OI-subsumption as a technical condition for Proposition 3 below. It should be noted, however, that our results remain valid for many refinement operators that are not specifically based on OI-subsumption, including all refinement operators that only add new literals to clauses. Also note that we do not use OI-subsumption as a covering operator but only to structure the space of hypotheses. Therefore there is no loss in what hypotheses can be learnt.

The next definition formally introduces the combination of refinement operators and saturations.

Definition 4 (Saturated refinement operator)

Let $\mathcal {L}$ be a first-order language. Let $\rho$ be a refinement operator on the set $\mathcal {C}$ of all $\mathcal {L}$-clauses containing at most n variables. Let $\mathcal {B}$ be a clausal theory. Let $\sigma _\mathcal {B} : \mathcal {C} \rightarrow \mathcal {C}$ be a function that maps a clause C to its saturation $C'$ w.r.t. $\mathcal {B}$. Then the function $\rho _{\mathcal {B}} = \sigma _\mathcal {B} \circ \rho$ is called the saturation of $\rho$ w.r.t. $\mathcal {B}$.

Clearly, the saturation of a refinement operator w.r.t. some clausal theory $\mathcal {B}$ is a refinement operator as well. However, it can be the case that $\rho$ is complete whereas its saturation is not. As we will show next, this is not a problem for completeness w.r.t. the given theory $\mathcal {B}$ in the sense that saturations of all clauses from the given class $\mathcal {C}$ are guaranteed to be eventually constructed by the combined operator, when $\rho$ is a complete refinement operator.

Proposition 3

Let $\mathcal {L}$ be a first-order language. Let $\rho$ be a complete refinement operator on the set of $\mathcal {L}$-clauses $\mathcal {C}$, $\mathcal {B}$ be clausal theory, $\sigma _\mathcal {B}$ a function that maps a clause C to its saturation $C'$ w.r.t. $\mathcal {B}$ and let $\rho _\mathcal {B}$ be the saturation of $\rho$ w.r.t. $\mathcal {B}$. Let $C \in \mathcal {C}$ be a clause, $\mathcal {S}_C$ and let $\mathcal {S}_C^{\mathcal {B}}$ be the sets of clauses that can be obtained from C by repeated application of $\rho$ and $\rho _\mathcal {B}$, respectively. Then for any clause $D \in \mathcal {S}_C$ there is a clause $D' \in \mathcal {S}_C^\mathcal {B}$ such that $\sigma _{\mathcal {B}}(D) \approx _{\textit{iso}} D'$.

Proof

We first note that if $A \preceq _{OI}B$ then $\sigma _\mathcal {B}(A) \preceq _{OI}\sigma _\mathcal {B}(B)$ (assuming an extended definition of OI-subsumption such that $A \preceq _{OI}\mathbf {T}$ for any A), which follows from the monotonicity of the entailment relation $\models$. Let us define $\mathcal {X} = \{ \sigma _\mathcal {B}(A) | A \in \mathcal {S}_C \}$. Note that $\mathcal {X}$ and $\mathcal {S}_C^\mathcal {B}$ are not defined in the same way ($\mathcal {X}$ is the set of saturations of clauses in $\mathcal {S}_C$ whereas $\mathcal {S}_C^\mathcal {B}$ is the set of clauses that can be obtained by the saturated refinement operator $\rho _\mathcal {B}$ from the clause C). We need to show that these two sets are equivalent. Clearly, $\mathcal {S}_C^\mathcal {B} \subseteq \mathcal {X}$. To show the other direction, let us assume (for contradiction) that there is a clause $X \in \mathcal {X}$ for which there is no clause $Y \in \mathcal {S}_C^\mathcal {B}$ which is isomorphic to X. Let us assume that X is a minimal clause with this property, meaning that for any clause $X'$ contained in the set $\mathcal {Z}_X = \{Z \in \mathcal {X} | Z \preceq _{OI}X \wedge X \not \approx _{\textit{iso}} Z\}$ there is a clause $Y' \in \mathcal {S}_C^\mathcal {B}$ which is isomorphic to $X'$. Clearly, if there is one such clause X then there is also a minimal one which follows from the fact that all the considered clauses are finite and $\preceq _{OI}$ is a partial order. Let us take a clause $X' \in \mathcal {Z}_X$ which is maximal¹⁰ w.r.t. the ordering induced by $\preceq _{OI}$ and let $Y'$ be the respective isomorphic clause from $\mathcal {S}_C^\mathcal {B}$. Then $\rho (Y')$ must contain a clause $Y''$, $Y' \not \approx _{\textit{iso}} Y''$, that OI-subsumes X, which follows from completeness of the refinement operator $\rho$. However, then $\sigma _\mathcal {B}(Y'')$ must be contained in $\mathcal {S}_C^\mathcal {B}$. It must also hold that $\sigma _\mathcal {B}(Y'') \preceq _{OI}\sigma _\mathcal {B}(X) = X$. Here, $\sigma _\mathcal {B}(Y'') \preceq _{OI}\sigma _\mathcal {B}(X)$ follows from the already mentioned observation that if $A \preceq _{OI}B$ then $\sigma _\mathcal {B}(A) \preceq _{OI}\sigma _\mathcal {B}(B)$, and the equality $\sigma _\mathcal {B}(X) = X$ follows from the idempotence of $\sigma _\mathcal {B}$, noting that X is already a saturation of some clause. However, this is a contradiction with the maximality of $X'$ and the corresponding $Y'$.    $\square$

3.3 Pruning Isomorphic Saturations

When searching the space of clauses or, in particular, saturations of clauses, we should avoid searching through isomorphic clauses. It is easy to see that the sets of clauses generated by a (saturated) complete refinement operator $\rho$ from two isomorphic clauses C and $C'$ will contain clauses that are isomorphic (i.e. for any clause in the first set there will be an isomorphic clause in the second set and vice versa). Therefore it is safe to prune isomorphic clauses during the search.

When searching through the hypothesis space of clauses, most ILP algorithms maintain some queue of candidate clauses. This is the case, for instance, in algorithms based on best-first search (Progol, Aleph [12]). Other algorithms, e.g. those based on level-wise search, maintain similar data structures (e.g. Warmr [5]). Many of the clauses that are stored in such queues or similar data structures will be equivalent, even if they are not isomorphic. Existing methods, even if they were removing isomorphic clauses during search¹¹, have to consider each of these equivalent clauses separately, which may greatly affect their performance. This is where using saturations of clauses w.r.t. some background knowledge is most useful because it can replace the different implicitly equivalent clauses by their saturation.

In theory, one could try to test isomorphism of all pairs of clauses currently in the queue data structures. However, this would be prohibitively slow in most practical cases. To efficiently detect equivalences by checking isomorphism of saturations, we replace the queue data structure (or a similar data structure used by the given algorithm) by a data structure that is based on hash tables. When a new hypothesis H is constructed by the algorithm, we first compute its saturation $H'$. Then, we check whether the modified queue data structure already contains a clause that is isomorphic to $H'$. To efficiently check this, we use a straightforward generalization of the Weisfeiler-Lehman labeling procedure [22]. We then only need to check whether two clauses are isomorphic if they have the same hash value. We similarly check whether $H'$ is isomorphic to a clause in the so-called closed set of previously processed hypotheses. If $H'$ is neither isomorphic to a clause in the queue nor to a clause in the closed set, it is added to the queue.

Example 6

Let us again consider the two clauses from Example 3: $H_1 = \textit{x}(A) \vee \lnot \textit{animal}(A) \vee \lnot \textit{cod}(A)$ and $H_2 = \textit{x}(A) \vee \lnot \textit{fish}(A) \vee \lnot \textit{cod}(A)$. Suppose that the theory $\mathcal {B}$ encodes the taxonomy of animals and contains the rules $\lnot \textit{cod}(X) \vee \textit{fish}(X)$ and $\lnot \textit{fish}(X) \vee \textit{animal(X)}$. Computing the saturations of $H_1$ and $H_2$, we obtain $H_1' = \textit{x}(A) \vee \lnot \textit{animal}(A) \vee \lnot \textit{cod}(A) \vee \lnot \textit{fish}(A)$ and $H_2' = \textit{x}(A) \vee \lnot \textit{fish}(A) \vee \lnot \textit{cod}(A) \vee \lnot \textit{animal}(A)$, which are isomorphic. Therefore both of them can be replaced by the same saturations while the corresponding algorithm keeps searching the hypothesis space.

Similarly as shown above for the two clauses from Example 3, saturations could be used to detect equivalence of the two clauses from Example 4 w.r.t. the corresponding background knowledge theory $\mathcal {B}$.

In addition to equivalence testing, saturations can be used to filter trivial hypotheses, i.e. hypotheses covering every example, without explicitly computing their coverage on the dataset (which would be very costly on large datasets). We illustrate this use of saturations in the next example.

Example 7

Consider a domain theory $\mathcal {B} = \lnot \textit{professor}(X) \vee \lnot \textit{student}(X)$ which states that no one can be both a student and a professor. Let us also consider a hypothesis $H = \textit{employee}(X) \vee \lnot \textit{professor}(X) \vee \lnot \textit{student}(X)$. If the domain theory $\mathcal {B}$ is correct, H should cover all examples from the dataset and is thus trivial. Accordingly, the saturation of H contains every literal, and is in particular equivalent to $\mathbf {T}$.

3.4 Learning Domain Theories for Pruning

The domain theories that we want to use for pruning hypothesis spaces can be learned from the given training dataset. Every clause C in such a learned domain theory should satisfy $e \models C$ for all examples e in the dataset. We construct such theories using a level-wise search procedure, starting with an empty domain theory. The level-wise procedure maintains a list of candidate clauses (modulo isomorphism) with i literals. If a clause C in the list of candidate clauses covers all examples (i.e. $e \models C$ for all e from the dataset) then it is removed from the list and if there is no clause in the domain theory which $\theta$-subsumes C, then C is also added to the domain theory. Each of the remaining clauses in the list, i.e. those which do not cover all examples in the dataset, are then extended in all possible ways by the addition of a literal. This is repeated until a threshold on the maximum number of literals is reached. The covering of examples by the candidate clauses is checked using $\theta$-subsumption as outlined in Sect. 2.

It is worth pointing out that if we restrict the domain theories, e.g. to contain only clauses of length at most 2 or only Horn clauses, the saturation process will be guaranteed to run in polynomial time (which follows from the polynomial-time solvability of 2-SAT and Horn-SAT).

3.5 Why Relative Subsumption is Not Sufficient

Although the motivation behind relative subsumption [15] is similar to ours, relative subsumption has two main disadvantages that basically disqualify it for the purpose of pruning the hypothesis space. The first problem is that pruning hypotheses that are equivalent w.r.t. relative subsumption may not guarantee completeness of the search. This is the same issue as with pruning based on plain $\theta$-subsumption which, unlike pruning based on isomorphism, may lead to incompleteness of the search. Note that this is already the case in the more restricted setting of graph mining under homomorphism [18]. The second issue with relative subsumption is that it would need to be tested for all pairs of candidate hypotheses, whereas the pruning based on saturations and isomorphism testing allows us to use the more efficient hashing strategy based on the Weisfeiler-Lehman procedure.

4 Experiments

In this section we evaluate the usefulness of the proposed pruning method on real datasets. We test it inside an exhaustive feature construction algorithm which we then evaluate on a standard molecular dataset KM20L2 from the NCI GI 50 dataset collection [17]. This dataset contains 1207 examples (molecules) and 64404 facts.

4.1 Methodology and Implementation

The evaluated feature construction method is a simple level-wise algorithm which works similarly to the Warmr frequent pattern mining algorithm [5]. It takes two parameters: maximum depth d and maximum number of covered examples t (also called “maximum frequency”). It returns all connected¹² clauses which can be obtained by saturating clauses containing at most d literals, and which cover at most t examples. Unlike in frequent conjunctive pattern mining where minimum frequency constraints are natural, when mining in the setting of learning from interpretations, the analogue of the minimum frequency is the maximum frequency constraint¹³.

The level-wise algorithm expects as input a list of interpretations (examples) and the parameters t and $d > 0$. It proceeds as follows:

 

Step 0::

set $i := 0$ and $L_0 := \{ \square \}$ where $\square$ denotes the empty clause.

Step 1::

construct a set $L_{i+1}$ by extending each clause from $L_i$ with a negative literal (in all possible ways).

Step 2::

replace clauses in $L_{i+1}$ by their negative saturations and for each set of mutually isomorphic clauses keep only one of them.

Step 3::

remove from $L_{i+1}$ all clauses which cover more than t examples in the dataset.

Step 4::

if $L_{i+1}$ is empty or $i+1 > d$ then finish and return $\bigcup _{j = 0}^{i+1} L_j$. Otherwise set $i := i+1$ and go to step 1.

 

As can be seen from the above pseudocode, we restricted ourselves to mining clauses which contain only negative literals. This essentially corresponds to mining positive conjunctive queries, which is arguably the most typical scenario. Nonetheless, it would be easy to allow the algorithm to search for general clauses, as the $\theta$-subsumption solver used in the implementation actually allows efficient handling of negations.

We implemented the level-wise algorithm and the domain theory learner in Java¹⁴. To check the coverage of examples using $\theta$-subsumption, we used an implementation of the $\theta$-subsumption algorithm from [8]. For theorem proving, we used an incremental grounding solver which relies on the Sat4j library [1] for solving ground theories and the $\theta$-subsumption engine from [8].

4.2 Results

Fig. 1.

Left panels: Runtime of the level-wise algorithm using saturations for pruning (red) and without using saturations (blue). Right panels: Number of clauses constructed by the algorithm using saturations (red) and without using saturations (blue). Top panels display results for maximal number of covered examples equal to dataset size minus one and bottom panels for this parameter set to dataset size minus 50, which corresponds to minimum frequency of 50. One minute, one hour, and ten hours are highlighted by yellow, green, and purple horizontal lines. Runtimes are extrapolated by exponential function and shown in dashed lines. (Color figure online)

We measured runtime and the total number of clauses returned by the level-wise algorithm without saturations and with saturations. Both algorithms were exactly the same, the only difference being that the second algorithm first learned a domain theory and then used it for computing the saturations. Note in particular that both algorithms used the same isomorphism filtering. Therefore any differences in computation time must be directly due to the use of saturations.

We performed the experiments reported here on the NCI dataset KM20L2. The learned domain theories were restricted to contain only clauses with at most two literals. We set the maximum number of covered examples equal to the number of examples in the dataset minus one (which corresponds to a minimum frequency constraint of 1 when we view the clauses as negated conjunctive patterns). Then we also performed an experiment where we set it equal to the number of examples in the dataset minus 50 (which analogically corresponds to a minimum frequency constraint of 50). We set the maximum time limit to 10 h.

The results of the experiments are shown in Fig. 1. The pruning method based on saturations turns out to pay off when searching for longer clauses where it improves the baseline by approximately an order of magnitude and allows it to search for longer hypotheses within the given time limit. When searching for smaller clauses, the runtime is dominated by the time for learning the domain theory, which is why the baseline algorithm is faster in that case. The number of generated clauses, which is directly proportional to memory consumption, also becomes orders of magnitude smaller when using saturations for longer clauses. Note that for every clause constructed by the baseline algorithm, there is an equivalent clause constructed by the algorithm with the saturation-based pruning. We believe these results clearly suggest the usefulness of the proposed method, which could potentially also be used inside many existing ILP systems.

5 Related Work

The works most related to our approach are those relying on a special case of Plotkin’s relative subsumption [15] called generalized subsumption [2]. Generalized subsumption was among others used in [10]. In Sect. 3.5 we discussed the reasons why relative subsumption is not suitable for pruning. Background knowledge was also used to reduce the space of hypotheses in the Progol 4.4 system [12], which uses Plotkin’s relative clause reduction. Note that the latter is a method for removing literals from bottom clauses, whereas in contrast our method is based on adding literals to hypotheses. Hence, the Progol 4.4 strategy is orthogonal to the methods presented in this paper. Another key difference is that our approach is able to learn the background knowledge from the training data whereas all the other approaches use predefined background knowledge. Finally, our approach is not limited to definite clauses, which is also why we do not use SLD resolution. On the other hand, as our method is rooted in first-order logic (due to the fact that we use the learning from interpretations setting) and not directly in logic programming, it lacks some of the expressive power of logic programming.

6 Conclusions

In this paper, we introduced a generally applicable method for pruning hypotheses in ILP, which goes beyond mere isomorphism testing. We showed that the method is able to reduce the size of the hypothesis space by orders of magnitudes, and also leads to a significant runtime reduction. An interesting aspect of the proposed method is that it combines induction (domain theory learning) and deduction (theorem proving) for pruning the search space. In future, it would be interesting to combine these two components of our approach more tightly.