Abstract
This paper studies specifications and proofs of distributed algorithms when only message history variables are used, using Basic Paxos and Multi-Paxos for distributed consensus as precise case studies. We show that not using and maintaining other state variables yields simpler specifications that are more declarative and easier to understand. It also allows easier proofs to be developed by needing fewer invariants and facilitating proof derivations. Furthermore, the proofs are mechanically checked more efficiently.
We show that specifications in TLA+ and proofs in TLA+ Proof System (TLAPS) are reduced by 25% and 27%, respectively, for Basic Paxos, and 46% (from about 100 lines to about 50 lines) and 48% (from about 1000 lines to about 500 lines), respectively, for Multi-Paxos. Overall we need 54% fewer manually written invariants and our proofs have 46% fewer obligations. Our proof for Basic Paxos takes 26% less time than Lamport et al.’s for TLAPS to check, and our proofs for Multi-Paxos are checked by TLAPS within 1.5 min whereas prior proofs for Multi-Paxos fail to be checked in the new version of TLAPS.
This work was supported in part by NSF grants CCF-1414078 and CCF-1248184 and ONR grant N000141512208. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of these agencies.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Reasoning about correctness of distributed algorithms is notoriously difficult due to a number of reasons including concurrency, asynchronous networks, unbounded delay, and arbitrary failures. Emerging technologies like autonomous cars are bringing vehicular clouds closer to reality [9], decentralized digital currencies are gathering more attention from academia and industry than ever [31], and with the explosion in the number of nano- and pico- satellites being launched, a similar trend is expected in the field of space exploration as well [29]. All of these systems deal with critical resources like human life, currency, and intricate machinery. This only amplifies the need for employing formal methods to guarantee their correctness.
Verification of distributed algorithms continues to pose a demanding challenge to computer scientists, exacerbated by the fact that paper proofs of these algorithms cannot be trusted [33]. The usual line of reasoning in static analysis of such systems involves manually writing invariants and then using theorem provers to verify that the invariants follow from the specification and that they imply correctness.
A distributed system comprises a set of processes communicating with each other by message passing while performing local actions that may be triggered upon receiving a set of messages and may conclude with sending a set of messages [14, 15]. As such, data processed by any distributed process fall into two categories: (i) History Variables: Sets of all messages sent and receivedFootnote 1 and (ii) Derived Variables: Local data maintained for efficient computation. Derived variables are often used to maintain results of aggregate queries over sent and received messages.
While reading and writing pseudocode, derived variables are helpful because instead of writing the definition of the variable everywhere, the variable is used instead. Human readers would recall the definition and convince themselves how the algorithm works. While this approach works well for humans, the same is not true for provers. For specifications written with derived variables, invariants have to be added to their proofs which, at the very least, establish that the derived variable implements its definition.
One reason to use derived variables in formal specifications is their existence in pseudocode. Another reason is the lack of high-level languages that provide elegant support for quantifications, history variables, and automatic optimal maintenance of aggregate queries over history variables. The barrier of lack of executable language support for such richness is overcome by high-level languages like DistAlgo [21], which provides native support for history variables, quantifications, and aggregate queries. This motivated us to dispense with derived variables, and study specifications written with only history variables and the impact of this change on their proofs.
Note that uses of history variables provide higher-level specifications of systems in terms of what to compute, as opposed to how to compute with employing and updating derived variables. It makes proofs easier, independent of the logics used for doing the proofs, because important invariants are captured directly in the specifications, rather than hidden under all the incremental updates. On the other hand, it can make model checking much less efficient, just as it can make straightforward execution much less efficient. This is not only because high-level queries are time consuming, but also because maintaining history variables can blow up the state space. This is why automatic incrementalization [10, 23, 27, 28] is essential for efficient implementations, including implementations of distributed algorithms [20, 22]. The same transformations for incrementalization can drastically speed up both program execution and model checking.
Contributions. We first describe a systematic style to write specifications of distributed algorithms using message history variables. The only variables in these specifications are the sets of sent and received messages. We show (i) how these are different from the usual pseudocode, (ii) why these are sufficient for specifying all distributed algorithms, and (iii) when these are better for the provers than other specifications. A method is then explained which, given such specifications, allows us to systematically derive many important invariants which are needed to prove correctness. This method exploits the monotonic increase of the sets of sent and received messages—messages can only be added or read from these sets, not updated or deleted.
We use three existing specifications and their Safety proofs as our case studies: (i) Basic Paxos for single-valued consensus by Lamport et al., distributed as an example with the TLA+ Proof System (TLAPS) [19], (ii) Multi-Paxos for multi-valued consensus [2], and (iii) Multi-Paxos with preemption [2]. Paxos is chosen because it is famous for being a difficult algorithm to grasp, while at the same time it is the core algorithm for distributed consensus—the most fundamental problem in distributed computing. We show that our approach led to significantly reduced sizes of specifications and proofs, numbers of needed manually written invariants, and proof checking times. Our specifications and proofs are available at https://github.com/sachand/HistVar.
Paper Overview. Section 2 details our style of writing specifications using Basic Paxos as an example. We then describe our strategy to systematically derive invariants in Sect. 3 while also showing how using history variables leads to needing fewer invariants. We discuss Multi-Paxos briefly in Sect. 4. Results comparing our specifications and proofs with existing work is detailed in Sect. 5. Section 6 concludes with related work.
2 Specifications Using Message History Variables
We demonstrate our approach by developing a specification of Basic Paxos in which we only maintain the set of sent messages. This specification is made to correspond to the specification of Basic Paxos in TLA+ written by Lamport et al. [19]. This is done intentionally to better understand the applicability of our approach. We also simultaneously show Lamport’s description of the algorithm in English [17] to aid the comparison, except we rename message types and variable names to match those in his TLA+ specification: prepare and accept messages are renamed  and
and  respectively, their responses are renamed
respectively, their responses are renamed  and
and  , respectively, and variable n is renamed b and bal in different places.
, respectively, and variable n is renamed b and bal in different places.
Distributed consensus. The basic consensus problem, called single-value consensus or single-decree consensus, is to ensure that a single value is chosen from among the values proposed by the processes. The safety requirements for consensus are [17]:
-
Only a value that has been proposed may be chosen.
-
Only a single value is chosen.
This is formally defined as

where \(\mathcal {V}\) is the set of possible proposed values, and \(\phi \) is a predicate that given a value v evaluates to true iff v was chosen by the algorithm. The specification of \(\phi \) is part of the algorithm.
Basic Paxos. Paxos solves the problem of consensus. Two main roles of the algorithm are performed by two kinds of processes:
-
\(\mathcal {P}\) is the set of proposers. These processes propose values that can be chosen.
-
\(\mathcal {A}\) is the set of acceptors. These processes vote for proposed values. A value is chosen when there are enough votes for it.
A set \(\mathcal {Q}\) of subsets of the acceptors, that is \(\mathcal {Q} \subseteq 2^{\mathcal {A}}\), is used as a quorum system. It must satisfy the following properties:
-
\(\mathcal {Q}\) is a set cover for \(\mathcal {A}\)—\(\bigcup _{Q \in \mathcal {Q}} Q = \mathcal {A}\).
-
Any two quorums overlap—\(\forall \,Q1, Q2 \in \mathcal {Q} : Q1 \cap Q2 \ne \emptyset \).
The most commonly used quorum system takes any majority of acceptors as an element in \(\mathcal {Q}\). For e.g., if \(\mathcal {A} = \{1, 2, 3\}\), then the majority based quorum set is \(\mathcal {Q} = \{\{1, 2\}, \{2, 3\}, \{1, 3\}, \{1, 2, 3\}\}\). Quorums are needed because the system can have arbitrary failures. If a process waits for replies from all other processes, as in Two-Phase Commit, the system will hang in the presence of even one failed process. In the mentioned example, the system will continue to work even if acceptor 3 fails because at least one quorum, which is \(\{1, 2\}\), is alive.
Basic Paxos solves the problem of single-value consensus. It defines predicate \(\phi \) as

where \(\mathcal {B}\) is the set of proposal numbers, also called ballot numbers, which is any set that can be strictly totally ordered.  means that a message of type
means that a message of type  with ballot number b and value v was sent by acceptor a (to some set of processes). An acceptor votes by sending such a message.
with ballot number b and value v was sent by acceptor a (to some set of processes). An acceptor votes by sending such a message.
Variables. Lamport et al.’s specification of Basic Paxos has four global variables.
-
msgs— history variable maintaining the set of messages that have been sent. Processes read from or add to this set but cannot remove from it. We rename this to sent in both ours and Lamport et al.’s specifications for clarity purposes. This is the only variable maintained in our specifications.
-
maxBal—for each acceptor, the highest ballot seen by it.
-
maxVBal and maxVal—for each acceptor, maxVBal is the highest ballot in which it has voted, and maxVal is the value it voted for in that ballot.
Algorithm steps. The algorithm consists of repeatedly executing two phases. Each phase comprises two actions, one by acceptors and one by proposers.
-
Phase 1a. Figure 1 shows Lamport’s description in English followed by Lamport et al.’s and our specifications in TLA+. Send is an operator that adds its argument to sent, i.e., \(Send(m) \mathrel {\smash {\triangleq }} sent' = sent \cup \{m\}\).
-
1.
The first conjunct in Lamport et al.’s specification is not mentioned in the English description and is not needed. Therefore it was removed.
-
2.
The third conjunct is also removed because the only variable our specification maintains is sent, which is updated by Send.
-
1.
-
Phase 1b. Figure 2 shows the English description and the specifications of Phase 1b. The first two conjuncts in both specifications capture the precondition in the English description. The remaining conjuncts specify the action.
-
1.
The first conjunct states that message m received by acceptor a is of type
 .
. -
2.
The second conjunct ensures that the proposal number bal in the
 message m is higher than that of any
message m is higher than that of any  request responded to by a. In Lamport et al.’s specification, derived variable maxBal[a] maintains the highest proposal number that a has ever responded to, in
request responded to by a. In Lamport et al.’s specification, derived variable maxBal[a] maintains the highest proposal number that a has ever responded to, in  and
and  messages, and its second conjunct uses \(m{.}bal > maxBal[a]\). Using sent only, we capture this intent more directly, as
messages, and its second conjunct uses \(m{.}bal > maxBal[a]\). Using sent only, we capture this intent more directly, as  , because those m2’s are the response messages that a has ever sent.
, because those m2’s are the response messages that a has ever sent. -
3.
The third conjunct is the action of sending a promise (
 message) not to accept any more proposals numbered less than bal and with the highest-numbered proposal (if any) that a has accepted, i.e., has sent a
message) not to accept any more proposals numbered less than bal and with the highest-numbered proposal (if any) that a has accepted, i.e., has sent a  message. This proposal is maintained in Lamport et al.’s specification in derived variables maxVBal and maxVal. We specify this proposal as \(max\_prop(a)\), which is either the set of proposals that have the highest proposal number among all accepted by a or if a has not accepted anything, then \(\{[bal \mapsto -1, val \mapsto \bot ]\}\) as the default, where \(-1 \notin \mathcal {B}\) and is smaller than all ballots and \(\bot \notin \mathcal {V}\). This corresponds to initialization in Lamport et al.’s specification as shown in Fig. 5.
message. This proposal is maintained in Lamport et al.’s specification in derived variables maxVBal and maxVal. We specify this proposal as \(max\_prop(a)\), which is either the set of proposals that have the highest proposal number among all accepted by a or if a has not accepted anything, then \(\{[bal \mapsto -1, val \mapsto \bot ]\}\) as the default, where \(-1 \notin \mathcal {B}\) and is smaller than all ballots and \(\bot \notin \mathcal {V}\). This corresponds to initialization in Lamport et al.’s specification as shown in Fig. 5. -
4.
The remaining conjuncts in Lamport et al.’s specification maintain the variable maxBal[a]. A compiler that implements incrementalization [23] over queries would automatically generate and maintain such a derived variable to optimize the corresponding query.
-
1.
-
Phase 2a. Figure 3 shows Phase 2a. The specifications differ from the English description by using a set of quorums, \(\mathcal {Q}\), instead of a majority. The only difference between the two specifications is the removed
 conjunct when using sent only. It is important to note that the English description fails to mention the first conjunct—a conjunct without which the specification is unsafe. Every
conjunct when using sent only. It is important to note that the English description fails to mention the first conjunct—a conjunct without which the specification is unsafe. Every  message must have a unique ballot.
message must have a unique ballot.Note that the first conjunct in Lamport et. al.’s specification (and therefore ours as well) states that none of the
 messages sent so far has bal equal to b. This is not directly implementable in a real system because this quantification query requires accessing message histories of all processes. We leave this query as is for two main reasons: (i) The focus of this paper is to demonstrate the use of history variables against derived variables and compare them in the light of simpler specification and verification. This removes derived variables but leaves queries on history variables unchanged even though they are not directly implementable. (ii) There is a commonly-used, straightforward, efficient way to implement this query - namely realizing ballot as a tuple in \(\mathbb {N} \times \mathcal {P}\) [16]. So a proposer only executes Phase 2a on a ballot proposed by itself (i.e., sent a
messages sent so far has bal equal to b. This is not directly implementable in a real system because this quantification query requires accessing message histories of all processes. We leave this query as is for two main reasons: (i) The focus of this paper is to demonstrate the use of history variables against derived variables and compare them in the light of simpler specification and verification. This removes derived variables but leaves queries on history variables unchanged even though they are not directly implementable. (ii) There is a commonly-used, straightforward, efficient way to implement this query - namely realizing ballot as a tuple in \(\mathbb {N} \times \mathcal {P}\) [16]. So a proposer only executes Phase 2a on a ballot proposed by itself (i.e., sent a  message with that ballot) and, for efficient implementation, only executes Phase 2a on the highest ballot that it has proposed.
message with that ballot) and, for efficient implementation, only executes Phase 2a on the highest ballot that it has proposed. -
Phase 2b. Figure 4 shows Phase 2b. Like Phase 1b, we replace the second conjunct with the corresponding query over sent and remove updates to the derived variables.
Complete algorithm specification. To complete the algorithm specification, we define, and compare, vars, Init, Next, and Spec which are typical TLA+ operator names for the set of variables, the initial state, possible actions leading to the next state, and the system specification, respectively, in Fig. 5.
Lamport et al.’s initialization of maxVBal and maxVal to \(-1\) and \(\bot \), respectively, is moved to our definition of \(max\_prop\) in Fig. 2. We do not need initialization of maxBal because if no  or
or  messages have been sent, the universally quantified queries over them would be vacuously true. In Lamport et al.’s specification, this is achieved by initializing maxBal to \(-1\), which is smaller than all ballots, and thus, the conjunct \(m{.}bal > maxBal[a]\) in Fig. 2 holds for the first
messages have been sent, the universally quantified queries over them would be vacuously true. In Lamport et al.’s specification, this is achieved by initializing maxBal to \(-1\), which is smaller than all ballots, and thus, the conjunct \(m{.}bal > maxBal[a]\) in Fig. 2 holds for the first  message received.
message received.
3 Invariants and Proofs Using Message History Variables
Invariants of a distributed algorithm can be categorized into the following three kinds:
-
1.
Type invariants. These ensure that all data processed in the algorithm is of valid type. For example, messages of type
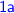 must have a field \(bal \in \mathcal {B}\). If an action sends a
must have a field \(bal \in \mathcal {B}\). If an action sends a  message with bal missing or \(bal \notin \mathcal {B}\), a type invariant is violated.
message with bal missing or \(bal \notin \mathcal {B}\), a type invariant is violated. -
2.
Message invariants. These are invariants defined on message history variables. For example, each message of type
 has a unique bal. This is expressed by the invariant
has a unique bal. This is expressed by the invariant  .
. -
3.
Process invariants. These state properties about the data maintained in derived variables. For example, in Lamport et al.’s specification, one such invariant is that for any acceptor a, \(maxBal[a] \ge maxVBal[a]\).
Figure 6 shows and compares all invariants used in Lamport et al.’s proof vs. ours. The following operators are used in the invariants for brevity:

Type invariants reduced to one. Lamport et al. define four type invariants, one for each variable they maintain. Messages is the set of all possible valid messages. We require only one, (I1). This invariant asserts that the type of all sent messages is valid. (I2-4) are not applicable to our specification.
Process invariants not needed. Lamport et al. define four process invariants, (I5-8), regarding variables maxVal, maxVBal, and maxBal. They are not applicable to our specification, and need not be given in our proof.
-
(I5) Because maxBal[a] is the highest ballot ever seen by a and maxVBal[a] is the highest ballot a has voted for, we have
 (4)
(4)where
 . Note that max is not in TLA+ and has to be user-defined. Invariant (I5) is needed in Lamport et al.’s proof but not ours because they use derived variables whereas we specify the properties directly. For example, for Lamport et al.’s Phase 1b, one cannot deduce \(m{.}bal > maxVBal[a]\) without (I5), whereas in our Phase 1b, definitions of 2bs and \(max\_prop\) along with the second conjunct are enough to deduce it.
. Note that max is not in TLA+ and has to be user-defined. Invariant (I5) is needed in Lamport et al.’s proof but not ours because they use derived variables whereas we specify the properties directly. For example, for Lamport et al.’s Phase 1b, one cannot deduce \(m{.}bal > maxVBal[a]\) without (I5), whereas in our Phase 1b, definitions of 2bs and \(max\_prop\) along with the second conjunct are enough to deduce it. -
(I6) Lamport et al.’s proof needs this invariant to prove (I11). Because the initial values are part of Init and are not explicitly present in their Phase 1b, this additional invariant is needed to carry this information along. We include the initial values when specifying the action in Phase 1b and therefore do not need such an invariant.
-
(I7) This invariant is obvious from the definition of VotedForIn in Eq. (3) and property of maxVBal in Eq. (4). The premise \(maxVBal[a] \ge 0\) is needed by Lamport et al.’s proof to differentiate from the initial value \(-1\) of maxVBal[a].
-
(I8) This states that a has not voted for any value at a ballot greater than maxVBal[a]. This invariant need not be manually given in our proofs because it is implied from the definition of maxVBal[a].
Message invariants not needed or more easily proved. Before detailing the message invariants, we present a systematic method that can derive several useful invariants used by Lamport et al. and thus make the proofs easier. This method is based on the following properties of our specifications and distributed algorithms:
-
1.
sent monotonically increases, i.e., the only operations on it are read and add.
-
2.
Message invariants hold for each sent message of some type, i.e., they are of the form
 , or more conveniently if we define
, or more conveniently if we define  , we have \(\forall \,m \in sent_{\tau }: \varPhi (m)\).
, we have \(\forall \,m \in sent_{\tau }: \varPhi (m)\). -
3.
\(sent = \emptyset \) initially, so the message invariants are vacuously true in the initial state of the system.
-
4.
Distributed algorithms usually implement a logical clock for ordering two arbitrary messages. In Paxos, this is done by ballots.
We demonstrate our method by deriving (I15). The method is applied for each message type used in the algorithm. Invariant (I15) is about  messages. We first identify all actions that send
messages. We first identify all actions that send  messages and then do the following:
messages and then do the following:
-
1.
Increment.
 messages are sent in Phase 2b as specified in Fig. 4. We first determine the increment to sent, \(\varDelta (sent)\), the new messages sent in Phase 2b. We denote a message in \(\varDelta (sent)\) by \(\delta \) for brevity. We have, from Fig. 4,
messages are sent in Phase 2b as specified in Fig. 4. We first determine the increment to sent, \(\varDelta (sent)\), the new messages sent in Phase 2b. We denote a message in \(\varDelta (sent)\) by \(\delta \) for brevity. We have, from Fig. 4,  (5)
(5) -
2.
Analyze. We deduce properties about the messages in \(\varDelta (sent)\). For
 messages, we deduce the most straightforward property that connects the contents of messages in \(\varDelta (sent)\) with the message m, from Fig. 4,
messages, we deduce the most straightforward property that connects the contents of messages in \(\varDelta (sent)\) with the message m, from Fig. 4,  (6)
(6) -
3.
Integrate. Because (i) sent monotonically increases, and (ii) \(\phi \) is an existential quantification over sent, \(\phi \) holds for all increments to
 . Property (i) means that once the existential quantification in \(\phi \) holds, it holds forever. Integrating both sides of Eq. (6) in the space of
. Property (i) means that once the existential quantification in \(\phi \) holds, it holds forever. Integrating both sides of Eq. (6) in the space of  messages yields (I15), i.e.,
messages yields (I15), i.e.,  (7)
(7)The case for \(\phi \) being universally quantified over sent is discussed with invariant (I12).
Other message invariants. (I9) and (I10) follow directly from Eq. (4) and need not be manually specified for our proof. We also derive (I11), (I12), and (I14) as describe in the following.
-
(I11) Like (I15), (I11) can also be systematically derived, from our Phase 1b in Fig. 2. This invariant is less obvious when variables maxVal and maxVBal are explicitly used and updated because (i) they are not updated in the same action that uses them, requiring additional invariants to carry their meaning to the proofs involving the actions that use them, and (ii) it is not immediately clear if these variables are being updated in Lamport et al.’s Phase 2b in Fig. 4 because a
 message is being sent or because a
message is being sent or because a 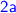 message was received.
message was received. -
(I12) To derive (I11) and (I15), we focused on where the contents of the new message come from. For (I12), we analyze why those contents were chosen. From our Phase 1b with definitions of 2bs and \(max\_prop\) in Fig. 2, we have
 (8)
(8)\(\phi \) has two disjuncts—the first has a universal quantification and the second has negated existential, which is universal in disguise. If sent is universally quantified, integration like for (I15) is not possible because the quantification only holds at the time of the action. As new messages are sent in the future, the universal may become violated.
The key is the phrase at the time. One way to work around the universal is to add a time field in each message and update it in every action as a message is sent, like using a logical clock. Then, a property like \(\phi (\delta ) = \forall \,m \in sent_{\tau }: \psi (m)\) can be integrated to obtain
$$\begin{aligned} \varPhi (sent_{\tau }) = \forall \,m2 \in sent_{\tau }: \forall \,m \in sent: m{.}time < m2.time \Rightarrow \psi (m) \end{aligned}$$(9)Because ballots act as the logical clock in Paxos, we do not need to specify a separate logical clock and we can perform the above integration on Eq. (8) to obtain the invariant (I12).
-
(I14) This invariant is of the form \(\forall \,m1, m2 \in sent_{\tau }, t: \psi (m1, t) \wedge \psi (m2, t) \Rightarrow m1 = m2\). In this case, \(\psi (m, t) \triangleq m{.}bal = t\). Deriving invariants like (I14) is nontrivial unless \(\psi \) is already known. In some cases, \(\psi \) can be guessed. The intuition is to look for a universal quantification (or negated existential) in the specification of an action. The ideal case is when the quantification is on the message type being sent in the action. Potential candidates for \(\psi \) may be hidden in such quantifications. Moreover, if message history variables are used, these quantifications are easier to identify.
Starting with a guess of \(\psi \), we identify the change in the counting measure (cardinality) of the set \(\{t: m \in sent_{\tau } \wedge \psi (m, t)\}\) along with that of \(sent_{\tau }\). In the case of (I14), we look for \(\varDelta (|\{m{.}bal: m \in sent_{2a}\}|)\). From our Phase 2a in Fig. 3, we have
 (10)
(10)Rewriting \(\phi \) as \(\{b\} \not \subseteq \{m{.}bal: m \in sent_{2a}\}\), it becomes clear that \(\varDelta (|\{m{.}bal: m \in sent_{2a}\}|) = 1\). Meanwhile, \(\varDelta (|\{m \in sent_{2a}\}|) = 1\). Because the counting measure increases by the same amount for both, (I14) can be derived safely.
4 Multi-Paxos
Specification. We have developed new specifications of Multi-Paxos and Multi-Paxos with Preemption that use only message history variables, by removing derived variables from the specifications described in Chand et al. [2]. This is done in a way similar to how we removed derived variables from Lamport et al.’s specification of Basic Paxos.
The most interesting action here was preemption. With preemption, if an acceptor receives a  or
or  message with bal smaller than the highest that it has seen, it responds with a
message with bal smaller than the highest that it has seen, it responds with a  message that contains the highest ballot seen by the acceptor. Upon receiving such a message, the receiving proposer would pick a new ballot that is higher than the ballots of all received
message that contains the highest ballot seen by the acceptor. Upon receiving such a message, the receiving proposer would pick a new ballot that is higher than the ballots of all received  messages.
messages.
This is a good opportunity to introduce the other message history variable, received, the set of all messages received. It is different from sent because a message could be delayed indefinitely before being received, if at all. In [2], derived variable proBallot is introduced to maintain the result of this query on received messages. We contrast this with our new specification in Fig. 7. Receive(m) adds message m to received, i.e., \(Receive(m) \triangleq received' = received \cup \{m\}\).
Verification. While we observed a 27% decrease in proof size for Basic Paxos, for Multi-Paxos this decrease was 48%. Apart from the points described in Sect. 3, an important player in this decrease was the removal of operator MaxVotedBallotInSlot from Chand et al.’s specifications. This operator was defined as

Five lemmas were needed in Chand et al.’s proof to assert basic properties of the operator. For example, lemma MVBISType stated that if \(D \subseteq [bal : \mathcal {B}, slot : \mathcal {S}, val : \mathcal {V}]\), then the result of the operator is in \( \mathcal {B} \cup \{-1\}\). Removing these lemmas and their proofs alone resulted in a decrease of about 100 lines (about 10%) in proof size.
5 Results
Table 1 summarizes the results of our specifications and proofs that use only message history variables, compared with those by Lamport et al. and Chand et al. We observe an improvement of around 25% across all stats for Basic Paxos and a staggering 50% for Multi-Paxos and Multi-Paxos with Preemption. Following, we list some important results:
-
The specification size decreased by 13 lines (25%) for Basic Paxos, from 52 lines for Lamport et al.’s specification to 39 lines for ours. For Multi-Paxos, the decrease is 36 lines (46%), from 78 lines for Chand et al.’s to 42 lines for ours, and for Multi-Paxos with Preemption, the decrease is 45 lines (46%), from 97 to 52.
-
The total number of manually written invariants decreased by 54% overall—by 9 (60%) from 15 to 6 for Basic Paxos, by 8 (50%) from 16 to 8 for Multi-Paxos, and by 9 (53%) from 17 to 8 for Multi-Paxos with Preemption. This drastic decrease is because we do not maintain the variables maxBal, maxVBal, and maxVal as explained in Sect. 3.
-
The proof size for Basic Paxos decreased by 83 lines (27%), from 310 to 227. This decrease is attributed to the fact that our specification does not use other state variables besides sent. This decrease is 468 lines (47%), from 988 to 520, for Multi-Paxos, and is 494 lines (48%), from 1032 to 538 for Multi-Paxos with Preemption.
-
Proof by contradiction is used twice in the proof by Lamport et al. and thrice for the proofs in Chand et al. We were able to remove all of these because our specification uses queries as opposed to derived variables. The motive behind removing proofs by contradiction is to have easier to understand constructive proofs.
-
The total number of proof obligations decreased by 46% overall—by 57 (24%) from 239 to 182 for Basic Paxos, by 450 (49%) from 918 to 468 for Multi-Paxos, and by 468 (49%) from 959 to 491 for Multi-Paxos with Preemption.
-
The proof-checking time decreased by 11 s (26%), from 42 to 31 for Basic Paxos. For Multi-Paxos and Multi-Paxos with Preemption, TLAPS took over 3 min for the proofs in [2] and failed (due to updates in the new version of TLAPS) to check the proofs of about 5 obligations. In contrast, our proofs were able to be checked completely in 1.5 min or less.
 invariants, (I13) and (I14) are
invariants, (I13) and (I14) are  invariants, and (I9) and (I15) are
invariants, and (I9) and (I15) are  invariants for Basic Paxos.
invariants for Basic Paxos.6 Related Work and Conclusion
History Variables. History variables have been at the center of much debate since they were introduced in the early 1970s [5,6,7]. Owicki and Gries [25] use them in an effort to prove properties of parallel programs, criticized by Lamport in his writings [13]. Contrary to ours, their history variables were ghost or auxiliary variables introduced for the sole purpose of simpler proofs. Our history variables are sent and received, whose contents are actually processed in all distributed system implementations.
Recently, Lamport and Merz [18] present rules to add history variables, among other auxiliary variables, to a low-level specification so that a refinement mapping from a high-level one can be established. The idea is to prove invariants in the high-level specification that serves as an abstraction of the low-level specification. In contrast, we focus on high-level specifications because our target executable language is DistAlgo, and efficient lower-level implementations can be generated systematically from high-level code.
Specification and Verification. Several systems [4, 8, 30], models [3, 24, 32], and methods [1, 11, 12, 26] have been developed in the past to specify distributed algorithms and mechanically check proofs of the safety and liveness properties of the algorithms. This work is orthogonal to them in the sense that the idea of maintaining only message history variables can be incorporated in their specifications as well.
Closer to us in terms of the specification is the work by Padon et al. [26], which does not define any variables and instead defines predicate relations which would correspond to manipulations of our history variables. For example,  is denoted by \(start\_round\_msg(b)\). Instead of using TLA+, the temporal logic of actions, they specify Paxos in first-order logic to later exploit benefits of Effectively Propositional Logic, such as satisfiability being decidable in it.
is denoted by \(start\_round\_msg(b)\). Instead of using TLA+, the temporal logic of actions, they specify Paxos in first-order logic to later exploit benefits of Effectively Propositional Logic, such as satisfiability being decidable in it.
In contrast, we present a method to specify distributed algorithms using history variables, implementable in high-level executable languages like DistAlgo, and then show (i) how such specifications require fewer invariants for proofs and (ii) how several important invariants can be systematically derived.
Notes
- 1.
This is different than some other references of the term history variables that include sequences of local actions, i.e., execution history [6].
References
Abadi, M., Lamport, L.: The existence of refinement mappings. Theoret. Comput. Sci. 82(2), 253–284 (1991)
Chand, S., Liu, Y.A., Stoller, S.D.: Formal verification of multi-paxos for distributed consensus. In: Fitzgerald, J., Heitmeyer, C., Gnesi, S., Philippou, A. (eds.) FM 2016. LNCS, vol. 9995, pp. 119–136. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-48989-6_8
Charron-Bost, B., Schiper, A.: The Heard-Of model: computing in distributed systems with benign faults. Distrib. Comput. 22(1), 49–71 (2009)
Chaudhuri, K., Doligez, D., Lamport, L., Merz, S.: The TLA+ proof system: building a heterogeneous verification platform. In: Cavalcanti, A., Deharbe, D., Gaudel, M.-C., Woodcock, J. (eds.) ICTAC 2010. LNCS, vol. 6255, p. 44. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14808-8_3
Clarke, E.M.: Proving correctness of coroutines without history variables. Acta Inform. 13(2), 169–188 (1980)
Clint, M.: Program proving: coroutines. Acta inform. 2(1), 50–63 (1973)
Clint, M.: On the use of history variables. Acta Inform. 16(1), 15–30 (1981)
Drăgoi, C., Henzinger, T.A., Zufferey, D.: PSync: a partially synchronous language for fault-tolerant distributed algorithms. ACM SIGPLAN Notices 51(1), 400–415 (2016)
Gerla, M., Lee, E.-K., Pau, G., Lee, U.: Internet of vehicles: from intelligent grid to autonomous cars and vehicular clouds. In: 2014 IEEE World Forum on Internet of Things (WF-IoT), pp. 241–246. IEEE (2014)
Gorbovitski, M.: A system for invariant-driven transformations. Ph.D. thesis, Computer Science Department, Stony Brook University (2011)
Hawblitzel, C., Howell, J., Kapritsos, M., Lorch, J.R., Parno, B., Roberts, M.L., Setty, S., Zill, B.: IronFleet: proving practical distributed systems correct. In: Proceedings of the 25th Symposium on Operating Systems Principles, pp. 1–17. ACM (2015)
Küfner, P., Nestmann, U., Rickmann, C.: Formal verification of distributed algorithms. In: Baeten, J.C.M., Ball, T., de Boer, F.S. (eds.) TCS 2012. LNCS, vol. 7604, pp. 209–224. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-33475-7_15
Lamport, L.: My writings : proving the correctness of multiprocess programs. https://lamport.azurewebsites.net/pubs/pubs.html. Accessed 10 Oct 2017
Lamport, L.: The implementation of reliable distributed multiprocess systems. Comput. Netw. 2(2), 95–114 (1978)
Lamport, L.: The temporal logic of actions. ACM Trans. Program. Lang. Syst. (TOPLAS) 16(3), 872–923 (1994)
Lamport, L.: The part-time parliament. ACM Trans. Comput. Syst. (TOCS) 16(2), 133–169 (1998)
Lamport, L.: Paxos made simple. ACM Sigact News 32(4), 18–25 (2001)
Lamport, L., Merz, S.: Auxiliary variables in TLA+. ArXiv e-prints, March 2017
Lamport, L., Merz, S., Doligez, D.: Paxos.tla. https://github.com/tlaplus/v1-tlapm/blob/master/examples/paxos/Paxos.tla. Accessed 6 Feb 2018
Liu, Y.A., Brandvein, J., Stoller, S.D., Lin, B.: Demand-driven incremental object queries. In: Proceedings of the 18th International Symposium on Principles and Practice of Declarative Programming (PPDP), pp. 228–241. ACM (2016)
Liu, Y.A., Stoller, S.D., Lin, B.: From clarity to efficiency for distributed algorithms. ACM Trans. Program. Lang. Syst. (TOPLAS) 39(3), 12 (2017)
Liu, Y.A., Stoller, S.D., Lin, B., Gorbovitski, M.: From clarity to efficiency for distributed algorithms. In: Proceedings of the 27th ACM SIGPLAN Conference on Object-Oriented Programming, Systems, Languages and Applications (OOPSLA), pp. 395–410. ACM (2012)
Liu, Y.A.: Systematic Program Design: From Clarity To Efficiency. Cambridge University Press, Cambridge (2013)
Lynch, N.A., Tuttle, M.R.: Hierarchical correctness proofs for distributed algorithms. In: Proceedings of the sixth annual ACM Symposium on Principles of distributed computing, pp. 137–151. ACM (1987)
Owicki, S., Gries, D.: An axiomatic proof technique for parallel programs i. Acta Inform. 6(4), 319–340 (1976)
Padon, O., Losa, G., Sagiv, M., Shoham, S.: Paxos made EPR: decidable reasoning about distributed protocols. Proc. ACM Program. Lang. 1(OOPSLA), 108 (2017)
Paige, R., Koenig, S.: Finite differencing of computable expressions. ACM Trans. Program. Lang. Syst. (TOPLAS) 4(3), 402–454 (1982)
Rothamel, T., Liu, Y.A.: Generating incremental implementations of object-set queries. In: Proceedings of the 7th International Conference on Generative Programming and Component Engineering, pp. 55–66. ACM (2008)
Schilling, K.: Perspectives for miniaturized, distributed, networked cooperating systems for space exploration. Robot. Auton. Syst. 90, 118–124 (2017)
Sergey, I., Wilcox, J.R., Tatlock, Z.: Programming and proving with distributed protocols. Proc. ACM Program. Lang. 2(POPL), 28 (2017)
Tschorsch, F., Scheuermann, B.: Bitcoin and beyond: a technical survey on decentralized digital currencies. IEEE Commun. Surv. Tutor. 18(3), 2084–2123 (2016)
Wilcox, J.R., Woos, D., Panchekha, P., Tatlock, Z., Wang, X., Ernst, M.D., Anderson, T.: Verdi: a framework for implementing and formally verifying distributed systems. In: ACM SIGPLAN Notices, vol. 50, pp. 357–368. ACM (2015)
Zave, P.: Using lightweight modeling to understand Chord. ACM SIGCOMM Comput. Commun. Rev. 42(2), 49–57 (2012)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Chand, S., Liu, Y.A. (2018). Simpler Specifications and Easier Proofs of Distributed Algorithms Using History Variables. In: Dutle, A., Muñoz, C., Narkawicz, A. (eds) NASA Formal Methods. NFM 2018. Lecture Notes in Computer Science(), vol 10811. Springer, Cham. https://doi.org/10.1007/978-3-319-77935-5_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-77935-5_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-77934-8
Online ISBN: 978-3-319-77935-5
eBook Packages: Computer ScienceComputer Science (R0)








 .
. message m is higher than that of any
message m is higher than that of any  request responded to by a. In Lamport et al.’s specification, derived variable maxBal[a] maintains the highest proposal number that a has ever responded to, in
request responded to by a. In Lamport et al.’s specification, derived variable maxBal[a] maintains the highest proposal number that a has ever responded to, in  and
and  messages, and its second conjunct uses
messages, and its second conjunct uses  , because those m2’s are the response messages that a has ever sent.
, because those m2’s are the response messages that a has ever sent. message) not to accept any more proposals numbered less than bal and with the highest-numbered proposal (if any) that a has accepted, i.e., has sent a
message) not to accept any more proposals numbered less than bal and with the highest-numbered proposal (if any) that a has accepted, i.e., has sent a  message. This proposal is maintained in Lamport et al.’s specification in derived variables maxVBal and maxVal. We specify this proposal as
message. This proposal is maintained in Lamport et al.’s specification in derived variables maxVBal and maxVal. We specify this proposal as  conjunct when using sent only. It is important to note that the English description fails to mention the first conjunct—a conjunct without which the specification is unsafe. Every
conjunct when using sent only. It is important to note that the English description fails to mention the first conjunct—a conjunct without which the specification is unsafe. Every  message must have a unique ballot.
message must have a unique ballot. messages sent so far has bal equal to b. This is not directly implementable in a real system because this quantification query requires accessing message histories of all processes. We leave this query as is for two main reasons: (i) The focus of this paper is to demonstrate the use of history variables against derived variables and compare them in the light of simpler specification and verification. This removes derived variables but leaves queries on history variables unchanged even though they are not directly implementable. (ii) There is a commonly-used, straightforward, efficient way to implement this query - namely realizing ballot as a tuple in
messages sent so far has bal equal to b. This is not directly implementable in a real system because this quantification query requires accessing message histories of all processes. We leave this query as is for two main reasons: (i) The focus of this paper is to demonstrate the use of history variables against derived variables and compare them in the light of simpler specification and verification. This removes derived variables but leaves queries on history variables unchanged even though they are not directly implementable. (ii) There is a commonly-used, straightforward, efficient way to implement this query - namely realizing ballot as a tuple in  message with that ballot) and, for efficient implementation, only executes Phase 2a on the highest ballot that it has proposed.
message with that ballot) and, for efficient implementation, only executes Phase 2a on the highest ballot that it has proposed.

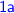 must have a field
must have a field  message with bal missing or
message with bal missing or  has a unique bal. This is expressed by the invariant
has a unique bal. This is expressed by the invariant  .
.

 . Note that
. Note that  , or more conveniently if we define
, or more conveniently if we define  , we have
, we have  messages are sent in Phase 2b as specified in Fig.
messages are sent in Phase 2b as specified in Fig. 
 messages, we deduce the most straightforward property that connects the contents of messages in
messages, we deduce the most straightforward property that connects the contents of messages in 
 . Property (i) means that once the existential quantification in
. Property (i) means that once the existential quantification in  messages yields (I15), i.e.,
messages yields (I15), i.e., 
 message is being sent or because a
message is being sent or because a 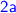 message was received.
message was received.

