Sound Black-Box Checking in the LearnLib

Abstract

In Black-Box Checking (BBC) incremental hypotheses of a system are learned in the form of finite automata. On these automata LTL formulae are verified, or their counterexamples validated on the actual system. We extend the LearnLib’s system-under-learning API for sound BBC, by means of state equivalence, that contrasts the original proposal where an upper-bound on the number of states in the system is assumed. We will show how LearnLib’s new BBC algorithms can be used in practice, as well as how one could experiment with different model checkers and BBC algorithms. Using the RERS 2017 challenge we provide experimental results on the performance of all LearnLib’s active learning algorithms when applied in a BBC setting. The performance of learning algorithms was unknown for this setting. We will show that the novel incremental algorithms TTT, and ADT perform the best.

J. Meijer—Supported by STW SUMBAT grant: 13859.

J. van de Pol—Supported by the 3TU.BSR project.

1 Introduction

There are many formal methods for analyzing the desired behavior of systems. Examples include complex industrial critical systems, such as wafer steppers, and X-ray diffraction machines. In these systems both liveness (something good eventually happens), and safety (something bad never happens) are essential. It is key for testers and developers of these systems to have easily usable tooling available to investigate liveness and safety properties of systems. We present an instance of such tooling known as Black-Box Checking (BBC), originally developed by Peled et al. [23] which we implemented in the LearnLib. We show its ease of use, why our method is sound even when not assuming an upper-bound on the number of states in the System Under Learning (SUL), and show how well it performs with an actual case study.

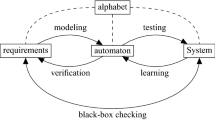
The essence of using formal methods is relating requirements on one hand, and a system on the other. The requirements are often formulated with some kind of temporal logic, such as Linear Temporal Logic (LTL). These formulas then express the liveness and safety properties of the system. In formal methods traditionally, the three main complementary methods are verification, testing, and learning. Verification involves checking whether some abstract instance (e.g. in the form of an automaton) of the specification adheres to a set of requirements. Testing involves checking whether the system conforms to an abstract instance of the specification. If such an abstract instance is modeled as an automaton, Model-Based Testing (MBT) [30] is typically applied. Conversely, an abstract instance can also be learned from a system. If such an instance is in the form of an automaton, and the system can only be accessed as a black-box, then this procedure is called Active Automata Learning (AAL) [27]. LearnLib [12] is a toolset that contains a wide variety of AAL algorithms. Many of these algorithms are inspired by Angluin’s famous $\mathrm {L}^*$ algorithm [1]. Figure 1 provides an overview of the aforementioned approaches. Figure 1 also shows the concept of an alphabet. An alphabet contains the symbols in which requirements must be written, and in what language the system communicates with the environment. This means that to make the system perform an action an input must be sent that is a symbol in the alphabet. To observe the reaction of the system, the output must also be a symbol in the alphabet.

Fig. 1.

Formal methods

Testing, verification, and learning can be used in a complementary fashion, because all of them have their advantages. Verification is typically done through model checking. Model checking has been around for several decades and efficient model checkers are readily available. The advantage of testing is a highly automated approach to check whether a system conforms to a specific model. There are many mature MBT tools available, such as JTorX [3]. From a practical perspective, learning an automaton from a system is also quite straightforward, because the only requirements are a definition of the alphabet, and some kind of adapter between a learning algorithm and system. These adapters are often quite easy to build. The three methods also have disadvantages. For example when verification is performed, it is known which requirement hold on an abstract notion of the system, but it is unknown which of those requirements also hold on the actual system. Testing has the disadvantage that the abstract notion (e.g. an automaton) has to be built and maintained by hand. Writing specifications for automata can be tedious, since it is often done with specification languages that may be unfamiliar to the developers of the system. Verifying requirements on an automaton that is obtained through learning is also difficult. Because it can take quite a long time before learning algorithms produce such an automaton. Even when such an automaton is obtained, verifying requirements is not straightforward, because the learned automaton can be incorrect. Black-box checking tries to alleviate those problems. It resolves the need for maintenance of an abstract notion of a system so that requirements can be directly checked on a system.

When BBC is applied to industrial cases, the guess of an upper-bound on the number of states to have a sound BBC procedure can be either dangerous (the guess is too low), or unpractical (the guess is too high). We resolve this by allowing the LearnLib to check for state equivalence in the SUL. Our implementation in the LearnLib is Free and Open Source, this alleviates the current scarcity of tool support. To investigate how efficient several active learning algorithms are for BBC, we contribute the following.

• Two variations of black-box checking algorithms.

• A novel sound black-box checking approach that uses state equivalences, instead of an upper-bound on the number of states in the SUL.

• A modular design, allowing new model checkers to be added easily, or smarter strategies to be implemented for detecting spurious counterexamples.

• A thorough reproducible experimental setup, with several algorithms.

The rest of the paper is structured as follows. Section 2 provides preliminary definitions and procedures for model checking, active learning and black-box checking. Section 3 describes how one can check whether a SUL accepts an infinite lasso-shaped word, and how this is implemented in the LearnLib. In Sect. 4 we discuss related work, such as other model checkers, active learning algorithms and the LBTest toolset. Section 5 details the result of our case study, and Sect. 6 concludes our work.

2 Preliminaries

The LearnLib mainly contains AAL algorithms for DFAs and Mealy machines. We provide a definition for both, and a definition for LTSs were multiple labels per edge are allowed. Typically, model checkers, such as LTSmin verify LTL properties on LTSs. Hence we provide LTL semantics for LTSs, and provide straightforward translations from DFAs and Mealy machines to LTSs. We also provide actual implementations of these translations in the LearnLib. Furthermore, this section gives a short introduction to active learning, and black-box checking.

Definition 1

(Edge Labeled Transition System). An edge Labeled Transition System (LTS) is defined as a tuple $\mathcal {L} = \langle S, s_0, \delta , L, T, \lambda \rangle$, where S is a finite nonempty set of states, $s_0 \in S$ is the initial state, $\delta : S \rightarrow 2^S$ is the transition function, L is the set of edge labels, T is the set of edge label types, and $\lambda : S \times S \rightarrow 2^{T \times L}$: is the edge labeling function. A path in $\mathcal {L}$ is an infinite sequence of states beginning in $s_0$. The set of paths is ${\text {Paths}}(\mathcal {L}) = \{s_0s_1\ldots \in S^\omega \mid \forall i > 0 :s_i \in \delta (s_{i-1})\}$. A trace is an infinite sequence of sets of tuples of labels: ${\text {Traces}}(\mathcal {L}) = \{ \lambda (s_0,s_1)\lambda (s_1,s_2)\ldots \in (2^{T \times L})^\omega \mid s \in {\text {Paths}}(\mathcal {L}) \}$.

Definition 2

(Deterministic Finite Automaton). A Deterministic Finite Automaton (DFA) is defined as a tuple $\mathcal {D} = \langle S, s_0, \varSigma , \delta , F \rangle$, where S is a finite nonempty set of states, $s_0 \in S$ is the initial state, $\varSigma$ is a finite alphabet, $\delta : S \times \varSigma \rightarrow S$ is the total transition function, $F \subseteq S$ is the set of accepting states. The language of $\mathcal {D}$ is denoted $L(\mathcal {D})$. A DFA is Prefix-Closed iff $\forall s \in S, \forall i \in \varSigma :\delta (s, i) \in F \implies s \in F$. In other words $\forall \sigma _1\ldots \sigma _n \in L(\mathcal {D}) :\sigma _1\ldots \sigma _{n-1} \in L(\mathcal {D})$. The LTS of a non-empty, prefix-closed DFA $\mathcal {D}$ is $\mathcal {L}_\mathcal {D} = \langle F, s_0, \delta _\mathcal {L}, \varSigma , \{letter\}, \lambda _\mathcal {L}\rangle$, where $\delta _\mathcal {L}(s) = \bigcup _{i \in \varSigma } \delta (s, i)$, and $\lambda _\mathcal {L}(s, s') = \{(letter, l) \mid l \in \varSigma \wedge \delta (s, l) = s' \}$.

Fig. 2.

Example DFA

Example 1

(DFA). An example prefix-closed DFA for the regular expression $(ab)^*a?$ is given in Fig. 2a (the trap state is implicit). The LTS is given in Fig. 2b. The traces in the LTS are: $\{\{(letter,a)\}\{(letter,b)\}\ldots \}$.

Definition 3

(Mealy Machine). A Mealy machine is defined as a tuple $\mathcal {M} = \langle S,s_0,\varSigma ,\varOmega ,\delta ,\lambda \rangle$, where S is a finite nonempty set of states, $s_0 \in S$ is the initial state, $\varSigma$ is a finite input alphabet, $\varOmega$ is a finite output alphabet, $\delta : S \times \varSigma \rightarrow S$ is the total transition function, and $\lambda : S \times \varSigma \rightarrow \varOmega$ is the total output function. The LTS of $\mathcal {M}$ is $\mathcal {L}_\mathcal {M} = \langle S, s_0, \delta _\mathcal {L}, \varSigma \cup \varOmega , \{input, output\}, \lambda _\mathcal {L}\rangle$, where $\delta _\mathcal {L}(s) = \bigcup _{i \in \varSigma } \delta (s, i)$, and $\lambda _\mathcal {L}(s, s') = \{ \{ (in, i), (out, o) \} \mid i \in \varSigma \wedge \delta (s, i) = s' \wedge o \in \varOmega \wedge \lambda (s, i) = o \}$.

Fig. 3.

Example Mealy machine

Example 2

(Mealy Machine). An example Mealy machine is given in Fig. 3a. The LTS is given in Fig. 3b. The traces of the LTS are: $\{\{(in,a),(out,1)\}\{(in,a),(out,2)\}\ldots \}$.

Throughout this paper the following assumptions are made.

• All DFAs reject the empty language (because an LTS thereof is not defined).

• All DFAs are prefix-closed (Mealy machines are by definition prefix-closed).

• All DFAs and Mealy machines are minimal (automata constructed through active learning are always minimal; our definition of prefix-closed only holds on minimal automata).

• All SULs are deterministic.

2.1 LTL Model Checking

An LTL formula expresses a property that should hold over all infinite runs of a system. This means that if a system does not satisfy an LTL property, there generally exists a counterexample that is an infinite word which exhibits a lasso structure.

Definition 4

(LTL). Given an LTS $\mathcal {L} = \langle S, s_0, \delta , L, T, \lambda \rangle$, LTL formulae over $\mathcal {L}$ adhere to the following grammar:¹ $\phi \,{:}{:}= \mathtt {true}\mid \phi _1 \wedge \phi _2 \mid \lnot \phi \mid \mathop {\mathtt {X}}\phi \mid \phi _1\mathbin {\mathtt {U}}\phi _2 \mid t = l,$ where $t \in T$, and $l \in L$. Given an LTL formula $\phi$, all infinite words that satisfy $\phi$ are given by the set ${\text {Words}}(\phi ) = \{\sigma \in (2^{T \times L})^\omega \mid \sigma \models \phi \}$, where the satisfaction relation $\mathop {\models } \subseteq (T \times L)^\omega \times \mathop {\mathrm {LTL}}$ is defined inductively over $\phi$ by the following properties. Let $\sigma = A_0A_1A_2\ldots \in (2^{T \times L})^\omega$, and $\sigma [j\ldots ] = A_jA_{j+1}A_{j+2}\ldots$:

$$ \sigma \models {\left\{ \begin{array}{ll} \mathtt {true}, &{}\\ \phi _1 \wedge \phi _2 &{} \mathrm {iff~} \sigma \models \phi _1 \wedge \sigma \models \phi _2,\\ \lnot \phi &{} \mathrm {iff~} \sigma \not \models \phi ,\\ \mathop {\mathtt {X}}\phi &{} \mathrm {iff~} \sigma [1\ldots ] = A_1A_2A_3\ldots \models \phi ,\\ \phi _1\mathbin {\mathtt {U}}\phi _2 &{} \mathrm {iff~} \exists j \ge 0 :\sigma [j\ldots ] \models \phi _2 \wedge \forall 0 \le i < j :\sigma [i\ldots ] \models \phi _1,\\ t = l &{} \mathrm {iff~} (t, l) \in A_0\mathrm {.} \end{array}\right. } $$

Finally $\mathcal {L} \models \phi \iff {\text {Traces}}(\mathcal {L}) \subseteq {\text {Words}}(\phi )$.

Example 3

(LTL for DFAs). An example LTL formula that holds for the LTS $\mathcal {L}$ in Fig. 2b is: $\phi = \mathop {\mathtt {X}}(letter = b)$. All the words that satisfy the formula are in ${\text {Words}}(\phi ) = \{\{(letter,a)\}\{(letter,b)\}\ldots , \{(letter,b)\}\{(letter,b)\}\ldots \}$. Clearly, ${\text {Traces}}(\mathcal {L}) \subseteq {\text {Words}}(\phi )$, so $\mathcal {L} \models \phi$.

An example for Mealy machines is analogous. Finally we provide a formal definition of a lasso as follows.

Definition 5

(Lasso). Given an LTS $\mathcal {L}$, a trace $\sigma \in {\text {Traces}}(\mathcal {L})$ is a lasso if it can be split in a finite prefix p, such that $p \sqsubset \sigma$, and a finite loop q, such that $pq^\omega = \sigma$.

2.2 Active Learning

For our purposes, active learning is the process of learning a sequence of hypotheses $\mathcal {H}_1\mathcal {H}_2\ldots \mathcal {H}_F$, such that their behavior converges to some target automaton (DFA, or Mealy machine). The key components are illustrated in Fig. 4.

Fig. 4.

Active learning

Learner: an algorithm that can form hypotheses based on queries and counterexamples.

Equivalence oracle ($=$): an oracle that decides whether two languages are equal. The oracle decides between the language of the current hypothesis of the learner, and the language of the SUL. If the languages are not equivalent the oracle will provide a counterexample that distinguishes both languages. The language of the SUL is a set of finite traces.

Membership oracle ($\in$): an oracle that decides whether or not a word is a member of the language of the SUL.

SUL: In the case an active learning algorithm is applied to an actual system, a SUL interface is used that can step through a system, to answer membership queries. In the LearnLib, the SUL interface exposes the methods pre and post that can reset a system (i.e. put it back to the initial state), step that stimulates the system with one input symbol and returns the corresponding output, canFork and fork that may fork a SUL, i.e. provide some copy (that behaves identically to) a system. In active learning, this is used to pose queries in parallel. We will show it is useful for performing state equivalence checks in BBC too.

Definition 6

(query). Given a DFA $\mathcal {D} = \langle S, s_0, \varSigma , \delta , F\rangle$, and a SUL, a query is a function $q :\varSigma ^* \rightarrow \mathbb {B}$, where $\mathbb {B} = \{\bot , \top \}$ denotes the set of Booleans, indicating whether the input word is in the language of the SUL or not.

Example 4

(Active Learning). Given an alphabet $\varSigma = \{a,b\}$, and a DFA $\mathcal {D}$ to be learned such that ${\text {L}}(\mathcal {D}) = (ab)^*a?$, an active learning algorithm could first produce the hypothesis $\mathcal {D}_1$ in Fig. 5a (the trap state is explicit), where the language accepted is ${\text {L}}(\mathcal {D}_1) = \mathrm {a}^*$. At some point the equivalence oracle generates $aa \in \varSigma ^*$, and performs the membership query ${\text {q}}(aa) = \bot$. The equivalence oracle recognizes that $aa \in {\text {L}}(\mathcal {D}_1)$, and concludes it found a counterexample to $\mathcal {D}_1$. The learner refines $\mathcal {D}_1$, and produces the final hypothesis in Fig. 5b. Note that this example hides the complexity of actually refining the hypothesis. In the LearnLib refining a hypothesis is done with the method Learner.refineHypothesis() that accepts a query (counterexamples) and subsequently poses additional membership queries. More details on refining hypotheses are outside of the scope of this paper; they can be found in e.g. [1, 27].

Fig. 5.

Active learning

Finding a counterexample to the current hypothesis by means of an equivalence oracle is expensive in terms of time. In the worst-case the equivalence oracle has to try out all words of maximum length n in $\varSigma ^n$. Some smart equivalence oracles (e.g. ones using the partial W-method [8]) can find a counterexample quite quickly, if there is one. However, the number of membership queries to find the counterexample is still orders of magnitudes larger than the size of the hypothesis. E.g. any word of maximum length 2 that could serve as a counter example for the first hypothesis in Example 4 is in $\{\epsilon ,a,b,aa,ab,ba,bb\}$. When hypotheses grow larger, the set of possible counterexamples grows with an even larger degree.

2.3 Black-Box Checking

Compared to active learning, BBC (Fig. 6) adds a procedure that checks a set of properties $\{P_1, \ldots , P_n\}$ on each hypothesis produced by the Learner. The components added are as follows.

Fig. 6.

Black-box checking extension

Model checker ($\models$): an algorithm that checks whether an hypothesis satisfies a property. If the hypothesis does not satisfy the property it provides some counterexamples to the property. The language of the counterexamples is a subset of the language of the checked hypothesis.

Emptiness oracle ($\varnothing$): an oracle that decides whether the intersection of two languages is empty. The oracle decides between the language of the counterexamples given by the model checker, and the language of the SUL. If the intersection is not empty it will provide a counterexample, which is a word in the intersection and as such, a counterexample to the property checked by the model checker.

Inclusion oracle ($\subseteq$): an oracle that decides whether one language is included in another. The oracle decides whether the language of the counterexamples given by the model checker is included in the language of the SUL. If the language is not included, the oracle will provide a counterexample such that it is a word not in the language of the SUL, and thus a counterexample to the current hypothesis. One can view the combination of the model checker, emptiness oracle, and inclusion oracle as a black-box oracle.

In traditional active learning there are two kinds of sets of membership queries; learning queries (done by the learner) and equivalence queries (done by the equivalence oracle). With BBC there are two more types of queries; inclusion queries (done by the inclusion oracle), and emptiness queries (done by the emptiness oracle). The decision between performing inclusion queries, and emptiness queries depends on whether the property can be falsified with the current hypothesis. We generalize both to model checking queries. The key observation why adding properties to verify to the learning algorithm can be useful, follows from the observation that black-box checking queries are very cheap compared to equivalence queries. Given an alphabet $\varSigma$, a naive equivalence oracle has to perform arbitrary membership queries for words in $\varSigma ^*$, while the black-box oracle has to perform only membership queries for a subset of the language of the current hypothesis.

Given that black-box checking queries are much cheaper than equivalence queries a sketch of the black-box checking algorithm (Figs. 5 and 6) is as follows. Initially (①) the learner constructs an hypothesis using membership queries (②). This hypothesis is, together with a set of properties, given to the model checker (➋). If the model checker finds counterexamples for a property and the current hypothesis, the counterexamples are given to the emptiness oracle (➌). The emptiness oracle performs membership queries (➍) to try to find a counterexample from the model checker that is not spurious. If a real counterexample for a property is found, it is reported to the user (➎), and the property is not considered for future hypotheses. Otherwise, there could be a spurious one, and thus the set of counterexamples are given to the inclusion oracle. The inclusion oracle performs membership queries (➏) to find a counterexample for the current hypothesis (➐), the learner performs membership queries (②) to complete the next hypothesis. If the hypothesis is refined, the black-box oracle repeats steps (➋, ..., ➐) until the model checker can not find any new counterexample. In the latter case we enter the traditional active learning loop (Fig. 4): the equivalence oracle tries to find a counterexample for the current hypothesis (③) using membership queries (④). If a counterexample is found (⑤) the learner will construct the next hypothesis using membership queries (②) and the black-box oracle is put back to work. If the equivalence does not find a counterexample (④) the final hypothesis is reported to the user. Note that a black-box oracle can be implemented in two ways. The black-box oracle can first try to find a counterexample for every property before finding a refinement for the current hypothesis. The second implementation finds a counterexample for a single property and if such a counterexample does not exist, find a counterexample for the current hypothesis, before checking the next property. One may favor the first implementation if there is a high chance a property can be disproved with the current hypothesis, or refining the current hypothesis becomes quite expensive.

Example 5

(Black-Box Checking). Consider again the first hypothesis $\mathcal {D}$, produced by an active learning algorithm from Fig. 5a, that accepts the language $a^*$, and the LTL formula $\phi = \mathop {\mathtt {X}}(letter = b)$, from Example 3. An LTL model checker checks whether $\mathcal {D} \models \phi$. The model checker concludes $\mathcal {D}$ does not model $\phi$, and produces the lasso $a^\omega$ as a counterexample. The model checker unrolls the loop of the lasso an arbitrary number of 3 times, and provides the singleton language $L( CEs ) = \{aaa\}$ to the emptiness oracle ($\varnothing$). The emptiness oracle checks whether the intersection of the language of the SUL ($L( SUL )$), and $L( CEs )$ is empty. To this end, a membership query $q(aaa) = \bot$ is performed. This means indeed $L( SUL ) \cap L( CEs ) = \varnothing$ and the property can not be falsified. Next, $L( CEs )$ is given to the inclusion oracle ($\subseteq$) that checks $L( CEs ) \subseteq L( SUL )$. To this end the inclusion oracle performs the same membership query $q(aaa) = \bot$. The inclusion oracle concludes that $L( CEs ) \not \subseteq L( SUL )$, and thus provides $aaa \not \in L( SUL )$ as a counterexample to the learner. The essence of this example is that Fig. 5a, can be refined without performing any equivalence query. This example (like Example 4) hides to complexity of refining a hypothesis too. Refining a hypothesis in the LearnLib in the context of BBC can also be done with Learner.refineHypothesis().

3 Sound Black-Box Checking

The main contribution is (1.) the concept of sound BBC, that involves checking whether a SUL accepts a lasso-shaped infinite word, and (2.) an overview of the implementation in the LearnLib.

3.1 Validating Lassos with State Equivalence

Making the BBC procedure sound involves checking whether infinite lasso-shaped words given as counterexamples by the model checker are accepted by the SUL. Obviously in practice checking whether a SUL accepts an infinite word is impossible. However, this can be resolved if one considers what goes on inside a black-box system. We need to check if the SUL also exhibits a particular lasso through its state space when stimulated with a finite word (that also produces the same output as given by the model checker). This can be achieved by observing particular states the SUL evolves through when stimulated. Note that this view of a SUL is still quite a black-box view; we only record the states, we do not enforce the SUL to move to a particular state. We introduce a new notion of a query, namely an $\omega$-query, which in addition to the input word and output of the SUL also contains which states need to be recorded, and which states where actually visited. Compared with traditional BBC, sound BBC requires an emptiness oracle for lassos, denoted $\varnothing _\omega$, and a membership oracle for lassos, denoted $\in _\omega$.

Definition 7

$\mathbf {(\omega \text {-}query).}$ Given a DFA $\mathcal {D} = \langle S, s_0, \varSigma , \delta , F\rangle$, and another set of states Z from the SUL, an $\mathrm {\omega }$-query is a function $q_\omega :\varSigma ^* \times 2^\mathbb {N} \rightarrow \mathbb {B} \times {Z^*}$, where $\mathbb {B} = \{\bot ,\top \}$ denotes the set of Booleans, indicating whether the input word is in the language of the SUL or not, $2^\mathbb {N}$ the set of possible symbol indices after which a state has to be recorded, and $Z^*$ a sequence of possible recorded states. A definition for an $\omega$-query for Mealy machines is analogous.

Example 6

${ (}\omega \text {-}query{ ).}$ An example property that does not hold for the final DFA $\mathcal {D}$ in Fig. 5b is $\phi = (letter = b)$. Whenever a model checker determines whether $\mathcal {D} \models \phi$, it may give the lasso $l = a(ba)^\omega$ as a potential counterexample for $\phi$. The language $L( CEs ) = \{l\}$ is given to the lasso emptiness oracle $\varnothing _\omega$, which will unroll the loop of the lasso an arbitrary number of 3 times, and asks the omega membership oracle ($\in _\omega$) for $q_\omega (abababa,\{1,3,5\}) = (\top , s_1s_1s_1)$. Here it is clear the SUL cycles through state $s_1$, and thus accepts the infinite lasso-shaped word l.

In general, determining whether a state sequence is a closed loop can be done with Definition 8 (we record states at the beginning of each loop iteration). This definition allows us to check whether a SUL accepts a lasso in the most general way. E.g. to check whether a SUL accepts lasso $p(q_1q_2\ldots q_n)^\omega$ in a finite number of steps, we also check if the SUL accepts structurally different shaped (but equivalent) lassos, such as $pq_1(q_2\ldots q_nq_1)^\omega$, $p(q_1q_2\ldots q_nq_1q_2\ldots q_n)^\omega$ etc.

Definition 8

(closed-loop). Given an $\omega$-query ${\mathrm{q}_\omega }(pq^n,I) = \{\top ,s\}$, a state sequence $s = s_0s_1\ldots s_n$ is a closed-loop iff $n > 0$, and $\exists 0 \le i < j \le n :s_i = s_j$, and $I = \{\vert p \vert , \vert p \vert + \vert q \vert , \ldots , \vert p \vert + \vert q \vert \cdot n\}$.

3.2 Implementation in the LearnLib

We extend the interface of the LearnLib following Fig. 6, with a new type of query, and more oracles. The purpose of queries is to have a well defined way of exchanging information between the learner and the SUL. Oracles find counterexamples to claims, that may in practice, be undecidable to do.

SUL: The SUL interface is extended with methods boolean canRetrieveState() indicating whether states can actually be observed in the SUL, if this is not possible then sound BBC is not possible, Object getState() returning the current state of the SUL, boolean deepCopies() indicating whether the object returned by getState() is a deep copy.

ModelChecker: A ModelChecker may find a counterexample to a property and hypothesis. A counterexample is a subset of the language of the hypothesis. LTSmin [4, 15] is an available implementation of a ModelChecker for LTL in the LearnLib.

OmegaQuery: An OmegaQuery is a specialization of a Query. An answered Query contains information about whether a word is in the language of the SUL. An OmegaQuery specializes this behavior to infinite words.

OmegaMembershipOracle: An oracle that decides whether an infinite word is in the language of the SUL. To this end it poses OmegaQueries. There are several implementations available; one that simulates DFAs and Mealy machines, and one that wraps around a SUL.

EmptinessOracle: An EmptinessOracle generates words that are in a given automaton, and tests whether those words are also in the SUL. The current implementation, generates words in a breadth-first manner. A limit can be placed on the maximum number of words. An EmptinessOracle is used to check whether any word in the language given as a counterexample by the ModelChecker is present in the SUL. A specialization of an EmptinessOracle is a LassoEmptinessOracle that uses OmegaQueries to check whether infinite lasso-shaped words are not in the SUL.

InclusionOracle: Similar to the EmptinessOracle; it generates a limited number of words in a breadth-first manner, but checks whether words are in the language of the SUL. Note that both of these oracles may perform the same queries; this is a practical issue and is usually resolved by using a SULCache so that in case of a cache-hit the SUL is not stimulated. The InclusionOracle, and EmptinessOracle may have different strategies (BFS vs. DFS), and hence are not merged together into a single oracle. Separation of concerns (finding a counterexample to the current hypothesis, vs. finding a counterexample to a property), is also considered a good design principle.

BlackBoxProperty: a BlackBoxProperty is a property for a black-box system. It may be disproved, or used to find a counterexample to the current hypothesis. To these ends, it requires a ModelChecker, EmptinessOracle, InclusionOracle, and the property itself, such as an LTL formula. Note that LTL counterexamples for safety properties not necessarily exhibit a lasso structure. A future improvement could exploit this and hence the EmptinessOracle is given to BlackBoxProperty, and not to a BlackBoxOracle.

BlackBoxOracle: an oracle that disproves a set of BlackBoxProperties, or find a counterexample to the current hypothesis in the same set of BlackBoxProperties. Currently, there are two implementations available. One implementation iterates over the set of properties that are still unknown, and tries to disprove any of them before refining the current hypothesis. The other implementation iterates over the set of properties that are still unknown, and before disproving a next property it first tries to refine the current hypothesis with the current property. Both implementations at their core compute a least fixed-point of a set of properties they can not disprove. The latter implementation is used in the experiments later. In the case where an OmegaMembershipOracle wraps around a SUL there are two implementations available, based on the implementation of SUL.deepCopies(). If a SUL does not make a deep copy of the state of the SUL it could be the case that if SUL.step() is executed, a previously obtained state with SUL.getState() would also be modified, e.g. the assertion in the Java snippet

may not hold. To resolve this; if SUL.deepCopies() does not hold, then SUL.forkable() must hold. Two instances of a SUL are used, i.e. one regular instance, and a forked instance to compare two states. More specifically an OmegaMembershipOracle that wraps around a SUL that does not make deep copies of states in fact uses hash codes of states, and if the hash codes of two states are equal, the OmegaMembershipOracle will step one instance of the SUL through the access sequence of one state, and the forked instance of the SUL through the access sequence of the second state.

In case SUL.deepCopies() does hold, checking equality of two states is straightforward; one can simply invoke Object.equals() on the two states. Listing 1.1 shows how the running example can be implemented in the LearnLib. Note that we show how a membership oracle can answer queries by simulating a DFA. In Sect. 5 we show how one can learn a Mealy machine by implementing LearnLib’s SUL interface.

4 Related Work

Related work in context of this work can be found in three main areas. First, there is a tool that already does BBC, called LBTest [21]. Second, other than the LearnLib there is another active learning framework called libalf [5]. Third, aside from LTSmin there are other model checkers such as NuSMV [6], and SPIN [9]. Currently, LBTest is not Free and Open Source Software (FOSS). The LearnLib on the other hand is licensed under the Apache 2 license and thus freely available, even for commercial use. This argument is important because BBC is very successful when applied to industrial critical systems [17, 19]. Our new implementation in the LearnLib is also licensed under the Apache 2 license. Our reasoning for implementing BBC in the LearnLib, and not libalf is that LearnLib is actively maintained, while libalf is not.

We choose to select the LTSmin [15] model checker, because LTSmin, similar to the LearnLib has a liberal BSD license, and is still actively maintained. Compared to NuSMV, LTSmin has an explicit-state model checker, while NuSMV is a symbolic model checker using BDDs. In principle NuSMV would also suffice as a model checker in this work. We have designed our BBC approach in such a way that in the future integrating NuSMV with the LearnLib is easy. Another popular model checker is SPIN. The disadvantage of using the SPIN model checker is that the counterexamples it produces are state-based, while active learning algorithms require action-based counterexamples [26].

BBC is not new to the LearnLib, several years ago a similar study was performed, named dynamic testing [24]. Recently new active learning algorithms such as ADT [7], and TTT [13] have been added to the LearnLib, and their performance in the context of BBC is still unknown. Both ADT, and TTT may very well compare to the main learning algorithm Incremental Kripke Learning (IKL) [20] in LBTest, which is a so-called incremental learning algorithm. Incremental learning algorithms try to produce new hypotheses more quickly, in order to reduce the number of learning queries. Traditional active learning algorithms, such as L^* produce fewer hypotheses, where each new hypothesis requires more learning queries. The latter makes sense in the context of active learning, because this minimizes the number of equivalence queries necessary. In the context of active learning incremental learning algorithms may actually degrade performance; while they may perform well in the number of learning queries, they may require more equivalence queries to refine the hypotheses, resulting in longer run times, see [11, Sect. 5.5]. In BBC model checking queries can be used to refine hypotheses. Model checking queries are negligible compared to equivalence queries [20], making the ADT, and TTT algorithms excellent candidates for a BBC study.

5 Results

BBC in the presence of a good amount of LTL formulae can greatly reduce the number of learning queries, and equivalence queries required to disprove the LTL formulae compared to active learning. Note that, although BBC introduces additional model checking queries (performed by the equivalence oracle, or inclusion oracle), these model checking queries are dwarfed by the amount of equivalence queries (and even learning queries). We will thus refrain from reporting the amount model checking queries here (they can be found online², alongside reproduction instructions). What we will show is the following.

• How many learning queries, and equivalence queries it takes to disprove as many LTL formulae as possible in the traditional active learning setting. This means evaluating all LTL formulae after active learning algorithms produce the final hypothesis.

• The amount of learning queries, and equivalence queries in the BBC setting to disprove as many LTL formulae as possible.

Currently there are eight active learning algorithms implemented in the LearnLib for Mealy machines, which are as follows: ADT [7], DHC [22], Discrimination Tree [10], L^* [1], Kearns and Vazirani [16], Maler and Pnueli [18], Rivest and Schapire [25], and TTT [13]. To investigate the performance of these algorithms in a BBC setting we take problem instances, and LTL formulae from the 2017 RERS challenge. The Rigorous Examination of Reactive Systems (RERS) challenge³ is a yearly recurring verification challenge [14]. There are two main categories. In one category one has to solve properties for problems which are parallel in nature [29]. The other category involves sequential problems [28]. The RERS sequential problems are provided in Java (among others); the Java problem structure is given in Listing 1.2.

One can see that it is straightforward to actively learn a Mealy machine from a Problem instance. The alphabet is specified with the field String[] inputs. The state of a problem instance is determined by the valuations of some instance variables (a175, a52, a176, a166, a167, and a62). An input can be given to the calculateOutput method, which returns an output. The problem instance can be reset with the reset() method. A SUL implementation of a RERS Problem is easy: SUL.post() invokes Problem.reset(), SUL.step() invokes Problem.calculateOutput(). To achieve sound BBC, we must be able to retrieve the current state of a Problem instance. We choose not to make deep copies of a state of a Problem, hence SUL.deepCopies() does not hold. This means an OmegaMembershipOracle, must use Object.hashCode(), and Object.equals(). These methods can be easily generated with project Lombok⁴, by annotating a class with @EqualsAndHashCode. Lastly, the SUL can be forked by creating a new SUL instance, with a new Problem instance.

Fig. 7.

Experimental results (Color figure online)

We benchmark the LearnLib active learning algorithms with nine different RERS problems from the 2017 RERS challenge in a BBC setting. Each problem comes with 100 different LTL formulae, where typically approximately half of the formulae hold, and the other half does not hold. When active learning algorithms are able to learn the complete Mealy machine, this Mealy machine will be minimal. In case of the RERS problems the size of those Mealy machine range from tens of states to several thousands. Additionally this requires a few hundred to several thousand learning queries, and several thousand to millions equivalence queries. In Fig. 7 the top graph shows the legend. The second graph shows the number of learning queries for the smallest RERS problem, and the third graph the number of equivalence queries. The last graph shows the number of learning queries for the largest RERS problem. The x-axes show on a logarithmic scale the number of queries required to disprove a certain number of properties. The y-axes show the amount of properties that are disproved. A dashed line shows the relation between queries and falsified properties in an active learning setting, while a normal line shows the relation in a BBC setting. The further a line appears to the left; the better the algorithm. A dashed line is always purely vertical, because active learning algorithms do not disprove properties on-the-fly (i.e. the same number of queries is required to disprove all properties). In the case of BBC (uninterrupted lines) properties are disproved on-the-fly. This means fewer queries may be required to disprove the first properties. One can also see that in some cases an uninterrupted line, and dashed line of the same color are not equally high. This means that within the used timeout of 1 h active learning did not construct the complete hypothesis, and thus disproves fewer properties. Interestingly, almost all algorithms use fewer learning queries when used in the context of BBC. And even more interesting, some algorithms only use equivalence queries to disprove the last few properties. Obviously this is a great result. Figure 7 also shows that (as suspected) the incremental TTT, and ADT algorithms produce more equivalence queries compared to a classic algorithm like Rivest and Schapire. The performance of the eight algorithms is quite consistent throughout the larger problem instances. The ADT algorithm seems to perform really well, but the TTT is quite competitive too, this can be seen especially in the largest RERS problem. Also the last graph⁵ shows that TTT seems to need fewer learning queries, but ADT seems to be able to disprove more properties within 1 h. The great performance of ADT is particularly interesting since it is only developed recently. The ADT algorithm is developed to reduce the number of resets of the SUL. Now it seems to be the best choice for BBC too among the benchmarked algorithms and RERS problem instances.

6 Conclusion

We have presented a black-box checking implementation for the LearnLib. This includes a novel sound approach for liveness LTL properties, where we can check if a system-under-learning accepts an infinite lasso-shaped word. This contrasts the original proposal where an (hard to guess) upper-bound on the number of states of the system-under-learning is assumed. Our implementation is available under a liberal free and open source license, such that it can be put to practice quite easily. Our results (Fig. 7) show that recently added ADT, and TTT active learning algorithms perform the best in a black-box checking setting. In contrast to some other learning algorithms in the LearnLib, ADT, and TTT are incremental learning algorithms, meaning they construct more hypotheses while using less learning queries. In an active learning setting this may degrade performance, because more equivalence queries are required. In a black-box checking setting this appeared to be an advantage, because model checking queries replace expensive equivalence queries. Further work may show how ADT, and TTT compare with the IKL algorithm in LBTest. Software testers now have a free ease-of-use sound black-box checking implementation available for industrial use cases. Future work may show whether additional model checkers such as NuSMV provide comparable results, or if there exist different valuable strategies for finding (spurious) counterexamples to properties. In our case study we applied a perfect state equivalence function to the RERS problems, it would be interesting to apply our approach to cases where only part of the state can be observed, or when the SUL is hardware, instead of software.