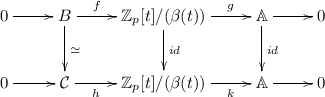Keywords

1 Introduction

RSA cryptosystem is one of the most famous public key scheme and is based on the existence of an one-way trapdoor function, which is easy to compute and difficult to invert without knowing some information. However, some attacks are possible when, e.g., the private key is small [23] or the public key is small [5]. Further attacks have been reviewed in [11] exploiting possible extra information (such as the knowledge of linear relations occurring between two plaintexts). Moreover, RSA leaks some vulnerabilities in broadcast applications [9]. Hence, during the years, RSA-like schemes (see, e.g., [2, 6, 13, 15, 17]) have been proposed in order to overcome some of the previous vulnerabilities.

In this paper, we present a novel RSA-like scheme that is more secure than RSA in some of the previous situations, like broadcast scenarios or considering the Wiener attack and others. Our scheme is based on a particular group equipped with a non-standard product that we have found working on a cubic field related to the cubic Pell equation (which is a generalization of the Pell equation, one of the most famous equations in number theory). This group appears to have many interesting properties and connections that should be further investigated. In fact, we would like to point out that in this work we give a first idea about the potentiality of this group in cryptographic applications, with the aim of providing an original point of view for exploiting number theory in cryptography and opening new studies. Certainly, our scheme should be more investigated under several perspectives, such as its efficiency. However, it appears very promising due to the definition itself and the many properties and connections to different topics.

The paper is structured as follows. In Sect. 2, we introduce a group with a non-standard product starting from a cubic field. Section 3 is devoted to the presentation of our cryptosystem and its discussion. Moreover, we see that powers with respect to our product can be evaluated by means of a generalization of the Rédei rational functions (Rédei rational functions are classical and very interesting functions in number theory). In Sect. 4 we present the conclusion.

2 A Product Related to the Cubic Pell Equation

The Pell equation \(x^2 - dy^2 = 1\), for d positive integer non-square and x, y unknowns, is one of the most famous Diophantine equations. Its generalization to the cubic case is given by the following equation:

$$\begin{aligned} x^3 + r y^3 + r^2 z^3 - 3 r x y z = 1 \end{aligned}$$
(1)

where r is a given non-cubic integer and x, y, z unknown numbers whose values we are seeking over the integers. This equation is considered the more natural generalization of the Pell equation, since it arises considering the unitary elements of a cubic field as well as the Pell equation can be introduced considering unitary elements of a quadratic field. Specifically, let \((\mathbb F, +, \cdot )\) be a field and \(t^3 - r\) an irreducible polynomial in \(\mathbb F[t]\). Let us consider the quotient field \(\mathbb A = \mathbb F[t] / (t^3 - r) = \{ x + y t + z t^2 : x, y, z \in \mathbb F \}\). The quotient field \(\mathbb A\) naturally induces a product between triples of elements of \(\mathbb F\) as follows:

$$(x_1, y_1, z_1) \bullet (x_2, y_2, z_2) := (x_1 x_2 + (y_2 z_1 + y_1 z_2) r, x_2 y_1 + x_1 y_2 + r z_1 z_2, y_1 y_2 + x_2 z_1 + x_1 z_2)$$

for \((x_1, y_1, z_1), (x_2, y_2, z_2) \in \mathbb F^3\) and the norm of an element is given by

$$N(x, y, z) := x^3 + r y^3 + r^2 z^3 - 3 r x y z,$$

see, e.g., [1], p. 98. Considering the unitary elements we get the cubic Pell curve

$$\mathcal C = \{ (x, y, z) \in \mathbb F^3 : x^3 + r y^3 + r^2 z^3 - 3 r x y z = 1 \}.$$

In [4], Christofferson widely studied the more general equation

$$x^3 + rb^2 y^3 + r^2b z^3 - 3 rb x y z = c,$$

whose the cubic Pell equation is a particular case for \(b = c = 1\) and r not a cube, providing also a complete bibliography up to 1956. It is worth noting that it is still lacking an algorithm for generating the solutions of such an equation (for any value of r) similar to that for the quadratic Pell case (see, e.g., [1]).

Proposition 1

\((\mathcal C, \bullet )\) is a commutative group with identity (1, 0, 0) and the inverse of an element (x, y, z) is

$$(\bar{x}, \bar{y}, \bar{z}) := (-x + r y z, r z^2 - x y, y^2 - x z).$$

Proof

The proof is straightforward and is left to the reader.

Remark 1

In \(\mathbb F^3\) an element (x, y, z) is invertible with respect to \(\bullet \) if and only if \(N(x, y, z) \not = 0\) and its inverse is

$$\left( \frac{\bar{x}}{N(x, y, z)}, \frac{\bar{y}}{N(x, y, z)}, \frac{\bar{z}}{N(x, y, z)} \right) .$$

Remark 2

When \(\mathbb F = \mathbb R\), the cubic Pell curve \(\mathcal C\) contains the solutions of the cubic Pell equation.

Remark 3

The Pell equation can be introduced considering the unitary elements of \(\mathbb R[t]/(t^2 - d)\), d positive integer non-square, where the product between elements is

$$(x_1, y_1) (x_2, y_2) = (x_1 x_2 + d y_1 y_2, x_1 y_2 + y_1 x_2).$$

Starting from \(\mathbb A\), we can introduce a new group with a non-standard product having interesting properties that can be also exploited for creating a novel RSA-like cryptosystem. Let us consider the quotient group \(B := \mathbb A^* / \mathbb F^*\). An element in B is the equivalence class of elements in \(\mathbb A^*\), i.e., \([m + n t + p t^2] \in B\) is the equivalence class of \(m + n t + p t^2 \in \mathbb A^*\) defined by

$$[m + n t + p t^2] := \{ \lambda m + \lambda n t + \lambda p t^2 : \lambda \in \mathbb F^* \}.$$

We can now rewrite the elements of B. Given \(m + n t + p t^2 \in \mathbb A^*\), if \(m \not = 0\) and \(n = p = 0\), then

$$[m + n t + p t^2] = [m] = [1_{\mathbb F^*}].$$

If \(n \not = 0\) and \(p = 0\), then

$$[m + n t + p t^2] = [m + n t] = [m + t]. $$

Finally, if \(p \not = 0\), then

$$[m + n t + p t^2] = [m + n t + t^2].$$

Thus, the group B is

$$B = \{[m + n t + t^2] : m,n \in \mathbb F\} \cup \{[m + t] : m \in \mathbb F\} \cup \{ [1_{\mathbb F^*}] \}.$$

Now, we can write the elements of B with a new notation. Fixed an element \(\alpha \not \in \mathbb F\), the elements of B can be written as couples of the kind (m, n), with \(m, n \in \mathbb F\), or \((m, \alpha )\), with \(m \in \mathbb F\), or \((\alpha , \alpha )\). Hence the group B is

$$B = (\mathbb F \times \mathbb F) \cup (\mathbb F \times \{\alpha \}) \cup (\{\alpha \} \times \{\alpha \}).$$

With this new notation and remembering that \(\mathbb A =\mathbb F[x]/(t^3 - r)\), we can obtain a commutative product \(\odot \) in B, where \((\alpha , \alpha )\) is the identity, having the following rules:

  • \((m, \alpha ) \odot (p, \alpha ) = (m p, m + p)\)

  • \((m, n) \odot (p, \alpha ) = {\left\{ \begin{array}{ll} \left( \frac{m p +r}{n + p}, \frac{m + n p}{n + p} \right) , \quad \text {if} \quad n + p \not = 0 \\ \left( \frac{m p +r}{m - n^2}, \alpha \right) , \quad \text {if} \quad n = -p, m - n^2 \not =0 \\ (\alpha , \alpha ), \quad \text {otherwise} \end{array}\right. }\)

  • \((m, n) \odot (p, q) \!=\! {\left\{ \begin{array}{ll} \left( \frac{m p + (n + q) r}{m + p + n q}, \frac{n p + m q + r}{m + p + n q} \right) , \,\,\text {if} \,\, m + p + n q \not = 0 \\ \left( \frac{m p + (n + q) r}{n p + m q + r}, \alpha \right) , \,\, \text {if} \,\, m + p + n q = 0, n p + m q + r \!\not =\! 0 \\ (\alpha , \alpha ), \,\, \text {otherwise} \end{array}\right. }\)

As a consequence, the following proposition holds.

Proposition 2

\((B, \odot )\) is a commutative group with identity \((\alpha , \alpha )\). The inverse of an element (m, n), with \(m - n^2 \not = 0\), is \(\left( \frac{n r - m^2}{m - n^2}, \frac{r - m n}{m - n^2} \right) \). The inverse of an element \((m^2, m)\) is \((-m, \alpha )\). Viceversa, the inverse of an element \((m, \alpha )\) is \((-m^2, m)\).

Remark 4

When \(\mathbb F = \mathbb R\), the element \(\alpha \) can be viewed as \(\infty \) and the points in B of the kind \((m, \infty )\), \((\infty , \infty )\) as points at infinity.

Furthermore, if we consider \(\mathbb {F}= \mathbb {Z}_{p}\) where p is prime, then we have a field, so \(B=\mathbb {A}^*/ \mathbb {F}^*=\mathbb {Z}_{p}^*[t]/\mathbb {Z}_{p}^*\) is a field too. It is easy to notice that the point \(0=[0:0:0] \notin B\) and we can consider the equivalence relation \(\sim \) induced by the action of \(\mathbb {Z}_{p}^*\) on the set \(\mathbb {Z}_{p}^*[t]\) such that \(b_{1}\sim b_{2} \iff \exists \lambda \in \mathbb {Z}_{p}^*: b_{1}= \lambda b_{2}\) and now it is clear that B is a projective space.

Remark 5

If \(\mathbb {F}\) is not a finite field, let us denote B as \(B_{0}\), \(B_{1}= B_{0}^{*} / \mathbb {F^*}\), \(B_{n}= B_{n-1}^{*} / \mathbb {F^*}\) and so \(\forall n\) , then we have \(B_{n+1} \subset B_{n}\) and so we have a directed system, in fact \(\forall n\) \(B_{n} \subset B_{0}\); moreover let us consider the family of maps \(\{ \phi _{n, n+1} \}_{n}\) with \(\phi _{n, n+1}: B_{n+1} \hookrightarrow B_{n}\), where \(\phi _{n, n}= id_{B_{n}}\), such that \(\phi _{n, n+1} \circ \phi _{n+1, m} = \phi _{n, m}\) and \(\phi _{n, m}: B_{m} \hookrightarrow B_{n}\). At this point it is clear that \(\left( \{B_{n}\}, {\phi _{n, n+1}} \right) \) is a projective system, hence we naturally consider the inverse limit \( \varprojlim B_{i}\), that is equipped with a family of projection maps \(\{p_{n}\}_{n}\) such that the inverse limit has the following universal property, showed by the commutative diagram

figure a

with \(\pi _{n} \circ p_{n}^{-1}=id_{B_{n}}\)

Remark 6

We consider \(\mathbb {F}\) as a topological field, so that \(\mathcal {C}\) has the topology induced as a subset of \(\mathbb {F}^3\). The cubic Pell curve

$$\mathcal C = \{ (x, y, z) \in \mathbb F^3 : N(x, y, z):=x^3 + r y^3 + r^2 z^3 - 3 r x y z = 1 \},$$

endowed with the non standard product we have previously defined, can be studied as a topological group. Indeed the group operation

$$\mathcal {C}\times \mathcal {C} \longrightarrow \mathcal {C} ,\left( (x_{1},y_{1},z_{1}), (x_{2},y_{2},z_{2})\right) \longmapsto (x_{1}x_{2}, y_{1}y_{2},z_{1}z_{2})$$

is a continuous mapping and the inversion map \(\mathcal {C} \longrightarrow \mathcal {C}, (x,y,z) \longmapsto (\bar{x}, \bar{y}, \bar{z})\) is likewise continuous, according to the fact that \(N(x, y, z)=1\). If \(\mathbb {F}=\mathbb {R}\), then we can consider \(\mathcal {C}\) equipped with the Euclidean topology, otherwise if \(\mathbb {F}=\mathbb {Z}_{p}\), then the discrete topology is the most natural topology we can put on it, but maybe it is not the only one interesting, even if the only one that is \(T_{0}\).

3 A Public-Key Cryptosystem

3.1 The Scheme

When \(\mathbb F = \mathbb Z_p\) (and fixing \(\alpha = \infty \)), the situation is interesting for cryptographic applications. Indeed, in this case we have \(\mathbb A = GF(p^3)\), i.e., \(\mathbb A\) is the Galois field of order \(p^3\). Thus, by construction, B is a cyclic group of order \(\frac{p^3 - 1}{p - 1} = p^2 + p + 1\), with respect to a well-defined product, and an analogous of the little Fermat’s theorem holds:

$$\begin{aligned} (m,n)^{\odot p^2 + p + 1} \equiv (\infty , \infty ) \pmod p, \end{aligned}$$
(2)

where the power is evaluated by using the product \(\odot \), for any \(m \in \mathbb Z_p\) and \(n \in \mathbb Z_p \cup \{\infty \}\).

Remark 7

It follows from (2) that

$$(m,n)^{\odot (p^2 + p + 1)(q^2 + q + 1)} \equiv (\infty , \infty ) \pmod N,$$

where \(N = pq\), for p and q prime numbers. This does not mean that, when B is constructed over \(\mathbb Z_N\), B is a group. In this case we only have an analogous of the Euler’s theorem. In other words when we construct B over \(\mathbb Z_p\) (p prime) our product \(\odot \) works like the standard product in \(\mathbb Z_p\). Moreover, when we consider B over \(\mathbb Z_N\), our product \(\odot \) works like the standard product in \(\mathbb Z_N\).

As a consequence we can construct a public-key cryptosystem similar to the RSA scheme, but using our product \(\odot \).

The following steps describe the keys generation:

  • choose two prime numbers p, q

  • compute \(N = p q\)

  • choose an integer e such that \((e, (p^2 + p + 1) (q^2 + q + 1)) = 1\)

  • choose a non-cube integer r in \(\mathbb Z_p\), \(\mathbb Z_q\) and \(\mathbb Z_N\)

  • compute d such that \(ed \equiv 1 \pmod {(p^2 + p + 1) (q^2 + q + 1)}.\)

The public encryption key is (N, e, r) and the secret decryption key is (p, q, d). Given a pair of messages \(m_1\) and \(m_2\) in \(\mathbb Z_N\), they can be encrypted by

$$(c_1, c_2) \equiv (m_1, m_2)^{\odot e} \pmod N.$$

The receiver can decrypt the messages evaluating

$$(c_1, c_2)^{\odot d} \pmod N.$$

3.2 Some Remarks

In the following, we discuss some peculiarities of our cryptosystem.

First, our scheme is more secure than RSA in broadcast scenarios, i.e., when the plaintext is encrypted for different receivers using the same public exponent and it is possible to recover the plaintext message by solving a set of congruences of polynomials [9]. However, this attack can not be applied when the trapdoor function is not a simple monomial power as in RSA [12]. Thus, this kind of attacks fails in our scheme.

Another classical attack against the RSA scheme is the Wiener attack [23]. Said e and d the public and private exponents, respectively, in the RSA scheme the following relation holds

$$ed - k\varphi (N) = 1$$

for a certain integer k, where \(\varphi \) is the Euler totient function and \(N=pq\) (for p and q prime numbers) is the modulo with respect to messages are encrypted and decrypted. For large values of N the following bounds hold:

$$\begin{aligned} N - 3 \sqrt{N}< \varphi (N) < N \end{aligned}$$
(3)

The Wiener attack exploits properties of continued fractions. Indeed, thanks to the previous inequalities, we have

$$|\frac{k}{d} - \frac{e}{N} |< \frac{1}{2d^2},$$

i.e., by Legendre theorem, d is the denominator of a convergent of the continued fraction expansion of \(\frac{e}{N}\) and consequently the private exponent d can be recovered. In our case, the role of \(\varphi (N)\) is substituted by \((p^2 + p + 1)(q^2 + q + 1)\). This leads to a less efficient evaluation of the decryption exponent, however in this situation inequalities similar to (3) can not be found, making the Wiener attack not usable against our scheme. Moreover, for the same reason, further attacks exploiting continued fractions, reviewed in [7], fail in our case.

Remark 8

The private exponent d can be effectively recovered by using the Wiener attack if it is less than \(N^{1/4}\), where N is the RSA-modulo. A typical size of the RSA-modulo is 1024–bit. Thus, in this case, it is required that the size of d must be at least 256 bits long in order to avoid the Wiener attack, but this is unfortunate for low-power devices [3]. Using the proposed scheme, the dimension of the private exponent could be less than 256 bits without being affected by the Wiener attack.

Finally, our scheme appears to be robust against another class of attack presented in [20] (see also [11], Sect. 3.1, for a review of the attack). We recall this attack here for the reader. It is supposed that it is known a linear relation between two plaintexts \(M_1\) and \(M_2\):

$$M_2 = M_1 + \varDelta $$

where \(\varDelta \) is known and \(C_1 \equiv M_1^e \pmod N\), \(C_2 \equiv M_2^e \pmod N\). In this case, the attack can retrieve the plaintext messages evaluating the greatest common divisor of the polynomials

$$x^e - C_1 \pmod N, \quad (x + \varDelta )^e - C_2 \pmod N.$$

In our case, the situation is more complicated, since the exponentiation yields rational functions and not polynomials. Moreover, in our case, we deal with bivariate polynomials.

3.3 Evaluation of the Powers with Respect to \(\odot \) by Means of Generalized Rédei Functions

The Rédei rational functions were introduced by Rédei in [21] from the development of \((z + \sqrt{d})^n\), where z is an integer and d a non-square positive integer. We can define the Rédei polynomials \(N_n(d,z)\) and \(D_n(d,z)\) as follows:

$$(z + \sqrt{d})^n = N_n(d,z) + D_n(d,z) \sqrt{d}, \quad \forall n \ge 0.$$

The Rédei polynomials have the following closed form:

$$N_n(d,z) = \sum _{k = 0}^{[n/2]} \left( {\begin{array}{c}n\\ 2k\end{array}}\right) d^k z^{n - 2k}, \quad D_n(d,z) = \sum _{k = 0}^{[n/2]} \left( {\begin{array}{c}n\\ 2k + 1\end{array}}\right) d^k z^{n - 2k - 1}.$$

The Rédei rational functions are defined by

$$Q_n(d,z) = \frac{N_n(d,z)}{D_n(d,z)}, \quad \forall n \ge 1$$

and can be also evaluated by means of powers of matrices. Indeed, we have

$$\begin{pmatrix} z &{} d \\ 1 &{} z \end{pmatrix}^n = \begin{pmatrix} N_n &{} dD_n \\ D_n &{} N_n \end{pmatrix},$$

see [8].

They are classical and interesting functions in number theory since, for instance, they provide approximations of square roots, are permutations in finite fields and Rédei polynomials belong to the class of the Dickson polynomials [14]. Moreover, they have been applied in several contexts, like the creation of a cryptographic system based on the Dickson scheme [18] and the generation of pseudorandom sequences [22].

Here, we see that the powers of elements in B can be evaluated by means of a certain generalization to the cubic case of the Rédei functions.

Starting from the development of \((z_1 + z_2 \root 3 \of {r} + \root 3 \of {r^2})^n\), with \(z_1, z_2, r \in \mathbb F\) and r non-cube, we can introduce three sequences of polynomials \(A_n(r, z_1, z_2)\), \(B_n(r, z_1, z_2)\), \(C_n(r, z_1, z_2)\) that generalize the Rédei polynomials. We define

$$(z_1 + z_2 \root 3 \of {r} + \root 3 \of {r^2})^n = A_n(r, z_1, z_2) + B_n(r, z_1, z_2) \root 3 \of {r} + C_n(r, z_1, z_2) \root 3 \of {r^2}, \quad \forall n \ge 0.$$

Hence, the rational functions \(\frac{A_n}{C_n}\) and \(\frac{B_n}{C_n}\), for \(n \ge 1\) can be considered a generalization to the cubic case of the Rédei rational functions.

Remark 9

Let us observe that for introducing the generalized Rédei functions, it is not necessary to work in a field. Indeed, the previous definition works even in the case that \(z_1, z_2, r\) belongs to a commutative ring with identity. Indeed, the original Rédei polynomials were introduced in \(\mathbb Z\). We have chosen to define the generalized Rédei polynomials in the field \(\mathbb F\) only for being consistent with the notation used for introducing B as a group and not introducing new notation.

In the following proposition, we see that also the generalized Rédei polynomials can be evaluated by means of a matricial approach.

Proposition 3

Let \(A_n(r, z_1, z_2), B_n(r, z_1, z_2), C_n(r, z_1, z_2)\) be the generalized Rédei polynomials, then

$$\begin{pmatrix} z_1 &{} r &{} rz_2 \\ z_2 &{} z_1 &{} r \\ 1 &{} z_2 &{} z_1 \end{pmatrix}^n = \begin{pmatrix} A_n &{} rC_n &{} rB_n \\ B_n &{} A_n &{} rC_n \\ C_n &{} B_n &{} A_n \end{pmatrix}, \quad \forall n \ge 0$$

Proof

In the following, for the seek of simplicity we omit the dependence on \(r, z_1, z_2\). We prove the thesis by induction on n.

Basis: for \(n=0\) we have \(A_0 = 1, B_0 = 0, C_0 = 0\) and \((z_1 + z_2 \root 3 \of {r} + \root 3 \of {r^2})^0=1\), i.e.,

$$\begin{pmatrix} z_1 &{} r &{} rz_2 \\ z_2 &{} z_1 &{} r \\ 1 &{} z_2 &{} z_1 \end{pmatrix}^0 = \begin{pmatrix} A_0 &{} 0 &{} 0 \\ 0 &{} A_0 &{} 0 \\ 0 &{} 0 &{} A_0 \end{pmatrix}.$$

Similarly, it is straightforward to check the cases \(n = 1, 2\).

Inductive step: we assume the statement holds for some natural number \(n - 1\) and we prove that holds for n too. We have

$$\begin{pmatrix} z_1 &{} r &{} rz_2 \\ z_2 &{} z_1 &{} r \\ 1 &{} z_2 &{} z_1 \end{pmatrix}^n =\begin{pmatrix} z_1 &{} r &{} rz_2 \\ z_2 &{} z_1 &{} r \\ 1 &{} z_2 &{} z_1 \end{pmatrix}^{n-1} \begin{pmatrix} z_1 &{} r &{} rz_2 \\ z_2 &{} z_1 &{} r \\ 1 &{} z_2 &{} z_1 \end{pmatrix}$$
$$= \begin{pmatrix} A_{n-1} &{} rC_{n-1} &{} rB_{n-1} \\ B_{n-1} &{} A_{n-1} &{} rC_{n-1} \\ C_{n-1} &{} B_{n-1} &{} A_{n-1} \end{pmatrix} \begin{pmatrix} z_1 &{} r &{} rz_2 \\ z_2 &{} z_1 &{} r \\ 1 &{} z_2 &{} z_1 \end{pmatrix}. $$

Thus, we have to show that

$${\left\{ \begin{array}{ll} A_n = z_1A_{n-1} + rz_2C_{n-1} + rB_{n-1} \\ B_n = z_1B_{n-1} + z_2A_{n-1} + rC_{n-1} \\ C_n = z_1C_{n-1} + z_2B_{n-1} + A_{n-1} \end{array}\right. }.$$

By definition of generalized Rédei polynomials, we have

$$(z_1 + z_2 \root 3 \of {r} + \root 3 \of {r^2})^{n} = A_n + B_n \root 3 \of {r} + C_n \root 3 \of {r^2}.$$

On the other hand

$$(z_1 + z_2 \root 3 \of {r} + \root 3 \of {r^2})^{n} = (z_1 + z_2 \root 3 \of {r} + \root 3 \of {r^2})^{n-1}(z_1 + z_2 \root 3 \of {r} + \root 3 \of {r^2})$$
$$= (A_{n-1} + B_{n-1} \root 3 \of {r} + C_{n-1} \root 3 \of {r^2})(z_1 + z_2 \root 3 \of {r} + \root 3 \of {r^2})$$

from which, expanding the last product, the thesis easily follows.

In the next proposition, we see that these functions can be used in order to evaluate powers of elements \((z_1, z_2)\) in B.

Proposition 4

Given \((z_1, z_2) \!\in \! B\) and let \(A_n(r, z_1, z_2), B_n(r, z_1, z_2), C_n(r, z_1, z_2)\) be the generalized Rédei polynomials, we have

$$(z_1, z_2)^{\odot n} = {\left\{ \begin{array}{ll} \left( \frac{A_n}{C_n}, \frac{B_n}{C_n} \right) , \quad \text {if} \quad C_n \not = 0 \\ \left( \frac{A_n}{B_n}, \alpha \right) , \quad \text {if} \quad B_n \not = 0, \ C_n = 0 \\ (\alpha , \alpha ), \quad \text {if}\quad B_n = C_n = 0 \end{array}\right. },$$

for \(n \ge 1\).

Proof

By the previous proposition, we have

$$\begin{pmatrix} A_n &{} rC_n &{} rB_n \\ B_n &{} A_n &{} rC_n \\ C_n &{} B_n &{} A_n \end{pmatrix} \begin{pmatrix} A_m &{} rC_m &{} rB_m \\ B_m &{} A_m &{} rC_m \\ C_m &{} B_m &{} A_m \end{pmatrix} = \begin{pmatrix} A_{m+n} &{} rC_{m+n} &{} rB_{m+n} \\ B_{m+n} &{} A_{m+n} &{} rC_{m+n} \\ C_{m+n} &{} B_{m+n} &{} A_{m+n} \end{pmatrix},$$

from which we get

$${\left\{ \begin{array}{ll} A_{m+n} = A_m A_n + r B_m C_n + r B_n C_m \\ B_{m+n} = A_m B_n + A_n B_m + r C_m C_n \\ C_{m+n} = A_m B_n + B_m B_n + A_n C_m \end{array}\right. }.$$

Thus, if \(C_m, C_n \not =0\) and \(C_{m+n} = A_m B_n + B_m B_n + A_n C_m \not = 0\), i.e., \(\frac{A_n}{C_n} + \frac{A_m}{C_m} + \frac{B_mB_n}{C_nC_m} \not =0\) (that is the condition \(m+p+nq\not =0\) for the product \((m,n)\odot (p,q)\)), we have

$${\left\{ \begin{array}{ll} \frac{A_{m+n}}{C_{m+n}} = \frac{\frac{A_{n}}{C_{n}} \frac{A_{m}}{C_{m}} + r \frac{B_{m}}{C_{m}} + r \frac{B_{n}}{C_{n}}}{\frac{A_{m}}{C_{m}} + \frac{B_{n}}{C_{n}} \frac{B_{m}}{C_{m}} + \frac{A_{n}}{C_{n}}} \\ \frac{B_{m+n}}{C_{m+n}} = \frac{\frac{B_{n}}{C_{n}} \frac{A_{m}}{C_{m}} + \frac{B_{m}}{C_{m}} \frac{A_n}{C_n} + r}{\frac{A_{m}}{C_{m}} + \frac{B_{n}}{C_{n}} \frac{B_{m}}{C_{m}} + \frac{A_{n}}{C_{n}}} \end{array}\right. }$$

and this is equivalent to say that

$$\left( \frac{A_{m+n}}{C_{m+n}}, \frac{B_{m+n}}{C_{m+n}} \right) = \left( \frac{A_{n}}{C_{n}}, \frac{B_{n}}{C_{n}} \right) \odot \left( \frac{A_{m}}{C_{m}}, \frac{B_{m}}{C_{m}} \right) .$$

In the case that \(B_{m+n}\not =0\) \(C_{m+n} = A_m B_n + B_m B_n + A_n C_m = 0\), i.e., \(\frac{A_n}{C_n} + \frac{A_m}{C_m} + \frac{B_mB_n}{C_nC_m} =0\) (that is the condition \(m+p+nq=0\) for the product \((m,n)\odot (p,q)\)), then we have

$$\left( \frac{A_{m+n}}{B_{m+n}}, \alpha \right) = \left( \frac{A_{m}}{C_{m}}, \frac{B_{m}}{C_{m}} \right) \odot \left( \frac{A_{n}}{C_{n}}, \frac{B_{n}}{C_{n}} \right) .$$

Now, considering that \(\left( \frac{A_{1}}{C_{1}}, \frac{B_{1}}{C_{1}} \right) = (z_1, z_2)\), the thesis follows.

When we consider elements of the kind \((z, \alpha )\) in B, the previous generalized Rédei functions can not be applied for evaluating the powers. However, in the following proposition, we see how these powers can be evaluated in a similar way.

Proposition 5

Given \((z_1, \alpha ) \in B\) and let \(\bar{A}_n(r, z_1)\), \(\bar{B}_n(r, z_1)\), \(\bar{C}_n(r, z_1)\) be polynomials defined by

$$(z_1 + \root 3 \of {r})^n = \bar{A}_n(r, z_1) + \bar{A}_n(r, z_1) \root 3 \of {r} + \bar{A}_n(r, z_1) \root 3 \of {r^2}, \quad \forall n \ge 1.$$

We have that

  1. 1.

    \(\begin{pmatrix} z_1 &{} 0 &{} r \\ 1 &{} z_1 &{} 0 \\ 0 &{} 1 &{} z_1 \end{pmatrix}^n = \begin{pmatrix} \bar{A}_n &{} \bar{C}_n &{} r \bar{B}_n \\ \bar{B}_n &{} \bar{A}_n &{} \bar{C}_n \\ \bar{C}_n &{} \bar{B}_n &{} \bar{A}_n \end{pmatrix}, \quad \forall n \ge 0\)

  2. 2.

    \((z_1, \alpha )^{\odot n} = {\left\{ \begin{array}{ll} \left( \frac{\bar{A}_n}{\bar{C}_n}, \frac{\bar{B}_n}{\bar{C}_n} \right) , \quad \text {if} \quad \bar{C}_n \not = 0 \\ \left( \frac{\bar{A}_n}{\bar{B}_n}, \alpha \right) , \quad \text {if} \quad \bar{B}_n \not = 0, \ \bar{C}_n = 0 \\ (\alpha , \alpha ), \quad \text {if} \quad \bar{B}_n = \bar{C}_n = 0 \end{array}\right. }\)

Proof

The proofs are similar to proofs of Propositions 3 and 4 and are left to the reader.

Remark 10

As we have already pointed out, the generalized Rédei functions can be used for evaluating powers in B even in the case that we are working in a ring and not in the field \(\mathbb F\). Let us note that in this case B is not a group but the product is well-defined and the powers can be evaluated by Propositions 4 and 5. In this case conditions “\(\not =0\)” means “is invertible”.

4 Conclusion

In this paper, we have proposed a novel RSA-like scheme that is more secure than RSA in broadcast applications and is not affected by the Wiener attack. Moreover, it appears more robust than RSA with respect to other attacks that exploit the knowledge of a linear relation occurring between two plaintexts. This scheme has been developed by using a new group equipped with a non-standard product whose powers can be evaluated by means of some generalized Rédei functions. This group and its product have shown many interesting properties and relations highlighting that they are worth investigating due to their perspectives. Certainly, in this work we have only given an idea of their use in cryptographic applications, but the present scheme should be further discussed and improved. In the following, we advise some further studies:

  • In [16], the author exhibits an algorithm of complexity \(O(log_2(n))\) with respect to addition, subtraction and multiplication to evaluate Rédei rational functions over a ring. It will be interesting to study a similar algorithm in order to obtain an efficient method for evaluating the generalized Rédei functions introduced in this paper, so that the encryption cost of our algorithm is equal to the encryption cost of the RSA scheme or less considering that in our scheme we encrypt two messages at once.

  • We conjecture that \((B, \odot )\) and \((\mathcal {C}, \bullet )\) are isomorphic. Proving this fact and finding the isomorphism lead to important consequences. First, the isomorphism could be exploited in order to improve our scheme following the ideas of RSA-like schemes based on isomorphism between two groups (see, e.g., [12, 19]). Moreover, in this way a method for generating the solutions of the cubic Pell equation could be found (note that such a method is still missing [1]). As a special case, we will also state that the number of solutions of the cubic Pell equation in \(\mathbb Z_p\) is \(p^2 + p + 1\) (as numerical simulations appear to confirm). One could try to show that \(B \simeq \mathcal {C}\) using the Short Five Lemma [10]: if in the following diagram we have two exact sequences, that is \(\ker g = \text {Im}f\) and \(\ker k= \text {Im}h\), whew both k and g are surjections and both h and f are injections, under the hypothesis that two of the down arrows are isomorphism, then the last down arrow is an isomorphism too.

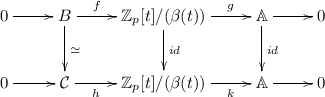
    figure b

    So our goal is to find an appropriate \((\beta (t))\) and the maps previously introduced, with particular attention to the degree of the polynomial \((\beta (t))\). For now, we were only able to find the following morphism

    $$\epsilon : {\left\{ \begin{array}{ll} B \rightarrow \mathcal {C} \\ (m, n) \mapsto \left( \frac{m^3 + 6 m n r + n^3 r + r^2}{m^3 + r n^3 + r^2 - 3 r m n}, \frac{3 (m^2 n + m r + n^2 r)}{m^3 + r n^3 + r^2 - 3 r m n}, \frac{3 (m^2 + m n^2 + nr)}{m^3 + r n^3 + r^2 - 3 r m n}\right) \\ (m, \alpha ) \mapsto \left( 1, \frac{3m^2}{m^3+r}, \frac{3m}{m^3+r}\right) \\ (\alpha , \alpha ) \mapsto (1,0,0) \end{array}\right. }$$

    Moreover, let us recall that \(\mathbb Z_p\) has non-cubic residues only when \(p \equiv 1 \pmod 3\), and consequently 3 divides \(p^2 + p + 1\). Thus, when we consider \(\mathbb F = \mathbb Z_p\), we are able to construct the group B only for the prime numbers p such that \(p^2 + p + 1\) is divisible by 3. Then we have observed that we have \(|Im \epsilon |= \frac{|B |}{3}\).

  • The scheme should be studied from a computational point of view, in order to give more precise and effective results about its efficiency and security. In this paper, we have only investigated some improvements regarding the security from a theoretical point of view.