Abstract
This chapter deals with the problem of modelling the behaviour of massive concrete structures. In the last decades, the developments in the field of computational mechanics were significant, so nowadays several numerical techniques are available to this goal, depending on the scale level considered but also on which phenomena/processes are taken into account. In this chapter, we limit the description to approaches/models that can be implemented using the Finite Element Method, which is still the worldwide most used numerical technique. This chapter presents two distinct groups of models. The first group covers deterministic models starting from the simplest ones, which consider simply the thermo-chemo-mechanical behaviour of the material, to more sophisticated approaches which consider also the fluid phases; i.e., they consider concrete as a multiphase porous material. In this first part, a specific section is dedicated to mechanical behaviour modelling considering damage of the material, plasticity, etc. The second group of the models takes into consideration stochastic nature of cracking. These models are formulated specifically for giving a detailed information about cracks spacing and opening in concrete structures in service life conditions.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
- Massive Concrete Structures
- Multiphase Porous Media
- Steel Fibre-reinforced Concrete (SFRC)
- Autogenous Shrinkage
- Hydration Degree
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
7.1 Introduction
Computational analysis has become crucial in almost all disciplines, together with theory and experimental analysis. Every model is a simplification of reality intended to promote its understanding. A model uses a simplified physical formulation, mathematical framework and numerical tools in order to find the solution. Successful models pass the validation stage where modelling results correspond sufficiently well to reality.
Computational approaches are also playing an increasing role in industry. In fact, validated models can save significant amount of experiments, time, and resources, can mitigate potential problems and even find optimal solution. For instance, in the case of massive concrete structures, numerical modelling often follows objectives such as determination of temperature field during hardening, effect of concrete composition, estimation of cracking potential with consequences to durability, economical benefits.
In civil and environmental engineering, most of the processes/phenomena are mathematically described by a set of partial differential equations (PDEs), usually nonlinear in material laws. For example, a set of PDEs describes heat and mass transfer, mechanical effects, hydrodynamic effects, electric and magnetic fields, and all their interactions (multiphysics problems). There exists a significant amount of numerical techniques for solving such a kind of complex mathematical systems, some of them limited to the research world. In the context of this state-of-the-art report, we consider the most commonly used numerical method—the Finite Element Method. Often, obtaining a prediction from a theory requires massive computing, so it is necessary to develop and implement special algorithms for parallel computation to be able to exploit the full potential of the technology and maintain scientific and productive competitiveness. Virtually, all manufacturers of high-end chips in the last few years have adopted a multiprocessor organisation, typically with 4–8 processors per chip (but solutions with up to 18 cores are available). This number is expected to grow to 100–1000 in the next decade. Hence, high-parallelism and low-communication algorithms are no longer the prerogative of supercomputing and are instead becoming pervasive, but a description of such kind of solvers and tools is beyond the scope of this chapter.
Hardening concrete is undoubtedly one of the most difficult structural materials for modelling. The difficulties arise from a complex concrete microstructure, which is additionally subjected to transformations as a result of cement hydration. Initially, it is a mixture of liquids and solids of varying diameters and shapes. Such a multiphase medium is characterised by strong viscous and plastic properties. With progressing cement, hydration concrete becomes a solid, with elastic, viscous and plastic characteristics, where the mutual proportions of these features depend on the progress of the concrete hardening process. Moreover, in addition to the chemical reactions resulting in the hydration of the material, several physical phenomena take place (e.g. phase changes) and numerous fields are interacting with each other (thermal, hygral, mechanical, etc.) making the problem a typical multifield–multiphysics problem (Gawin et al. 2006a).
Concrete represents a multiscale material which spans characteristic lengths from about 10−10 to 10−2 m. The finest atomistic scale of C-S-H determines several macroscopic properties such as elasticity, strength, creep, shrinkage, which manifest on higher scales (Bernard et al. 2003; Pichler et al. 2011). Hydration takes place up to micrometre scale of cement paste, and large aggregates have impact on fracture properties.
Recent advances in multiscale models demonstrated models’ capabilities to capture those effects and to set up microstructure-property link. Indeed, nowadays several multiscale technics, of mathematical or numerical nature, are available for considering the material behaviour at different scales: the formulation of constitutive relationships starting from the microcomponents of the material up to the macroscale is an example of the application of multiscale strategy (see Chap. 3 for thermal properties).
Taking into account only concrete scale and its changes during hardening, two possibilities appear to model its early-age behaviour:
-
to use pure thermo-chemical, and possibly mechanical, models, or
-
to formulate a multifield model.
In the first class of models, concrete is treated as a continuum at macroscopic level and only the solid phase of the material is considered, taking into account the thermal field and the chemical reactions (e.g. the hydration process), which affect the mechanical performance of the material for a large extent.
The second group of models is based on the multifield concept; i.e., they consider one or more phases: not only the solid phase, which is typically the concrete skeleton, but also the liquid and gaseous components filling the pores of the material. Depending on the number of the phases considered and on the scale level chosen for the initial formulation of the mathematical model, the multifield models can be subdivided into two main groups corresponding to two different approaches.
The first approach is related to phenomenological models, where concrete is treated as a continuous medium. A detailed analysis of physical processes related to phase transitions and chemical processes occurring in hardening concrete is neglected in these models, and a macroscopic description of the thermal–moisture–mechanical phenomena is used as a multiphysical description.
The second approach is related to multiphase models based on Multiphase Porous Media Mechanics (MPMM), in which a precise analysis of the physical phenomena and the influence of the material’s internal structure on these phenomena are made. Starting from the microscopic level, appropriate constitutive equations are defined for the solid, liquid and gaseous phases of the medium and then averaged at macroscopic scale for a multiphase medium.
This state-of-the-art report gives a basic overview of the main approaches available in the literature for modelling the behaviour of concrete at early ages and beyond, starting from the simplest ones and then increasing the level of complexity.
First, the pure thermo-chemo-mechanical models are introduced in Sect. 7.2. Then, multifield single-fluid phase thermo-chemo-mechanical models and their extension with a moisture transport are presented and described in Sect. 7.3. Both these groups of models can be considered based on a typical phenomenological approach (i.e. concrete is treated as a homogeneous medium directly at macroscopic level). The last class of deterministic models taken into consideration is the one of multifield multiphase models described in Sect. 7.4 based on porous media mechanics. Each model group contains validation examples showing its effectiveness in the numerical simulation of the main phenomena/processes taking place in massive concrete structures.
Whatever is the model adopted for the description of the general behaviour of the material, it is needed to consider the effects of thermal field, chemical reactions and solid skeleton-fluid phase interactions on its mechanical performance. This means the necessity to choose an appropriate constitutive relationship, describing specifically its mechanical behaviour. Thus, damage and plasticity material models are briefly discussed in Sect. 7.5 in connection with Chap. 4. Section 7.6 focuses on models with stochastic nature. These models are formulated specifically for giving a detailed information about cracks’ spacing and opening in concrete structures in service life conditions.
7.2 Thermo-Chemo-Mechanical Models
Thermo-chemo-mechanical models consider coupling among heat transport, evolution of underlying microstructure via chemical reactions and solid mechanics. Moisture (humidity, water) transport is neglected, leading to zero drying shrinkage. Such simplification is feasible for massive structures in their early age (except for element surface), while for long-term calculation a chemo-hydro-thermo-mechanical model should be preferred (see Sects. 7.3 and 7.4).
During early age, several phenomena occur simultaneously. In thermal-chemo-mechanical models, the following ones are generally taken into account: hydration linked to the temperature evolution due to exothermic cement reaction, thermal conduction and dilatation, autogenous shrinkage, mechanical properties evolution and mechanical degradation due to cracks and/or damage (which could be visco-elastic damage models or plastic models).
7.2.1 Thermal Conduction Through the Concrete
The prediction of temperature evolution in a massive concrete structure is based on the heat equation with a source term:
in which Q ξ is the latent heat of hydration [Jm−3], T [K] is the temperature, α is the hydration degree, k is the thermal conductivity [Wm−1K−1], and c is the volumetric heat capacity [Jm−3K−1]. The latent heat of hydration, the thermal conductivity and the volumetric heat capacity could be kept constant (see Waller 2000; Mounanga 2004; Mounanga et al. 2006) or evolve slightly with the temperature (Morabito 2001) and the hydration (see Faria et al. 2006; Ruiz et al. 2001; Lura and Van Breugel 2001).
7.2.2 Constitutive Relationships/Couplings
One can distinguish between two types of couplings: thermo-chemical and chemo-mechanical couplings with the corresponding constitutive relationships, which are analysed and discussed in the following sections.
Thermo-chemical Coupling
The thermal properties, namely thermal conductivity, heat capacity and coefficient of thermal expansion, are generally functions of the temperature and also evolve at early age with the changes in the microstructure of the cement-based materials. For instance, Hansen et al. (1982) reported a decrease of thermal conductivity from 0.88 to 0.78 W/(mK) during hydration of rapid hardening Portland cement, w/c = 0.5 at T = 30 °C, while Mounanga (2004) obtained an increase. Generally, this aspect is not explicitly taken into account in simulations or even experimentally, but different authors report an impact of the variation of these properties on the structural response. For instance, Briffaut et al. (2012) performed simulations, at the structure level, in which the heat capacity and the thermal conductivity evolved with respect to the degree of hydration. In their simulation, the evolution of the heat capacity impacted the stress response more strongly than the evolution of the thermal conductivity. Lura and van Breugel (2001) reported that a given variation of the heat capacity may lead to a variation of the same order of magnitude in the computed temperatures and stresses. The same authors also found that up to 5% of variation in the thermal conductivity, an almost negligible effect is observed on the temperature and stress responses and that the CTE affects actively the thermo-chemo-mechanical response (a variation of 16% in the CTE is reported to increase the cracking risk by about 15%) (see Lura and Van Breugel 2001). On the other hand, Hilaire (2014) reported a not very pronounced impact of the CTE evolution on the mechanical response at early age.
The thermal source of the heat equation depends on the evolution of hydration which is achieved using chemical affinity (see Ulm and Coussy 1998, 2001; Lackner and Mang 2004; Regourd and Gauthier 1980):
where E a is the activation energy [Jmol−1], R is the ideal gas constant 8.3145 [JK−1mol−1], T is the temperature [K], α is the hydration degree, and \(\tilde{A}(\alpha )\) is the chemical affinity [s−1].
Many kinds of expression describing the evolution of the chemical affinity have been used (see among others Lackner and Mang 2004; Cervera et al. 1999a; Benboudjema and Torrenti 2008; Briffaut et al. 2012; Sciumè et al. 2013), but there remains experimental fitting. Buffo-Laccarière et al. (2007) proposed an expression for multiphasic hydration degree evolution linked to chemical activation and physical water accessibility to anhydrous cement product which allows for composed cement.
The energy of activation is also a function of the temperature and may vary as a function of the mechanisms deemed to drive hydration (Lothenbach et al. 2008). Again, the variation of the energy of activation with respect to age and temperature is often neglected in TC analyses.
Chemo-mechanical Coupling/Evolution of Mechanical Properties (Elastic, Plastic or Damage)
This kind of model is generally based on uncoupled strains decomposition:
where \({\varvec{\upvarepsilon}}_{M}\) is the mechanical strain tensor, \({\varvec{\upvarepsilon}}_{bc}\) is the basic creep strain tensor, \({\varvec{\upvarepsilon}}_{au}\) is the autogenous strain tensor, \({\varvec{\upvarepsilon}}_{T}\) is the thermal strain tensor, and finally, \({\varvec{\upvarepsilon}}\) is the total strain tensor. Nevertheless, some authors used coupling between creep and damage (see Chap. 4) and between creep and hydration (chemo-visco-elastic coupling see Chap. 4).
Autogenous shrinkage is directly related to the evolution of hydration in the material. Experimental results show that autogenous shrinkage evolution is almost linear with respect to the hydration degree as soon as the percolation threshold has been overcame (see Laplante 1993; Mounanga 2004; Mounanga et al. 2006). Therefore, autogenous shrinkage can be modelled by the following equation (Ulm and Coussy 1998):
where κ is a constant material parameter [-], α0 is the mechanical percolation threshold [-] (Torrenti and Benboudjema 2005), α ∞ is the final hydration degree (which depends on the concrete mix Waller 2000), and \(\left\langle \cdot \right\rangle\!_{+}\) is the positive part operator. A small expansion (so-called swelling) can also be measured at the beginning of hydration, depending on the w/c ratio and the type of cement.
The mechanical strains could be elastic ones (Faria et al. 2006) but could also consider plasticity (Ulm and Coussy 1998, 2001; Lackner and Mang 2004) or damage (Benboudjema and Torrenti 2008; Briffaut et al. 2011; Cervera et al. 1999b). In this last case, the relationship between apparent stress \({\varvec{\upsigma}}\), effective stress \({\tilde{\varvec{\upsigma}}}\), damage D, elastic stiffness tensor E, elastic strain and previously defined strain reads:
where \({\varvec{\upvarepsilon}}_{ttc}\) is the transient thermal creep strain.
The Young’s modulus E and the tensile strength f t increase due to hydration as follows (De Schutter 1999; Stefan et al. 2010, see also Chap. 4):
where ft∞ is the final tensile strength (i.e. when \(\alpha = \alpha_{\infty }\)) [Pa], E∞ is the final Young’s modulus [GPa], \(\bar{\alpha }^{{a_{E} }}\), and \(\bar{\alpha }^{{a_{ft} }}\) are constant material parameters.
The Poisson’s ratio is relatively stable for mature concrete. Neville et al. (1983) recommend a value equal to 0.2 for most of concrete mixes. However, De Schutter and Taerwe (1996) suggests an evolution depending on the hydration degree:
where ν is the Poisson’s ratio and α is the hydration degree. Note that for a hydration degree equal to 0, the Poisson’s ratio is equal to 0.5 which is the common value for an incompressible fluid.
The evolution of the damage is linked to the elastic equivalent tensile strain and could use strain from Rankine criterion (Cervera et al. 1999b) or Mazars approach (Benboudjema and Torrenti 2008; Briffaut et al. 2011).
Strain softening induces inherent mesh dependency and produces failure without energy dissipation (see Pijaudiet-Cabot and Bažant 1987). In order to dissipate the same amount of energy after mesh refinement, when strains localise in one row of finite elements, a characteristic length l c is introduced as a localisation limiter (Rots 1988; Cervera and Chiumenti 2006). Fracture energy of an element g f is related to the material fracture energy G f and the characteristic length l c :
where V ef is the volume of the finite element.
The fracture energy also depends on the hydration degree (De Schutter and Taerwe 1997):
where δ is a material property that must be fitted from experimental data and G f∞ is the material fracture energy at the end of hydration process.
Ulm and Coussy (1998) propose a chemo-mechanical cross-effect in a context where plasticity is considered. These authors link the chemo-plastic cross-effects to the strength growth and plastic hardening/softening properties of the material when irreversible skeleton evolutions occur.
Thermo-mechanical Coupling
The thermal strain \({\varvec{\upvarepsilon}}_{th}\) is linked to the temperature variation and to the coefficient of thermal expansion CTE which is a function of the hydration degree and of the temperature. Nevertheless, constant value allows to obtain sufficiently accurate prediction (Loukili et al. 2000):
where T0 is the reference temperature [K].
Thermo-chemo-mechanical Coupling
In thermo-chemo-mechanical model, when creep is taken into account, viscous parameter could also be affected by the hydration degree and the temperature. For instance, when rheological modelling is used, the viscosity and the stiffness of the component should be affected (Benboudjema and Torrenti 2008; Briffaut et al. 2012).
It is noteworthy that the properties such as heat capacity and CTE are, for thermo-elastic composites, linked according to some cross-relationships (Chen et al. 2012).
An additional thermo-chemo-mechanical coupling arises on the light of Bažant and collaborators micro-prestress solidification theory (Bažant et al. 1997, 2004). According to these authors, a micro-prestress relaxation within the concrete matrix appears at the microlevel and is related to the hydration reaction. This effect is thermo-activated per se (Bažant et al. 2004).
7.2.3 Validation of the Thermo-Chemo-Mechanical Models on Massive Structures at Early Age
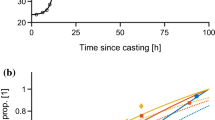
The chemo-thermal problem is often decoupled from the mechanical problem. Several comparisons of model estimations and experimental measurements can be found in the literature (e.g. Craeye et al. 2009; Fairbairn et al. 2004; Faria et al. 2006; Honorio et al. 2014; Ulm and Coussy 1998, 2001). An example of thermal prediction on a massive concrete structure (wall thickness 1.2 m; height 2.4 m) is given in Fig. 7.1.
Temperature prediction on Civaux Wall (thickness 1.2 m; height 2.4 m) during hydration (Briffaut 2010)
7.3 Multifield Models: Single-Fluid Models
This group of multifield models deals with the heat and moisture transport in a porous material accompanied with mechanical response. The material can represent cement paste, mortar, or concrete as a continuum directly defined at macroscale. Even if the model is a multifield model, it is still based on a phenomenological approach. In the view of the model description, thermo refers to heat transport, chemo stands for chemical reactions occurring due to cement hydration, and hygro describes moisture or water vapour transport as a single transported fluid phase, followed with solid mechanical analysis.
In the simplest approach, thermo-(chemo)-hygro models proceed using a staggered approach where temperature and relative humidity fields are computed first. Both fields are then passed to mechanical model which accounts for strain-related quantities, such as thermal strain caused by temperature, drying strain originating from relative humidity, autogenous shrinkage strain due to drop in relative humidity. Several mechanical parameters may depend on the microstructure evolution, such as increasing Young’s modulus or increasing tensile strength (de Shutter 2002). This section shows several examples of material sub-models, their coupling and validations on real structures.
7.3.1 Phenomena Taken into Consideration
Heat transport (thermo-) takes into account heat conduction (diffusion), heat convection and radiation. The transport is often enhanced with heat generated due to mostly exothermic cement hydration, or extended for enthalpy of water evaporation from concrete surface (Černý and Rovnaníková 2002). Modelling heat transport solely in hydrating concrete is used rarely; it finds its place especially in massive concrete structures where moisture gradient could be neglected and thermal gradients present substantial strains (Park et al. 2008).
Chemical phenomena deal mainly with the evolution of hydrating microstructure; i.e., it describes kinetics of hydrating clinker minerals, their hydration, evolution of volume fractions or generated heat. The most elaborated hydration models take into account cement chemistry, cement fineness, temperature, supplementary cementitious materials, and water availability (Thomas et al. 2011). Temperature acceleration often requires coupling with a heat transport model since reaction speed approximately doubles with a 10 °C increase (Černý and Rovnaníková 2002).
Moisture transport describes gas diffusion, effusion and solution diffusion, being driven by a gradient of water vapour pressure (Künzel 1995). The moisture in a porous material can be present in the form of solid, liquid or vaporous form, and it becomes convenient to quantify moisture as a total water content in this single-fluid model. Most hygral models express total water content as a relative humidity, using water vapour sorption isotherm for recalculation (Künzel 1995).
Mechanical part describes the effect of strains on structural behaviour in hydrating concrete. Under standard circumstances, strains contain autogenous shrinkage, temperature expansion/contraction or drying shrinkage. Mechanical models used in the analysis compute time-dependent material behaviour (creep, shrinkage) and time-independent load response (plasticity, damage).
Each part is represented with more or less sophisticated sub-model, which could operate on different scales using a multiscale formulation. For example, concrete can be treated as a heterogeneous material for prediction of hydration heat (Park et al. 2008), and elasticity and strength can be linked to cement hydration (Shutter 2002).
7.3.2 Coupled Formulation and Data Flow
The multiphysical thermo-(chemo)-hygro-mechanical formulation leads at least to three governing equations. Each sub-model contains a state variable to be solved and may depend on other state variable, leading to mutual coupling:
-
Thermo: enthalpy balance equation with unknown temperature field T [K], see Eq. 7.1.
-
Chemo: hydration kinetic equation could be added, with, e.g., unknown degree of hydration α [-], see Eq. 7.2.
-
Hygro: mass balance equation for moisture transport with unknown relative humidity h [-]. Some models use moisture content by mass w\([{\rm kg}_{H_{2}O}/m_{concrete}^{3}]\) instead, being a thermodynamically equivalent quantity related to h by sorption/desorption isotherm.
-
Linear momentum conservation equation (static equilibrium) with unknown displacement field u[m]. Various material constitutive laws (viscoelastic, plastic, damage) define stress/strain relationship between displacement field u and stress σ, see Sect. 7.5.
A monolithic formulation of thermo-(chemo)-hygro-mechanical problem requires that all unknowns are solved in one system of equations, leading generally to large systems. A simpler strategy for approximate solution is often employed, using one-way coupling when outputs from one sub-model are passed to another one, solving sub-models’ set of equations separately. Such staggered solution strategy is the most popular method of decoupling (Baggio et al. 1995; Červenka et al. 2014; Wu et al. 2014).
A characteristic thermo-hygro-mechanical model using a staggered approach is shown in Fig. 7.2. First, heat transport sub-model with a possible hydration sub-model computes temperature field T. Second, moisture transport sub-model evaluates field of relative humidity h which also depends on temperature. Alternatively, if hydration is formulated such as humidity-dependent, the corrector phase may be added to find equilibrium in both sub-models with compatible humidity field. Temperature and relative humidity fields are passed further to time-dependent mechanical sub-model.
A classical setup of thermo-chemo-hygro-mechanical model implementing a staggered solution strategy
Strain decomposition belongs to the key assumptions of the mechanical model. Under small deformations, total strain tensor could be decomposed to (Thelandersson 1987)
where the indices denote elastic, fracture, plastic, creep, thermal, autogenous, and drying shrinkage strain components, respectively. Several strain components may depend on temperature, such as creep, and on humidity, such as drying shrinkage strain (Bažant et al. 2015). T and h are known from the underlying sub-models.
Analysis of Eq. 7.14 shows that strain components could be separated into long-term and short-term contributions. Long-term (time-dependent) mechanical laws define strain evolution in time such as strains ε cr , ε T , ε au , ε d,sh . On the other hand, short-term (time-independent, frozen time) mechanical laws have no notion of time and evaluate ε e , ε f , ε p strains. These strains are related to concrete elasticity, concrete cracking and concrete crushing, where time-dependent evolution of concrete properties is often accounted for inside the constitutive laws (Červenka et al. 2014). Most of short-term constitutive laws are based on stress criteria, such as principal stress/tensile strength or plasticity surface.
7.3.3 Mathematical Formulation and Constitutive Relationships
7.3.3.1 Stand-Alone Heat Transport
Chapter 3 describes in detail the heat balance equation, heat source, boundary conditions with thermal properties of concrete and its components.
7.3.3.2 Stand-Alone Moisture Transport
Moisture transport in concrete has been modelled since the 1930s, and since that time, it has been recognised that concrete moisture diffusivity strongly depends on moisture content (Pickett 1942). Moisture transport model has been formulated by Bažant and Najjar (1972) who quantified nonlinear concrete diffusivity and showed it decreases an order of magnitude when passing from saturated to dry concrete state. The mass balance equation for water vapour transport reads:
where w [kg/m3] is moisture (evaporable water) content, t [s] is time, J w [kg/(m2s)] is moisture flux, and w s [kg/m3] is water source, e.g. water consumption during hydration. Defining concrete moisture capacity C h [kg/m3], one can relate moisture content w with relative humidity h [-] as
Bažant and Najjar (1972) assumed C h being a constant over the whole desorption range, see Fig. 7.3 for three w/cs.
Example of desorption isotherms for structural concrete (Hansen 1986) and linearisation
They arrived to the mass balance equation for moisture transport with h as the unknown:
where J [m/s] is the liquid and vapour diffusion flux density, C [m2/s] is diffusivity depending on h, h s captures humidity decrease due to self-desiccation during hydration, and K is a hygrothermic coefficient [K−1]. Bažant and Najjar proposed S-shape function for diffusivity as:
with characteristic values for mature concrete C1 = 150 × 10−12 − 2200 × 10−12 m2/s, α0 = 0.05 − 0.10 (it is the initial hydration degree), h c = 0.75 − 0.90, N = 6 − 16 (Bažant and Najjar 1972). Figure 7.4 shows such an example for structural concrete. More refined values for structural concrete were proposed (Fib 2010; Abbasnia et al. 2013) as well as simpler approximations (Ayano and Wittman 2002; Xi et al. 1994). Note that the S-shape function gives a nonlinear stationary profile of relative humidity across a concrete member, favouring higher relative humidity.
Example of concrete moisture diffusivity (Bažant and Najjar 1972)
Dirichlet boundary condition for (7.17) prescribes a fixed value of h, while humidity convection on a surface can be conveniently approximated with a humidity transfer coefficient as:
where h ∞ is relative humidity far away from a surface. β p can be approximated for concrete (Kwak et al. 2006):
which gives a value β p = 2.74 × 10−8 m/s for w/c = 0.44, advised also by other authors (Andreasik 1982; Aurich et al. 2009).
7.3.3.3 Heat and Moisture Coupled Transport
Coupling of heat and moisture transport leads generally to a system of two differential balance equations for heat and moisture transport
where H is the total enthalpy [J/m3], q is the heat flux density [W/m2], Q H is the heat source [W/m3], J is the liquid and vapour diffusion flux density [kg/(m2s)], and Q w is the moisture source [kg/(m3s)]. Constitutive equations defining flux densities q and J have been used by several authors (Andreasik 1982; Klemczak 2011), and their general forms yield:
where d ij are diffusion coefficients for heat or moisture transport.
Further, attention is focused to quite popular coupled model for building materials which was pioneered by Künzel (1995). He defined constitutive equations by taking into account separate liquid and moisture transport in a porous material, quantifying dependence of thermal conductivity on moisture content and dependence of water vapour permeability on temperature. Elaboration of Eqs. 7.22–7.25 leads to the final form:
where dH/dT [J/(m3K)] is a heat capacity, λ [W/(mK)] is a thermal conductivity, dQ s /dt [W/m3] is an outflow of heat per unit volume, e.g. hydration heat source, h v [J/kg] is evaporation enthalpy of water, δ p [kg/(msPa)] is water vapour permeability, p sat [Pa] is water vapour saturation pressure depending on temperature, dw/dh [kg/m3] is moisture storage capacity, D φ [kg/(ms)] is liquid conduction coefficient, and w n [kg/m3/s] is non-evaporable (chemically bound) water flux density, i.e. consumed water due to hydration. The moisture diffusivity depends again on relative humidity, in a similar fashion as in Fig. 7.4.
7.3.4 Validations of Single-Fluid Models
7.3.4.1 Validation of a Stand-Alone Moisture Transport Model
A short example of drying concrete cylinder illustrates the Bažant-Najjar’s model for moisture transport (Bažant and Najjar 1972). A concrete cylinder with 6 inches in diameter was exposed at 7 days to environmental humidity with 0.5 (Hanson 1968). The best fit over all datapoints gave parameters from Eq. 7.19 as C1 = 579 × 10−12 m2/s, α0 = 0.002, h c = 0.85, N = 3, better than in the original article (Bažant and Najjar 1972) (Fig. 7.5).
Validation of cylinder drying (Hanson 1968)
7.3.4.2 Validation of Oparno Bridge’s Arch
A reinforced concrete arch bridge, completed in 2010, was erected in the Czech Republic, on a highway between Prague and Dresden. Two arches with a span of 135 m support prestressed bridge decks, as shown in Fig. 7.6.
Two arches of Oparno Bridge during construction (Photograph by Jan L. Vítek)
Emphasis on durability with reduced cracking and application of concrete with OPC 431 kg/m3 led to the need for internal cooling during concrete hardening. The analysed cross section is located above the scaffolding as shown in Fig. 7.6. The left symmetric part has outer dimensions of 3.5 × 2.17 m, the analysis considered first a 2D cross-sectional model (Červenka et al. 2014). The most critical time for the temperature evolution occurred during summer casting with the peak ambient air temperature over 30 °C. CEM I 42.5R was used for concrete C45/55, and its reaction kinetics was well known.
Figure 7.7 shows the temperature T and the moisture fields at 0, 32, 42, 60 h of hydration. It was exercised that water cooling efficiently mitigated hydration heat and maintained the core temperature under 65 °C. Without water cooling, the maximum temperature would exceed 85 °C, which was unacceptable. Figure 7.8 validates temperatures from the thermo-hygral model.
Temperature (top) and relative humidity (bottom) fields in the left symmetric part of the arch cross section. The outer dimensions of the displayed cross section are 3.5 × 2.17 m. Six cooling pipes are embedded, and the cooling water was turned off at 40 h
Temperature validation in the core of the bridge arch
The results of the transport analysis entered mechanical analysis which computed cracks (see Fig. 7.8 for the evolution of temperature). The cracks’ pattern originates from heat dissipation through the surface (Fig. 7.9).
Crack pattern in a 1-m long segment in the Oparno Bridge
7.3.4.3 Validation of ConCrack’s Restrained Beam
The validation of the coupled hydro-thermo-hydro-mechanical analysis originates from the well-documented RG8 ConCrack experiment (Mazars 2014). Figure 7.10 shows the overall geometry of the RG8 beam with two massive heads on both sides and two restraining steel struts. The central beam part was made of reinforced concrete C50/60, w/c = 0.46, with dimensions of 0.5 × 0.8 × 5.1 m. The benchmark experiment provided material and structural data, internal temperature in three points, and displacements of two points C, D located on the beam axis 2.5 m apart. Maximum temperature in the core attained 53.7 °C at 30 h.
Validation of RG8 ConCrack experiment—experiment overview (by CEOS.fr), cracks at 30 days, displacement of points C-D and strain decomposition at the core point
Thermo-hygro-mechanical simulation used Künzel’s heat-moisture model, B3 creep model and fracture-plastic material model in ATENA software (Červenka et al. 2014). Figure 7.10 validates further C-D displacement and displays strain decomposition in the core point. Note that thermal strain with subsequent cooling contributes the most to cracking at early ages.
7.3.4.4 Validation of a Restrained Wall in Oslo
A restrained wall served as a forerunner experiment for Bjørvika submerged tunnel project, built in Oslo between 2005 and 2012. The wall utilised low-heat concrete with a minimal risk of early-age cracking and high watertightness. Figure 7.11 shows two walls built on a raft concrete slab (Ji 2008). The left wall is made from SV-40 concrete containing low-heat OPC I with silica fume at the amount of 424 kg/m3. This left wall is validated using a thermo-chemo-mechanical model implemented in OOFEM (Patzák and Rypl 2012), neglecting moisture transport (Šmilauer et al. 2016).
Field test of a restrained wall in Oslo (Ji 2008)
A semi-adiabatic calorimeter gave temperature evolution on a concrete cube with 247-mm edge. This small-scale test served for calibration of affinity hydration model with perfect result (Leal da Silva et al. 2015).
The restrained concrete wall was cast on older concrete raft slab according to Fig. 7.11. The quarter-simulated wall had reduced dimensions of 0.5 × 2 × 7.5 m due to symmetry conditions. A fixed temperature 20 °C served at the bottom, fluctuating temperature between 8 and 21 °C provided ambient temperature-exposed surfaces. Heat transfer coefficients of 3.75 W/(m2K) acted on vertical surfaces covered with a formwork, the top had 5.75 W/(m2K) with a foil cover, and the bottom had 10 W/(m2K). The formwork removal at 216 h increased the coefficients to 19 W/(m2K). Figure 7.12 shows temperature field with the maximum temperature at 30 h and temperature validation in gage 15 which is located in the middle of the wall, 1.2 m above the bottom.
Temperature field at 30 h and the validation
The mechanical part used B3 creep model for concrete with corresponding parameters, coefficient of thermal expansion of 10−5 K−1. The evolution of autogenous shrinkage, tensile strength and fracture energy was defined accordingly (Fib 2010). The wall’s bottom was supported with horizontal stiffness of 1000 MN/m3 to mimic high stiffness of the underlying old concrete. The first cracks on the surface appeared already in 12 h, but they closed by 60 h due to cooling. Minor cracks formed after 70 h close to the interface with the old concrete, where high shear stress led to tension on inclined planes. At time 260 h, vertical cracks formed through the whole beam section close to gage 15, leading to a drop of principal stress (Fig. 7.13). The widest cracks attained the width of 0.42 mm, and the maximum tensile stress in reinforcement reached 25 MPa (Fig. 7.14). The localisation into crack bands was not indicated in the experiment signalising better tensile strength of concrete than that adopted from Model Code (Fib 2010).
Validation of horizontal strain, principal stress and tensile strength at gage 15
First principal stress, cracks and stress in reinforcement at 300 h
7.4 Multifield Models: Advanced Multiphase Modelling
In this part, the models will be discussed considering more than one fluid inside the pore network of concrete. This class of models regards concrete as a porous material and is based essentially on the mechanics of porous media.
This group of models aims at the simulation of the overall thermo-hygral and mechanical behaviour of the material, considering sometimes also some chemical aspects (e.g. the reactions of hydration and dehydration). To analyse hygro-thermal phenomena in porous media, two different approaches are currently used: phenomenological and mechanistic ones. In phenomenological approaches (e.g. Bažant and Thonguthai 1978, 1979; Bažant and Kaplan 1996), moisture and heat transport are described by diffusive-type differential equations with temperature- and moisture content-dependent coefficients. The model coefficients are usually determined by inverse problem solution, starting from experimental tests results, to obtain the best agreement between theoretical prediction and experimental evidence. An advantage of such a kind of models is that they are very accurate for interpolation but rather poor for extrapolation of the known experimental results. Moreover, various physical phenomena are lumped together and important processes, such as phase changes, are neglected. An example of such a class of models is described in Sect. 7.3.
Mechanistic models (Gawin et al. 2002, 2003, 2006a, b, c, 2008, 2009) are more complicated from the mathematical point of view, and contrary to phenomenological ones, their coefficients have a clear physical meaning. This kind of models is often obtained from microscopic balance equations written for each constituent of the medium, which are then averaged in space by applying special averaging operators.
Several mathematical and numerical models, usually based on extensive laboratory tests, have been developed for the analysis of heat and mass transfer in concrete at early ages and beyond, e.g. Benboudjema and Torrenti (2008), Cervera et al. (1999a, b), Gawin et al. (2006a, b). However, one should remember that every interpretation possesses all limitations and simplifications that are assumed in the mathematical model which the simulation is based on. Thus, for this purpose one should use models considering possibly the whole complexity and mutual interactions of the analysed physical processes. Hence, a proper choice may be models based on mechanics of multiphase porous media, taking into account chemical reactions (e.g. reactions related to hydration, silica-alkali reactions and other reactions due to chemically aggressive environments), phase changes, cracking and thermo-chemical material degradation, as well as their mutual couplings and influence on the hygral, thermal, chemical and mechanical properties of concrete. These physical aspects of the behaviour of concrete treated as a multiphase porous material are described in the following sections.
7.4.1 Concrete as Multiphase Porous Material
Concrete is essentially a mixture of two components: aggregates and paste. The aggregate component is usually sand, gravel or crushed stone. It is mainly responsible for the unit weight, the elastic modulus and the dimensional stability of concrete. The paste component is typically used to bind aggregates in concrete and mortar. It is a porous medium, which is composed of a solid skeleton, produced from the hydration of Portland cement, and pores, which are filled by different fluid phases. The principal solid phases generally present in the hydrated cement paste (hcp) that can be resolved by an electron microscope are the calcium silicate hydrates C-S-H which are very important in determining the properties of the paste such as strength and permeability, and the calcium hydroxide Ca(OH)2 (also called portlandite). The pore structure is relevant for concrete. It contributes to the mechanical strength of concrete, but it also allows the interaction with the external environment which takes place through the connected pores. Besides, it is the container of the liquid water and gas phases (vapour and dry air). Figure 7.15 gives a schematic representation of cement paste seen as a partially saturated medium.
Schematic representation of a non-saturated porous material
For a given representative elementary volume (REV)Ω, the volume of pores Ω p allows to define the porosity \(n =\Omega _{p} /\Omega\). Furthermore, the degree of saturation of pores with liquid water is introduced as \(S_{w} =\Omega _{w} /\Omega _{p}\). It is an experimentally determined function of the relative humidity RH (obtained through the sorption isotherms). The remaining volume of pores is filled with a gaseous mixture with a gas saturation: \(S_{g} = \left( {1 - S_{w} } \right) =\Omega _{g} /\Omega _{p}\) (Ω w and Ω g are the volumes of the liquid and gas phases, respectively).
The interfacial surface tension of water in a capillary pore leads to a concave meniscus between liquid water and gas phase, as shown in Fig. 7.16. This may give rise to a discontinuity in fluid pressure. The difference between the liquid water pressure p w and the gas pressure (dry air p a + vapour p v ) is called the capillary pressure p c and is a function of the liquid water saturation S w :
Schematic representation of the representative elementary volume (REV)
Assuming the contact angle γ between liquid phase and solid matrix to be zero, the capillary pressure of water p c can be related to the pore radius r with the Laplace equation:
where σ(T) is the surface tension of water which depends upon temperature and χ is the curvature of the meniscus. Any change in the curvature of meniscus will change the equilibrium between liquid and vapour phases. A relation between the liquid water and the vapour can be obtained by means of Kelvin’s equation considering that liquid is incompressible and the vapour is a perfect gas.
Water can exist in the hydrated cement paste in many forms:
-
capillary and physically adsorbed water; their loss is mainly responsible for the shrinkage of the material while drying;
-
interlayer water; it can be lost only during strong drying, which leads to considerably shrinkage of the C-S-H structure.
All these types of water can evaporate up to 105 °C (at atmospheric pressure and slow rate of heating). Another type of water, which is non-evaporable water, is chemically bound water. It is considered to be an integral part of the structure of various cement hydration products, and it is released when the hydrates decompose on heating. Based on the Feldman–Sereda model (Feldman and Sereda 1968), the different types of water associated with the C-S-H are illustrated in Fig. 7.17.
Probable structure of hydrated silicates (based on Feldman and Sereda 1968)
In fact, there is a third phase in the concrete microstructure, known as transition zone, which represents the interfacial region between the particles of coarse aggregates and the hcp. Concrete has microcracks in the transition zone even before a structure is loaded. This has a great influence on the stiffness of concrete. In the composite material, the transition zone serves as a bridge between the two components: the mortar matrix and the coarse aggregate particles. Therefore, the broken bridges (i.e. voids and microcracks in this zone) would not permit stresses transfer.
For what has been described above, concrete can be treated as a multiphase/multicomponent porous material. Because of this, in the last fifteen years, mechanics of multiphase porous media proved to be a theory enabling an efficient modelling of cement-based materials (Gawin et al. 2003, 2006a, b, 2008, 2009; Pesavento et al. 2008, 2012). It allows for considering the porous and multiphase nature of the materials, their chemical transformations, water phase changes and different behaviour of moisture below and above the critical temperature of water, mutual interactions between the thermal, hygric and degradation processes, as well as several material nonlinearities, especially those due to temperature changes, material cracking and thermo-chemical degradation.
In modelling, it is usually assumed that the material phases are in thermodynamic equilibrium state locally. In this way, their thermodynamic state is described by one common set of state variables and not by separate sets for every component of the material, which allows reducing the number of unknowns in a mathematical model. Thus, there is, for example, one common temperature for the multiphase material and not different temperature values for the skeleton, liquid water, vapour and dry air, etc. When fast hygro-thermal phenomena in a material are analysed (e.g. during a rapid heating and/or drying), the assumption is debatable, but it is almost always used in modelling, giving reasonable results from a physical point of view and in part confirmed by the available experimental results.
Concrete is here considered to be a multiphase medium where the voids of the solid skeleton could be filled with various combinations of liquid and gas phases as in Fig. 7.16. In the specific case, the fluids filling pore space are the moist air (mixture of dry air and vapour), capillary water and physically adsorbed water. The chemically bound water is considered to be part of the solid skeleton until it is released on heating.
Below the critical temperature of water T cr , the liquid phase consists of physically adsorbed water, which is present in the whole range of moisture content, and capillary water, which appears when degree of water saturation S w exceeds the upper limit of the hygroscopic region, S ssp (i.e. below S ssp there is only physically adsorbed water). Above the temperature T cr , the liquid phase consists of the adsorbed water only. In the whole temperature range, the gas phase is a mixture of dry air and water vapour.
Thanks to the mechanics of porous media and the schematisation of the material described above, it is possible to analyse three different classes of phenomena which characterises the behaviour of concrete at early ages and beyond:
-
hygral phenomena,
-
thermal phenomena,
-
mechanical phenomena,
-
chemical processes.
7.4.1.1 Hygral Phenomena
In order to analyse the physical processes taking place in the material under variable conditions in terms of temperature and pressure, we can consider a concrete element heated from the environment.
When temperature increases in a concrete structure (e.g. in a wall), water vapour pressure is continuously increasing in a zone close to the heated surface. This derives principally from the evaporation of water inside the wall, when the temperature reaches and passes the boiling point of water. Vapour pressure is also due to the water that is liberated during the dehydration of cement paste. This increase in the water vapour pressure in the hot region will create a thermodynamic imbalance between the hot and the cold regions. This will entail a diffusion process of the water vapour and of the dry air through the wall and towards the external atmosphere to maintain the equilibrium between liquid and vapour (see Fig. 7.18).
Mass sources/sinks and mass transport mechanisms in a non-saturated porous medium subjected to heating
For appropriate prediction of the moisture distribution in a concrete structure, one needs to know the material properties that control the movement of the fluids inside a porous medium. Permeability and diffusivity are the most important properties of the cementitious materials, from this point of view. These are very sensitive to porosity changes or microcracking phenomena. In fact, the increases in permeability and porosity of such materials are currently accepted as providing a reliable indication of their degradation whether it has thermal, mechanical or physicochemical origins. Therefore, in this document these properties and their evolutions will be analysed also in the view of what is described in Chaps. 3 and 4.
7.4.1.2 Thermal Phenomena
Concerning thermal phenomena, it can be stated that in most cases the main mechanism for heat transport is heat conduction. Heat conduction responds to gradients of temperature T. However, additional heat transfer will also be accomplished by advection due to the movement of the three phases: solid, liquid and gas. The latent heat inherent to phase changes may also have significant thermal effects (Gawin et al. 2003), see also Fig. 7.19.
Heat sources/sinks and heat transport mechanisms in a porous medium
The evolution of the temperature distribution in any structure is governed by the thermal properties of the material, particularly heat capacity and thermal conductivity. In case of concrete, it is difficult to determine these properties because of the numerous phenomena that occur simultaneously within the microstructure of concrete and cannot be separated easily. These phenomena are affected in particular by the evolution of the porosity, by the moisture content, by the type and amount of aggregate, by changes in the chemical composition and by the latent heat consumption generated by certain chemical phenomena. Because of these effects, a unique relation cannot rigorously describe the dependence of concrete properties on temperature.
7.4.1.3 Mechanical Phenomena
When mechanically loaded and simultaneously heated, the overall measured strain of concrete is assumed as an additive combination of different components. These components can be conventionally classified into three families according to the origin of driving mechanisms:
-
Mechanical strains that occur due to an applied mechanical load only. Elastic strain, cracking strain and basic creep strain are main mechanical components.
-
Thermo-hygral strains related to the occurrence of physicochemical processes within the material such as drying, temperature raising, hydration and other chemical reactions. Thermal expansion and shrinkage (both capillary and chemical shrinkage) are the most important components. They are carried out in (mechanically) load-free configurations.
-
Interaction strains are additional components generated when the above-mentioned physicochemical processes occur during a concomitant applied load. In this case, indeed, the overall measured strain differs from the sum of all strains induced by each single mechanism. For instance, additional elastic strain, due to the evolution of Young’s modulus with temperature, is an illustration of interaction strains. Also, drying and creep strains belong to this category. For example, drying creep is shown when the structural element can exchange water with the environment (i.e. shrinkage is taking place) and is loaded at the same time.
7.4.1.4 Chemical Processes
Description of chemical reactions taking place in concrete at early ages (and beyond) and their couplings with the thermo-hygral state of the material (e.g. self-drying) can be found in Chap. 3. Here, one underlines that in the numerical modelling the hydration is often considered as a single chemical reaction; i.e., only the overall process is described through the formulation of a proper evolution equation.
7.4.2 Heat and Mass Transfer
The general approach to heat and mass transfer processes in a partially saturated open porous medium is to start from a set of balance equations governing the time evolution of mass and heat of solid matrix and fluids filling the porous network, taking into account the exchange between the phases and with the surrounding medium. These balance equations are supplemented with an appropriate set of constitutive relationships, which permit to reduce the number of independent state variables that control the physical process under investigation.
The formulation of the mathematical model is based usually on here main approaches:
-
(1)
Mixture theories (Bear 1988);
-
(2)
Volume averaging theories (Whitaker 1980);
-
(3)
Hybrid mixture theories (Hassanizadeh and Gray 1979a, b, 1980).
In the first approach, the governing equations of the model and its constitutive equations are both formulated directly at macroscale. In the second and in the third approach, the governing equations are defined at microscopic level and then upscaled at macrolevel by applying some averaging operators (mass, volume, area operators, mainly). In the case of volume averaging approach also the constitutive relationships are formulated at microscale.
The Hybrid Mixture Theory and the Volume Averaging Theory allow for taking into account both bulk phases and interfaces of the multiphase system, assure that the Second Law of Thermodynamics is satisfied at macrolevel, that no un-wanted dissipations are generated and that the definition of the relevant quantities involved is thermodynamically correct.
Recently, it has been shown that with the combination of Hybrid Mixture Theory and the Thermodynamically Constrained Averaging Theory (TCAT, Gray and Miller 2005), also the satisfaction of the second law of thermodynamics for all constituents at microlevel is guaranteed (Gray et al. 2009).
Starting from this latter approach, in the following section a full set of balance equations is presented. They can be obtained by using the procedure of space averaging of the microscopic balance equations, written for the individual constituents of the medium (i.e. the governing equations at local level). The theoretical framework is based on the works of Lewis and Schrefler (1998), Gray and Schrefler (2007). A detailed description of the procedure can be found in (Pesavento 2000; Gawin et al. 2003, 2006a, b, c, 2008, 2009; Pesavento et al. 2008, 2012).
7.4.2.1 Final Form of the Governing Equations
The hygro-chemo-thermal state of cement-based materials considered as multiphase porous media is described by three primary state variables: the capillary pressure p c , the gas pressure p g and the temperature T, as well as one internal variable describing advancement of the hydration processes, i.e. degree of hydration, α. This choice is of particular importance: the chosen quantities must describe a well-posed initial-boundary value problem, should guarantee a good numerical performance of the solution algorithm and should make their experimental identification simple. A detailed discussion about the choice of state (i.e. primary) variables can be found in Sect. 7.4.3.
The mathematical model describing the material performance consists of three equations: two mass balances (continuity equations of water and dry air), enthalpy (energy) balance and one evolution equation (degree of dehydration). For convenience of the reader, the final form of the model equations, expressed in terms of the primary state variables, is listed below. The full development of the equations is presented in (Gawin et al. 2006a, b).
Mass balance equation of dry air takes into account both the diffusive (described by the term L.30.7) and advective air flow (L.30.8), the variations of the saturation degree of water (L.30.1) and air density (L.30.4), as well as the variations of porosity caused by: hydration process (L.30.5), temperature variation (L.30.2), skeleton density changes due to dehydration (L.30.6) and by skeleton deformations (L.30.3). The mass balance equation has the following form:
in which ρ π is the density of the π-phase (π = s, w, g) and β s is the thermal expansion coefficient of the solid phase, ρ a is the dry air density, α the hydration degree, and \({\mathbf{J}}_{g}^{a}\) the dry air diffusive flux. In the previous equation and in the following ones, vs is the velocity of the solid phase, while vπs is the relative velocity of the π-fluid phase (π = w, g) with respect to the solid skeleton.
Mass balance equation of water species (vapour + liquid water) considers the diffusive (L.31.6) and advective flows of water vapour (L.31.7) and water (L.31.8), the mass sources related to phase changes of vapour (evaporation–condensation, physical adsorption–desorption) (the sum of those mass sources equals to zero) and hydration (R.31.1), and the changes of porosity caused by variation of: temperature (L.31.3), hydration process (L.31.10), variation of skeleton density due to hydration (L.31.9) and deformations of the skeleton (L.31.2), as well as the variations of: water saturation degree (L.31.1) and the densities of vapour (L.31.4) and liquid water (L.31.5). This gives the following equation (Gawin et al. 2006a, b):
where ρ v is the water vapour density, \({\mathbf{J}}_{g}^{v}\) is the water vapour diffusive flux, and \(\dot{m}_{hydr}\) is the water mass source/sink due to hydration process.
In Eq. 7.31, β swg is the thermal expansion coefficient of the multiphase porous medium, defined by:
in which β π is the thermal expansion coefficient of each phase (π = s, w, g).
Enthalpy balance equation of the multiphase medium, accounting for the conductive (L.33.3) and convective (L.33.2) heat flows, the heat effects of phase changes (R.33.1) and dehydration process (R.33.2), and the heat accumulated by the system (L.33.1), can be written as follows:
where \(\widetilde{{\mathbf{q}}}\) is the conductive thermal flux, vw and vg are the velocities of the liquid and gas phase, respectively, and the thermal capacity of the multiphase porous medium (ρC p ) eff and the enthalpies of vaporisation \(\Delta H_{vap}\) and hydration \(\Delta H_{hydr}\) are:
in which \(C_{p}^{\pi }\) is the specific heat of the π-phase (π = s, w, g).
In Eq. 7.33, the vapour mass source is given by (Gawin et al. 2006a, b):
with:
Equation 7.35 considers the advective flow of water (R.35.4), the mass sources related to dehydration (R.35.7) and the changes of porosity caused by: variation of temperature (R.35.3), dehydration process (R.35.6), variation of skeleton density due to dehydration (R.35.5) and deformations of the skeleton (R.35.2), as well as the variations of water saturation degree (R.35.1).
The governing equations in the form described above are now complemented by the constitutive equations.
7.4.2.2 Constitutive Equations
Fluid state equations
The liquid water is considered to be incompressible such that its density depends on the temperature only. The vapour, dry air and the gas mixture are considered to behave as ideal gases, which gives (π = v, a, g):
where p π is the pressure, M π is the molar mass, and R is the universal gas constant. Furthermore, the pressure and density of the gas mixture can be related to the partial pressures and densities of the constituents through the Dalton’s law:
which gives:
Liquid–Vapour Equilibrium
By assuming that the evaporation process occurs without energy dissipation, that is, liquid and vapour water have equal free enthalpies, one can derive the generalised Clausius–Clapeyron equation, which is a relationship between liquid and vapour pressure:
where the capillary pressure at equilibrium
has been introduced for the porous medium and p vs is the saturation vapour pressure, which only depends on temperature.
Mass fluxes
According to the definition of the velocities in the governing equations (7.30) (Gawin et al. 2006a), the mass fluxes can be as follows:
which represents the Darcy’s law for the liquid (π = w) and gaseous (π = g) phases, respectively, and where k is the intrinsic permeability, k rπ is the relative permeability, μ π is the dynamic viscosity, and g is the gravity acceleration.
The mass fluxes related to the diffusion are defined as:
where \({\mathbf{J}}_{g}^{a}\) and \({\mathbf{J}}_{g}^{v}\) are the fluxes of the dry air and water vapour in the gas phases (i.e. the humid air), respectively, and \({\mathbf{D}}_{g}^{a}\) is the diffusion tensor of the dry air.
Conductive Heat Flux
In the energy balance Eq. 7.33, the heat conduction process in the porous medium can be described by Fourier’s law which relates the temperature to the heat flux as follows:
where λ(S w ,T) is the effective thermal conductivity which in general is a function of the temperature and of the degree of saturation with liquid water of the pores.
Sorption–desorption isotherm
Solving the presented equations aims at determining the spatial and temporal distribution of temperature, masses of constituents and corresponding pressures within the porous medium. By introducing the previous constitutive equations, the problem involves, at this stage, as main unknowns (S w , p c , p g , T, m vap ) or alternatively (S w , p v , p a , T, m vap ). This set is reduced by introducing an additional explicit relationship (van Genuchten 1980; Baroghel-Bouny et al. 1999; Pesavento 2000; Gawin et al. 2003):
which is the sorption–desorption isotherm, characterising phenomenologically the microstructure of the porous medium (pore size distribution).
Moreover, it is needed to consider that the microstructure of the cement paste shows important changes during hydration (refinement of the porous network), so it is important to take into account this aspect in the mathematical formulation of the isotherms.
To do this, the classical analytical expression proposed by Van Genuchten (1980) can be slightly modified to take into account the hydration degree (see Fig. 7.20), which is a measure of the hydration extent (see the next subsections for its definition):
(Adapted from Sciumé et al. 2013)
Desorption isotherms: the numbers in the diagram indicate the hydration degree.
where a and b are the classical parameters of the Van Genuchten’s law, and c and Γ i are the newly introduced parameters (Sciumè et al. 2013).
Using this additional relationship, the reduced set of unknowns is then (p c , p g , T, m vap ) where a choice is made here to retain the state variables (p c , p g ) instead of (p v , p a ) or (p w , p a ). Moreover, the set of unknowns can be further reduced. Because of this, mass conservation equations of liquid and vapour defined as in (Schrefler 2002; Gawin et al. 2003) have been summed to eliminate the evaporation source term m vap and thus obtain the mass balance equation for the water species (that means liquid water plus water vapour), Eq. 7.31.
7.4.3 Key Points for Modelling Cement-Based Materials as Multiphase Porous Media
Dealing with cement-based materials as multiphase porous media introduces some physical and theoretical difficulties, which should be overcome to be able to formulate a mathematical model giving reliable results for the material. These key points are discussed in the following subsections.
Choice of state variables
A proper choice of state variables for description of the multiphase porous materials is of particular importance. From a practical point of view, the physical quantities used should be possibly easy to measure during experiments, and from a theoretical point of view, they should uniquely describe the thermodynamic state of the medium. They should also assure a good numerical performance of the computer code based on the resulting mathematical model. As already mentioned previously, the necessary number of state variables may be significantly reduced if the existence of local thermodynamic equilibrium at each point of the medium is assumed (Schrefler 2002). In such a case, the physical state of different phases of water can be described by the same variable.
Having in mind all the aforementioned remarks, the state variables chosen for the presented model will be now briefly discussed. Use of temperature, which is the same for all constituents of the medium because of the assumption about the local thermodynamic equilibrium state, and use of solid skeleton displacement vector are rather obvious; thus, it needs no further explanation. As a hygrometric state variable, various physical quantities which are thermodynamically equivalent may be used, e.g. moisture content by volume or by mass, liquid water saturation degree, vapour pressure, relative humidity or capillary pressure. Analysing materials in the whole range of temperatures, one must remember that at temperatures higher than the critical point of water (i.e. 374.15 °C or 647.3 K) there is no capillary (or free) water present in the material pores, and there exists only the gas phase of water, i.e. vapour. Then, very different moisture contents may be encountered at the same moment in a cement-based material, ranging from full saturation with liquid water (e.g. in some nuclear vessels or in so-called moisture clog zone in a heated concrete, see England and Khoylou 1995, or in concrete at early ages), up to almost completely dry material. Moreover, some quantities (e.g. saturation or moisture content) which can be chosen as primary variables are not continuous at interfaces between different materials.
For these reasons, apparently it is not possible to use, in a direct way, one single variable for the whole range of moisture contents. However, it is possible to use a single variable that has a different meaning depending on the state. The moisture state variable selected in the model is capillary pressure (Gawin et al. 2002, 2003, 2006a) that was shown to be a thermodynamic potential of the physically adsorbed water and, with an appropriate interpretation, can be also used for description of water at pressures higher than the atmospheric one. The capillary pressure has been shown to assure good numerical performance of the computer code (Gawin et al. 2002, 2003, 2006a, b, c) and is very convenient for analysis of stress state in concrete, because there is a clear relation between pressures and stresses (Gray et al. 2009).
Therefore, as already shown, the chosen primary state variables of the presented model are the volume averaged values of: gas pressure, p g , capillary pressure, p c , temperature, T, and displacement vector of the solid matrix, u.
For temperatures lower than the critical point of water, T < T cr , and for capillary saturation range, S w > S ssp (T) (S ssp is not only the upper limit of the hygroscopic moisture range as mentioned earlier, but also the lower limit of the capillary one), the capillary pressure is defined according to Eq. 7.41.
For all other situations, and in particular for T ≥ T cr or where condition S w < S ssp is fulfilled (there is no capillary water in the pores), the capillary pressure substitutes—only formally—the water potential Ψ c , defined as:
where M w is the molar mass of water, R is the universal gas constant, and fvs is the fugacity of water vapour in thermodynamic equilibrium with a saturated film of physically adsorbed water (Gawin et al. 2002). For physically adsorbed water at lower temperatures (S w < S ssp and T < T cr ), the fugacity fvs should be substituted in the definition of the potential Ψ c , by the saturated vapour pressure p vs . Having in mind Kelvin’s equation, valid for the equilibrium state of capillary water with water vapour above the curved interface (meniscus) we can notice that in the situations where Eq. 7.47 is valid, the capillary pressure may be treated formally as the water potential multiplied by the density of the liquid water, according to the relation:
Thanks to this similarity, it is possible to “formally” use the capillary pressure during computations even in the low moisture content range, where the capillary water is not present in the pores and capillary pressure has no physical meaning.
7.4.4 Constitutive Laws for Crack Evolution
In the following, some peculiar aspects of the mechanical behaviour of the material strictly related to its porous nature are illustrated, taking into account that most of the phenomena/processes involved are described in Chap. 4, e.g. creep and microfracturing.
Furthermore, a more detailed discussion about the formulation of proper constitutive relationships for describing damage mechanics and visco-plasticity can be found in Sect. 7.5.
7.4.4.1 Momentum Balance
For completeness, the momentum balance equation is recalled here. Introducing the Cauchy stress second-order tensor σtotal (x, t) at any point x in the studied domain Ω, and at time t, and the applied forces per unit volume vector f (x, t), the momentum balance equations can be written, in a quasi-static case, i.e. neglecting the inertia effects, as:
These equations are complemented by the boundary conditions, which are either the prescription of displacements on some part of the boundary of the studied domain \(\Gamma _{u} = \partial\Omega _{u}\):
or the prescription of surface forces on the complementary part \(\Gamma _{u}^{q} = \partial\Omega _{u}^{q}\) the boundary:
where n denotes the outward normal vector.
7.4.4.2 Effective Stress Principle
Here, cement-based materials are treated as multiphase porous media; hence, for analysing the stress state and the deformation of the material, it is necessary to consider not only the action of an external load, but also the pressure exerted on the skeleton by fluids present in its voids. Hence, the total stress tensor σtotal acting in a point of the porous medium may be split into the effective stress ε s τ s , which accounts for stress effects due to changes in porosity, spatial variation of porosity and the deformations of the solid matrix, and a part accounting for the solid phase pressure exerted by the pore fluids (Pesavento et al. 2008; Gray et al. 2009)
where I is the second-order unit tensor, b H is the Biot coefficient, and p s is some measure of solid pressure acting in the system, i.e. the normal force exerted on the solid surface of the pores by the surrounding fluids.
Taking into account several simplifications (Pesavento et al. 2008; Gray et al. 2009), the relationship describing the effective stress principle can be written in the following manner:
where \(x_{s}^{ws}\) is the fraction of skeleton area in contact with the water and P s is an alternative measure of the “solid pressure”. The effective stress principle in the form of Eq. 7.54 allows to consider not only the capillary effects but also the disjoining pressure (Gawin et al. 2004; Pesavento et al. 2008; Gray et al. 2009).
7.4.4.3 Strain Decomposition
As already mentioned in Sect. 7.4.1.3, different strain components can be identified in a maturing element of concrete, both at early ages or at long term. Accordingly, the overall measured strain tensor ε may conventionally be split as following (Gawin et al 2004):
where ε el is the elastic strain, ε f is the cracking induced strain, ε T is the thermal strain, ε chem is the chemical strain (i.e. due to the hydration), ε cr is the creep strain which can be split into two parts: basic creep and drying creep.
In the following, some of these strain components will be analysed and discussed in view of a specific formulation of a mechanical constitutive model, also taking into account what has been presented in Chaps. 3 and 4.
7.4.4.4 An Example of a Mechanical Constitutive Model for Concrete
Concrete is modelled as a visco-elastic damageable material, whose mechanical properties depend on the hydration degree (De Schutter and Taerwe 1996). The relationship between apparent stresses σtotal, effective stresses \({\tilde{\varvec{\sigma}}}\) (in the sense of damage mechanics), damage D, elastic stiffness matrix E, elastic strains ε el , creep strains ε cr , shrinkage strains ε sh (caused by the fluid pressures as shortly described in Sect. 7.4.4.2), thermal strains- ε T and total strains ε reads:
Young’s modulus E, the tensile strength f t and the Poisson’s ratio ν vary due to hydration according to the equations proposed by De Schutter and Taerwe (1996) and De Schutter (2002).
Creep strain is computed using a rheological model made of a Kelvin-Voigt chain and two dashpots combined in serial way (see Fig. 7.21). The first two cells (aging Kelvin-Voigt chain and one single dashpot) are used to compute the basic creep, and the last cell (single dashpot) is dedicated to the drying creep strain. The scalar model in Fig. 7.21 is extended in 3D through the definition of a creep Poisson’s ratio (Sciumè et al. 2013).
Creep rheological model
The thermal strain ε th is related to the temperature variation:
in which β s is the thermal dilatation coefficient (kept constant) and 1 is the unit tensor.
To compute shrinkage, the elastic and the viscous parts have to be considered:
taking into account the solid pressure (see Eqs. 7.53–7.54), the constitutive model to compute the elastic shrinkage reads
where K T is the bulk modulus of the solid skeleton and b H is the Biot modulus. The viscous part of shrinkage strain, \(\dot{\varvec{\varepsilon}}_{sh}^{visc}\), is computed using the creep rheological model (represented in Fig. 7.21) in which the stress is now \(\dot{\varvec{\varepsilon}}_{sh}^{visc}\).
Damage D is linked to the elastic equivalent tensile strain, \(\hat{\varepsilon }\). To take into account the coupling between creep and cracking, the expression of \(\hat{\varepsilon }\) proposed by Mazars (1986) is modified by Mazzotti and Savoia (2003) and reads:
where β is a coefficient calibrated experimentally, which allows for considering that often cracking may occur even at lower tensile stress than the expected tensile strength. The damage criterion is given by:
where κ0(α) is the tensile strain threshold, which is computed from the evolution of tensile strength, and the Young’s modulus (De Schutter and Taerwe 1996). Considering the equivalent tensile strain, \(\hat{\varepsilon }\), and with respect to criterion Eq. 7.62 D is given by the equations proposed by Benboudjema and Torrenti (2008); the adopted damage model allows taking into account also evolution of fracture energy during hydration (De Schutter and Taerwe 1997).
To overcome the mesh dependency related to the local damage formulation, the model is regularised in tension with the introduction of a characteristic length related to the size of each finite element (Rots 1988; Cervera and Chiumenti 2006).
7.4.5 Boundary Conditions
With the momentum balance equation, the set of governing equations is complete, Eqs. 7.30, 7.31, 7.33 and 7.50. For the model closure, we need the initial and boundary conditions. The initial conditions (ICs) specify the values of primary state variables at time instant t = 0 in the whole analysed domain Ω and on its boundary Γ, (Γ = Γπ \(\Gamma _{\pi } \cup\Gamma _{\pi }^{q}\); π = g, c, t, u):
The boundary conditions (BCs) describe the values of the primary state variables at time instants t > 0 (Dirichlet’s BCs) on the boundary Γ π :
or heat and mass exchange, and mechanical equilibrium condition on the boundary \(\Gamma _{\pi }^{q}\) (the BCs of Cauchy’s type or the mixed BCs):
where n is the unit normal vector, pointing towards the surrounding gas, qa, qv, qw and qT are respectively the imposed fluxes of dry air, vapour, liquid water and the imposed heat flux, and \(\bar{\varvec{\sigma}}\) is the imposed traction, ρv∞ and \(T_{\infty }\) are the mass concentration of water vapour and the temperature in the far field of undisturbed gas phase, e is emissivity of the interface, and σ o the Stefan–Boltzmann constant, while α c and β c are convective heat and mass exchange coefficients.
The boundary conditions, with only imposed fluxes given, are called Neumann’s BCs. The purely convective boundary conditions for heat and moisture exchange are also called Robin’s BCs.
7.4.6 Numerical Formulation
The set of nonlinear partial differential equations that controls the processes of mass and heat transport (Eqs. 7.30 and 7.31) plus the one Eq. 7.33 is usually discretised in the space domain by means of Finite Element Method. Also Equation 7.50 is usually discretised in the space domain by means of Finite Element Method.
According to the FEM procedure, the governing equations are written by using the weighted residual method, and the standard Galerkin procedure is usually adopted. Time discretisation is achieved by means of the standard Finite Difference Method. A non-symmetric, nonlinear system is finally obtained, and linearisation, usually by means of the Newton–Raphson method, is required (Zienkiewicz and Taylor 2000).
The final set of discretised, linearised governing equations is solved as a monolithic system or, alternatively, by means of a staggered coupled procedure (see Gawin et al. 2003, 2006a, b, 2008; Sciumè et al. 2013).
Starting from the previous initial-boundary value problem, the variational formulation can be obtained. Then, the standard Galerkin discretisation, replacing the weighting functions with the shape functions, is adopted. For the state variables, we can write:
The resulting system of equations can be written in the following concise discretised matrix form:
with
where the nonlinear matrix coefficients C ij (xj), K ij (x j ) and (x j ) are defined in detail in Pesavento (2000), Gawin et al. (2003, 2006a, b).
The time discretisation is accomplished through a fully implicit finite difference scheme (backward difference):
where superscript i (i = g, c, t, u) denotes the state variable, n is the time step number, and Δt is the time step length.
The equation set (7.69) can be linearised according to the following scheme:
where k is the iteration index and \(\frac{{\partial {\varvec{\Psi}}_{i} }}{{\partial {\mathbf{x}}}}\) is Jacobian matrix.
More details concerning numerical techniques used for solution of the model equations can be found in Pesavento (2000) Gawin et al. (2003, 2006a, b, 2008, 2009).
7.4.6.1 Solution Strategy
A monolithic approach is often adopted for solution of the linearised system. In this approach, all the equations are solved at the same time and all the state variables are updated simultaneously during the iterative procedure. This approach guarantees the optimal convergence of the system especially when dealing with strong nonlinearities (Pesavento 2000; Gawin et al. 2003; Bianco et al. 2003).
Alternatively, the system can be solved using a staggered procedure that permits to solve the equations sequentially (Sciumè et al. 2013). A specific iterative algorithm to account for the interaction between all the transfer processes to conserve their full coupling is required. Staggered procedures show a superior flexibility compared to monolithic ones if successive fields have to be introduced in the problem. Moreover, an appropriate partitioning reduces the size of the discretised problem to be solved at each time step. For further details, see Sciumè et al. (2013).
7.4.7 Application of the Proposed Approach
In this section, two application cases are presented. The mechanical constitutive law used for this purpose is the one described in Sects. 7.4.2 and 7.4.4. For sake of brevity tables with the assumed parameters that are not reported here, can be found in the referred papers.
7.4.7.1 Cracking of a Reinforced Concrete Beam Under Variable Environmental Condition
As typical application of the approach based on TCAT and validation of the resulting model, the results of the numerical simulation of cracking of a massive concrete beam are shown. The analysed test is a large beam specimen built for ConCrack (2011): the international Benchmark for Control of Cracking in Reinforced Concrete Structures (Fig. 7.22). This benchmark has been organised within the French national project CEOS (Comportement et Evaluation des Ouvrages Speciaux vis-à-vis de la fissuration et du retrait) dedicated to the analysis of the behaviour of special large specimens concerning cracking and shrinkage.
Experimental specimen (right) and finite elements mesh (left)
Here, one of the experiments of the benchmark programme and its numerical simulation are presented. The test is divided in two phases. During the first 48 h after casting, the structure is thermally isolated and protected from drying. Then, after two days the isolation and the formwork are removed and the structure is conserved during two months in the open environment. During the two phases of the test, the longitudinal strains of the structure are globally restrained by two metallic struts. After two months, the structure is loaded by a static bending test. For more details on the analysed test, see the reference Web page of the benchmark (https://www.concrack.org). The mesh of concrete is made of 3D elements (Fig. 7.22, left). Truss elements rigidly linked with the concrete 3D mesh are used to model the struts. The local damage model of Mazars (1986) has been used. This approach allows predicting cracking in mode I (De Sa et al. 2008; De Sa and Benboudjema 2012) which is the case here, since cracking is induced by shrinkage restraint. The model is regularised in tension with the introduction of a characteristic length, l c , related to the size of each finite element (Rots 1988; Cervera and Chiumenti 2006) to overcome the possible mesh dependency. The model for concrete at early age is that of Sciumè et al. (2013).
The boundary conditions are assumed to be of convective type for both heat and mass exchange, see Simoni and Schrefler (2014) for details. For the material parameters, see Sciumè et al. (2012).
During the first and second phases, the longitudinal displacements of the specimen have been globally restrained by the two metallic struts. Therefore, during hydration the thermal extension of the concrete has been restrained and so in this phase the concrete cross section was compressed. After the hydration, it is the shrinkage of the beam that has been contrasted. The position of the displacement measurement points are depicted in Fig. 7.23 and the deformed configuration and the damage at day 60 in Fig. 7.24. The solution is not symmetric due to the non-symmetric solar irradiation: this has been experimentally measured by the benchmark organizers and taken into account in the modelling process.
Position of the displacement measurement points (and coordinates)
Deformed configuration (× 500) and damage after 60 days. Face exposed to the sun (left) and face not exposed to the sun (right)
The comparison between the experimentally and numerically obtained relative displacements and axial force is shown in Fig. 7.25. Note the complex displacement evolution.
Relative displacement between the point C and D (left). Axial force in the two metallic struts that restrain shrinkage (right)
After two months, a static four-point bending test has been carried out until rupture. Compression has been applied by eight jacks and live controlled by a pressure sensor with an independent data registration system. The load was applied with increments of 50 kN, and each loading step is kept during 20 min. The comparison between the experimental and numerical crack pattern and the force versus displacement diagram is shown in Fig. 7.26. The comparison in Figs. 7.25 and 7.26 with experimental results shows that the adopted approach is able to simulate such complicated multifield fracture phenomena in realistic engineering structures. For more results concerning hydration and thermal field, the reader is referred to the Website of ConCrack (2011) and the final report.
Comparison between the numerical and experimental crack pattern (left). Force versus displacements during the bending test (right)
7.4.7.2 Modelling of Repaired Beam
The numerical simulation of the thermo-hygro-mechanical behaviour of two repaired beams is presented in this subsection (see Sciumè et al. 2013). Numerical results are compared with the experimental ones of the reference experiment performed by Bastien Masse (2010).
The geometry of the reinforced beams is represented in Fig. 7.27. Three identical reinforced beams were cast for the experiment. At thirty days after the casting, two of these beams, after the hydrodemolition of 30 mm of the upper part, had been repaired: one using the ordinary concrete (OC) (very similar to that using to cast the three beams) and the other using the ultra-high-performance fibre-reinforced concrete (UHPC). The third beam is the reference specimen. Two fibre-optic sensors (FO-h and FO-b) were placed inside the beams. More details on the experimental procedure (laboratory conditions, specimen equipment, etc.) can be found in Bastien Masse (2010).
Geometry and FE mesh of the repaired beam
The beams have been modelled in 2D plane stress; for more information about the assumed boundary conditions and the FE discretization, refer to Sciumè et al. (2013).
Is important to highlight that the THCM history of the two beams before the repair and the wetting procedure for the preparation of the substrate have been also taken into account within the modelling process (the numerical simulations start from the casting of the beams), and this has been critical to succeed in predictive numerical results.
Before performing the simulation of the beams, the input parameters for the two considered concretes have been identified. This has been done exploiting experiments performed by Bastien Masse (2010) for the characterisation of the two repair materials. Comparison between experimental results and numerical ones for adiabatic calorimetry, creep properties, Young’s modulus and Poisson’s ration evolution, autogenous and drying shrinkage is shown in Fig. 7.28.
(Adapted from Sciumé et al. 2013)
Experimental tests exploited to identify the model parameters: a adiabatic calorimetry, b creep test, c Young’s modulus and Poisson’s ration evolution, d autogenous and drying shrinkage for OC, e autogenous and drying shrinkage for UHPC. Symbols are experimental data, while solid and dashed lines are numerical results.
In Fig. 7.29, for the two repair cases, relative humidity at 1 h, 1 week and 1 month after repair is depicted. In the UHPC, self-desiccation has also a relevant impact on the decrease of relative humidity.
(Adapted from Sciumé et al. 2013)
Relative humidity at 1 h, 1 week and 1 month after repair for the two simulated cases.
Figure 7.30 shows the numerical and the experimental results for the vertical displacement of the three beams measured using the linear potentiometer placed in the lower middle point of the beams. A good agreement between the experimental results and the numerical ones can be observed. The deflection of the reference beam is mainly due to its weight and also to the not symmetric position of the steel reinforcements: in other words the shrinkage of the upper and lower part of the beam generates an eccentric force which increases the deflection of the beam. In the repaired beams, the deflections are accentuated by the autogenous and drying shrinkage of the fresh restoration materials.
(Adapted from Sciumé et al. 2013)
Experimental (open symbols) and numerical results (solid lines) for the vertical displacement of the middle points of the three beams. The time “zero” corresponds to the application of the repairs.
After 2 months, the two repaired beams have been submitted to a three-point bending test, and also in this case, the presented model has shown good accuracy in predicting experimental results (Sciumè et al. 2013).
7.5 Constitutive Laws for Crack Evolution
Damage of concrete is connected with formation of discrete cracks. The study of damage in which damage is modelled in a discrete manner is the interest of fracture mechanics. Discrete crack models perform well in representation of structural behaviour governed by a few dominant cracks with large crack widths and which location and direction of propagation can be known a priori, and as such are suitable for modelling of laboratory tests. More often damage of concrete due to crack formation is represented with smeared models of cracking. Smeared crack models are good for representation of typical, properly designed reinforced concrete structures characterised by many cracks of small widths. The cracked material is treated as continuum, and its cracked parts are assigned with modified properties. Usually, it is assumed that the cracked element can no longer transfer the load in the direction perpendicular to the crack plane (tensile stresses) but can still transfer the parallel (shear) stresses (Hofstetter and Mang 1995).
7.5.1 Damage Models
The failure of concrete is connected with formation of a crack under certain level of stress. Formation of the crack is a local phenomenon; however, homogenisation techniques can be used to transform a cracked element into a continuum medium and apply non-local damage models. Continuous damage models are based on phenomenological approach to description of an elastic material containing cracks, in which the effect of microcracking on the elastic stiffness of concrete (a quasi-brittle material) is introduced with internal state variables which act on the elastic stiffness of the material (Pijaudier-Cabot 1995). In the simplest damage model, the effect of damage is represented as degradation of the modulus of elasticity of concrete:
where σ ij is the stress component, ε kl is the strain component, and \(E_{ijkl}^{damaged}\) is the stiffness coefficient of the damaged material. Ladevèze (1983) has introduced a model which contains two damage variables d and δ, which are equal to 0 in undamaged material and reach 1 at complete failure. By assuming d = δ, Mazars (1984) has proposed a simplified formulation of this model which reads:
where E 0 and ν 0 are elastic modulus and Poisson’s ratio of undamaged isotropic material and δ ij is a Kronecker delta.
Most commonly used non-local damage models are scalar isotropic models, which introduce a scalar variable to represent damage. Nevertheless, there are formulations based on plasticity models (see, e.g. Leblond et al. 1992) or anisotropic damage models (see, e.g. Pijaudier-Cabot et al. 1994; Valanis 1991).
Damage can be controlled by either energy release rate or by tensile strain. In the first approach, there is no distinction between the effect of damage in compression and tension, while the other model does not have such limitations; thus, it is more suitable for modelling of concrete. However, since the level of the compressive stresses induced by the early-age effects is relatively small in the discussed massive concrete structures, many authors apply damage criteria which account for material degradation only in tension. For that purpose, stress–strain relationship with strain softening in tension is used (such relationships were proposed, e.g., by Bažant and Oh (1983) or Gutsch and Rostásy (1994)). These models involve tensile strength of concrete, f t , and fracture energy, G f .
The most popular strain-based damage model was introduced by Mazars (1984) and developed by Mazars and Bournazel (1996) for the purpose of modelling early-age concrete, modified and presented in its latest form by Benboudjema and Torrenti (2008). The damage criterion which determines the formation of cracking is defined as:
where \(\underline{\varepsilon }\) is the equivalent tensile strain and \(\varepsilon_{ctu} (\alpha )\) is the tensile strain capacity defined as a ratio between the tensile strength, f t (α), and the modulus of elasticity, E(α), at the time of analysis, t, expressed as a function of degree of hydration, α(t):
After the threshold strain is exceeded \(\underline{\varepsilon } > \varepsilon_{ctu} (\alpha )\), cracking appears. It is assumed that part of the element is sound and part of the element is cracked; only the sound part of the element can transfer the stress, which is the effective stress, \(\underline{\sigma }\):
The influence of progressing cracking on stress, σ, is expressed with the damage, D, and effective stress \(\underline{\sigma }\):
The damage, D, describing the softening behaviour of concrete in tension is given by the formula:
where A t and B t are material parameters defining softening branch of σ − ε diagram.
When modelling softening of concrete as damage progresses, it must be remembered that the results of numerical analysis are strongly mesh-dependent (Azenha et al. 2009, 2011; Benboudjema and Torrenti 2008; Jendele et al. 2014). It is advised to discretise the analysed structure based on the density of the fracture energy, G f , and internal length, l c (Hillerborg et al. 1976). The internal length bridges the gap between damage and fracture mechanics as the fracture energy is a function of this length (Pijaudier-Cabot 1995).
In order to apply damage models, two characteristics of the material need to be defined (Pijaudier-Cabot 1995): softening stress–strain curve and internal length of the non-local continuum. These characteristics can be obtained either experimentally or with the inverse analysis (FEM calculations on simple structural elements).
7.5.2 Plasticity Models
Other approach to modelling early-age concrete is based on plasticity models, defined for three-dimensional complex stress states in which damage of the element—its occurrence and character—is defined by a failure criterion. Failure criterion can be graphically represented by a spatial surface, called failure surface. Behaviour of concrete element after reaching failure surface is defined by the appropriate material model, as is its behaviour before damage.
In modelling early-age concrete, the simplest material model is viscoelastic model, which extensions led to definition of other models based on plasticity, i.e. viscoelastic–plastic, elasto-viscoplastic and viscoelasto-viscoplastic models. A concise presentation and comparison of these models were presented by Klemczak (2007). In the viscoelastic model, the stress–strain relationship has a form:
where notation Δεcr (ti+1) is given by the formula:
Dve is a viscoelasticity matrix:
where
in which C(t, τ) is a creep function.
In viscoelastic–plastic model, the strain tensor consists additionally of a plastic strain component:
The magnitude of plastic strain is determined by the law of plastic flow:
where dλ is a scalar proportionality coefficient and g is the surface of plastic potential, defined in the stress space as:
The yield surface evolution, which characterises plastic behaviour of concrete, for maturing concrete depends on the plastic parameter κ = κ(εp) and the age of concrete t:
The yield surface f represents real physical states; thus, the point representing the current state of stress in the stress space must always remain on the yield surface. This means that each load must correspond to such a change of hardening parameter that the point representing the state of stress is located on the yield surface. This consistency condition may be written as:
The stress–strain relationship for the viscoelasto-plastic model can be defined as:
or in the following form:
with:
where n is a vector normal to the yield surface, m is a vector normal to the plastic potential surface, and h is the hardening modulus given as:
The failure criterion for a viscoelasto-plastic model is defined as follows:
Finally, viscous behaviour of concrete can be considered in the plastic phase, which led to formulation of viscoplastic models. One approach to determination of viscoplastic strains is based on the overstress concept, which states that viscoelastic strain develops only when a stress path goes outside the yield surface. The viscoelastic strain rate is proportional to the excess stress. There are two main proposal of models based on this concept: Perzyna model (Perzyna 1966) and Duvant-Lions model (De Borst et al. 2001). The first model is more general by assuming a function of the excess stress, while in the other one the viscoelastic strain rate is directly proportional to the vector of stress increase above plastic state. It must be, however, emphasised that in both proposals it is possible that stress path goes outside the yield surface; thus, the consistency condition df = 0 is not satisfied.
The consistency condition is satisfied in a consistency concept of the viscoplastic model in which the viscoplastic strain is defined as:
where \(\dot{\lambda }\) is a positive scalar called a consistent parameter (De Borst et al. 2001; Winnicki 2001).
Stress–strain relationship can be expressed in the following rate form:
The yield surface and failure surface are expressed as functions of hardening parameter and its rate:
Such formulation satisfies the consistency condition. The age of concrete is implicitly considered in the adopted hardening law κ = κ(εvp, t).
Damage of the element is defined by failure criterion. When defining the failure surface for concrete, it was observed in the experimental tests (Chen 1982; Majewski 2003) that the shape of deviatoric section is close to triangular in the zone of tensile and low-compressive stresses and similar to circular in the zone of high-compressive stresses. The deviatoric section is smooth and convex, but it is not a circle and the surface is not a solid of revolution. The meridians are smooth, convex and curvilinear but for practical ranges can be approximated with straight lines.
There have been multiple proposals for the failure surface to represent the behaviour of concrete under the complex stress state. The single- and double-parameter failure criteria used for description of the failure surface for concrete, such as the Rankine, Mohr–Coulomb and Drucker–Prager failure criteria, are commonly applied for description of the failure surface of concrete (Jendele et al. 2014; Lackner and Mang 2004); however, each of them fails to represent some major characteristic of the concrete behaviour. Thus, more advanced approaches are used, e.g. three- or five-parameter Willam–Warnke criterion or four-parameter Ottosen criterion. The criteria are expressed either with stress invariants (I 1 , J 2 and θ) or by means of the mean and octahedral stress (σ m , τ oct and θ).
The three-parameter Willam–Warnke criterion provides good representation of concrete behaviour within the range of mean stresses from 4/3f c to 1/3f t . However, because of the assumption of linearity of meridians, the strength within bi- and three-axial tensile stresses and three-axial compression is overestimated (Majewski 2003). This shortcoming is removed in Ottosen failure criterion and five-parameter Willam–Warnke criterion where curvilinear meridians are defined. According to the five-parameter Willam–Warnke criterion, deviatoric section is still defined with a triple elliptical shape, but the ratio of the meridians radii is not constant but depends on the level of mean stresses. Meridians are defined with curved lines (second-order parabolas) which requires introduction of two additional parameters. Both failure surfaces are “open” in the direction of compressive stresses on the mean stresses axis.
To remove the shortcomings of these criteria and limit the complexity of the model, Majewski proposed a modified three-parameter Willam–Warnke failure criterion (Majewski 2003, 2004). In his approach, meridians are straight lines, but instead of defining meridians in such a way that meridian crosses the points representing the values of appropriate strengths of concrete, the best straight-line approximation was derived. Moreover, to limit the stresses in high-compressive stresses range, a closing cap was defined (tension cutoff) (see Fig. 7.31).
(MWW3, adopted after Majewski 2003)
Deviatoric and axiatoric sections of failure surface with the modified three-parameter Willam–Warnke criterion
Under the same assumptions, the modified Willam–Warnke criterion was adopted by Klemczak (2007) for early-age concrete. MWW3 was calibrated based on the laboratory tests (see Fig. 7.32a). Development of the failure surface was considered as mechanical properties defining the shape of the surface (compressive and tensile strengths) change in time (see Fig. 7.32b).
(Adopted after Klemczak 2007)
MWW3 failure surface for hardening concrete: a. calibration based on experimental results, b. development during hardening process.
Damage intensity factor was proposed by Majewski (2003) to determine the level of damage of the element. DIF relates the actual stress level \(\tau_{oct}^{{}}\) with respect to the stress at failure surface \(\tau_{okt}^{f}\) (Fig. 7.33):
(Adopted after Majewski 2003)
Graphical interpretation of damage intensity factor.
The value of the damage intensity factor equal to unity signifies reaching of failure surface and damage, which character depends on the location where the failure surface was reached. In case of massive concrete structures under early-age effects, failure surface is predominantly reached within hydrostatic tensile stresses, which is equivalent with formation of a splitting crack in the direction perpendicular to the principal tensile stress.
Behaviour of concrete after damage (i.e. reaching failure surface) is governed by the applied softening law. If the stress path reaches the failure surface in the area of mean tensile stress, where failure manifests as a splitting crack, a substantial anisotropy of the concrete appears. Then, when describing material after failure the law of softening and material anisotropy is considered.
7.6 Probabilistic Modelling of Mechanical Behaviour
This section presents some alternative methods to modelling the mechanical behaviour of concrete structures in service life conditions. On the contrary of what was described in Sect. 7.5, in which all the models and constitutive laws have a deterministic nature, this new class of models is based on a probabilistic approach. They are capable to give a detailed information about cracks spacing and opening.
7.6.1 Probabilistic Explicit and Semi-Explicit Cracking Model for Concrete
7.6.1.1 Probabilistic Explicit Cracking Model
The presented model was first developed at IFSTTAR by Rossi and Richer (1987) and Rossi and Wu (1992) and recently improved by Tailhan et al. (2010). It describes the behaviour of concrete via its two major characteristics: heterogeneity and sensitivity to scale effects (see Rossi et al. 1994). The physical basis of the model (presented in detail in Rossi and Richer 1987; Rossi and Wu 1992) can be summarised as follows:
-
The heterogeneity of concrete is due to its composition. The local mechanical characteristics (Young’s modulus E b , tensile strength f t , shear strength τc) are randomly distributed.
-
The scale effects are a consequence of the heterogeneity of the material. The mechanical response directly depends on the volume of material that is stressed.
-
The cracking process is controlled by defects in the cement paste, by the heterogeneity of the material, and by the development of tensile stress gradients.
The following points specify how the numerical model accounts for these physical evidences:
-
The model is developed in the framework of the finite element method, each element representing a given volume of (heterogeneous) material.
-
The tensile strength is distributed randomly on all elements of the mesh using a probability distribution function whose characteristics depend on the ratio: volume of the finite element/volume of the largest aggregate and the compressive strength (as a depends on the mesh, while the volume of the largest aggregate is a property of the concrete, see Rossi and Richer 1987; Rossi and Wu 1992; Tailhan et al. 2010).
-
The shear strength is also distributed randomly on all elements using a distribution function: (1) its mean value is independent of the mesh size and is assumed equal to the half of the average compressive strength of the concrete, and (2) its deviation depends on the element’s size and is the same (for elements of same size) as that of the tensile strength.
-
In the explicit cracking model, developed, in priority, to perform 2D simulations, the cracks are explicitly represented by interface elements of zero thickness. These elements connect volume elements representing uncracked plain concrete. Failure criteria of Rankine in tension and Tresca in shear are used. As far as tensile or shear stresses remain lower than their critical values, the interface element ensures the continuity of displacements between the nodes of the two neighbouring volume elements. The material cell gathering these two volume elements and the interface element remains therefore elastic. Once one of the preceding failure criteria is reached, the interface element opens and an elementary crack is created. Its tensile and shear strengths as well as its normal and tangential stiffness values become equal to zero (Rossi and Richer 1987; Rossi and Wu 1992; Tailhan et al. 2010). In case of crack reclosure, the interface element recovers its normal stiffness and follows a classical Coulomb’s law (Rossi et al 1996).
Note that in this model, the creation and the propagation of a crack is the result of the creation of elementary failure planes that randomly appear and can coalesce to form the macroscopic cracks (see Fig. 7.34). Note also that, in fact, the finite element volume considered to determinate the tensile strength distribution function is, in the explicit cracking model, the total volume of two volume elements interfaced by one interface element (see Fig. 7.34).
Probabilistic concrete cracking model
To conclude, it can be said that this probabilistic model is in fact a deterministic one with probabilised parameters. Hence, it is necessary to perform a large number of computations to statistically validate the results following a Monte Carlo method, because only one simulation is not relevant when a probabilistic model is used. The number of numerical simulations needed is related to the structural problem concerned and the scattering of the structural response. In this way, it is easy to perform a safety analysis of the loaded structure.
7.6.1.2 Probabilistic Semi-Explicit Cracking Model
The semi-explicit cracking model is based on the same physical assumptions than the explicit one. The main difference between the two approaches is related to the way of modelling the cracks. As a matter of fact, in the semi-explicit cracking model, cracks are not modelled by using interface elements but by using volume elements (linear triangles in 2D or linear tetrahedron in 3D).
The failure criteria of Rankine in tension and Tresca in shear are thus applied at the gravity centre of the elements. When one of these criteria is reached in one element, all the components of the matrix of rigidity of the volume element become equal to zero. It is a “kill element” approach. By this way, a crack is modelled by a hole.
Note that, in the frame of this semi-explicit cracking model, the finite element volume considered to determinate the tensile strength distribution function is the volume of the volume element itself.
7.6.2 Concrete-Rebar Bond Model
A simple and robust model has been developed and validated at IFSTTAR (see Phan et al. 2013a, b, 2015). It takes into account the nonlinear behaviour of the concrete-rebar bond in the frame of damage mechanics. It can represent physical phenomena such as interface sliding, cracks appearance and degradation process. The concrete-rebar bond is modelled as interface elements. Their role is to:
-
Ensure the displacement continuity between the concrete and the steel before the slip of the interface and before the cracking of the concrete, thus ensuring the transfer of stresses between steel and concrete.
-
Represent the macroscopic mechanical effect of the rebar at the ribs—which is not explicitly represented in the mesh.
-
Simulate a local failure between steel and concrete along the rebar resulting from a loss of the local adhesion due to shear cracking.
-
Simulate the local friction between the concrete and the steel after the interface failure.
The model is implemented in 2D and 3D. It models the concrete-rebar bond as a material zone that progressively degrades in shear (the tensile failure is neglected). Prior to total failure, stresses are continuously transmitted through the interface.
The interface model is based on a damage model that maintains a constant level of stress when the critical shear has been reached (see Fig. 7.35). When the relative tangential displacement between the concrete and the rebar exceeds a critical value, the interface element is declared broken (Rossi 1993). After failure, a Mohr–Coulomb type of friction behaviour is maintained (see Fig. 7.36).
a Steel–concrete interface behaviour law and b damage evolution
Mohr–Coulomb friction after failure of the steel–concrete interface
The interface model is deterministic. This is a valid approximation because the cracking process around the rebar is governed by the presence of the ribs (rather than the heterogeneity of concrete) (Rossi 1993).
Only the values of the maximum shear stress, C, and of the tangential critical relative displacement, \(\delta_{t}^{cri}\), have to be determined. This is done by numerical inverse analysis of tie-beam tests.
7.6.3 Probabilistic Explicit Cracking Model for FRC
The extension of the probabilistic explicit model to analyse the cracking process of FRC structures is very simple.
The first step is to create cracks in the matrix, that means, in the concrete. It is realised by opening the interface elements as described in Sect. 7.6.1.
Thus, after cracking, the interface element rigidity is considered different for normal and tangential displacements. In 2D, normal and tangential rigidities of the interface element are \(K_{n}^{'}\) and \(K_{t}^{'}\), respectively. This post-cracking elastic behaviour exists until it reaches a limit, \(\delta_{0}\), related to the normal displacement. Once this limit value is reached, the mechanical behaviour of the interface element changes. As a matter of fact, the normal stress is considered as linearly decreasing with the normal displacement in order to take into account the damage of the bond between the concrete and the fibre and the pull-out of the fibre. The decreasing evolution is obtained with a damage model.
Finally, the interface element is considered definitely broken, and its normal and tangential rigidities are equal to zero, when the normal displacement occurring during the damage step reaches a critical value \(\delta_{c}\). This value corresponds to the state where the effect of fibres is considered negligible.
The post-cracking total energy dissipated during the linear increase and followed by the linear decrease of the normal stress is considered randomly distributed on the mesh elements as for the material tensile strength. However, the random distribution results from a log-normal distribution function with a mean value independent of the mesh elements size and a standard deviation increasing with the decrease in the mesh elements size, which is physically logical (see Rossi 2012). In practice, to model a given structure, the distribution function is determined in the following manner:
-
The mean value is directly obtained by performing a certain number of uniaxial tensile tests on notched specimens (the post-cracking energy is classically determined from the load-crack opening curve) or indirectly by performing an inverse approach based on numerical simulations of bending test.
-
The standard deviation, which depends on the mesh elements size, is determined by an inverse analysis approach that consists of simulating uniaxial tests (on notched specimens) or bending tests with different element mesh sizes. As a matter of fact, knowing from the mean value of the post-cracking energy, several numerical simulations are realised for each mesh size and the standard deviation related to each mesh size is obtained by fitting the experimental results (in terms of mean and standard deviation of the numerical responses compared to their corresponding experimental values). By this way, it is possible to find a relation between the standard deviation and the finite element mesh size.
The numerical mechanical behaviour adopted for the post-cracking step is illustrated in Fig. 7.37. Only the normal stress–normal displacement curve is considered in this figure.
Modelling of the post-cracking behaviour of FRC
7.6.4 Example of Application of the Numerical Model Related to RC Structures
This example of validation of the numerical model was published in Phan et al. (2013b).
The structure concerned is a reinforced slab–beam submitted to three-point bending, 3.30 m long (3.00 m between supports), 0.80 m wide, and 0.15 m thick (an element must have a thickness ≤1/5 of its width to be considered a slab). All details (geometry, reinforcement, loading conditions, etc.) concerning this RC structure are given in Fig. 7.38.
Slab–beam dimensions, type of reinforcement and loading conditions
The mean compressive strength of the concrete studied was 55 MPa.
The mechanical properties of the steel rebars were:
-
Young’s modulus: 200000 MPa,
-
Linear hardening modulus 1120 MPa,
-
Elastic limit strength: 640 MPa,
-
Ultimate limit strength: 720 MPa,
-
Ultimate strain: 12%.
Tie-beam tests were performed in parallel of this structural test to get (by inverse approach, see Sect. 7.6.3) the values of the parameters of the concrete-rebars bond model.
These values were the following: C = 16 MPa and \(\delta_{t}^{cri}\) = 23 μm.
3D simulation of the beam–slab was performed. The finite element mesh used is shown in Fig. 7.39.
3D finite elements mesh of the beam–slab
The finite elements used were:
-
hexahedral linear elements for the steel bar,
-
3D linear interface elements for the concrete/steel bond,
-
tetrahedral linear elements for the concrete.
Figure 7.40 shows a comparison between experience and numerical simulation concerning the global behaviour of the structure represented by the load–deflection curve.
Load–deflection curves—comparison between experience and numerical simulation
Figure 7.41 shows an example of cracking profile obtained with the numerical simulations.
Slab–beam test—example of cracking profile obtained with the 3D simulations
Figures 7.42 and 7.43 summarise comparison between numerical simulations and experimental tests in terms of mean, min and max curves related, respectively, to the number of cracks versus load and to the cracks opening versus load.
Slab–beam test—number of cracks versus load—mean, min, max curves—comparison between experience and numerical simulations
Slab–beam test—cracks opening versus load—mean, min, max curves—Comparison between experience and numerical simulations
7.6.5 Example of Application of the Numerical Model Related to FRC Structures
This example of validation of the numerical model has been published in (Rossi et al. 2015). The FRC structure concerned was a steel fibre-reinforced concrete (SFRC) beam submitted to four-point bending. The experimental campaign that allows the comparison of experimental and numerical results was conducted at Ecole Polytechnique de Montréal, Canada (de Montaignac de Chauvance 2011). The dimensions (length, width, height) of the beam were the following: 2600 × 400 × 300 mm. The testing apparatus used for this experimental campaign is shown in Fig. 7.44.
Beams’ dimensions, testing apparatus and instrumentation related to the experimental tests
The SFRC used was a self-compacting one containing 78 kg/m3 of hooked-end steel fibres. These fibres were 35 mm long and had a diameter of 0.55 mm. This SFRC achieved an average compressive strength of approximately 60 MPa at 28 days.
In order to characterise the tensile behaviour, uniaxial tension tests were performed on this SFRC. The RILEM uniaxial tension test was conducted on notched core cylinders (h = 100 mm and Ø = 85 mm). Six specimens for each mix were cored horizontally from a 500 × 600 × 400 mm block casted in addition to the beams.
These tensile tests were performed to determinate, by inverse approach, the parameters of tensile behaviour model of the SFRC (Sect. 7.6.4).
The parameters of the tensile behaviour model related to the studied SFRC were the following:
-
Average tensile strength: 2.46 MPa,
-
Tensile strength standard deviation: 0.34 MPa,
-
Average post-cracking energy: 4.26 MPa.mm,
-
Post-cracking energy standard deviation: 0.88 MPa.mm,
-
δ 0 : 0.05 mm,
-
δ C : 4 mm.
The finite element mesh used to simulate the beam behaviour is shown in Fig. 7.45.
Finite elements mesh of the SFRC beam
Figure 7.46 shows a comparison between the global behaviour of the SFRC beam obtained with the experience and with the numerical simulation. This global behaviour is considered in the frame of the load–deflection curve of the beam.
Load–deflection curve—comparison between experience and numerical simulation
Figure 7.47 shows an example of cracking pattern obtained with the numerical simulation.
Example of cracking pattern obtained with the numerical simulation
Figure 7.48 proposes a comparison between the evolution (with the loading moment) of the maximum crack opening displacement obtained experimentally with the one obtained numerically.
Maximum crack opening displacement versus loading moment—comparison between experience and numerical simulation
References
Abbasnia, R., Shekarchi, M., & Ahmadi, J. (2013). Evaluation of concrete drying shrinkage related to moisture loss. ACI Materials Journal, 110, 269–277.
Andreasik, M. (1982). Naprężenia termiczno–skurczowe w masywach betonowych. Ph.D. thesis. Cracow University of Technology, Cracow, Poland.
Aurich, M., Filho, A. C., Bittencourt, T. N., & Shah, S. P. (2009). Finite element modeling of concrete behaviour at early age. Revista IBRACON de Estruturas e Materiais, 2, 37–58.
Ayano, T., & Wittmann, F. H. (2002). Drying, moisture distribution, and shrinkage of cement-based materials. Materials and Structures, 35, 134–140.
Azenha, M., Faria, R., & Ferreira, D. (2009). Identification of early-age concrete temperatures and strains: Monitoring and numerical simulation. Cement & Concrete Composites, 31, 369–378.
Azenha, M., Sousa, C., Faria, R., & Neves, A. (2011). Thermo–hygro–mechanical modelling of self-induced stresses during the service life of RC structures. Engineering Structures, 33, 3442–3453.
Baggio, P., Majorana, C. E., & Schrefler, B. A. (1995). Thermo-hygro-mechanical analysis of concrete. International Journal for Numerical Methods in Fluids, 20, 573–595.
Baroghel-Bouny, V., et al. (1999). Characterization and identification of equilibrium and transfer moisture properties for ordinary and high-performance cementitious materials. Cement and Concrete Research, 29, 1225–1238.
Bastien Masse, M. (2010). Étude du comportement déformationnel des bétons de réparation. Master Thesis. Université de Montréal.
Bažant, Z. P., Cusatis, G., & Cedolin, L. (2004). Temperature effect on concrete creep modeled by microprestress-solidification theory. Journal of Engineering Mechanics, 130, 691–699.
Bažant, Z. P., Hauggaard, A. B., Baweja, S., & Ulm, F.-J. (1997). Microprestress-solidification theory for concrete creep. I: Aging and drying effects. Journal of Engineering Mechanics 123, 1188–1194.
Bažant, Z. P., Jirásek, M., et al. (2015). RILEM draft recommendation: TC-242-MDC multi-decade creep and shrinkage of concrete: material model and structural analysis. Materials and Structures, 48, 753–770.
Bažant, Z. P., & Najjar, L. J. (1972). Nonlinear water diffusion in nonsaturated concrete. Materials and Structures, 5, 3–20.
Bažant, Z. P., & Oh, B. H. (1983). Crack band theory for fracture of concrete. Materials and Structures, 16, 155–177.
Bažant, Z. P., & Thonguthai, W. (1978). Pore pressure and drying of concrete at high temperature. Journal of the Engineering Mechanics Division ASCE, 104, 1059–1079.
Bažant, Z. P., & Thonguthai, W. (1979). Pore pressure in heated concrete walls: theoretical prediction. Magazine of Concrete Research, 31(107), 67–76.
Bažant, Z. P., & Kaplan, M. F. (1996). Concrete at high temperatures: material properties and mathematical models. Harlow: Longman.
Bear, J. (1988). Dynamics of fluids in porous media. New York: Dover.
Benboudjema, F., & Torrenti, J. M. (2008). Early-age behaviour of concrete nuclear containments. Nuclear Engineering and Design, 238(10), 2495–2506.
Bernard, O., Ulm, F.-J., & Lemarchand, E. (2003). A multiscale micromechanics-hydration model for the early-age elastic properties of cement-based materials. Cement and Concrete Research, 33, 1293–1309.
Bianco, M., Bilardi, G., Pesavento, F., Pucci, G., & Schrefler, B. A. (2003). A frontal solver tuned for fully-coupled non-linear hygro-thermo-mechanical problems. International Journal of Numerical Methods in Engineering, 57(13), 1801–1818.
Briffaut, M. (2010). Etude de la fissuration au jeune âge des structures massives: influence de la vitesse de refroidissement, des reprises de bétonnage et des armatures. Dissertation (in French), ENS Cachan.
Briffaut, M., Benboudjema, F., Torrenti, J.-M., & Nahas, G. (2011). Numerical analysis of the thermal active restrained shrinkage ring test to study the early age behavior of massive concrete structures. Engineering Structures, 33(4), 1390–1401.
Briffaut, M., Benboudjema, F., Torrenti, J.-M., & Nahas, G. (2012). Effects of early-age thermal behaviour on damage risks in massive concrete structures. European Journal of Environmental and Civil Engineering, 16, 589–605. https://doi.org/10.1080/19648189.2012.668016.
Buffo-Lacarrière, L., Sellier, A., Escadeillas, G., & Turatsinze, A. (2007). Multiphasic finite element modeling of concrete hydration. Cement and Concrete Research, 37, 131–138.
Černý, R., & Rovnaníková, P. (2002). Transport processes in concrete. Abingdon: Spon press.
Červenka, V., Červenka, J., Jendele, L., & Šmilauer, V. (2014). ATENA simulation of crack propagation in CONCRACK benchmark. European Journal of Environmental and Civil Engineering, 18(7), 828–844.
Cervera, M., & Chiumenti, M. (2006). Mesh objective tensile cracking via a local continuum damage model and a crack tracking technique. Computer Methods in Applied Mechanics and Engineering, 196, 304–320.
Cervera, M., Prato, T., & Oliver, J. (1999a). Thermo-chemo-mechanical model for concrete. I: Hydration and aging. Journal of Engineering Mechanics, 127, 1018–1027.
Cervera, M., Olivier, J., & Prato, T. (1999b). A thermo-chemo-mechanical model for concrete. II: damage and creep. Journal of Engineering Mechanics (ASCE), 125(9), 1028–1039.
Chen, W.-F. (1982). Plasticity in reinforced concrete. New York: McGraw-Hill.
Chen, Y., Huang, R., Huang, Z., & Sun, L. (2012). Effective specific heats of multi-phase thermoelastic composites. Acta Mechanica Solida Sinica, 25, 262–276. https://doi.org/10.1016/S0894-9166(12)60024-X.
ConCrack. (2011). International benchmark for control of cracking in R.C. Structures. https://www.concrack.org.
Craeye, B., De Schutter, G., Van Humbeeck, H., & Van Cotthem, A. (2009). Early age behaviour of concrete supercontainers for radioactive waste disposal. Nuclear Engineering and Design, 239, 23–35. https://doi.org/10.1016/j.nucengdes.2008.10.006.
De Borst, R., Heeres, O. M., & Suiker, A. S. (2001). Some recent issues in computational plasticity. In Proceedings of European Conference on Computational Mechanics, Kraków 2001.
de Montaignac de Chauvance, R. (2011). Analyse du comportement d’éléments fléchis en béton renforcé de fibes métalliques. Du matériau à la structure. Dissertation (in french), Thesis of’Ecole Polytechnique de Montréal, Canada (in french).
De Sa, C., & Benboudjema, F. (2012). Modeling of concrete nonlinear mechanical behavior at high temperatures with different damage-based approaches. Materials and Structures, 44, 1411–1429.
De Sa, C., Benboudjema, F., Thiery, M., & Sicard, J. (2008). Analysis of microcracking induced by differential drying shrinkage. Cement & Concrete Composites, 30, 947–956.
De Schutter, G. (1999). Degree of hydration based Kelvin model for the basic creep of early age concrete. Materials and Structures, 32, 260–265.
De Schutter, G. (2002a). Finite element simulation of thermal cracking in massive hardening concrete elements using degree of hydration based material laws. Computers & Structures, 80, 2035–2042.
De Schutter, G. (2002b). Influence of hydration reaction on engineering properties of hardening concrete. Materials and Structures, 35, 447–452.
De Schutter, G., & Taerwe, L. (1996). Degree of hydration based description of mechanical properties of early-age concrete. Materials and Structures, 29(6), 335–344.
De Schutter, G., & Taerwe, L. (1997). Fracture energy of concrete at early ages. Materials and Structures, 30, 67–71.
England, G., & Khoylou, N. (1995). Moisture flow in concrete under steady state non-uniform temperature states: experimental observations and theoretical modeling. Nuclear Engineering and Design, 156, 83–107.
Fairbairn, E. M. R., Silvoso, M. M., Toledo Filho, R. D., Alves, J. L. D., & Ebecken, N. F. F. (2004). Optimization of mass concrete construction using genetic algorithms. Computers & Structures, 82, 281–299. https://doi.org/10.1016/j.compstruc.2003.08.008.
Faria, R., Azenha, M., & Figueiras, J. A. (2006). Modelling of concrete at early ages: application to an externally restrained slab. Cement & Concrete Composites, 28, 572–585.
Feldman, R. F., & Sereda, P. J. (1968). The model for hydrated Portland cement as deduced from sorption-length change and mechanical properties. Materials and Construction, 1, 509–520.
Fib. (2010). Model Code for concrete structures 2010. International Federation for Structural Concrete (fib).
Gawin, D., Pesavento, F., & Schrefler, B. A. (2002). Modelling of hygro-thermal behaviour and damage of concrete at temperature above critical point of water. International Journal of Numerical and Analytical Methods in Geomechanics, 26(6), 537–562.
Gawin, D., Pesavento, F., & Schrefler, B. A. (2003). Modelling of thermo-chemical and mechanical damage of concrete at high temperature. Computer Methods in Applied Mechanics and Engineering, 192, 1731–1771. https://doi.org/10.1016/S0045-7825(03)00200-7.
Gawin, D., Pesavento, F., & Schrefler, B. A. (2004). Modelling of deformations of high strength concrete at elevated temperatures. Materials and Structures, 37(268), 218–236.
Gawin, D., Pesavento, F., & Schrefler, B. A. (2006a). Hygro-thermo-chemo-mechanical modelling of concrete at early ages and beyond. Part I: Hydration and hygro-thermal phenomena. International Journal for Numerical Methods in Engineering, 67(3), 299–331. https://doi.org/10.1002/nme.1615.
Gawin, D., Pesavento, F., & Schrefler, B. A. (2006b). Hygro-thermo-chemo-mechanical modelling of concrete at early ages and beyond. Part II: Shrinkage and creep of concrete. International Journal for Numerical Methods in Engineering, 67(3), 332–363. https://doi.org/10.1002/nme.1636.
Gawin, D., Pesavento, F., & Schrefler, B. A. (2006c). Towards prediction of the thermal spalling risk through a multi-phase porous media model of concrete. Computer Methods in Applied Mechanics and Engineering, 195(41–43), 5707–5729.
Gawin, D., Pesavento, F., & Schrefler, B. A. (2008). Modeling of cementitious materials exposed to isothermal calcium leaching, with considering process kinetics and advective water flow. Part 1: Theoretical model. Solids and Structures, 45, 6221–6240. https://doi.org/10.1016/j.ijsolstr.2008.07.010.
Gawin, D., Pesavento, F., & Schrefler, B. A. (2009). Modeling deterioration of cementitious materials exposed to calcium leaching in non-isothermal conditions. Computer Methods in Applied Mechanics and Engineering, 198, 3051–3083. https://doi.org/10.1016/j.cma.2009.05.005.
Gray, W. G., & Miller, C. T. (2005). Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 1. Motivation and overview. Advances in Water Resources, 28, 161–180.
Gray, W. G., & Schrefler, B. A. (2007). Analysis of the solid phase stress tensor in multiphase porous media. International Journal for Numerical and Analytical Methods in Geomechanics, 31(4), 541–581.
Gray, W. G., Schrefler, B. A., & Pesavento, F. (2009). The solid phase stress tensor in porous media mechanics and the Hill-Mandel condition. Journal of the Mechanics and Physics of Solids, 57, 539–554. https://doi.org/10.1016/j.jmps.2008.11.005.
Gutsch, A., & Rostásy, F. S. (1994). Young concrete under high tensile stresses—creep, relaxation and cracking. In Proceedings of the International RILEM Conference on Thermal Cracking in Concrete at Early Ages, London.
Hansen, K. K. (1986). Sorption isotherms: A catalogue. Kgs. Lyngby, Denmark: Technical University of Denmark.
Hansen, P. F., Hansen, J. H., Kjaer, V., & Pedersen, E. J. (1982). Thermal properties of hardeing cement pastes. In Proceedings of RILEM International Conference on Concrete at Early-Ages. Paris.
Hanson, J. A. (1968). Effects of curing and drying environments on splitting tensile strength. American Concrete Institute Journal, 65, 535–543.
Hassanizadeh, S. M., & Gray, W. G. (1979a). General conservation equations for multi-phase systems: 1. Averaging procedure. Advances in Water Resources, 2, 131–144.
Hassanizadeh, S. M., & Gray, W. G. (1979b). General conservation equations for multi-phase systems: 2. Mass, momenta, energy and entropy equations. Advances in Water Resources, 2, 191–203.
Hassanizadeh, S. M., & Gray, W. G. (1980). General conservation equations for multi-phase systems: 3. constitutive theory for porous media flow. Advances in Water Resources, 3, 25–40.
Hilaire, A. (2014). Etude des déformations différées des bétons en compression et en traction, du jeune au long terme: Application aux enceintes de confinement. Dissertation (in french), École normale supérieure de Cachan - ENS Cachan, Paris.
Hillerborg, A., Modeer, M., & Petersson, P. (1976). Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cement and Concrete Research, 6, 773–782.
Hofstetter, G., & Mang, H. A. (1995). Computational mechanics of reinforced concrete structures. Wiesbaden, Germany: Vieweg.
Honorio, T., Bary, B., & Benboudjema, F. (2014). Evaluation of the contribution of boundary and initial conditions in the chemo-thermal analysis of a massive concrete structure. Engineering Structures, 80, 173–188. https://doi.org/10.1016/j.engstruct.2014.08.050.
Jendele, L., Šmilauer, V., & Cervenka, J. (2014). Multiscale hydro–thermo–mechanical model for early-age and mature concrete structures. Advances in Engineering Software, 72, 134–146.
Ji, G. (2008). Cracking risk of concrete structures in the hardening phase: Experiments, material modeling and finite element analysis. Ph.D. thesis, Trondheim, Norway.
Klemczak, B. (2007). Adapting of the Willam-Warnke failure criteria for young concrete. Archives of Civil Engineering, 53(2), 323–339.
Klemczak, B. (2011). Prediction of coupled heat and moisture transfer in early-age massive concrete structures. Numerical Heat Transfer, Part A: Applications, 60(3), 212–233.
Künzel, H. (1995). Simultaneous heat and moisture transport in building components. Stutgart: IRB.
Kwak, H.-G., Ha, S.-J., & Kim, J.-K. (2006). Non-structural cracking in RC walls: Part I. Finite Element Formulation, Cement and Concrete Research, 36(4), 749–760.
Lackner, R., & Mang, H. A. (2004). Chemoplastic material model for the simulation of early-age cracking: From the constitutive law to numerical analyses of massive concrete structures. Cement & Concrete Composites, 26, 551–562.
Ladeveze, P. (1983). Sur une theorie de l’endomagement anisotrope. Internal Report no 34 Laboratoire de Mecanique et Technologie, Cachan, France.
Laplante, P. (1993). Propriétés mécaniques des bétons durcissants: Analyse comparée des bétons classiques et à très hautes performances. Dissertation (in french), ENPC.
Leal da Silva, W. R., Šmilauer, V., & Štemberk, P. (2015). Upscaling semi-adiabatic measurements for simulating temperature evolution of mass concrete structures. Materials and Structures, 48(4), 188–197.
Leblond, J. B., Perrin, G., & Devaux, J. (1992). Bifurcation effects in ductile metals with damage delocalisation. ASME Journal of Applied Mechanics
Lewis, R. W., & Schrefler, B. A. (1998). The finite element method in the static and dynamic deformation and consolidation of porous media (2nd ed.). Chichester: Wiley.
Liu, B. Y. H., & Jordan, R. C. (1963). A rational procedure for predicting the long-term average performance of flat-plate solar energy collectors. Solar Energy, 7(2), 53–74.
Lothenbach, B., Matschei, T., Möschner, G., & Glasser, F. P. (2008). Thermodynamic modelling of the effect of temperature on the hydration and porosity of Portland cement. Cement and Concrete Research, 38, 1–18. https://doi.org/10.1016/j.cemconres.2007.08.017.
Loukili, A., Chopin, D., Khelidj, A., & Le Touzo, J. Y. (2000). A new approach to determine autogenous shrinkage of mortar at an early age considering temperature history. Cement and Concrete Research, 30, 915–922.
Lura, P., & Van Breugel, K. (2001). Thermal properties of concrete. Sensitivity studies. In IPACS (Improved Production of Advanced Concrete Structures) Project, Luleå
Majewski, S. (2003). Mechanika betonu konstrukcyjnego w ujeciu sprężysto–plastycznym. Monograph 45. Gliwice, Poland: Silesian University of Technology.
Majewski, S. (2004). MWW3–Elasto–plastic model for concrete. Archives of Civil Engineering, 50(1), 11–43.
Mazars, J. (1984). Application de la mecanique de l’endommagement au comportement non lineaire et a la rupture du beton de structure. Dissertation, Universite Paris VI.
Mazars, J. (1986). A description of micro and macroscale damage of concrete structures. Engineering Fracture Mechanics, 25(5–6), 729–737.
Mazars, J. (2014). Control of cracking, a major issue for reinforced concrete structures. European Journal of Environmental and Civil Engineering, 18(7), 721–723.
Mazars, J., & Bournazel, J. P. (1996). Modelling of damage processes due to volumic variations for maturing and matured concrete. In Proceedings of the International RILEM Conference on Concrete: from Material to Structure, Arles, France.
Mazzotti, C., & Savoia, M. (2003). Nonlinear creep damage model for concrete under uniaxial compression. Journal of Engineering Mechanics, 129(9), 1065–1075.
Morabito, P. (2001). Thermal properties of concrete. Variations with the temperature and during the hydration phase. In Project IPACS, Luleå.
Mounanga, P. (2004). Étude expérimentale du comportement de pâtes de ciment au très jeune âge: Hydratation, retraits, propriétés thermophysiques. Dissertation (in French), Université de Nantes, Nantes.
Mounanga, P., Baroghel-Bouny, V., Loukili, A., & Khelidj, A. (2006). Autogenous deformations of cement pastes: Part I. Temperature effects at early age and micro–macro correlations. Cement and Concrete Research, 36, 110–122.
Neville, A. M., Dilger, W. H., & Brooks, J. J. (1983). Creep of plain and structural concrete. Longman Group Construction Press.
Park, K.-B., Jee, N.-Y., Yoon, I.-S., & Lee, H.-S. (2008). Prediction of temperature distribution in high-strength concrete using hydration model. ACI Materials Journal, 105(2), 180–186.
Patzák, B., & Rypl, D. (2012). Object-oriented, parallel finite element framework with dynamic load balancing. Advances in Engineering Software, 47(1), 35–50.
Perzyna, P. (1966). Fundamental problems in viscoplasticity. Advances in Applied Mechanics, 9, 243–377.
Pesavento, F. (2000). Non-linear modeling of concrete as multiphase porous material in high temperature conditions. Dissertation, University of Padova.
Pesavento, F., Gawin, D., & Schrefler, B. A. (2008). Modeling cementitious materials as multiphase porous media: theoretical framework and applications. Acta Mechanica, 201, 313–339. https://doi.org/10.1007/s00707-008-0065-z.
Pesavento, F., Gawin, D., Wyrzykowski, M., Schrefler, B. A., & Simoni, L. (2012). Modeling alkali-silica reaction in non-isothermal, partially saturated cement based materials. Computer Methods in Applied Mechanics and Engineering (CMAME), 225–228, 95–115. https://doi.org/10.1016/j.cma.2012.02.019.
Phan, T. S., et al. (2013a). Numerical modeling of the rebar/concrete interface: Case of the flat steel rebars. Materials and Structures, 46(6), 1011–1025.
Phan, T. S., Tailhan, J.-L., & Rossi, P. (2013b). 3D numerical modelling of concrete structural element reinforced with ribbed flat steel rebars. Structural Concrete, 14(4), 378–388.
Phan, T. S., Rossi, P., & Tailhan, J.-L. (2015). Numerical modelling of the concrete/rebar bond. Cement & Concrete Composites, 59, 1–9.
Pichler, B., & Hellmich, C. (2011). Upscaling quasi-brittle strength of cement paste and mortar: A multi-scale engineering mechanics model. Cement and Concrete Research, 41, 467–476.
Pickett, G. (1942). The effect of change in moisture-content of the creep of concrete under a sustained load. Journal of the American Concrete Institute, 13, 333–355.
Pijaudier-Cabot, G., & Bažant, Z. P. (1987). Nonlocal Damage Theory. Journal of Engineering Mechanics, 113(10), 1512–1533.
Pijaudier-Cabot, G. (1995). Non local damage. In H.-B. Mühlhaus (Ed.), Continuum models for materials with microstructure. London: Wiley.
Pijaudier-Cabot, G., La Borderie, C., & Fichant, S. (1994). Damage mechanics for concrete modelling: applications and comparisons with plasticity and fracture mechanics. In N. Bicanic, et al. (Eds.) Proceedings of EURO-C. Pineridge Press Pubs.
Regourd, M., & Gauthier, E. (1980). Behavior of cement under accelerated hardening. Annales de I’ITBTP (in French) (Vol. 179, pp. 65–96).
Rossi, P. (1993). Comportement dynamique des bétons: du matériau à la structure. Annales de l’Institut technique du bâtiment et des travaux publics (Vol. 511). Institut technique du bâtiment et des travaux publics (in french).
Rossi, P. (2012). Experimental study of scaling effect related to post-cracking behaviours of metal fibres reinforced concretes. European Journal of Environmental and Civil Engineering, 16(10), 1261–1268.
Rossi, P., et al. (1994). Scale effect on concrete in tension. Materials and Structures, 27, 437–444.
Rossi, P., Daviau-Desnoyers, D., & Tailhan, J.-L. (2015). Analysis of cracking in steel fibre reinforced concrete (SFRC) structures in bending using probabilistic modelling. Structural Concrete, 3, 381–388.
Rossi, P., & Richer, S. (1987). Numerical modelling of concrete cracking based on a stochastic approach. Materials and Structures, 20(119), 334–337.
Rossi, P., Ulm, F. J., & Hachi, F. (1996). Compressive behaviour of concrete: physical mechanisms and modelling. ASCE Engineering Mechanics, 122(11), 1038–1043.
Rossi, P., & Wu, X. (1992). Probabilistic model for material behaviour analysis and appraisement of concrete. Magazine of Concrete Research, 44(161), 271–280.
Rots, J. G. (1988). Computational modeling of concrete fracture. Dissertation, Delft University of Technology, Delft (Netherlands).
Ruiz, J., Schindler, A., Rasmussen, R., Kim, P., Chang, G. (2001). Concrete temperature modeling and strength prediction using maturity concepts in the FHWA HIPERPAV software. In: Proceedings of 7th International Conference on Concrete Pavements, Orlando, USA.
Schrefler, B. A. (2002). Mechanics and thermodynamics of saturated-unsaturated porous materials and quantitative solutions. Applied Mechanics Review, 55(4), 351–388.
Sciumè, G., Benboudjema, F., De Sa, C., Pesavento, F., Berthaud, Y., & Schrefler, B. A. (2013). A multiphysics model for concrete at early age applied to repairs problems. Engineering Structures, 57, 374–387.
Sciumè, G., Schrefler, B.A., & Pesavento, F. (2012). Thermo-hygro-chemo-mechanical modelling of the behaviour of a massive beam with restrained shrinkage. In Proceedings of CONCRACK 3, International Workshop on Crack Control of Mass Concrete and Related Issues Concerning Early-Age Concrete Structures. Paris, France: RILEM, JCI.
Simoni, L., & Schrefler, B. A. (2014). Multi field simulation of fracture. In S. P. A. Bordas (Ed.), Advances in applied mechanics—AAMS (Vol. 47, pp. 367–519). UK: Academic Press.
Šmilauer, V., Baquerizo, L., Matschei, T., Havlásek, P., Leal da Silva, W. R., & Hájková, K. (2016). ConTemp—A virtual thermo-mechanical simulator for hydrating reinforced concrete blocks with extension to service life. Service life of cement-based materials and structures (pp. 463–472). Bagneux: Rilem Publications s.a.r.l.
Stefan, L., Benboudjema, F., Torrenti, J. M., & Bissonnette, B. (2010). Prediction of elastic properties of cement pastes at early ages. Computational Materials Science, 47, 775–784.
Tailhan, J.-L., et al. (2010). From Local to Global Probabilistic Modeling of Concrete Cracking. Annals of Solid and Structural Mechanics, 1, 103–115.
Thelandersson, S. (1987). Modelling of combined thermal and mechanical action in concrete. ASCE Engineering Mechanics, 113(6), 893–906.
Thomas, J. J., Biernacki, J. J., Bullard, J. W., Bishnoi, S., Dolado, J. S., Scherer, G. W., et al. (2011). Modeling and simulation of cement hydration kinetics and microstructure development. Cement and Concrete Research, 41(12), 1257–1278.
Torrenti, J. M., & Benboudjema, F. (2005). Mechanical threshold of concrete at an early age. Materials and Structures, 38, 299–304.
Ulm, F.-J., & Coussy, O. (1998). Couplings in early-age concrete: From material modeling to structural design. International Journal of Solids and Structures, 35, 4295–4311. https://doi.org/10.1016/S0020-7683(97)00317-X.
Ulm, F.-J., & Coussy, O. (2001). What is a “massive” concrete structure at early ages? Some dimensional arguments. Journal of Engineering Mechanics, 127, 512–522.
Valanis, K. C. (1991). A global damage theory and the hyperbolicity of the wave problem. ASME Journal of Applied Mechanics, 58, 311–316.
van Genuchten, M. T. (1980). A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Science Society of America Journal, 44(5), 892–898.
Waller, V. (2000). Relations entre composition des bétons, exothermie en cours de prise et résistance en compression. Dissertation (in French), Ecole Nationale des Ponts et Chaussées, Marne-La-Vallée.
Whitaker, S. (1980). Heat and mass transfer in granular porous media. Advances in Drying, 1.
Winnicki, A. (2001). Viscoplastic consistency model—basic features. In Proceedings of European Conference on Computational Mechanics, Kraków, 2001.
Wu, T., Temizer, I., & Wriggers, P. (2014). Multiscale hydro-thermo-chemo-mechanical coupling: Application to alkali-silica reaction. Journal of Computational Material Science, 84, 381–395.
Xi, Y., Bažant, Z. P., Molina, L., & Jennings, H. M. (1994). Moisture diffusion in cementitious materials. Moisture capacity and diffusion. Advanced Cement Based Materials, 1(6), 258–266.
Zienkiewicz, O. C., & Taylor, R. L. (2000). The finite element method, The basis (Vol. 1). Oxford: Butterworth-Heinemann.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 RILEM
About this chapter
Cite this chapter
Pesavento, F., Knoppik, A., Šmilauer, V., Briffaut, M., Rossi, P. (2019). Numerical Modelling. In: Fairbairn, E., Azenha, M. (eds) Thermal Cracking of Massive Concrete Structures. RILEM State-of-the-Art Reports, vol 27. Springer, Cham. https://doi.org/10.1007/978-3-319-76617-1_7
Download citation
DOI: https://doi.org/10.1007/978-3-319-76617-1_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-76616-4
Online ISBN: 978-3-319-76617-1
eBook Packages: EngineeringEngineering (R0)