Variational Analysis of Nematic Shells

Abstract

In this note we present some recent results on the Mathematical Analysis of Nematic Shells. The type of results we present deal with the analysis of defectless configurations as well as the analysis of defected configurations. The mathematical tools include Topology, Analysis of Partial Differential Equations as well as Variational Techniques like Γ convergence.

1 Introduction: The Model and the Role of the Topology

The occasion of writing this note came because the second author of this paper was invited to lecture at the

$$\displaystyle \begin{aligned} \text{\textit{INdAM-ISIMM Workshop on Trends on Applications of Mathematics to Mechanics}} \end{aligned}$$

in Rome. These note contains the results presented in the seminar. More precisely, these results are the outcome of a research line started in 2012 and culminated in the papers [9, 35, 36] and [8]. In this note we try to convey the main ideas behind the results and leave the detailed proofs to the above mentioned papers.

A Nematic Shell is a rigid colloidal particle with a typical dimension in the micrometer scale coated with a thin film of nematic liquid crystal whose molecular orientation is subjected to a tangential anchoring. The study of these structures has received a good deal of interest, especially in the physics community (see, e.g., [6, 23, 26, 27, 30, 37, 39, 41, 42] and [28]).

From a mathematical point of view, a Nematic Shell is usually identified with a two dimensional compact (oriented by the choice of the unit normal field ${\boldsymbol {\gamma }}:M\to \mathbb {R}^3$) surface M without boundary with the local orientation of the molecules described via a unit norm tangent vector field, named director in analogy with the “flat” case. More precisely, the local orientation of the molecules is described via a unit-norm tangent vector field $\mathbf {n}:M \to \mathbb {R}^3$ with n(x) ∈T _x M for any x ∈ M, T _x M being the tangent plane at the point x.

The study of these structures is particularly interesting and challenging due to its interdisciplinary character as it combines in a non trivial way physics, geometry, topology and variational techniques. In particular, the interplay between the geometry and the topology of the fixed substrate and the tangential anchoring constraint is a source of difficulties that will accompany us for the whole analysis. Indeed, as observed in [41] and [6], the liquid crystal equilibrium (and all its stable configurations, in general) is the result of the competition between two driving principles: on the one hand the minimization of the “curvature of the texture” penalized by the elastic energy, and on the other the frustration due to constraints of geometrical and topological nature, imposed by anchoring the nematic to the surface of the underlying particle. Different theoretical approaches for the treatment of Nematic Shells are available. Differences arise in the choice of the form of the elastic part of the free energy which could be of intrinsic or extrinsic nature. More precisely, theories which employ only covariant derivatives will be named intrinsic (see [26, 38, 39, 41]) while theories that comprise also how the shell sits in the three dimensional space will be named extrinsic (see [27] and [28]). When restricting to the simpler one-constant approximation, the extrinsic energy has the form

$$\displaystyle \begin{aligned} W(\mathbf{n}):= \frac \kappa2 \int_M | \mathrm{D}\mathbf{n}|{}^2 + |\mathrm{d} {\boldsymbol{\gamma}}(\mathbf{n}) \mathbf{n}|{}^2\,\mathrm{d} S, \end{aligned} $$

(1)

while the intrinsic energy has the form

$$\displaystyle \begin{aligned} W_{\mathrm{intr}}(\mathbf{n}):= \frac \kappa2 \int_M | \mathrm{D}\mathbf{n}|{}^2\,\mathrm{d} S. \end{aligned} $$

(2)

In the definitions above n is a tangent vector field with unit norm, κ is a positive constant (from now on κ will be taken equal to one), the symbol D denotes the covariant derivative on M, and dγ, the differential of the Gauss map, is the so called shape operator. We refer to the quantity ∫ _M |Dn|² as the Dirichlet (or elastic) energy of n.

The extrinsic energy (1) has been derived by Napoli & Vergori (see [27] and [28]) by using a formal dimension reduction. More precisely, starting from the Oseen-Frank energy W ^OF (see [40]) on a tubular neighborhood M _h of thickness h (satisfying a suitable constraint related to the curvature of M), Napoli and Vergori obtain that the limit

$$\displaystyle \begin{aligned} \lim_{h\searrow 0} \frac 1h W^{\mathrm{OF}}(\mathbf{n},M_h) = W_{\mathrm{extr}}(\mathbf{n}). \end{aligned}$$

is well defined for any fixed and sufficiently smooth field n with the property of being independent of the thickness direction and tangent to leaf of the foliation M _h . The form of the limit energy is as follows

$$\displaystyle \begin{aligned} W_{\mathrm{extr}}(\mathbf{n}):=\frac 12 \int_M K_1 (\operatorname{{\mathrm{div}_s}} \mathbf{n})^2 + K_2 (\mathbf{n} \cdot \operatorname{{\mathrm{curl}_s}} \mathbf{n})^2 +K_3 |\mathbf{n} \times \operatorname{{\mathrm{curl}_s}} \mathbf{n}|{}^2\,\mathrm{d} S, \end{aligned} $$

(3)

where the differential operators div_s and curl_s in the display above are proper surface counterparts of the divergence and the curl operators (see [28]). The positive constants K ₁, K ₂, K ₃ are the analogous of the Frank’s constants in the euclidean case (see [40]). Finally, the energy (1) corresponds to the one-constant approximation, namely the energy W _extr with K ₁ = K ₂ = K ₃ = κ.

It is worthwhile noting that the above formal argument can be made rigorous using the theory of Γ-convergence in the spirit of [24] (see [14] for the derivation of the surface Q tensor energy).

An important problem in the modern Materials Science is the analysis and the control of the complex microstructures that the material may develop. As observed in [19], the appearance of microstructures is usually related to the occurrence of the so-called defects, which are localized regions where the material behavior appears to be drastically different from the prototypical one. This is the case of Nematic Liquid Crystals for which defects can be easily seen in experiments. Defects are regions where the director field changes abruptly, due to the topological behavior of the field surrounding them. A prominent example of the appearance of defects is that of Nematic Shells which may develop topological defects due to the interplay between the topology of the substrate, the boundary conditions and the constraints on the director field (see [9]).

More precisely, when dealing with Nematic Shells, the topology of the shell and, possibly, of the boundary conditions is responsible for the emergence of defects which manifest in points in the shell where the director field is not well defined and consequently its energy ((1) or (2)) is infinite. The link between the topology of the shell M and the number of singularities that a unit norm vector field must have is given by the Poincaré-Hopf Index Theorem: If a unit norm has singularities of degree d _i located at the points x ₁, …, x _k then

$$\displaystyle \begin{aligned} \sum_{i=1}^{k}d_i = \chi(M), \end{aligned}$$

where χ(M) is the Euler Characteristic of M. For example, a spherical shell has χ(M) = 2, thus implying the necessity of having defects with total degree equal to 2. A crucial step in the analysis of a variational problem is the understanding of the correct functional framework where to set, for example, the minimization of the given energy. In the context of Nematic Shells, a closer inspection of the energy (3) reveals that there exist constants such that (see Proposition 1)

$$\displaystyle \begin{aligned} \frac{ K_*}{2} \int_{M}\big(\vert \mathrm{D} \mathbf{n} \vert^2 + \vert{\mathrm{d}{\boldsymbol{\gamma}} }(\mathbf{n})\vert^2\big)\mathrm{d} S\le W_{\mathrm{extr}}(\mathbf{n})\le \frac{ K^*}2 \int_{M}\big(\vert \mathrm{D} \mathbf{n} \vert^2 + \vert \mathrm{d} {\boldsymbol{\gamma}}(\mathbf{n}) \vert^2\big)\mathrm{d} S, \end{aligned}$$

Consequently, the natural choice for the functional framework would be to set the analysis in the space of tangent vector fields such that |n| and |Dn| belong to L ²(M), which means that we have to consider the Sobolev set

As it happens for smooth vector fields, the topology of the shell may introduce possible obstructions to this program. This is again related to the Poincaré-Hopf index Theorem. In particular, the following theorem clarifies the situation for vector fields with W ^{1, 2} regularity

Theorem 1.1

Let M be a compact smooth surface without boundary, embedded in $\mathbb {R}^3$ . Let χ(M) be the Euler characteristic of M. Then

$$\displaystyle \begin{aligned} W^{1,2}_{\mathrm{tan}}(M, \, \mathbb{S}^2) \neq \emptyset \,\,\Leftrightarrow \chi(M) = 0. \end{aligned}$$

The proof of this theorem is given in [36] and it is based on a purely PDE argument. Interestingly, Theorem 1.1 is a consequence of the more general results contained in [9] regarding the extension of the Poincaré-Hopf Theorem to vector fields with VMO regularity defined on compact manifolds with, possibly, boundary. Theorem 1.1 is in a certain sense a borderline case for the existence of unit norm vector fields with Sobolev regularity. In fact, defining for p ≥ 1, the Sobolev set of tangent vector fields

we have that

• For p ≥ 2, $W^{1,p}_{\tan }(M;\mathbb {S}^2)\neq \emptyset$ if and only if χ(M) = 0

• For 1 ≤ p < 2, $W^{1,p}_{\tan }(M;\mathbb {S}^2) \neq \emptyset$.

The first item when p > 2 is a consequence of the classical Poincaré-Hopf Theorem and of the embedding W ^{1, p} ⊂ C ⁰ for p > 2 in two dimensions. The case p = 2 follows from Theorem 1.1. The second item follows from the fact that a vector field that behaves like $\frac {x}{\vert x\vert }$ around the singularities belong to $W^{1,p}_{\tan }(M;\mathbb {S}^2)$ for 1 ≤ p < 2 as a direct computation shows.

Coming back to the analysis of the energy (1), Theorem 1.1 gives that for shells M with χ(M) ≠ 0 the energy (1) is infinite and thus clearly not adequate to describe this situation.

The rest of the paper is divided according to Theorem 1.1. More precisely, we will first discuss in Sect. 2 the results for shells with Euler Characteristic equal to zero and then in Sect. 3 we will concentrate on shells with non zero Euler Characteristic.

When χ(M) = 0, we obtain results regarding the existence of minimizers, the existence of the gradient flow and also some quantitative results on the structure of the minimizers for axisymmetric toroidal shells. The proofs of the results use ideas borrowed from the theory of harmonic maps.

Moreover, starting from a variant of the well known XY spin model, we perform the rigorous derivation via Γ-convergence of the energy (1) in terms of a discrete to continuum limit. More precisely, we consider a family of triangulations $\mathcal {T}_\varepsilon$ of M with the vertices $i\in \mathcal {T}^{0}_\varepsilon$ lying on M and with mesh size ε, i.e. $\varepsilon = \max _{T\in \mathcal {T}_\varepsilon }\mathrm {diam}(T)$. At any point $i\in \mathcal {T}^0_{\varepsilon }$ sits a unit-norm tangent vector v _ε (i) ∈T _i M named spin. We consider the following discrete energy

$$\displaystyle \begin{aligned} XY_\varepsilon(\mathbf{v}_\varepsilon) := \frac{1}{2} \sum_{i\neq j\in \mathcal{T}^0_\varepsilon} \kappa^{ij}_\varepsilon \left| \mathbf{v}_\varepsilon(i) - \mathbf{v}_\varepsilon(j) \right|{}^2, \end{aligned} $$

(4)

where the coefficients $\kappa _{\varepsilon }^{ij}$ are the entries of the stiffness matrix of the Laplace-Beltrami operator of M. We show that, as ε → 0, the discrete energy XY _ε converges to the continuum energy (1), in the sense of Γ-convergence.

The XY spin model has been widely used in the physics community due to its simple use and effectiveness (among the others, we refer to the works of Berezinskii [4] and of Kosterlitz and Thouless [22] who were awarded the 2016 Nobel Prize for Physics, together with Haldane) but has also attracted the attention of the mathematics community, see for instance [1, 2, 7].

For shells M with χ(M) ≠ 0, the energy (1) is clearly not well defined due to Theorem 1.1 and we have to face the emergence of configurations with defects. In Sect. 3 we will discuss the location of defects and their energetics. A possible strategy would be to relax one the above constraints, for instance the unit-norm constraint as in the Ginzburg-Landau theory (see, for instance, [5, 20, 21, 31, 32] and the recent papers [17] and [18] for the analysis on a Riemannian manifold). In this note, we present the approach of [8] and instead of a continuous model we rather consider the discrete XY spin model (4). Defects emerge when we let ε → 0 in (4). In particular, we will address the Γ-convergence of the energy

$$\displaystyle \begin{aligned} XY_\varepsilon(\cdot) - \pi\mathcal{K} \vert \log\varepsilon\vert, \end{aligned}$$

where $\mathcal {K}$ is an even, positive integer, such that $\vert \chi (M)\vert \le \mathcal {K}$. What appears in the limit is the so called Renormalized Energy (introduced and studied first in [5] and then in many other contributions, see [3, 32] and references therein) that describes the energetics and the interaction between defects. The Renormalized Energy we obtain is given by the sum of a purely intrinsic part and of an extrinsic part related to the shape operator of M and thus the location of the defects also depends on how the shell “sits” in the three dimensional space. At the level of minimizers, we have the following expansion

$$\displaystyle \begin{aligned} \min XY_\varepsilon = \pi|\chi(M)|\vert\log\varepsilon\vert+ \mathbb{W}(\mathbf{v}) + \sum_{i=1}^{|\chi(M)|}\gamma(x_i) + \mathrm{o}_{\varepsilon\to 0}(1), \end{aligned}$$

where $\mathbf {v}\in W^{1,2}_{\tan , \mathrm {loc}}(M\setminus \{x_1, \ldots , x_{|\chi (M)|}\}; \, \mathbb {S}^2)$ is the “continuum limit” of the sequence of discrete minimizers and γ(x _i ) is a positive quantity that takes into account the energy located in the core of the defects x _i of v. An interesting feature that is not shared in the planar case, both continuous and discrete (see [5] and [2]), nor in the curved continuous case (see [17] and [18]), is that the core energy γ(x _i ) depends on the singularity x _i .

The interest in analyzing configurations with defects goes beyond the aesthetic appeal of the question. In fact, the defect’s points could serve as anchoring bonds between colloidal particles, as precognized by Nelson [29] and recently realized in [43]. Thus, the understanding of the defects formation and of their energetics and location could be of impact for this new chemistry for meta materials.

We conclude this long introduction with some differential geometry notation that we use. We refer to the book [13] for all the material regarding differential geometry.

Given a compact two dimensional surface M with metric g, embedded in $\mathbb {R}^3$ and oriented with the normal γ, we denote the area element induced by the choice of the orientation with dS. We denote with ∇ the connection with respect to the standard metric of $\mathbb {R}^3$, and we let D _v u be the covariant derivative of u in the direction v (u and v are smooth tangent vector fields in M), with respect to the Levi Civita (or Riemannian) connection D of the metric g on M.

Now, if u and v are extended arbitrarily to smooth vector fields on $\mathbb {R}^3$, we have the Gauss Formula :

$$\displaystyle \begin{aligned} \nabla_{\mathbf{v}} \mathbf{u} = \mathrm{D}_{\mathbf{v}} \mathbf{u} + \langle \mathrm{d}{\boldsymbol{\gamma}}(\mathbf{u}),\mathbf{v}\rangle {\boldsymbol{\gamma}}. \end{aligned} $$

(5)

This decomposition is orthogonal, thus there holds

$$\displaystyle \begin{aligned} \vert\nabla \mathbf{u}\vert^2 = \vert\mathrm{D} \mathbf{u}\vert^2 + \vert \mathrm{d}{\boldsymbol{\gamma}}(\mathbf{u})\vert^2. \end{aligned} $$

(6)

Beside the covariant derivative, we introduce another differential operator for vector fields on M, which takes into account also the way that M embeds in $\mathbb {R}^3$. Let u be a smooth vector field on M. We extend it smoothly to a vector field $\tilde {\mathbf {u}}$ on $\mathbb {R}^3$ and we denote its standard gradient by $\nabla \tilde {\mathbf {u}}$ on $\mathbb {R}^3$. For x ∈ M, we define

$$\displaystyle \begin{aligned} \nabla_{\mathrm{s}} \mathbf{u}(x):=\nabla \tilde{\mathbf{u}}(x)P_{M}(x), \end{aligned}$$

where P _M (x) := (Id−γ ⊗γ)(x) is the orthogonal projection on T _x M. In other words, ∇_s is the restriction of the standard derivative in $\mathbb {R}^3$ to directions that are tangent to M. This differential operator is well-defined, as it does not depend on the particular extension $\tilde {\mathbf {u}}$. In general, ∇_s u ≠ Du = P _M (∇u) since the matrix product is non commutative. Moreover, thanks to (5) and (6) there holds

$$\displaystyle \begin{aligned} \vert \nabla_{\mathrm{s}} \mathbf{u}\vert^2 = \vert\mathrm{D}\mathbf{u}\vert^2 + \vert \mathrm{d}{\boldsymbol{\gamma}}(\mathbf{u})\vert^2. \end{aligned}$$

Note that, by identifying u with a map $\mathbf {u} = (\mathbf {u}^1, \, \mathbf {u}^2, \, \mathbf {u}^3)\colon M\to \mathbb {R}^3$, the k-th row of the matrix representing ∇_s u coincides with the Riemannian gradient (that we still denote with ∇_s) of u ^k.

2 Shells of Zero Euler Characteristic

According to Theorem 1.1, unless otherwise stated, throughout this section we will consider M to be a compact and smooth two-dimensional surface without boundary such that

(7)

and we will leave to the next Sect. 3 the case of a shell M with χ(M) ≠ 0. This section is organized as follows. First of all, in Sect. 2.1 we will discuss the minimization of the full energy (3) while in Sect. 2.2 we will study the gradient flow of the energy (1) with respect to the scalar product of L ². Finally, in Sect. 2.3 we discuss the rigorous derivation (in terms of Γ-convergence) of the energy (1) from the discrete energy (4). It is an open problem to justify in terms of a microscopic derivation the full energy (3), even in the euclidean case.

2.1 Existence of Minimizers

We let M satisfy (7), in such a way that $W^{1,2}_{\mathrm {tan}}(M, \, \mathbb {S}^2) \neq \emptyset$, we have the following (see [15] for the flat case)

Proposition 1

Let M be a smooth, compact surface in $\mathbb {R}^3$ , without boundary, satisfying (7) and let $W:W^{1,2}_{\mathrm {tan}}(M, \, \mathbb {S}^2) \to \mathbb {R}$ be the energy functional (1). Set $K_*:=\min \left \{K_1,K_2,K_3\right \}$ and K ^∗ := 3(K ₁ + K ₂ + K ₃). We have that

$$\displaystyle \begin{aligned} \frac{ K_*}{2} \int_{M}\big(\vert \mathrm{D}\mathbf{n} \vert^2 + \vert\mathrm{d} {\boldsymbol{\gamma}}(\mathbf{n})\vert^2\big)\mathrm{d} S\le W_{\mathrm{extr}}(\mathbf{n})\le \frac{ K^*}2 \int_{M}\big(\vert \mathrm{D}\mathbf{n} \vert^2 + \vert\mathrm{d} {\boldsymbol{\gamma}}(\mathbf{n})\vert^2\big)\mathrm{d} S. \end{aligned}$$

Moreover, the energy W is sequentially lower semicontinuous with respect to the weak convergence of $W^{1,2}(M;\mathbb {R}^3)$.

Thus, the existence of a minimizer of the energy W follows from the direct method of calculus of variations.

Proposition 2

There exists $\mathbf {n}\in W^{1,2}_{\mathrm {tan}}(M, \, \mathbb {S}^2)$ such that $W_{\mathrm {extr}}(\mathbf {n}) = \inf _{\mathbf {u} \in W^{1,2}_{\mathrm {tan}}(M, \, \mathbb {S}^2)}$ W _extr(u).

The proof of the existence of minimizers is simple being the energy quadratic. It is interesting to discuss how the energy selects the minimizers. We leave to [36] the discussion on the relation between the different tunings of K ₁, K ₂, K ₃ and the energy landscape for constant deviation angle (namely the angle that n forms with one of vectors generating the tangent plane to M, see formula (8) below) and we rather concentrate on the one-constant approximation. We observe that the energy (1) has the form of a “phase transition energy” since it is the sum of a Dirichlet part and of a (vectorial) double well potential part. In fact the purely extrinsic part |dγ(n)|² is minimized when n is oriented along the direction of minimal principal curvature (i.e. minimal normal curvature). Thus, the energy (1) favors a parallel configuration (i.e. a vector field such that Dn = 0) in the direction of minimal principal curvature. Already considering only the Dirichlet part (i.e. the intrinsic energy) the minimization experiences an interesting frustration of geometric nature due to the fact that the existence of globally defined unit norm parallel vector fields requires the Gaussian curvature to vanish. The effect of the competition between the two terms of the energy is particularly interesting on the axisymmetric torus. Thus, we fix M to be the axisymmetric torus, namely the surface parametrized by $X: [0,2\pi ]\times [0,2\pi ]\to \mathbb {R}^3$ where

R and r are usually known as major and minor radius, respectively. We let e ₁ and e ₂ be the unit tangent vectors given by

$$\displaystyle \begin{aligned} \mathbf{e}_1 =\frac{X_\theta}{|X_\theta|},\,\,\,\,\,\mathbf{e}_2 = \frac{X_\phi}{|X_\phi|}, \end{aligned}$$

and we let c ₁ and c ₂ be the principal curvatures

$$\displaystyle \begin{aligned} c_1 = \frac{1}{r},\,\,\,\,\,\,c_2(\theta,\phi) = \frac{\cos \theta}{R + r\cos\theta}. \end{aligned}$$

Then, we proceed as in [36] and we represent the director field n as

$$\displaystyle \begin{aligned} \mathbf{n} = \cos\alpha \, \mathbf{e}_1 + \sin\alpha \, \mathbf{e}_2. \end{aligned} $$

(8)

The angle α is named deviation angle. We restrict to vector fields $\mathbf {n}\in W^{1,2}_{\mathrm {tan}}(M, \, \mathbb {S}^2)$ with zero winding number (the general case is discussed in [36]). Thus the deviation angle turns out to be periodic, namely $\alpha \in H^1_{\mathrm {per}}(Q)$. The energy expressed in terms of α is particularly appealing for the analysis. Setting W(α) = W(n), with n given by (8), we have

$$\displaystyle \begin{aligned} W(\alpha)=\frac 1 2\int_Q \left\{\kappa|\nabla_{\mathrm{s}} \alpha|{}^2 +\eta\cos{}(2\alpha)\right\} \mathrm{d} S + \kappa \pi^2 \left(\frac{2-\mu^2}{\sqrt{\mu^2-1}}+2\mu\right), \end{aligned} $$

(9)

where $\eta (\theta ,\phi ):=\kappa \frac {c_1^2-c_2^2(\theta ,\phi )}{2}= \kappa \frac {R^2+2Rr\cos \theta }{2r^2(R+r\cos \theta )^2}$, and $\mu :=\frac Rr$. The number μ is called aspect ratio and plays a prominent role in the minimization. In the next Proposition we discuss the dependence of minimizers on the aspect ratio μ. In particular, we discuss the stability of the minimizers.

Proposition 3

Let μ := R/r. There exists $\mu ^* \in (2/\sqrt {3} ,2]$ such that the constant values α = π/2 + mπ, $m\in \mathbb {Z}$ , are local minimizers for W in $H^1_{\mathrm {per}}(Q)$ if and only if μ ≥ μ ^∗ . Moreover, if μ ≥ 2, there exists no non-constant solution w to the Euler Lagrange equation

$$\displaystyle \begin{aligned} -\varDelta_{\mathrm{s}} \alpha =\frac \kappa2(c_1^2-c_2^2)\sin (2\alpha) \,\,\,\,\mathit{\text{ in }} Q \end{aligned}$$

such that

$$\displaystyle \begin{aligned} \frac{\pi}{2} +m\pi \leq w \leq \frac \pi 2 +(m+1)\pi. \end{aligned}$$

The proof of the proposition is in [36]. It is worthwhile noting that it is an interesting open problem to analytically determine the exact value of the critical threshold μ ^∗. Numerics indicates that μ ^∗≈ 1.52.

Proposition 3 is important since it describes how the Napoli-Vergori energy (1) acts. In particular, it shows the differences—for a toroidal shell—with the classical intrinsic energy (2). It turns out that the presence of the extrinsic term related to the shape operator acts as a selection principle for equilibrium configurations. More precisely, when μ := R/r is sufficiently large then (see Proposition 3) the only constant solution is α = π/2 + mπ ($m\in \mathbb {Z}$). Moreover, when R/r < μ ^∗ a new class of non constant solutions appears (see Fig. 1, obtained discretizing the gradient flow equation). We make the following observation: This new solution tries to minimize the effect of the curvature by orienting the director field along the meridian lines (α = 0), which are geodesics on the torus, near the hole of the torus, while near the external equator the director is oriented along the parallel lines α = π/2, which are lines of curvature. The fact that the solution α = π/2 is no longer stable for sufficiently small μ is due to the high bending energy associated to α = π/2 in the internal hole of the torus. In fact, in a small strip close to the internal equator of the torus, we can approximate (see [36])

$$\displaystyle \begin{aligned} c_1^2 -c_2^2 \approx \frac{1}{r^2}-\frac{1}{(R-r)^2},\quad \mathrm{d} S \approx r(R-r)\mathrm{d}\theta\,\mathrm{d}\phi, \end{aligned}$$

Fig. 1

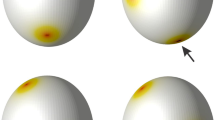
Configuration of the scalar field α and of the vector field n of a numerical solution to the gradient flow of (9) in the case R/r = 1.2 (left). Zoom-in of the central region of the same fields (right). The colour represents the angle α ∈ [0, π], the arrows represent the corresponding vector field n

and therefore

$$\displaystyle \begin{aligned} (c_1^2-c_2^2)\cos{}(\pi)\mathrm{d} S \approx \mu \frac{2-\mu}{\mu-1}\mathrm{d}\theta\,\mathrm{d}\phi, \end{aligned} $$

which tends to + ∞ as μ → 1.

Due to its “double well”-like structure, the energy (9) favors a smooth transition between α = π/2 and α = 0. In this sense, the new solution can be understood as an interpolation between α = π/2 and α = 0, which are the two constant stationary solutions of the system.

2.2 Existence of Solutions of the Gradient Flow of (1)

We then focus on the L ²-gradient flow of the one-constant approximation energy (1). The study of the gradient flow for the energy (1) could be seen as a starting point for the analysis of an Ericksen-Leslie type model for nematic shells. This problem has already been addressed in [38] where various well-posedness and long-time behavior results have been obtained for an Ericksen-Leslie type model on Riemannian manifolds. However, it should be pointed out that the model in [38] is purely intrinsic and does not take into account the way the substrate on which the nematic is deposited sits in the three-dimensional space. Moreover, in the equation describing the evolution of n (called d therein) the constraint |n| = 1 is not considered.

We prove (see Theorem 2.1) the well-posedness of the L ²-gradient flow of (1), i.e.

$$\displaystyle \begin{aligned} \begin{cases} \partial_t \mathbf{n} -\varDelta_g \mathbf{n} + \mathfrak{B}^2 \mathbf{n} = \vert \mathrm{D}\mathbf{n}\vert^2 \mathbf{n} + \vert \mathrm{d}{\boldsymbol{\gamma}}(\mathbf{n})\vert^2 \mathbf{n}\quad \text{in } M \times (0,+\infty), \\ \mathbf{n}(x,0) = \mathbf{n}_0\,\,\,\,\text{ a.e. in } M. \end{cases} \end{aligned} $$

(10)

Here Δ _g is the rough Laplacian and $\mathfrak {B}^2$ is the linear operator $(\mathfrak {B}^2 \mathbf {u}, \mathbf {v})_{\mathbb {R}^3}:= (\mathrm {d}{\boldsymbol {\gamma }}(\mathbf {u}),\mathrm {d}{\boldsymbol {\gamma }}(\mathbf {v}))_{\mathbb {R}^3}$ for any u, v tangent vector fields. The right-hand side of (10) is a result of the unit-norm constraint on the director n. The initial datum n ₀ is taken in $W^{1,2}_{\mathrm {tan}}(M, \, \mathbb {S}^2)$ and we look for weak solutions with bounded energy. A proof of the existence relying on (i) discretization, (ii) a priori estimates, (iii) convergence of discrete solutions, would encounter a difficulty here, as the nonlinear term |Dn|² in the right-hand side of (10) is not continuous with respect to the weak-W ^{1, 2} convergence expected from the a priori estimates. We overcome this problem with techniques employed in the study of the heat flow for harmonic maps (see [10, 11]): we first relax the unit-norm constraint with a Ginzburg-Landau approximation, i.e., we allow for vectors n with |n|≠ 1, but we penalize deviations from unitary length at the order 1/ε ², for a small parameter ε > 0. More precisely, we construct (via a time discretization argument) a sequence of fields n ^ε which solve

$$\displaystyle \begin{aligned} \begin{cases} \partial_t \mathbf{n}^\varepsilon -\varDelta_g \mathbf{n}^\varepsilon + \mathfrak{B}^2\mathbf{n}^\varepsilon + \frac{1}{\varepsilon^2}(\vert \mathbf{n}^\varepsilon\vert^2 - 1) \mathbf{n}^\varepsilon = 0, \text{ a.e. in } M \times (0,+\infty),\\ \mathbf{n}^\varepsilon(x,0) = \mathbf{n}_0\,\,\,\,\text{ a.e. in } M. \end{cases} \end{aligned}$$

The above equation has a gradient flow structure. Thus, we have

$$\displaystyle \begin{aligned} \| \partial_t \mathbf{n}^\varepsilon(t)\|{}^2 +\frac{\mathrm{d}}{\mathrm{d} t}W(\mathbf{n}^\varepsilon(t)) + \frac{1}{4\varepsilon^2}\frac{\mathrm{d}}{\mathrm{d} t}\int_{M} (\vert \mathbf{n}^\varepsilon(t)\vert^2-1)^2\mathrm{d} S = 0. \end{aligned}$$

which produces the following energy estimate when the initial condition n ₀ has finite energy

$$\displaystyle \begin{aligned} \| \partial_t\mathbf{n}^\varepsilon\|{}^2_{L^2(0,T;L^2_{\mathrm{tan}}(M))} &+ \| \mathrm{D} \mathbf{n}^\varepsilon\|{}^2_{L^\infty(0,T;L^2_{\mathrm{tan}}(M))} + \| \mathrm{d} {\boldsymbol{\gamma}}(\mathbf{n}^\varepsilon) \|{}^2_{L^\infty(0,T;L^2_{\mathrm{tan}}(M))} \\ &+\sup_{t\in(0,T)}\frac{1}{4\varepsilon^2}\int_M (\vert \mathbf{n}^\varepsilon(t)\vert^2-1)^2 \mathrm{d} S \le 3W(\mathbf{n}_0).{} \end{aligned} $$

Via standard compactness arguments, one obtains the existence of limit vector field n with the energy regularity specified by the above estimate. The difficult part is clearly to pass to the limit in the approximate equation and to show that the field n is indeed a weak solution of (10) The crucial observation (borrowed from [10, 11]) is that for a smooth unit-norm field n, (10) is equivalent to

$$\displaystyle \begin{aligned} (\partial_t \mathbf{n} -\varDelta_g \mathbf{n} + \mathfrak{B}^2\mathbf{n}) \times \mathbf{n} =0. \end{aligned} $$

(11)

To highlight the importance of the reformulation (11), let us consider the case of an harmonic map $u:\varOmega \to \mathbb {S}^2$ with $\varOmega \subset \mathbb {R}^n$ an open set. Being an harmonic map, u solves the nonlinear elliptic equation

$$\displaystyle \begin{aligned} \varDelta u + u\vert \nabla u\vert^2 = 0 \,\,\,\text{ in } \varOmega. \end{aligned} $$

(12)

Now, taking the vector product of the equation with u, one obtains that u solves (12) if and only if it solves

$$\displaystyle \begin{aligned} \varDelta u\times u= 0 \,\,\,\text{ in } \varOmega, \end{aligned}$$

which is equivalent to

$$\displaystyle \begin{aligned} \sum_{i=1}^{n}\frac{\partial}{\partial x_i}(u\times \frac{\partial u}{\partial x_i}) = 0\,\,\,\text{ in } \varOmega. \end{aligned} $$

(13)

Note that, differently from (12), the equation (13) is in divergence form and thus is it more treatable in weak regularity contexts. The above strategy can be implemented in our case and gives that (see [25, Lemma 7.5.4] for a similar argument)

Lemma 1

A vector field $\mathbf {n}\in W^{1,2}(0,T;L^2_{\mathrm {tan}}(M))\cap L^\infty (0,T;W^{1,2}_{\mathrm {tan}}(M, \, \mathbb {S}^2))$ is a weak solution of (10) if and only if it solves

$$\displaystyle \begin{aligned} \begin{aligned} -\int_{M}(\partial_t \mathbf{n}\times \mathbf{n}, {\boldsymbol{\gamma}})_{\mathbb{R}^3}\, \psi \,\mathrm{d} S+ \int_{M}g^{ij}(\mathrm{D}_i\mathbf{n},{\boldsymbol{\gamma}}\times \mathbf{n})_{\mathbb{R}^3} \, \partial_{j}\psi \,\mathrm{d} S - \int_{M}(\mathfrak{B}^2\mathbf{n}\times\mathbf{n},{\boldsymbol{\gamma}})_{\mathbb{R}^3} \, \psi\,\mathrm{d} S = 0 \end{aligned} \end{aligned} $$

(14)

for any smooth function $\psi :M\to \mathbb {R}$.

Thus the strategy is as follows. First of all, we test the weak formulation of (10) with the vector field ϕ = ψ γ ×n ^ε where $\psi :M\to \mathbb {R}$ is smooth. We obtain

$$\displaystyle \begin{aligned} \begin{aligned} &-\int_{M}(\partial_t \mathbf{n}^\varepsilon\times \mathbf{n}^\varepsilon, {\boldsymbol{\gamma}})_{\mathbb{R}^3} \, \psi\,\mathrm{d} S + \int_{M}g^{ij}(\mathrm{D}_i\mathbf{n}^\varepsilon,{\boldsymbol{\gamma}}\times \mathbf{n}^\varepsilon)_{\mathbb{R}^3} \, \partial_{j}\psi\,\mathrm{d} S \\ &\qquad \qquad \qquad - \int_{M}(\mathfrak{B}^2\mathbf{n}^\varepsilon\times\mathbf{n}^\varepsilon,{\boldsymbol{\gamma}})_{\mathbb{R}^3}\psi\,\mathrm{d} S = 0, \end{aligned} \end{aligned} $$

(15)

where the penalization term has disappeared thanks to $(a,b\times a)_{\mathbb {R}^3} = (b, a\times a)_{\mathbb {R}^3}= 0$, for $a,b\in \mathbb {R}^3$. Now, (15) has a “divergence” structure and thus is adequate for the limit procedure with respect to the convergences given by the energy estimate. Consequently, we pass to the limit in (15) and we obtain that n solves (14) that is equivalent to (10) thanks to the above lemma. Thus, we have (see [36, Theorem 5.1] for the details)

Theorem 2.1

Let M be a two-dimensional compact surface satisfying (7). Given $\mathbf {n}_0\in W^{1,2}_{\mathrm {tan}}(M, \, \mathbb {S}^2)$ there exists a global weak solution to (10) with n(⋅, 0) = n ₀(⋅) in M.

2.3 Justification of the Energy (1): A Discrete to Continuum Approach

In this subsection we show how the energy (1) emerges as the discrete to continuum limit of a discrete energy of XY type. We recall that we will use the very same discrete energy to understand the generation of defects for shells with non zero Euler Characteristic in the next Sect. 3. The main tool of our analysis will be the concept of Γ-convergence for which we refer to the book of G. Dal Maso [12].

The discrete energy we consider is defined on a triangulation of the surface M. Thus, before introducing the discrete energy, we have to (briefly) introduce the discrete formalism. We refer to the paper [8] for the details of the construction.

For any ε ∈ (0, ε ₀], we let $\mathcal {T}_\varepsilon$ be a triangulation of M, that is, a finite collection of non-degenerate affine triangles $T\subseteq \mathbb {R}^3$ with the following property: the intersection of any two triangles T, $T^\prime \in \mathcal {T}_\varepsilon$ is either empty or a common subsimplex of T, T ^′. The parameter ε is the mesh size, namely we assume $\varepsilon =\max _{T\in \mathcal {T}_\varepsilon }\mathrm {diam}(T)$. The set of vertices of $\mathcal {T}_\varepsilon$ will be denoted by $\mathcal {T}^0_\varepsilon$. We will always assume that $\mathcal {T}^0_\varepsilon \subseteq M$. We set $\widehat {M}_\varepsilon := \cup _{T\in \mathcal {T}_\varepsilon } T$, so $\widehat {M}_\varepsilon$ is the piecewise-affine approximation of M induced by $\mathcal {T}_\varepsilon$. Given a piecewise-smooth function $\mathbf {u}\colon \widehat {M}_\varepsilon \to \mathbb {R}^k$, we denote by ∇ _ε u the restriction of the derivative ∇u to directions that lie in the triangles of $\widehat {M}_\varepsilon$.

We will only consider family of triangulations $(\mathcal {T}_\varepsilon )$ that satisfy the following conditions.

(H₁ ):

There exists a constant Λ > 0 such that, for any ε ∈ (0, ε ₀] and any $T\in \mathcal {T}_\varepsilon$, the (unique) affine bijection ϕ: T _ref → T satisfies

$$\displaystyle \begin{aligned} \operatorname{\mathrm{Lip}}(\phi)\leq\varLambda\varepsilon, \qquad \operatorname{\mathrm{Lip}}(\phi^{-1})\leq \varLambda\varepsilon^{-1}, \end{aligned}$$

where $T_{\mathrm {ref}}\subseteq \mathbb {R}^2$ be a reference triangle of vertices (0, 0), (1, 0) and (0, 1). Here Lip(ϕ) denotes the Lipschitz constant of ϕ, Lip(ϕ) :=sup_{x ≠ y}|x − y|⁻¹|ϕ(x) − ϕ(y)|.

(H₂ ):

For any ε ∈ (0, ε ₀] and any i, $j\in \mathcal {T}^0_\varepsilon$ with i ≠ j, the stiffness matrix $\kappa ^{ij}_\varepsilon$ of the Laplace Beltrami operator on M satisfies

$$\displaystyle \begin{aligned} \kappa_\varepsilon^{ij} := -\int_{\widehat{M}_\varepsilon} \nabla_{\varepsilon}\widehat{\varphi}_{\varepsilon, i} \cdot\nabla_{\varepsilon}\widehat{\varphi}_{\varepsilon, j} \,\mathrm{d} S \geq 0, \end{aligned}$$

where the hat function $\widehat {\varphi }_{\varepsilon , i}$ is the unique piecewise-affine, continuous function $\widehat {M}_\varepsilon \to \mathbb {R}$ such that $\widehat {\varphi }_{\varepsilon , i}(j) = \delta _{ij}$ for any $j\in \mathcal {T}^0_\varepsilon$.

(H₃ ):

For any ε ∈ (0, ε ₀], $\widehat {M}_\varepsilon \subseteq U$ and the restriction of the nearest-point projection $\widehat {P}_\varepsilon := P_{|\widehat {M}_\varepsilon }\colon \widehat {M}_\varepsilon \to M$ has a Lipschitz inverse. Moreover, we have $\operatorname {\mathrm {Lip}}(\widehat {P}_\varepsilon ) + \operatorname {\mathrm {Lip}}(\widehat {P}_\varepsilon ^{-1})\leq \varLambda$ for some ε-independent constant Λ.

An important consequence of the assumption (H₃) is that the restriction of the nearest-point projection $\widehat {P}_\varepsilon \colon \widehat {M}_\varepsilon \to M$ has a Lipschitz inverse $\widehat {P}_\varepsilon ^{-1}\colon M \to \widehat {M}_\varepsilon$. Following [16], we use $\widehat {P}_\varepsilon$ and $\widehat {P}_\varepsilon ^{-1}$ to construct the so called metric distorsion tensor. This object will be important in our analysis since it will permit to rewrite our discrete energy as an energy for a proper vector field interpolating the discrete spins. To introduce the metric distorsion tensor, we proceed as follow. For any x ∈ M such that $\widehat {P}_\varepsilon ^{-1}(x)$ falls in the interior of a triangle of $\widehat {M}_\varepsilon$ (so that $\widehat {P}_\varepsilon ^{-1}$ is smooth in a neighbourhood of x), we let the metric distorsion tensor A _ε (x) to be the unique linear operator T _x M →T _x M that satisfies

$$\displaystyle \begin{aligned} \left(\mathbf{A}_\varepsilon(x)\mathbf{X}, \, \mathbf{Y}\right) = \left(\mathrm{d} \widehat{P}_\varepsilon^{-1}(x) [\mathbf{X}], \, \mathrm{d} \widehat{P}_\varepsilon^{-1}(x) [\mathbf{Y}]\right) \end{aligned} $$

(16)

for any X, Y ∈ T _x M. The metric distorsion tensor is symmetric and positive definite, since the right-hand side of (16) is. Consequently, we introduce a norm $\|\cdot \|{ }_{L^\infty (M)}$ on L ^∞(M; TM ⊗T^∗ M) by

$$\displaystyle \begin{aligned} \|\mathbf{A}\|{}_{L^\infty(M)} := \underset{x\in M}{\operatorname{\mbox{ess sup}}} \ \|\mathbf{A}(x) \|{}_{\mathrm{T} M\otimes\mathrm{T}^* M}, \end{aligned}$$

where $\|\cdot \|{ }_{\mathrm {T} M\otimes \mathrm {T}^* M}$ is the operator norm. The following lemma (see [8, Lemma 2]) is important.

Lemma 2

Suppose that $(\mathcal {T}_\varepsilon )$ satisfies (H1) and (H3) . Then, there holds

$$\displaystyle \begin{aligned} \|\mathbf{A}_\varepsilon - \operatorname{\mathrm{Id}}\|{}_{L^\infty(M)} + \|\mathbf{A}^{-1}_\varepsilon - \operatorname{\mathrm{Id}}\|{}_{L^\infty(M)} \leq C\varepsilon. \end{aligned}$$

Let g _ε  ∈ L ^∞(M; T^∗ M ^⊗2) be the metric on M defined by g _ε (X, Y) := (A _ε X, Y), for any smooth fields X and Y on M. Given a function u ∈ W ^{1, 2}(M), one can define the Sobolev W ^{1, 2}-seminorm of u with respect to g _ε , i.e.

$$\displaystyle \begin{aligned} |u|{}_{W^{1,2}_\varepsilon(M)}^2 := \int_M \left(\mathbf{A}_\varepsilon^{-1}\nabla_{\mathrm{s}} u, \, \nabla_{\mathrm{s}} u\right) (\det \mathbf{A}_\varepsilon)^{1/2} \, \mathrm{d} S, \end{aligned} $$

(17)

where ∇_s denotes the Riemaniann gradient and dS the volume form on M (with respect to the metric induced by $\mathbb {R}^3$). By construction (16), the map $\widehat {P}_\varepsilon ^{-1}$ is an isometry between M, equipped with the metric g _ε , and $\widehat {M}_\varepsilon$, with the metric induced by $\mathbb {R}^3$. Therefore, given $v\in W^{1, 2}(\widehat {M}_\varepsilon ; \, \mathbb {R})$ and a Borel set U ⊆ M, there holds

$$\displaystyle \begin{aligned} |v\circ\widehat{P}_\varepsilon^{-1}|{}_{W^{1,2}_\varepsilon(U)}^2 = \int_{\widehat{P}_\varepsilon^{-1}(U)} |\nabla_{\varepsilon} v|{}^2 \,\mathrm{d} S. \end{aligned}$$

Arguing component-wise, we see that the same equality holds for a (not necessarily tangent) vector field $\mathbf {v}\colon \widehat {M}_\varepsilon \to \mathbb {R}^3$ in place of v.

Using assumption (H₃), to any discrete vector field $\mathbf {v}_\varepsilon \in \mathrm {T}(\mathcal {T}_\varepsilon ; \, \mathbb {S}^2)$ we can associate a continuous field $\mathbf {w}_\varepsilon \colon M\to \mathbb {R}^3$ by setting

$$\displaystyle \begin{aligned} \mathbf{w}_\varepsilon:=\widehat{\mathbf{v}}_\varepsilon\circ\widehat{P}_\varepsilon^{-1}, \end{aligned} $$

(18)

where $\widehat {\mathbf {v}}_\varepsilon \colon \widehat {M}_\varepsilon \to \mathbb {R}^3$ is the affine interpolant of v _ε . The field w _ε is Lipschitz-continuous and satisfies w _ε  = v _ε on $\mathcal {T}^0_\varepsilon$, but it is not tangent to M nor unit-valued, in general. However, one can still prove some useful properties that we collect in a single lemma (see [8, Lemma 3, Lemma 4, Lemma 5] for the proofs).

Lemma 3

Suppose that (H1) , (H2) , (H3) are satisfied. Then, for any ε ∈ (0, ε ₀] and any discrete field $\mathbf {v}_\varepsilon \in \mathrm {T}(\mathcal {T}_\varepsilon ; \, \mathbb {S}^2)$ , w _ε is Lipschitz-continuous with Lipschitz constant

$$\displaystyle \begin{aligned} \operatorname{\mathrm{Lip}}(\mathbf{w}_\varepsilon)\leq C\varepsilon^{-1}. \end{aligned}$$

Moreover, w _ε satisfies the following

• For any subset $\widehat {U}\subseteq \widehat {M}_\varepsilon$ that can be written as union of triangles of $\mathcal {T}_\varepsilon$ , there holds

  $$\displaystyle \begin{aligned} XY_\varepsilon(\mathbf{v}_\varepsilon, \, \widehat{U}) := \frac 12 \sum_{i, j\in \mathcal{T}^0_\varepsilon\cap\widehat{U}}\kappa_\varepsilon^{ij} \left| \mathbf{v}_\varepsilon(i) - \mathbf{v}_\varepsilon(j) \right|{}^2 = \frac 12 |\mathbf{w}_\varepsilon|{}^2_{W^{1,2}_\varepsilon(P(\widehat{U}))}. \end{aligned} $$

  (19)

• There exists a positive constant C such that

  $$\displaystyle \begin{aligned} \left\| \left(\mathbf{w}_\varepsilon, \, {\boldsymbol{\gamma}}\right) \right\|{}_{L^\infty(M)} \leq C\varepsilon,\,\mathit{\text{ and }} \frac{1}{\varepsilon^2} \int_{\widehat{M}_\varepsilon} \left(1 - |\mathbf{w}_\varepsilon|{}^2\right)^2 \leq C \, XY_\varepsilon(\mathbf{v}_\varepsilon). \end{aligned} $$

  (20)

Another immediate but important consequence of the lemma above is a compactness result for discrete sequences v _ε with equi-bounded energy with respect to ε.

Lemma 4

Let $\mathbf {v}_\varepsilon \in \mathrm {T}(\mathcal {T}_\varepsilon ; \, \mathbb {S}^2)$ be a sequence such that

$$\displaystyle \begin{aligned} XY_\varepsilon(\mathbf{v}_\varepsilon) \le C \qquad \mathrm{for any} \varepsilon>0, \end{aligned}$$

then there exists $\mathbf {v}\in W^{1,2}_{\mathrm {tan}}(M, \, \mathbb {S}^2)$ and a subsequence of ε such that, defining w _ε as in (18), there holds

$$\displaystyle \begin{aligned} \mathbf{w}_\varepsilon \xrightarrow{\varepsilon \to 0} \mathbf{v} \,\,\,\,\,\mathit{\text{ strongly in }} L^2(M;\mathbb{R}^3). \end{aligned} $$

(21)

Then, we have the following.

Theorem 2.2

Suppose that the assumptions (H1) , (H2) and (H3) are satisfied. Then, XY _ε Γ-converges with respect to weak convergence of $L^2(M;\mathbb {R}^3)$ to the functional

$$\displaystyle \begin{aligned} W(\mathbf{v}):= \begin{cases} \frac 12\int_{M}\vert\mathrm{D}\mathbf{v}\vert^2 + \vert \mathrm{d}{\boldsymbol{\gamma}}[\mathbf{v}]\vert^2 \mathrm{d} S, &\,\,\mathit{\text{ if }} \mathbf{v}\in W^{1,2}_{\tan}(M;\mathbb{S}^2)\\ + \infty, &\,\,\mathit{\text{ otherwise in }} L^2(M;\mathbb{R}^3). \end{cases} \end{aligned}$$

The proof follows standard argument in the analysis of discrete to continuum limits via Γ-convergence (see, e.g., [1, 7] and the Lecture Notes [34] for a slightly different model). We highlight the main points for future reference since, to the best of our knowledge, the proof of this result is not contained in any contribution.

Proof (Proof—Γ-liminf Inequality)

We are given a sequence of discrete vector fields v _ε and we aim to prove that there exists a unit norm tangent vector field v such that w _ε  →v weakly in $L^2(M;\mathbb {R}^3)$ (actually much more is true) and

$$\displaystyle \begin{aligned} \liminf_{\varepsilon\to 0}XY_\varepsilon(\mathbf{v}_\varepsilon) \ge W(\mathbf{v}). \end{aligned} $$

(22)

Without loss of generality, we may assume that there exists a constant C such that XY _ε (v _ε ) ≤ C for any ε (if not (22) is trivially satisfied). Thus, we have that the sequence w _ε defined in (18) is bounded, uniformly with respect to ε, in $W^{1,2}_{\varepsilon }(M)$. Then, the compactness result in Lemma 4 gives that there exists a subsequence, still denoted with w _ε , and a vector field $\mathbf {v}\in W^{1,2}(M;\mathbb {R}^3)$ for which

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \mathbf{w}_\varepsilon \xrightarrow{\varepsilon \to 0} \mathbf{v} \,\,\,\,\text{ strongly in } L^2(M;\mathbb{R}^3). \end{array} \end{aligned} $$

(23)

This convergence, combined with (20), give that v is tangent and |v| = 1, namely $\mathbf {v}\in W^{1,2}_{\mathrm {tan}}(M, \, \mathbb {S}^2)$. Finally, since there holds (see (17))

$$\displaystyle \begin{aligned} XY_\varepsilon(\mathbf{v}_\varepsilon) = \frac 12 |\mathbf{w}_\varepsilon|{}^2_{W^{1,2}_\varepsilon(M)} = \frac 12 \sum_{i=1}^3|\mathbf{w}_\varepsilon^i|{}^{2}_{W^{1,2}_\varepsilon(M)} = \frac 12\sum_{i=1}^3 \int_M \left(\mathbf{A}_\varepsilon^{-1}\nabla_{\mathrm{s}} \mathbf{w}_\varepsilon^i, \, \nabla_{\mathrm{s}} \mathbf{w}_\varepsilon^i\right) (\det \mathbf{A}_\varepsilon)^{1/2} \, \mathrm{d} S, \end{aligned}$$

Lemma 2 and the semicontinuity of norms with respect to weak convergence gives

$$\displaystyle \begin{aligned} \liminf_{\varepsilon \to 0}\frac 12 |\mathbf{w}_\varepsilon|{}^2_{W^{1,2}_\varepsilon(M)} \ge \frac 12 \int_{M}\vert \nabla_{\mathrm{s}} \mathbf{v}\vert^2 \mathrm{d} S = W(\mathbf{v}), \end{aligned}$$

that is (22).

Proof (Proof—Γ-limsup Inequality: Existence of a Recovery Sequence)

Given $\mathbf {v}\in W^{1,2}_{\mathrm {tan}}(M, \, \mathbb {S}^2)$, we have to construct a sequence of discrete vector fields $\mathbf {v}_\varepsilon \in \mathrm {T}(\mathcal {T}_\varepsilon ; \, \mathbb {S}^2)$ such that w _ε  →v weakly in $L^2(M;\mathbb {R}^3)$ and

$$\displaystyle \begin{aligned} \limsup_{\varepsilon \to 0}XY_\varepsilon(\mathbf{v}_\varepsilon)\le W(\mathbf{v}). \end{aligned}$$

The construction is as follows. First of all, we can assume that v is smooth, otherwise we can approximate it with a density argument (see [33] and [9]). Now, we let v _ε be the discrete vector field given by the restriction of v to the nodes of the triangulation, namely v _ε (i) := v(i) for $i\in \mathcal {T}^{\varepsilon }_{0}$. Then, constructing w _ε as in (18), it is not difficult to realize that w _ε  →v strongly in $L^2(M;\mathbb {R}^3)$ and that

$$\displaystyle \begin{aligned} \limsup_{\varepsilon\to 0}XY_\varepsilon(\mathbf{v}_\varepsilon) \le W(\mathbf{v}), \end{aligned}$$

hence the thesis follows.

3 Shells of Non-Zero Euler Characteristic: Emergence of Defects

In this last section we are interested in understanding the energetics of defected configurations and, consequently, locate the defects on the surface M. The results we present are taken from [8] to which we refer for all the details and proofs. First of all, we introduce the notion of vorticity and its discrete counterpart which, as it happens for the discrete flat case and for the Ginzburg Landau case, encodes the topological informations of the discrete sequence v _ε . Moreover, the concentration of the discrete vorticity in the ε → 0 limit will be the indication of the emergence of defects. We leave the precise introduction of this measure to the paper [8]. However, for the sake of clarity we briefly sketch it here.

We first consider the continuum setting. Given a map $\mathbf {u}\in (W^{1, 1}\cap L^\infty )(M;\,\mathbb {R}^3)$, we define the vorticity of u as the 1-form

whose action on a smooth, tangent field w on M is given by

The role of the vorticity (actually of its differential) is expressed in the following lemma (see [8, Lemma 6]).

Lemma 5

Let $\mathbf {u}\in W^{1,1}_{\mathrm {tan}}(M; \, \mathbb {S}^2)$ be a unit, tangent field. Suppose that there exist a finite number of points x ₁, …, x _p such that

$$\displaystyle \begin{aligned} \mathbf{u}\in W^{1,2}_{\mathrm{loc}}(M\setminus\{x_1, \, \ldots, \, x_p\}; \, \mathbb{R}^3). \end{aligned}$$

Then

$$\displaystyle \begin{aligned} \star\mathrm{d}\jmath(\mathbf{u}) = 2\pi\sum_{i = 1}^p \operatorname{\mathrm{ind}}(\mathbf{u}, \, x_i) \delta_{x_i} - G \qquad \mathrm{in} \mathcal{D}^\prime(M). \end{aligned}$$

In the lemma, ⋆ is the Hodge dual operator and ind(u, x _i ) the local degree of u at the point x _i , that is, the winding number of u around the boundary of a small disk centred at x _i (see e.g. [9] for more details).

Now, given a discrete field $\mathbf {v}_\varepsilon \in \mathrm {T} (\mathcal {T}_\varepsilon ; \, \mathbb {S}^2)$, we define the discrete vorticity measure $\widehat {\mu }_\varepsilon (\mathbf {v}_\varepsilon )$ as follows. For any given triangle $T\in \mathcal {T}_\varepsilon$ we let (i ₀, i ₁, i ₂) be its vertices, sorted in counter-clockwise order with respect to the orientation induced by γ and we let i ₃ := i ₀. The measure $\widehat {\mu }_\varepsilon (\mathbf {v}_\varepsilon )$ is defined as a linear combination of Dirac delta measures supported on the baricenters of triangles $T\in \mathcal {T}_\varepsilon$, and the weights are given in such a way that

It turns out that the right-hand side approximates the integral $\int _T\mathrm {d}\jmath (\widehat {\mathbf {v}}_\varepsilon )$, where $\widehat {\mathbf {v}}_\varepsilon \colon \widehat {M}_\varepsilon \to \mathbb {R}^3$ is the affine interpolant of v _ε , hence $\widehat {\mu }_\varepsilon (\mathbf {v}_\varepsilon )$ is a discretization of $\mathrm {d}\jmath (\widehat {\mathbf {v}}_\varepsilon )$. In the limit ε → 0, the appearance of defects is related to the convergence $\widehat {\mu }_\varepsilon (\mathbf {v}_\varepsilon )\to 2\pi \mu - G \, \mathrm {d} S$, where μ is a measure concentrated on a finite number of points $\left \{x_1,\ldots ,x_k\right \}$ in M. This convergence is to be intended in the sense of the flat topology, that is, the dual-norm topology on $W^{1,\infty }(\mathbb {R}^3)^\prime$.

The location of the defects is achieved by the analysis of the so called Renormalized Energy $\mathbb {W}$ introduced by Brezis, Bethuel and Hélein for the Ginzburg Landau equation in [5]. In [8], we obtain the Renormalized Energy as the (first order) Γ-limit of the discrete energy XY _ε as in [2, 3, 32] for the euclidean case.

Following [2], we introduce the following class of vector fields in M: for any k, $\mathcal {V}_k$ is the set of fields $\mathbf {v}\in L^2(M; \, \mathbb {S}^2)$ such that there exist $(x_i)_{i=1}^k\in M^k$, $(d_i)_{i=1}^k \in \{-1, \, 1\}^k$ such that

$$\displaystyle \begin{aligned} \begin{aligned} \mathbf{v}\in W^{1,2}_{\tan, \mathrm{loc}}\left(M\setminus \bigcup_{i=1}^{k}x_i; \, \mathbb{S}^2\right), \qquad \star\mathrm{d}\jmath(\mathbf{v}) = 2\pi\sum_{i = 1}^k d_i \delta_{x_i} - G . \end{aligned} \end{aligned}$$

Given an even number $\mathcal {K}\in \mathbb {N}$ such that $\mathcal {K}\geq |\chi (M)|$, we define the intrinsic Renormalized Energy as (see [2, Eq. (4.22)]):

$$\displaystyle \begin{aligned} \mathbb{W}_{\mathrm{intr}}(\mathbf{v}) := \begin{cases} \lim_{\delta \to 0} \left(\dfrac{1}{2}\displaystyle\int_{M_\delta}\vert \mathrm{D}\mathbf{v}\vert^2\mathrm{d} S - \mathcal{K}\pi\vert \log\delta\vert\right) &\text{for }\mathbf{v}\in \mathcal{V}_{\mathcal{K}}\\ -\infty &\text{for }\mathbf{v}\in \mathcal{V}_{k},\,\,k <\mathcal{K},\\ +\infty &\text{otherwise in } L^2(M; \, \mathbb{R}^3), \end{cases} \end{aligned}$$

where, given $\mathbf {v}\in \mathcal {V}_{\mathcal {K}}$ and δ > 0 so small that the balls B _δ (x _i ) are pairwise disjoint, we have set $M_\delta :=M\setminus \bigcup _{i=1}^{\mathcal {K}}B_\delta (x_i)$. The definition above is shown to be well posed (see [8]). It is important to note that for $\mathbf {v}\in \mathcal {V}_{\mathcal {K}}$ there holds

$$\displaystyle \begin{aligned} \vert \mathrm{d} {\boldsymbol{\gamma}}[\mathbf{v}]\vert \le C \,\,\,\,\text{ a.e. in } M, \end{aligned} $$

(24)

where the constant C depends only on M. Thus, the following quantity exists in [−∞, +∞]:

$$\displaystyle \begin{aligned} \mathbb{W}(\mathbf{v}) := \mathbb{W}_{\mathrm{intr}}(\mathbf{v}) + \frac{1}{2}\int_{M}\vert \mathrm{d} {\boldsymbol{\gamma}}[\mathbf{v}]\vert^2 \mathrm{d} S. \end{aligned}$$

$\mathbb {W}$ will be called the Renormalized Energy. Note that $\mathbb {W}$ contains both an intrinsic and an extrinsic term but, due to (24), the latter is always finite. This shows, as expected, that the concentration of the energy is due to the Dirichlet part of $\mathbb {W}$ in (1).

A source of difficulties that emerges in the analysis of this discrete energy is related to the fact that for a curved shell the vertices of the triangulation do not necessarily sit on a structured lattice. In particular, this problem reflects on the study of the so called core energy, namely the energy concentrated in each defect, for which the typical scaling arguments used in the planar case (see [5] and [2]) are not available. As already anticipated, as a result of our analysis we will obtain a core energy that depends of the singularity and moreover it will depend on the (limit) triangulation around each defect x _i . To obtain such a result, we have to enforce our assumptions on the triangulation $\mathcal {T}_\varepsilon$ around the singularities in the limit ε → 0. At base, we require that our triangulation $\mathcal {T}_\varepsilon$ is somehow scale invariant. We express this requirement as follows.

(H₄ ):

For any x ∈ M there exists a triangulation $\mathcal {S} = \mathcal {S}(x)$ on $\mathbb {R}^2$ such that, for any δ > 0 smaller than the injectivity radius of M, there holds

$$\displaystyle \begin{aligned} \lim_{\varepsilon\searrow 0} \ d(\mathcal{S}_{\varepsilon}, \, \mathcal{S}_{|B_{\delta/\varepsilon}}) \, \left| \log\varepsilon \right| = 0, \end{aligned}$$

where d(⋅, ⋅) is a properly defined distance between triangulations (see [8] for the details) and $\mathcal {S}_{|B_{\delta /\varepsilon }}$ denotes the restriction of $\mathcal {S}$ to the ball B _δ/ε.

In [8, Theorem B] the following theorem is proved

Theorem 3.1

Suppose that the assumptions (H1) , (H2) , (H3) and (H4) are satisfied. Then the following Γ-convergence result holds.

• (i) Compactness. Let $\mathcal {K}\in \mathbb {N}$ and let v _ε be a sequence in $\mathrm {T}(\mathcal {T}_\varepsilon ; \, \mathbb {S}^2)$ for which there exists a positive constant $C_{\mathcal {K}}$ such that

  $$\displaystyle \begin{aligned} XY_\varepsilon(\mathbf{v}_\varepsilon) - \mathcal{K}\pi \vert \log\varepsilon\vert \le C_{\mathcal{K}}. \end{aligned} $$

  (25)

  Then, up to a subsequence, there holds

  $$\displaystyle \begin{aligned} \hat{\mu}_\varepsilon(\mathbf{v}_\varepsilon)\xrightarrow{\operatorname{\mathrm{flat}}} 2\pi\mu - G \mathrm{d} S \end{aligned} $$

  (26)

  for some $\mu = \sum _{i=1}^k d_i \delta _{x_i}$ with $\sum _{i=1}^k \vert d_i\vert \le \mathcal {K}$ . If $\lvert \mu \rvert = \mathcal {K}$ , then $k=\mathcal {K}\equiv \chi (M) \mod 2$ , |d _i | = 1 for any i. Moreover, there exists $\mathbf {v}\in \mathcal {V}_{\mathcal {K}}$ and a subsequence such that

  $$\displaystyle \begin{aligned} \mathbf{w}_\varepsilon \to \mathbf{v} \mathit{\text{ strongly in }} L^2(M;\mathbb{R}^3) \mathit{\text{ and weakly in }} W^{1,2}_{\mathrm{loc}}(M\setminus \bigcup_{i=1}^{\mathcal{K}}x_i; \mathbb{R}^3), \end{aligned} $$

  (27)

  where w _ε is the interpolant of v _ε defined by (18).

• (ii) Γ- $\liminf$ inequality. Let $\mathbf {v}_\varepsilon \in \mathrm {T}(\mathcal {T}_\varepsilon ; \, \mathbb {S}^2)$ be a sequence satisfying (25) with $\mathcal {K}\equiv \chi (M)\mod 2$ and converging to some $\mathbf {v}\in \mathcal {V}_{\mathcal {K}}$ as in (26)–(27). Then, there holds

  $$\displaystyle \begin{aligned} \liminf_{\varepsilon\to 0} \left(XY_\varepsilon(\mathbf{v}_\varepsilon) - \mathcal{K} \pi\vert \log\varepsilon\vert\right) \ge \mathbb{W}(\mathbf{v}) + \sum_{i=1}^{\mathcal{K}}\gamma(x_i), \end{aligned}$$

  where γ(x _i ) is the core energy around each defect x _i .

• (iii) Γ- $\limsup$ inequality. Given $\mathbf {v}\in \mathcal {V}_{\mathcal {K}}$ , there exists $\mathbf {v}_\varepsilon \in \mathrm {T}(\mathcal {T}_\varepsilon ; \, \mathbb {S}^2)$ such that $\hat {\mu }_\varepsilon (\mathbf {v}_\varepsilon )\xrightarrow { \operatorname {\mathrm {flat}}}\star \mathrm {d}\jmath (\mathbf {v})$ , w _ε  →v as in (27) and

  $$\displaystyle \begin{aligned} \lim_{\varepsilon\to 0}\left(XY_\varepsilon(\mathbf{v}_\varepsilon) - \mathcal{K} \pi\vert \log\varepsilon\vert\right) = \mathbb{W}(\mathbf{v}) + \sum_{i=1}^{\mathcal{K}}\gamma(x_i). \end{aligned}$$