Keywords

1 Introduction

A variety of splines with different properties are used in calculations in many engineering projects [1, 3]. Among them are analysis-suitable T-splines of arbitrary degree, which are useful for modeling cracks in plane problems, and for the solution of boundary-value problems, cubic, bicubic and biquadratic B-splines, trigonometric, orthogonal splines. These splines are applied to the construction of curves and surfaces, to the designing of ship hulls, to the transformation of a sound signal’s frequency and to many others [1,2,3,4,5,6,7,8,9,10,11,12,13].

This paper is a continuation of the series of papers devoted to the construction and investigation of the properties of integro-differential polynomial splines of the fifth order [7, 14, 15]. In this paper we discuss the construction of polynomial splines which use three integrals over subintervals in addition to the values of the function in the nodes. As in previous papers, we construct the approximation separately for each subinterval. As usual, local spline approximation uses values of the approximated function and, sometimes, values of its derivatives.

2 Approximation of the Function

Suppose that n, m are natural numbers, while a, b, c, d, h are real numbers, h = (b-a)/n. Let the function \( u\left( x \right) \) be such that \( u \in C^{5} \left[ {a - 3h,b} \right]. \) We have the grid of interpolation nodes \( x_{i} \) such that \( x_{ - k} = a - kh,k = 3,2,1 \), \( x_{0} = a,x_{i + 1} = x_{i} + h,i = 0, \ldots ,n,x_{n} = b \).

Suppose that \( u\left( {x_{i} } \right),i = 0,1, \ldots ,n \) and \( \int_{{x_{i - 1} }}^{{x_{i} }} {u\left( \xi \right)d\xi } , \int_{{x_{i - 2} }}^{{x_{i} }} {u\left( \xi \right)d\xi } ,\int_{{x_{i - 3} }}^{{x_{i} }} {u\left( \xi \right)d\xi , i = 0, \ldots ,n} \) are known. We denote \( \tilde{\tilde{u}}\left( x \right) \) as an approximation of function u(x) in interval \( \left[ {x_{i} ,x_{i + 1} } \right] \subset \left[ {a,b} \right] \):

$$ \begin{aligned} \tilde{\tilde{u}}(x) & = u(x_{i} )w_{i} (x) + u(x_{i + 1} )w_{i + 1} (x) + \int\limits_{{x_{i - 1} }}^{{x_{i} }} u (\xi )d\xi w_{i}^{ < - 1,0 > } (x) + \int\limits_{{x_{i - 2} }}^{{x_{i} }} u (\xi )d\xi \,w_{i}^{ < - 2,0 > } (x) \\ & \quad + \int\limits_{{x_{i - 3} }}^{{x_{i} }} u (\xi )d\xi \,w_{i}^{ < - 3,0 > } (x). \\ \end{aligned} $$

We obtain basic splines \( w_{i} \left( x \right), \) \( w_{i + 1} \left( x \right), \) \( w_{i}^{ < - 1,0 > } (x),w_{i}^{ < - 2,0 > } \left( x \right),w_{i}^{ < - 3,0 > } \left( x \right) \) from system: \( \tilde{\tilde{u}}(x) \equiv u(x),\quad u(x) = x^{i - 1} ,\quad i = 1,2,3,4,5. \)

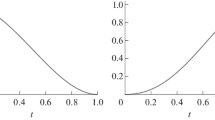
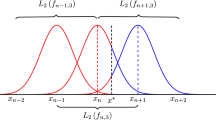
If \( x = x_{i} + th,\quad t \in [0,1], \) then the basic splines can be written in the form:

$$ w_{i} (x_{i} + th) = \frac{{(1 - t)(125t^{3} + 577t^{2} + 736t + 222)}}{222}, w_{i + 1} (x_{i} + th) = \frac{{t(12 + 33t + 24t^{2} + 5t^{3} )}}{74}, $$
$$ w_{i}^{ < - 1,0 > } (x_{i} + th) = \frac{{t(t - 1)(155t^{2} + 603t + 516)}}{148h}, w_{i}^{ < - 2,0 > } (x_{i} + th) = \frac{{t(1 - t)(55t^{2} + 171t + 90)}}{148h}, $$
$$ w_{i}^{ < - 3,0 > } (x_{i} + th) = \frac{{t(t - 1)(85t^{2} + 197t + 92)}}{1332h}. $$

We can also construct the approximation in this form:

$$ \begin{aligned} V\left( x \right) & = u\left( {x_{i} } \right)\omega_{i} \left( x \right) + u\left( {x_{i + 1} } \right)\omega_{i + 1} \left( x \right) + \int\limits_{{x_{i - 1} }}^{{x_{i} }} {u(\xi )d\xi } \, \omega_{i}^{ < - 1,0 > } \left( x \right) + \int\limits_{{x_{i - 2} }}^{{x_{i - 1} }} {u(\xi )d\xi \,\omega_{i}^{ < - 2, - 1 > } } \left( x \right) \\ & \quad + \int\limits_{{x_{i - 3} }}^{{x_{i - 2} }} {u(\xi )d\xi \,\omega_{i}^{ < - 3, - 2 > } } \left( x \right),x \in \left[ {x_{i} ,x_{i + 1} } \right]. \\ \end{aligned} $$
(1)

We obtain basic splines \( \omega_{i,0} \left( x \right),\;\;\omega_{i + 1,0} \left( x \right), \)\( \omega_{i}^{ < s,s + 1 > } \left( x \right),s = - 1, - 2, - 3 \), from the system:

$$ V(x) = u(x),\quad u(x) = x^{i - 1} ,\quad i = 1,2,3,4,5. $$
(2)

If \( x = x_{i} + th,\quad t \in \left[ {0,1} \right] \), then the basic splines can be written in the following form:

$$ \omega_{i} (x_{i} + th) = \frac{{(1 - t)(125t^{3} + 577t^{2} + 736t + 222)}}{222}, \omega_{i + 1} (x_{i} + th) = \frac{{t(12 + 33t + 24t^{2} + 5t^{3} )}}{74}, $$
$$\begin{aligned} \omega_{i}^{ < - 1,0 > } (x_{i} + th) &= \frac{{t(t - 1)(985t^{2} + 4085t + 3926)}}{1332h}, \\ \omega_{i}^{ < - 2, - 1 > } (x_{i} + th) &= - \frac{{t(t - 1)(205t^{2} + 671t + 359)}}{666h},\end{aligned} $$
$$ \omega_{i}^{ < - 3, - 2 > } (x_{i} + th) = \frac{{t(t - 1)(85t^{2} + 197t + 92)}}{1332h}. $$

Our aim is to determine if \( V(x) = \tilde{\tilde{u}} \left( x \right). \)

Lemma 1.

Let function \( u \in C^{5} [a - 3h,b] \). The next statement is valid:

$$ V(x) = \tilde{\tilde{u}}(x),\quad x \in [x_{i} ,x_{i + 1} ],\quad i = 0,1, \ldots ,n - 1. $$

Proof.

It can be shown that the next relations are valid:

$$ I_{1} = w_{i}^{ < - 1,0 > } \left( {x_{i} + th} \right) + w_{i}^{ < - 2,0 > } \left( {x_{i} + th} \right) + w_{i}^{ < - 3,0 > } \left( {x_{i} + th} \right) = \omega_{i}^{ < - 1,0 > } \left( {x_{i} + th} \right), $$
$$ I_{2} = w_{i}^{ < - 2,0 > } (x_{i} + t{\mkern 1mu} h) + w_{i}^{ < - 3,0 > } (x_{i} + t{\mkern 1mu} h) = \omega_{i}^{ < - 2, - 1 > } (x_{i} + t{\mkern 1mu} h), $$
$$ I_{3} = w_{i}^{ < - 3,0 > } (x_{i} + t{\mkern 1mu} h) = \omega_{i}^{ < - 3, - 2 > } (x_{i} + t{\mkern 1mu} h). $$

Therefore, we obtain:

$$ \begin{aligned} \tilde{\tilde{u}}\left( {x_{i} \, + \, th} \right) & = \, u\left( {x_{i} } \right)\omega_{i,0} \left( x \right) \, + \, u\left( {x_{i + 1} } \right)\omega_{i + 1,0} \left( x \right) + \int\limits_{{x_{i - 1} }}^{{x_{i} }} {u(\xi )d\xi \;} I_{1} + \int\limits_{{x_{i - 2} }}^{{x_{i - 1} }} {u(\xi )d\xi \,I_{2} } \\ & \quad + \int\limits_{{x_{i - 3} }}^{{x_{i - 2} }} {u(\xi )d\xi \;} I_{3} = u\left( {x_{i} } \right)\omega_{i,0} \left( x \right) + u\left( {x_{i + 1} } \right)\omega_{i + 1,0} \left( x \right) + \int\limits_{{x_{i - 1} }}^{{x_{i} }} {u(\xi )d\xi \,} \omega_{i}^{ < - 1,0 > } \left( {x_{i} + th} \right) \\ & \quad + \int\limits_{{x_{i - 2} }}^{{x_{i - 1} }} {u(\xi )d\xi } \;\omega_{j}^{ < - 2, - 1 > } \left( {x_{j} + th} \right) + \int\limits_{{x_{i - 3} }}^{{x_{i - 2} }} {u(\xi )d\xi \,\omega_{i}^{ < - 3, - 2 > } \left( {x_{i} \, + \, th} \right) = V\left( {x_{i} + th} \right).} \\ \end{aligned} $$

The proof is complete.

Lemma 2.

Let the function be such that \( u \in C^{5} [a - 3h,b] \). The next statements are valid:

$$ \begin{array}{*{20}l} {(1)\quad V\left( {x_{i} } \right) = u\left( {x_{i} } \right),} \hfill & {(2)\quad V\left( {x_{i + 1} } \right) = u\left( {x_{i + 1} } \right),} \hfill & {(3)\quad \mathop \smallint \limits_{{x_{i - 1} }}^{{x_{i} }} V\left( x \right)dx = \mathop \smallint \limits_{{x_{i - 1} }}^{{x_{i} }} u\left( x \right)dx,} \hfill \\ \end{array} $$
$$ \begin{array}{*{20}l} {(4)\quad \mathop \smallint \limits_{{x_{i - 2} }}^{{x_{i - 1} }} V\left( x \right)dx = \mathop \smallint \limits_{{x_{i - 2} }}^{{x_{i - 1} }} u\left( x \right)dx,} \hfill & {(5)\quad \mathop \smallint \limits_{{x_{i - 3} }}^{{x_{i - 2} }} V\left( x \right)dx = \mathop \smallint \limits_{{x_{i - 3} }}^{{x_{i - 2} }} u\left( x \right)dx.} \hfill \\ \end{array} $$

Proof.

Firstly, let us notice that statements (1)–(2) follow from the next relations:

$$ \omega_{i} (x_{i} ) = 1, \omega_{i} (x_{i + 1} ) = 0, \omega_{i + 1} (x_{i} ) = 0, \omega_{i + 1} (x_{i + 1} ) = 1, \omega_{i}^{ < - 1,0 > } (x_{i} ) = 0, $$
$$ \omega_{i}^{ < - 1,0 > } (x_{i + 1} ) = 0, \omega_{i}^{ < - 2, - 1 > } (x_{i} ) = 0, \omega_{i}^{ < - 2, - 1 > } (x_{i + 1} ) = 0, \omega_{i}^{ < - 3, - 2 > } (x_{i} ) = 0, $$
$$ \omega_{i}^{ < - 3, - 2 > } (x_{i + 1} ) = 0. $$

Similarly, statements (3)–(5) follow from the next relations:

$$ \int_{{x_{i - 1} }}^{{x_{i} }} {\omega_{i} } (x)dx = 0, \int_{{x_{i - 1} }}^{{x_{i} }} {\omega_{i + 1,0} } (x)dx = 0, \int_{{x_{i - 1} }}^{{x_{i} }} {\omega_{i}^{ < - 1,0 > } } (x)dx = 1, \int_{{x_{i - 1} }}^{{x_{i} }} {\omega_{i}^{ < - 2, - 1 > } } (x)dx = 0, $$
$$ \int_{{x_{i - 1} }}^{{x_{i} }} {\omega_{i}^{ < - 3, - 2 > } } (x)dx = 0. $$
$$ \int_{{x_{i - 2} }}^{{x_{i - 1} }} {\omega_{i} } (x)dx = 0, \int_{{x_{i - 2} }}^{{x_{i - 1} }} {\omega_{i + 1,0} } (x)dx = 0, \int_{{x_{i - 2} }}^{{x_{i - 1} }} {\omega_{i}^{ < - 1,0 > } } (x)dx = 0, \int_{{x_{i - 2} }}^{{x_{i - 1} }} {\omega_{i}^{ < - 2, - 1 > } } (x)dx = 1, $$
$$ \int_{{x_{i - 2} }}^{{x_{i - 1} }} {\omega_{i}^{ < - 3, - 2 > } } (x)dx = 0, \int_{{x_{i - 3} }}^{{x_{i - 2} }} {\omega_{i} } (x)dx = 0, \int_{{x_{i - 3} }}^{{x_{i - 2} }} {\omega_{i + 1,0} } (x)dx = 0, \int\limits_{{x_{i - 3} }}^{{x_{i - 2} }} {\omega_{i}^{ < - 1,0 > } } (x)dx = 0, $$
$$ \int\limits_{{x_{i - 3} }}^{{x_{i - 2} }} {\omega_{i}^{ < - 2, - 1 > } } (x)dx = 0, \int\limits_{{x_{i - 3} }}^{{x_{i - 2} }} {\omega_{i}^{ < - 3, - 2 > } } (x)dx = 1. $$

The proof is complete.

Now we can find the points \( \zeta_{1} , \zeta_{2} , \zeta_{3} \) such that

$$ u\left( { \zeta_{1} } \right)h = \mathop \smallint \limits_{{x_{i - 1} }}^{{x_{i} }} u\left( \xi \right) d\xi , \zeta_{1} \epsilon\left[ {x_{i - 1} ,x_{i} } \right], u\left( { \zeta_{2} } \right)h = \mathop \smallint \limits_{{x_{i - 2} }}^{{x_{i - 1} }} u\left( \xi \right) d\xi , \zeta_{2} \epsilon\left[ {x_{i - 2} ,x_{i - 1} } \right], $$
$$ u\left( { \zeta_{3} } \right)h = \mathop \smallint \limits_{i - 3}^{{x_{i - 2} }} u\left( \xi \right) d\xi ,\zeta_{3} \epsilon\left[ {x_{i - 3} ,x_{i - 2} } \right]. $$

We can construct approximation \( \tilde{u}(x) \), \( x \in [x_{j} ,x_{j + 1} ] \), in the form:

$$ \begin{aligned} \tilde{u}\left( x \right) & = u\left( {x_{j} } \right)\omega_{j,0} \left( x \right) + u\left( {x_{j + 1} } \right)\omega_{j + 1,0} \left( x \right) \\ & \quad + u\left( {\zeta_{1} } \right)h\omega_{j}^{{\left\langle { - 1,0} \right\rangle }} \left( x \right) + u\left( {\zeta_{2} } \right)h\omega_{j}^{{\left\langle { - 2, - 1} \right\rangle }} \left( x \right) + u\left( {\zeta_{3} } \right)h\omega_{j}^{{\left\langle { - 3, - 2} \right\rangle }} \left( x \right). \\ \end{aligned} $$

The interpolation of the Lagrange type with nodes \( \zeta_{1} , \zeta_{2} , \zeta_{3} \), \( \zeta_{4} = x_{j} \), \( \zeta_{5} = x_{j + 1} , \) has the form

$$ \tilde{U}\left( x \right) = \sum\nolimits_{i = 1}^{5} {u\left( {\zeta_{i} } \right)W\left( x \right)/\left( {\left( {x - \zeta_{i} } \right)W^{{\prime }} \left( {\zeta_{i} } \right)} \right)} ,x \in [x_{j} ,x_{j + 1} ], $$
(3)

where \( W\left( x \right) = \left( {x - \zeta_{1} } \right)\left( {x - \zeta_{2} } \right)\left( {x - \zeta_{3} } \right)\left( {x - \zeta_{4} } \right)\left( {x - \zeta_{5} } \right). \)

The remainder term of the Lagrange interpolation (3) is as follows:

$$ U^{\left( 5 \right)} \left( \eta \right)\left( {x - x_{j} } \right)\left( {x - x_{j + 1} } \right)\left( {x - \zeta_{1} } \right)\left( {x - \zeta_{2} } \right)\left( {x - \zeta_{3} } \right)/5!, \eta \epsilon\,\left[ {x_{j - 3} ,x_{j + 1} } \right]. $$

Table 1 shows actual errors of approximation of functions constructed with formula (1) and theoretical errors of approximation of functions constructed with formula (3) when \( \left[ {a,b} \right] = \left[ { - 1,1} \right],h = 0.1. \) Calculations were done in Maple with Digits = 15.

Table 1. Actual errors \( max_{{t \in \left[ {0,1} \right]}} \left| {V - u} \right| \) constructed with formula (1) and theoretical errors of approximation (3)
Full size table

3 Comparison with Lagrange Type Splines

Suppose we know the values of function \( u \in C^{5} [a - 3h,b] \) in the points x i . We consider the interpolation with Lagrange type splines

$$ \begin{aligned} W\left( x \right) & = u\left( {x_{j} } \right)\omega_{j} \left( x \right) + u\left( {x_{j + 1} } \right)\omega_{j + 1} \left( x \right) + u\left( {x_{j - 1} } \right)\omega_{j - 1} \left( x \right) + u\left( {x_{j - 2} } \right)\omega_{j - 2} \left( x \right) \\ & \quad + u\left( {x_{j - 3} } \right)\omega_{j - 3} \left( x \right),x \in \left[ {x_{j} ,x_{j + 1} } \right] \\ \end{aligned} $$
(4)

It can be found that \( \omega_{j + 1} \left( x \right) = \left( {x - x_{j} } \right)\left( {x - x_{j - 1} } \right)\left( {x - x_{j - 2} } \right)\left( {x - x_{j - 3} } \right)/Z_{j + 1} \),

$$ Z_{j + 1} = \left( {x_{j + 1} - x_{j} } \right)\left( {x_{j + 1} - x_{j - 1} } \right)\left( {x_{j - 1} - x_{j - 2} } \right)\left( {x_{j + 1} - x_{j - 3} } \right), $$
$$ \omega_{j} \left( x \right) = \left( {x - x_{j + 1} } \right)\left( {x - x_{j - 1} } \right)\left( {x - x_{j - 2} } \right)\left( {x - x_{j - 3} } \right)/Z_{j} , $$
$$ Z_{j} = \left( {x_{j} - x_{j + 1} } \right)\left( {x_{j} - x_{j - 1} } \right)\left( {x_{j} - x_{j - 2} } \right)\left( {x_{j} - x_{j - 3} } \right), $$
$$ \omega_{j - 1} \left( x \right) = \left( {x - x_{j + 1} } \right)\left( {x - x_{j} } \right)\left( {x - x_{j - 2} } \right)\left( {x - x_{j - 3} } \right)/Z_{j - 1} , $$
$$ Z_{j - 1} = \left( {x_{j - 1} - x_{j + 1} } \right)\left( {x_{j - 1} - x_{j} } \right)\left( {x_{j + 1} - x_{j - 2} } \right)\left( {x_{j + 1} - x_{j - 3} } \right), $$
$$ \omega_{j - 2} \left( x \right) = \left( {x - x_{j + 1} } \right)\left( {x - x_{j} } \right)\left( {x - x_{j - 1} } \right)\left( {x - x_{j - 3} } \right)/Z_{j - 2} , $$
$$ Z_{j - 2} = \left( {x_{j - 2} - x_{j + 1} } \right)\left( {x_{j - 2} - x_{j} } \right)\left( {x_{j - 2} - x_{j - 1} } \right)\left( {x_{j - 2} - x_{j - 3} } \right), $$
$$ \omega_{j - 3} \left( x \right) = \left( {x - x_{j + 1} } \right)\left( {x - x_{j} } \right)\left( {x - x_{j - 1} } \right)\left( {x - x_{j - 2} } \right)/Z_{j - 3} , $$
$$ Z_{j - 3} = \left( {x_{j - 3} - x_{j + 1} } \right)\left( {x_{j - 3} - x_{j} } \right)\left( {x_{j - 3} - x_{j - 1} } \right)\left( {x_{j - 3} - x_{j - 2} } \right). $$

Lemma 3.

Suppose \( u \in C^{5} [a - 3h,b] \). There is a point \( \eta \in [x_{j - 3} ,x_{j + 1} ] \), such that

$$ u\left( x \right) - W\left( x \right) = \frac{{u^{\left( 5 \right)} (\eta )}}{5!}\quad (x - x_{j} )(x - x_{j + 1} )(x - x_{j - 1} )\left( {x - x_{j - 2} } \right)\left( {x - x_{j - 3} } \right),x \in \left[ {x_{j} ,x_{j + 1} } \right]. $$

Proof.

The points \( x_{j - i} , \, i \, = - 1,0,1,2,3 \) are the points of interpolation. Using the formula of the remainder term of Lagrange interpolation we obtain the formula.

Corollary.

If \( M = \mathop {max}\limits_{{x \in \left[ {a - 3h,b} \right]}} \, \left| {u^{\left( 5 \right)} \left( x \right)} \right| \) and we put \( x = x_{j} + th,\quad t \in \left[ {0,1} \right] \), then

$$ \left| {W\left( {x_{j} + th} \right) - u\left( {x_{j} + th} \right)} \right| \le 3.63Mh^{5} /5! $$

Proof.

Obviously,

$$ \left| {W\left( {x_{j} + th} \right) - u\left( {x_{j} + th} \right)} \right| \le Mh^{5} \left| {t\left( {t - 1} \right)\left( {t + 1} \right)\left( {t + 2} \right)\left( {t + 3} \right)} \right|/5! $$

It can be obtained, that

\( max_{{t \in \left[ {0,1} \right]}} \left| {t\left( {t - 1} \right)\left( {t + 1} \right)\left( {t + 2} \right)\left( {t + 3} \right)} \right| = 3.63 \),

when \( t \approx 0.6444 \).

The proof is complete.

Table 2 shows actual and theoretical errors of approximation of functions constructed with formula (4) when \( \left[ {a,b} \right] = \left[ { - 1,1} \right],\quad h = 0.1. \) Calculations were done in Maple with Digits = 15.

Table 2. Actual and theoretical errors \( max_{{t \in \left[ {0,1} \right]}} \left| {V - u} \right| \) of approximation constructed with formula (4)
Full size table

4 Conclusion

Here we investigated approximation using the values of integrals of the function over the subintervals immediately to the left of this subinterval. If the values of the integral of the function are unknown, we will use quadrature formulae with the fifth order of approximation.