A Note on Diffusion Processes with Jumps

Abstract

We focus on stochastic diffusion processes with jumps occurring at random times. After each jump the process is reset to a fixed state from which it restarts with a different dynamics. We analyze the transition probability density function, its moments and the first passage time density. The obtained results are used to study the lognormal diffusion process with jumps which is of interest in the applications.

This work was supported by INDAM-GNCS.

1 Introduction and Description of the Model

Stochastic processes with jumps play a relevant role in many fields of applications. For example, in [3, 7, 10], diffusion processes with jumps are studied in order to model an intermittent treatment for tumor diseases, in [4] birth-and-death processes with jumps are analyzed as queuing models with catastrophes, in [5] a non-homogeneous Ornstein-Uhlenbeck with jumps is considered in relation to neuronal activity. In these contexts, a jump is random event that changes the state of the process leading it to another random state from which the dynamics restarts with the same or different law.

We consider diffusion processes assuming that the jumps occur at random times chosen with a fixed probability density function (pdf). After each jump the process is reset to a fixed state from which it restarts with a different dynamics.

Let $\{\widetilde{X}_k(t),\,t\ge t_0\ge 0\}$ ($k=0,1,\ldots$) be a stochastic diffusion process. Following [6], we construct the stochastic process X(t) with random jumps. Starting from the initial state $\rho _0=X(t_0)$, the process X(t) evolves according to $\widetilde{X}_0(t)$ until a jump occurs that shifts the process to a state $\rho _1$. From here, X(t) restarts according to $\widetilde{X}_1(t)$ until another jump occurs resetting the process to $\rho _2$ and so on. The effect of the k-th jump ($k=1,2,\ldots$) is to shift the state of X(t) in $\rho _k$. Then, the process evolves like $\widetilde{X}_{k}(t)$, until a new jump occurs.

X(t) consists of cycles, whose durations, $I_1,\;I_2,\ldots$, representing the time intervals between two consecutive jumps, are independent random variables distributed with pdf $\psi _k(\cdot )$. We denote by $\varTheta _1,\varTheta _2,\ldots$ the times in which the jumps occur. We set $\varTheta _0=t_0$ that corresponds the initial time and for $k=1,2,\ldots$, let $\gamma _k(\tau )$ be the pdf of the random variable $\varTheta _k$. The variables $I_k$ and $\varTheta _k$ are related, indeed $\varTheta _1=I_1$ and for $k>1$ it results $\varTheta _k=I_1+I_2+\ldots I_k$. Hence, the pdf $\gamma _k(\cdot )$ of $\varTheta _k$ and the pdf $\psi _k(\cdot )$ of $I_k$ are related, indeed $\gamma _1(t)=\psi _1(t)$ and $\gamma _k(t)=\psi _1(t)*\psi _2(t)*\cdots *\psi _k(t)$, where “$*$” denotes the convolution operator.

In the paper we study X(t) by analyzing the transition pdf, its moments and the first passage time of X(t) through a constant boundary. We consider some particular cases when the inter-jumps $I_k$ are deterministic or exponentially distributed. Finally, the lognormal diffusion process with jumps is studied.

2 Some Probabilistic Features of the Process

Let $f(x,t|y,\tau )\!=\!\frac{\partial }{\partial x}P[X(t)\le x|X(\tau )\!=\!y]$, $\widetilde{f}_k(x,t|y,\tau )\!=\!\frac{\partial }{\partial x} P[\widetilde{X}(t)\le x|\widetilde{X}(\tau )\!=\!y]$ be the transition pdf’s of X(t) and $\widetilde{X}_k(t)$, respectively. The densities f and $\widetilde{f}_k$ are related. Indeed, considering the age of the process with jumps, we have the following expression of the transition pdf of the process X(t)

$$\begin{aligned} f(x,t|\rho _0,t_0)= & {} \left( 1-\int _{0}^{t-t_0}\psi _1(s)\,ds\right) \widetilde{f}_0(x,t|\rho _0,t_0)\nonumber \\+ & {} \sum _{k=1}^\infty \int _{t_0}^t \left( 1-\int _0^{t-\tau }\psi _k(s)ds\right) \widetilde{f}_k(x,t|\rho _k,\tau )\,\gamma _k(\tau )\,d\tau . \end{aligned}$$

(1)

We analyze the right hand side of (1). The first term represents the case in which there are not jumps in the interval $(t_0,t)$, so that X(t) evolves as $\widetilde{X}_0(t)$. The factor $1-\int _{0}^{t-t_0}\psi _1(s)\,ds$ represents the probability that the first jump occurs after the time t. The sum in (1) concerns the circumstance that one or more jumps occur in $(t_0,t)$. In this case, the last jump, the k-th one, occurs at the time $\tau \in (t_0,t)$ with probability $1-\int _{0}^{t-\tau }\psi _k(s)\,ds$; then X(t) evolves according to $\widetilde{X}_k(t)$ to reach x at time t, starting from $\rho _k$.

Denoting by $m^{(n)}(x,t|y,\tau )=E[X^n(t)|X(\tau )=y]$ and $\widetilde{m}_k^{(n)}(x,t|y,\tau )=E[\widetilde{X}^n(t)|\widetilde{X}(\tau )=y]$ the conditional moments of X(t) and $\widetilde{X}_k(t)$, respectively, from (1) it follows

$$\begin{aligned} m^{(n)}(t|\rho _0,t_0)= & {} \left( 1-\int _{0}^{t-t_0}\psi _1(s)\,ds\right) \widetilde{m}_0^{(n)}(t|\rho _0,t_0)\nonumber \\+ & {} \sum _{k=1}^\infty \int _{t_0}^t \left( 1-\int _0^{t-\tau }\psi _k(s)ds\right) \widetilde{m}_k^{(n)}(t|\rho _k,\tau )\,\gamma _k(\tau )\,d\tau . \end{aligned}$$

(2)

To analyze the first passage time (FPT) of X(t), we consider a state $S>\rho _k$ $(k=0,1,2\ldots )$. For $X(t_0)<S$ we denote by $T_{\rho _0}(t_0)=\inf \{t\ge t_0:\,X(t)>S\}$ the random variable FPT of X(t) through S and with $g(S,t|\rho _0,t_0)=\frac{\partial }{\partial t}P\left\{ T_{\rho _0}(t_0)<t\right\}$. Similarly let $\widetilde{T}_{\rho _0}(t_0)=\inf \{t\ge t_0:\, \widetilde{X}(t)>S\}$ with $\widetilde{X}(t_0)<S$ be the FPT for $\widetilde{X}(t)$ through S and $g(S,t|\rho _0,t_0)=\frac{\partial }{\partial t}P\left\{ T_{\rho _0}(t_0)<t\right\}$. Recalling that X(t) consists of independent cycles and that $\widetilde{X}_k(t)$ evolves in $I_k$, the following relation can be obtained

$$\begin{aligned}&g(S,t|\rho _0,t_0)=\left[ 1-\int _{0}^{t-t_0}\psi (s)\,ds\right] \widetilde{g}_0(S,t|\rho _0,t_0)\\&+\sum _{k=1}^\infty \int _{t_0}^t \biggl [1-\int _0^{t-\tau }\psi (s)ds\biggr ] \widetilde{g}_k(S,t|\rho _k,\tau ) \gamma _k(\tau )\,d\tau \biggl \{\prod _{j=0}^{k-1} \Bigl [1-P(\widetilde{T_j}(\varTheta _j)<\varTheta _{j+1})\Bigr ] \biggr \}, \nonumber \end{aligned}$$

(3)

where the product $\prod _{j=0}^{k-1} \Bigl [1-P(\widetilde{T_j}(\varTheta _j)<\varTheta _{j+1})\Bigr ]$ represents the probability that none of the processes $\widetilde{X}_0(t), \widetilde{X}_1(t),\ldots , \widetilde{X}_{k-1}(t)$ crosses S before $\tau$.

3 Deterministic Inter-jumps

We assume that the jumps occur at fixed times denoted by $\tau _1,\tau _2,\ldots ,\tau _N$. Therefore, X(t) consists of a combination of processes $\widetilde{X}_k(t)$ with $\widetilde{X}_k(\tau _k)={X}(\tau _k)=\rho _k$. Assuming that $\tau _0=t_0$, $\tau _{N+1}=\infty$, one has

$$ {X(t)}=\sum _{k=0}^{N} {\widetilde{X}_k(t)} \mathbf {1}_{\left( \tau _k,\tau _{k+1}\right) }(t) \quad \mathrm{with} \quad \mathbf {1}_{\left( \tau _k,\tau _{k+1}\right) }(t)=\left\{ \begin{array}{ll} 1,&{}\quad t \in \left( \tau _k,\tau _{k+1}\right) \\ 0,&{} \quad t\notin \left( \tau _k,\tau _{k+1}\right) . \end{array} \right. $$

After the time $\tau _N$, the process X(t) evolves as $\widetilde{X}_N(t)$. For $k=0,1,\ldots ,N$, $\varTheta _k=\tau _k$ a.s. and $I_k$ are degenerate random variables; in particular, denoting by $\delta$ the delta Dirac function, the pdf ’s of $\varTheta _k$ and of $I_k$ are

$$ \gamma _k(t)=\delta (t-\tau _k),\qquad \psi _k(t)=\delta \left[ t-(\tau _k-\tau _{k-1})\right] , $$

respectively. We note that

$$\begin{aligned} \int _{a}^b \delta (s-\tau _k) ds=H(b-a-\tau _k),\qquad H(x)=\int _{-\infty }^x \delta (u)\,du=\left\{ \begin{array}{ll} 0,&{}\quad x<0\\ 1,&{} \quad x> 0, \end{array} \right. \end{aligned}$$

(4)

where $H(\cdot )$ is the Heaviside unit step function. Hence, from (1) one has:

$$\begin{aligned} f(x,t|\rho _0,t_0)= & {} \left[ 1-H\left( t-\tau _1\right) \right] \widetilde{f}_0(x,t|\rho _0,t_0)\\+ & {} \sum _{k=1}^\infty H\left( t-\tau _k\right) \left[ 1-H\left( t-\tau _k-(\tau _k-\tau _{k-1})\right) \right] \widetilde{f}_k\left( x,t|\rho _k,\tau _k\right) , \end{aligned}$$

from which, recalling (4), it follows:

$$\begin{aligned} f(x,t|\rho _0,t_0)=\sum _{k=0}^{N} {\widetilde{f}_k(x,t|\rho _k,\tau _k)} \mathbf {1}_{\left( \tau _k,\tau _{k+1}\right) }(t). \end{aligned}$$

(5)

Similarly, from (2) the conditional moments of X(t) can be obtained.

Concerning the FPT problem, we note that since $\varTheta _k= \tau _k$ a.s., one has

$$ 1-P[\widetilde{T}_k(\tau _k)<\tau _{k+1}]=1-\int _{\tau _k}^{\tau _{k+1}} \widetilde{g}_k(S,\tau |\rho _k,\tau _k)d\tau ; $$

so, following the procedure used to obtain (5), one has:

(6)

4 Exponentially Distributed Inter-jumps

We assume that, for $k\ge 1$, $\rho _k=\rho$ and $I_k$ are identically distributed with pdf $\psi _k(s)=\psi (s)=\xi e^{-\xi s}$ for $s>0$. In this case the pdf of $\varTheta _k$ is an Erlang distribution with parameters $(k,\xi )$, i.e. $\gamma _k(t)= \xi ^k t^{k-1} e^{-\xi t} /(k-1)!$ for $t>0$. From (1) and (2) the transition pdf and the conditional moments of X(t) result:

$$\begin{aligned} f(x,t|\rho ,t_0)=e^{-\xi (t-t_0)} \widetilde{f}_0(x,t|\rho ,t_0)+e^{-\xi t} \sum _{k=1}^\infty \int _{t_0}^t \frac{\xi ^k \tau ^{k-1}}{(k-1)!}\widetilde{f}_k(x,t|\rho ,\tau )d\tau , \end{aligned}$$

(7)

$$\begin{aligned} m^{(n)}(t|\rho ,t_0)=e^{-\xi (t-t_0)} \widetilde{m}_0^{(n)}(t|\rho ,t_0)+e^{-\xi t} \sum _{k=1}^\infty \int _{t_0}^t \frac{\xi ^k \tau ^{k-1}}{(k-1)!}\widetilde{m}_k^{(n)}(t|\rho ,\tau )d\tau , \end{aligned}$$

(8)

respectively. Moreover, concerning the FPT pdf, from (3) one has:

$$\begin{aligned}&g(S,t|\rho ,t_0)=e^{-\xi (t-t_0)} \widetilde{g}(S,t|\rho ,t_0)\nonumber \\&+\sum _{k=1}^\infty \int _{t_0}^{t} \frac{(\xi \tau )^{k-1} e^{-\xi \tau }}{(k-1)!}\xi e^{-\xi (t-\tau )} \widetilde{g}_k(S,t|\rho ,\tau )d\tau \biggl \{\prod _{j=0}^{k-1} \biggr [1-P(\widetilde{T}_j(\varTheta _j)<\varTheta _{j+1})\biggr ] \biggr \}.\quad \end{aligned}$$

(9)

We assume that each $\widetilde{X}_k(t)$ evolves as $\widetilde{X}(t)$, from (7) and (8) one obtains:

$$\begin{aligned} f(x,t|\rho ,t_0)=e^{-\xi (t-t_0)} \widetilde{f}(x,t|\rho ,t_0)+\xi \int _{t_0}^t e^{-\xi (t-\tau )} \widetilde{f}(x,t|\rho ,\tau )d\tau ; \end{aligned}$$

(10)

$$\begin{aligned} m^{(n)}(t|\rho ,t_0)=e^{-\xi (t-t_0)} \widetilde{m}^{(n)}(t|\rho ,t_0)+\xi \int _{t_0}^t e^{-\xi (t-\tau )} \widetilde{m}^{(n)}(t|\rho ,\tau )d\tau , \end{aligned}$$

(11)

in agreement with the analogue results in [1, 2]. Moreover, if the involved processes are time homogeneous, one has that $P(\widetilde{T_j}({\varTheta _j})<\varTheta _{j+1})=P(\widetilde{T}(0)<I_{j+1})=P(\widetilde{T}(0)<I)$, where $\widetilde{T}(0)$ is the FPT of $\widetilde{X}_0(t)$ through the threshold S and $I_k{\mathop {=}\limits ^{d}} I$. Therefore, Eq. (9) becomes:

$$\begin{aligned}&g(S,t-t_0|\rho )= e^{-\xi (t-t_0)} \widetilde{g}(S,t-t_0|\rho )+\sum _{k=1}^\infty \int _{0}^{t-t_0} \frac{\left( \xi \tau \left[ 1-P(\widetilde{T}(0)<I)\right] \right) ^{k-1}}{(k-1)!} \nonumber \\&\qquad \times \,xi e^{-\xi t} \widetilde{g}(S,t-\tau |\rho )d\tau \left[ 1-P(\widetilde{T}(0)<I)\right] \nonumber \\&\qquad =e^{-\xi (t-t_0)} \widetilde{g}(x,t-t_0|\rho )\nonumber \\&\qquad \quad +\,\xi \left[ 1-P(\widetilde{T}(0)<I)\right] e^{-\xi t}\int _{0}^{t-t_0} e^{\xi \tau \left[ 1-P(\widetilde{T}(0)<I)\right] } \widetilde{g}(S,t-\tau |\rho )d\tau . \end{aligned}$$

(12)

5 The Lognormal Process with Jumps

We construct a new process with jumps on the lognormal process. This is an interesting process to study because it and its transformations are largely used in the applications. For example, in [8] a gamma-type diffusion process is transformed in a lognormal process to model the trend of the total stock of the private car-petrol. So, the study is performed on a lognormal process to provide a statistical methodology by which it can be fitted real data and obtain forecasts that, in statistical term, are quite accurate. In this context, a process with jumps can take into consideration the possibility of stock collapsed and a threshold can represent a control value. Also such process with stock collapses can be studied to give forecasts and, eventually, prevent problems. More recently, in [9], a gamma diffusion process with exogenous factors is transformed also in a lognormal process to describe the electric power consumption during a period of economic crisis. The transformation in the lognormal process allows to infer on parameters to give forecasts and, moreover, an application on the total consumption in Spain is considered. In this context, we can construct a process with jumps to take into consideration the possibility of a breakdown. Regarding this process with breakdowns, a threshold can represent a control value that gives an alarm in some cases which can be of interest for the authority.

Let $\widetilde{X}_k(t)$ be the lognormal time homogeneous diffusion processes with drift $A_1^{k}(x)=a_kx$ and infinitesimal variance $A_2^k(x)=\sigma _k^2x^2$. For $\widetilde{X}_k(t)$ one has

$$\begin{aligned} \widetilde{f}_k(x,t|\rho _k,t_k)={1\over x\sigma _k\sqrt{2\pi (t-\tau _k)}}\exp \biggl \{-{[\log ({x\over \rho _k})- (a_k-{\sigma _k^2\over 2})(t-\tau _k)]^2\over 2\sigma _k^2(t-\tau _k)}\biggr \}, \end{aligned}$$

(13)

$$\begin{aligned} \widetilde{m}_k^{(n)}(t|\rho _k,\tau _k)=\exp \left\{ n \left[ \log \rho _k+\left( a_k-{\sigma _k^2\over 2}\right) (t-\tau _k)\right] +{n^2\over 2}\sigma _k^2(t-\tau _k)\right\} , \end{aligned}$$

(14)

$$\begin{aligned} \widetilde{g}_k(S,t|\rho _k,\tau _k)= {|\log ( {S\over \rho _k})|\over \sqrt{2\pi \sigma _k^2(t-\tau _k)^3}} exp\biggl \{-{[\log ({S\over \rho _k})- (a_k-{\sigma _k^2\over 2})(t-\tau _k)]^2\over 2\sigma _k^2(t-\tau _k)}\biggr \}. \end{aligned}$$

(15)

5.1 Lognormal Process with Deterministic Jumps

Let $\tau _1,\tau _2,\ldots ,\tau _N$ be the instants in which jumps occur. From (5), recalling (13) one obtains the transition pdf of X(t):

$$ f(x,t|\rho _0,t_0)=\sum _{k=0}^{N}\, \frac{ \mathbf {1}_{\left( \tau _k,\tau _{k+1}\right) }(t)}{x\,\sqrt{2 \pi \sigma _k^2 (t-\tau _k)}}\exp {\biggl \{-\frac{[\log ({x\over \rho _k})-(a_k-{\sigma _k^2\over 2}) (t-\tau _k)]^2}{2 {\sigma _k}^2 (t-\tau _k)}\biggr \}} $$

and, making use of (14), the conditional moments of X(t) can be obtained from (2). Moreover, the FPT pdf is obtainable by (6) by remarking that from (15) one has:

$$\begin{aligned}&\int _{\tau _j}^{\tau _{j+1}} \widetilde{g}_j(S,\tau |\rho _j,\tau _j)\tau ={1\over 2}\mathrm{Erfc}\biggl [ {\log ({S\over \rho _j})+(a_j-{\sigma ^2_j\over 2})(t_{j+1}-t_j)\over \sqrt{2\sigma _j^2(t_{j+1}-t_j)}}\biggr ]\\&\qquad +\,{1\over 2}\exp \biggl \{- {2(a_j-{\sigma ^2_j\over 2})\log ({S\over \rho _j})\over \sigma _j^2}\biggr \}\mathrm{Erfc}\biggl [ {\log ({S\over \rho _j})-(a_j-{\sigma ^2_j\over 2})(t_{j+1}-t_j)\over \sqrt{2\sigma _j^2(t_{j+1}-t_j)}}\biggr ], \end{aligned}$$

where $\mathrm{Erfc}(x)= (2/\sqrt{\pi })\int _x^\infty e^{-t^2}dt$ denotes the complementary error function.

5.2 Lognormal Process with Exponentially Distributed Jumps

Let $I_k$ be identically distributed random variables with $\psi _k(s)\equiv \psi (s)=\xi e^{-\xi s}$, so that the expression (7) holds, with $\widetilde{f}_k(x,t|\rho ,\tau _k)$ defined in (13). Moreover, making use of the moments of the single process $\widetilde{X}_k(t)$, also the moments of X(t) can be evaluated via (8). Similarly, recalling (15), from (9) the FPT pdf can be written.

Now we consider the special case in which $\rho _k=\rho$ and $\widetilde{X}_k(t) {\mathop {=}\limits ^{d}} \widetilde{X}(t)$ with $A_1^{(k)}(x)=a x$ and $A_2^{(k)}(x)=\sigma ^2x^2$. In this case, from (10) and (13) one has:

$$\begin{aligned} f(x,t|\rho ,t_0)= & {} \frac{e^{-\xi (t-t_0)}}{x\,\sqrt{2 \pi \sigma ^2(t-t_0)}} \exp {\left\{ -\frac{[\log ({x\over \rho })-(a-{\sigma ^2\over 2}) (t-t_0)]^2}{2 \sigma ^2 (t-t_0)}\right\} }\\+ & {} \xi \int _{t_0}^t \frac{e^{-\xi (t-\tau )}}{x\sqrt{2 \pi \sigma ^2(t-\tau )}} \exp {\left\{ -\frac{[\log ({x\over \rho })-(a-{\sigma ^2\over 2}) (t-\tau )]^2}{2 \sigma ^2 (t-\tau )}\right\} }d\tau , \end{aligned}$$

where

$$\begin{aligned}&\int _{t_0}^t \frac{e^{-\xi (t-\tau )}}{x\sqrt{2 \pi \sigma ^2(t-\tau )}} \exp {\left\{ -\frac{[\log ({x\over \rho })-(a-{\sigma ^2\over 2}) (t-\tau )]^2}{2 \sigma ^2 (t-\tau )}\right\} }d\tau \\&\quad =\,\frac{e^{\log ({x\over \rho })\bigl (a-{\sigma ^2\over 2}-\sqrt{(a-{\sigma ^2\over 2})^2+2\sigma ^2 \xi }\bigr )}}{2x \sqrt{\mu ^2+2\sigma ^2 \xi }} \biggl [\mathrm{Erfc}\biggr (\frac{\log ({x\over \rho })-(t-t_0) \sqrt{(a-{\sigma ^2\over 2})^2+2\sigma ^2 \xi }}{\sqrt{2 (t-t_0) \sigma ^2}}\biggr )\\&\quad -\,e^{\frac{2\log ({x\over \rho })\sqrt{(a-{\sigma ^2\over 2})^2+2\sigma ^2 \xi }}{\sigma ^2}}\mathrm{Erfc}\biggr (\frac{\log ({x\over \rho })+(t-t_0) \sqrt{(a-{\sigma ^2\over 2})^2+2\sigma ^2 \xi }}{\sqrt{2 (t-t_0) \sigma ^2}}\biggr )\Biggr ]. \end{aligned}$$

Fig. 1.

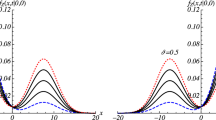
The mean of X(t) (full line) and the mean of $\widetilde{X}_0(t)$ (dashed line) are plotted for the deterministic jumps (on the left) and for exponential jumps (on the right). For the deterministic case $\rho _k= 0.1,0.3,0.2,0.1,0.2$, $a_k=0.1,0.2,0.3,0.4,0.1$, $\tau _k=0,5,8,11,14$ for $k=0,1,2,3,4$. For the exponential case the parameters are $\rho =0.1$, $a=0.3$ and $\xi =0.2$. In both cases $\sigma =1$.

Moreover, the conditional moments of X(t) can be evaluated from (11) with $\widetilde{m}^{(n)}(t|\rho , t_0)$ given in (14); so it follows:

$$\begin{aligned} m^{(n)}(t|\rho ,t_0)= & {} e^{-\xi (t-t_0)}\widetilde{m}^{(n)}(t|\rho ,t_0)+{\xi \rho ^n\over n(a-{\sigma ^2\over 2})+n^2{\sigma ^2\over 2}-\xi }\nonumber \\\times & {} \Bigl [\exp \Bigl \{[n\Bigl (a-{\sigma ^2\over 2}\Bigr )+n^2{\sigma ^2\over 2}-\xi ](t-t_0)\Bigr \}-1\Bigr ]. \end{aligned}$$

(16)

Concerning the FPT pdf, recalling that $\widetilde{g}_j(S,\tau |\rho ,t_j)=\widetilde{g}(S,\tau |\rho ,t_j)$ is defined in (15), from (12) one has:

$$\begin{aligned} g(S,t|\rho ,t_0)= & {} e^{-\xi (t-t_0)}\frac{\log ({S\over \rho })}{\sqrt{2 \pi \sigma ^2 (t-t_0)^3}}\exp {\biggl \{-\frac{[\log ({S\over \rho })-(a-{\sigma ^2\over 2}) (t-t_0)]^2}{2 \sigma ^2 (t-t_0)}\biggr \}}\\+ & {} \xi e^{-\xi (t-t_0)} \bigl [1-P(\widetilde{T}(0)<I)\bigr ]\int _{t_0}^{t} e^{\xi \tau \bigl [1-P(\widetilde{T}(0)<I)\bigr ]}\frac{\log ({S\over \rho })}{\sqrt{2 \pi \sigma ^2 (t-\tau )^3}} \\\times & {} \exp {\biggl \{-\frac{[\log ({S\over \rho })-(a-{\sigma ^2\over 2}) (t-\tau )]^2}{2 \sigma ^2 (t-\tau )}\biggr \}}d\tau , \end{aligned}$$

with

$$\begin{aligned}&P(\widetilde{T}(0)<I)=-\frac{1}{2} \xi \biggl \{L\biggl [\mathrm{Erfc}\biggl (\frac{-\log ({S\over \rho })+(a-{\sigma ^2\over 2}) \theta }{\sqrt{2 \sigma ^2 \theta }}\biggr )\biggr ] \\&\qquad \qquad \qquad \quad +\,L\biggl [\mathrm{Erfc}\biggr (\frac{-\log ({S\over \rho })-(a-{\sigma ^2\over 2}) \theta }{\sqrt{2 \sigma ^2 \theta }}\biggr )\biggr ]\biggr \}, \end{aligned}$$

where L is the Laplace Transform.

In Fig. 1 the mean of X(t) (full line) and the mean of $\widetilde{X}_0(t)$ (dashed line) are plotted for the deterministic jumps (on the left) and for exponential jumps (on the right).

6 Conclusion and Future Developments

Stochastic diffusion processes with jumps occurring at random times have been studied by analyzing the transition pdf and its moments, the FPT density in the presence of constant and exponential distributed jumps. Particular attention has been payed on the lognormal process with jumps.

As future develops one could insert a dead time after a jump representing a delay period after that the process re-starts. This period can be represented by a random variable and the expressions for the transition pdf, the conditional moments and the FPT density can be obtained. Moreover, one can consider other probability distributions for the inter-jump intervals. In general, one can construct other processes with jumps, unknown in literature, on diffusion processes that are of interest in the applications. Finally, a general methodology to infer on parameters could be interesting to fit real data and provide forecasts in application context.