Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The models for the description of growth phenomena, originally associated to the evolution of animals populations, currently play an important role in several fields like that economic, biological, medical, ecological, among others. For this reason many efforts are oriented to the development of always more sophisticated mathematical models for the description of a particular type of behaviour. The most representative curves for modeling growth are of exponential-type as the logistic and Gompertz curves because they are characterized by a finite carrying capacity, that represents, in general terms, the limitation of the natural resources. Specifically, the Gompertz curve is frequently used because in several contexts it seems to fit the experimental data in enough precise way. It is described by the equation:

$$\begin{aligned} x(t)=\exp \Bigl \{{m\over \beta }[1-e^{-\beta (t-t_0)}] + \ln x_0\,e^{-\beta (t-t_0)}\Bigr \}, \end{aligned}$$
(1)

where m and \(\beta \) are positive constants that represent the growth parameters of the population. Equation (1) is able to describe growth dynamics in a lot of contexts so, for instance animal, vegetable, tumor growth. Equation (1) is solution of the following ordinary differential equation:

$$\begin{aligned} {dx\over dt}=m\beta -\beta x\ln x,\qquad x(t_0)=x_0. \end{aligned}$$

We note that in (1) the carrying capacity is \(K=\lim _{t\rightarrow \infty } x(t)=\exp \{m/\beta \}\). However, in several contexts, the carrying capacity can depend from the initial size of the population (cf. [4, 6, 8], for example). In order to take into account this aspect, in [8] the authors modified Eq. (1) as follows

$$\begin{aligned} x(t)=x_0\exp \Bigl \{{m\over \beta }\,[e^{-\beta t_0}-e^{-\beta t}] \Bigr \}. \end{aligned}$$
(2)

Equation (2) is the solution of

$$\begin{aligned} {dx\over dt}=m\,e^{-\beta t}x,\qquad x(t_0)=x_0. \end{aligned}$$
(3)

We note explicitly that the limit for long time of (2) depends from the initial size of the population being \(K=x_0\exp \bigl \{{m/\beta }\,e^{-\beta t_0}\bigr \}\).

In this paper, we consider the stochastic diffusion process associated to (2), denoted by X(t). Then we derive the process \(X_C(t)\) by modifying the growth parameter m to introduce the effect of a therapy interpreted as a continuous time dependent function C(t). We study both the processes by focusing on the First Passage Time (FPT) problem. Moreover, in experimental studies the effect of a new therapy has to be tested so the term C(t) is usually unknown. The knowledge of such functional form is fundamental since it allows to introduce an external control to the system and to explain how the therapy acts. Further, the study of some problems related to the process \(X_C(t)\), i.e. modeling and forecasting, requires the knowledge of C(t). For these reasons, the functional form of C(t) has to be estimated. In this direction we propose a two-step estimation procedure applicable when data from a control group, modeled by means of X(t), and from one or more treated groups, described by \(X_C(t)\), are available. In the first step the parameters of the control group, are estimated by maximum likelihood method (see [8, 9]). In the second step the function C(t) is estimated making use of relationships between the processes X(t) and \(X_C(t)\). Finally, in order to evaluate the goodness of the proposed procedure a simulation study is presented.

The paper is organized as follows. In Sect. 2 the stochastic model \(X_C(t)\) is introduced, the transition distribution and the related moments are provided. In Sect. 3 we study the FPT through suitable boundaries of interest in real applications. In Sect. 4 a two-step procedure is proposed to estimate the parameters of \(X_C(t)\). A simulation is also provided to validate the procedure. Some conclusions close the paper.

2 The Stochastic Model

In the following we consider the stochastic version of the Eq. (3). Precisely, let X(t) be a stochastic process defined in \({\mathbb R}^+\) described by the following stochastic differential equation (SDE)

$$\begin{aligned} dX(t)=m\,e^{-\beta t} X(t)dt+\sigma X(t)\,dW(t), \qquad X(t_0)=x_0\; a.s. \end{aligned}$$
(4)

It can be obtained from (3), following a standard procedure (see, for instance [5]). The parameters m and \(\beta \) are positive constants that represent the growth rates of the population \(X(t), \sigma >0\) is the width of random fluctuations and W(t) represents a standard Brownian motion.

In real-life situations, intrinsic growth rates of the population can be modify by means of exogenous terms generally depending on time. Examples of such situations could be suitable food treatments in growth of animals (see [1]) or therapeutic treatments in tumor growth (see for instance [2, 3, 7]). In order to model such situations, we modify the drift of X(t) by introducing a continuous time dependent function C(t) to model the effect of an exogenous factor, namely therapy, obtaining the stochastic process \(X_C(t)\) described by the following SDE

$$\begin{aligned} dX_C(t)= [m-C(t)]e^{-\beta t}X_C(t) dt+ \sigma X_C(t) dW(t), \qquad X_C(t_0)=x_0\; a.s. \end{aligned}$$
(5)

The solution of (5) is a diffusion process with sample paths

$$\begin{aligned} X_C(t)= x_0\exp \left\{ \int _{t_0}^t[m-C(s)]\,e^{-\beta s}\,ds-{\sigma ^2\over 2}\,(t-t_0)+\sigma \,[W(t)-W(t_0)]\right\} . \end{aligned}$$
(6)

Clearly, the solution of (4) can be obtained by (6) choosing \(C(t)=0\). Equation (5) defines a stochastic diffusion process taking values in \(\mathbb {R}^+\), characterized by drift and infinitesimal variance given by

$$\begin{aligned} A_1^C(x,t)=[m-C(t)]e^{-\beta t}x, \qquad A_2^C(x) = \sigma ^2 x^2, \end{aligned}$$

respectively. Let \(f_C(x,t|y,\tau )={\partial \over \partial x} P[X_C(t)\le x|X_C(\tau )=y]\) be the transition probability density function (pdf) of \(X_C(t)\). The function \(f_C(x,t|y,\tau )\) is solution of the Fokker-Planck equation:

$$\begin{aligned} {\partial f_C(x,t|y,\tau )\over \partial t}=-[m-C(t)]e^{-\beta t}{\partial \over \partial x}[xf_C(x,t|y,\tau )]+{\sigma ^2\over 2} {\partial \over \partial x^2}[x^2f_C(x,t|y,\tau )] \end{aligned}$$
(7)

and of the Kolmogorov equation:

$$\begin{aligned} {\partial f_C(x,t|y,\tau )\over \partial \tau }+[m-C(\tau )]e^{-\beta \tau }y{\partial f_C(x,t|y,\tau )\over \partial y} +{\sigma ^2y^2\over 2}{\partial f_C(x,t|y,\tau )\over \partial y^2}=0. \end{aligned}$$
(8)

Furthermore, \(f_C(x,t|y,\tau )\) satisfies the initial delta condition: \(\lim _{t\rightarrow \tau }f_C(x,t|y,\tau )=\lim _{\tau \rightarrow t}f_C(x,t|y,\tau )=\delta (x-y)\). Note that the transformation

$$\begin{aligned} z=\ln x+d(t),\qquad z_0=\ln y+d(\tau ) \end{aligned}$$

with

$$\begin{aligned} d(t)={\sigma ^2\over 2}t+{m\over \beta }e^{-\beta t}+\int ^tC(\theta )e^{-\beta \theta }d\theta , \end{aligned}$$

reduces (7) and (8) to the analogous equations for a Wiener process Z(t) defined in \({\mathbb R}\) with drift and infinitesimal variance \(B_1=0, B_2=\sigma ^2\), respectively. So one obtains

$$\begin{aligned} f_C(x,t|y,\tau )={1\over x\sqrt{2\pi \sigma ^2(t-\tau )}} \exp \biggl \{-{[\ln (x/y)+d(t)-d(\tau )]^2\over 2\sigma ^2(t-\tau )}\biggr \}. \end{aligned}$$

Moreover one has

$$\begin{aligned}&E[X^k_C(t)|X_C(\tau )=y]=y\,\exp \biggl \{-k\Bigl [{m\over \beta }\,\left( e^{-\beta t}-e^{-\beta \tau }\right) \\&\qquad \qquad \qquad +\int _{\tau }^t C(\theta )e^{-\beta \theta }\,d\theta \Bigr ] +{k(k-1)\over 2}\sigma ^2(t-\tau )\biggr \}. \end{aligned}$$

3 First Passage Time Through a Single Boundary

Let

$$\begin{aligned} T_{x_0,S(t)}^C =\left\{ \begin{array}{ll} \displaystyle {\inf _{t\ge t_0}\{t\;:\; X_C(t)>S(t)|X_C(t_0)=x_0\}},&{}x_0<S(t_0)\\ \displaystyle {\inf _{t\ge t_0}\{t\;:\; X_C(t)<S(t)|X_C(t_0)=x_0\}},&{}x_0>S(t_0) \end{array} \right. \end{aligned}$$

be the FPT of \(X_C(t)\) through the boundary S(t) and let \(g_C[S(t),t|x_0,t_0]\) be the FPT pdf. If \(S(t)\in C^2[t_0,+\infty )\) the FPT pdf \(g_C[S(t),t|x_0,t_0]\) is solution of the following second kind Volterra integral equation:

$$\begin{aligned}&g_C[S(t),t|x_0,t_0]=2\rho \Bigl [\psi _C[S(t),t|x_0,t_0] -\!\!\int _{t_0}^tg_C[S(\tau ),\tau |x_0,t_0]\,\psi _C[S(t),t|S(\tau ),\tau ]d\tau \Bigr ] \end{aligned}$$

with

$$\begin{aligned} \psi _C[S(t),t|y,\theta ]= & {} {f_C[S(t),t|y,\theta ]\over 2}\Bigl \{S^\prime (t)-[m-C(t)]e^{-\beta t}S(t) \\&-S(t){\ln [S(t)/S(\theta )-\int _\theta ^t[m-C(s)]e^{-\beta s}\,ds\over t-\theta }\Bigr \} \end{aligned}$$

Note that if

$$\begin{aligned} S(t)=A\exp \Bigl \{Bt+\int ^t[m-C(s)]\,e^{-\beta s}\,ds\Bigr \} \end{aligned}$$

with \(A>0\) and \(B\in {\mathbb R}\), then \(\psi _C[S(t),t|S(\tau ),\tau ]=0, \forall \tau \in [t_0,t]\), so that the FPT pdf can be expressed in the following closed form:

$$\begin{aligned} g_C[S(t),t|x_0,t_0]\!=\! {\Big |\ln {S(t_0)\over x_0}\Bigr |\over \sqrt{2\pi \sigma ^2(t\!-\!t_0)^3}} \exp \biggl \{-{\Bigl [({\sigma ^2\over 2}\!+\!B)(t\!-\!t_0)\!+\!\ln {S(t_0)\over x_0}\Bigr ]^2\over 2\sigma ^2(t\!-\!t_0)}\biggr \}, \;\; S(t_0)\ne x_0. \end{aligned}$$

Moreover, by choosing in (9) \(C(t)=Be^{\beta t}\) and \( A=px_0\exp \Bigl \{{m\over \beta }e^{-\beta t_0}\Bigr \}\), one has

$$\begin{aligned} S(t) = pE[X(t)|X(t_0)=x_0]=p x_0\exp \Bigl \{{m\over \beta }(e^{-\beta t_0}-e^{-\beta t})\Bigr \} \end{aligned}$$
(9)

that, for \(0<p<1\), represents a percentage of the mean of the process X(t). In other words, for the process \(\{X_C(t);\,t_0\le t\}\) characterized by infinitesimal moments

$$\begin{aligned} A_1^C(x,t)=\bigl [m-Be^{\beta t}\bigr ]e^{-\beta t}x,\quad A_2^C(x) =\sigma ^2 x^2, \end{aligned}$$
(10)

the FPT pdf through boundary (9) is given by

$$\begin{aligned} g_C[S(t),t|x_0,t_0]={|\ln p|\over \sqrt{2\pi \sigma ^2(t-t_0)^3}} \exp \Bigl \{-{[(\sigma ^2/2+B)(t-t_0)+\ln p]^2\over 2\sigma ^2(t-t_0)}\Bigr \}. \end{aligned}$$
(11)

For the process defined in (10) with \(m=0.75, \beta =0.18, \sigma = 0.07\), in Fig. 1 the FPT pdf (11) is plotted for \(p=0.7\) (on the left) and \(p=0.85\) (on the right) for various choices of B.

Fig. 1.
figure 1

FPT pdf (11) for \(X_C(t)\) in (10) with \(m=0.75, \beta =0.18, \sigma = 0.07\) through S(t) in (9) for \(p=0.7\) (left) and \(p=0.85\) (right) and some values of B.

Full size image

4 Inference

In this section we propose a two step estimation procedure that can be used when data from a control group and from one or more treated groups are available. In the first step, from the control group, modeled by means of X(t), the parameters \(m,\beta \) and \(\sigma \) are estimated by maximum likelihood method (see [8, 9]). In the second step the function C(t) is estimated making use of some relationships relating the process X(t) describing the control group, i.e. an untreated group, and \(X_C(t)\) modeling the treated group. The idea is to take the model X(t) as a starting point and then to use the information provided by the treated group to fit the function C(t). Therefore, after estimating the parameters of X(t), C(t) is estimated by the trajectories of the treated and non treated groups by means of suitable relations between the two models.

In order to relate the trajectories of the processes \(X_C(t)\) and X(t), we assume that \(X_C(t_0)=X(t_0)= x_0\), i.e. the therapy is applied from time \(t_0\), so that from Eq. (6) one obtains:

$$\begin{aligned} X_C(t)=\exp \biggl \{- \int _{t_0}^tC(s)\,e^{-\beta s}ds\biggr \}\,X(t). \end{aligned}$$
(12)

From (12), looking at the conditional mean functions, we find

$$\begin{aligned} E[X_C(t)|X_C(t_0)=x_0]=\exp \biggl \{- \int _{t_0}^tC(s)\,e^{-\beta s}ds\biggr \}\,E[X(t)|X(t_0)=x_0] \end{aligned}$$

from which we have

$$\begin{aligned} C(t)= -e^{\beta t} {d\over dt}\ln \left( {E[X_C(t)|X_C(t_0)=x_0]\over E[X(t)|X(t_0)=x_0]}\right) . \end{aligned}$$

4.1 Proposed Methodology

The data required for the proposed strategy are the values of \(d_1\) sample paths of a non-treated group \((x_{ij}, i= 1, \ldots ,d_1, \;j = 1, \ldots ,n)\) and \(d_2\) sample paths of a treated group \((x^C_{ij}, i= 1, \ldots ,d_2, \;j = 1, \ldots ,n)\), observed in the same time instants \(t_1,\ldots ,t_n\).

  • From the data of the control group, estimate the parameters of process X(t). From this first step, we obtain ML estimations \(\widehat{m}, \widehat{\beta }\) and \(\widehat{\sigma }^2\).

  • Denoting by \(x_j\) and \(x^C_j\) the means of \(x_{ij}\) and of \(x^C_{ij}\) at any instant \(t_j\), respectively, i.e.

    $$\begin{aligned} x_j={1\over d_1}\sum _{i=1}^{d_1}x_{ij},\qquad x_j^C={1\over d_2}\sum _{i=1}^{d_2}x_{ij}^C, \end{aligned}$$

    we obtain

    $$\begin{aligned} \gamma _j= - \ln \left[ {x_j^C\over x_j}\right] . \end{aligned}$$

  • Interpolate the points \(\gamma _j\) for \(j=1,2, \ldots n\) (for example by using cubic spline interpolation) obtaining the function \(\widehat{\gamma }(t)\). Finally, consider the following function as an approximation of C(t).

    $$\begin{aligned} \widehat{C}(t)= - e^{\widehat{\beta }t} \;\widehat{\gamma }^{\;\prime }(t). \end{aligned}$$

4.2 A Simulation Study

In order to evaluate the goodness of the proposed procedure we present a simulation study. We consider some specific functions for therapies: constant, linear, logarithmic and periodic. 50 sample paths of the control group X(t) with \(m=0.1,\;\beta =0.01,\;\sigma =0.01\) and \(t_0=0\) have been simulated assuming a random initial state \(x_0\) chosen according \(\varLambda (1,0.16)\).

The paths include 300 observations of the process starting from \(t_1=t_0=0\) with \(t_i-t_{i-1}=2\).

The first step of the procedure gives the estimation of the control group parameters: \(\widehat{m}=0.09578, \widehat{\beta }= 0.01085\) and \( \widehat{\sigma }= 0.0157\). Hence, as control group we consider the stochastic process X(t) with infinitesimal moments

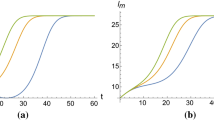
$$\begin{aligned} A_1(x,t)=0.09578\,e^{-0.01085\,t}\,x, \qquad A_2(x)=0.0157^2\,x^2. \end{aligned}$$
(13)

Then, 50 sample paths of the treated group \(X_C(t)\) have been simulated with \(X_C(t_0)=X(t_0)=x_0\) and considering the following therapies: \(C(t)\!=\!-0.005, C(t)\!=\!\pm 0.001 t, C(t)\!=\!0.005 \sin (t), C(t)\!=\!0.02\ln (1+0.15 t)\). The results obtained by applying the proposed procedure are shown in Fig. 2. The dashed curves represent the functions C(t) whereas the full curves represent the corresponding estimation \(\widehat{C}(t)\). We note explicitly that in the considered cases the proposed procedure is able to capture the trend of C(t). To evaluate the performance of the proposed procedure we calculate the mean absolute error (MAE), root mean square error (RMSE) and

$$\begin{aligned} d=1-\frac{\sum _{i=1}^N(\widehat{C}(t_i)-C(t_i))^2}{\sum _{i=1}^N\bigl (|\widehat{C}(t_i)-\overline{C(t)}|+|C(t_i)-\overline{C(t)}|\bigr )^2} \end{aligned}$$

where N is the number of estimated values for the considered cases and \(\overline{C(t)}\) is the mean of function C(t). The results are shown in Table 1 for the aforementioned cases. For all the choices of the function C(t) the procedure provides very satisfactory estimates of the function C(t).

Fig. 2.
figure 2

For the process (13), C(t) and its estimate are shown for different cases.

Full size image
Table 1. MAE, RMSE and d for the considered therapies.
Full size table

5 Conclusions

We have analyzed a non-homogeneous Gompertz-type stochastic diffusion processes characterized by a carrying capacity depending on the initial state. For such a process we have considered a perturbation of a growth parameter by introducing the effect of a exogenous term C(t) generally depending on time and we have studied the first passage time of the process through a time dependent boundary. Moreover, a two-step procedure has been proposed in order to estimate the model parameters and to fit the function C(t) when data from a control group and one or more treated groups are available. Our simulation study has shown that the proposed procedure is able to capture the trend of C(t) in a very satisfactory way.