Keywords

1 Introduction

Nowadays a lot of economic situations are described by the mathematical model of discrete optimal location discrete problems. The situations, where the decision is made by the monopolist only, have been mostly studied. Such situations are common for the normal economic behaviour. Thus there appear the problems aimed to minimise the expenses such as: simple plant location problem [7], p-median problem [13], capacitated plant location problem [16], which have already become classical. In the modern economic situation, it is often demanded to take into consideration the current rivalry at the market. From this point of view there is a great interest to the competitive facility location models, as they describe most complicated situations and require the special methods of solution. The models differ particularly in the competitors’ behaviour [10].

The static competitive facility location problems imply that the competitor’s decision is known and will not be changed. Let us take into consideration the situation when a Company plans to enter the market of existing products and services, so that its p shops served as big share of the market as it is possible. The facilities produce goods of the same kind; the prices are similar; the customers’ choice of the shops depends only on the distance from the located ones [14]. If the customers take into account the size of the shop, its assortment, the quality of the service, then such circumstances are described by the static probabilistic models. The different kinds of which are described e.g. in [3, 6, 8].

Even more complicated is the situation when the competitor’s decision is not known beforehand. The deterministic multilevel sequential problems can be considered among such formulations. The bi-level models distinguish the Leader (the company) and the Follower (the competitor). At first the Leader enters the market and establishes a set of facilities S1 which consists of p facilities. Then the Follower, being aware of that decision, establishes the set of facilities S2 which consists of r facilities. Each customer chooses the place to be served among the facilities from the sets S1 or S2 according to his/her own preferences. Each served customer brings definite profit, therefore all the market is divided between the Leader and the Follower. Those problems are called (r|p)-centroid problems. The interesting results for that kind of problem have been gained e.g. in [4, 9, 15].

Besides the probabilistic bi-level sequential problems, competitive facility location with competition of customers and others should be taken into consideration. Some solutions for them can be found in [5, 10].

This paper deals with the static competitive facility location problems with the elastic demand. The three types of threshold algorithms [1] have been developed for that task. The computational experiments have been carried out in order to compare them.

The comparative analysis of the algorithms, according to the nature and the value of the threshold, has been carried out for the special test examples with up to 300 locations. The results of the computational experiments are given below.

2 Problem Formulation

Berman and Krass [6] and Aboolian et al. [3] develop a spatial interaction model with variable expenditure by introducing non-constant expenditure functions into spatial interaction location models. Aboolian et al. [2] proposed a new model where optimal location and design decisions for a set of new facilities are seeking. Here we develop approximate algorithms for the location and design problem described in [2]. In this problem, Company plans to locate its facilities which differ from one another in design: size, range, etc. Let R be the set of facility designs, \(r\in R.\) There are \(w_i\) customers at the point i of discrete set \(N=\{1,2,\ldots , n\}.\) All customers have the same demand, so each item can be considered as one client with weight \(w_i\). Clients of each point choose to use the facilities of Company or its competitors depending on their attractiveness and distance. The distance \(d_{ij}\) between the points i and j is measured, for example, in Euclidean metric or equals to the shortest distance in the corresponding graph. It is assumed that \(C\subset P\) is the set of pre-existing competitor facilities and it will not change. The Company may open its markets in \(S=P\setminus C\) taking into account the budget B and the cost of opening \(c_{jr}\) facility \(j\in S\) with design \(r\in R.\) The Company’s goal is to attract a maximum number of customers, i.e. to serve the largest share of total demand.

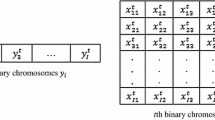
Let us write out the mathematical model according to [2]. Variables \(x_{jr}=1\), if facility j is opened with design variant r and \(x_{jr}=0\) otherwise, \(j\in S, r\in R.\) Utility \(u_{ij} = \sum _{r=1}^{R} {k_{ijr} x_{jr}},\) where the supplementary coefficients

$$k_{ijr}=a_{jr}(d_{ij}+1)^{-\beta }.$$

They depend on the sensitivity \(\beta \) of customers to distance to facility and attractiveness \(a_{jr}.\) The total utility for the customers in point \(i \in N\) from the facilities controlled by the competitors is \(U_{i}(C) = \sum _{j \in C} {u_{ij}}.\)

The demand function has an exponential form:

$$g(U_{i}) = 1 - \exp \bigg (-\lambda _{i} U_{i}\bigg ),$$

where \(\lambda _{i}\) is the characteristic of elastic demand in point i,  \(\lambda _{i}>0;\) \(U_{i}\) is the total utility for a customer at \(i \in N\) from all open facilities:

$$U_{i} = \sum _{j \in S} {\sum _{r=1}^{R} {k_{ijr} x_{jr}}} + U_{i}(C)=U_{i}(S)+U_{i}(C).$$

It is assumed that the demand of the customers at \(g(U_{i})\) is a concave increasing function.

The company’s total share of facility \(i \in N\) is measured by:

$$MS_{i} = \frac{U_{i}(S)}{U_{i}(S) + U_{i}(C)} = \frac{\sum _{j \in S} \sum _{r=1}^{R} {k_{ijr} x_{jr}}}{\sum _{j \in S} {\sum _{r=1}^{R} {k_{ijr} x_{jr}}} + \sum _{j \in C} {u_{ij}}}. $$

Then the mathematical model looks like:

$$\begin{aligned} \max \sum _{i \in N} {w_{i}\cdot g(U_{i})\cdot MS_{i}}, \end{aligned}$$
(1)
$$\begin{aligned} \sum _{j \in S} {\sum _{r \in R} {c_{jr} x_{jr}}} \le B, \end{aligned}$$
(2)
$$\begin{aligned} \sum _{r \in R} {x_{jr}} \le 1, j\in S, \end{aligned}$$
(3)
$$\begin{aligned} x_{jr} \in \{0,1\}, \quad r \in R, j \in S. \end{aligned}$$
(4)

Based on above notation, the objective function (1) looks as follows:

$$\begin{aligned}&\max \sum _{i\in N} w_{i}\cdot \bigg (1-\exp \bigg (-\lambda _{i} \bigg (\sum _{j\in S}{\sum _{r=1}^{R}{k_{ijr}x_{jr}}} + U_{i}(C)\bigg )\bigg )\bigg )\nonumber \\&\qquad \cdot \bigg (\frac{\sum _{j \in S} {\sum _{r=1}^{R}k_{ijr} x_{jr}}}{\sum _{j \in S} {\sum _{r=1}^{R} {k_{ijr} x_{jr}}} + \sum _{j \in C} {u_{ij}}}\bigg ). \end{aligned}$$
(5)

The objective function (5) reflects the Company’s goal to maximize the share of customers demand. Inequality (2) takes into account the available budget. Condition (3) shows that only one variant of the design can be selected.

3 Threshold Algorithms

The number of algorithms known for solution of the competitive facility and design problem is little. In [2], an adapted weighted greedy heuristic algorithm is proposed. Earlier we developed Variable Neighborhood Search algorithms [12]. In this paper, we offer Threshold Algorithms [1] for this problem.

Let s be a feasible solution of a combinatorial minimization problem. The general scheme of threshold algorithms is the following:

  1. 1.

    Select an initial solution \(s_0,\) compute the initial value of the objective function \(f(s_0),\) define the record value as \(f^*:=f(s_0).\) Set the iteration counter \(k=0\), set the threshold value \(t_k\) and the type of neighborhood \(N(s_k).\)

  2. 2.

    Until the stopping criterion is not satisfied, do the following:

    1. 2.1

      Select the new solution randomly in the neighborhood of the current one: \(s_j\in N(s_k).\)

    2. 2.2

      If the difference does not exceed the threshold \(f(s_j)-f(s_k)<t_k,\) then \(s_{(k+1)}:=s_j.\)

    3. 2.3

      If \(f^*>f(s_k),\) then update the best found solution value \(f^*:=f(s_k).\)

    4. 2.4

      Set \(k:=k+1.\)

There are three variants of this algorithm depending on the setting of the sequence of the threshold value \(\{ t_k\}\):

  1. (1)

    Iterative improvement: the sequence \(t_k=0,k=0,1,2,...,\) is a variant of local descent with a monotonous improvement of the objective function;

  2. (2)

    Threshold accepting: \(t_k=c_k,\) \(k=0,1,2,..., c_k\ge 0,\) \(c_k\!\ge \! c_{k+1}\) and \(\lim \limits _{k\rightarrow \infty }c_k\!\rightarrow \! 0\) are the local search variants when the objective function deterioration is assumed until some fixed threshold, and the threshold continually goes down to zero;

  3. (3)

    Simulated annealing: the sequence \(t_k\ge 0,k=0,1,2,...,\) is a random variable with the expectation \(E(t_k)=c_k\ge 0\) which is the local search variant, when the objective function arbitrary deterioration is assumed but the transition probability is inversely related to the deterioration value. For any two feasible solutions \(s_i\) and \(s_j\) the probability of accepting \(s_j\) from \(s_i\) at the iteration k is:

$$P_{s_i s_j}=\left\{ \begin{array} {lr} 1 &{} \ \ \ if \ \ \ f(s_j)\le f(s_i), \\ \exp {\frac{f(s_i)-f(s_j)}{c_k}} &{} \ \ \ if \ \ \ f(s_j)>f(s_i), \end{array} \right. s_j\in N(s_i).$$

At the present time the simulated annealing algorithm shows good results for a wide range of optimization problems. The randomized nature of this algorithm allows asymptotic convergence to optimal solutions under special conditions [1].

We adapted threshold algorithms for the maximization problem. These algorithms belong to the class of local search methods. The neighborhood selection plays an important role in their development for individual tasks. The Lin-Kernighan neighborhood have been used in the proposed variants of algorithms. In addition, a special neighborhood is constructed as follows. Let the vector \(z=(z_i)\) be such that \(z_i\) corresponds to facility i: \(z_i=r\) iff \(x_{ir}=1\). Then feasible solution \(z'\) is called neighboring for z if it can be obtained with the following moves: (a) choose one of the open facilities p with design variant \(z_p\) and reduce the number of design variant up to 0 (close the facility); (b) select the facility q which is closed; then open the facility q with the design variant \(z_p\).

4 Computatinal Experiments

To study the algorithms a series of testing instances similar to the real data of the applied problem [2] has been constructed in [12]. The testing instances consist of two sets with uniform distribution of distances in the interval [0;30] (Series 1) and with Euclidean distances (Series 2). They contain 96 instances for location of 60, 80, 100, 150, 200 and 300 facilities; 3 types of design variants are used, the budget limited is 3, 5, 7 and 9; the demand parameter is \(\lambda _{i} = 1, i\in N\); the customer sensitivity to the distance is high (\(\beta =2\)).

It must be mentioned that there is a problem of the choice of the parameter values so that the algorithm could produce good results for a wide range of instances. After the series of preliminary experiments the following parameter values for the simulated annealing algorithm have been found: the temperature interval length l = 10, the initial temperature \(t_0\) = 150, the cooling (minimal) temperature value \(t_{cool}\) = 5, the cooling coefficient r = 0.99, the number of points in the Lin-Kernighan neighborhood K = 3. The threshold value equal to 5 was chosen for the threshold accepting algorithm.

Table 1 shows the values of deviations from the upper bounds (UB) [12] for test instances with uniform distribution of distances in a single run of the algorithms. For example, the average deviations for the uniform distribution of distances instances of 300 locations are: 6.627% for the iterative improvement; 8.308% for the threshold accepting; 1.523% for the simulated annealing algorithm. The test instances with Euclidean distances proved to be difficult for all considered algorithms. The deviations in this case are: 15.325% for the iterative improvement; 18.296% for the threshold accepting; 14.231% for the simulated annealing algorithm. In 8 test instances the best found goal function values of simulated annealing was within 0.001% from UB (in 6 and in 2 test instances for iterative improvement and threshold accepting respectively). It was noted that in some instances, vector solutions of the algorithms coincide with the vectors of UB: in 42 cases for iterative improvement, in 23 test instances for threshold accepting and in 75 cases for simulated annealing algorithm. For instances with Euclidean distances this values are 23, 11 and 27 respectively.

Since algorithms are of a probabilistic nature, they are tested repeatedly. We ran 1000 each of the algorithms for each of the test instances. For this computational experiment, the following results are obtained. The average deviations for the instances with uniform distribution of distances of 300 locations are: 6.771% for the iterative improvement; 8.36% for the threshold accepting algorithm; 1.044% for the simulated annealing algorithm. The deviations in case of the Euclidean distances are: 16.017% for the iterative improvement; 18.71% for the threshold accepting algorithm; 14.734% for the simulated annealing algorithm. This indicates that Series 2 is more complicated for the proposed algorithms. On the other hand, such deviations may display that the upper bounds for the second series are inaccurate. For Series 1, the 95% confidence interval for the probability of obtaining the deviations less than 0.001% for simulated annealing is between [0.111;0.115], for iterative improvement is [0.044;0.047] and for threshold accepting is [0.030;0.032]. For Series 2, the 95% confidence interval for the probability of obtaining the deviations less than 12% for simulated annealing is [0.112;0.116], for iterative improvement is [0.075;0.078] and for threshold accepting is [0.030;0.032]. The Wilcoxon test [11] showed statistically significant differences between the values of the objective functions of the investigated algorithms with significance level 0.05. The simulated annealing algorithm in both series of test instances gives the best value of the objective function. At the same time, an iterative improvement algorithm has an advantage over the threshold accepting algorithm, which is confirmed by statistically significant differences in both series.

Table 1. Deviations from upper bounds in case of uniform distribution of distances
Full size table

Table 2 contains the information about minimal (min), average (av) and maximal (max) CPU time (in seconds) for the proposed algorithms until the stopping criterion was met. The experiments have been carried out using a PC Intel i5-2450M, 2.50 GHz, memory 4 GB. The time for the instances with Euclidean distances and with the uniform distribution of distances is approximately the same. Note that well-known commercial software is rather time-consuming. For instance, for one of the instances of 60 locations the CPU time of CoinBonmin (GAMS) was 63 h and the objective function deviation from the upper bounds was 12.919%. All proposed algorithms yielded equal objective function values with deviation 11.796%, running time was less than 1.638 s for it.

Table 2. CPU time (sec)
Full size table

5 Conclusion

This paper is devoted to the development of approximate algorithms for one variant of the static probabilistic competitive facility location and design problem. Its mathematical model is based on a nonlinear objective function, and the share of the served demand is elastic. That complicates the task of finding an optimal solution.

The threshold algorithms for the search of approximate solutions have been built, their parameter setting has been carried out. It should be noticed that the iterative improvement and the simulated annealing algorithms are comparable in the objective function for the instances up to 100 locations. The maximum counting duration of the built algorithms does not exceed 20 s. and the minimal deviations from upper bounds was less then 0.001%. The analysis of the algorithms for the instances with a large number of locations has proved the advantage of the simulated annealing algorithm over the threshold algorithms and its applicability to complex problems.