1 Introduction

Among the numerous applications there is a great interest in location problems [1]. In many cases, it is necessary to place the facilities in several locations and to assign a number of customers to be served to them so, that the total expenses were the least. In the well-known classical models, such as Simple Plant Location Problem, p-median Problem, and others [1]; the decision is made by one person, not taking into consideration the customers’ opinions and other circumstances.

However, the customers very often have their own preferences, and several rival companies struggle for serving them. Such situations are described in competitive market location problems which most accurately characterize the actual business environment. The paper deals with a discrete type of such a task in which the facilities can be opened at a finite set of possible locations and the clients are in a discrete set of points. The rival companies have already occupied some of them and are unable to change their decision. The new Company is aware of the existing competition. The customers choose the facilities taking into account their attractiveness. This task is related to the Static Probabilistic Competitive Facility Location Problems [2] one of them was develosped by Berman and Krass [3].

We take into consideration a special case of the model in [3] which was proposed in [4] and is called “facility location and design problem”. Aboolian et al. proposed a spatial interaction model for describing demand cannibalization. In [4], the demand is a function of the total utility and the objective function is nonlinear. This location problem is quite complicated both from the theoretical and the practical points of view. Obtaining optimal solutions for large instances of the problem using the exact algorithms, including software packages, can require significant time and computer resources. In [4], the adapted weighted greedy heuristic algorithm is proposed for the solution of the discrete competitive facility location and design problem. Therefore, it is interesting to develop modern decision methods for the considered problem.

A lot of attention has been given to the methods of finding approximate solutions recently [5], they include the class of local search algorithms [6]. Variable Neighborhood Search Algorithm (VNS) belongs to this class, it is successfully used for solution of many applied tasks. The basic idea of VNS is to explore a set of predefined neighborhoods successively in order to provide a better solution. The Variable Neighborhood Search Approach [7] for the location and design problem is developed in this paper. A new version of the VNS is proposed, the specific types of neighborhoods are described. The numerical experiments based on the specially generated instances [8] have been carried out, the comparison of Variable Neighborhood Search Algorithm and Greedy Weight Heuristic [4] have been executed. CoinBonmin is used for the analysis of the quality of the obtained solutions [9]. The results show that VNS can find new best known solutions to the large instances of the problem with a small relative error.

The rest of the paper is organized as follows. Section 2 contains the formulation of the problem. Section 3 describes the schemes of the Neighborhood Search Algorithm and Greedy Weight Heuristic. The new version of VNS for the considered problem is proposed in Sect. 3 as well. Section 4 presents the results of the numerical experiments. Section 5 concludes the paper.

2 Problem Formulation

The article deals with the situation when a new Company plans to enter the market of existing products and services. It makes a decision to open a supermarket chain, which will differ in size or the set of goods provided from the existing ones. Such differences are called “design options”. Customers select companies based on their attractiveness and distance from their location. The aim of the Company is to interest the greatest number of the customers thus serving the largest share of the demand. This percentage is not fixed for the company and depends on where and which option the new enterprise will be opened on.

The problem has several applications. One of them appeared in Toronto (Canada) and is described by Kraas, Berman, Aboolian. The mathematical model has been formulated in [4]. Let R be the set of facility designs, \(r\in R.\) There are \(w_i\) customers at the point i of discrete set \(N=\{1,2,\cdots n\}\) in the problem. All the customers have the same demands, so each item can be considered as one client with the weight \(w_i\). Let the distance \(d_{ij}\) between the points i and j be measured in Euclidean metric or it equals to the shortest part leght in the corresponding graph. Let \(P\subseteq N\) be the set of potential facility locations. It is assumed that \(C\subset P\) is the set of preexisting rival facilities. The Company may open its branches in \(S=P\setminus C\) taking into account the available budget B,  attractiveness \(a_{jr}\), and the cost of opening \(c_{jr}\) facility \(j\in S\) with design \(r\in R.\)

Such flexible choice of customer is represented in the gravity-type spatial interaction models. These models are known as the brand share models in the marketing literature [10]. According to these models, the utility \(u_{ij}\) of a facility at location \(j\in S\) for a customer at point \(i\in N\) can be written as exponential function. Let \(x_{jr}=1\), if the facility j is opened with the design variant r and \(x_{jr}=0\) otherwise, \(j\in S, r\in R.\)

To determine the usefulness \(u_{ij}\) of the facility \(j\in S\) for the customer \(i\in N\) the coefficients \(k_{ijk}\) have been introduced: \(k_{ijk}=a_{jr}(d_{ij}+1)^{-\beta }.\) They depend on the sensitivity \(\beta \) of the customers to the distance from the facility.

The utility \(u_{ij}\) \(= \sum _{r=1}^{R} {k_{ijr} x_{jr}}.\) The total utility of the customer \(i \in N\) received from the competitive facilities is

$$U_{i}(C) = \sum _{j \in C} {u_{ij}}.$$

The demand function is

$$g(U_{i}) = 1 - \exp \bigg (-\lambda _{i} U_{i}\bigg ),$$

where \(\lambda _{i}\) is the flexible demand characteristic in point i;  \(U_{i}\) is the total utility for a customer at \(i \in N\) from all open facilities:

$$U_{i} = \sum _{j \in S} {\sum _{r=1}^{R} {k_{ijr} x_{jr}}} + U_{i}(C).$$

The total share of the company in the facility \(i \in N\):

$$MS_{i} = \frac{U_{i}(S)}{U_{i}(S) + U_{i}(C)} = \frac{\sum _{j \in S} \sum _{r=1}^{R} {k_{ijr} x_{jr}}}{\sum _{j \in S} {\sum _{r=1}^{R} {k_{ijr} x_{jr}}} + \sum _{j \in C} {u_{ij}}}. $$

The mathematical model looks like:

$$\begin{aligned} \sum _{i \in N} {w_{i}\cdot g(U_{i})\cdot MS_{i}} \rightarrow max \end{aligned}$$
(1)
$$\begin{aligned} \sum _{j \in S} {\sum _{r=1}^{R} {c_{jr} x_{jr}}} \le B, \end{aligned}$$
(2)
$$\begin{aligned} \sum _{r=1}^{R} {x_{jr}} \le 1, \end{aligned}$$
(3)
$$\begin{aligned} x_{jr} \in \{0,1\}, \quad r \in R, j \in S. \end{aligned}$$
(4)

Based on the above notation, the objective function (1) looks as

$$\begin{aligned} \sum _{i\in N}\! w_{i}\bigg (\! 1-\exp \bigg (\! -\lambda _{i} \bigg (\!\sum _{j\in S}{\sum _{r=1}^{R}{k_{ijr}x_{jr}}} + U_{i}(C)\!\bigg )\!\bigg )\!\bigg )\cdot \end{aligned}$$
(5)
$$ \cdot \bigg (\frac{\sum _{j \in S} {\sum _{r=1}^{R}k_{ijr} x_{jr}}}{\sum _{j \in S} {\sum _{r=1}^{R} {k_{ijr} x_{jr}}} + \sum _{j \in C} {u_{ij}}}\bigg ) \rightarrow max.$$

The objective function (5) reflects the Company’s aim to maximize the volume of the customers’ demand. Inequality (2) takes into account the available budget. Condition (3) shows that only one variant of the design can be selected for each facility.

3 Algorithms

The of well-known software GAMS (CoinBonmin) for the location and design problem can calculate an approximate solution which is not guaranteed to be optimal [9]. Solving such problem requires a significant investment of time and computing resources. In this regard, one of the approaches to its solution is in employment of the approximate heuristic methods. In this paper, the Variable Neighborhoods Search algorithm [7, 11] has been constructed and compared to the Greedy Weight Heuristic one for the considered problem, the scheme of the Variable Neighborhood Search algorithm (VNS) is given below.

$$\text {The scheme of the VNS algorithm}$$

Initialization. Select the set of neighborhood structures \(N_k, k=1,\ldots ,k_{max},\) that will be used in the search; find the initial solution x;  choose the stopping condition.

Repeat the following steps until the stopping condition is met.

  1. (1)

    Set \(k:=1.\)

  2. (2)

    Until \(k=k_{max},\) repeat the following steps.

  1. (a)

    Shaking. Generate a point \(x\prime \) at random from the k-th neighborhood of x \((x\prime \in N_k(x));\)

  2. (b)

    Local search. Apply a local search method with \(x\prime \) as the initial solution; denote \(x\prime \prime \) as the obtained local optimum;

  3. (c)

    Move or not. If this local optimum is better than the incumbent, move there \(x:=x\prime \prime ,\) and continue the search with \(N_1, k:=1;\) otherwise, set \(k:=k+1.\)

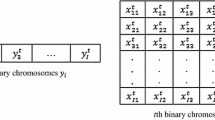
The new types of neighborhoods used for the algorithm are described below. Let the vector \(z=(z_i)\) be such that \(z_i\) corresponds to facility i: \(z_i=r\) iff \(x_{ir}=1\). The feasible initial solution z is obtained using a special deterministic procedure.

Neighborhood 1 (N1). Feasible solution \(z'\) is called neighboring for z if it can be obtained with the following steps:

  1. (a)

    choose randomly one of the open facilities p with the scenario \(z_p\) and close it;

  2. (b)

    select the facility q which is closed and has the highest attractiveness; then open the facility q with the scenario \(z_p\).

Neighborhood 2 (N2). Feasible solution \(z'\) is called neighboring for z if it can be obtained with the following operations:

  1. (a)

    choose randomly one of the open facilities p with the scenario \(z_p\) and reduce the number of the scenario;

  2. (b)

    select randomly the facility q and increase the number of its scenario.

Neighborhood 3 (N3). Unlike the Neighborhood 2 at step (b) select randomly the facility q which is closed; then open the facility q with the scenario \(z_p\).

Lin–Kernighan neighborhood was applied as Neighborhood 4 [12].

In order to describe Greedy Weight Heuristic let us introduce the following terms: L is a set of facility design pairs (j, r), where \(j \in S\) is the location of the facility, \(r \in R\) is the design scenario chosen for that location. Z(L) is the objective function value associated with the location-design set L. Let \(\rho _{jr}(L) = Z(L\cup (j,r)) - Z(L)\) be the improvement of the objective function obtained by adding the location-design pair (j, r) to the location-design set L. Set T is the location-design pairs that should be excluded from further consideration. The outline of Greedy Weight Heuristic is as follows:

Step 1: \(L^0 = \emptyset , T^0 = \emptyset , t = 1\)

Step 2: Let \((j(t),r(t)) = arg\ max_{(j,r)\not \in T^{t-1}} {\big \lbrace \frac{\rho _{jr}(L^{t-1})}{c_{jr}} \big \rbrace }\)

If \(\sum _{(j,r)\in L^{t-1}}c_{jr}+c_{j(t)r(t)}\le B\) then

set \(L^t=L^{t-1}+\{(j(t),r(t))\},\) \( T^t=T^{t-1}+\lbrace (j(t),r)|r \in R\rbrace \)

and set \(t=t+1\).

Return to Step 2.

Else go to Step 3.

Endif

Step 3: If \(Z(L^{t-1})\ge Z(j(t),r(t))\), then

\(L^H = L^{t-1}\) is the adapted greedy solution with value \(Z(L^H)\).

Else set \(L^1 = \lbrace (j(t),r(t))\rbrace \), \(T^1 = \lbrace (j(t),r)|r \in R\rbrace \), \(t=2\)

Return to Step 2.

Endif

Stop

The described algorithms have been programmed on a computer and experimentally investigated. The results are contained in the following section.

4 Experimental Study

The validation of the VNS algorithm has been conducted for the following data: the neighborhoods N1, N2, N3 and Lin–Kernighan are used, local descent has been carried out with the help of the neighborhood of Lin–Kernighan with 9 points. Stopping criteria for the VNS has been the complete neighborhood exploration without an improvement of the solution.

Table 1 Best known solutions
Full size table

There are three options for the enterprises development (\( R = \) 3): the small one with the cost of opening \( c_ {j1} = \) 1; the medium one with the cost of opening \(c_ {j2} = \) 2; the large one with the cost of opening \( c_ {j3} = 3 \) for all \( j \in S \). At each point of the demand a business can be opened, i.e., \( P = N \). The budget varies from 3 to 9 in the increments of 2 units. For example, having the budget of 9 units the Company can open 3 large enterprises or 9 small or it can combine them. The problem has been considered for random distances (\( d_ {ij} \in [0,30], i \ne j, d_ {ij} = d_ {ji} \)) and satisfying the triangle inequality (coordinate \( x \in [0, 100] \), coordinate \( y \in [0,150] \)). The number of obtained locations is 60, 80, 100, 150, 200, 300. It has been assumed that the problem possesses a high sensitivity to the distance (\( \beta = 2 \)) and a nonfixed demand, i.e., \( \lambda = 1 \).

Experiments were carried out on PC Intel i5–2450M, 2.50 GHz, 4GB memory. The test cases with Euclidean distances are proved to be difficult for the CoinBonmin solver. In particular, the maximum CPU time for the test problems with \(|N|=60\) was more than 63 h. Therefore, CoinBonmin was given 10 min of CPU time for each example of higher dimensions. Solver CoinBonmin found the best known solutions in 13 cases out of 80 (see Table 1). The VNS and GWH algorithms found new best known solutions for all the test problems with Euclidean distances with dimensions from 80 to 300 in less time. The average time of the VNS algorithm until the stopping criterion was triggered is 181.35 s. (GWH 2.29 s). In all the cases, the best solutions of the VNS were equal to the best solutions of GWH.

Table 2 CPU time (sec)
Full size table
Fig. 1
figure 1

The average improvement of new best known solutions obtaining by VNS upon CoinBonmin

Full size image
Fig. 2
figure 2

The average deviation of GWH from the CoinBonmin results (It is information about how many percent on average GWH results worse than CoinBonmin results)

Full size image

Table 2 contains the information about minimal (min), average (av), and maximal (max) CPU time (in seconds) of the proposed algorithms for the test problems. GAMS found records for all the tasks in the test cases with arbitrary distances. The average improvement of the VNS from GAMS was 1.55%, the average deviations of the GWH from GAMS was 12.5%. The results are presented in Figs. 1 and 2. The VNS algorithm improved the record values found by GWH in all test instances with arbitrary distances.

5 Conclusion

In this paper, we have created a new version of the Variable Neighborhood Search algorithm and implemented the Greedy Weight Heuristic for the location and design problem. New neighborhoods of a special type have been proposed, the experimental tuning of parameters for both algorithms have been carried out. Two sets of specially structured test examples have been generated. The proposed algorithms have been able to gain new best known solutions or solutions with small relative error. Therefore, the obtained results have indicated the usefulness of the proposed algorithms for solving the problem.