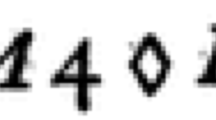Computation in Early Mesopotamia

Abstract

The history of Mesopotamian mathematics begins around 3300 BCE with the development of written systems for recording the control and flow of goods and other economic resources such as land. Numeration was bound up with measurement and was a collection of concrete systems. One of the key developments over the subsequent thousand years or so was the gradual rationalization of these complex concrete systems and the consequent emergence of an abstract conception of number and techniques of computation that applied regardless of metrological category. Throughout their history Mesopotamian scribes organized knowledge in the form of lists. In mathematics there were also lists, but along with lists came metrological and mathematical tables, two-dimensional arrays of data that organized information both vertically and horizontally. A key example is tables giving lists of lengths of sides of square or rectangular fields, along with their areas; the problem of computation of areas remained a constant concern throughout the period covered here. In this chapter, we cover the development of Mesopotamian computation from the archaic period up to the edge of the emergence of the fully abstract sexagesimal computational system for which they are renowned, tracing, as far as can be seen with currently available sources, the long developmental process.

Introduction

Origins are murky. The closer we approach beginnings the more fragmentary and partial the sources. Our own prejudices and preconceptions can lead us to misinterpret what evidence there is. We have to be particularly careful to guard against this tendency when studying the very early history of mathematics . It is easy to assume that mathematics, and especially elementary mathematics, is universal and therefore ancient categories of thought and concepts match ours. They do not.

The quest for a deeper understanding of how Mesopotamians conceived of and implemented their mathematics has been difficult, involved many scholars over decades of work, and is far from complete, particularly with respect to the third millennium, the subject of this chapter. The history of the development of the field from the pioneers of the 1930s to the 1990s is wonderfully told in Jens Høyrup’s excellent “Changing Trends” paper (Høyrup 1996); for an updating of the story see (Melville 2016).

The best-known period of Mesopotamian mathematics is the Old Babylonian (ca. 2000–1600 BCE). From this period we have an abundance of mathematical texts using the sexagesimal place-value system and relatively clear hints of computational techniques and physical aids. However, the introduction of the abstract sexagesimal place value system late in the 3rd millennium (typically located in the Ur III period of 2100–2000 BCE) led to a radical disjunction in computational practice and we cannot suppose that instruments and aids in use in the Old Babylonian period and later were also used before then. A discussion of Old Babylonian practice appears elsewhere in this volume. The one tool we are certain third millennium scribes used to aid their computation is the mathematical list or table, a characteristic Mesopotamian technique of organizing data. A short table summarizing the standard modern periodization of early Mesopotamian history is included at the end of this chapter.

Much of the literature on early (that is, before 2100 BCE) Mesopotamian mathematics is technical and intended (only) for specialists. As an introduction to those seeking general orientation to the overall field, I recommend Eleanor Robson’s chapter on Mesopotamian mathematics in the source book edited by Victor Katz (Robson 2007), and her book (Robson 2008). Robson’s bibliographies will provide excellent pathways into the literature. For a deeper look at the third millennium in particular, the best starting point remains (Nissen et al. 1993).

One of the most important developments of third millennium Mesopotamian mathematics is the gradual emergence of an abstract conception of number from quantity notation tied to specific metrological units. Exactly how this occurred is still not clear, and historians argue greatly over how to interpret evidence at different stages of this development.

Another cause for debate is the interpretation of arithmetic, algorithmic procedures, and the possible role of geometric analysis. These topics are touched on below although a detailed description of the nuances of the various positions scholars have taken is beyond the scope of this paper.

Some Background

The period considered in this chapter takes place before the development of the abstract sexagesimal place-value system, the base-60 cuneiform system that allowed context-free computations, especially multiplication. In the third millennium BCE before the Ur III period, computation was context-dependent, and the development of an abstract concept of number, and of an abstract numerical script is a process that spans the thousand years of our concern.

Mathematical exercises in Mesopotamia were computational. Typical problems were structured so that the solution required computing some specific quantity. The happy accident of writing on clay means that the archaeological record of the extent and development of mathematics in early Mesopotamia is more complete than that for any other culture. However, it also means that what we have is only what they chose to write down. Anything not in the written record, such as oral instruction or possible auxiliary counting aids, is largely lost to us. Archaeology has not been particularly helpful in understanding third-millennium computational practices. We have tablets, some with archaeological context, many not; we know what students learned, but have much less idea of how they learned it.

Writing in Mesopotamia arose in response to bureaucratic demands: the need to record and control the flow of goods. Thus, from the beginning, writing and mathematics were deeply intertwined. The archaic period (ca. 3350–3000 BCE) presented scribes with a complex series of metrological systems, each with its own notation, and trainees had to learn to manipulate the different quantities and symbols, and explore the linkages between systems, for instance between the length and area systems when computing quantities to do with fields or houses.

The main tool for education of beginners was the auxiliary table. Metrological data were gathered into systematically organized tables that allowed students to learn and explore connections between systems. An example of such a table is given in Fig. 1. Its contents are discussed later in the chapter.

Fig. 1

Source Cuneiform Digital Library Initiative, P106078, http://cdli.ucla.edu/dl/photo/P010678.jpg. http://cdli.ucla.edu/search/archival_view.php?ObjectID=P010678

VAT 12593. Table of lengths and areas.

Another well-known characteristic of Mesopotamian mathematics was its algorithmic nature. Learning how to solve problems involved learning step-by-step procedures. Precisely how these computational algorithms were developed can not usually be determined, but various classes of procedures for dealing with different types of problems can be observed.

As the writing system, metrological notation, and society changed over the course of the third millennium, mathematical problems and procedures naturally changed as well. However, the centrality of writing (after all, the records we have are from scribes), the use of tables, and the algorithmic habit provide a constant theme.

In this chapter, we present a series of snapshots of mathematics and computational practices, analyzing tablets from several different locations and times. The Sargonic period (ca. 2340–2200 BCE) produced a number of interesting metrological geometric problems; the recent publication of table texts from the Early Dynastic IIIa and b periods (ca. 2600–2340 BCE) has provided some new insights into length-area computations; there is an important collection of mathematical tablets from Šuruppak from around 2500 BCE, and the archaic period (ca. 3000 BCE) is represented by a large collection of tablets mostly from Uruk. This trajectory into the ever more distant past will help uncover constant themes as well as emphasize the differences in different periods.

Fig. 2

Source CDLI wiki: http://cdli.ox.ac.uk/wiki/lib/exe/fetch.php?media=carte-ediii.jpg. http://cdli.ox.ac.uk/wiki/doku.php?id=cartes_atlas

Map of Near East.

Third-millennium Mesopotamia was an agrarian society with large urban settlements (Adams 1981) (see Fig. 2). For the administrators of a redistributive economy, two constant key computations were determining quantities of goods or rations for multiples of people, given the basic amount for a single person (in various categories), and finding the areas of fields, given the lengths of the sides. The latter computation was important for estimating harvest, seed, animal and labor requirements, taxation, and allotting land to individuals. These two kinds of problems gave rise to the two major types of (what we would term) multiplication—repeated addition, and length-area conversions. Repeated addition operated in a single metrological domain such as repeatedly adding quantities of grain, while length and area computations required understanding the linkages between two different systems, in this case the length and area systems. The abstraction of the sexagesimal place-value system allowed the unification of calculation procedure for these two kinds of ‘multiplication’. For a detailed treatment of the terminology and conceptualization of Mesopotamian arithmetic, see Høyrup (2002a, b).

Sargonic Mathematics (2340–2200 BCE)

The extant corpus of Sargonic mathematical tablets is very small, fewer than twenty texts are known (a list of tablets with their publication histories is given in Foster-Robson 2004). Almost all examples concern length-area computations of rectangular or square fields. Additionally, there is one example of a problem of division of trapezoidal area that we will not discuss further here. [For more on that tablet (IM 58045), see Friberg (1990), Robson (2007), and Friberg (2014).]

The length-area problems come in two guises. In one, the task is to compute an area given the lengths of the sides. In the other type the goal is to find the length of one side of a rectangular field given the area and the length of the other side. The second problem is, of course, extremely artificial and unlikely to arise in actual surveying practice, but even the direct problem of computing the area tends to have a quite artificial construction. The sizes and shapes of the areas (fields) are also not necessarily realistic (Liverani 1990; see also Foster-Robson 2004) and it is clear that the problems are exercises in conversions between length and area units, a problem for which Sargonic metrology was almost uniquely unsuited.

In this period, the key length-unit was the nindan (ca. 6 m) and the key area unit was the sar of 1 nindan square (ca. 36 m²). The sar provided a very clear linkage between the two systems. However, it was the only convenient unit linkage. The nindan was the largest length unit in use, sitting atop a complex system of smaller units. Multiples of the nindan were recorded with cuneiform discrete notation. On the other hand, the area sar was the smallest area unit, sitting at the bottom of a complex system of larger units. Since there were no subunits available, fractions of a sar were recorded with made-up sixtieths (gin) borrowed from weight metrology.

The relationships between the length units (slightly simplified) are given in (Table 1), and the area units in (Table 2). For more details on metrology see Powell (1990).

Table 1 Sargonic length units

Table 2 Sargonic area units

Here we give two representative examples of Sargonic length-area problems, one direct and one inverse (originally published as texts 27 and 29 in Limet 1973) (Figs. 3 and 4).

Fig. 3

Source Cuneiform Digital Library Initiative, P213161, http://cdli.ucla.edu/search/archival_view.php?ObjectID=P213161

Sargonic text 1.

Fig. 4

Source Cuneiform Digital Library Initiative, P213163, http://cdli.ucla.edu/search/archival_view.php?ObjectID=P213163

Sargonic text 2.

A translation of each problem is:

• 1. 11 nindan, 1 kuš-numun, 1 giš-bad, 1 šu-bad. Its area 1 iku ¼ iku 2 ½ sar 6 gin 15 gin-tur. It was found.

• 2. The average long sides are 2 40 nindan. What is the short side? The area is 1 iku. Its short side is 3 kuš-numun, 1 giš-bad, 1 šu-bad.

Note that the ‘problems’ contain a bare minimum of information, especially the first, which mostly consists of a length and an area. No task is stated, no procedure is given, no shape is mentioned, and it doesn’t even say that it is about a field. The second problem at least states a question, but again does not mention a field or state explicitly the shape. The term ‘average’ in the second example refers to a standard procedure for estimating the area of a not-quite rectangular shape by multiplying the average of the lengths with average of the widths.

The laconic and partial written evidence makes the task of the historian attempting to reconstruct ancient mathematical practices all the harder, although in the cases such as this, much of the context can be deduced from other examples.

The artificiality of the problems is clear. In the first problem, the length is given in what Friberg terms ‘wide-span’ numbers, that is, a quantity spanning a range of units from large to small. The area then comes out as a complicated awkward quantity. Additionally, the length, 11 nindan, 1 kuš-numun, 1 giš-bad, 1 šu-bad, with a series of 1s, is hardly chosen at random. For the second problem, the area is a simple quantity and the lengths again span the available units. It is also worth noting that the second field is around 960 m long and about 3 m wide.

In 2004 Foster and Robson published a new tablet from a private collection and took the opportunity to revisit the entire Sargonic corpus, summarizing the state of knowledge (Foster-Robson 2004); the next year, Friberg published another Sargonic tablet and also surveyed the overall corpus (Friberg 2005). Their interpretations are starkly different and there is no consensus among historians as to the correct view of Sargonic conceptions of mathematics.

Correct calculations offer little hint of how the answers were found; analysis of errors in mathematical computations can be helpful for historians. Sometimes the failure mode can reveal the underlying procedure. There is an error in the computation of the Foster-Robson tablet, and the authors use the mistake as the basis of their interpretation, arguing that the given answer “makes sense only if we assume that the scribe has treated the area measurement in iku as if it were in sar…and this type of error could only come about if scribes were expected to convert standard mixed metrological notation into sexagesimal multiples and fractions of a base unit” (2004, 6). Thus, Foster and Robson see “convincing evidence for sexagesimalisation” (2004, 1) in the Sargonic period. Hence, Foster and Robson provide a “summary of calculation ” for the second problem listed above as: $1\,40 \div 2\,40 = 0;37\,30 = 0;30 + 0;05 + 0;02\,30$, that is, as a sexagesimal calculation with conversions back into metrological units as the last step, just as the procedure would have been done in the Old Babylonian period.

Friberg rejected the Foster-Robson interpretation of Sargonic mathematics , and in particular the computational errors as providing evidence for an early sexagesimalization, stating his goal at the beginning of his paper, “It has been claimed repeatedly by several authors… most recently Foster and Robson that sexagesimal numbers in place value notation must have been used in the complicated computations needed to solve the problems stated in the [Sargonic] metric division exercises and square-side-and-area exercises, always without explicit solution procedures. The aim of the present paper is to show that it is easy to explain those computations in less anachronistic ways” (2005, 1).

The less anachronistic way Friberg had in mind was to view of the problems as “metric geometry”. Where Foster and Robson saw computation with numbers, Friberg saw manipulation of figures with given lengths and areas, hence his term “metric geometry”. In this case, the Sargonic length-area problems are part of his sweeping re-assessment of Mesopotamian mathematics extending Høyrup’s “cut-and-paste” geometrical interpretation of Old Babylonian quadratic mathematics (Høyrup 2002a, b) back to the early third millennium. Indeed, Friberg considers the metric-geometric area manipulations as the source of the later interest in quadratic problems.

Friberg referred to problems of the inverse type, as in the second example above, as “metric division problems”, and stated, “the object of the exercise is not to divide a number by another number, but to divide a given area by a given length” (2005, 2). That is, a geometrical rather than arithmetic procedure.

For the second problem above, Friberg observed that 1 iku is a square of $10 \times 10$ nindan and then applied the following “factorization algorithm ”:

“1 iku:

= 10 nindan · 10 nindan (a square with the side 10 nindan has the area 1 iku)

= 40 nindan · 2 nindan 3 kuš-numun (one side multiplied by 4, the other by ¼)

= 2 40 nindan · 3 1/2 1/4 kuš-numun (the length multiplied by 4, the side by ¼)

Hence, the answer is that the short side is 3 1/2 1/4 kuš-numun = 3 kuš-numun 1 giš-bad 1 šu-bad” (2005, 6).

This presentation is still numerical. A clearer view of Friberg’s geometric interpretation is given in Fig. 5 (where we have abbreviated the units nindan (n), kuš-numun (kn), giš-bad (gb), šu-bad (šb); the transliteration of the units here is slightly different from that of Friberg).

Fig. 5

Friberg’s metric geometry

Friberg’s metric geometry interpretation is detailed, complicated, and subtle and here we have given only a simple example without his detailed justifications. While his proposal is not without difficulties, it does act as a corrective to an excessive focus on metric quantities as numbers.

Sargonic scribes left no record of precisely how they conceived of their mathematical exercises nor did they explain how they achieved their results. If they visualized models of their fields to manipulate, they did not say so; if they had some kind of counting board for computation , they also did not say. A proper understanding of Sargonic mathematical processes awaits further research.

Mathematical Tables from the Early Dynastic III Period (2600–2340 BCE)

While the meagre Sargonic corpus of mathematics texts does not include any of the table texts that were such an important part of mathematical practice, the preceding Early Dynastic III period (ED III) includes five known examples, of which three have only recently been published and subjected to detailed analysis. All concern length-area metrology, relating lengths of sides and resulting areas of square or rectangular surfaces.

The most well-known is VAT 12593 (Deimel 1923, 82; Nissen et al. 1993; see Fig. 1 for a photograph). This is a large tablet from EDIIIa Šuruppak (ca. 2500 BCE) with a table of lengths and area of square fields of descending size from 1 gešu (that is, 600) nindan to 5 nindan, with corresponding areas decreasing from 3 šar 2 buru to ¼ iku. The reverse of the tablet is badly broken and presumably the table originally continued down to smaller sizes. The table is organized in three columns, first the lengths of the front of the field (sag), secondly the width, marked sa₂ indicating it is equal to the front, and thirdly the areas, labelled gan₂ in the first row to indicate that the areas represent fields (Tables 3 and 4).

Table 3 Transliteration of VAT 12593 (obverse)

Table 4 Transliteration of VAT 12593 (reverse)

For the lengths, the aš sign represents 1 nindan, the u sign 10 nindan, the geš 60 nindan, and gešu 600 nindan. For the areas, we have 1 eše = 6 iku and 1 bur = 3 eše as in the Sargonic texts discussed above. For the larger units, we have 1 buru = 10 bur and 1 sar = 6 buru.

The precise purpose of such a text is not exactly clear, and we do not have sufficient evidence to be certain of how these tables were used. Nor is it clear how the underlying computations of areas were made. It is unlikely that the original computations were performed in the order in which the information is presented in the table, from large quantities to small. That argues that the table is some kind of summary. It could have been written to show that certain simple length-area relationships had been memorized, or it could have functioned as a reference table as an aid to calculating more complicated situations, presumably by subdividing a surface into smaller, regular pieces. Computation of field areas presents us with a nice balance of arithmetic and geometry.

In their discussion of this tablet, Nissen, Damerow and Englund suggested the table was an exercise, rather than a practical aid, writing, “The exact purpose of this table of areas of square fields is not known. We may exclude the possibility that it served as some sort of table of calculations used to consult particular values. The list was more likely to have been written as an exercise containing easily determinable field surfaces every land-surveyor was required to know which could be added together in calculating complicated surfaces” (1993, 139). Certainly the well-known Old Babylonian multiplication tables were largely exercises in showing mastery of a topic, rather than aids for those with poor memories and perhaps this example falls into that genre.

The only other known EDIIIa table text, MS 3047, was published by Friberg in 2007. Similar in shape and format to VAT 12593, the obverse of the tablet contains a table of lengths and areas for rectangular shapes where the length of the rectangle is always 60 times its width. In contrast to VAT 12593, the values increase in size in each line and, rather surprisingly, the table concludes with a total area. Accounting texts from Šuruppak frequently include long lists of individual entries summarized by a total, but it is unusual to see this appearing in a mathematical text. The reverse of MS 3047 contains a mysterious table that Friberg suggested represented a geometric progression of areas, but it cannot yet be completely understood.

These two EDIIIa (2600–2500 BCE) tables are complemented by three ED IIIb (2500–2340 BCE) texts. The first published, A 681 (Luckenbill 1930), has a rather different layout from the two Šuruppak texts. Instead of a table divided into columns to be read across the tablet from left to right, this one gives lengths of squares and corresponding areas to be read down each column individually.

The next ED IIIb text to appear, CUNES 50-08-001, was also published in Friberg (2007). This is a large, multi-column tablet with five different tables of square areas, ranging from the very large 1 šaru (that is, 36000 nindan) to very small 1 šu-bad (1/24 nindan).

Most recently, we have the tablet published by Feliu (2012). This tablet contains two tables. The first is an almost exact duplicate of VAT 12593, the other computes areas of rectangular shape where one side is held fixed throughout the table while the other varies in each line.

These few tables, all ostensibly on the same topic, that of computation of rectangular and square areas, present us with a great diversity of practice. While some of them may have been informed or derived from actual surveying practice, that is, fields of realistic sizes, others, and especially CUNES 50-08-001 seem concerned with a theoretical extension of practical surveying beyond the bounds of the metrological system. Given that the extension to small area units comes from invoking sexagesimal fractions from weight metrology, we are again confronted with the question of how much a proto-sexagesimal metrological idea was in the air centuries before the development of the abstract sexagesimal place-value system. We are also left to question the extent to which tables of areas should be viewed as arithmetical calculations and how much as metrological geometric constructs. Friberg said of CUNES 50-08-001 that it was “a clear forerunner of the invention of sexagesimal numbers in place value notation” (2007, 426). On the other hand, Proust (forthcoming) has a detailed review of the corpus of five tablets, in which it is argued that a metric geometric approach is possible behind the older (EDIIIa) tablets while the systematic exploration found in CUNES 50-08-001 represented a shift in conceptualizing multiplication, and in particular the construction of areas from given linear measures, from a geometric orientation to an arithmetic one. That is, Proust sees these area tables as providing a marker of an increasing arithmetization of mathematical thinking.

Friberg’s notion of metric geometry as detailed in (2005, 2007, 2014) requires sophisticated manipulation of shapes and a careful knowledge of metrological relationships. One begins with a simple shape and deforms it into the desired final result. Such procedures can yield complicated word problems, but are not needed for the simple tables from Šuruppak discussed above. Proust’s proposed geometric approach to the area tables starts from the observation that the key linkage between lengths and areas at this time is not the sar of 1 square nindan, but the iku, the area of a square 10 nindan on a side. From this it is a simple matter to construct reference shapes for all larger area units and combine them to produce the desired squares for the tables. Not much more than counting is required, and certainly no abstract multiplication Proust (forthcoming). Thus a geometric approach obviates complicated calculations.

Mathematical Problem Texts from Šuruppak (ca. 2500 BCE)

The texts from Šuruppak date from around 2500 BCE and come from a narrow period, a few months to a few years. A large number of administrative texts have allowed a reconstruction of parts of the organization of the city (Pomponio and Visicato 1994; Visicato 1995, 2000). There is a term for ‘scribe’, and a hundred are known from the economic documents. Šuruppak was part of a group of half a dozen cities that were preparing for war at the time the documents were written. We can assume they lost as the city was then largely abandoned.

Among the administrative texts are a small number of mathematical ones, including a group that can be considered as the world’s oldest known mathematical word problems. One of these problems is to compute the area of a very large square, 5 gešu nindan (ca. 18 km) on a side (TSS 188, Jestin 1937). As is the case with the later Sargonic problem texts discussed above, the actual tablet contains not much more than quantities. No task is specified, and no procedure explained (Fig. 6).

Fig. 6

Source Cuneiform Digital Library Initiative, P010773. http://cdli.ucla.edu/dl/lineart/P010773_l.jpg. http://cdli.ucla.edu/search/archival_view.php?ObjectID=P010773

TSS 188, computation of a large area.

The text was analyzed by Friberg (2007, 148–149). The given answer is incorrect. Recall that the largest entry on the table VAT 12593 gave the area of a square of side 1 gešu nindan as 3 šar 2 buru. The problem on this tablet is to determine an area 25 times as great.

The relevant portion of the area metrology is given in the factor diagram below.

Friberg observed that the given answer is precisely what would have been obtained if the area of a 1 gešu nindan square had been incorrectly looked up in a table or recalled as 3 šar 3 buru instead of 3 šar 2 buru. Friberg briefly summarized the subsequent calculation in an equation without indicating the details of how the intermediate steps were conceived or carried out. His description implies an essentially arithmetical procedure.

Starting from an incorrect base area also upsets all the nice linkages that occur for the larger units and it really should have been apparent that something had gone wrong if following Proust’s subdivision of a diagram approach. However, the initial error could propagate effortlessly through the resulting computations if some kind of repeated addition or ‘correspondence’ procedure had been used. The issue arises because of the limitations of the specific notation in use during this period.

If the large surface was conceived as a 5 by 5 grid of smaller areas then computing the larger area becomes a simple problem in addition. If one square had area 3 šar 3 buru then two squares would have area 7 šar, 3 squares 1 šaru 3 buru, four squares 1 šaru 4 šar and five squares 1 šaru 7 šar 3 buru. Since five squares form a row or column, the calculation could then operate on rows to get the final result. In this model only simple addition and an understanding of the unit conversions inherent in the factor diagram is needed. All intermediate values are maintained in the standard metrological notation. Also, note that multiples of a given unit are recorded with repetitions of a unit, so tallying and bundling are the only requirements. These computations could have easily been carried out either in writing on some kind of temporary scratch pad surface, or using a simple additive counting board with symbolic markers for the different units.

We have emphasized the importance of core linkages between metrological systems. The use of correspondences based on simple linkages was first suggested by Friberg in his analysis of an Ebla mathematical text as a division problem. Friberg formulated the problem as: “Given that you have to count with 1 gubar [an Ebla capacity unit] for 33 persons, how much do you count with for 260,000 persons?” (Friberg 1986, 19). Friberg made the crucial observation that division of 260,000 by 33 was not possible using Eblaite notation and thus a different procedure must have been used.

A similar proposal for dealing with division problems from Šuruppak was given in Melville (2002) and Friberg (2007, 410–415) summarizes an improved version of the original suggestions for both the Ebla and Šuruppak problems. Below we give two examples, one simple, one more complicated, to illustrate the technique.

The tablet TSS 81 (Jestin 1937) reads (in the translation from the Digital Corpus of Cuneiform Mathematical Texts, see http://oracc.museum.upenn.edu/dccmt/): “40 sons of builders (each) received 2 ban as a flour gift. (Total) 3 lidga, 1 barig, 2 ban of flour” (Fig. 7).

Fig. 7

Source Cuneiform Digital Library Initiative, P010737. http://cdli.ucla.edu/dl/lineart/P010737_l.jpg. http://cdli.ucla.edu/search/archival_view.php?ObjectID=P010737

TSS 81, ration computations.

The modern approach would be to take an abstract multiple $( {40 \times 2 = 80} )$ of the base unit ban and then convert the 80 ban into the correct units. However, the capacity notation in Šuruppak precluded writing more than 5 ban (see Melville 2002 for details). Quantity notation was tied to the measurement system and not abstracted out as a number. Instead, the scribe must have worked up from the base correspondence of 1 person to 2 ban up to the correspondence of 40 people to the total quantity of 3 lidga, 1 barig, 2 ban using some kind of tabular arrangement and aggregating and bundling the quantity units.

A similar approach must also have been used for the ration ‘division ’ problem from Šuruppak (TSS 50, Jestin 1937): “A granary of barley. Each man received 7 sila of grain. Its men: 4 šaru 5 šar 4 gešu 2 geš 5 u 1; 3 sila of barley remains” (Fig 8).

Fig. 8

Source Cuneiform Digital Library Initiative, P010721. http://cdli.ucla.edu/dl/lineart/P010721_l.jpg. http://cdli.ucla.edu/search/archival_view.php?ObjectID=P010721

TSS 50, ration computations.

The scribe must have worked up from the correspondence of 1 man to 7 sila up through the various capacity units to the granary at the top. In fact, there is another copy of this problem, TSS 671 (Jestin 1937), or at least an attempted answer. In this case, the answer given is incorrect, but if some system of correspondences was used, the given solution required only one simple error in the middle of the computation . The challenge for the scribe was managing correspondences between two different metrological domains, each with different notation and different relationships between larger and smaller units.

While it is dangerous to generalize from such a modest sample, the fact that these division problems dominate the small corpus of mathematical problems suggests that the construction and solution of complex metro-mathematical division problems was popular 4500 years ago. As Friberg observed, “the fact that three of the four oldest known mathematical problem texts were concerned with exactly the same kind of ‘non-trivial’ division problems must be significant: the obvious implication is that the ‘current fashion’ among mathematicians about four and a half millennia ago was to study non-trivial division problems involving large…numbers and ‘non-regular’ divisors such as 7 and 33” (Friberg 1986, 22). The theory of correspondences suggests that these problems may have been solved using simple repetition and bundling with a collection of intermediate steps organized in a list or tabular fashion.

Archaic Mathematics (ca. 3000 BCE)

Although more is now known about the mathematics of the Archaic period around 3000 BC than was the case a few decades ago, much is still mysterious. The best introduction remains (Nissen et al. 1993).

Writing and mathematics were introduced in mesopotamia for administrative purposes, in order to monitor and record the flow of goods in a bureaucratic context. As Foster observed, “Accountability means the obligation to keep records for property that does not belong to the record-keeper. Although some have suggested that Sumerian accountability grew out of the difficulty of managing large quantities or transactions too complicated to remember, this misses the fundamental purpose of institutional record-keeping of all periods” (Foster 2005, 78). Thus, most of the sources we have derive from an institutional context and reflect institutional needs and priorities; what other kinds of mathematics there may have been in society have not left similar traces.

Another complication with the archaic texts is that it is often difficult to tell if a tablet represents an actual administrative document, a practice model document, or an exercise. In this context, Friberg used the term ‘metro-mathematical text’, commenting that “the term is appropriate because it is often difficult or impossible to distinguish a complicated and mathematically interesting administrative-economic text from a carefully designed mathematical exercise constructed in order to demonstrate the use of, and manipulation with, various kinds of measures and their numerical notations” (Friberg 1997, 2).

One indicator of artificiality that Friberg used was the presence of round or “almost-round” quantities, especially in areas of fields. One might expect fields in administrative archives to come in all shapes and sizes. The presence of lengths or areas that are conspicuously round (especially large and conspicuously round) or that differ from a round number either by a simple fraction or a small quantity suggests an artificial exercise. The frequency of occurrence of such measures convinced Friberg that many of these texts were educational and led to his geometric division interpretation extending back into the earliest script phases (Friberg 1997, 2014).

Friberg’s argument is delicate and one must take care in its interpretation. One example that he uses in both papers (1997 and 2014) is an archaic text where the areas of five rectangular fields are computed and then the total is recorded (MSVO 1, 2, Englund and Grégoire 1991). The total area is written as 3 šar 5 buru 2 bur 2 eše 5 iku, not an obviously round quantity. However, converting this into a multiple of iku, Friberg noted that the total is 4193 iku or, as he wrote, “$7 \cdot 10 \cdot 60\,iku - 7\,iku$”, commenting that, “This nearly round area number is hardly accidental” (2014, 4). Friberg is not suggesting that the quantity 4200 iku was written out, as that would not be possible in the contemporary notation, but that an underlying geometrical sense was used to construct problems where the solution comes very close to a regular figure. The point being that in problems involving fields, especially areas of fields, some kind of geometric representation may have been used, presumably marked on some temporary surface such as a dust board, the ground, or clay, but that this aid is not recorded on the final tablet that has come down to us. The only trace of the geometry is in the quantities chosen.

Early writing was largely curviform, drawn by a reed stylus onto wet clay. Quantity notation was somewhat different. The other end of the stylus was pressed into the clay either at an angle, producing a horizontal or vertical wedge shape, or straight down producing a circle. Two different sizes of stylus were used and the notation could combine them so, for example, producing a small circle inside a large wedge. These basic signs were decorated in various ways to extend to a repertoire of about 50 different quantity signs. How far this practical disjunction in way of writing quantities reflected a conceptual distinction is unclear.

Each sign represented a certain sized unit when referring to a particular metrological domain such as lengths, areas, capacities, time, or discrete goods. As there were more units than signs, many of the signs, especially the simple basic ones, appeared in several different contexts, where the same pair of signs could stand for different multiples depending on what was being measured. For example, the circular sign obtained by pressing the end of the stylus vertically into the clay represented 6 wedges in the capacity system, 10 wedges in the system used for discrete goods and 18 wedges in the area system. Unravelling this complex collection of metrological units and their relationships was a correspondingly difficult task. The main description of the results is in Nissen et al. (1993). Multiples of each basic unit were recorded with repetitions of the unit sign—three times a circle was shown as three circles. It is not known for certain how computations were carried out. All that was written down was the result of a computation , and there are no texts explaining arithmetic procedures. However, as we have seen above, there are some hints, but they are slight and open to contradictory interpretations.

Calculation

The question of precisely what kinds of computational aids and tools the Mesopotamian scribe could call upon, and exactly how certain kinds of calculations were carried out is problematic. The evidence is thin, indirect, and contradictory. We are considering a period of over a thousand years with evidence of slow but steady conceptual development. There is not necessarily a single answer. More than 20 years ago, with reference to the archaic period, Peter Damerow and Robert Englund wrote,

How such calculations were performed is not understood in detail. Instruments that could have served as calculation aids are as yet not attested in archaeological finds, or have not been identified as such. Lexical lists from later periods, however, suggest that the Sumerians used tallying boards made of wood, which being perishable would not have been unearthed in excavation. There is also some evidence that the sign SANGA, designating the chancellor of an economic unit, derives from a pictogram depicting such a tallying board. This, in fact, is supported by the cuneiform sign ŠID which, also having developed from this sign, was employed as an ideogram with the meaning “account”. (Nissen et al. 1993, 134)

Sadly, at least with respect to archaeology, not much has changed in the intervening years. There is still no incontrovertible evidence for any kind of counting board. However, we can say a little more.

First, the lexical evidence. There is a Sumerian term (giš-šudum-ma) translated as “tally-stick”. However, the word only appears (twice) in much later Old Babylonian literary sources. The term is not attested in the third-millennium sources at all and, while it is indeed possible that Sumerians made use of tally-sticks, such would be more a record device than a calculation aid. The second term (giš-nig-šid) appears in lexical lists (long lists of related words) but does not appear outside of them. The Sumerian giš is a determinative signifying an object made out of wood, so if the term referred to a real object it would be some kind of wooden device aiding in accounting. One of the problems with interpreting the lexical texts is that in them Sumerian scribes strove for an idealized completeness that did not always reflect reality. The fact that such objects are not ever mentioned in administrative documents is problematic, perhaps more so than their absence from the archeological record.

The hint provided by the shape of the archaic sign sanga is more intriguing. Before the term “scribe” appeared in the middle of the third millennium, there was a category of officials associated with receipt and disbursement of goods called sanga who often needed to determine totals of numerous entries or ratios of ingredients to go towards making goods (beer, for example). The sign is very well attested and came in a number of variants, of which the most common type was:

(CDLI signlist, http://cdli.ucla.edu/tools/SignLists/protocuneiform/archsigns.html)

The suggestive shape has led some to argue that the sign represents some kind of counting board with a receptacle for counters on the side. The farthest anyone has committed themselves in print is Jøran Friberg, who in a parenthetical aside remarked, “the sign sanga itself may be the picture of a box for number tokens”. (Friberg 2007, 151)

What makes the weakness of the evidence more frustrating is that the third millennium seems bracketed by the use of counters. Before writing developed, there was a widespread system of ‘tokens’ in use in Mesopotamia, and it appears that at least some of these tokens acted as ‘counters’ recording quantities of types of goods. The exact details of the relationships of early counters to the goods is unclear and whether they merely acted as a record of quantities or were used for calculations is completely unknown (Lieberman 1980; Schmandt-Besserat 1992; Englund 1993; Friberg 1994). At the other end of the period, both Proust and Høyrup have argued for the presence of a counting board in Old Babylonian mathematics (Proust 2000; Høyrup 2002a, b). But this is after the development of the abstract sexagesimal system, and their arguments depend in part on analysis of errors in many-place computations which would not have occurred the same way in earlier periods. Perhaps the new kinds of computation called forth new technology.

Another approach is to consider the kinds of calculations scribes were called upon to perform. We have seen that the archaic system had a wide range of quantity notation with often narrowly specified subject matter. Over the course of the following thousand years, number was gradually abstracted out of quantity. However, within this range of systems, there were distinct similarities. Each metrological system contained multiple different units. In all cases, multiples of a unit were given by repetition of the unit, either repeating the whole sign or by modifying a base sign with a series of strokes. There were thus three kinds of operations of increasing difficulty that were needed: simple accumulation, replacement or bundling of units within a sequence, and relations between units in different systems.

In the first case, simple accumulation, ‘addition’ is merely copying. That is, what we might think of as ‘$2 + 2 = 4$’ becomes in an accumulation or tallying system ‘$II + II = IIII$’, with the particular sign for the unit varying with context. The next level is bundling the appropriate collection of a small unit into one of the next larger unit. This operation could be learned either solely through writing or with some sort of physical aids. What complicated the issue for Mesopotamian scribes as opposed to modern children confronting, say, number rods, is that each individual system contained multiple different sized bundles to scale from one unit to the other. Context was vital, and this the written system was able to express clearly.

The third, and by far the most difficult, problem was establishing linkages between metrological domains that used different kinds of multiples in the span of their units. We have seen examples of this in the problem of giving rations to people, where the capacity units do not nicely correspond to the discrete system used to count people, and, above all, in the core problem of computing the area of a field from measurements of the sides. Length and area units did not align well. The evidence we have is that scribes responded to this challenge by developing tables reflecting simple square and rectangular cases, and possibly diagrams, but not the use of counting boards.

The main basis of Sumerian scribal education lay in copying and memorization. Scribes developed their writing and linguistic skills through copying exemplars and gradually memorizing signs and forms. It is probable that mathematics was learned the same way. Proust’s reconstruction of elementary mathematics education at Nippur during the Old Babylonian period shows that students learned lists of metrological signs, then mathematical tables (in this later period multiplication tables), and only entered on doing even simple calculations once they were thoroughly grounded in the intricacies of the metrological systems (Proust 2007). This pedagogical approach had deep roots.

If mathematical calculation , and in the third millennium this meant accumulation and correspondences, only came late in scribal education, it may well be that such calculations were carried out in written form. The professional identity of a scribe depended on the exclusive ability to write and, certainly in the archaic period, the complexity of quantity notation argues for a written form of computation , although this must remain speculative in the absence of better evidence.

Appendix: Periodization

The absolute chronology of Mesopotamia is an area of current vigorous scholarly debate, especially before the first millennium. The further back in time one goes, the larger the uncertainties. For convenience here we follow the middle chronology periodization adopted by the Cuneiform Digital Library Initiative (CDLI), as follows:

Period	Date
Uruk IV	~3350 to 3200
Uruk III	~3200 to 3000
Early Dynastic I–II	~2900 to 2700
Early Dynastic IIIa	~2600 to 2500
Early Dynastic IIIb	~2500 to 2340
Sargonic	~2340 to 2200
Ur III	~2100 to 2000
Old Babylonian	~2000 to 1600