Soft Decision Feedback Turbo Equalizer Based on Channel Estimation

Abstract

In order to improve the system BER performance, combining the decoding structure of the feedback iteration in Turbo code, a soft decision feedback equalizer based on channel estimation (CE-SDFE) was proposed. In the initial iteration, CE-SDFE is equivalent to RLS-DFE. In the next iteration, the feedback LLR information is utilized to reconstruct the IQ symbol sequence. The feedback symbol sequence is regenerated by using the IQ symbol sequence and the estimated channel impulse response. We use the weighted sum of the received symbol sequence and the feedback symbol sequence as the input of feedforward filter, and the weighted sum of the soft decision symbol sequence and the reconstructed IQ symbol sequence as the input of feedback filter. The weighting coefficient is generated according to the signal-to-noise ratio and multipath path number. The simulation results show the effectiveness of the proposed algorithm.

1 Introduction

In wireless communication system, multipath propagation can cause inter-symbol interference (ISI), ISI will cause distortion of the signal, thus affecting the quality of data transmission [1]. In general, the equalizer is used to eliminate the influence of ISI, and then the decoder is used to reduce the bit error rate. Equalizers and decoders are used to eliminate the effects of channel noise and interference, and the independent use of both can guarantee the reliability of communication to a certain extent [2]. However, when the channel environment is poor, to further improve the reliability of the system, we can consider the combination of equalization and decoding to obtain the joint gain, and this joint technology has encountered a significant increase in complexity.

The turbo code [3] proposed in 1993, its feedback iterative decoding structure and its idea of iterative use of soft information provides a new way to solve the high complexity of joint technology. Turbo equalization technology is the use of Turbo code iterative ideas, in the equalization and decoding between the continuous soft information iterative time domain equalization technology, which can greatly reduce the bit error rate [4].

We combined with the feedback structure of feedback iteration in Turbo code and its idea of iterative use of soft information to improve the performance of the receiver. In this paper, we propose a soft decision feedback equalization based on channel estimation (CE-SDFE). In the initial iteration, CE-SDFE is equivalent to RLS-based decision feedback equalizer (RLS-DFE) [5]. In the next iteration, the feedback LLR information is utilized to reconstruct the IQ symbol sequence. The feedback symbol sequence is regenerated by using the IQ symbol sequence and the estimated channel impulse response. The input of feedforward filter is the weighted sum of the received symbol sequence and the feedback symbol sequence, and the input of feedback filter is the weighted sum of the soft decision symbol sequence and the reconstructed IQ symbol sequence. The weighting coefficient is generated according to the signal-to-noise ratio and multipath path number. The simulation results show the effectiveness of the proposed algorithm.

2 RLS-Based Decision Feedback Equalizer

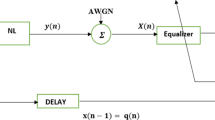
Decision feedback equalizer [6] consists of two parts: feedforward filter (FFF) and feedback filter (FBF), the structure shown in Fig. 1. The feedforward filter consists of a feedforward transversal filter, which takes the received symbol sequence as input and suppresses the forward ISI linearly. The feedback filter takes the past decision symbol as input and estimates the interference of the preceding symbol to the following symbol.

Fig. 1.

Decision feedback equalizer.

Thus, the output of the decision feedback equalizer can be represented as

$$ \bar{x}_{k} = \sum\limits_{{n = - K_{1} }}^{0} {b_{n} y_{k - n} } + \sum\limits_{n = 1}^{{K_{2} }} {b_{n} \hat{x}_{k - n} } , $$

(1)

where $\hat{x}_{k}$ is the estimated value of the kth information symbol, $\left\{ {b_{n} } \right\}$ is the tap coefficient of the filter and $\left\{ {\hat{x}_{k - 1} , \ldots ,\hat{x}_{{k - K_{2} }} } \right\}$ is the decision of the previous symbols. The feedforward filter contains $K_{1} + 1$ taps, and the feedback filter contains $K_{2}$ taps. Here we define $N = K_{1} + K_{2} + 1$. In the k times, the filter coefficient of DFE is defined as $B_{N} (k) = [b_{{ - K_{1} }} ,\,\ldots\,b_{0} , \ldots ,b_{{K_{2} }} ]^{T}$, and the input symbols is defined as $Y_{N} (k) = [y_{{k + K_{1} }} , \ldots y_{k} , \ldots ,x_{{k - K_{2} }} ]^{T}$. The matrix form of the DFE output can be expressed as

$$ \bar{x}_{k} = B_{N}^{H} (k)Y_{N} (k). $$

(2)

Since the parameters of the wireless channel are variable, the equalizer’s tap coefficients must be synchronized to track changes. For the adjustment of the tap coefficient, it is necessary to adopt the adaptive adjustment method, that is adaptive equalization. The RLS algorithm is utilized to optimize $B_{N} (k)$. RLS algorithm is a special case of Kalman filter algorithm, also known as Kalman algorithm [7]. Kalman filtering is the development of Wiener filtering, which minimizes the trace of the correlation matrix of the filtered state error [8]. Compared with the LMS class algorithm, both the LMS algorithm and the RLS algorithm are based on the least cost function [9], but the choice of the cost function is different. The cost function of the RLS algorithm is

$$ \xi (n) = \sum\limits_{k = 0}^{n} {w^{n - k} \left| {e(k)} \right|^{2} } , $$

(3)

where w represents a weighting factor $0 < w < 1$. For RLS-DFE, when the input is the known symbols, the error is defined as

$$ e(k) = p_{k} - \bar{x}_{k} = p_{k} - B_{N}^{H} (k)Y_{N} (k). $$

(4)

When the input is the known symbols, the error is defined as

$$ e(i) = \hat{x}_{k} - \bar{x}_{k} = \hat{x}_{k} - B_{N}^{H} (k)Y_{N} (k). $$

(5)

We introduce exponential weighting into past data, which is appropriate when the channel characteristics are time-variant. Minimization of $\xi (n)$ with respect to the coefficient vector $B_{N} (n)$ yields the set of linear equations

$$ R_{N} (n)B_{N} (n) = D_{N} (n), $$

(6)

where $R_{N} (n)$ is the signal correlation matrix of the received symbol sequence which can be represented as

$$ R_{N} (n) = \sum\limits_{k = 0}^{n} {w^{n - k} Y_{N}^{*} (k)Y_{N}^{T} (k)} . $$

(7)

and $D_{N} (n)$ is the cross-correlation vector:

$$ D_{N} (n) = \sum\limits_{k = 0}^{n} {w^{n - k} \bar{x}_{k} Y_{N}^{*} (k)} . $$

(8)

The solution of Eq. 6 is

$$ B_{N} (n) = R_{N}^{ - 1} (n)D_{N} (n). $$

(9)

It is inefficient to solve the set of N linear equations for each new signal component that is received. To avoid this, we proceed as follows. First, $R_{N} (n)$ may be computed recursively as

$$ R_{N} (n) = wR_{N} (n - 1) + Y_{N}^{*} (n)Y_{N}^{T} (n), $$

(10)

where we call Eq. 10 the time-update equation for $R_{N} (n)$.

We use the matrix-inverse identity to calculate $R_{N}^{ - 1} (n)$:

$$ R_{N}^{ - 1} (n) = \frac{1}{w}\left[ {R_{N}^{ - 1} (n - 1) - \frac{{R_{N}^{ - 1} (n - 1)Y_{N}^{*} (n)Y_{N}^{T} (n)R_{N}^{ - 1} (n - 1)}}{{w + Y_{N}^{T} (n)R_{N}^{ - 1} (n - 1)Y_{N}^{*} (n)}}} \right]. $$

(11)

For convenience, we define $P_{N} (n) = R_{N}^{ - 1} (n)$. It is also convenient to define an N-dimensional vector, called the Kalman gain vector, as

$$ K_{N} (n) = \frac{{P_{N} (n - 1)Y_{N}^{*} (n)}}{{w + Y_{N}^{T} (n)P_{N} (n - 1)Y_{N}^{*} (n)}}. $$

(12)

With these definitions, Eq. 11 becomes

$$ P_{N} (n) = \frac{1}{w}\left[ {P_{N} (n - 1) - K_{N} (n)Y_{N}^{T} (n)P_{N} (n - 1)} \right]. $$

(13)

Since

$$ B_{N} (n) = P_{N} (n)D_{N} (n). $$

(14)

and

$$ D_{N} (n) = wD_{N} (n - 1) + \bar{x}_{n} Y_{N}^{*} (n). $$

(15)

The time-update equation of $B_{N} (n)$ can be represented as

$$ B_{N} (n) = B_{N} (n - 1) + K_{N} (n)e_{N} (n). $$

(16)

3 Soft Decision Feedback Equalizer Based on Channel Estimation

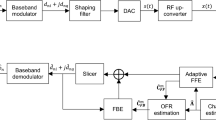
According to the description of RLS-DFE in the previous section, we propose a soft decision feedback turbo equalizer based on channel estimator based on channel estimation, as it is shown in Fig. 2. In CE-SDFE, the feedforward and feedback filter’s tap number are determined based on the estimated channel delay [10]. The input of the equalizer feedforward filter is

$$ {\mathbf{z}}_{N} = P_{r} {\mathbf{y}}_{N} + P_{e} {\mathbf{y}}_{N}^{b} , $$

(17)

where ${\mathbf{y}}_{N}$ is the sampled symbol sequence, ${\mathbf{y}}_{N}^{d}$ is the feedback symbol sequence, $P_{r}$ represents a weighting coefficient of the sampled symbol sequence, $P_{e}$ represents the weight coefficient of the feedback symbol sequence, $P_{r}$ and $P_{e}$ satisfy $P_{r} + P_{e} = 1$.

Fig. 2.

Soft decision feedback turbo equalizer based on channel estimation.

The input of the feedback filter is

$$ P_{r}^{d} \hat{x}_{n} + P_{e}^{d} x_{n}^{d} , $$

(18)

where $\hat{x}_{n}$ represent the soft decision of the equalizer output $\bar{x}_{n}$, $x_{n}^{d}$ represent the feedback data symbol, $P_{r}^{d}$ represents the weighting coefficient of $\hat{x}_{n}$, $P_{e}^{d}$ represents the weighting coefficient of $x_{n}^{d}$, $P_{r}^{d}$ and $P_{e}^{d}$ satisfy $P_{r}^{d} + P_{e}^{d} = 1$.

In the first iteration, CE-SDFE is equivalent to RLS-DFE, and the concrete steps can be described as:

• ① Parameter initialization: $P_{r} = 1$, $P_{e} = 0$, ${\mathbf{y}}_{N}^{b} = \left\{ 0 \right\}$, $P_{r}^{d} = 1$, $P_{e}^{d} = 0$, The input of feedforward filter is ${\mathbf{z}}_{N} = {\mathbf{y}}_{N}$; Initialize the equalizer parameters as described in Sect. 2.

• ② Channel response estimate: The input of channel estimator is a sequence of sampled symbols ${\mathbf{y}}_{N}$ and a sequence of known symbols ${\mathbf{P}}$, and the output of estimator is the channel impulse response ${\mathbf{h}}_{k}$. The estimator is implemented using the RLS filter.

• ③ Adaptive equalization: The input of feedforward filter is ${\mathbf{z}}_{N}$, the output is $\bar{x}_{n}$. When $n \in I_{p}$, the corresponding reference symbol is a known symbol, the feedback error was

  $$ e(n) = p_{n} - \bar{x}_{n} , $$

  (19)

  The known symbol $p_{n}$ was the input of the feedback filter;

  When $n \in I_{d}$, the corresponding reference symbol is an unknown data symbol. A soft decision $\hat{x}_{n}$ was obtain on $\bar{x}_{n}$, and the feedback error was

  $$ e(n) = \hat{x}_{n} - \bar{x}_{n} , $$

  (20)

  The soft decision result $\hat{x}_{n}$ is the input of the feedback filter;

• ④ Decoder: when the equalizer outputs all the data symbols, we need to descramble the data symbol firstly, and obtain $\left\{ {\bar{x}_{n}^{r} } \right\}$. The second step is to calculate the log-likelihood ratio $\left\{ {\lambda_{n,j} } \right\}$ based on $\left\{ {\bar{x}_{n}^{r} } \right\}$ and channel estimation information. Finally, the deinterleaving and Viterbi deciding are performed on $\left\{ {\lambda_{n,j} } \right\}$ to obtain the decoding result $\left\{ {l_{n} } \right\}$.

When the initial iteration is completed, the CE-SDFE needs to adjust the input of the feedforward filter and the feedback filter using the result of demodulation decoding and intermediate information. The specific steps can be described as follows:

• ① Burst frame symbol sequence reconstruction: First, the priori LLR information is calculated using the decoding results $\left\{ {l_{n} } \right\}$ and $\left\{ {\lambda_{n,j} } \right\}$. And then $\left\{ {\lambda_{n,j}^{e} } \right\}$ and $\left\{ {\lambda_{n,j} } \right\}$ will be added to obtain the LLR information $\left\{ {\lambda_{n,j}^{d} } \right\}$. Then $\left\{ {\lambda_{n,j}^{d} } \right\}$ is used to reconstruct the data symbol sequence $\left\{ {x_{n}^{r} } \right\}$, Finally, the sequence $\left\{ {x_{n}^{r} } \right\}$ is scrambled and framed to reconstruct the burst symbol sequence ${\mathbf{x}}_{N}^{d}$.

• ② Feedback symbol sequence generation: generated using the estimated channel impulse response ${\mathbf{h}}_{k}$ and ${\mathbf{x}}_{N}^{d}$.

• ③ Calculate the weighting coefficients $P_{r}$, $P_{e}$, $P_{r}^{d}$, $P_{e}^{d}$: The weight coefficients $P_{e}$ and $P_{e}^{d}$ need to be determined based on the number of channels estimated by the channel, the signal-to-noise ratio and the data symbol modulation:

  When the number of paths equal to 1,

  $$ \begin{array}{*{20}l} {P_{e} = 2\text{Q} \left( {\sqrt {\left( {2\log_{2} L_{d} } \right)\sin^{2} \left( {\frac{\pi }{{L_{d} }}} \right)\rho } } \right),P_{r} = 1 - P_{e} } \hfill \\ {P_{e}^{d} = 2\text{Q} \left( {\sqrt {\left( {2\log_{2} L_{d} } \right)\sin^{2} \left( {\frac{\pi }{{L_{d} }}} \right)\rho } } \right),P_{r}^{d} = 1 - P_{e}^{d} } \hfill \\ \end{array} , $$

  (21)

  where $\text{Q} ( \cdot )$ represents the Q functions, $L_{d}$ represents the total number of elements in the data symbol map vector set, $\rho$ represents the normalized signal to noise ratio.

  When the number of paths is greater than 1,

  $$ \begin{array}{*{20}l} {P_{e} = 0,P_{r} = 1} \hfill \\ {P_{e}^{d} = 2\text{Q} \left( {\sqrt {\left( {2\log_{2} L_{d} } \right)\sin^{2} \left( {\frac{\pi }{{L_{d} }}} \right)\rho } } \right),P_{r}^{d} = 1 - P_{e} } \hfill \\ \end{array} . $$

  (22)

• ④ Adaptive equalization: The input of feedforward filter is ${\mathbf{z}}_{N} = P_{r} {\mathbf{y}}_{N} + P_{e} {\mathbf{y}}_{N}^{b}$, the output is $\bar{x}_{n}$. When $n \in I_{p}$, the feedback error was

  $$ e(n) = p_{n} - \bar{x}_{n} , $$

  (23)

  The known symbol $p_{n}$ was the input of the feedback filter;

  When $n \in I_{d}$, the corresponding reference symbol is an unknown data symbol. A soft decision $\hat{x}_{n}$ was obtain on $\bar{x}_{n}$, and the feedback error was

  $$ e(n) = P_{r}^{d} \hat{x}_{n} + P_{e}^{d} x_{n}^{d} - \bar{x}_{n} , $$

  (24)

  The input of the feedback filter is $P_{r}^{d} \hat{x}_{n} + P_{e}^{d} x_{n}^{d}$.

• ⑤ Decoder: when the equalizer outputs all the data symbols, we need to descramble the data symbol firstly, and obtain $\left\{ {\bar{x}_{n}^{r} } \right\}$. The second step is to calculate the log-likelihood ratio $\left\{ {\lambda_{n,j} } \right\}$ based on $\left\{ {\bar{x}_{n}^{r} } \right\}$ and channel estimation information. Finally, the deinterleaving and Viterbi deciding are performed on $\left\{ {\lambda_{n,j} } \right\}$ to obtain the decoding result $\left\{ {l_{n} } \right\}$.

4 Simulation Results

In this section Monte Carlo simulation result for CE-SDFE are presented to verify the feasibility of the adaptive equalization algorithm. In the simulation, we use the signal frame length of 440, which consist of 128 known 8PSK symbol and 312 data symbols. The adaptive equalization algorithm is simulated by 10000 Monte Carlo experiments using Gaussian channel and fading channel.

Figure 3 shows the bit error rate of the receiver under AWGN channel. In the simulation, the realization of the system need to consider synchronization, parameter estimation and so on. The simulation results show that when the number of iterations is 0 and the bit error rate is 10⁻⁵, snr is 8.5 dB. By iteration, The BER performance of this algorithm is improved to 8 dB.

Fig. 3.

BER performance for AWGN channel.

Figure 4 shows the convergence performance of the DFE filter when SNR is 5 dB. The simulation has the same channel condition with Fig. 3. The simulation results show that the MSE performance can converge to about 0.2 when the number of iterations is equal to 0. The feedback error is small due to the soft decision of the unknown symbol. When the number of iterations is equal to 4, the MSE can converge to 0.001.

Fig. 4.

MSE performance for AWGN channel.

Figure 5 shows the bit error rate of the receiver under fading channel. The fading channel consist of two delay path which have the same power, and the delay is 1 ms.

Fig. 5.

BER performance for fading channel.

In the simulation, the realization of the system need to consider synchronization, parameter estimation and so on. The simulation results show that when the number of iterations is 0 and the bit error rate is 10−5, snr is 8.5 dB. By iteration, The BER performance of this algorithm is improved to 8 dB. The simulation results show that when the number of iterations is 0 and the bit error rate is 10−2, snr is 15 dB. By iteration, The BER performance of this algorithm is improved to 13 dB.

Figure 6 shows the convergence performance of the DFE filter when SNR is 10 dB. The simulation has the same channel condition with Fig. 5. The simulation results show that the MSE performance can converge to about 0.2 when the number of iterations is equal to 0.

Fig. 6.

MSE performance for fading channel.

5 Conclusion

We combined with the feedback structure of feedback iteration in Turbo code and its idea of iterative use of soft information to improve the performance of the receiver. In this paper, we propose a soft decision feedback equalization based on channel estimation. In the initial iteration, CE-SDFE is equivalent to RLS-DFE. In the next iteration, the feedback LLR information is utilized to reconstruct the IQ symbol sequence. The feedback symbol sequence is regenerated by using the IQ symbol sequence and the estimated channel impulse response. The input of feedforward filter is the weighted sum of the received symbol sequence and the feedback symbol sequence, and the input of feedback filter is the weighted sum of the soft decision symbol sequence and the reconstructed IQ symbol sequence. The weighting coefficient is generated according to the signal-to-noise ratio and multipath path number. The simulation results show that the proposed algorithm has improved BER performance and MSE performance under Gaussian channel and fading channel condition, but the iteration increases the computational complexity and needs the relationship between the equalization performance and the number of iterations in practical.