The Diffraction of a Two-Dimensional Curved Shock Wave Using Geometric Shock Dynamics

Abstract

The diffraction of a cylindrical shock wave segment around convex sharp corners is considered. This investigation is approached from a numerical and analytical perspective. The numerical investigation was carried out using ANSYS Fluent while Whitham’s theory of geometric shock dynamics was used as a basis for the analytical approach. A model based on Whitham’s theory was developed, wherein the cylindrical shock profile is viewed as being composed of connected plane shocks with varying orientation. As the length of these plane shocks approaches zero, their combined shape approximates the cylindrical shock’s profile. Upon diffraction, disturbance waves propagate along this sequence of plane shocks; the theory of sound was used to model the propagation of these disturbances (taking into account the variation of shock orientation). Using this method, the inflection point (the point where the disturbed and undisturbed portions of the shock meet) was calculated. The results from the calculation were compared to those from ANSYS Fluent and they showed good correlation. A further attempt was made at modelling an elliptical shock, which produced unexpected results. In plane and cylindrical shocks, the disturbed region grows weaker; yet, it grows stronger in elliptical shock producing another wave between the reflected shock and the wall.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

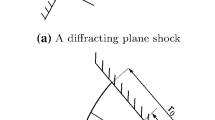
In this paper, the diffraction of curved shock waves around convex corners is presented. To a certain extent, this work can be viewed as an extension of the work of Skews [5], where the diffraction of a plane shock wave around convex corners was investigated (Fig. 1a) using the theory of sound.

Fig. 1

Illustrations of plane and curved shock diffraction showing the point of inflection and sound wave behind the shock

In that work, it was shown that Whitham’s theory of Geometric Shock Dynamics (GSD) [6] was adequate for predicting the profiles of strong shocks although its accuracy decreased as the shock weakens. The inaccuracies inherent in Whitham’s theory when considering weak shocks were attributed to it ignoring post-shock conditions (the free propagation assumption). In light of that, Milton [4] accounted for the post-shock conditions, while Itoh et al. [3] generalised the resulting expression for both strong and weak shocks.

Upon encountering a convex corner, the curvature and shape of the shock change. The angle made by the line joining the point where shock curvature begins to change to the corner with the x-axis is the angle $\nu$. On the shape of the diffracted plane shock, it was shown that the shape was self-similar in time, wherein the angle $\nu$ is independent of time. Moreover, the angle $\nu$ was shown to be independent of the wall angle (Fig. 1).

Here, it is shown that qualitatively, a curved shock behaves just as a plane shock does albeit with quantitative differences. While the flow behind a plane shock is uniform, the same cannot be said for a curved shock. As the curved shock propagates in its channel, it converges on itself and accelerates. Therefore, unlike a plane shock, the speed of sound and of the perturbed gas behind the shock are always changing.

For this investigation, ANSYS Fluent v 15.0 solver was used for the CFD simulations and MATLAB 8.0.0.783 was used for solving the generalised equations of geometric shock dynamics.

2 Diffraction Model

Diffraction occurs when a shock wave encounters a convex corner (Fig. 1). Expansion waves propagating along the shock cause the shock’s shape and Mach number to change. In addition, a reflected wave travelling at the local speed of sound is generated behind the shock.

To calculate shock Mach number, the area Mach number relationship can be used which when combined with GSD allows for the calculation of the shock’s profile.

2.1 Geometric Shock Dynamics

The shock Mach number can be related to the cross-sectional area of the channel through which it propagates. Chester [1], Chisnell [2] and Whitham [6] independently showed that by ignoring post-shock conditions, Eq. 1 can be used to calculate the shock’s speed. The expression was subsequently revised by Milton [4] and Itoh et al. [3] (Accounting for reflected waves behind the shock) resulting in a correction factor ($\eta (A,M_s)/M_s$) added to the right-hand side of Eq. 1:

$$\begin{aligned} -\frac{1}{A}\frac{dA}{dM_s} = \frac{2M_s}{(M_s^2-1)K(M_s)} \end{aligned}$$

(1)

$$\begin{aligned} \frac{\partial }{\partial \alpha }\left( \frac{1}{M} \frac{\partial A}{\partial \alpha }\right) +\frac{\partial }{\partial \beta }\left( \frac{1}{A} \frac{\partial M}{\partial \beta }\right) =0 \end{aligned}$$

(2)

In addition to the relationship between area and Mach number, Whitham [6] derived a geometric relation (Eq. 2) for a shock on a curvilinear coordinate system (Fig. 2). In order to account for the change in shape of a shock’s profile, Whitham introduced the concept of a disturbance propagating along the shock. The disturbance propagates at a Mach number c(M) which depends on the shock’s Mach number. Introducing this concept allows the reduction of Eq. 2 into conservative form (Eqs. 3 and 4):

$$\begin{aligned} \theta + \int \frac{dM}{Ac} = \text {constant along } \frac{dy}{dx}=\tan (\theta +\nu ) \end{aligned}$$

(3)

$$\begin{aligned} \theta - \int \frac{dM}{Ac} = \text {constant along } \frac{dy}{dx}=\tan (\theta -\nu ) \end{aligned}$$

(4)

Fig. 2

Curvilinear coordinate system for the derivation of GSD where $\overline{PQ}=M\delta \alpha$, $\overline{SP}=A\delta \beta$, $\overline{SR}=\left( M+\frac{\partial {M}}{\partial {\beta }}\delta \beta \right) \delta \alpha$ and $\overline{RQ}=\left( A+\frac{\partial {A}}{\partial {\alpha }}\delta \alpha \right) \delta \beta$

In Eqs. 3 and 4, the line along which the invariant ($\theta \pm \int \frac{dM}{Ac}$) is constant represents the characteristic which is the locus followed by disturbances in the laboratory frame of reference. Equations 3 and 4 represent upward and downward moving disturbances on the shock front. $\theta$ is the shock’s orientation relative to the x-axis, M is the shock’s Mach number, A is the channel’s cross-sectional area, and c is the Mach number of the disturbance. In the characteristic equation, $\nu$ is the angle made by the line joining the disturbance to the corner with the line parallel to the wall at the corner.

3 Diffraction Around a Convex Sharp Corner

In general, when a shock encounters a convex corner, a sequence of disturbances of decreasing strength propagate along the shock front causing it to bend. Consider a case of simple waves wherein the disturbances originate from one end of the shock. In the following section, a plane shock is considered then with that insight generalised to cylindrical shocks. Furthermore, only the first disturbance that propagates along the shock is considered. Since we consider a simple wave, then we may neglect one of Eqs. 3 or 4.

3.1 Plane Shock

Assuming an upward moving disturbance, we neglect Eq. 4. When the shock is incident at the corner, its orientation and Mach number are $\theta _0 \, \mathrm{and} \, M_0$, respectively. Taking these as the initial conditions of the shock, we can find the constant of the invariant and hence re-write Eq. 3 as

$$\begin{aligned} \theta + \int _1^M \frac{dM}{Ac} = \theta _0 + \int _1^{M_0} \frac{dM}{Ac} \end{aligned}$$

(5)

Since the Mach number of an undisturbed plane shock is constant, it follows from Eq. 5 that $\theta = \theta _0$. Furthermore, since the Mach number of the plane shock is constant, it follows that $\nu$, a function of the shock’s Mach number, is also constant (say $\nu _0$).

From the above argument and Eq. 3, the locus of the first disturbance is then given by the straight line (Eq. 10), which is also the characteristic of the first disturbance (Fig. 3):

$$\begin{aligned} y = \tan (\theta _0+\nu _0)(x-x_0)+y_0 \end{aligned}$$

(6)

Fig. 3

Diffraction of a plane shock with orientation $\theta$ with respect to the x-axis

3.1.1 Theory of Sound

Using the theory of sound [5], the locus of the first disturbance was calculated. A schematic of the concept is shown in Fig. 1a. Using the theory, it was shown that $\nu$ can reliably be calculated from Eq. 7 instead of 9 which is based on Whitham’s theory:

$$\begin{aligned} \tan {(\nu )} = \sqrt{\left( \frac{(M^2-1)((\lambda -1)M^2+2)}{(\lambda +1)M^4} \right) } \end{aligned}$$

(7)

$$\begin{aligned} \tan (\nu ) =\sqrt{\frac{(M^2-1)((\lambda -1)M^2+2)}{((\lambda +1)M^2))}}\frac{1}{M} \end{aligned}$$

(8)

$$\begin{aligned} \tan (\nu ) = \sqrt{\frac{1}{2}\frac{(M^2-1)K(M)}{(\lambda +1)M^2}} \end{aligned}$$

(9)

Equation 8 is a rearrangement of 7; the numerator is the Mach number (c(M)) of the disturbance along with the shock according to the theory of sound while the denominator is the Mach number of the shock. Thus, $\tan (\nu )$ is the ratio of the distance travelled along the shock to the distance travelled by the shock (Fig. 4a). In an attempt to extend the theory of sound to curved shocks, it might be tempting to consider the intersection of a sound wave with the curved shock but in Sect. 3.3, we show a different way for extension. Figure 4b shows the concept applied to a curved shock.

Fig. 4

Diffraction of a plane shock with orientation $\theta _0$

3.2 Cylindrical Shock

The orientation of a cylindrical shock varies along the shock (Fig. 5), while the Mach number of the undisturbed part of the shock varies with time. As a consequence, the locus of the first disturbance is not expected to be linear. As with a plane shock, taking the initial conditions at the wall when the shock had orientation $\theta _i$ and Mach number $M_i$ (at position $i = 0$), the invariant reduces to Eq. 5. Since the shock’s Mach number is not constant as the shock propagates, Eq. 5 can be rearranged to give the change in shock orientation when the shock Mach number changes from $M_i$ to $M_{i+1}$. This is then used to calculate the orientation of the point on the shock occupied by the moving disturbance.

Fig. 5

An illustration of the variation of shock orientation along a cylindrical shock wave segment profile

$$\begin{aligned} \theta _{i+1} = \theta _{i} + \int _{M_{i+1}}^{M_i} \frac{dM}{Ac} \end{aligned}$$

(10)

From Eq. 3, the characteristic corresponding to Eq. 10 is

$$\begin{aligned} \frac{dy}{dx}= & {} \tan (\theta +\nu )\nonumber \\ y_{i+1}= & {} y_{i} +(x_{i+1}-x_{i})\tan (\theta _{i+1} + \nu _{i+1}) \end{aligned}$$

(11)

While Eq. 11 is linear between i and $i+1$, it will not be linear for all i since the gradient $\tan (\theta _{i+1} + \nu _{i+1})$ is variable. Therefore, the characteristic of the first disturbance which is also its locus will not be a straight line.

3.3 A Physical Interpretation

When a shock is incident on a corner, Whitham [6] showed that disturbance signals ($c(M_s)$) propagate along the shock causing the shock to change shape. For the case of a diffracting shock, the corner sends a sequence of disturbances that is decreasing in strength ($c_1> c_2> c_3 > \cdots$). An assumption made in this paper is that, other than initiating the disturbance signals and acting as a boundary constraint (i.e. The shock is always perpendicular to the wall), the wall has no other impact on the shock’s diffraction.

Before we consider the diffraction of a curved shock we recall Eq. 7, derived by Skews [5]. In comparison with experimental data, Eq. 7 was found to predict the inflection point ($\nu _0$) of a diffraction shock well (see Fig. 1a).

For a cylindrical shock, Eq. 7 will not directly apply. However, with reference to Fig. 6 it can be used. Key to this argument is that the curvature of the shock is not communicated to all points that make up the shockwave. When the cylindrical shock is incident on the corner (A) (Fig. 6), the system can be treated as a plane shock, tangential to the curved shock at point A moving at the curved shock’s speed ($M_0$) at A. With that view, Eq. 7 can be applied to calculate the inflection point ($\nu _0$). After a time $\varDelta t$ when the shock has propagated a distance $\varDelta x$, the inflection point will be propagated to point B.

Fig. 6

An illustration of the new model

According to Skews [5], point B represents the first disturbance that was generated by the corner. Alluding to the assumption made above that the wall serves no other purpose than as a signal generator and boundary condition, point B can be treated as a virtual corner. This is so because

• There is a signal $c(M_s)$ which, relative to point C, D, $\ldots$ was generated at points B.

• The direction of propagation of point B is perpendicular to the shock at B (A virtual wall). This can be compared with Whitham’s [6] assumption that in the ray shock network, the rays can be treated as the walls of stream tubes.

That being the case, the shock at point B can be treated as a planar shock tangential to the curved shock at B with the wall slightly inclined according to the virtual wall described above. Equation 7 can then be applied to find the new inflection point $\nu _1$ measured with respect to the virtual wall. Note that because the shock’s speed is not constant then $\nu _1 \ne \nu _2 \ne \nu _3 \ne \cdots$. Corrolary, the locus of the inflection point will be curved. As $\varDelta t$ becomes infinitesimal, a smooth locus for the inflection point can be obtained.

The above method should similarly apply to any shock with a smooth profile. It is also easy to see how it generalises back to a plane shock.

4 CFD and GSD Simulation Profiles

As expected, the diffraction of a cylindrical shock is qualitatively similar to that of a plane shock with similar features being observed behind both plane and cylindrical shocks. Quantitative differences are to be expected considering that the flow behind a cylindrical shock is non-uniform unlike that of a plane shock. Figures 7 and 8 show a CFD simulation of a 165 mm radius shock diffracting around a $27.5^\circ \, \mathrm{and} \, \mathrm{a} \, 45^\circ$ corner.

Fig. 7

Diffraction of a 165 mm radius cylindrical shock around a corner of $27.5^\circ$

Fig. 8

Diffraction of a 165 mm radius cylindrical shock around a corner of $45^\circ$

Fig. 9

The locus of the inflection on 200 mm shock at Mach 1.5

4.1 Point of Inflection

Upon diffraction, the shock’s curvature changes from convex to concave. The point where the shock changes from concave to convex is its inflection point. Using the method presented in Sect. 3.2 in conjunction with Geometric Shock Dynamics, points of inflection were calculated for cylindrical shocks with radii 50 mm, 100 mm and 200 mm at Mach numbers 1.2 and 1.5. The resulting loci were compared to those determined from CFD simulations.

In Figs. 9, 10, 11 and 12, the circular data points represent CFD data and the line is the locus calculated using the method presented here. For the cases considered, the fit was found to be good. For example, for the 200 mm shock, the model presented in Sect. 6 was satisfactory at 95% confidence level using a $\chi ^2$ goodness of fit statistic. From the figures it can be seen that, as the shock radius increases, the locus of the inflection point on the shock becomes more linear as expected.

Fig. 10

The locus of the inflection on a 100 mm shock at Mach 1.2

Fig. 11

The locus of the inflection on a 100 mm shock at Mach 1.5

Fig. 12

The locus of the inflection on a 50 mm shock at Mach 1.5

In calculating $\nu$, Eq. 7 was used. Whitham’s Eq. 9 was found to be inadequate for weak plane shocks and for this reason might be inadequate for cylindrical shocks as well.

5 Conclusion

A method to calculate the locus of the first disturbance is presented which generalises from curved to plane shocks. While it was applied only to cylindrical shocks, it should apply equally well to other shock shapes with a smooth profile. This method does not give the shape of the diffracted section of the shock wave. However, by accounting for the other disturbances generated at the wall, it might be possible to calculate the shape shock since the same method is successful with plane shocks.

Fig. 13

An illustration of the convergence of an ellipse. Shown here are the normals of an elliptic profile and how any two normals always intersect at distinct points

Fig. 14

Diffraction of an elliptic shock around a $27.5^{\circ }$ convex corner

6 Future Work: Elliptical Shocks

While cylindrical shock diffraction patterns are qualitatively similar to those of plane shocks, elliptical shocks are slightly different. This difference could be accorded more to geometry than physics. In particular, the normals of a cylindrical shock converge onto a single point (the centre), those of an ellipse form a locus (an astroid) (Fig. 13). Therefore, the manner in which an elliptical shock converges on itself will be considerably different. Any two normals will intersect along the astroid and where they intersect marks the point of wave focusing. Thus, for an elliptic shock, focusing occurs continuously unlike a cylindrical shock which focuses only at the centre point. Figure 14 shows the simulation results of the diffraction of an elliptic shock around a $27.5^{\circ }$ convex corner. The profile of the diffracted shock starts off as one would expect from plane and cylindrical shocks. At a time of 0.0004 s, a second reflection appears, attached to the diffracted shock. Using the concept of a disturbance on the shock’s profile, as the part of the shock that has not yet diffracted propagates, it gradually converges on itself causing disturbances to propagate towards the wall. Because the shock is converging, its increasing means that the sequence of disturbances sent towards the wall is of increasing strength. The point where they meet is the where the second reflection occurs.