13.1 Introduction

In the past few decades, many applications of speech communication systems have been investigated, but it is well known that these systems always suffer from the deterioration of speech quality under adverse noise conditions. In a study of speech enhancement, many types of statistical signal estimation methods have been proposed, e.g., the maximum likelihood estimator of short-time spectral amplitude (spectral subtraction (SS) [1,2,3,4]), the minimum mean-square error estimator of the complex-valued spectrum (Wiener filtering (WF) [5]), the Bayesian estimator of short-time spectral amplitude (the minimum mean-square error short-time spectral amplitude (MMSE-STSA) estimator [6] and the minimum mean-square error log-spectral amplitude estimator (MMSE-LSA) [7]), and the MAP estimator [8]. SS is the commonly used noise reduction method that has high noise reduction performance with low computational complexity. However, in this method, artificial distortion, referred to as musical noise, arises owing to nonlinear signal processing, leading to a serious deterioration of sound quality [9, 10]. Therefore, to assess and control the generation of musical noise, several studies were conducted using higher-order statistics [11,12,13].

To achieve high-quality noise reduction with low musical noise, an iterative SS method has been proposed [14,15,16]. This method is performed through signal processing, in which weak SS processes are iteratively applied to the input signal. Also, Inoue et al. have reported the very interesting phenomenon that this method with appropriate parameters gives equilibrium behavior in the growth of higher-order statistics with increasing number of iterations [17]. This means that almost no musical noise is generated even with high noise reduction, which is one of the most desirable properties of single-channel nonlinear noise reduction methods. Following this finding, Miyazaki et al. have derived the optimal parameters satisfying the no-musical-noise-generation condition by analysis based on higher-order statistics [18]. We have defined this method as musical-noise-free speech enhancement, where no musical noise is generated even for a high signal-to-noise ratio (SNR) in iterative SS. In this chapter, firstly, we explain the overview of musical-noise-free iterative SS.

In conventional iterative SS, however, it is assumed that the input noise signal is stationary, meaning that we can estimate the expectation of noise power spectral density from a time-frequency period of a signal that contains only noise. In contrast, under real-world acoustical environments, such as a nonstationary noise field, although it is necessary to dynamically estimate noise, this is very difficult. Therefore, in this chapter, secondly, we describe an advanced iterative signal extraction method using a microphone array that can be applied to nonstationary noise [19]. This method consists of iterative blind dynamic noise estimation by independent component analysis (ICA) [20,21,22,23] and musical-noise-free speech extraction by modified iterative SS, where multiple iterative SS is applied to each channel while maintaining the multichannel property reused for ICA.

Thirdly, in relation to the above-mentioned method, we discuss the justification of applying ICA to signals nonlinearly distorted by SS. We theoretically clarify that the degradation in ICA-based noise estimation obeys an amplitude variation in room transfer functions between the target user and microphones. Next, to reduce speech distortion, we introduce a channel selection strategy into ICA, where we automatically choose less varied inputs to maintain the high accuracy of noise estimation. Furthermore, we introduce a time-variant noise power spectral density (PSD) estimator [24] instead of ICA to improve the noise estimation accuracy. From objective and subjective evaluations, it is revealed that the presented method outperforms various types of the conventional methods.

Note that there exist many investigations for musical noise assessment using higher-order statistics [25,26,27,28,29] and the study on musical-noise-free speech enhancement was carried out for several methods except for iterative SS, namely, iterative WF [30], the iterative MMSE-STSA estimator [31] and the iterative generalized MMSE-STSA estimator [32]. In this chapter, however, only SS-based method is dealt with because of ease in the mathematical derivations and readers’ understanding. Also, the theoretical analysis and results in ICA-based noise estimation are valid for other independent linear factor analysis algorithms, e.g., independent vector analysis [33,34,35] and independent low-rank matrix analysis [36,37,38,39]. However, we focus our attention on only ICA in this chapter owing to its simpleness.

13.2 Single-Channel Speech Enhancement with Musical-Noise-Free Properties

13.2.1 Conventional Non-iterative Spectral Subtraction

We apply a short-time discrete Fourier transform (DFT) to the observed signal, which is a mixture of target speech and noise, to obtain the time-frequency signal. We formulate conventional non-iterative SS [1] in the time-frequency domain as follows:

$$\begin{aligned} Y(f,\tau ) = \left\{ \begin{array}{ll} \sqrt{ |X(f,\tau )|^{2}-\beta \mathrm{E} [ |{N}|^{2} ] } \exp ({j{\arg }(X(f,\tau ))}) \\ \,(\mathrm{if}\,\, |X(f,\tau )|^{2}>\beta \mathrm{E} [ |{N}|^{2} ]), \\ \eta X(f,\tau ) \quad (\mathrm{otherwise}), \end{array} \right. \end{aligned}$$
(13.1)

where \({Y}(f,\tau )\) is the enhanced target speech signal, \({X}(f,\tau )\) is the observed signal, f denotes the frequency subband, \(\tau \) is the frame index, \(\beta \) is the oversubtraction parameter, and \(\eta \) is the flooring parameter. Here, \(\mathrm{E}[|N|^2]\) is the expectation of the random variable \(|N|^2\) corresponding to the noise power spectra. In practice, we can approximate \(\mathrm{E}[|N|^2]\) by averaging the observed noise power spectra \(|N(f,\tau )|^2\) in the first K-sample frames, where we assume the absence of speech in this period and noise stationarity. However, this often requires high-accuracy voice activity detection. In addition, many methods for dynamic estimation of the expectation of the noise PSD have been proposed [4], but always suffered from difficulty in rapidly changing nonstationary noise.

Generally speaking, conventional spectral subtraction suffers from the inherent problem of musical noise generation. For example, a large oversubtraction parameter affords a large noise reduction but considerable musical noise is also generated. To reduce the amount of musical noise generated, we often increase the flooring parameter, but this decreases noise reduction; thus, there exists a trade-off between noise reduction and musical noise generation.

13.2.2 Iterative Spectral Subtraction

In an attempt to achieve high-quality noise reduction with low musical noise, an improved method based on iterative SS was proposed in previous studies [14,15,16]. This method is performed through signal processing, in which the following weak SS processes are recursively applied to the noise signal (see Fig. 13.1). (I) The average power spectrum of the input noise is estimated. (II) The estimated noise prototype is then subtracted from the input with the parameters specifically set for weak subtraction, e.g., a large flooring parameter \(\eta \) and a small subtraction parameter \(\beta \). (III) We then return to step (I) and substitute the resultant output (partially noise reduced signal) for the input signal.

Fig. 13.1
figure 1

Block diagram of iterative SS

Full size image

13.2.3 Modeling of Input Signal

In this chapter, we assume that the input signal X in the power spectral domain is modeled using the gamma distribution as

$$\begin{aligned} P(x) = \frac{x^{\alpha -1}}{\varGamma (\alpha )\theta ^\alpha }\exp (-x/\theta ), \end{aligned}$$
(13.2)

where \(x \ge 0,~\alpha > 0\), and \(\theta >0\). Here, \(\alpha \) is the shape parameter, \(\theta \) is the scale parameter, and \(\varGamma (\alpha )\) is the gamma function, defined as

$$\begin{aligned} \varGamma (\alpha ) = \int _0^\infty t^{\alpha -1}\exp (-t)dt. \end{aligned}$$
(13.3)

If the input signal is Gaussian noise, its complex-valued DFT coefficients also have the Gaussian distributions in the real and imaginary parts. Therefore, the p.d.f. of its power spectra obeys the chi-square distribution with two degrees of freedom, which corresponds to the gamma distribution with \(\alpha \!=\!1\). Also, if the input signal is super-Gaussian noise, the p.d.f. of its power spectra obeys the gamma distribution with \(\alpha \!<\!1\). We make assumption here that \(\theta \) is assumed to be the deterministically known noise PSD and estimation artifacts of the noise PSD are not taken into account in this chapter. Also, the estimation of \(\alpha \) for real-world (short-term) data is explained in, e.g., Ref. [40].

Fig. 13.2
figure 2

Example of generation of tonal component after signal processing, where input signal is speech with white Gaussian noise and output is processed signal by SS

Full size image

13.2.4 Metric of Musical Noise Generation: Kurtosis Ratio

We speculate that the amount of musical noise is highly correlated with the number of isolated power spectral components and their level of isolation (see Fig. 13.2). In this chapter, we call these isolated components tonal components. Since such tonal components have relatively high power, they are strongly related to the weight of the tail of their probability density function (p.d.f.). Therefore, quantifying the tail of the p.d.f. makes it possible to measure the number of tonal components. Thus, we adopt kurtosis, one of the most commonly used higher-order statistics, to evaluate the percentage of tonal components among all components. A larger kurtosis value indicates a signal with a heavy tail, meaning that the signal has many tonal components. Kurtosis is defined as

$$\begin{aligned} \mathrm{kurt}=\frac{\mu _{4}}{\mu _{2}^{2}}, \end{aligned}$$
(13.4)

where “\(\mathrm{kurt}\)” is the kurtosis and \(\mu _m\) is the mth-order moment, given by

$$\begin{aligned} \mu _{m}=\int _{0}^{\infty }x^{m}P(x)dx, \end{aligned}$$
(13.5)

where P(x) is the p.d.f. of the random variable X. Note that \(\mu _m\) is not a central moment but a raw moment. Thus, (13.4) is not kurtosis in the mathematically strict definition but a modified version; however, we still refer to (13.4) as kurtosis in this chapter.

In this study, we apply such a kurtosis-based analysis to a time-frequency period of subject signals for the assessment of musical noise. Thus, this analysis should be conducted during, for example, periods of silence in speech when we evaluate the degree of musical noise arising in remaining noise. This is because we aim to quantify the tonal components arising in the noise-only part, which is the main cause of musical noise perception, and not in the target-speech-dominant part.

Although kurtosis can be used to measure the number of tonal components, note that the kurtosis itself is not sufficient to measure the amount of musical noise. This is obvious since the kurtosis of some unprocessed noise signals, such as an interfering speech signal, is also high, but we do not recognize speech as musical noise. Hence, we turn our attention to the change in kurtosis between before and after signal processing to identify only the musical-noise components. Thus, we adopt the kurtosis ratio as a measure to assess musical noise [11,12,13]. This measure is defined as

$$\begin{aligned} \text {kurtosis ratio}=\frac{\mathrm{kurt}_{\mathrm{proc}}}{\mathrm{kurt}_{\mathrm{org}}}, \end{aligned}$$
(13.6)

where \(\mathrm{kurt}_{\text {proc}}\) is the kurtosis of the processed signal and \(\mathrm{kurt}_{\text {org}}\) is the kurtosis of the original (unprocessed) signal. This measure increases as the amount of generated musical noise increases. In Ref. [11], it was reported that the kurtosis ratio is strongly correlated with the human perception of musical noise. Figure 13.3 shows an example of the relation between the kurtsis ratio (in log scale) and a human-perceptual score of degree of musical noise generation, where we can confirm the strong correlation.

Fig. 13.3
figure 3

Relation between kurtsis ratio (in log scale) and human-perceptual score of degree of musical noise generation [11]

Full size image

13.2.5 Musical Noise Generation in Non-iterative Spectral Subtraction

In conventional non-iterative spectral subtraction, the long-term-averaged power spectrum of a noise signal is utilized as the estimated noise power spectrum. Then, the estimated noise power spectrum multiplied by the oversubtraction parameter \(\beta \) is subtracted from the observed power spectrum. When a gamma distribution is used to model the noise signal, its mean is \(\alpha _\mathrm{n} \theta _\mathrm{n}\), where \(\alpha _\mathrm{n}\) and \(\theta _\mathrm{n}\) are the shape and scale parameters of noise, respectively (the subscript “\(\mathrm n\)” indicates that the parameters belong to noise). Thus, the amount of subtraction is \(\beta \alpha _\mathrm{n} \theta _\mathrm{n}\). The subtraction of the estimated noise power spectrum in each frequency band can be considered as a shift of the p.d.f. in the zero-power direction, given by

$$\begin{aligned} \frac{1}{\theta _\mathrm{n}^{\alpha _\mathrm{n}} \varGamma (\alpha _\mathrm{n})} (z+\beta \alpha _\mathrm{n} \theta _\mathrm{n})^{\alpha _\mathrm{n}-1} \exp \left\{ -\frac{z+\beta \alpha _\mathrm{n} \theta _\mathrm{n}}{\theta _\mathrm{n}}\right\} , \end{aligned}$$
(13.7)

where z is the random variable of the p.d.f. after spectral subtraction.

As a result, negative-power components with nonzero probability arise. To avoid this, such negative components are replaced by observations that are multiplied by a positive value \(\eta \) (flooring parameter). This means that the region corresponding to the probability of the negative components, which forms a section cut from the original gamma distribution, is compressed by the effect of the flooring, resulting in

$$\begin{aligned} \frac{1}{(\eta ^2\theta _\mathrm{n})^{\alpha _\mathrm{n}} \varGamma (\alpha _\mathrm{n})} z^{\alpha _\mathrm{n} -1}\exp \left\{ -\frac{z}{\eta ^2\theta _\mathrm{n}}\right\} . \end{aligned}$$
(13.8)

Note that the flooring parameter \(\eta \) is squared in the p.d.f. because the multiplication of \(\eta \) is conducted in the amplitude spectrum domain (see the second branch in (13.1)) but we now consider its effect in the power spectrum domain.

Finally, the floored components are superimposed on the laterally shifted p.d.f. Thus, the resultant p.d.f. after spectral subtraction, \(P_{\mathrm {SS}}(z)\), can be written as

$$\begin{aligned}&P_{\mathrm {SS}}(z)= \nonumber \\&\left\{ \begin{array}{ll} \frac{1}{\theta _\mathrm{n}^{\alpha _\mathrm{n}}\varGamma (\alpha _\mathrm{n})} (z+\beta \alpha _\mathrm{n} \theta _\mathrm{n})^{\alpha _\mathrm{n}-1} \exp \left\{ -\frac{z+\beta \alpha _\mathrm{n}\theta _\mathrm{n}}{\theta _\mathrm{n}}\right\} \\ +\frac{1}{(\eta ^2\theta _\mathrm{n})^{\alpha _\mathrm{n}}\varGamma (\alpha _\mathrm{n})} z^{\alpha _\mathrm{n}-1}\exp \left\{ -\frac{z}{\eta ^2\theta _\mathrm{n}}\right\} &{} (0 \le z < \beta \alpha _\mathrm{n}\eta ^2 \theta _\mathrm{n}), \\ \frac{1}{\theta _\mathrm{n}^{\alpha _\mathrm{n}}\varGamma (\alpha _\mathrm{n})} (z+\beta \alpha _\mathrm{n}\theta _\mathrm{n})^{\alpha _\mathrm{n}-1} \exp \left\{ -\frac{z+\beta \alpha _\mathrm{n}\theta _\mathrm{n}}{\theta _\mathrm{n}}\right\} &{} (\beta \alpha _\mathrm{n}\eta ^2 \theta _\mathrm{n} \le z), \end{array} \right. \end{aligned}$$
(13.9)

To characterize non-iterative spectral subtraction, the mth-order moment of z is required. For \(P_{\mathrm {SS}}(z)\), the mth-order moment is given by

$$\begin{aligned} \mu _m^\mathrm{SS} =&\int _0^{\infty } z^m\cdot P_{\mathrm {SS}}(z)d{z} \nonumber \\ =&\int _{0}^{\infty } z^m\frac{1}{\theta _\mathrm{n}^{\alpha _\mathrm{n}}\varGamma (\alpha _\mathrm{n})} (z+\beta \alpha _\mathrm{n} \theta _\mathrm{n})^{\alpha _\mathrm{n}-1} \exp \left\{ -\frac{z+\beta \alpha _\mathrm{n} \theta _\mathrm{n}}{\theta _\mathrm{n}}\right\} d{z} \nonumber \\&+ \int _0^{\beta \alpha _\mathrm{n} \eta ^2 \theta _\mathrm{n}} z^m \frac{1}{(\eta ^2\theta _\mathrm{n})^{\alpha _\mathrm{n}}\varGamma (\alpha _\mathrm{n})}z^{\alpha _\mathrm{n}-1} \exp \left\{ -\frac{z}{\eta ^2\theta _\mathrm{n}}\right\} d{z}, \end{aligned}$$
(13.10)

where z is the random variable of the p.d.f. after spectral subtraction. We now expand the first term of the right-hand side of (13.10). Here, let \(t=(z+\beta \alpha _\mathrm{n}\theta _\mathrm{n})/\theta _\mathrm{n}\), then \(\theta _\mathrm{n} dt=d{z}\) and \(z=\theta _\mathrm{n} (t-\beta \alpha _\mathrm{n})\). Consequently,

$$\begin{aligned}&\int _{0}^{\infty } z^m \frac{1}{\theta _\mathrm{n}^{\alpha _\mathrm{n}}\varGamma (\alpha _\mathrm{n})} (z+\beta \alpha _\mathrm{n}\theta _\mathrm{n})^{\alpha _\mathrm{n}-1} \exp \left\{ -\frac{z+\beta \alpha _\mathrm{n}\theta _\mathrm{n}}{\theta _\mathrm{n}}\right\} d{z}\nonumber \\&= \int _{\beta \alpha _\mathrm{n}}^{\infty } \theta _\mathrm{n}^m (t-\beta \alpha _\mathrm{n})^m \frac{1}{\theta _\mathrm{n}^{\alpha _\mathrm{n}}\varGamma (\alpha _\mathrm{n})} (\theta _\mathrm{n} t)^{\alpha _\mathrm{n}-1}\exp \{-t\}\theta _\mathrm{n} dt\nonumber \\&= \frac{\theta _\mathrm{n}^m}{\varGamma (\alpha _\mathrm{n})} \int _{\beta \alpha _\mathrm{n}}^{\infty } \sum _{l=0}^{m} (-\beta \alpha _\mathrm{n})^l \frac{\varGamma (m+1)}{\varGamma (l+1)\varGamma (m-l+1)} t^{m-l} t^{\alpha _\mathrm{n}-1}\exp \{-t\} dt\nonumber \\&= \frac{\theta _\mathrm{n}^m}{\varGamma (\alpha _\mathrm{n})} \sum _{l=0}^{m} (-\beta \alpha _\mathrm{n})^l \frac{\varGamma (m+1)}{\varGamma (l+1)\varGamma (m-l+1)} \varGamma (\alpha _\mathrm{n}+m-l,\beta \alpha _\mathrm{n}), \end{aligned}$$
(13.11)

where we use the binomial theorem given by

$$\begin{aligned} (t+a)^m = \sum _{l=0}^{m} a^l \frac{\varGamma (m+1)}{\varGamma (l+1)\varGamma (m-l+1)} t^{m-l}, \end{aligned}$$
(13.12)

and \(\varGamma (a,b)\) is the upper incomplete gamma function defined as

$$\begin{aligned} \varGamma (a,b) = \int _b^{\infty } t^{a-1}\exp \{-t\} dt. \end{aligned}$$
(13.13)

Next we consider the second term of the right-hand side of (13.10). Here, let \(t=z/(\eta ^2\theta _\mathrm{n})\), then \(\eta ^2\theta _\mathrm{n} dt=d{z}\). Thus,

$$\begin{aligned}&\int _0^{\beta \alpha _\mathrm{n} \eta ^2 \theta _\mathrm{n}} z^m \frac{1}{(\eta ^2\theta _\mathrm{n})^{\alpha _\mathrm{n}}\varGamma (\alpha _\mathrm{n})}z^{\alpha _\mathrm{n}-1} \exp \left\{ -\frac{z}{\eta ^2\theta _\mathrm{n}}\right\} d{z}\nonumber \\&= \int _0^{\beta \alpha _\mathrm{n}} (\eta ^2\theta _\mathrm{n} t)^m \frac{1}{(\eta ^2\theta _\mathrm{n})^{\alpha _\mathrm{n}}\varGamma (\alpha _\mathrm{n})} (\eta ^2\theta _\mathrm{n} t)^{\alpha _\mathrm{n}-1}\exp \left\{ -t\right\} \eta ^2\theta _\mathrm{n} dt\nonumber \\&= \frac{\eta ^{2m}\theta _\mathrm{n}^m}{\varGamma (\alpha _\mathrm{n})} \int _0^{\beta \alpha _\mathrm{n}} t^{\alpha _\mathrm{n}-1+m}\exp \left\{ -t\right\} dt \nonumber \\&=\frac{\eta ^{2m}\theta _\mathrm{n}^m}{\varGamma (\alpha _\mathrm{n})} \gamma (\alpha _\mathrm{n} +m,\beta \alpha _\mathrm{n}), \end{aligned}$$
(13.14)

where \(\gamma (a,b)\) is the lower incomplete gamma function defined as

$$\begin{aligned} \gamma (a,b) = \int _0^{b} t^{a-1}\exp \{-t\} dt. \end{aligned}$$
(13.15)

As a result, the mth-order moment after spectral subtraction, \(\mu _m^\mathrm{SS}\), is a composite of (13.11) and (13.14), and is given by [17]

$$\begin{aligned} \mu _m^\mathrm{SS} = \theta _\mathrm{n}^m {\mathscr {M}}(\alpha _\mathrm{n},\beta ,\eta ,m), \end{aligned}$$
(13.16)

where

$$\begin{aligned} {{\mathscr {M}}(\alpha _\mathrm{n},\beta ,\eta ,m)} =&{\mathscr {S}}(\alpha _\mathrm{n},\beta ,\eta ) + \eta ^{2m} {\mathscr {F}}(\alpha _\mathrm{n},\beta ,\eta ),\end{aligned}$$
(13.17)
$$\begin{aligned} {\mathscr {S}}(\alpha _\mathrm{n},\beta ,m)=&\sum _{l=0}^{m} (-\beta \alpha _\mathrm{n})^l \frac{\varGamma (m\!+\!1)\varGamma (\alpha _\mathrm{n}\!+\!m\!-\!l,\beta \alpha _\mathrm{n})}{\varGamma (\alpha _\mathrm{n})\varGamma (l\!+\!1)\varGamma (m\!-\!l\!+\!1)}, \end{aligned}$$
(13.18)
$$\begin{aligned} {\mathscr {F}}(\alpha _\mathrm{n},\beta ,m)=&\frac{\gamma (\alpha _\mathrm{n}\!+\!m,\beta \alpha _\mathrm{n})}{\varGamma (\alpha _\mathrm{n})}. \end{aligned}$$
(13.19)

From (13.4), (13.16), and (13.17), the kurtosis after SS can be expressed as

$$\begin{aligned} \mathrm{kurt}= \frac{{{\mathscr {M}}(\alpha _\mathrm{n},\beta ,\eta ,4)}}{{\mathscr {M}}^2(\alpha _\mathrm{n},\beta ,\eta ,2)} . \end{aligned}$$
(13.20)

Using (13.6) and (13.20), we also express the kurtosis ratio as

$$\begin{aligned} \mathrm{kurtosis~ratio}=&\frac{{\mathscr {M}}(\alpha _\mathrm{n},\beta ,\eta ,4)/{\mathscr {M}}^2(\alpha _\mathrm{n},\beta ,\eta ,2)}{{\mathscr {M}}(\alpha _\mathrm{n},0,0,4)/{\mathscr {M}}^2(\alpha _\mathrm{n},0,0,2)}. \end{aligned}$$
(13.21)

Also, as a measure of the noise reduction performance, the noise reduction rate (NRR) [41], the output SNR minus the input SNR in dB, can be given in terms of a 1st-order moment as [17]

$$\begin{aligned} \mathrm{NRR} =10\log _{10} \frac{{\alpha _\mathrm{n}}}{ { {\mathscr {M}}(\alpha _\mathrm{n},\beta ,\eta ,1)}}. \end{aligned}$$
(13.22)

13.2.6 Musical-Noise-Free Speech Enhancement

In [18], Miyazaki et al. proposed musical-noise-free noise reduction, where no musical noise is generated even for a high SNR in iterative SS. In the study, some of the authors discovered an interesting phenomenon that the kurtosis ratio sometimes does not change even after SS via mathematical analysis based on (13.21) [17]. This indicates that the kurtosis ratio can be maintained at unity even after iteratively applying SS to improve the NRR, and thus no musical noise is generated owing to the domino-toppling phenomenon. Following this finding, the authors derived the optimal parameters satisfying the musical-noise-free condition [18] by finding a fixed-point status in the kurtosis ratio, i.e., by solving

$$\begin{aligned} \frac{{\mathscr {M}}(\alpha _\mathrm{n},0,0,4)}{ {\mathscr {M}}^2(\alpha _\mathrm{n},0,0,2)} =\frac{{\mathscr {M}}(\alpha _\mathrm{n},\beta ,\eta ,4)}{{\mathscr {M}}^2(\alpha _\mathrm{n},\beta ,\eta ,2)}. \end{aligned}$$
(13.23)

The inductive result is that the kurtosis ratio never changes even at a large number of (ideally “infinite”) iterations. In this situation, sufficient noise reduction can be gained if the NRR improvement in each iteration is even small but positive. This corresponds to musical-noise-free noise reduction. In summary, we can formulate a new theorem on musical-noise-free conditions as follows.

(I) Fixed-point kurtosis condition: The kurtosis should be equal before and after spectral subtraction in each iteration. This corresponds to a fixed point for the 2nd- and 4th-order moments.

(II) NRR growth condition: The amount of noise reduction should be larger than 0 dB in each iteration, relating to a change in the 1st-order moment.

Although the parameters to be optimized are \(\eta \) and \(\beta \), we hereafter derive the optimal \(\eta \) given a fixed \(\beta \) for ease of closed-form analysis. First, we change (13.20) for

$$\begin{aligned} \mathrm{kurt}(\alpha _\mathrm{n},\beta ,\eta ) =\frac{{\mathscr {S}} (\alpha _\mathrm{n},\beta ,4) +\eta ^8 {\mathscr {F}} (\alpha _\mathrm{n},\beta ,4)}{\left( {\mathscr {S}} (\alpha _\mathrm{n},\beta ,2) +\eta ^4 {\mathscr {F}} (\alpha _\mathrm{n},\beta ,2)\right) ^2}. \end{aligned}$$
(13.24)

Next, the fixed-point kurtosis condition corresponds to the kurtosis being equal before and after spectral subtraction, thus

$$\begin{aligned} \frac{{\mathscr {S}} (\alpha _\mathrm{n},\beta ,4) +\eta ^8 {\mathscr {F}} (\alpha _\mathrm{n},\beta ,4)}{\left( {\mathscr {S}} (\alpha _\mathrm{n},\beta ,2) +\eta ^4 {\mathscr {F}} (\alpha _\mathrm{n},\beta ,2)\right) ^2} =\frac{(\alpha _\mathrm{n}+3)(\alpha _\mathrm{n}+2)}{(\alpha _\mathrm{n}+1)\alpha _\mathrm{n}}. \end{aligned}$$
(13.25)

Let \({\mathscr {H}}=\eta ^4\), and (13.25) yields the following quadratic equation in \({\mathscr {H}}\).

$$\begin{aligned}&\left( {\mathscr {F}}(\alpha _\mathrm{n},\beta ,4){(\alpha _\mathrm{n}\!+\!1)\alpha _\mathrm{n}}\!-\!{\mathscr {F}}^2(\alpha _\mathrm{n},\beta ,2){(\alpha _\mathrm{n}\!+\!3)(\alpha _\mathrm{n}\!+\!2)}\right) {\mathscr {H}}^2\nonumber \\ -&2{\mathscr {S}}(\alpha _\mathrm{n},\beta ,2){\mathscr {F}}(\alpha _\mathrm{n},\beta ,2){(\alpha _\mathrm{n}\!+\!3)(\alpha _\mathrm{n}\!+\!2)}{\mathscr {H}}\nonumber \\ +&{\mathscr {S}}(\alpha _\mathrm{n},\beta ,4){(\alpha _\mathrm{n}\!+\!1)\alpha _\mathrm{n}}\!-\!{\mathscr {S}}^2(\alpha _\mathrm{n},\beta ,2){(\alpha _\mathrm{n}\!+\!3)(\alpha _\mathrm{n}\!+\!2)}\!=\!0. \end{aligned}$$
(13.26)

Thus, we can derive a closed-form estimate of \({\mathscr {H}}\) from the given noise shape parameter \(\alpha _\mathrm{n}\) and oversubtraction parameter \(\beta \) as

$$\begin{aligned} {\mathscr {H}}=&\{{{\mathscr {F}}(\alpha _\mathrm{n} ,\beta ,4){(\alpha _\mathrm{n} \!+\!1)\alpha _\mathrm{n} }\!-\!{\mathscr {F}}^2(\alpha _\mathrm{n} ,\beta ,2){(\alpha _\mathrm{n} \!+\!3)(\alpha _\mathrm{n} \!+\!2)}}\}^{-1}\nonumber \\&\Biggl [{\mathscr {S}}(\alpha _\mathrm{n} ,\beta ,2){\mathscr {F}}(\alpha _\mathrm{n} ,\beta ,2){(\alpha _\mathrm{n} \!+\!3)(\alpha _\mathrm{n} \!+\!2)} \nonumber \\&\pm \Bigl [ \left\{ {\mathscr {S}}(\alpha _\mathrm{n} ,\beta ,2){\mathscr {F}}(\alpha _\mathrm{n} ,\beta ,2){(\alpha _\mathrm{n} \!+\!3)(\alpha _\mathrm{n} \!+\!2)}\right\} ^2 \nonumber \\&-\left\{ {\mathscr {F}}(\alpha _\mathrm{n} ,\beta ,4){(\alpha _\mathrm{n} \!+\!1)\alpha _\mathrm{n} }\!-\!{\mathscr {F}}^2(\alpha _\mathrm{n} ,\beta ,2){(\alpha _\mathrm{n} \!+\!3)(\alpha _\mathrm{n} \!+\!2)} \right\} \nonumber \\&\left\{ {\mathscr {S}}(\alpha _\mathrm{n} ,\beta ,4){(\alpha _\mathrm{n} \!+\!1)\alpha _\mathrm{n} }\!-\!{\mathscr {S}}^2(\alpha _\mathrm{n} ,\beta ,2){(\alpha _\mathrm{n} \!+\!3)(\alpha _\mathrm{n} \!+\!2)}\right\} \Bigl ]^{\frac{1}{2}} \Biggl ]. \end{aligned}$$
(13.27)

Finally, \(\eta ={\mathscr {H}}^{1/4}\) is the resultant flooring parameter that satisfies the fixed-point kurtosis condition.

From (13.22), the NRR growth condition is expressed as

$$\begin{aligned} \mathrm{NRR} \!=\! 10\log _{10} \frac{\alpha _\mathrm{n}}{{\mathscr {S}}(\alpha _\mathrm{n},\beta ,1) +\eta ^2 {\mathscr {F}}(\alpha _\mathrm{n},\beta ,1)} \!>\!0. \end{aligned}$$
(13.28)

Here, since \(\eta >0\), we can solve the inequality as

$$\begin{aligned} 0<\eta <\sqrt{ \frac{{\alpha _\mathrm{n}-{\mathscr {S}}(\alpha _\mathrm{n},\beta ,1)}}{{\mathscr {F}}(\alpha _\mathrm{n},\beta ,1)}}. \end{aligned}$$
(13.29)

In summary, we can choose the parameters simultaneously satisfying the fixed kurtosis point condition and NRR growth condition using (13.27) and (13.29). Figure 13.4 shows an example of the kurtosis ratio in optimized iterative SS, where Gaussian noise is assumed. We can confirm the flat trace of the kurtosis, indicating no musical noise generation.

Fig. 13.4
figure 4

Relation between NRR and kurtosis ratio obtained from theoretical analysis for case of Gaussian noise

Full size image

13.3 Extension to Multichannel Blind Signal Processing

13.3.1 Blind Spatial Subtraction Array

In the previous section, we assumed that the input noise signal is stationary, meaning that we can estimate the expectation of a noise signal from a time-frequency period of a signal that contains only noise, i.e., speech absence. However, in actual environments, such as a nonstationary noise field, it is necessary to dynamically estimate the noise PSD.

To solve this problem, Takahashi et al. previously proposed blind spatial subtraction array (BSSA) [42], which involves accurate noise estimation by ICA followed by a speech extraction procedure based on SS (see Fig. 13.5). BSSA improves the noise reduction performance, particularly in the presence of both diffuse and nonstationary noises; thus, almost all the environmental noise can be dealt with. However, BSSA always suffers from musical noise owing to SS. In addition, the output signal of BSSA degenerates to a monaural (not multichannel) signal, meaning that ICA cannot be reapplied; thus, we cannot iteratively estimate the noise power spectra. Therefore, it is impossible to directly apply iterative SS to the conventional BSSA.

Fig. 13.5
figure 5

Block diagram of BSSA [42]

Full size image

13.3.2 Iterative Blind Spatial Subtraction Array

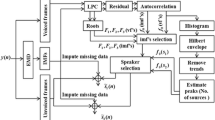
In this section, we introduce a multi-iterative blind signal extraction method integrating iterative blind noise estimation by ICA and iterative noise reduction by SS. As mentioned previously, the conventional BSSA cannot iteratively and accurately estimate noise by ICA because the conventional BSSA performs a delay and sum (DS) operation before SS. To solve this problem, Takahashi et al. have proposed an improved BSSA structure that performs multiple independent SS in each channel before DS; we call this structure channelwise SS [43,44,45]. Using this structure, we can equalize the number of channels of the observed signal to that of the signals after channelwise SS. Therefore, we can iteratively apply noise estimation by ICA and speech extraction by SS (see Fig. 13.6). Also, the advantage of the structure is that ICA has the possibility of adaptively estimating the distorted wavefront of a speech signal to some extent even after SS, because ICA is a blind signal identification method that does not require knowledge of the target signal direction. Details of this issue will be discussed in Sect. 13.3.3. Hereafter, we refer to this type of BSSA as iterative BSSA.

Fig. 13.6
figure 6

Block diagram of iterative BSSA [19]

Full size image

We conduct iterative BSSA in the following manner, where the superscript [i] represents the value in the ith iteration of SS (initially \(i=0\)).

(I):

The observed signal vector of the K-channel array in the time-frequency domain, \(\mathbf {X}^{[0]}(f,\tau )\), is given by

$$\begin{aligned} \mathbf {X}^{[0]}(f,\tau )=\mathbf {H}(f)S(f,\tau )+\mathbf {N}(f,\tau ), \end{aligned}$$
(13.30)

where \(\mathbf {H}(f)=[H_1(f),H_2(f)\ldots , H_K(f)]^\mathrm{T}\) is a column vector of the transfer functions from the target signal position to each microphone, \(S(f,\tau )\) is the target speech signal, and \(\mathbf {N}(f,\tau )\) is a column vector of the additive noise.

(II):

Next, we perform signal separation using ICA as [20]

$$\begin{aligned} \mathbf {O}^{[i]}(f,\tau ) =&\mathbf {W}_{\mathrm{ICA}}^{[i]}(f) \mathbf {X}^{[i]}(f,\tau ), \end{aligned}$$
(13.31)
$$\begin{aligned} \mathbf {W}^{[i][p+1]}_{\mathrm{ICA}}(f) =&\mu [\mathbf {I}-\langle \mathbf {\varphi }(\mathbf {O}^{[i]}(f,\tau )) (\mathbf {O}^{[i]}(f,\tau ))^{\mathrm H} \rangle _\tau ] \nonumber \\&\cdot \mathbf {W}_{\mathrm{ICA}}^{[i][p]}(f) +\mathbf {W}_{\mathrm{ICA}}^{[i][p]}(f), \end{aligned}$$
(13.32)

where \(\mathbf {W}^{[i][p]}_\mathrm{ICA}(f)\) is a demixing matrix, \(\mu \) is the step-size parameter, [p] is used to express the value of the pth step in the ICA iterations, \(\mathbf {I}\) is the identity matrix, \(\langle \cdot \rangle _{\tau }\) denotes a time-averaging operator, and \(\mathbf {\varphi }(\cdot )\) is an appropriate nonlinear vector function. Then, we construct a noise-only vector,

$$\begin{aligned} \mathbf {O}^{[i]}_\mathrm{noise}(f,\tau ) =&[O_{1}^{[i]}(f,\tau ), \ldots , O_{U-1}^{[i]},0, \nonumber \\&O_{U+1}^{[i]}(f,\tau ),\ldots , O_{K}^{[i]}(f,\tau )]^\mathrm{T}, \end{aligned}$$
(13.33)

where U is the signal number for speech, and we apply the projection back operation to remove the ambiguity of the amplitude and construct the estimated noise signal, \(\mathbf {Z}^{[i]}(f,\tau )\), as

$$\begin{aligned} \mathbf {Z}^{[i]}(f,\tau ) = \mathbf {W}^{[i]}_{\mathrm{ICA}}(f)^{-1}\mathbf {O}_\mathrm{noise}^{[i]}(f,\tau ). \end{aligned}$$
(13.34)
(III):

Next, we perform SS independently in each input channel and derive the multiple target-speech-enhanced signals. This procedure can be given by

$$\begin{aligned}&X_{k}^{[i+1]}(f,\tau ) = \nonumber \\&\left\{ \begin{array}{ll} \sqrt{ |X_{k}^{[i]}(f,\tau )|^{2}-\beta |Z_{k}^{[i]}(f,\tau )|^{2} } \exp ({j \arg ({X}_{k}^{[i]}(f,\tau ))}) \\ (\mathrm{if}\,\, |X_{k}^{[i]}(f,\tau )|^{2}>\beta |Z_{k}^{[i]}(f,\tau )|^{2}) , \\ \eta X_{k}^{[i]}(f,\tau ) \,\,(\mathrm{otherwise}), \end{array} \right. \end{aligned}$$
(13.35)

where \({X}_{k}^{[i+1]}(f,\tau )\) is the target-speech-enhanced signal obtained by SS at a specific channel k. Then we return to step (II) with \(\mathbf {X}^{[i+1]}(f,\tau )\). When we obtain sufficient noise reduction performance, we proceed to step (IV).

(IV):

Finally, we obtain the resultant target-speech-enhanced signal by applying DS to \(\mathbf {X}^{[*]}(f,\tau )\), where \(*\) is the number of iterations after which sufficient noise reduction performance is obtained. This procedure can be expressed by

$$\begin{aligned} Y(f,\tau )&= \mathbf {W}_\mathrm{DS}^\mathrm{T}(f)\mathbf {X}^{[*]}(f,\tau ), \end{aligned}$$
(13.36)
$$\begin{aligned} \mathbf {W}_\mathrm{DS}(f)&= [W_1^\mathrm{(DS)}(f),\ldots , W_K^\mathrm{(DS)}(f)], \end{aligned}$$
(13.37)
$$\begin{aligned} W_k^\mathrm{(DS)}(f)&= \frac{1}{K} \exp (-2 \pi j (f/M) f_\mathrm{s} d_k \sin \theta _U / c), \end{aligned}$$
(13.38)
$$\begin{aligned} \theta _{U}&= \sin ^{-1} \frac{\arg \left( \frac{\left[ \mathbf {W}^{[*]}_\mathrm{ICA}(f)^{-1}\right] _{kU}}{\left[ \mathbf {W}^{[*]}_\mathrm{ICA}(f)^{-1}\right] _{k'U}} \right) }{2 \pi f_\mathrm{s} c^{-1} (d_k - d_{k'})}, \end{aligned}$$
(13.39)

where \(Y(f,\tau )\) is the final output signal of iterative BSSA, \(\mathbf {w}_\mathrm{DS}\) is the filter coefficient vector of DS, M is the DFT size, \(f_\mathrm{s}\) is the sampling frequency, \(d_k\) is the microphone position, c is the sound velocity, and \(\theta _{U}\) is the estimated direction of arrival of the target speech obtained by ICA’s demixing matrix [46]. Moreover, \([\mathbf {A}]_{lj}\) represents the entry in the lth row and jth column of \(\mathbf {A}\).

13.3.3 Accuracy of Wavefront Estimated by Independent Component Analysis After Spectral Subtraction

In this subsection, we discuss the accuracy of the estimated noise signal in each iteration of iterative BSSA. In actual environments, not only point-source noise but also non-point-source (e.g., diffuse) noise often exists. It is known that ICA is proficient in noise estimation rather than speech estimation under such a noise condition [42, 47, 48]. This is because the target speech can be regarded as a point-source signal (thus, the wavefront is static in each subband) and ICA acts as an effective blocking filter of the speech wavefront even in a time-invariant manner, resulting in good noise estimation. However, in iterative BSSA, we should address the inherent question of whether the distorted speech wavefront after nonlinear noise reduction such as SS can be blocked by ICA or not; thus, we determine whether the speech component after channelwise SS can become a point source again.

Hereafter, we quantify the degree of point-source-likeness for SS-applied speech signals. For convenience of discussion, a simple two-channel array model is assumed. First, we define the speech component in each channel after channelwise SS as

$$\begin{aligned} \hat{S}_1(f,\tau )&= H_1(f)S(f,\tau ) + \varDelta S_1(f,\tau ), \end{aligned}$$
(13.40)
$$\begin{aligned} \hat{S}_2(f,\tau )&= H_2(f)S(f,\tau ) + \varDelta S_2(f,\tau ), \end{aligned}$$
(13.41)

where \(S(f,\tau )\) is the original point-source speech signal, \(\hat{S}_k(f,\tau )\) is the speech component after channelwise SS at the kth channel, and \(\varDelta S_k(f,\tau )\) is the speech component distorted by channelwise SS. Also, we assume that \(S(f,\tau )\), \(\varDelta S_1(f,\tau )\), and \(\varDelta S_2(f,\tau )\) are uncorrelated with each other. Obviously, \(\hat{S}_1(f,\tau )\) and \(\hat{S}_2(f,\tau )\) can be regarded as being generated by a point source if \(\varDelta S_1(f,\tau )\) and \(\varDelta S_2(f,\tau )\) are zero, i.e., a valid static blocking filter can be obtained by ICA as

$$\begin{aligned}&[\mathbf {W}_\mathrm{ICA}(f)]_{11} \hat{S}_1(f,\tau ) + [\mathbf {W}_\mathrm{ICA}(f)]_{12} \hat{S}_2(f,\tau ) \nonumber \\&=([\mathbf {W}_\mathrm{ICA}(f)]_{11}H_1(f) + [\mathbf {W}_\mathrm{ICA}(f)]_{12}H_2(f))S(f,\tau ) \nonumber \\&=0, \end{aligned}$$
(13.42)

where we assume \(U=1\) and, e.g., \([\mathbf {W}_\mathrm{ICA}(f)]_{11} = H_2(f)\) and \([\mathbf {W}_\mathrm{ICA}(f)]_{12} = -H_1(f)\). However, if \(\varDelta S_1(f,\tau )\) and \(\varDelta S_2(f,\tau )\) become nonzero as a result of SS, ICA does not have a valid speech-blocking filter with a static (time-invariant) form.

Second, the cosine distance between speech power spectra \(|\hat{S}_1(f,\tau )|^2\) and \(|\hat{S}_2(f,\tau )|^2\) is introduced in each frequency subband to indicate the degree of point-source-likeness as

$$\begin{aligned} \mathrm{COS}(f)= \frac{\sum _\tau |\hat{S}_1(f,\tau )|^2|\hat{S}_2(f,\tau )|^2}{\sqrt{\sum _\tau |\hat{S}_1(f,\tau )|^4}\sqrt{\sum _\tau |\hat{S}_2(f,\tau )|^4}}. \end{aligned}$$
(13.43)

From (13.43), the cosine distance reaches its maximum value of unity if and only if \(\varDelta S_1(f,\tau ) = \varDelta S_2(f,\tau ) = 0\), regardless of the values of \(H_1(f)\) and \(H_2(f)\), meaning that the SS-applied speech signals \(\hat{S}_1(f,\tau )\) and \(\hat{S}_2(f,\tau )\) can be assumed to be produced by the point source. The value of \(\mathrm{COS}(f)\) decreases with increasing magnitudes of \(\varDelta S_1(f,\tau )\) and \(\varDelta S_2(f,\tau )\) as well as with increasing difference between \(H_1(f)\) and \(H_2(f)\); this indicates the non-point-source state.

Third, we evaluate the degree of point-source-likeness in each iteration of iterative BSSA by using \(\mathrm{COS}(f)\). We statistically estimate the distorted speech component of the enhanced signal in each iteration. Here, we assume that the original speech power spectrum \(|S(f,\tau )|^2\) obeys a gamma distribution with a shape parameter of 0.1 (this is a typical value for speech [49,50,51,52,53,54]) as

$$\begin{aligned} |S(f,\tau )|^2 \sim \frac{x^{-0.9}}{\varGamma (0.1)\theta _\mathrm{s}^{0.1}}\exp (-x/\theta _\mathrm{s}), \end{aligned}$$
(13.44)

where \(\theta _\mathrm{s}\) is the speech scale parameter. Regarding the amount of noise to be subtracted, the 1st-order moment of the noise power spectra is equal to \(\theta _\mathrm{n}\alpha _\mathrm{n}\) when the number of iterations, i, equals zero. Also, the value of \(\alpha _\mathrm{n}\) does not change in each iteration when we use the specific parameters \(\beta \) and \(\eta \) that satisfy the musical-noise-free condition because the kurtosis ratio does not change in each iteration. If we perform SS only once, the rate of noise decrease is given by

$$\begin{aligned} {\mathscr {M}}(\alpha _\mathrm{n},\beta ,\eta ,1)/\alpha _\mathrm{n}, \end{aligned}$$
(13.45)

and thus, the amount of residual noise after the ith iteration is given by

$$\begin{aligned} \mu _1^{[i]}&= \theta _\mathrm{n}\alpha _\mathrm{n}\left\{ {\mathscr {M}}(\alpha _\mathrm{n},\beta ,\eta ,1)/ \alpha _\mathrm{n}\right\} ^{i} \nonumber \\&= \theta _\mathrm{n} {\mathscr {M}}^i(\alpha _\mathrm{n},\beta ,\eta ,1) \alpha _\mathrm{n}^{1-i}. \end{aligned}$$
(13.46)

Next, we assume that the speech and noise are disjoint, i.e., there are no overlaps in the time-frequency domain, and that speech distortion is caused by subtracting the average noise from the pure speech component. Thus, the speech component \(|\hat{S}_k^{[i+1]}(f,\tau )|^2\) at the kth channel after the ith iteration is represented by subtracting the amount of residual noise (13.46) as

$$\begin{aligned}&|{\hat{S}}_k^{[i+1]}(f,\tau )|^2= \nonumber \\&\left\{ \begin{array}{ll} |{\hat{S}_k}^{[i]}(f,\tau )|^2 - \beta {\theta }_\mathrm{n} {\mathscr {M}}^i(\alpha _\mathrm{n},\beta ,\eta ,1) \alpha _\mathrm{n}^{1-i} \\ (\mathrm{if}\,\, |{\hat{S}_k}^{[i]}(f,\tau )|^2 > \beta {\theta }_\mathrm{n} {\mathscr {M}}^i(\alpha _\mathrm{n},\beta ,\eta ,1) \alpha _\mathrm{n}^{1-i} ) , \\ \eta ^2 |{\hat{S}_k}^{[i]}(f,\tau )|^2 \,\,(\mathrm{otherwise}). \end{array} \right. \end{aligned}$$
(13.47)

Here, we define the input SNR as the average of both channel SNRs,

$$\begin{aligned} \mathrm{ISNR}(f)&= \frac{1}{2}\left( \frac{0.1|H_1(f)|^2\theta _\mathrm{s}}{\alpha _\mathrm{n}\theta _\mathrm{n}} + \frac{0.1|H_2(f)|^2\theta _\mathrm{s}}{\alpha _\mathrm{n}\theta _\mathrm{n}}\right) \nonumber \\&= \frac{0.1\theta _\mathrm{s}}{2\alpha _\mathrm{n}\theta _\mathrm{n}}(|H_1(f)|^2+|H_2(f)|^2). \end{aligned}$$
(13.48)

If we normalize the speech scale parameter \(\theta _\mathrm{s}\) to unity, from (13.48), the noise scale parameter \(\theta _\mathrm{n}\) is given by

$$\begin{aligned} \theta _\mathrm{n}&= \frac{0.1(|H_1(f)|^2+|H_2(f)|^2)}{2\alpha _\mathrm{n} \mathrm{ISNR}(f)}, \end{aligned}$$
(13.49)

and using (13.49), we can reformulate (13.47) as

$$\begin{aligned}&|{\hat{S}}_k^{[i+1]}(f,\tau )|^2= \nonumber \\&\left\{ \begin{array}{ll} |{\hat{S}_k}^{[i]}(f,\tau )|^2 \!-\! \beta \frac{0.1(|H_1(f)|^2\!+\!|H_2(f)|^2)}{2\mathrm{ISNR}(f)} {\mathscr {M}}^i(\alpha _\mathrm{n},\beta ,\eta ,1) \alpha _\mathrm{n}^{-i} \\ (\mathrm{if} \, |{\hat{S}_k}^{[i]}(f,\tau )|^2 \!>\! \beta \frac{0.1(|H_1(f)|^2\!+\!|H_2(f)|^2)}{2\mathrm{ISNR}(f)} {\mathscr {M}}^i(\alpha _\mathrm{n},\beta ,\eta ,1) \alpha _\mathrm{n}^{-i} ) , \\ \eta ^2 |{\hat{S}_k}^{[i]}(f,\tau )|^2 \,\,(\mathrm{otherwise}). \end{array} \right. \end{aligned}$$
(13.50)

Furthermore, we define the transfer function ratio (TFR) as

$$\begin{aligned} \mathrm{TFR}(f) = |{H_1(f)}/{H_2(f)}|^2, \end{aligned}$$
(13.51)

and if we normalize \(|H_1(f)|^2\) to unity in each frequency subband, \(|H_1(f)|^2+|H_2(f)|^2\) becomes \(1+1/\mathrm{TFR}(f)\). Finally, we express (13.50) in terms of the input SNR \(\mathrm{ISNR}(f)\) and the transfer function ratio \(\mathrm{TFR}(f)\) as

$$\begin{aligned}&|{\hat{S}}_k^{[i+1]}(f,\tau )|^2= \nonumber \\&\left\{ \begin{array}{ll} |{\hat{S}_k}^{[i]}(f,\tau )|^2 \!-\! \beta \frac{0.1(1\!+\!1/\mathrm{TFR}(f))}{2\mathrm{ISNR}(f)} {\mathscr {M}}^i(\alpha _\mathrm{n},\beta ,\eta ,1) \alpha _\mathrm{n}^{-i} \\ (\mathrm{if}\,\, |{\hat{S}_k}^{[i]}(f,\tau )|^2 \!>\! \beta \frac{0.1(1\!+\!1/\mathrm{TFR}(f))}{2\mathrm{ISNR}(f)} {\mathscr {M}}^i(\alpha _\mathrm{n},\beta ,\eta ,1) \alpha _\mathrm{n}^{-i} ) , \\ \eta ^2 |{\hat{S}_k}^{[i]}(f,\tau )|^2 \,\,(\mathrm{otherwise}). \end{array} \right. \end{aligned}$$
(13.52)

As can be seen, the speech component is subjected to greater subtraction and distortion as \(\mathrm{ISNR}(f)\) and/or \(\mathrm{TFR}(f)\) decrease.

Figure 13.7 shows the relation between the TFR and the corresponding value of \(\mathrm{COS}(f)\) calculated by (13.43) and (13.52). In Fig. 13.7, we plot the average of \(\mathrm{COS}(f)\) over whole frequency subbands. The noise shape parameter \(\alpha _\mathrm{n}\) is set to 0.2 with the assumption of super-Gaussian noise (this corresponds to the real noises used in Sect. 13.5), the input SNR is set to 10, 5, or 0 dB, and the noise scale parameter \(\theta _\mathrm{n}\) is uniquely determined by (13.49) and the previous parameter settings. The TFR is set from 0.4 to 1.0 (\(|h_1(f)|\) is fixed to 1.0). Note that the TFR is highly correlated to the room reverberation and the interelement spacing of the microphone array; we determined the range of the TFR by simulating a typical moderately reverberant room and the array with 2.15 cm interelement spacing used in Sect. 13.5 (see the example of the TFR in Fig. 13.8). For the internal parameters used in iterative BSSA in this simulation, \(\beta \) and \(\eta \) are 8.5 and 0.9, respectively, which satisfy the musical-noise-free condition. In addition, the smallest value on the horizontal axis is 3 dB in Fig. 13.7 because DS is still performed even when \(i=0\).

From Figs. 13.7a and b, which correspond to relatively high input SNRs, we can confirm that the degree of point-source-likeness, i.e., \(\mathrm{COS}(f)\), is almost maintained when the TFR is close to 1 even if the speech components are distorted by iterative BSSA. Also, it is worth mentioning that the degree of point-source-likeness is still above 0.9 even when the TFR is decreased to 0.4 and i is increased to 6. This means that almost 90% of the speech components can be regarded as a point source and thus can be blocked by ICA. In contrast, from Fig. 13.7c, which shows the case of a low input SNR, when the TFR is dropped to 0.4 and i is more than 3, the degree of point-source-likeness is lower than 0.6. Thus, less than 60% of the speech components can be regarded as a point source, and this leads to poor noise estimation.

Fig. 13.7
figure 7

Relation between number of iterations of iterative BSSA and cosine distance. Input SNR is a 10 dB, b 5 dB, and c 0 dB

Full size image
Fig. 13.8
figure 8

Typical examples of \(\mathrm{TFR}(f)\) (\(|H_1(f)/H_2(f)|^2\)) in each frequency subband

Full size image

13.4 Improvement Scheme for Poor Noise Estimation

13.4.1 Channel Selection in Independent Component Analysis

In this subsection, we introduce a channel selection strategy in ICA for achieving high accuracy of noise estimation. As mentioned previously, speech distortion is subjected to \(\mathrm{ISNR}(f)\) and \(\mathrm{TFR}(f)\), and the accuracy of noise estimation is degraded along with speech distortion. Figure 13.8 shows typical examples of the TFR. From Fig. 13.8, we can confirm that the TFRs in different combinations of microphones are not the same in each frequency subband; at a specific frequency, one microphone pair has higher \(\mathrm{TFR}(f)\) than another pair, and vice versa at another frequency. Thus, we are able to select an appropriate combination of microphones to obtain a higher TFR.

Therefore, we introduce the channel selection method into ICA in each frequency subband, where we automatically choose less varied inputs to maintain high accuracy of noise estimation. Hereafter, we describe the detail of the channel selection method. First, we calculate the average power of the observed signal \({X_k}(f,\tau )\) at the kth channel as

$$\begin{aligned} \mathrm{E}_\tau [|{X_k}(f,\tau )|^2] \!=\! \mathrm{E}_\tau [|{S}(f,\tau )|^2] |{H_k}(f)|^2 \!+\! \mathrm{E}_\tau [|{N_k}(f,\tau )|^2]. \end{aligned}$$
(13.53)

Here, \(\mathrm{E}_\tau [|{S}(f,\tau )|^2]\) is a constant, and if we assume a diffuse noise field, \(\mathrm{E}_\tau [|{N_k}(f,\tau )|^2]\) is also a constant. Thus, we can estimate the relative order of \(|H_k(f)|^2\) by comparing (13.53) for every k.

Next, we sort \(\mathrm{E}_\tau [|{X_k}(f,\tau )|^2]\) in descending order and select the channels corresponding to a high amplitude of \(|{H_k}(f)|^2\) satisfying the following condition:

$$\begin{aligned} \max _k \mathrm{E}_\tau [|{X_k}(f,\tau )|^2] \cdot \xi \le \mathrm{E}_\tau [|{X}_k(f,\tau )|^2], \end{aligned}$$
(13.54)

where \(\xi (<1)\) is the threshold for the selection.

Finally, we perform noise estimation based on ICA using the selected channels in each frequency subband, and we apply the projection back operation to remove the ambiguity of the amplitude and construct the estimated noise signal.

13.4.2 Time-Variant Noise Power Spectral Density Estimator

In the previous section, we revealed that the speech components cannot be regarded as a point source, and this leads to poor noise estimation in iterative BSSA. To solve this problem, we introduce a time-variant noise PSD estimator [24] instead of ICA to improve the noise estimation accuracy. This method has been developed for future high-end binaural hearing aids and performs a prediction of the left noisy signal from the right noisy signal via the Wiener filter, followed by an auto-PSD of the difference between the left noisy signal and the prediction. By applying the noise PSD estimated from this estimator to (13.35), we can perform speech extraction. The procedure of this noise PSD estimator is described in Appendix.

Fig. 13.9
figure 9

Kurtosis ratio obtained from experiment for traffic noise under 10-dB NRR condition

Full size image
Fig. 13.10
figure 10

Cepstral distortion obtained from experiment for traffic noise under 10-dB NRR condition

Full size image
Fig. 13.11
figure 11

Kurtosis ratio obtained from experiment for railway station noise under 10-dB NRR condition

Full size image
Fig. 13.12
figure 12

Cepstral distortion obtained from experiment for railway station noise under 10-dB NRR condition

Full size image

13.5 Experiments in Real World

13.5.1 Experimental Conditions

We conducted objective and subjective evaluation experiments to confirm the validity of iterative BSSA under the diffuse and nonstationary noise condition. The size of the experimental room was \(4.2 \times 3.5 \times 3.0~\mathrm{m}^3\) and the reverberation time was approximately 200 ms. We used a two-, three-, or four-element microphone array with an interelement spacing of 2.15 cm, and the direction of the target speech was set to be normal to the array. All the signals used in this experiment were sampled at 16 kHz with 16-bit accuracy. The DFT size was 1024, and the frame shift length was 256. We used 5 male and 5 female speakers (one utterance per speaker) as sources of the original target speech signal. The input SNR was -5, 0, 5, and 10 dB.

13.5.2 Objective Evaluation

We conducted an objective experimental evaluation under the same NRR condition. First, Figs. 13.9, 13.10, 13.11, and 13.12 show the kurtosis ratio and cepstral distortion obtained from the experiments with real traffic noise and railway station noise, where we evaluate 10-dB NRR (i.e., output SNRs = 5, 10, 15, and 20 dB) signals processed by five conventional methods, namely, the MMSE-STSA estimator, the Log MMSE estimator incorporating speech-presence uncertainty [55], single-channel musical-noise-free iterative spectral subtraction, the multichannel speech enhancement method integrating the minimum variance beamformer and the Log MMSE estimator for postfiltering, and BSSA, in addition to several types of iterative BSSAs (using ICA or a time-variant noise estimator with/without channel selection). Here, we did not apply the channel selection method to the two-microphone case because ICA or time-variant noise estimation requires at least two-channel signals. Also, we applied a minimum statistics noise PSD estimator [4] to the MMSE STSA estimator and musical-noise-free iterative spectral subtraction, and we use the decision-directed approach for a priori SNR estimation in the MMSE STSA estimator and the log MMSE estimator. From Figs. 13.9 and 13.11, we can confirm that the iterative BSSA methods outperform the MMSE STSA estimator, the Log MMSE estimator, and the conventional BSSA in terms of kurtosis ratio. In particular, the kurtosis ratios of the iterative BSSA methods are mostly close to 1.0. This means that the iterative methods did not generate any musical noise. However, the iterative BSSA methods lead to greater speech distortion compared with the conventional BSSA (see Figs. 13.10 and 13.12). Therefore, a trade-off exists between the amount of musical noise generation and speech distortion in the conventional BSSA and iterative BSSA methods. This result implies the disadvantage of iterative BSSA, i.e., large speech distortion, which has been theoretically predicted in Sect. 13.3.3. However, since the speech distortion of the proposed iterative BSSA with channel selection is lower than that of the original iterative BSSA, we can confirm the validity of the channel selection method.

Fig. 13.13
figure 13

Subjective evaluation results for a traffic noise and b railway station noise

Full size image
Fig. 13.14
figure 14

Spectrogram for a clean signal, b observed signal, c signal extracted by BSSA, and d signal extracted by iterative BSSA

Full size image

13.5.3 Subjective Evaluation

Since we found the above-mentioned trade-off, we next conducted a subjective evaluation for setting the performance competition. In the evaluation, we presented a pair of 10-dB NRR signals processed by the conventional BSSA and four of iterative BSSAs (using ICA or a time-variant noise estimator with/without channel selection) in random order to 10 examinees, who selected which signal they preferred from the viewpoint of total sound quality, e.g., less musical noise, less speech distortion, and so forth.

The result of this experiment is shown in Fig. 13.13 for (a) traffic noise and (b) railway station noise. It is found that the output signals of some iterative BSSAs are preferred to that of the conventional BSSA, indicating the higher sound quality of the iterative methods in terms of human perception. This result is plausible because humans are often more sensitive to musical noise than to speech distortion as indicated in past studies, e.g., [12].

To visually understand the above-mentioned result, Fig. 13.14 shows part of the spectrograms of (a) a clean signal, (b) an observed signal, (c) a signal extracted by BSSA, and (d) a signal extracted by iterative BSSA, where the input SNR is set to 5 dB with real traffic noise and the NRR is 10 dB. From Fig. 13.14, it is confirmed that iterative BSSA reduces the number of isolated components in time-frequency domain sequences, which is a factor contributing to musical noise, compared with BSSA. Also, there are no major differences in the speech components of the clean signal, the signal processed by BSSA, and the signal processed by iterative BSSA; thus, we can conclude that the intelligibility of iterative BSSA is no less than that of BSSA.

13.6 Conclusions and Remarks

In this chapter, we addressed a musical-noise-free blind speech extraction method using a microphone array that can be applied to nonstationary noise. Firstly, we introduced iterative BSSA using a new BSSA structure, which generates almost no musical noise even with increasing noise reduction performance.

Secondly, in relation to the method, we discussed the justification of applying ICA to signals nonlinearly distorted by SS. We theoretically clarified that the degradation in ICA-based noise estimation obeys an amplitude variation in room transfer functions between the target user and microphones. Therefore, we gave the introduction of a channel selection strategy in ICA and a time-variant noise PSD estimator to improve the noise estimation accuracy.

Finally, from the objective evaluation experiments, we confirmed a trade-off between the amount of musical noise generation and speech distortion in the conventional and iterative BSSA. However, in a subjective preference test, iterative BSSA obtained a higher preference score than the conventional BSSA. Thus, iterative BSSA is advantageous to the conventional BSSA in terms of sound quality.

Implementation on a small hardware still receives much attention in industrial applications. Due to the limitation of space, however, the authors skip the discussion on this issue. Instead, several studies [56,57,58,59,60] have dealt with the issue of real-time implementation of ICA and BSSA, which would be helpful for the readers.