Recent Advances in Multichannel Source Separation and Denoising Based on Source Sparseness

Abstract

This chapter deals with multichannel source separation and denoising based on sparseness of source signals in the time-frequency domain. In this approach, time-frequency masks are typically estimated based on clustering of source location features, such as time and level differences between microphones. In this chapter, we describe the approach and its recent advances. Especially, we introduce a recently proposed clustering method, observation vector clustering, which has attracted attention for its effectiveness. We introduce algorithms for observation vector clustering based on a complex Watson mixture model (cWMM), a complex Bingham mixture model (cBMM), and a complex Gaussian mixture model (cGMM). We show through experiments the effectiveness of observation vector clustering in source separation and denoising.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

11.1 Introduction

When a desired sound is recorded by distant microphones, it is mixed with other sounds, which often degrade speech quality and intelligibility as well as automatic speech recognition (ASR) performance. To resolve this problem, techniques such as source separation, denoising, and dereverberation have been studied extensively. This chapter focuses on source separation and denoising; see [1] for dereverberation.

Figure 11.1 illustrates source separation and denoising we deal with in this paper. Suppose we record $N (\ge 1)$ source signals in the presence of background noise by using $M (\ge 2)$ microphones. Our goal is to estimate each source signal from the observed signals. Note that there is not only a multichannel approach [2,3,4,5] using multiple microphones but also a single-channel approach using a single microphone [6,7,8,9]. A main advantage of the multichannel approach is that it can perform source separation and denoising with little or even no distortion in the desired source signal.

Fig. 11.1

Source separation and denoising we deal with in this paper

Especially, multichannel source separation and denoising based on source sparseness [10,11,12,13,14,15,16,17,18,19,20] have turned out to be highly effective and robust in the real world [16, 17, 19, 20]. Various signals including speech are known to have sparseness in the time-frequency domain: a small percentage of the time-frequency components of a signal capture a large percentage of its overall energy [10]. The source sparseness is often exploited by assuming that the observed signals are dominated by a single source signal or by background noise at each time-frequency point. We call this a sparseness assumption. The dominating source signal or background noise at each time-frequency point can be represented by masks. Once we have obtained these masks, we can estimate the source signals either by applying the masks directly to the observed signals (masking) [10,11,12,13,14, 16, 17, 19, 21] or by applying beamformers designed based on the masks [15, 18, 20, 22].

The key to the effectiveness of this approach is accurate estimation of the masks, which is usually performed based on either spatial information [10,11,12,13,14,15,16,17,18,19,20] or spectral information [21, 22]. We focus on the former, which employs source location features extracted from the observed signals, such as time and level differences between microphones. The sparseness assumption implies that the source location features form clusters, each of which corresponds to a source signal or the background noise. These clusters can be found by clustering the source location features to obtain the masks. This is typically done by fitting a mixture model to the features, where the appropriate design of the features and the mixture model is significant to mask estimation accuracy.

In this chapter, we introduce a recently proposed clustering method, observation vector clustering, which has attracted attention for its effectiveness [11, 13, 15,16,17,18,19,20]. This method has been employed in many evaluation campaigns successfully [17, 20]. We introduce algorithms for observation vector clustering based on a complex Watson mixture model (cWMM), a complex Bingham mixture model (cBMM), and a complex Gaussian mixture model (cGMM).

The rest of this chapter is organized as follows. Section 11.2 overviews source separation and denoising based on the observation vector clustering. Section 11.3 introduces algorithms for observation vector clustering based on the cWMM, the cBMM, and the cGMM. Section 11.4 describes experiments, and Sect. 11.5 concludes this chapter.

11.2 Source Separation and Denoising Based on Observation Vector Clustering

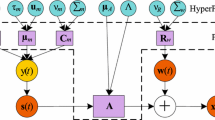
This section overviews source separation and denoising based on observation vector clustering. Figure 11.2 shows the overall processing flow of this method. In mask estimation, masks are estimated from the observed signals. In source signal estimation, source signals are estimated by masking or beamforming based on the estimated masks.

Fig. 11.2

Overall processing flow of source separation and denoising based on observation vector clustering

11.2.1 Mask Estimation

Figure 11.3 shows the processing flow of mask estimation in Fig. 11.2. In feature extraction, a source location feature vector is extracted from the observed signals. In frequency-wise clustering, clustering of the extracted feature vector is performed in each frequency bin. As a result, posterior probabilities are obtained, which indicate how much the individual clusters contribute to each time-frequency point. In permutation alignment, the masks are obtained from the posterior probabilities; the details will be explained later.

Fig. 11.3

Processing flow of mask estimation in Fig. 11.2

Feature Extraction

In feature extraction in Fig. 11.3, a source location feature vector is extracted at each time-frequency point. Conventionally, time and level differences between microphones were often employed as source location features. In contrast, in the observation vector clustering, we operate directly on an observation vector composed of multichannel complex spectra.

Let $y^{(m)}_{tf}\in \mathbb {C}$ denote the observed signal at the mth microphone in the short-time Fourier transform (STFT) domain. Here, $m\in \{1,\dots ,M\}$ denotes the microphone index; $t\in \{1,\dots ,T\}$ the frame index; $f\in \{1,\dots ,F\}$ the frequency bin index; M the number of microphones in the array; T the number of frames; F the number of frequency bins up to the Nyquist frequency. We define the observation vector by $\mathbf {y}_{tf}\triangleq \begin{bmatrix} y^{(1)}_{tf}&y^{(2)}_{tf}&\dots&y^{(M)}_{tf} \end{bmatrix}^\textsf {T}\in \mathbb {C}^M,$ where the superscript $^\textsf {T}$ denotes transposition.

We employ the observation vector $\mathbf {y}_{tf}$ as the feature vector $\mathbf {z}_{tf}$:

$$\begin{aligned} \mathbf {z}_{tf}=\mathbf {y}_{tf}. \end{aligned}$$

(11.1)

In this case, $\mathbf {z}_{tf}$ lies in the complex linear space $\mathbb {C}^M$. Alternatively, we can also employ a normalized observation vector $\frac{\mathbf {y}_{tf}}{\Vert \mathbf {y}_{tf}\Vert }$ as the feature vector $\mathbf {z}_{tf}$:

$$\begin{aligned} \mathbf {z}_{tf}=\frac{\mathbf {y}_{tf}}{\Vert \mathbf {y}_{tf}\Vert }, \end{aligned}$$

(11.2)

where $\Vert \cdot \Vert$ denotes the Euclidean norm. In this case, $\mathbf {z}_{tf}$ lies on the unit hypersphere $S^{M-1}$ in $\mathbb {C}^M$ centered at the origin, because $\Vert \mathbf {z}_{tf}\Vert =1$ (see Fig. 11.4).

Fig. 11.4

Example of the source location feature vector for two sources. Here, $\mathbb {C}^M$ has been simplified to $\mathbb {R}^3$ for illustration

In the following, we describe our modeling of the observation vector $\mathbf {y}_{tf}$. We consider both noiseless and noisy cases.

First, we consider the noiseless case, where $N (\ge 2)$ source signals are recorded by the microphones without noise. The number of sources, N, is assumed to be given throughout this chapter. In this noiseless case, $\mathbf {y}_{tf}$ is modeled by $\mathbf {y}_{tf}=\sum _{n=1}^Ns^{(n)}_{tf}\mathbf {h}^{(n)}_{tf}$. Here, $s^{(n)}_{tf}$ denotes the nth source signal in the STFT domain, and $\mathbf {h}^{(n)}_{tf}$ denotes the steering vector for the nth source. The steering vector $\mathbf {h}^{(n)}_{tf}$ represents the acoustic transfer characteristics from the nth source to the microphones. Under the sparseness assumption, the above model can be approximated by $\mathbf {y}_{tf}=s^{(\nu )}_{tf}\mathbf {h}^{(\nu )}_{tf}$, where $\nu =d_{tf}$ denotes the index of the source signal that dominates $\mathbf {y}_{tf}$ at the time-frequency point (t, f). Here, both $s^{(n)}_{tf}$ and $\mathbf {h}^{(n)}_{tf}$ are unknown.

Next, we consider the noisy case, where $N(\ge 1)$ source signal(s) are recorded by the microphones in the presence of background noise. In this case, $\mathbf {y}_{tf}$ is modeled by $\mathbf {y}_{tf}=\sum _{n=1}^Ns^{(n)}_{tf}\mathbf {h}^{(n)}_{tf}+\mathbf {v}_{tf}$, where $\mathbf {v}_{tf}$ denotes the contribution of the background noise to $\mathbf {y}_{tf}$. Under the sparseness assumption, this model can be approximated by

$$\begin{aligned} \mathbf {y}_{tf}= {\left\{ \begin{array}{ll} s^{(\nu )}_{tf}\mathbf {h}^{(\nu )}_{tf}+\mathbf {v}_{tf},&{}\text {if }\ d_{tf}=\nu \in \{1,\dots ,N\},\\ \mathbf {v}_{tf},&{}\text {if }\ d_{tf}=0. \end{array}\right. } \end{aligned}$$

(11.3)

Here, $d_{tf}$ denotes the index of the source signal or the background noise that dominates $\mathbf {y}_{tf}$ at the time-frequency point (t, f), where the case $d_{tf}=0$ corresponds to the background noise and the cases $d_{tf}\in \{1,\dots ,N\}$ to the source signals. Note that the background noise $\mathbf {v}_{tf}$ is assumed to be contained in $\mathbf {y}_{tf}$ at all time-frequency points, because it is usually not sparse. $s^{(n)}_{tf}$, $\mathbf {h}^{(n)}_{tf}$, and $\mathbf {v}_{tf}$ are all unknown.

In both cases, our goal is to estimate $s^{(n)}_{tf}$ given $\mathbf {y}_{tf}$.

Frequency-Wise Clustering

In frequency-wise clustering in Fig. 11.3, clustering of the feature vector $\mathbf {z}_{tf}$ is performed in each frequency bin. As a result, the posterior probability $\tilde{\gamma }^{(k)}_{tf}$ is obtained for each cluster k, which indicates how much the kth cluster contributes to the time-frequency point (t, f).

The clustering can be performed by fitting a mixture model

$$\begin{aligned} p(\mathbf {z}_{tf}|\varTheta _f)&=\sum _{k}\alpha ^{(k)}_fp\bigl (\mathbf {z}_{tf}\big |\tilde{d}_{tf}=k,\varTheta _f\bigr ) \end{aligned}$$

(11.4)

to $\mathbf {z}_{tf}$. Here, $\tilde{d}_{tf}$ denotes the index of the cluster that $\mathbf {z}_{tf}$ belongs to; $\alpha ^{(k)}_f\triangleq P\bigl (\tilde{d}_{tf}=k\big |\varTheta _f\bigr )$ the prior probability of $\tilde{d}_{tf}=k$; $p\bigl (\mathbf {z}_{tf}\big |\tilde{d}_{tf}=k,\varTheta _f\bigr )$ the conditional probability density function of $\mathbf {z}_{tf}$ under $\tilde{d}_{tf}=k$; $\sum _k$ the sum over all possible values of k (i.e., $\sum _{k=1}^K$ for the noiseless case; $\sum _{k=0}^K$ for the noisy case); $\varTheta _f$ the set of all model parameters in (11.4). $\alpha ^{(k)}_f$ satisfies $\sum _k\alpha ^{(k)}_f=1$ and $\alpha ^{(k)}_f\ge 0$.

$\varTheta _f$ is estimated by the maximization of the log-likelihood function

$$\begin{aligned} L(\varTheta _f)&=\sum _{t=1}^T\ln p(\mathbf {z}_{tf}|\varTheta _f), \end{aligned}$$

(11.5)

which can be done by the expectation-maximization (EM) algorithm. Once $\varTheta _f$ has been estimated, we obtain the posterior probability $\tilde{\gamma }^{(k)}_{tf}$ based on Bayes’ theorem [23] as follows:

$$\begin{aligned} \tilde{\gamma }^{(k)}_{tf}&\triangleq P\bigl (\tilde{d}_{tf}=k\big |\mathbf {z}_{tf},\varTheta _f\bigr )\end{aligned}$$

(11.6)

$$\begin{aligned}&=\frac{\alpha ^{(k)}_fp\bigl (\mathbf {z}_{tf}\big |\tilde{d}_{tf}=k,\varTheta _f\bigr )}{\displaystyle \sum _{l}\alpha ^{(l)}_fp\bigl (\mathbf {z}_{tf}\big |\tilde{d}_{tf}=l,\varTheta _f\bigr )}. \end{aligned}$$

(11.7)

Here, $\tilde{\gamma }^{(k)}_{tf}$ satisfies $\sum _k\tilde{\gamma }^{(k)}_{tf}=1$ and $\tilde{\gamma }^{(k)}_{tf}\ge 0$.

Permutation Alignment

In permutation alignment in Fig. 11.3, the masks are obtained by using the posterior probabilities $\tilde{\gamma }^{(k)}_{tf}$.

The index k of the clusters and the index n of the source signals and the background noise do not necessarily coincide, but there is permutation ambiguity between them. This implies that $\tilde{\gamma }^{(k)}_{tf}$ for the same k may correspond to different source signals at different frequencies. Therefore, we need to permute the cluster indexes k so that each k corresponds to the same source signal or background noise in all frequency bins, which is called permutation alignment. As a result of the permutation alignment, we obtain the masks $\gamma ^{(n)}_{tf}$.

Many methods have been proposed for permutation alignment [16, 24,25,26]. Especially, Sawada et al. [16] has proposed an effective method based on correlation of posterior probabilities $\tilde{\gamma }^{(k)}_{tf}$ between frequencies.

11.2.2 Source Signal Estimation

In source signal estimation in Fig. 11.2, source signals are estimated by masking or beamforming based on the estimated masks.

Masking

When masking is employed, the source signals are estimated by multiplying an observed signal by the estimated masks $\gamma ^{(n)}_{tf}$ as follows:

$$\begin{aligned} \hat{s}^{(n)}_{tf}=\gamma ^{(n)}_{tf}y^{(\mu )}_{tf}. \end{aligned}$$

(11.8)

Here, $\mu$ denotes the index of the reference microphone.

Beamforming

Here we consider the noisy case. Among many types of beamformers, we focus on the MVDR beamformer. The MVDR beamformer is especially suitable for the front end of ASR, because it can perform source separation and denoising without distorting the desired source signal.

The output of the MVDR beamformer is given by

$$\begin{aligned} \hat{s}^{(n)}_{tf}=\frac{\mathbf {h}^{(n)\textsf {H}}_{tf}\bigl (\varvec{\varPhi }^{\mathbf {y}}_f\bigr )^{-1}\mathbf {y}_{tf}}{\mathbf {h}^{(n)\textsf {H}}_{tf}\bigl (\varvec{\varPhi }^{\mathbf {y}}_f\bigr )^{-1}\mathbf {h}^{(n)}_{tf}}. \end{aligned}$$

(11.9)

$\varvec{\varPhi }^{\mathbf {y}}_f$ denotes the covariance matrix of $\mathbf {y}_{tf}$ , which can be estimated by

$$\begin{aligned} \hat{\varvec{\varPhi }}^{\mathbf {y}}_f=\frac{1}{T}\sum _{t=1}^T\mathbf {y}_{tf}\mathbf {y}_{tf}^\textsf {H}. \end{aligned}$$

(11.10)

In the MVDR beamformer, accurate estimation of the steering vector $\mathbf {h}^{(n)}_{tf}$ is crucial.

Conventionally, $\mathbf {h}^{(n)}_{tf}$ was estimated based on the assumptions of planewave propagation and a known array geometry. These assumptions are often violated in the real world, and lead to degraded performances of the MVDR beamformer and therefore ASR. Here we present mask-based steering vector estimation, which does not rely on these assumptions, and therefore is more robust in the real world.

First, a covariance matrix $\varvec{\varPsi }^{(n)}_f$ corresponding to the nth source signal plus the background noise is estimated by

$$\begin{aligned} \varvec{\varPsi }^{(n)}_f=\frac{\sum _{t=1}^T\gamma ^{(n)}_{tf}\mathbf {y}_{tf}\mathbf {y}_{tf}^\textsf {H}}{\sum _{t=1}^T\gamma ^{(n)}_{tf}}, \end{aligned}$$

(11.11)

and a noise covariance matrix $\varvec{\varPsi }^{(0)}_f$ is estimated by

$$\begin{aligned} \varvec{\varPsi }^{(0)}_f=\frac{\sum _{t=1}^T\gamma ^{(0)}_{tf}\mathbf {y}_{tf}\mathbf {y}_{tf}^\textsf {H}}{\sum _{t=1}^T\gamma ^{(0)}_{tf}}. \end{aligned}$$

(11.12)

The noise contribution to $\varvec{\varPsi }^{(n)}_f$ is reduced by subtracting $\varvec{\varPsi }^{(0)}_f$from $\varvec{\varPsi }^{(n)}_f$. The steering vector $\mathbf {h}^{(n)}_{tf}$ is estimated as a principal eigenvector of the resultant matrix $\varvec{\varPsi }^{(n)}_f-\varvec{\varPsi }^{(0)}_f$.

11.3 Mask Estimation Based on Modeling Directional Statistics

Several mixture models for the feature vector $\mathbf {z}_{tf}$ have been proposed to estimate the masks accurately. These mixture models include the cWMM, the cBMM, and the cGMM, which are specific examples of the general mixture model (11.4).

11.3.1 Mask Estimation Based on Complex Watson Mixture Model (cWMM)

Sawada et al. [13, 16] and Tran Vu et al. [15] have proposed to estimate masks based on modeling the feature vector (11.2) by a complex Watson mixture model (cWMM). The cWMM is composed of complex Watson distributions of Mardia et al. [27], and the complex Watson distribution is an extension of a real Watson distribution of Watson [28].

The probability density function (PDF) of the cWMM is given by

$$\begin{aligned} p(\mathbf {z}_{tf};\varTheta _{\text {W},f})&=\sum _k\alpha ^{(k)}_fp_\text {W}\Bigl (\mathbf {z}_{tf};\mathbf {a}^{(k)}_f,\kappa ^{(k)}_f\Bigr ), \end{aligned}$$

(11.13)

where $p_\text {W}$ denotes a complex Watson distribution

$$\begin{aligned} p_\text {W}(\mathbf {z};\mathbf {a},\kappa )&\triangleq \frac{(M-1)!}{2\pi {}^M\mathscr {K}(1,M;\kappa )}\exp \Bigl ({\kappa \bigl |\mathbf {a}^\textsf {H}\mathbf {z}\bigr |^2}\Bigr ).\end{aligned}$$

(11.14)

Both the complex Watson distribution and the cWMM are defined on the unit hypersphere in $\mathbb {C}^M$:

$$\begin{aligned} S^{M-1}\triangleq \Bigl \{\mathbf {z}\in \mathbb {C}^M\Big |\Vert \mathbf {z}\Vert =1\Bigr \}, \end{aligned}$$

(11.15)

which is illustrated in Fig. 11.4. Each complex Watson distribution in (11.13) models the distribution of $\mathbf {z}_{tf}$ for a cluster. k denotes the cluster index.

$$\begin{aligned} \varTheta _{\text {W},f}\triangleq \Bigl \{\alpha ^{(k)}_f,\mathbf {a}^{(k)}_f,\kappa ^{(k)}_f\Big |{}^\forall k\Bigr \} \end{aligned}$$

(11.16)

denotes the set of all model parameters of the cWMM (11.13), where $\alpha ^{(k)}_f$ satisfies

$$\begin{aligned} \alpha ^{(k)}_f&\ge 0,\end{aligned}$$

(11.17)

$$\begin{aligned} \sum _k\alpha ^{(k)}_f&=1, \end{aligned}$$

(11.18)

$\mathbf {a}^{(k)}_f$ denotes a parameter representing the mean orientation of $\mathbf {z}_{tf}$ for the kth cluster satisfying

$$\begin{aligned} \bigl \Vert \mathbf {a}^{(k)}_f\bigr \Vert =1, \end{aligned}$$

(11.19)

and $\kappa \in \mathbb {R}$ denotes a parameter representing the concentration of the distribution of $\mathbf {z}_{tf}$ for the kth cluster. $^\textsf {H}$ denotes conjugate transposition; $\mathscr {K}$ the confluent hypergeometric function of the first kind, also known as the Kummer function, which is defined by the following power series:

$$\begin{aligned} \mathscr {K}(\xi ,\eta ;\kappa )\triangleq 1+\frac{\xi }{\eta }\frac{\kappa }{1!}+\frac{\xi (\xi +1)}{\eta (\eta +1)}\frac{\kappa ^2}{2!}+\dots . \end{aligned}$$

(11.20)

To analyze the behavior of (11.14) as a function of $\mathbf {z}$, note that (11.14) depends on $\mathbf {z}$ through the term $\bigl |\mathbf {a}^\textsf {H}\mathbf {z}\bigr |$ only and increases[decreases] monotonically as $\bigl |\mathbf {a}^\textsf {H}\mathbf {z}\bigr |$ increases when $\kappa >0$[$\kappa <0$]. Note also that

$$\begin{aligned} 0\le \bigl |\mathbf {a}^\textsf {H}\mathbf {z}\bigr |\le 1, \end{aligned}$$

(11.21)

which follows from the Cauchy-Schwartz inequality and $\Vert \mathbf {z}\Vert =\Vert \mathbf {a}\Vert =1$. Therefore, for $\kappa >0$[$\kappa <0$], (11.14) has the global minima[maxima] at

$$\begin{aligned} \Bigl \{\mathbf {z}\in S^{M-1}\Big |\bigl |\mathbf {a}^\textsf {H}\mathbf {z}\bigr |=0\Bigr \}, \end{aligned}$$

(11.22)

increases[decreases] monotonically as $\bigl |\mathbf {a}^\textsf {H}\mathbf {z}\bigr |$ increases, and has the global maxima[minima] at

$$\begin{aligned} \Bigl \{\mathbf {z}\in S^{M-1}\Big |\bigl |\mathbf {a}^\textsf {H}\mathbf {z}\bigr |=1\Bigr \}. \end{aligned}$$

(11.23)

Note that (11.22) equals

$$\begin{aligned} \{\mathbf {z}\in {S}^{M-1}|\mathbf {a}^\textsf {H}\mathbf {z}=0\}, \end{aligned}$$

(11.24)

and (11.23) equals

$$\begin{aligned} \{\exp (\text {j}\theta )\mathbf {a}|\theta \in [0,2\pi )\}. \end{aligned}$$

(11.25)

It is straightforward to see that, for $\kappa =0$, (11.14) is constant (i.e., uniform distribution on $S^{M-1}$). Based on the above property, we impose a constraint

$$\begin{aligned} \kappa ^{(k)}_f>0, \end{aligned}$$

(11.26)

which is appropriate for our application.

Once the model parameters $\varTheta _{\text {W},f}$ have been estimated, the posterior probability $\tilde{\gamma }^{(k)}_{tf}$ can be obtained based on Bayes’ theorem [23] by

$$\begin{aligned} \tilde{\gamma }^{(k)}_{tf}\leftarrow \frac{{\alpha }^{(k)}_fp_\text {W}\Bigl (\mathbf {z}_{tf};\mathbf {a}^{(k)}_f,\kappa ^{(k)}_f\Bigr )}{\displaystyle \sum _l{\alpha }^{(l)}_fp_\text {W}\Bigl (\mathbf {z}_{tf};\mathbf {a}^{(l)}_f,\kappa ^{(l)}_f\Bigr )}. \end{aligned}$$

(11.27)

To estimate the model parameters $\varTheta _{\text {W},f}$, the cWMM (11.13) is fitted to the feature vector $\mathbf {z}_{tf}$, e.g., based on the maximization of the log-likelihood function

$$\begin{aligned} \sum _{t=1}^T\ln p(\mathbf {z}_{tf};\varTheta _{\text {W},f}). \end{aligned}$$

(11.28)

This is realized by, e.g., an expectation-maximization (EM) algorithm [23], which consists in alternate iteration of an E-step and an M-step. The E-step consists in updating the posterior probability ${\gamma }^{(k)}_{tf}$ by (11.27) using current estimates of the model parameters $\varTheta _{\text {W},f}$. The M-step consists in updating the model parameters $\varTheta _{\text {W},f}$ using the posterior probability ${\gamma }^{(k)}_{tf}$, which is realized by applying the following update rules:

$$\begin{aligned} \alpha ^{(k)}_{f}&\leftarrow \frac{1}{T}\sum _{t=1}^T \tilde{\gamma }^{(k)}_{tf},\end{aligned}$$

(11.29)

$$\begin{aligned} \mathbf {R}^{(k)}_f&\leftarrow \frac{\sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}\mathbf {z}_{tf}\mathbf {z}^\textsf {H}_{tf}}{\sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}}, \end{aligned}$$

(11.30)

$$\begin{aligned} \bigl (\lambda ^{(k)}_f,\mathbf {a}^{(k)}_f\bigr )&\leftarrow \text {the largest eigenvalue and a corresponding eigenvector of }\mathbf {R}^{(k)}_f, \end{aligned}$$

(11.31)

$$\begin{aligned} \mathbf {a}^{(k)}_f&\leftarrow \frac{\mathbf {a}^{(k)}_f}{\bigl \Vert \mathbf {a}^{(k)}_f\bigr \Vert },\end{aligned}$$

(11.32)

$$\begin{aligned} \kappa ^{(k)}_{f}&\leftarrow \frac{M\lambda ^{(k)}_f-1}{2\lambda ^{(k)}_f\bigl (1-\lambda ^{(k)}_f\bigr )}\Biggl [1+\sqrt{\displaystyle 1+\frac{4(M+1)\lambda ^{(k)}_f\bigl (1-\lambda ^{(k)}_f\bigr )}{M-1}}\Biggr ]. \end{aligned}$$

(11.33)

See Appendix 1 for derivation of this EM algorithm.

Fig. 11.5

Illustration of the cWMM and the cBMM for two sources

A major limitation of the cWMM lies in that the complex Watson distribution (11.14) can represent a distribution that is rotationally symmetric about the axis $\mathbf {a}$ (see Fig. 11.5). Indeed, as we have already noted, (11.14) is a function of $\bigl |\mathbf {a}^\textsf {H}\mathbf {z}\bigr |$, which can be regarded as the cosine of the angle between $\mathbf {a}$ and $\mathbf {z}$. However, the distribution of the feature vector $\mathbf {z}_{tf}$ for each cluster is not necessarily rotationally symmetric, depending on various conditions such as the array geometry and acoustic transfer characteristics. The cWMM therefore has a limited ability to approximate the distribution of $\mathbf {z}_{tf}$, which results in degraded mask estimation accuracy and therefore degraded performance of source separation and denoising. This motivates us to consider more flexible distributions, which are described in Sects. 11.3.2 and 11.3.3.

11.3.2 Mask Estimation Based on Complex Bingham Mixture Model (cBMM)

To overcome the above limitation of the cWMM, Ito et al. have proposed to estimate masks based on modeling the feature vector (11.2) by a complex Bingham mixture model (cBMM) [29]. The cBMM is composed of complex Bingham distributions of Kent [30], and the complex Bingham distribution is an extension of the real Bingham distribution of Bingham [31]. The complex Bingham distribution can represent not only rotationally symmetric but also elliptical distributions on the unit hypersphere (see Fig. 11.5), and can therefore better approximate the distribution of the feature vector $\mathbf {z}_{tf}$ than the complex Watson distribution. As a result, the cBMM can improve mask estimation accuracy and therefore source separation and denoising performance compared to the cWMM.

The PDF of the cBMM is given by

$$\begin{aligned} p\bigl (\mathbf {z}_{tf};\varTheta _{\text {B},f}\bigr )&=\sum _k\alpha ^{(k)}_fp_\text {B}\Bigl (\mathbf {z}_{tf};\mathbf {B}^{(k)}_f\Bigr ), \end{aligned}$$

(11.34)

where $p_\text {B}$ denotes a complex Bingham distribution

$$\begin{aligned} p_\text {B}\bigl (\mathbf {z};\mathbf {B}\bigr )&\triangleq c(\mathbf {B})^{-1}\exp \bigl (\mathbf {z}^\textsf {H}\mathbf {B}\mathbf {z}\bigr ). \end{aligned}$$

(11.35)

Here, $c(\mathbf {B})$ denotes the following function defined for a Hermitian matrix $\mathbf {B}$.

$$\begin{aligned} c(\mathbf {B})\triangleq \Biggl [2\pi ^M\sum _{m=1}^M\frac{\exp \Bigl (\beta _m\Bigr )}{\displaystyle \prod _{l\ne m}\Bigl (\beta _m-\beta _l\Bigr )}\Biggr ], \end{aligned}$$

(11.36)

where $\beta _m$, $m=1,\dots ,M$, denote the eigenvalues of $\mathbf {B}$. Both the complex Bingham distribution and the cBMM are defined on the unit hypersphere $S^{M-1}$. Each complex Bingham distribution in (11.34) models the distribution of $\mathbf {z}_{tf}$ for a cluster.

$$\begin{aligned} \varTheta _{\text {B},f}\triangleq \Bigl \{\alpha ^{(k)}_f,\mathbf {B}^{(k)}_f\Big |{}^\forall k\Bigr \} \end{aligned}$$

(11.37)

denotes the set of all model parameters of the cBMM, where $\mathbf {B}^{(k)}_f$ is a Hermitian parameter matrix, which represents not only the location and the concentration, but also the direction and the shape, of the complex Bingham distribution. Note that the expression for the normalization factor in (11.35) is valid only when the eigenvalues of $\mathbf {B}$ are all distinct, which is always satisfied in practice.

Once the model parameters $\varTheta _{\text {B},f}$ have been estimated, the posterior probability $\tilde{\gamma }^{(k)}_{tf}$ can be obtained by

$$\begin{aligned} \tilde{\gamma }^{(k)}_{tf}\leftarrow \frac{{\alpha }^{(k)}_fp_\text {B}\Bigl (\mathbf {z}_{tf};\mathbf {B}^{(k)}_f\Bigr )}{\displaystyle \sum _l{\alpha }^{(l)}_fp_\text {B}\Bigl (\mathbf {z}_{tf};\mathbf {B}^{(l)}_f\Bigr )}. \end{aligned}$$

(11.38)

As in the cWMM case, $\varTheta _{\text {B},f}$ can be estimated by the maximum likelihood method based on the EM algorithm. The E-step consists in updating $\tilde{\gamma }^{(k)}_{tf}$ by (11.38) using the current $\varTheta _{\text {B},f}$ value. The M-step consists in updating $\varTheta _{\text {B},f}$ using $\tilde{\gamma }^{(k)}_{tf}$, which is realized by applying the following update rules:

$$\begin{aligned} \alpha ^{(k)}_{f}&\leftarrow \frac{1}{T}\sum _{t=1}^T \tilde{\gamma }^{(k)}_{tf},\end{aligned}$$

(11.39)

$$\begin{aligned} \mathbf {R}^{(k)}_f&\leftarrow \frac{\sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}\mathbf {z}_{tf}\mathbf {z}^\textsf {H}_{tf}}{\sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}}, \end{aligned}$$

(11.40)

$$\begin{aligned} \bigl (\lambda ^{(k)}_{fm},\mathbf {a}^{(k)}_{fm}\bigr )&\leftarrow \,\text {the}\, m\text {th largest eigenvalue and a corresponding eigenvector}\nonumber \\&\ \ \ \ \ \ \text {of } \mathbf {R}^{(k)}_f, \end{aligned}$$

(11.41)

$$\begin{aligned} \mathbf {a}^{(k)}_{fm}&\leftarrow \frac{\mathbf {a}^{(k)}_{fm}}{\bigl \Vert \mathbf {a}^{(k)}_{fm}\bigr \Vert }, \end{aligned}$$

(11.42)

$$\begin{aligned} \mathbf {B}^{(k)}_{f}&\leftarrow \sum _{m=1}^M\Biggl (-\frac{1}{\lambda ^{(k)}_{fm}}+\frac{1}{\lambda ^{(k)}_{f1}}\Biggr )\mathbf {a}^{(k)}_{fm}\mathbf {a}^{(k)\textsf {H}}_{fm}. \end{aligned}$$

(11.43)

See Appendix 2 for derivation of the above algorithm.

Note that the parameter matrix $\mathbf {B}^{(k)}_f$ has the following indeterminacy

$$\begin{aligned} p_\text {B}\Bigl (\mathbf {z}_{tf};\mathbf {B}^{(k)}_f\Bigr )=p_\text {B}\Bigl (\mathbf {z}_{tf};\mathbf {B}^{(k)}_f+\xi \mathbf {I}\Bigr ),{}^\forall \xi \in \mathbb {R}, \end{aligned}$$

(11.44)

which follows from $\Vert \mathbf {z}_{tf}\Vert =1$. Here, $\mathbf {I}$ denotes the $M\times M$ identity matrix. To remove this indeterminacy, in the above algorithm, $\xi$ has been determined so that the largest eigenvalue of $\mathbf {B}^{(k)}_f$ equals zero.

11.3.3 Mask Estimation Based on Complex Gaussian Mixture Model (cGMM)

As an alternative method, Ito et al. have proposed to estimate masks based on modeling the feature vector (11.1) by a complex (time-varying) Gaussian mixture model (cGMM) [32], inspired by Duong et al. [33]. Note that the cGMM models the observation vector itself in (11.1), instead of its normalized version in (11.2). The cGMM is composed of complex Gaussian distributions, where the covariance matrices are parametrized by time-invariant spatial covariance matrices and time-variant power parameters.

The PDF of the cGMM is given by

$$\begin{aligned} p(\mathbf {z}_{tf};\varTheta _{\text {G},f})&=\sum _k\alpha ^{(k)}_fp_\text {G}\Bigl (\mathbf {z}_{tf};0,\phi ^{(k)}_{tf}\mathbf {B}^{(k)}_f\Bigr ), \end{aligned}$$

(11.45)

where $p_\text {G}$ denotes a complex Gaussian distribution

$$\begin{aligned} p_\text {G}\bigl (\mathbf {z};\mathbf {g},\varvec{\varSigma }\bigr )&\triangleq \frac{1}{\pi ^M\det \varvec{\varSigma }}\exp [-(\mathbf {z}-\mathbf {g})^\textsf {H}\varvec{\varSigma }^{-1}(\mathbf {z}-\mathbf {g})], \end{aligned}$$

(11.46)

with $\mathbf {g}$ being the mean and $\varvec{\varSigma }$ the covariance matrix. Both the complex Gaussian distribution and the cGMM are defined in $\mathbb {C}^M$. Each complex Gaussian distribution in (11.45) models the distribution of $\mathbf {z}_{tf}$ for a cluster.

$$\begin{aligned} \varTheta _{\text {G},f}\triangleq \Bigl \{\alpha ^{(k)}_f,\mathbf {B}^{(k)}_f\Big |{}^\forall k\Bigr \}\cup \Bigl \{\phi ^{(k)}_{tf}\Big |{}^\forall k, {}^\forall t\Bigr \} \end{aligned}$$

(11.47)

denotes the set of all model parameters of the cGMM, where $\mathbf {B}^{(k)}_f$ is a scaled covariance matrix modeling the direction of the observation vector in (11.1) (i.e., the normalized observation vector (11.2)), and $\phi ^{(k)}_{tf}$ is a power parameter modeling the magnitude of the observation vector.

Once the model parameters $\varTheta _{\text {G},f}$ have been estimated, the posterior probability $\tilde{\gamma }^{(k)}_{tf}$ can be obtained by

$$\begin{aligned} \tilde{\gamma }^{(k)}_{tf}\leftarrow \frac{{\alpha }^{(k)}_fp_\text {G}\Bigl (\mathbf {y}_{tf};0,\phi ^{(k)}_{tf}\mathbf {B}^{(k)}_f\Bigr )}{\displaystyle \sum _l{\alpha }^{(l)}_fp_\text {G}\Bigl (\mathbf {y}_{tf};0,\phi ^{(l)}_{tf}\mathbf {B}^{(l)}_f\Bigr )}. \end{aligned}$$

(11.48)

As in the cWMM and the cBMM cases, $\varTheta _{\text {G},f}$ can be estimated by the maximum likelihood method based on the EM algorithm. The E-step consists in updating $\tilde{\gamma }^{(k)}_{tf}$ by (11.48) using the current $\varTheta _{\text {G},f}$ value. The M-step consists in updating $\varTheta _{\text {G},f}$ using $\tilde{\gamma }^{(k)}_{tf}$, which is realized by applying the following update rules:

$$\begin{aligned} \alpha ^{(k)}_{f}&\leftarrow \frac{1}{T}\sum _{t=1}^T \tilde{\gamma }^{(k)}_{tf},\end{aligned}$$

(11.49)

$$\begin{aligned} \mathbf {B}^{(k)}_f&\leftarrow \frac{\sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}\mathbf {y}_{tf}\mathbf {y}^\textsf {H}_{tf}/\phi ^{(k)}_{tf}}{\sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}},\end{aligned}$$

(11.50)

$$\begin{aligned} \phi ^{(k)}_{tf}&\leftarrow \frac{1}{M}\mathbf {y}_{tf}^\textsf {H}\Bigl (\mathbf {B}^{(k)}_f\Bigr )^{-1}\mathbf {y}_{tf}. \end{aligned}$$

(11.51)

See Appendix 3 for derivation of the above algorithm.

11.4 Experimental Evaluation

We conducted source separation and denoising experiments to verify the effectiveness of observation vector clustering introduced in this chapter.

11.4.1 Source Separation

We first describe the source separation experiment. We assumed that the number of sources was known. We generated observed signals by convolving 8s-long English speech signals with room impulse responses measured in an experimental room (see Fig. 11.6). The sampling frequency of the observed signals was 8 kHz; the frame length 1024 points (128 ms); the frame shift 256 points (32 ms); the number of EM iterations 100. The permutation problem was resolved by Sawada’s method [16]. Source signal estimates were obtained based on masking as in (11.8).

Fig. 11.6

Configurations in room impulse response measurement

Fig. 11.7

Signal-to-distortion ratio (SDR) as a function of the reverberation time $\text {RT}_{60}$

Figure 11.7 shows the signal-to-distortion ratio (SDR) [34] as a function of the reverberation time $\text {RT}_{60}$, and Fig. 11.8 shows an example of source separation results. The SDRs were averaged over 16 trials with eight combinations of speech signals and two distances between a loudspeaker and the array center. The azimuths of sources were $70^\circ$ and $150^\circ$ for $N=2$, and $70^\circ$, $150^\circ$, and $245^\circ$ for $N=3$.

Fig. 11.8

Example of source separation results for $N=2$ and $\text {RT}_{60}=130$ ms. The horizontal axis represents the time, and the vertical the frequency. To focus on low frequencies, which contain most speech energy, only the frequency range of 0 to 2 kHz is shown. The temporal range shown corresponds to 10 s

11.4.2 Denoising

Now we move on to the denoising experiment. The performance was measured by the word error rate (WER) of ASR on the CHiME-3 task [35]. The CHiME-3 task consists in recognition of WSJ-5K prompts read from, and recorded by, a tablet device equipped with $M=6$ microphones in four noisy public areas: on the bus (BUS), cafe (CAF), pedestrian area (PED), and street junction (STR). For further details about the data, we refer the readers to [35].

Denoising was performed by using MVDR beamformers designed using the estimated masks as in Sect. 11.2.2. Assuming that the background noise arrive from all directions equally (i.e., noise is diffuse), we set $\kappa ^{(0)}_f=0$ for the cWMM, $\mathbf {B}^{(0)}_f=0$ for the cBMM, and $\mathbf {B}^{(0)}_f=\mathbf {I}$ for the cGMM. Permutation alignment was performed by the method proposed in [36], which is based on a common amplitude modulation property of speech. The frame length and the frame shift were 64 ms and 16 ms, respectively, and the window was hann.

ASR was performed by using a DNN-HMM-based acoustic model with a fully connected DNN (10 hidden layers) and an RNN-based language model. The acoustic model was trained on 18 hours of multicondition data.

The word error rate (WER) for the real data of the development set, averaged over all environments, was as follows:

• no denoising: 14.29$\,\%$,

• denoising with the cWMM: 10.2$\,\%$,

• denoising with the cBMM: 8.3$\,\%$,

• denoising with the cGMM: 9.3$\,\%$.

We see that the WER has been reduced significantly by mask-based MVDR beamforming.

11.5 Conclusions

In this chapter, we described multichannel source separation and denoising based on source sparseness. Particularly, we introduced recently proposed framework of observation vector clustering, which have been shown to be effective and robust in the real world. We also introduced specific algorithms for observation vector clustering, based on the cWMM, the cBMM, and the cGMM.

Appendices

Appendix 1 Derivation of cWMM-Based Mask Estimation Algorithm

Here we derive the cWMM-based mask estimation algorithm in Sect. 11.3.1. The derivation of the E-step is straightforward and omitted. The update rules for the M-step is obtained by maximizing the following Q-function with respect to $\varTheta _{\text {W},f}$:

$$\begin{aligned} Q(\varTheta _{\text {W},f})&\triangleq \sum _{t=1}^T\sum _k\tilde{\gamma }^{(k)}_{tf}\ln \Biggl [\alpha ^{(k)}_fp_\text {W}\Bigl (\mathbf {z}_{tf};\mathbf {a}^{(k)}_f,\kappa ^{(k)}_f\Bigr )\Biggr ] \end{aligned}$$

(11.52)

$$\begin{aligned}&=\sum _k\biggl (\sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}\biggr )\ln \alpha ^{(k)}_f -\sum _k\biggl (\sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}\biggr )\ln \mathscr {K}\Bigl (1,M;\kappa ^{(k)}_{f}\Bigr ) \end{aligned}$$

(11.53)

$$\begin{aligned}&{=}+\sum _k\kappa ^{(k)}_{f}\mathbf {a}^{(k)\textsf {H}}_f\biggl ( \sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}\mathbf {z}_{tf}\mathbf {z}^{\textsf {H}}_{tf} \biggr )\mathbf {a}^{(k)}_f+C \nonumber \\&=\sum _k\biggl (\sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}\biggr )\Biggl [\ln \alpha ^{(k)}_f -\ln \mathscr {K}\Bigl (1,M;\kappa ^{(k)}_{f}\Bigr )+\kappa ^{(k)}_{f}\mathbf {a}^{(k)\textsf {H}}_f\mathbf {R}^{(k)}_f\mathbf {a}^{(k)}_f\Biggr ]+C. \end{aligned}$$

(11.54)

Here, $\mathbf {R}^{(k)}_f$ is defined by

$$\begin{aligned} \mathbf {R}^{(k)}_f\triangleq \frac{ \sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}\mathbf {z}_{tf}\mathbf {z}^{\textsf {H}}_{tf}}{\sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}}, \end{aligned}$$

(11.55)

and C denotes a constant independent of $\varTheta _{\text {W},f}$.

The update rule for $\alpha ^{(k)}_f$ is obvious: note the constraint (11.18) and apply the Lagrangian multiplier method.

The update rule for $\mathbf {a}^{(k)}_f$ is obtained by maximizing $Q(\varTheta _{\text {W},f})$ subject to (11.19). Noting (11.26), we see that this is equivalent to maximizing $\mathbf {a}^{(k)\textsf {H}}_f\mathbf {R}^{(k)}_f\mathbf {a}^{(k)}_f$ subject to (11.19). From the linear algebra, $\mathbf {a}^{(k)}_f$ is therefore a unit-norm principal eigenvector of $\mathbf {R}^{(k)}_f$.

The update rule for $\kappa ^{(k)}_f$ is obtained by maximizing

$$\begin{aligned} -\biggl (\sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}\biggr )\ln \mathscr {K}\Bigl (1,M;\kappa ^{(k)}_{f}\Bigr )+ \biggl (\sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}\biggr )\kappa ^{(k)}_{f}\mathbf {a}^{(k)\textsf {H}}_f\mathbf {R}^{(k)}_f\mathbf {a}^{(k)}_f. \end{aligned}$$

(11.56)

Since $\mathbf {a}^{(k)}_f$ is a unit-norm principal eigenvector of $\mathbf {R}^{(k)}_f$, we have

$$\begin{aligned} \mathbf {a}^{(k)\textsf {H}}_f\mathbf {R}^{(k)}_f\mathbf {a}^{(k)}_f=\lambda ^{(k)}_f, \end{aligned}$$

(11.57)

where $\lambda ^{(k)}_f$ is the principal eigenvalue of $\mathbf {R}^{(k)}_f$. Therefore, we have the following nonlinear equation for $\kappa ^{(k)}_{f}$:

$$\begin{aligned} \frac{\partial }{\partial \kappa ^{(k)}_{f}}\mathscr {K}\Bigl (1,M;\kappa ^{(k)}_{f}\Bigr )=\lambda ^{(k)}_f\mathscr {K}\Bigl (1,M;\kappa ^{(k)}_{f}\Bigr ). \end{aligned}$$

(11.58)

Using (3.8) in [37], (11.58) is approximately solved as follows:

$$\begin{aligned} \kappa ^{(k)}_{f}=\frac{M\lambda ^{(k)}_f-1}{2\lambda ^{(k)}_f\Bigl (1-\lambda ^{(k)}_f\Bigr )}\Biggl [1+\sqrt{\displaystyle 1+\frac{4(M+1)\lambda ^{(k)}_f\Bigl (1-\lambda ^{(k)}_f\Bigr )}{M-1}}\Biggr ]. \end{aligned}$$

(11.59)

Appendix 2 Derivation of cBMM-Based Mask Estimation Algorithm

Here we derive the cBMM-based mask estimation algorithm in Sect. 11.3.2. The update rule for the E-step is obvious. The update rules for the M-step is obtained by maximizing the following Q-function with respect to $\varTheta _{\text {B},f}$:

$$\begin{aligned} Q(\varTheta _{\text {B},f})&\triangleq \sum _{t=1}^T\sum _k\tilde{\gamma }^{(k)}_{tf}\ln \Biggl [\alpha ^{(k)}_fp_\text {B}\Bigl (\mathbf {z}_{tf};\mathbf {B}^{(k)}_f\Bigr )\Biggr ] \end{aligned}$$

(11.60)

$$\begin{aligned}&=\sum _k\biggl (\sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}\biggr )\ln \alpha ^{(k)}_f -\sum _k\biggl (\sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}\biggr )\ln c\Bigl (\mathbf {B}^{(k)}_{f}\Bigr ) \end{aligned}$$

(11.61)

$$\begin{aligned}&{=}+\sum _k\text {tr}\Biggl [\mathbf {B}^{(k)}_{f}\biggl ( \sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}\mathbf {z}_{tf}\mathbf {z}^{\textsf {H}}_{tf} \biggr )\Biggr ] \nonumber \\&=\sum _k\biggl (\sum _{t=1}^T{\gamma }^{(k)}_{tf}\biggr )\Biggl [\ln \alpha ^{(k)}_f-\ln c\Bigl (\mathbf {B}^{(k)}_{f}\Bigr )+\text {tr}\Bigl (\mathbf {B}^{(k)}_{f}\mathbf {R}^{(k)}_{f}\Bigr )\Biggr ]. \end{aligned}$$

(11.62)

Here, $c(\mathbf {B})$ is defined by (11.36), and $\mathbf {R}^{(k)}_f$ by (11.55).

The update rule for $\alpha ^{(k)}_f$ is obvious.

To derive the update rule for $\mathbf {B}^{(k)}_{f}$, let us denote the mth largest eigenvalue of $\mathbf {R}^{(k)}_{f}$ by $\lambda ^{(k)}_{fm}$ and a corresponding unit-norm eigenvector by $\mathbf {v}^{(k)}_{fm}$. We assume that $\lambda ^{(k)}_{fm},$ $m=1,\dots ,M,$ are all distinct and positive, which is always true in practice. $\mathbf {R}^{(k)}_{f}$ is represented as

$$\begin{aligned} \mathbf {R}^{(k)}_{f}=\sum _{m=1}^M\lambda ^{(k)}_{fm}\mathbf {v}^{(k)}_{fm}\mathbf {v}^{(k)\textsf {H}}_{fm}. \end{aligned}$$

(11.63)

From a result in [38], $\mathbf {v}^{(k)}_{fm},$ $m=1,\dots ,M$, are also the eigenvectors of $\mathbf {B}^{(k)}_{f}$. Hence, $\mathbf {B}^{(k)}_{f}$ is represented in the form

$$\begin{aligned} \mathbf {B}^{(k)}_{f}=\sum _{m=1}^M\beta ^{(k)}_{fm}\mathbf {v}^{(k)}_{fm}\mathbf {v}^{(k)\textsf {H}}_{fm}. \end{aligned}$$

(11.64)

Substituting (11.63) and (11.64) into (11.62) and disregarding terms independent of $\beta ^{(k)}_{fm}, m=1,\dots ,M,$ we have

$$\begin{aligned} \biggl (\sum _{t=1}^T{\gamma }^{(k)}_{tf}\biggr )\Biggl [-\ln c\Bigl (\mathbf {B}^{(k)}_{f}\Bigr )+\sum _{m=1}^M \lambda ^{(k)}_{fm}\beta ^{(k)}_{fm} \Biggr ]. \end{aligned}$$

(11.65)

Therefore, we have

$$\begin{aligned} \frac{\partial \ln c\Bigl (\mathbf {B}^{(k)}_{f}\Bigr )}{\partial \beta ^{(k)}_{fm}}=\lambda ^{(k)}_{fm}. \end{aligned}$$

(11.66)

Using an approximation in [38], this nonlinear equation can be approximately solved as follows:

$$\begin{aligned} \beta ^{(k)}_{fm}\sim -\frac{1}{\lambda ^{(k)}_{fm}}. \end{aligned}$$

(11.67)

Substituting (11.67) into (11.64) and adding a matrix of the form $\xi \mathbf {I}$ so that the largest eigenvalue of $\mathbf {B}^{(k)}_{f}$ is zero, we obtain the following update rule for $\mathbf {B}^{(k)}_{f}$:

$$\begin{aligned} \mathbf {B}^{(k)}_{f}\leftarrow \sum _{m=1}^M\Biggl (-\frac{1}{\lambda ^{(k)}_{fm}}+\frac{1}{\lambda ^{(k)}_{f1}}\Biggr )\mathbf {v}^{(k)}_{fm}\mathbf {v}^{(k)\textsf {H}}_{fm}. \end{aligned}$$

(11.68)

Appendix 3 Derivation of cGMM-Based Mask Estimation Algorithm

Here we derive the cGMM-based mask estimation algorithm in Sect. 11.3.3. The derivation of the E-step is straightforward and omitted. The update rules for the M-step is obtained by maximizing the following Q-function with respect to $\varTheta _{\text {G},f}$:

$$\begin{aligned} Q(\varTheta _{\text {G},f})&\triangleq \sum _{t=1}^T\sum _k\tilde{\gamma }^{(k)}_{tf}\ln \biggl [\alpha ^{(k)}_fp_\text {G}\Bigl (\mathbf {y}_{tf};0,\phi ^{(k)}_{tf}\mathbf {B}^{(k)}_f\Bigr )\biggr ] \end{aligned}$$

(11.69)

$$\begin{aligned}&=\sum _k\biggl (\sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}\biggr )\ln \alpha ^{(k)}_f -M\sum _{t=1}^T\sum _k\tilde{\gamma }^{(k)}_{tf}\ln \phi ^{(k)}_{tf} \end{aligned}$$

(11.70)

$$\begin{aligned}&{=}-\sum _k\biggl (\sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}\biggr )\ln \det \mathbf {B}^{(k)}_{f}-\nonumber \sum _{t=1}^T\sum _k \frac{\tilde{\gamma }^{(k)}_{tf}}{\phi ^{(k)}_{tf}}\mathbf {y}_{tf}^\textsf {H}\Bigl (\mathbf {B}^{(k)}_f\Bigr )^{-1}\mathbf {y}_{tf}+C\nonumber \\&=\sum _k\biggl (\sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}\biggr )\ln \alpha ^{(k)}_f -M\sum _{t=1}^T\sum _k\tilde{\gamma }^{(k)}_{tf}\ln \phi ^{(k)}_{tf} \\&{=}-\sum _k\biggl (\sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}\biggr )\ln \det \mathbf {B}^{(k)}_{f}-\nonumber \sum _k\text {tr}\Biggl [\Bigl (\mathbf {B}^{(k)}_f\Bigr )^{-1}\Biggl (\sum _{t=1}^T\frac{\tilde{\gamma }^{(k)}_{tf}}{\phi ^{(k)}_{tf}}\mathbf {y}_{tf}\mathbf {y}_{tf}^\textsf {H}\Biggr )\Biggr ]+C.\nonumber \end{aligned}$$

(11.71)

Here, C denotes a constant independent of $\varTheta _{\text {G},f}$.

The update rule for $\alpha ^{(k)}_f$ is obvious.

From (11.70), the update rule for $\phi ^{(k)}_{tf}$ is given by

$$\begin{aligned} \phi ^{(k)}_{tf}=\frac{1}{M}\mathbf {y}_{tf}^\textsf {H}\Bigl (\mathbf {B}^{(k)}_f\Bigr )^{-1}\mathbf {y}_{tf}. \end{aligned}$$

(11.72)

As for $\mathbf {B}^{(k)}_{f}$, it should satisfy

$$\begin{aligned} -\biggl (\sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}\biggr )\Bigl (\mathbf {B}^{(k)}_{f}\Bigr )^{-1}+\Bigl (\mathbf {B}^{(k)}_f\Bigr )^{-1}\Biggl (\sum _{t=1}^T\frac{\tilde{\gamma }^{(k)}_{tf}}{\phi ^{(k)}_{tf}}\mathbf {y}_{tf}\mathbf {y}_{tf}^\textsf {H}\Biggr )\Bigl (\mathbf {B}^{(k)}_f\Bigr )^{-1}=0. \end{aligned}$$

(11.73)

Therefore, the update rule for $\mathbf {B}^{(k)}_{f}$ is

$$\begin{aligned} \mathbf {B}^{(k)}_f=\frac{\sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}\mathbf {y}_{tf}\mathbf {y}^\textsf {H}_{tf}/\phi ^{(k)}_{tf}}{\sum _{t=1}^T\tilde{\gamma }^{(k)}_{tf}}. \end{aligned}$$

(11.74)