Decentralized Progressive Shape Formation with Robot Swarms

Abstract

We tackle the problem of achieving any given shape defined as a point cloud in a distributed manner with a swarm of robots. The contributions of this paper are (i) An algorithm that transforms a point cloud into a acyclic directed graph; (ii) A motion control law that, from the acyclic directed graph, allows a swarm of robots to achieve the target shape in a decentralized manner; and (iii) A theoretical model, which provides sufficient conditions on the convergence of the control law. The key idea of our approach is to achieve the target shape progressively by inducing an ordering among the robots. More precisely, we construct an acyclic directed graph so that any free robot (i.e., not part of the shape) finds its location with respect to the already placed robots. We prove that, for a 2D shape, it is sufficient for a free robot to calculate its location with respect to two already placed robots to achieve this objective. We validate our method through accurate physics-based simulations of non-holonomic robots.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Swarm robotics [5] is a branch of collective robotics that focuses on decentralized approaches to the problem of coordinating large teams of robots. A common assumption in many existing approaches is that all of the robots involved in the execution of a certain algorithm are ready to take part in it. However, especially when swarm sizes involve more than a dozen robots, it is hardly conceivable that all of the robots will be available. Economical and technological constraints are major drivers in the limitation of the number of robots that can be deployed in a specific time frame. For instance, in exploratory missions of planets or deep ocean floors, it is probable that only a small number of robots can be successfully deployed in a single mission. In addition, future missions involving complex, heterogeneous robot swarms will naturally unfold in a phase-wise fashion. In a large-scale Mars exploration mission, for instance, a first wave of radiation-hardened robots might be dedicated to creating shelter and network infrastructure for future waves of cheaper, more mission-specific robots.

A new class of swarm algorithms is necessary, which focuses on swarms that are progressively deployed over time [3]. As a step in this direction, we present a progressive, decentralized algorithm that allows a robot swarm to achieve a specific shape. Shape formation is an important application for robot swarms. Typical examples include monitoring of large-scale areas, satellite displacement in orbit, and the creation of ad hoc, large-scale network infrastructure. In these applications, it is desirable that even if the final form of the target shape has not been attained yet, the already placed robots can begin performing their assigned tasks. Thus, the time taken to complete the shape is, at least to an extent, less important than the time taken to add a new robot to the shape and the precision of the positioning.

The core of our idea is to express the target shape as an acyclic directed graph, in which each robot finds and maintains its position by considering only two other robots in the shape, called the parents. All robots know the acyclic directed graph, but initially no robot is assigned to any specific position in the shape. The shape is constructed dynamically and in an iterative fashion—each robot joins upon being granted permission by one of the parents. Based solely on local communication, our algorithm is completely decentralized. The algorithm is also parallel, since at any time multiple robots can join different parts of the shape.

The rest of the paper is organized as follows. We discuss related work in Sect. 2. In Sect. 3, we illustrate a mathematical model that proves the convergence properties of our decentralized algorithm. In Sect. 4, we present an algorithm to construct an acyclic directed graph starting from a point cloud which represents the target shape. In Sect. 5, we describe the behavior the robots follow to achieve the target shape. We report experimental evaluation in Sect. 6. The paper is concluded by Sect. 7, in which we outline future research directions.

2 Related Work

The problem of formation control has been widely studied in the literature. Relevant, recent examples of decentralized methodologies are consensus-based approaches [11, 15, 20] and rigidity-based approaches [2, 7, 19]. The interested reader is referred to [6, 10] and references therein for a more comprehensive overview of the formation control problem.

Considering the vastness of the literature, and that we deal with the problem of achieving any given shape defined as a point cloud in a decentralized manner, we focus on approaches with a similar objective.

Spletzer and Fierro [17] consider the task of repositioning a formation of robots to a new shape while minimizing either the maximum distance that any robot travels, or the total distance traveled by the formation. Ravichandran et al. [14] present a scalable distributed reconfiguration algorithm to achieve arbitrary target configurations built on top of a distributed median consensus estimator which requires only local communication. Yu and Nagpal [21] present a theoretical study of decentralized control for sensing-based shape formation on modular multi-robot systems, where the desired shape is specified in terms of local sensor constraints between neighboring robot agents. Alonso-Mora et al. [1] consider arbitrary target patterns and detect a proper representation with an optimal robot deployment, using a method that is independent of the number of robots. Liu and Shell [8] tackle the problem of changing smoothly between formations of spatially deployed multi-robot systems, and show that this can be achieved by routing agents on a Euclidean graph that corresponds to paths computed on—and projected from—an underlying three-dimensional matching graph.

3 Mathematical Model

3.1 Problem Statement

Let us consider a team of N mobile robots moving in $\mathbb R^2$, each of which is assigned a label $i \in \{1,...,N\}$. For each robot, let the vector $\mathbf p_i(t)=[x_i(t), y_i(t)]^T \in \mathbb R^2$ describe its position with respect to a fixed global reference frame $\mathscr {O}_{xy}^g$. It is assumed that each robot has a dynamics

$$\begin{aligned} {\dot{\mathbf {p}}}_i= \mathbf u_i. \end{aligned}$$

(1)

We assume that each robot i does not know its absolute position $\mathbf p_i(t)$, but it can measure the relative distance $d_{ij}(t) = ||\mathbf p_i(t) - \mathbf p_j(t) ||$ and the relative bearing $\theta _{ij}(t)$ with respect to any neighboring robot j. We also assume that the nodes can communicate with their neighboring robots, i.e., the robots in their direct line-of-sight. Communication and distance/angle estimation can be achieved through situated communication [18] devices present on commercial robots such as the e-puck [9].

The problem statement can be defined as follows.

Problem 1

Given a desired formation expressed as a set of of desired positions $\{{\bar{\mathbf {q}}}_1, {\bar{\mathbf {q}}}_2, \ldots , {\bar{\mathbf {q}}}_N\}$, there exists a translation $\mathbf r \in \mathfrak {R}^2$ and a rotation $R(\theta )$ such that

$$ \lim _{t \rightarrow \infty } R(\theta ) \mathbf {p}_i(t) + \mathbf r = {\bar{\mathbf {q}}}_i. $$

In this problem formulation, we are not interested in having the formation converge to a specific position in the environment. Rather, we impose that the target shape can be arbitrarily rototranslated w.r.t. the fixed global reference frame. In the remainder of this section, for the sake of simplicity and without loss of generality, we will consider ${\bar{\mathbf {q}}}_1=[0, 0]^T$ and ${\bar{\mathbf {q}}}_2=[x_2, 0]^T$ with $x_2 > 0$. Under this assumption, we call $\mathbf {p}_i^{12}$ the coordinates of the i-th robot in the reference frame centered in $\mathbf {p}_1$. The x axis is oriented as the vector connecting $\mathbf {p}_1$ to $\mathbf {p}_2$, while the y axis is obtained through a $\pi /2$ anti-clockwise rotation of x around $\mathbf {p}_1.$ We then restate Problem 1 as the following control problem:

Problem 2

Given a desired formation $\{{\bar{\mathbf {q}}}_1, {\bar{\mathbf {q}}}_2, \ldots , {\bar{\mathbf {q}}}_n\}$ where ${\bar{\mathbf {q}}}_1=[0,0]^T$ and ${\bar{\mathbf {q}}}_2=[x_2, 0]^T$ and $x_2 > 0$, ensure that ${\dot{\mathbf {p}}}_{i} \rightarrow 0$ and $\mathbf {p}_i \rightarrow {\bar{\mathbf {q}}}_i$ $\forall i \in \{1, \ldots , N\}$.

3.2 Proposed Solution

For robot 1, a simple solution to Problem 2 is to maintain its current position, i.e.,

$$\begin{aligned} \mathbf {u}_1 = \mathbf {0}. \end{aligned}$$

(2)

For robot 2, an equally simple solution is to apply any control law of the form

$$\begin{aligned} \mathbf {u}_2 = \mathbf {f}_2(d_{1,2}(t)) \end{aligned}$$

(3)

that ensures that $d_{1,2}(t)$ globally asymptotically tends to $||{\bar{\mathbf {q}}}_1(t) - {\bar{\mathbf {q}}}_2(t) ||$. A distance-based attraction/repulsion law, such as the Coulomb potential [16], is a good choice for $\mathbf {f}_2$.

Concerning the other robots ($i>2$), we associate to each of them two parent nodes j and k and define a continuously differentiable potential field $\varPhi _i(\mathbf {p}_i, \mathbf {p}_j, \mathbf {p}_k),$ $\varPhi _i : \mathfrak {R}^2 \times \mathfrak {R}^2\times \mathfrak {R}^2 \rightarrow \mathfrak {R}$, such that, for any two bounded $\mathbf {p}_j$ and $\mathbf {p}_k$, these assumptions hold:  

A1::

$\varPhi _i(\mathbf {p}_i, \mathbf {p}_j, \mathbf {p}_k)$ is invariant to rototranslations:

$$ \varPhi _i( R(\theta ) \mathbf {p}_i + \mathbf {r}, R(\theta ) \mathbf {p}_j + \mathbf {r}, R(\theta ) \mathbf {p}_k + \mathbf {r}) = \varPhi _i(\mathbf {p}_i, \mathbf {p}_j, \mathbf {p}_k). $$

A2::

$\varPhi _i(\mathbf {p}_i, \mathbf {p}_j, \mathbf {p}_k)$ is unbounded for unbounded $\mathbf {p}_i$:

$$ \lim _{||\mathbf {p}_i||\rightarrow \infty } \varPhi _i(\mathbf {p}_i, \mathbf {p}_j, \mathbf {p}_k) = \infty . $$

A3::

If $p_j$ and $p_k$ are distinct, $\varPhi _i(\mathbf {p}_i, \mathbf {p}_j, \mathbf {p}_k)$ admits only one stationary point, which we denote as ${\bar{\mathbf {p}}}_i(\mathbf {p}_j,\mathbf {p}_k)$, and that point is a minimum of the potential field. This corresponds to forcing robot i to only have one possible position to reach when communicating with robots j and k.

A4::

There exist two finite scalars $\alpha _{\text {max}}$ and $\beta _{\text {min}}$ such that for any $\mathbf {p}_j,\, \mathbf {p}_k$

$$ -\nabla \varPhi _i( \mathbf {p}_i, \mathbf {p}_j, \mathbf {p}_k)^T \nabla \varPhi _i( \mathbf {p}_i, \mathbf {p}_j + \mathbf {d}_j, \mathbf {p}_k + \mathbf {d}_k) \le 0 $$

for any $||\mathbf {b}_j||,||\mathbf {b}_k||\le \alpha _{\text {max}},$ and for any $\mathbf {p}_i={\bar{\mathbf {p}}}_i(\mathbf {p}_j, \mathbf {p}_k)+\mathbf {d}_i$ with $||\mathbf {d}_i||\ge \beta _{\text {max}}$. This means that, for bounded perturbations of the parents $\mathbf {p}_j$ and $\mathbf {p}_k$, if $\mathbf {p}_i$ is sufficiently far from the equilibrium, the perturbed anti-gradient is still a direction of descent of the non-perturbed potential field.

  We prove the following theorem by using a control law in the form:

$$\begin{aligned} \mathbf {u}_i = -\nabla \varPhi _i(\mathbf {p}_i, \mathbf {p}_j, \mathbf {p}_k), \end{aligned}$$

(4)

Theorem 1

Consider the system described by Equation (1) controlled by control laws in the form of Equations (2)–(4) that comply with assumptions A1–A4. Under the constraints

• 1. If j and k are parents of i, then $j < i$ and $k < i$;

• 2. ${\bar{\mathbf {p}}}_i({\bar{\mathbf {q}}}_j, {\bar{\mathbf {q}}}_k) = {\bar{\mathbf {q}}}_i\quad \forall i \in \{1,\ldots ,N\}$;

Problem 2 is solved for any initial condition.

Since every position ${\bar{\mathbf {q}}}_i$ in the target shape is expressed with respect to two other positions ${\bar{\mathbf {q}}}_j$ and ${\bar{\mathbf {q}}}_k$, and $j<i$ and $k<i$, we can represent the target shape as an acyclic directed graph in which every node i is connected to its parents j and k. Thus, the process of positioning a specific robot i can ideally be seen as a cascade of positioning processes, which starts with robot 1 and proceeds with all other robots. If every step of the positioning dynamics is globally asymptotically stable, then the entire process converges to the desired shape. This is the core idea behind the proof in [12].

For some applications, assumptions A3 and A4 might prove too strong. For instance, the existence of a single stationary point topologically forbids the use of repulsion terms among robots that are usually used for collision avoidance. To fix this, consider the following relaxed condition:  

A3bis::

If $\mathbf {p}_j$ and $\mathbf {p}_k$ are distinct there exists ${\bar{\mathbf {p}}}_i(\mathbf {p}_j,\mathbf {p}_k)$ which is an isolated minimum of $\varPhi _i(\mathbf {p}_i,\mathbf {p}_j,\mathbf {p}_k)$.

  By using A3bis instead of A3 and dropping assumption A4, the formation is asymptotically stable. This means that there exists a basin of attraction around the configuration of equilibrium ${\dot{\mathbf {p}}}_i^{1,2} = {\bar{\mathbf {q}}}_i$ for which Problem 2 is solved.

Theorem 2

Consider the system described by Equation (1) controlled by Equations (2)–(4) that comply with assumptions A1, A2, and A3bis. Under the contraints:

• 1. If j and k are parents of i, then $j <i$ and $k <i$;

• 2. ${\bar{\mathbf {p}}}_i({\bar{\mathbf {q}}}_j,{\bar{\mathbf {q}}}_k) = {\bar{\mathbf {q}}}_i\quad \forall i \in \{1,\ldots ,N\}$;

Problem 2 is solved for initial conditions in a suitable neighborhood of the equilibrium configuration of ${\dot{\mathbf {p}}}_i^{1,2} = \mathbf {q}_i\quad \forall i \in \{1,\ldots ,N\}.$

The proof is reported in [12].

4 From Point Cloud to Acyclic Directed Graph

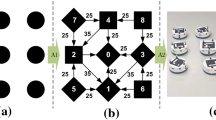
The target shape is expressed as a 2D point cloud. In this section, we present an algorithm that produces an acyclic directed graph starting from the 2D point cloud (see also Fig. 1). The specific frame of reference used to express the point cloud is not important, since the labeled graph must only encode the relative distances between a robot and its two predecessors.

Fig. 1

Depiction of the input and output of the algorithm presented in Sect. 4. The left side shows the input, an unlabeled point cloud. The right side illustrates the labeled acyclic directed graph output by the algorithm. In the output, numerical labels identify the position in the acyclic directed graph; arrows indicate the parents of a specific shape node, and the associated numbers denote the parent-child distance in cm. Square nodes are those located on the positive side with respect to the vector joining the two parents; diamond nodes are on the negative side. Sides are calculated considering the right-hand rule

The algorithm proceeds iteratively and collects the points in three lists:

• the unlabeled list contains the points for which no label was found yet;

• the delayed list contains the points for which a label was searched, but it was impossible to find one in the current iteration;

• the labeled list stores the labeled points.

The algorithm starts by storing all points as unlabeled, and by calculating the center of mass of the point cloud. The points are then sorted by their distance to the center of mass. The two closest points are labeled 0 and 1, 0 is stored as a predecessor of 1, and the points are moved to labeled. Using the center of mass allows the shape formation process to start at the center of the shape and to grow outwards, making it easier for joining robots to navigate to their target position.

Subsequent points are labeled as follows. First, a candidate point is drawn from the unlabeled set. Next, the viable predecessors among the points in labeled are searched. Two points are viable if, with the candidate point, they form a triangle in which every robot has unobstructed line-of-sight with the other two. If no pair of predecessor can be found, the candidate is moved to delayed and a new candidate point is drawn. As soon as two viable predecessors are found, the candidate point is stored into labeled and a new graph element is added (each node stores labeled node, predecessors, and positional information—see Fig. 1, right). The delayed points are moved back to unlabeled, and a new iteration of the algorithm is performed.

The algorithm ends when no points are present in unlabeled. If delayed is an empty set, the algorithm finished successfully, as all points have been labeled; otherwise, the algorithm fails.

5 Robot Behavior

Assumptions. At time zero, no robot is part of the structure. The process that brings a robot to the decision of triggering the shape formation behavior depends on the specific experiment under study. Here, we assume that a single robot makes such decision, i.e., the process is not started twice in the same swarm. For simplicity, we also assume that every robot knows the acyclic graph of the target shape. However, this assumption could be lifted. For instance, the robot that triggers the behavior could broadcast the data of the labeled graph chosen for the task at hand. Nearby robots, upon receiving this data, could help diffuse it either unconditionally, or only when they join the shape.

Fig. 2

A finite state machine representation of the robot behavior

Behavior Structure. The behavior is composed of four states (see Fig. 2):  

Free::

A robot is this state is not part of the structure, nor actively requesting to join. In this state, a robot monitors its neighborhood searching for a label i that is not currently part of the shape nor being requested by other robots. If such label is found and both parents for it are in direct line-of-sight, the robot switches to state Asking.

Asking::

A robot in this state broadcasts a request to join with label i. If the request receives no response for a predefined time, or if another robot is accepted, any rejected robot switches back to Free. Otherwise, the robot switches to state Joining.

Joining::

A robot in this state uses the two parents as references to join the shape. The robot navigates to the target position. As soon as its distance to the target is smaller than a tolerance $\varepsilon$, the robot switches to Joined.

Joined::

A robot in this state is part of the shape and performs two activities: (i) It maintains its position with respect to the relevant robots around it—the relevant robots are its direct parents and children; and (ii) It collects requests from Asking robots, granting access to the one in the best position to assume a specific label.

 

Communication. During the construction of the shape, every robot broadcasts a message to inform its neighbors of its current state. In addition, some states require extra information to be broadcast. When a robot is Asking, it broadcasts a request structured as a tuple $\langle \textsc {Asking}$,i,$z\rangle$, in which z is the request id. The latter is drawn uniformly at random between 1 and a sufficiently large number Z.¹ A robot in Asking state is such that the parents of label i are in direct line-of-sight. Thus, both parents receive the request. The parent with the higher label m is in charge of responding to the request. This parent collects the requests received in the last time step and ranks them from the simplest to achieve (i.e., the requesting robot is close to its target position) to the hardest to achieve. The best request is granted by broadcasting a message $\langle \textsc {Joined}$,m,i,$\bar{z},\texttt {granted}\rangle$, where $\bar{z}$ identifies the request for label i univocally. The accepted robot switches to Joining, while the other robots that asked for i switch back to state Free. Rarely, it might happen that two robots choose the same request id z for the same label i. In this case, the robot in charge replies with $\langle \textsc {Joined}$,m,i,repeat $\rangle$, which forces the conflicting robots to repeat their request, while informing other robots that their request for i was refused.

Navigation. The mathematical model described in Sect. 3 neglects aspects such as non-holonomic motion, body size, and collision avoidance to guarantee tractability. In a physical implementation of the algorithm, however, these aspects play a crucial role in system dynamics. As discussed in Sect. 3, we assume that the robots are capable of detecting their distance and angle to a number of neighbors in range. Navigation is based solely on this information—we do not require the robots to estimate their global position in the environment. Navigation is implemented following the well-known virtual physics approach [16], whereby virtual forces are calculated by overlapping multiple potential fields according to the state of the robots.  

Free::

When a robot is in this state, it must keep at a safe distance from the structure being built to prevent congestion. In addition, Free robots follow the external perimeter of the shape and search for free labels. This is obtained by combining two virtual forces: one that imposes a sufficiently large distance from the shape, and one that pushes the robots perpendicularly to any Joining or Joined robot in sight.

Asking::

Robots in this state must keep in sight to the two parents of the label being requested. The virtual force is calculated by imposing bounded repulsion to Free robots and bounded attraction to Joined robots.

Joining::

To join the shape, a robot must follow the complex, position-dependent force field depicted in Fig. 3, which corresponds to $-\nabla \varPhi _i(\mathbf {p}_i,\mathbf {p}_j,\mathbf {p}_k)$, discussed in Sect. 3.

Joined::

Robots that already joined the shape must keep their distance to their parents and direct children. In our implementation, we used a field based on Coulomb forces analogous to [16].

  In addition to these primary states, we added a fifth state, Escape, to deal with Free robots that got trapped in the middle of Joined robots. This extra behavior proved important to drop the failure rate of the shape formation process from about 30% to 0.37% (see Sect. 6). An example of the dynamics of the navigation behavior can be seen in Fig. 4.

Fig. 3

Virtual force field experienced by a joining robot with respect to its parents j and k. The black star indicates the target position to be reached by the joining robot. This force field is a realization of $-\nabla \varPhi _i(\mathbf {p}_i,\mathbf {p}_j,\mathbf {p}_k)$, discussed in Sect. 3

Fig. 4

The dynamics of the presented behavior with a heart-like shape formed by 114 robots. The black robots are Free, and the green-yellow robots are Joined. Screenshot taken with the ARGoS simulator. A video is available at http://carlo.pinciroli.net/DARS2016/heart.mp4

6 Experimental Evaluation

We evaluated the performance of our shape formation algorithm through a set a simulated experiments. We employed a realistic, physics-based simulator for multi-robot systems called ARGoS.² The models present in ARGoS have been validated, and robot controllers developed with this simulator have been succesfully ported to real platforms in many works [13].

Performance measures. We concentrated our analysis on three aspects of the shape formation process: completion time, joining time, and absolute positioning error. Completion time is the time necessary to form a complete shape. Joining time is the time elapsed between two successive join events, i.e., the moments in which the robots become part of the shape, switching to Joined. In the context of a progressive algorithm, this measure is more interesting than completion time, because it accounts for recruitment efficiency. The absolute positioning error $E_{ij}$ between robots i and j is calculated as $E_{ij} = \left| (d_{ij} - \bar{d_{ij}})/\bar{d_{ij}}\right|$ where $\bar{d_{ij}}$ is the expected distance between robots i and j (as stored in the labeled graph), and $d_{ij}$ is the actual distance measured at the end of the experiment.

The target shape. While our algorithm can form generic shapes, to ensure comparability among different experimental conditions, the robots are tasked with the formation of a grid. We worked with three grid sizes—$5 \times 5$, $10 \times 10$, and $15 \times 15$.

Experimental setup. The experimental arena is an empty square of side L, in which M robots are uniformly distributed with a certain density D. We considered three density configurations—broad ($D = 0.01$), medium ($D = 0.05$), and tight ($D = 0.1$). To enforce a specific value of D across different choices of M, we calculated $L = \sqrt{(N \pi R^2)/D}$, where R is the radius of the robot ($R = 8.5\,{\mathrm{cm}}$). For our experiments, we utilized the marXbot [4], a wheeled robot equipped with a range-and-bearing sensor that allows for situated communication; its maximum speed was set to 10 cm/s. We also studied the effect that different numbers of available robots have on the shape formation algorithm. To this aim, we defined N as the number of robots necessary to complete a shape (e.g., $N = 25$ for a $5 \times 5$ grid) and set $M = kN$, with $k \in \{1,2,3\}$. Every configuration $\langle \text {grid size}, D, k\rangle$ was tested 30 times, for a total of 810 runs.

Fig. 5

Experimental evaluation of the shape formation behavior presented in Sect. 5. Each box corresponds to the distribution of a performance measure of a specific experimental configuration $\langle \text {grid size}, D, k\rangle$ over 30 runs (see Sect. 6). The whiskers in the box plots indicate the 5th and 95th percentile. The top plot reports the completion time in seconds; the middle plot reports the joining time in seconds; and the bottom plot reports the positioning error

Discussion. Out of the 810 runs, in only 3 of them the shape was not completed, for a failure rate of 0.37%. In all of the failed runs, a Free robot remained trapped in the middle of the shape, unable to exit. These failures occurred in high-density configurations ($D = 0.1$), and involved a robot that remained trapped at the very beginning of the experiment, when the swarm dynamics is most chaotic. Low- and middle-density runs, on the other hand, all completed successfully. Regarding performance measures, the results are reported in Fig. 5. Both completion time and joining time decrease with k. When $k=1$, all of the robots must find their spot in the shape. Towards the end of an experiment, however, the number of available spots diminishes, and the remaining few robots must spend a long time looking for it. For higher values of k, however, the probability that a free robots finds a vacant label increases, thus lowering the joining time. The effect of the deployment density D is a slight decrease of completion time for tighter initial distributions. Although this effect is only minor, through observation we could notice that, with tighter initial distributions, the robots have to travel shorter distances and, as a consequence, tend to find vacant labels more frequently. The positioning error does not seem to be significantly affected in any configuration, remaining always lower than 8% and with a median slightly above 4%. The fact that these parameters do not affect the error is expected, because the behavior is designed to separate Free and Asking robots from Joining and Joined robots. None of the considered parameters can affect this separation. The actual value of the error is due to the parameter configuration of the force field that a robot follows to reach its place in the shape. With non-holonomic robots, it is common to be unable to reach the exact designated position due to motion limitations. For instance, a 8% error over a distance of 100 cm (i.e., the node distance in all of our experiments) corresponds to 8 cm, which is comparable to the radius of the marXbot ($R = 8.5\,{\mathrm{cm}}$).

7 Conclusions

Progressive deployment is a milestone towards the creation of real-world robot swarms for complex scenarios. In this paper, we presented an approach to the formation of any shape described through a 2D point cloud. Through a mathematical model, we provided sufficient conditions to ensure convergence; we proposed an algorithm to derive an acyclic directed graph from a 2D point cloud; and illustrated a decentralized robot behavior that attains the target shape represented by the acyclic directed graph. We validated our approach through a set of experiments that considered swarm size, available robots, and density of the initial robot distribution.

Future work involves the validation of our approach on real robots. In addition, joining and completion time could be improved by allowing Joined robots to guide Free robots to places where vacant labels are present.