Abstract
This paper presents a technique to reason about functional properties of shared-memory concurrent software by means of abstraction. The abstract behaviour of the program is described using process algebras. In the program we indicate which concrete atomic steps correspond to the actions that are used in the process algebra term. Each action comes with a specification that describes its effect on the shared state. Program logics are used to show that the concrete program steps adhere to this specification. Separately, we also use program logics to prove that the program behaves as described by the process algebra term. Finally, via process algebraic reasoning we derive properties that hold for the program from its abstraction. This technique allows reasoning about the behaviour of highly concurrent, non-deterministic and possibly non-terminating programs. The paper discusses various verification examples to illustrate our approach. The verification technique is implemented as part of the VerCors toolset. We demonstrate that our technique is capable of verifying data- and control-flow properties that are hard to verify with alternative approaches, especially with mechanised tool support.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
The major challenge when reasoning about concurrent or distributed software is to come up with an appropriate abstraction that provides sufficient detail to capture the intended properties, while at the same time making verification manageable. This paper presents a new powerful abstraction approach that enables reasoning about the intended properties of the program in a purely non-deterministic setting, and can abstract code at different levels of granularity. The presentation of the abstraction technique in this paper focuses on shared-memory concurrent programs and safety properties, but many extensions may be explored, for example for distributed programs or progress properties, as sketched in the paragraph on future work. The paper illustrates our approach by discussing multiple verification examples in which we verify various data- and control-flow properties. We demonstrate that the proposed technique can be used to verify program properties that are hard to verify with alternative approaches, especially in a practical manner via mechanised tools.
To motivate our approach, consider the program shown in Fig. 1. The figure shows a parallel version of the classical Euclidean algorithm for finding a greatest common divisor, \(\mathtt{gcd}(x,y)\), of two given positive integers x and y. This is done by forking two concurrent threads: one thread to decrement the value of x whenever possible, and one thread to decrement the value of y.
We are interested in verifying deductively that this program indeed computes the greatest common divisor of x and y. To accomplish this in a scalable fashion requires that our technique be modular, or more precisely procedure-modular and thread-modular, to allow the individual functions and threads to be analysed independently of one another. The main challenge in achieving this lies in finding a suitable way of capturing the effect of function calls and threads on the shared memory in a way that is independent of the other functions and threads. Our proposal is to capture these effects as sequences of exclusive accesses (in this example increments and decrements) to shared memory (in this example the variables x and y). We abstract such accesses into so-called actions, and their sequences into process algebraic terms.
In our example above we abstract the assignments \(x := x - y\) and \(y := y - x\) needed to decrease the values of x and y into actions \(\mathsf{decrx}\) and \(\mathsf{decry}\), respectively. Action behaviour is specified by means of contracts consisting of a guard and an effect; the explanation of the details of this are deferred to Sect. 3. Using these actions, we can specify the effects of the two threads by means of the process algebra terms \(\mathsf{tx}\) and \(\mathsf{ty}\), respectively, which are defined as follows:

Here the action \(\mathsf{done}\) indicates termination of a process. The functional behaviour of the program can then be specified by the process \(\mathsf{pargcd}\) defined as the term \(\mathsf{tx}() \parallel \mathsf{ty}()\). Standard process algebraic reasoning can be applied to show that executing \(\mathsf{pargcd}\) results in calculating the correct \(\mathtt{gcd}\).
Therefore, by proving that the implementation executes as prescribed by \(\mathsf{pargcd}\), we simultaneously establish its functional property of producing the correct result. The \(\mathsf{pargcd}\) process thus describes the program behaviour.
Once the program has been specified, the access exclusiveness of the actions is verified by a suitable extension of separation logic with permission accounting [5, 19]. On top of it, we develop rules that allow to prove, in a thread-local fashion, that the program indeed follows its prescribed process. The details of our technique applied to the above program are presented in Sect. 3.
In previous work [4, 27] we developed an approach that records the actions of a concurrent program as the program executes. Reasoning with this approach is only suitable for terminating programs, and occurs at the end of its execution, requiring the identification of repeating patterns. In contrast, the current approach requires a process algebra term upfront that describes the patterns of atomic concurrent actions, which allows the specification of functional behaviour of reactive, non-terminating programs. For instance, we can verify properties such as “the values of the shared variables x and y will be equal infinitely often”, expressed in LTL by the formula \(\Box \lozenge (x = y)\), of a program that forks separate threads to modify x and y, similarly to the above parallel GCD program.
Compared to many of the other modern logics to reason about concurrent programs, such as CAP [9], CaReSL [26], Iris [17], and TaDA [7], our approach does the abstraction at a different level. Our abstraction connects program code with individual actions, while these other approaches essentially encode an abstract state machine, describing how program steps evolve from one abstract program state to the next abstract program state, and explicitly consider the changes that could be made by the thread environment. As a result, in our approach the global properties are specified in a way that is independent of the program implementation. This makes it easier for non-experts to understand the program specification. The main contributions of this paper are:
-
An abstraction technique to specify and verify the behaviour of possibly non-terminating, shared-memory concurrent programs, where the abstractions are implementation-independent and may be non-deterministic;
-
A number of verification examples that illustrate our approach and can mechanically be verified via the VerCors toolset; and thus
-
Tool support for our model-based reasoning approach.
The remainder of this paper is organised as follows. Section 2 provides a brief background on separation logic and process algebras. Then, Sect. 3 illustrates in more detail how abstract models are used in the verification of the parallel GCD example. Section 4 elaborates on the proof rules as they are used by the VerCors tool set. Section 5 discusses two more verification examples that apply our approach: verifying a concurrent counter and verifying a locking protocol. Finally, Sect. 6 discusses related work and Sect. 7 concludes.
2 Background
Our program logic is an extension of Concurrent Separation Logic (CSL) with permission accounting [1, 19, 22]. The main difference with classical Hoare logic is that each allocated heap location is associated with a fractional permission \(\pi \), modelled as a rational number in the range \((0,1]\) [5, 6]. By allocating a heap location \(\ell \), the allocating thread gets full ownership over \(\ell \), represented by the  predicate. The
predicate. The  predicate gives writing permission to the specified heap location, whereas
predicate gives writing permission to the specified heap location, whereas  for \(\pi < 1\) only gives reading permission. The
for \(\pi < 1\) only gives reading permission. The  predicates may be split and merged along \(\pi \), so that
predicates may be split and merged along \(\pi \), so that  . In this case, \(\Leftrightarrow \) can be read as “splitting” from right to left, or “merging” from left to right. The \(*\) connector is the separating conjunction; the assertion \(\mathcal{P} *\mathcal{Q}\) means that the heap can be split into two disjoint parts, so that one part satisfies the assertion \(\mathcal{P}\) and the other part satisfies \(\mathcal{Q}\). CSL allows (splitted) points-to predicates that are separated via the \(*\)-connective to be distributed over concurrent threads (under certain conditions), thereby allowing to reason about race freedom and about functional behaviour of concurrent programs.
. In this case, \(\Leftrightarrow \) can be read as “splitting” from right to left, or “merging” from left to right. The \(*\) connector is the separating conjunction; the assertion \(\mathcal{P} *\mathcal{Q}\) means that the heap can be split into two disjoint parts, so that one part satisfies the assertion \(\mathcal{P}\) and the other part satisfies \(\mathcal{Q}\). CSL allows (splitted) points-to predicates that are separated via the \(*\)-connective to be distributed over concurrent threads (under certain conditions), thereby allowing to reason about race freedom and about functional behaviour of concurrent programs.
2.1 Dynamic Locking
To reason about dynamically allocated locks we use the program logic techniques proposed by Gotsman et al. [11]. Our language includes the \({{\mathbf {\mathsf{{init}}}}} \ \mathcal{L}\) statement, which initialises a new lock associated with the lock label \(\mathcal{L}\). The program logic requires that a resource invariant is specified for each initialised lock. A resource invariant is a predicate that expresses the ownership predicates protected by the lock. In the program logic a \(\mathsf{Lock}_1(\mathcal{L})\) predicate is produced by \({{\mathbf {\mathsf{{init}}}}} \ \mathcal{L}\), which represents the knowledge of the existence of a lock labelled \(\mathcal{L}\) and this predicate is required to obtain the lock later. Obtaining a lock labelled \(\mathcal{L}\) is done via the \({{\mathbf {\mathsf{{acquire}}}}} \ \mathcal{L}\) statement which, on the program logic level, consumes the \(\mathsf{Lock}_\pi (\mathcal{L})\) predicate and exchanges it for the resource invariant that is associated to \(\mathcal{L}\). Releasing a lock is done via the \({{\mathbf {\mathsf{{release}}}}} \ \mathcal{L}\) statement, which has the reverse effect: it takes the resource invariant of \(\mathcal{L}\) and exchanges it for \(\mathsf{Lock}_\pi (\mathcal{L})\). The \({{\mathbf {\mathsf{{destroy}}}}} \ \mathcal{L}\) statement destroys the lock \(\mathcal{L}\) and thereby consumes \(\mathsf{Lock}_1(\mathcal{L})\) in the program logic and gives back the resource invariant associated to \(\mathcal{L}\).
2.2 Process Algebra Terms
The abstract models we use to reason about programs are represented as process algebra terms. A subset of the \(\mu \)CRL [12, 13] language is used as a suitably expressive process algebra with data. The basic primitives are actions, each representing an indivisible process behaviour. Processes are defined by combining actions and recursive process calls, which both may be parameterised by data. Process algebra terms have the following structure:

where E are arithmetic expressions, B are Boolean expressions, a are action labels, and p are process labels. With \(\overline{E}\) we mean a sequence of expressions.
The empty process is denoted \(\varepsilon \) and the deadlock process by \(\delta \). The process \(a(\overline{E})\) is an action call and \(p(\overline{E})\) a recursive process invocation, with \(\overline{E}\) the argument sequence. Two process terms P and Q may compose either sequentially \(P \ \cdot \ Q\) or alternatively \(P + Q\). The parallel composition \(P \parallel Q\) allows the actions of P and Q to be interleaved during execution. The conditional construct \({{\mathbf {\mathsf{{if}}}}} \, B \, {{\mathbf {\mathsf{{then}}}}} \, P \, {{\mathbf {\mathsf{{else}}}}} \, Q\) resembles the classical “if-then-else”; it yields either P or Q, depending on the result of evaluating the expression B.
3 Motivating Example
This section demonstrates our approach by verifying functional correctness of the parallel GCD verification example that was discussed in the introduction. With functional correctness we mean verifying that, after the program terminates, the correct value has been calculated. In this example, the correct value is the mathematical GCD of the two (positive) values given as input to the algorithm.
Our approach uses the following steps:
-
(1)
Actions and their associated guards and effects are defined that describe in what ways the program is allowed to make updates to shared memory.
-
(2)
The actions are composed into processes by using the process algebraic connectives discussed in Sect. 2. These processes determine the desired behaviour of (parts of) the concrete program. Notably, processes that are composed in parallel correspond to forked threads in the program.
-
(3)
All defined processes that have a contract are verified. Concretely, we automatically verify whether the postconditions of processes can be ensured by all traces that start from a state in which the precondition is satisfied.
-
(4)
Finally we verify that every thread forked by the program behaves as specified by the process algebraic specification. If this is the case, the verification results that are established from (3) can be used in the program logic.
Tool support for model-based reasoning is provided as part of the VerCors verification tool set [2, 3]. The VerCors tool set aims to verify programs under various concurrency models, notably heterogeneous and homogeneous concurrency, written in high-level programming languages such as Java and C. Although most of the examples presented in this paper have been worked out and verified in PVL, the Prototypal Verification Language that we use to prototype new verification features, tool support is also provided for both Java and C.
All verification examples presented in this paper have been verified with the VerCors tool set. Moreover, all example programs are accessible via an online interface to VerCors, available at http://utwente.nl/vercors.
Parallel GCD. We demonstrate our model-based reasoning approach by capturing the functional behaviour of a parallel GCD algorithm. The parallel GCD verification problem is taken from the VerifyThis challenge held at ETAPS 2015Footnote 1 and considers a parallel version of the classical Euclidean algorithm.
The standard Euclidean algorithm is defined as a function \(\mathsf{gcd}\) such that, given two positive integers x and y, \(\mathtt{gcd}(x,x)=x\), \(\mathtt{gcd}(x,y) = \mathtt{gcd}(x-y,y)\) if \(x > y\), and \(\mathtt{gcd}(x,y) = \mathtt{gcd}(x,y-x)\) if \(y > x\). The parallel version of this algorithm uses two concurrent threads: the first thread continuously decrements the value of x when \(x > y\), the second thread continuously decrements the value of y when \(y > x\), and this process continues until x and y converge to the \(\mathtt{gcd}\) of the two original input values. Model-based reasoning is used to describe the interleaving of the concurrent threads and to prove functional correctness of the parallel algorithm in an elegant way. Figure 2 presents the setup of the \(\mathsf{pargcd}\) process, which models the behaviour of a parallel GCD algorithm with respect to the two global variables x and y. The \(\mathsf{pargcd}\) process uses three different actions, named: \(\mathsf{decrx}\), \(\mathsf{decry}\), and \(\mathsf{done}\). Performing the action \(\mathsf{decrx}\) captures the effect of decreasing x, provided that \(x > y\) before the action is performed. Likewise, performing \(\mathsf{decry}\) captures the effect of decreasing y. Finally, the \(\mathsf{done}\) action may be performed when \(x = y\) and is used to indicate termination of the algorithm.
The \(\mathsf{pargcd}\) process is defined as the parallel composition of two processes; the process \(\mathsf{tx}()\) describes the behaviour of the thread that decreases x, and \(\mathsf{ty}()\) describes the behaviour of the thread that decreases y. The \(\mathsf{pargcd}\) process requires that the shared variables x and y are both positive, and ensures that both x and y contain the \(\mathtt{gcd}\) of the original values of x and y. Proving that \(\mathsf{pargcd}\) satisfies its contract is done via standard process algebraic reasoning: first \(\mathsf{pargcd}\) is converted to a linear process (i.e. a process without parallel constructs), which is then analysed (e.g. via model checking) to show that every thread interleaving leads to a correct answer, in this case  .
.
Verifying Program Correctness. Figure 3 shows the \(\mathtt{startgcd}\) function, which is the entry point of the parallel GCD algorithm. According to \(\mathtt{startgcd}\)’s contract, two positive integers must be given as input and permission is required to write to x and y. On line 8 a model is initialised and named m, which describes that all further program executions behave as specified by the \(\mathsf{pargcd}\) process. Since \(\mathsf{pargcd}\) is defined as the parallel composition of the processes \(\mathsf{tx}\) and \(\mathsf{ty}\), its definition may be matched in the program code by forking two concurrent threads and giving each thread one of the components of \(\mathsf{tx}() \parallel \mathsf{ty}()\). In this case, the thread executing \(\mathtt{threadx}()\) continues from the process \(\mathsf{tx}()\) and the thread executing \(\mathtt{thready}()\) continues from \(\mathsf{ty}()\). By later joining the two threads and finishing the model by using the ghost statement \({{\mathbf {\mathsf{{finish}}}}}\) (which is only possible if \(\mathsf{pargcd}\) has been fully executed), we may establish that \(\mathtt{startgcd}\) satisfies its contract. However, we still have to show that the threads executing \(\mathtt{threadx}\) and \(\mathtt{thready}\) behave as described by the model m.
Figure 4 shows the implementation of \(\mathtt{threadx}\) and \(\mathtt{thready}\). Both procedures require a \(\mathsf{Lock}_{\pi }(lock)\) predicate, which gives the knowledge that a lock with resource invariant labelled lock has been initialised, and gives the possibility to acquire this lock and therewith the associated resource invariant. Moreover, both procedures require one half of the splitted \(\mathsf{Proc}_{1}(m,\mathsf{tx}() \parallel \mathsf{ty}())\) predicate that is established in Fig. 3 as result of initialising the model on line 8.
The connection between the process and program code is made via the \({{\mathbf {\mathsf{{action}}}}}\) (ghost) statements. To illustrate, in the function \(\mathtt{threadx}\) the decrement of x on line 13 is performed in the context of an action block, thereby forcing the \(\mathsf{tx}()\) process in the \(\mathsf{Proc}_{1/2}\) predicate to perform the \(\mathsf{decrx}\) action. The \({{\mathbf {\mathsf{{guard}}}}}\) of \(\mathsf{decrx}\) specifies the condition under which \(\mathsf{decrx}\) can be executed, and the \({{\mathbf {\mathsf{{effect}}}}}\) clause describes the effect on the (shared) state as result of executing \(\mathsf{decrx}\). Eventually, both threads execute the \(\mathsf{done}\) action to indicate their termination.
The VerCors tool set can automatically verify the parallel GCD verification example discussed above, including the analysis of the processes.
4 Program Logic
This section shortly elaborates on the assertion language and the proof rules of our approach, as used internally by the VerCors tool set to reason about abstractions. We do not present a full formalisation, for full details we refer to [27]. Only the proof rules related to model-based reasoning are discussed.
4.1 Assertion Language
Our program logic builds on standard CSL with permission accounting [6] and lock predicates [11]. The following grammar defines its assertion language:

where E are arithmetic expressions, B are Boolean expressions, x are variables, \(\pi \) are fractional permissions, \(\mathcal{L}\) are lock labels, and p are process labels. Note that the specification language implemented in VerCors supports more assertion constructs; we only highlight a subset to elaborate on our approach.
Instead of using a single points-to ownership predicate, like in standard CSL, our extensions require three different points-to predicates:
-
The
 predicate is the standard points-to predicate from CSL. It gives write permission to the heap location expressed by E in case \(\pi = 1\), and gives read access in case \(\pi \in (0,1]\). This predicate also represents the knowledge that the heap contains the value expressed by \(E'\) at location E.
predicate is the standard points-to predicate from CSL. It gives write permission to the heap location expressed by E in case \(\pi = 1\), and gives read access in case \(\pi \in (0,1]\). This predicate also represents the knowledge that the heap contains the value expressed by \(E'\) at location E. -
The process points-to predicate
 is similar to
is similar to 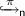 , but indicates that the heap location at E is bound by an abstract model. Since all changes to this heap location must be captured by the model, the
, but indicates that the heap location at E is bound by an abstract model. Since all changes to this heap location must be captured by the model, the  predicate only gives read permission to E, even when \(\pi = 1\).
predicate only gives read permission to E, even when \(\pi = 1\). -
The action points-to predicate
 gives read- or write access to the heap location E in the context of an \({{\mathbf {\mathsf{{action}}}}}\) block. As a precondition, \({{\mathbf {\mathsf{{action}}}}}\) blocks require
gives read- or write access to the heap location E in the context of an \({{\mathbf {\mathsf{{action}}}}}\) block. As a precondition, \({{\mathbf {\mathsf{{action}}}}}\) blocks require 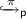 predicates for all heap locations that are accessed in their body. These predicates are then converted to
predicates for all heap locations that are accessed in their body. These predicates are then converted to  predicates, which give reading permission if \(\pi \in (0,1]\), and writing permission if \(\pi =1\).
predicates, which give reading permission if \(\pi \in (0,1]\), and writing permission if \(\pi =1\).
All three points-to ownership predicates can be split and merged along the associated fractional permission, to be distributed among concurrent threads:

Essentially, three different predicates are needed to ensure soundness of the verification approach. When a heap location \(\ell \) becomes bound by an abstract model, its  predicate is converted to an
predicate is converted to an  predicate in the program logic. As an effect, the value at \(\ell \) cannot just be changed, since the
predicate in the program logic. As an effect, the value at \(\ell \) cannot just be changed, since the  predicate does not permit writing to \(\ell \) (even when \(\pi =1\)). However, the value at \(\ell \) can be changed in the context of an action block, as the rule for action blocks in our program logic converts all affected
predicate does not permit writing to \(\ell \) (even when \(\pi =1\)). However, the value at \(\ell \) can be changed in the context of an action block, as the rule for action blocks in our program logic converts all affected  predicates to
predicates to  predicates, and
predicates, and  again allows heap writes. The intuition is that, by converting
again allows heap writes. The intuition is that, by converting  predicates to
predicates to  predicates, all changes to \(\ell \) must occur in the context of action blocks, and this allows us to describe all changes to \(\ell \) as process algebra terms. Consequently, by reasoning over these process algebra terms, we may reason about all possible changes to \(\ell \), and our verification approach allows to use the result of this reasoning in the proof system.
predicates, all changes to \(\ell \) must occur in the context of action blocks, and this allows us to describe all changes to \(\ell \) as process algebra terms. Consequently, by reasoning over these process algebra terms, we may reason about all possible changes to \(\ell \), and our verification approach allows to use the result of this reasoning in the proof system.
The second main extension our program logic makes to standard CSL is the \(\mathsf{Proc}_{\pi }(E,p,P)\) predicate, which represents the knowledge of the existence of an abstract model that: (i) is identified by the expression E, (ii) was initialised by invoking the process labelled p, and (iii) is described by the process term P. For brevity we omitted p from the annotations in all example programs, since this component is constant (it cannot be changed in the proof system). The third component P is the remaining process term that is to be “executed” (or “matched”) by the program. The \(\mathsf{Proc}_{\pi }\) predicates may be split and merged along the fractional permission and the process term, similar to the points-to ownership predicates:
4.2 Proof System
Figure 5 shows the proof rules for our model-based reasoning approach. For presentational purposes these rules are somewhat simplified: the rules  ,
,  , and
, and  require some extra side conditions that deal with process- and action arguments. We also omitted handing process arguments in
require some extra side conditions that deal with process- and action arguments. We also omitted handing process arguments in  . More details on these proof rules can be found in [27].
. More details on these proof rules can be found in [27].
The  rule allows reading from the heap, which can be done with any points-to permission predicate (that is,
rule allows reading from the heap, which can be done with any points-to permission predicate (that is,  for any permission type t). Writing to shared memory is only allowed by
for any permission type t). Writing to shared memory is only allowed by  with a full permission predicate that is not of type \(\mathsf{p}\); if the targeted heap location is bound by an abstract model, then all changes must be done in an action block (see the
with a full permission predicate that is not of type \(\mathsf{p}\); if the targeted heap location is bound by an abstract model, then all changes must be done in an action block (see the  rule).
rule).  handles the initialisation of a model, which on the specification level converts all affected
handles the initialisation of a model, which on the specification level converts all affected  predicates to
predicates to  and produces a full \(\mathsf{Proc}_1\) predicate.
and produces a full \(\mathsf{Proc}_1\) predicate.  handles model finalisation: it requires a fully executed \(\mathsf{Proc}_1\) predicate (holding the process \(\varepsilon \)) and converts all affected
handles model finalisation: it requires a fully executed \(\mathsf{Proc}_1\) predicate (holding the process \(\varepsilon \)) and converts all affected  predicates back to
predicates back to  . Finally,
. Finally,  handles action blocks. If a proof can be derived for the body S of the action block that: (i) respects the guard and effect of the action, and (ii) with the
handles action blocks. If a proof can be derived for the body S of the action block that: (i) respects the guard and effect of the action, and (ii) with the  predicates of all heap locations accessed in S converted to
predicates of all heap locations accessed in S converted to  , then a similar proof can be established for the entire action block. Observe that
, then a similar proof can be established for the entire action block. Observe that  requires and consumes the matching action call in the process term.
requires and consumes the matching action call in the process term.
5 Applications of the Logic
In this section we apply our approach on two more verification problems: (i) a concurrent program in which multiple threads increase a shared counter by one (see Sect. 5.1); and (ii) verifying control-flow properties of a fine-grained lock implementation (see Sect. 5.2). Also some interesting variants on these problems are discussed. For example (i) we verify the functional property that, after the program terminates, the correct value has been calculated. For (ii) we verify that clients of the lock adhere to the intended locking protocol and thereby avoid misusing the lock.
5.1 Concurrent Counting
Our second example considers a concurrent counter: a program where two threads concurrently increment a common shared integer. The basic algorithm is given in Fig. 6. The goal is to verify that \(\mathtt{program}\) increments the original value of counter by two, given that it terminates. However, providing a specification for \(\mathtt{worker}\) can be difficult, since no guarantees to the value of counter can be given after termination of \(\mathtt{worker}\), as it is used in a concurrent environment.
Existing verification approaches for this particular example [8] mostly require auxiliary state, a form of rely/guarantee reasoning, or, more recently, concurrent abstract predicates, which may blow-up the amount of required specifications and are not always easy to use. We show how to verify the program of Fig. 6 via our model-based abstraction approach. Later, we show how our techniques may be used on the same program but generalised to n threads.
Our approach is to protect all changes to counter by a process that we name \(\mathsf{parincr}\). The \(\mathsf{parincr}\) process is defined as the parallel composition \(\mathsf{incr}\parallel \mathsf{incr}\) of two processes that both execute the \(\mathsf{incr}\) action once. Performing \(\mathsf{incr}\) has the effect of incrementing counter by one. From a process algebraic point of view it is easy to see that \(\mathsf{parincr}\) satisfies its contract: every possible trace of \(\mathsf{parincr}\) indeed has the effect of increasing counter by two, and this can automatically be verified. We use this result in the verification of \(\mathtt{program}\) by using model-based reasoning. In particular, we may instantiate \(\mathsf{parincr}\) as a model m, split along its parallel composition, and give each forked thread a fraction of the splitted \(\mathsf{Proc}\) predicate. The interface specification of the \(\mathtt{worker}\) procedure thus becomes:

An annotated version of the concurrent counting program is presented in Fig. 7. The \({{\mathbf {\mathsf{{atomic}}}}}\) statement is used as a construct for statically-scoped locking; for simplicity we assume that writing permissions for counter are maintained by its resource invariant. Indeed, by showing that both threads execute the \(\mathsf{incr}\) action, the established result of incrementing counter by 2 can be concluded.
Generalised Concurrent Counting. The interface specification of \(\mathsf{worker}\) is generic enough to allow a generalisation to n threads. Instead of the \(\mathsf{parincr}\) process as presented in Fig. 7 one could consider the following process, which essentially encodes the process “\(\mathsf{incr} \parallel \cdots \parallel \mathsf{incr}\)” (n times) via recursion:

Figure 8 shows the generalised version of the concurrent counting program, in which we reuse the \(\mathsf{incr}\) action and the \(\mathtt{worker}\) procedure from Fig. 7. Here \(\mathtt{program}\) takes an extra parameter n that determines the number of threads to be spawned. The \(\mathtt{spawn}\) procedure has been added to spawn the n threads. This procedure is recursive to match the recursive definition of the \(\mathsf{parincr}(n)\) process. Again, each thread executes the \(\mathtt{worker}\) procedure. We verify that after running \(\mathtt{program}\) the value of counter has increased by n.
On the level of processes we may automatically verify that each trace of the process \(\mathsf{parincr}(n)\) is a sequence of n consecutive \(\mathsf{incr}\) actions. As a consequence, from the effects of \(\mathsf{incr}\) we can verify that \(\mathsf{parincr}(n)\) increases counter by n. On the program level we may verify that \(\mathtt{spawn}(m,n)\) fully executes according to the \(\mathsf{parincr}(n)\) process. To clarify, on line 6 the definition of \(\mathsf{parincr}(n)\) can be unfolded to \(\mathsf{incr} \parallel \mathsf{parincr}(n-1)\) and can then be split along its parallel composition. Then the forked thread receives \(\mathsf{incr}\) and the recursive call to \(\mathtt{spawn}\) receives \(\mathsf{parincr}(n-1)\). After calling \({{\mathbf {\mathsf{{join}}}}}\) on line 8, both the call to \(\mathtt{worker}\) and the recursive call to \(\mathtt{spawn}\) have ensured completing the process they received, thereby leaving the (merged) process \(\varepsilon \parallel \varepsilon \), which can be rewritten to \(\varepsilon \) to satisfy the postcondition of \(\mathtt{spawn}\). As a result, after calling \({{\mathbf {\mathsf{{finish}}}}}\) on line 18 we can successfully verify that counter has indeed been increased by n.
Unequal Concurrent Counting. One could consider an interesting variant on the two-threaded concurrent counting problem: one thread performing the assignment “\(counter = counter + v\)” for some integer value v, and the other thread concurrently performing “\(counter = counter * v\)”. Starting from a state where \(counter = c\) holds for some c, the challenge is to verify that after running the program we either have \(counter = (c + v) * v\) or \(counter = (c * v) + v\).
This program can be verified using our model-based approach (without requiring for example auxiliary state) by defining corresponding actions for the two different assignments. The global model is described as the process \(\mathsf{count}({{\mathbf {\mathsf{{int}}}}} \ n) := \mathsf{plus}(n) \parallel \mathsf{mult}(n)\), where the action \(\mathsf{plus}(n)\) has the effect of incrementing counter by n and \(\mathsf{mult}(n)\) has the effect of multiplying counter by n. The required program annotations are then similar to the ones used in Fig. 7.
All three variants on the concurrent counting problem can be automatically verified using the VerCors toolset.
5.2 Lock Specification
The third example demonstrates how our approach can be used to verify control-flow properties of programs, in this case the compare-and-swap lock implementation that is presented in the Concurrent Abstract Predicates (CAP) paper [9]. The implementation is given in Fig. 9. The \(\mathtt{cas}(x,c,v)\) operation is the compare-and-swap instruction, which atomically updates the value of x by v if the old value at x is equal to c, otherwise the value at x is not changed. A Boolean result is returned indicating whether the update to x was successful.
In particular, model-based reasoning is used to verify that the clients of this lock adhere to the intended locking protocol: clients may only successfully acquire the lock when the lock was unlocked and vice versa. Stated differently, we verify that clients may not acquire (nor release) the same lock successively.
The process algebraic description of the locking protocol is a composition of two actions, named \(\mathsf{acq}\) and \(\mathsf{rel}\), that model the process of acquiring and releasing the lock, respectively. A third action named \(\mathsf{done}\) is used to indicate that the lock is no longer used and can thus be destroyed. We use this process as a model to protect changes to the shared variable flag, so that all changes to flag must either happen as an \(\mathsf{acq}\) or as a \(\mathsf{rel}\) action. The \(\mathsf{acq}\) action may be performed only if flag is currently false and has the effect of setting flag to true. The \(\mathsf{rel}\) action simply has the effect of setting flag to false, whatever the current value of flag (therefore \(\mathsf{rel}\) does not need a guard). The locking protocol is defined by the processes \(\mathsf{Locked}() := \mathsf{rel} \cdot \mathsf{Unlocked}()\) and \(\mathsf{Unlocked}() := \mathsf{acq} \cdot \mathsf{Locked}() + \mathsf{done}\). This allows us to use the following interface specifications for the \(\mathtt{acquire}\) and \(\mathtt{release}\) procedures (with m a global identifier of an initialised model):

Specification-wise, clients of the lock may only perform \(\mathtt{acquire}\) when they have a corresponding process predicate that is in an “\(\mathsf{Unlocked}\)” state (and the same holds for \(\mathtt{release}\) and “\(\mathsf{Locked}\)”), thereby enforcing the locking protocol (i.e. the process only allows traces of the form: \(\mathsf{acq}, \mathsf{rel}, \mathsf{acq}, \mathsf{rel}, \cdots \)). The \(\mathtt{acquire}\) procedure performs the \(\mathsf{acq}\) action via the \(\mathtt{cas}\) operation: one may define \(\mathtt{cas}\) to update flag as an \(\mathsf{acq}\) action. Moreover, since \(\mathtt{cas}\) is an atomic operation, it can get all necessary ownership predicates from the resource invariant inv. Furthermore, calling \(\mathtt{destroy}()\) corresponds to performing the \(\mathsf{done}\) action on the process algebra level, which may only be done in the “\(\mathsf{Unlocked}\)” state.
The full annotated lock implementation is presented in Fig. 10. The \(\mathtt{init}\) and \(\mathtt{destroy}\) procedures have been added to initialise and finalise the lock and thereby to create and destroy the corresponding model. The \(\mathtt{init}\) consumes write permission to flag, creates the model, and transfers the converted write permission into the resource invariant inv. Both the atomic block (on line 28) and the \(\mathtt{cas}\) operation (on line 21) make use of inv to get permission to change the value of flag in an action block. The \(\mathtt{cas}\) operation on line 21 performs the \(\mathsf{acq}\) action internally, depending on the success of the compare-and-swap (indicated by its return value). This is reflected upon in the loop invariant. The \(\mathtt{destroy}\) procedure has the opposite effect of \(\mathtt{init}\): it consumes the (full) \(\mathsf{Proc}\) predicate (in state “\(\mathsf{Unlocked}\)”), destroys the model and the associated resource invariant, and gives back the converted write permission to flag.
In the current presentation, \(\mathtt{init}\) returns a single \(\mathsf{Proc}\) predicate in state \(\mathsf{Unlocked}\), thereby allowing only a single client. This is however not a limitation: to support two clients, \(\mathtt{init}\) could alternatively initialise and ensure the \(\mathsf{Unlocked}() \parallel \mathsf{Unlocked}()\) process. Furthermore, to support n clients (or a dynamic number of clients), \(\mathtt{init}\) could apply a construction similar to the one used in the generalised concurrent counting example (see Sect. 5.1).
Reentrant Locking. The process algebraic description of the locking protocol can be upgraded to describe a reentrant lock: a locking system where clients may \(\mathtt{acquire}\) and \(\mathtt{release}\) multiple times in succession. A reentrant lock that is acquired n times by a client must also be released n times before it is available to other clients. Instead of using the \(\mathsf{Locked}\) and \(\mathsf{Unlocked}\) processes, the reentrant locking protocol is described by the following process (with \(n \ge 0\)):
Rather than describing the lock state as a Boolean flag, like done in the single-entrant locking example, the state of the reentrant lock can be described as a multiset containing thread identifiers. In that case, \(\mathsf{acq}\) and \(\mathsf{rel}\) protect all changes made to the multiset in order to enforce the locking protocol described by \(\mathsf{Lock}\). The interface specifications of \(\mathtt{acquire}\) and \(\mathtt{release}\) then become:

Moreover, the \(\mathsf{Lock}(n)\) process could be extended with a \(\mathsf{done}\) action to allow the reentrant lock to be destroyed. The \(\mathsf{done}\) action should then only be allowed when \(n=0\). Both the simple locking implementation and the reentrant locking implementation have been automatically verified using the VerCors toolset.
5.3 Other Verification Examples
This section demonstrated the use of process algebraic models in three different verification examples, as well as some interesting variants on them. We showed how model-based reasoning can be used as a practical tool to verify different types of properties that would otherwise be hard to verify, especially with an automated tool. We considered data properties in the parallel GCD and the concurrent counting examples, and considered control-flow properties in the locking examples. Moreover, we showed how to use the model-based reasoning approach in environments with a dynamic number of concurrent threads.
Our approach can also be used to reason about non-terminating programs. Notably, a no-send-after-read verification example is available that addresses a commonly used security property: if confidential data is received by a secure device, it will not be passed on. The concrete send- and receive behaviour of the device can be abstracted by \(\mathsf{send}\) and \(\mathsf{recv}\) actions, respectively. Receiving confidential information is modelled as the \(\mathsf{clear}\) action. Essentially, we show that after performing a \(\mathsf{clear}\) action the device can no longer perform \(\mathsf{send}\)’s.
6 Related Work
The abstraction technique proposed in this paper allows reasoning about functional behaviour of concurrent, possibly non-terminating programs. A related approach is (impredicative) Concurrent Abstract Predicates (CAP) [9, 25], which also builds on CSL with permissions. In the program logic of CAP, regions of memory can be specified as being shared. Threads must have a consistent view of all shared regions: all changes must be specified as actions and all shared regions are equipped with a set of possible actions over their memory. Our approach uses process algebraic abstractions over shared memory in contrast to the shared regions of CAP, so that all changes to the shared memory must be captured as process algebraic actions. We mainly distinguish in the use of process algebraic reasoning to verify properties that could otherwise be hard to verify, and in the capability of doing this mechanically by providing tool support.
Other related approaches include TaDA [7], a program logic that builds on CAP by adding a notion of abstract atomicity via Hoare triples for atomic operations. CaReSL [26] uses a notion of shared regions similar to CAP, but uses tokens to denote ownership. These tokens are used to transfer ownership over resources between threads. Iris [17, 18] is a reasoning framework that aims to provide a comprehensive and simplified solution for recent (higher-order) concurrency logics. Sergey et al. [24] propose time-stamped histories to capture modifications to the shared state. Our approach may both capture and model program behaviour and benefits from extensive research on process algebraic reasoning [12]. Moreover, the authors provide a mechanised approach to interactively verify full functional correctness of concurrent programs by building on CSL [23]. Popeea and Rybalchenko [21] combine abstraction refinement with rely-guarantee reasoning to verify termination of multi-threaded programs.
In the context of verifying distributed systems, Session Types [15] describe communication protocols between processes [14]. However, our approach is more general as it allows describing any kind of behaviour, including communication behaviour between different system components.
7 Conclusion
This paper addresses thread-modular verification of possibly non-terminating concurrent programs by proposing a technique to abstract program behaviour using process algebras. A key characteristic of our approach is that properties about programs can be proven by analysing process algebraic program abstractions and by verifying that programs do not deviate from these abstractions. The verification is done in a thread-modular way, using an abstraction-aware extension of CSL. This paper demonstrates how the proposed technique provides an elegant solution to various verification problems that may be challenging for alternative verification approaches. In addition, the paper contributes tool support and thereby allow mechanised verification of the presented examples.
Future Work. We are currently working on mechanising the formalisation and the soundness proof of the proposed technique using Coq. At the moment, verification at the process algebra level is non-modular. As a next step, we plan to achieve modularity at this level as well, by combining our approach with rely-guarantee [16] and deny-guarantee reasoning [10]. We also plan to investigate how to mix and interleave abstract and concrete reasoning. In the current set up, reasoning is done completely at the level of the abstraction. If this part of the program is used as a component in a larger program, we plan to investigate how the verification results for the components can be used to reason about the larger program, if reasoning about the larger program is not done at this level of abstraction. Finally, in a different direction, we plan to extend the abstraction technique to reason about distributed software. For example, abstractions may be used to capture the behaviour of a single actor/agent as a process term, allowing process algebraic techniques such as [20] to be used for further verification.
Notes
- 1.
See also http://etaps2015.verifythis.org.
References
Amighi, A., Haack, C., Huisman, M., Hurlin, C.: Permission-based separation logic for multithreaded Java programs. LMCS 11(1), 1–66 (2015)
Blom, S., Darabi, S., Huisman, M., Oortwijn, W.: The VerCors tool set: verification of parallel and concurrent software. In: Polikarpova, N., Schneider, S. (eds.) IFM 2017. LNCS, vol. 10510, pp. 102–110. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-66845-1_7
Blom, S., Huisman, M.: The VerCors tool for verification of concurrent programs. In: Jones, C., Pihlajasaari, P., Sun, J. (eds.) FM 2014. LNCS, vol. 8442, pp. 127–131. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-06410-9_9
Blom, S., Huisman, M., Zaharieva-Stojanovski, M.: History-based verification of functional behaviour of concurrent programs. In: Calinescu, R., Rumpe, B. (eds.) SEFM 2015. LNCS, vol. 9276, pp. 84–98. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-22969-0_6
Bornat, R., Calcagno, C., O’Hearn, P.W., Parkinson, M.J.: Permission accounting in separation logic. In: POPL, pp. 259–270 (2005)
Boyland, J.: Checking interference with fractional permissions. In: Cousot, R. (ed.) SAS 2003. LNCS, vol. 2694, pp. 55–72. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-44898-5_4
da Rocha Pinto, P., Dinsdale-Young, T., Gardner, P.: TaDA: a logic for time and data abstraction. In: Jones, R. (ed.) ECOOP 2014. LNCS, vol. 8586, pp. 207–231. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44202-9_9
da Rocha Pinto, P., Dinsdale-Young, T., Gardner, P.: Steps in modular specifications for concurrent modules. In: MFPS, EPTCS, pp. 3–18 (2015). https://doi.org/10.1016/j.entcs.2015.12.002
Dinsdale-Young, T., Dodds, M., Gardner, P., Parkinson, M.J., Vafeiadis, V.: Concurrent abstract predicates. In: D’Hondt, T. (ed.) ECOOP 2010. LNCS, vol. 6183, pp. 504–528. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14107-2_24
Dodds, M., Feng, X., Parkinson, M., Vafeiadis, V.: Deny-guarantee reasoning. In: Castagna, G. (ed.) ESOP 2009. LNCS, vol. 5502, pp. 363–377. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00590-9_26
Gotsman, A., Berdine, J., Cook, B., Rinetzky, N., Sagiv, M.: Local reasoning for storable locks and threads. In: Shao, Z. (ed.) APLAS 2007. LNCS, vol. 4807, pp. 19–37. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-76637-7_3
Groote, J.F., Mousavi, M.R.: Modeling and Analysis of Communicating Systems. MIT Press, Cambridge (2014)
Groote, J.F., Ponse, A.: The syntax and semantics of \(\mu \)CRL. In: Ponse, A., Verhoef, C., van Vlijmen, S.F.M. (eds.) Algebra of Communicating Processes, pp. 26–62. Springer, London (1995). https://doi.org/10.1007/978-1-4471-2120-6_2
Honda, K., Marques, E.R.B., Martins, F., Ng, N., Vasconcelos, V.T., Yoshida, N.: Verification of MPI programs using session types. In: Träff, J.L., Benkner, S., Dongarra, J.J. (eds.) EuroMPI 2012. LNCS, vol. 7490, pp. 291–293. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-33518-1_37
Honda, K., Yoshida, N., Carbone, M.: Multiparty asynchronous session types. In: POPL, pp. 273–284. ACM (2008)
Jones, C.B.: Tentative steps toward a development method for interfering programs. ACM Trans. Program. Lang. Syst. 5(4), 596–619 (1983)
Jung, R., Swasey, D., Sieczkowski, F., Svendsen, K., Turon, A., Birkedal, L., Dreyer, D.: Iris: monoids and invariants as an orthogonal basis for concurrent reasoning. In: POPL, pp. 637–650. ACM (2015)
Krebbers, R., Jung, R., Bizjak, A., Jourdan, J.-H., Dreyer, D., Birkedal, L.: The essence of higher-order concurrent separation logic. In: Yang, H. (ed.) ESOP 2017. LNCS, vol. 10201, pp. 696–723. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54434-1_26
O’Hearn, P.W.: Resources, concurrency and local reasoning. Theoret. Comput. Sci. 375(1–3), 271–307 (2007)
Pang, J., van de Pol, J., Espada, M.: Abstraction of parallel uniform processes with data. In: SEFM, pp. 14–23. IEEE (2004)
Popeea, C., Rybalchenko, A.: Compositional termination proofs for multi-threaded programs. In: Flanagan, C., König, B. (eds.) TACAS 2012. LNCS, vol. 7214, pp. 237–251. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28756-5_17
Reynolds, J.C.: Separation logic: a logic for shared mutable data structures. In: Logic in Computer Science, pp. 55–74. IEEE Computer Society (2002). https://doi.org/10.1109/LICS.2002.1029817
Sergey, I., Nanevski, A., Banerjee, A.: Mechanized verification of fine-grained concurrent programs. In: PLDI, pp. 77–87. ACM (2015)
Sergey, I., Nanevski, A., Banerjee, A.: Specifying and verifying concurrent algorithms with histories and subjectivity. In: Vitek, J. (ed.) ESOP 2015. LNCS, vol. 9032, pp. 333–358. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46669-8_14
Svendsen, K., Birkedal, L.: Impredicative concurrent abstract predicates. In: Shao, Z. (ed.) ESOP 2014. LNCS, vol. 8410, pp. 149–168. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54833-8_9
Turon, A., Dreyer, D., Birkedal, L.: Unifying refinement and hoare-style reasoning in a logic for higher-order concurrency. In: ICFP, pp. 377–390 (2013)
Zaharieva-Stojanovski, M.: Closer to reliable software: verifying functional behaviour of concurrent programs. Ph.D. thesis, University of Twente (2015). https://doi.org/10.3990/1.9789036539241
Acknowledgements
This work is partially supported by the ERC grant 258405 for the VerCors project and by the NWO TOP 612.001.403 project VerDi.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Oortwijn, W., Blom, S., Gurov, D., Huisman, M., Zaharieva-Stojanovski, M. (2017). An Abstraction Technique for Describing Concurrent Program Behaviour. In: Paskevich, A., Wies, T. (eds) Verified Software. Theories, Tools, and Experiments. VSTTE 2017. Lecture Notes in Computer Science(), vol 10712. Springer, Cham. https://doi.org/10.1007/978-3-319-72308-2_12
Download citation
DOI: https://doi.org/10.1007/978-3-319-72308-2_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-72307-5
Online ISBN: 978-3-319-72308-2
eBook Packages: Computer ScienceComputer Science (R0)









 predicate is the standard points-to predicate from CSL. It gives write permission to the heap location expressed by E in case
predicate is the standard points-to predicate from CSL. It gives write permission to the heap location expressed by E in case  is similar to
is similar to 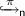 , but indicates that the heap location at E is bound by an abstract model. Since all changes to this heap location must be captured by the model, the
, but indicates that the heap location at E is bound by an abstract model. Since all changes to this heap location must be captured by the model, the  predicate only gives read permission to E, even when
predicate only gives read permission to E, even when  gives read- or write access to the heap location E in the context of an
gives read- or write access to the heap location E in the context of an 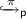 predicates for all heap locations that are accessed in their body. These predicates are then converted to
predicates for all heap locations that are accessed in their body. These predicates are then converted to  predicates, which give reading permission if
predicates, which give reading permission if 




