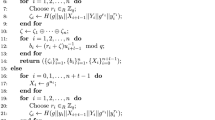1 Introduction

A secret sharing (SS) scheme is a method of sharing a secret among a set of n players so that some predefined authorized subsets of the players are able to recover the secret. The notion of threshold SS was introduced by Shamir [24] and Blakley [4] independently where the cardinality of any authorized set is larger than a given threshold. Later, Ito et al. [15] generalized this notion to a setting where the authorized subsets are an arbitrary family of subsets of the players, called access structures.

SS is now used as a central building block in many cryptographic and distributed applications such as unconditionally secure multiparty computation (MPC) [1, 2, 5, 7]. In addition, for natural application to unconditionally secure MPC [5, 7], the multiplicative property of SS is essential. We therefore focus on information-theoretically secure SS in this paper.

Motivated by open problems in the area of MPC such as unconditionally secure MPC with minimal interaction, Barkol et al. (Journal of Cryptology, 2010 [3]) introduced d-multiplicative SS and studied the type of access structures for which such secret sharing schemes exist. A secret sharing scheme is d-multiplicative if the scheme allows the players to multiply shared d (rather than two) secrets by locally converting their shares into an additive sharing of the product. They proved that d-multiplicative schemes exist if and only if no d unauthorized sets of players cover the whole set of players (type \(Q_d\)). In particular, t-private d-multiplicative secret sharing among n players is possible only if \(n > d\cdot t\) where t-private means that every set of t players is unauthorized. This result implies a limitation on the usefulness of SS in the context of MPC in the sense that a larger number of players n is required for maintaining the privacy level t as d increases. In other words, if we have a sufficient number of players, there is a possibility of simplifying complex tasks of MPC by computing the product of two or more elements directly and non-interactively without any setup.

In this paper, we aim to improve the usefulness of d-multiplicative SS (MSS) in the context of MPC while maintaining its advantages: no need for any interaction, any setup, or any computational assumption.

First, we introduce the notion of verifiably d-multiplicative SS, which is mainly formalized for the motivated applications of d-MSS given in [3]. In the motivated applications, each player adds random additive shares of 0 to each generated share and the receiver of the shares only obtains the summed value (i.e. the product). We therefore call a d-multiplicative scheme verifiable if the scheme enables the players to locally generate an additive sharing of a proof that the sum of shares (rather than each share) is correct. We expect that the verifiability can be used for making MPC secure in the presence of an active adversary by accepting the output only if the correctness is verified. A concrete application is beyond the scope of this paper and is a possible future work.

Secondly, we study the feasibility of verifiably d-multiplicative SS. We prove that verifiably d-multiplicative secret sharing is possible if the access structures of type \(Q_{d+1}\) where the privacy achieved is perfect and the error probability is zero. In the threshold case, type \(Q_{d+1}\) implies \(n>(d+1)\cdot t\). This means that we need to degrade the privacy level t or gather a larger number of players n. In addition, in the proposed error-free scheme, the share size of a proof increases with the number of unauthorized sets. A basic approach for overcoming this problem in the context of MPC is to require interaction among the players [20] or to use verifiable secret sharing [22], which relies on computationally secure commitment with a common reference string. That is, the advantages of d-MSS are spoiled.

To achieve the optimal bounds on n of d-MSS (i.e., \(n>d\cdot t\) for t-privacy, or type \(Q_d\)), we accept an error probability and prove that verifiably d-multiplicative schemes exist if and only if the access structure is of type \(Q_d\), where the privacy achieved is perfect, the error probability is non-zero but chosen arbitrarily, and each share of the proof only consists of two field elements.

The interesting point of these results is that a secret sharing scheme itself is not necessarly verifiable or linear. We note that the same results can be also obtained for non-perfect privacy from the result on the (im)possibility of non-perfect d-MSS in [26].

2 Preliminaries

In this section, we recall the definition of multiplicative and private properties, some results on feasibility, and a motivated application given in [3].

2.1 Notations and Definitions

A secret sharing scheme involves a dealer and n players \(P_1,\ldots ,P_n\), and specifies a randomized mapping from the secret s to an n-tuple of shares \((s_1, \ldots , s_n)\), where the share \(s_i\) is given to player \(P_i\). We assume that the secret is taken from a finite field \(\mathbb F\). We also assume that all shares \(s_i\) are taken from a finite share domain \(\mathcal{S}\). Let \(\mathcal{D}\) denote a discrete probability distribution from which the dealer’s randomness is chosen. To share a secret \(s\in \mathbb F\), the dealer chooses a random element \(r\in \mathcal{D}\) and applies a sharing function \(\mathsf{SHARE}:\mathbb F\times \mathcal{D}\rightarrow \mathcal{S}^n\) to compute \(\mathsf{SHARE}(s,r) = (s_1 ,\ldots ,s_n)\). For \(T\subseteq [n]\), let \(\mathsf{SHARE}(s, r )_T\) denote the restriction of \(\mathsf{SHARE}(s,r)\) to its T-entries.

Definition 1

( t -Private secret sharing [3]). A secret sharing scheme is said to be t-private if for every set \(T\subseteq [n]\) with \(|T|=t\) and every pair of secrets \(s, s'\in \mathbb F\), the random variables \(\mathsf{SHARE}(s,r)_T\) and \(\mathsf{SHARE}(s',r)_T\) induced by a random choice of \(r\in \mathcal{D}\) are identically distributed.

Definition 2

( d -Multiplicative secret sharing [3]). We call a secret sharing scheme d-multiplicative if it satisfies the following d-multiplicative property. Let \(s^{(1)}, \ldots , s^{(d)}\in \mathbb F\) be d secrets, and \(r^{(1)},\ldots ,r^{(d)}\in \mathcal{D}\) be d elements in the support of \(\mathcal{D}\). For \(1\le j\le d\), let \((s_1^{(j)}, \ldots , s_n^{(j)})=\mathsf{SHARE}(s^{(j)},r^{(j)})\). We require the existence of a function \(\mathsf{MULT}:[n]\times \mathcal{S}^d\rightarrow \mathbb F\) such that for all possible \(s^{(j)}\) and \(r^{(j)}\) as above, \(\sum _{i=1}^n \mathsf{MULT}(i,s_i^{(1)}, \ldots , s_i^{(d)})=\prod _{j=1}^d s^{(j)}\).

To generalize our results from the threshold case to general access structures, we show the notations and definitions of such secret sharing given in [3]. In contrast to traditional secret sharing specifying a collection of authorized player sets, the complementary notion of an adversary structure, specifying a collection of unauthorized sets, is used for convenience in [3].

Definition 3

( Adversary structure [3]). An n-player adversary structure is a collection of sets \(\mathcal{T}\subseteq 2^{[n]}\) that is closed under subsets; that is, if \(T\in \mathcal{T}\) and \(T'\subseteq T\) then \(T'\in \mathcal{T}\). Let \({\hat{\mathcal{T}}}\) be the collection of maximal sets in \(\mathcal{T}\) (namely those that are not contained in any other set from \(\mathcal{T}\)).

Definition 4

( \(\mathcal{T}\) -Private secret sharing [3]). Let \(\mathcal{T}\) be an n-player adversary structure. A secret sharing scheme is said to be \(\mathcal{T}\)-private if every pair of secret \(s,s'\in \mathbb F\) and every \(T\in {\mathcal{T}}\), the random variables \(\mathsf{SHARE}(s,r)_T\) and \(\mathsf{SHARE}(s',r)_T\) induced by a random choice of \(r\in \mathcal{D}\) are identically distributed.

Definition 5

( Adversary structure of type \(Q_d\) [3]). Let n, d be positive integers and \(\mathcal{T}\) be an n-player adversary structure. We say that \(\mathcal{T}\) is of type \(Q_d\) if for every d sets \(T_1,\ldots ,T_d\in \mathcal{T}\) we have \(T_1\cup \cdots \cup T_d\subset [n]\). That is, no d unauthorized sets cover the entire set of players.

The main result in [3] is a characterization of d-multiplicative secret sharing.

Theorem 1

(Theorem 4.6 in [3]). For any positive integers n, d and a n-player adversary structure \(\mathcal{T}\), there exists a d-multiplicative \(\mathcal{T}\)-private secret sharing scheme if and only if \(\mathcal{T}\) is of type \(Q_d\).

2.2 A Motivated Application

The motivated applications of the d-multiplicative property given in [3] are secure polynomial evaluation and general secure computation with minimal interaction. It has been shown that given a t-private d-multiplicative secret sharing for n players over \(\mathbb F\), there exists a t-private n-server secure polynomial evaluation protocol for multi-variate polymomials of degree d over \(\mathbb F\) where the communication complexity is linear in the input length (see Lemma 3.1 in [3]). In addition, the generalization from polynomials to arbitrary functions can be obtained by using randomizing polynomials [16] which enables to represent an arbitrary function by a vector of (randomized) degree-3 polynomials [3].

For simplicity, we briefly introduce the simplest case: A polynomial is the form \(x_{1}\cdot x_{2}\cdots x_{d}\); There are d clients, who holds inputs and wish to evaluate the polynomial without revealing their inputs each other, and n servers, who help perform the evaluation. Client j with \(1\le j\le d\) holds an input \(s^{(j)}\) and every server only knows the identity of the polynomial. Informally, a protocol should satisfy the following correctness and privacy requirements.

 

Correctness: :

All clients output \(s^{(1)}\cdots s^{(d)}\) (assuming that both client and servers follow the protocol).

t -Privacy: :

Any collusion involving a strict subset of the clients and at most t servers should not learn anything about the inputs of the other clients other than what follows from their own inputs and the output.

 

The formal definitions and security proof are not included in [3] (the related literatures [6, 12] are referred), and omitted here.

The t-private n-server protocol given in [3] proceeds as follows:

  • Round 1: Client j, \(1\le j\le d\), shares his input \(s^{(j)}\) by computing \(\mathsf{SHARE}(s^{(j)}\), \(r^{(j)})=(s^{(j)}_1, \ldots , s^{(j)}_n)\). After sharing his input, he sends the share \(s^{(j)}_i\) to Server i. In addition, Client j distributes between the servers random additive shares of 0, namely it sends to Server i a field element \(z^{(j)}_i\) such that the n elements \(z^{(j)}_i\) are random subject to the restriction that they add up to 0, i.e., \(\sum _{i=1}^{n}z^{(j)}_i=0\).

  • Round 2: Server i, \(1\le i\le n\), computes \(y_i= \mathsf{MULT}(i, s^{(1)}_i,\ldots ,s^{(d)}_i)+\sum _{j=1}^{d}z^{(j)}_i\), and sends \(y_i\) to all clients.

  • Output: Each client computes and outputs \(\sum _{i=1}^{n}y_i\). From the d-multiplicative property, this output is equal to \(s^{(1)}\cdots s^{(d)}\).

An important point to note here is that the generated shares \(y_i\) is randomized by additive shares of 0 and each client only obtains the summed value (i.e., the product). Thus, in this paper, the notion of verifiability is defined for the summed value rather than each share.

3 Verifiably Multiplicative Secret Sharing

We now define the verifiability of multiplication. We assume that malicious players who may behave arbitrary have the same structure as that against privacy. To verify the summed value rather than each additive share, we define a proof and its shares by vectors in \(\mathbb F^c\) for a positive integer c where the summation of two vectors \(a=(a_1,\ldots ,a_c)\) and \(b=(b_1,\ldots ,b_c)\) is performed by adding the corresponding components of the vectors, i.e., \(a+b=(a_1+b_1,\ldots ,a_c+b_c)\).

Definition 6

( \((\epsilon ,d)\) -Verifiably multiplicative secret sharing ). Let c be a positive integer. A \(\mathcal{T}\)-private secret sharing scheme is said to be \((\epsilon ,d)\)-verifiably multiplicative if the scheme is d-multiplicative and there are two functions \(\mathsf{PROOF}:[n]\times \mathcal{S}^d\rightarrow \mathbb F^c\) and \(\mathsf{VER}:\mathbb F\times \mathbb F^c \rightarrow \{1,0\}\) that satisfy the following properties.  

Correctness: :

For \(s^{(j)}\in \mathbb F\) and \(r^{(j)}\in \mathcal{D}\) with \(1\le j\le d\), let \((s_1^{(j)}, \ldots , s_n^{(j)})=\mathsf{SHARE}(s^{(j)},r^{(j)})\), \(m=\sum _{i=1}^n \mathsf{MULT}(i,s_i^{(1)}, \ldots , s_i^{(d)})\), and \(\sigma =\sum _{i=1}^n \mathsf{PROOF}(i\), \(s_i^{(1)}\), \(\ldots , s_i^{(d)})\). Then, \(\mathsf{VER}(m, \sigma )=1\).

Verifiability: :

An adversary that modifies any additive shares for any \(T\in \mathcal{T}\) can cause a wrong value to be accepted as the product with probability at most \(\epsilon \). More formally, we define the experiment \({Exp}(s^{(1)},\ldots ,s^{(d)}, T, \mathsf {Adv})\) with some d secrets \(s^{(1)},\ldots ,s^{(d)}\in \mathbb F\), unauthorized set \(T\in \mathcal{T}\), and interactive adversary \(\mathsf {Adv}\).  

\({Exp}(s^{(1)},\ldots ,s^{(d)}, T, \mathsf {Adv})\)::
1.:

For each j with \(1\le j\le d\), sample \(r^{(j)}\leftarrow \mathcal{D}\) and generate \((s^{(j)}_1\), \(\ldots \), \(s^{(j)}_n)=\mathsf{SHARE}(s^{(j)},r^{(j)})\).

2.:

Give \(\{(s^{(1)}_i,\ldots ,s^{(d)}_i)|i\in T\}\) to \(\mathsf {Adv}\).

3.:

\(\mathsf {Adv}\) outputs modified additive shares \(m_i'\in \mathbb F\) and \(\sigma _i'\in \mathbb F^c\) with \(i\in T\). For \(i\not \in T\), we define \(m_i'=\mathsf{MULT}(i,s^{(1)}_i,\ldots ,s^{(d)}_i)\) and \(\sigma _i'=\mathsf{PROOF}(i\), \(s^{(1)}_i\), \(\ldots \), \(s^{(d)}_i)\).

4.:

Compute \(m'=\sum _{i=1}^nm_i'\) and \(\sigma '=\sum _{i=1}^n\sigma _i'\).

5.:

If \(m'\not =s^{(1)}\cdots s^{(d)}\) and \(\mathsf{VER}(m',\sigma ')=1\), then output 1 else 0.

  We require that for any d secrets \(s^{(1)},\ldots ,s^{(d)}\in \mathbb F\), any unauthorized set \(T\in \mathcal{T}\), and any unbounded adversary \(\mathsf {Adv}\),

$$\begin{aligned} \Pr [{Exp}(s^{(1)},\ldots ,s^{(d)},T,\mathsf {Adv})=1]\le \epsilon . \end{aligned}$$

 

Given an \((\epsilon ,d)\)-verifiably multiplicative t-private secret sharing scheme, we can make the motivated application correct in the presence of at most t malicious servers. Specifically, the protocol satisfies the following strong correctness.

 

t -Correctness: :

All clients output \(s^{(1)}\cdots s^{(d)}\) or \(\bot \) assuming at most t malicious servers. That is, an incorrect value is not accepted.

  The protocol in Sect. 2 is modified as follows.

  • Round 1: Client j distributes between the servers random additive shares of the zero-vector, namely it sends to Server i a vector \(z^{(j)}_i\in \mathbb F^{c+1}\) such that the n vectors \(z^{(j)}_i\) are random subject to the restriction that they add up to the vector with all components being 0, i.e., \(\sum _{i=1}^{n}z^{(j)}_i=(0,\ldots ,0)\).

  • Round 2: Server i, \(1\le i\le n\), computes a vector \(y_i= (\mathsf{MULT}(i\), \(s^{(1)}_i\), \(\ldots \), \(s^{(d)}_i)\), \(\mathsf{PROOF}(i\), \(s^{(1)}_i\), \(\ldots \), \(s^{(d)}_i))+\sum _{j=1}^{d}z^{(j)}_i\), and sends \(y_i\) to all clients.

  • Output: Let \(y_i=(m_i,\sigma _i)\). Each client computes \(m=\sum _{i=1}^{n}m_i\) and \(\sigma =\sum _{i=1}^{n}\sigma _i\). It outputs m if \(\mathsf{VER}(m,\sigma )=1\), otherwise it outputs 0.

4 Feasibilities

Our main results are sufficient conditions for \((\epsilon ,d)\)-verifiably multiplicative \(\mathcal{T}\)-private secret sharing to be possible. For the error-free case \(\epsilon =0\), the condition is stronger than that of the previous d-multiplicative \(\mathcal{T}\)-private secret sharing, which does not require the verifiability.

Theorem 2

For any positive integers n, d, and an n-player adversary structure \(\mathcal{T}\), there exists a (0, d)-verifiably multiplicative \(\mathcal{T}\)-private secret sharing scheme if \(\mathcal{T}\) is of type \(Q_{d+1}\) where \(c=|{\hat{\mathcal{T}}}|\) (every proof consists of \(|{\hat{\mathcal{T}}}|\) elements of \(\mathbb F\)).

Then, we prove that the condition can be weakened to the optimal one, i.e., that of the previous d-multiplicative \(\mathcal{T}\)-private secret sharing (type \(Q_d\)) by relaxing the requirement on the error probability to \(\epsilon >0\) that is chosen arbitrarily.

Theorem 3

For any positive integers n, E, d, and an n-player adversary structure \(\mathcal{T}\), there exists a secret sharing scheme that is \((1/|\mathbb F|^E,d)\)-verifiably multiplicative and \(\mathcal{T}\)-private if and only if \(\mathcal{T}\) is of type \(Q_{d}\) where \(c=2E\) (every proof consists of two elements of \(\mathbb F^E\)).

We now prove Theorem 2.

Proof

(Theorem 2 ). We construct a (0, d)-verifiably multiplicative \(\mathcal{T}\)-private scheme for n players from the CNF scheme in [15], which is given for general access structures. In the CNF scheme, to share a given secret s, for \(T\in {\hat{\mathcal{T}}}\), \(r_T\) is randomly chosen from \(\mathbb F\) subject to the restriction that \(\sum _{T\in {\hat{\mathcal{T}}}}r_T=s\). Each share \(s_i\) is the set \(\{r_T|i\not \in T \}\). We note that in the t-private CNF scheme, \(s_i\) consists of exactly \({}_{n-1}C_t\) field elements. The \(\mathcal{T}\)-privacy property follows from the fact that every set \(T\in {\hat{\mathcal{T}}}\) jointly misses \(r_T\) and thus can learn no information about the secret. The d-multiplicative property is proven in [3] and a multiplication function \(\mathsf{MULT}\) exists. Thus, we prove the existence of \(\mathsf{PROOF}\) and \(\mathsf{VER}\). The key idea is to generate shares of the product for subsets of players \([n]\setminus T\) for every set of malicious players \(T\in \mathcal{T}\) and check the equality of all recovered values. Any set of malicious players is contained by some \(T\in {\hat{\mathcal{T}}}\). Thus, the value recovered from shares for \([n]\setminus T\) is correct, and the equality of all recovered values guarantees that the error-probability is zero. Based on this idea, we define \(\mathsf{PROOF}\) and \(\mathsf{VER}\) as follows. We number the subsets in \({\hat{\mathcal{T}}}\) from 1 to \(|{\hat{\mathcal{T}}}|\). Let \(s^{(1)},\ldots ,s^{(d)}\) be secrets. For \(1\le j\le d\), let \(r^{(j)}_T\) with \(T\in {\hat{\mathcal{T}}}\) denote the additive parts of \(s^{(j)}\). We write the product \(s^{(1)} \cdots s^{(d)}=(\sum _{T\in {\hat{\mathcal{T}}}}r^{(1)}_T)\cdots (\sum _{T\in {\hat{\mathcal{T}}}}r^{(d)}_T)\) as the sum of the \(|{\hat{\mathcal{T}}}|^d\) monomials of the form \(r^{(1)}_{T_{j_1}}\cdots r^{(d)}_{T_{j_d}}\). For each \(T_l\in {\hat{\mathcal{T}}}\), we partition the monomials into \(n-|T_l|\) disjoint sets \(X_{l,i}\) such that \(i\in [n]\setminus T_l\) and all monomials in set \(X_{l,i}\) is obtained from \(s_i\). The possibility of partition follows from the fact that every monomial as above can be assigned to a set \(X_{l,i}\) such that \(i\not \in T_{j_1}\cup \cdots \cup T_{j_d}\cup T_l\). The existence of such i follows from the assumption that \(\mathcal{T}\) is of type \(Q_{d+1}\). For each \(1\le i\le n\), \(\mathsf{PROOF}(i, \cdot )\) outputs \(\sigma _i=(\sigma _{i,1},\ldots ,\sigma _{i,|{\hat{\mathcal{T}}}|})\in \mathbb F^{|{\hat{\mathcal{T}}}|}\) where \(\sigma _{i,l}\) is the sum of the monomials in \(X_{l,i}\) if \(i\not \in T_l\), and otherwise 0. We note that if all players follow the scheme, then \(\sigma =\sum \sigma _i\) is the vector with all components being \(s^{(1)}\cdots s^{(d)}\). We define the verification function \(\mathsf{VER}(m,\sigma )\) to be 1 if and only if \(\sigma =(m,\ldots ,m)\) holds. Even if malicious players T provide incorrect shares, there is a component \(\sigma _l\) with \(T\subseteq T_l\) which is the correct value \(s^{(1)}\cdots s^{(d)}\). Thus, \(\mathsf{VER}\) detects the existence of an incorrect value without error.    \(\square \)

Next, we prepare a lemma for the proof of Theorem 3.

Lemma 1

Given d-multiplicative \(\mathcal{T}\)-private secret sharing schemes for n players over \(\mathbb F\) and \(\mathbb F^E\), there exists a \((1/|\mathbb F|^E,d)\)-verifiably multiplicative \(\mathcal{T}\)-private secret sharing scheme for n players where \(c=2 E\) (every proof consists of two elements of \(\mathbb F^E\)).

Proof

For notational convenience, we present the proof for the case \(E=1\). The generalization to an arbitrary \(E>1\) is shown later. Suppose there is a d-multiplicative \(\mathcal{T}\)-private secret sharing scheme for n players over \(\mathbb F\) and its multiplication function, denoted by \(\mathsf{SHARE}'\) and \(\mathsf{MULT}'\), with randomness domain \(\mathcal{D}'\) and share domain \(\mathcal{S}'\). We show a method of constructing a \((1/|\mathbb F|,d)\)-verifiably multiplicative \(\mathcal{T}\)-private secret sharing scheme for n players \((\mathsf{SHARE}\), \(\mathsf{MULT}\), \(\mathsf{PROOF}\), \(\mathsf{VER})\) with \(c=2\) from \((\mathsf{SHARE}'\), \(\mathsf{MULT}')\).

The key idea is as follows: For the product \(m=s^{(1)}\cdots s^{(d)}\), \(\mathsf{PROOF}\) generates additive shares of \(\alpha \in \mathbb F\) and those of \(\beta =\alpha \cdot m\), and then \(\mathsf{VER}\) checks whether \(\alpha \cdot m=\beta \). A similar technique is used for detection of cheaters in secret sharing by Cabello et al. [9] in which m is replaced with the secret s itself and \(\alpha \) and \(\beta \) are shared together with the secret. In contrast, in the scheme we present here, additive shares of \(\alpha \) and \(\beta \) are not shared beforehand and are computed by using only the d-multiplicative property. We note that the d-multiplication property imposes no linearity requirement on \(\mathsf{SHARE}\) itself. Thus, we need to convert non-additive shares of \(\alpha \) into additive ones. To realize such conversion, we additionally share “1” for padding the product \(1^{d-1}\) with \(\alpha \).

Specifically, we define \(\mathsf{SHARE}:\mathbb F\times \mathcal{D}\rightarrow \mathcal{S}\) as follows: \(\mathcal{D}=\mathbb F\times \mathcal{D}'^4\), \(\mathcal{S}=\mathbb F^4\), and \(\mathsf{SHARE}(s,(\alpha ,r_1,r_2,r_3,r_4))=(\mathsf{SHARE}'(s,r_1)\), \(\mathsf{SHARE}'(\alpha ,r_2)\), \(\mathsf{SHARE}'(\alpha \cdot s,r_3)\), \(\mathsf{SHARE}'(1,r_4))\). That is, randomly chosen \(\alpha \in \mathbb F\), \(\gamma =\alpha \cdot s\in \mathbb F\), and \(1\in \mathbb F\) are additionally shared.

Let \(s^{(1)}, \ldots ,s^{(d)}\) be d secrets. Let \(\alpha ^{(1)}, \ldots ,\alpha ^{(d)},\gamma ^{(1)}, \ldots ,\gamma ^{(d)}\) be chosen as the above, that is, \(\gamma ^{(j)}=\alpha ^{(j)}\cdot s^{(j)}\). For \(1\le i\le n\) and \(1\le j\le d\), \(s^{(j)}_i=(t^{(j)}_i,\alpha ^{(j)}_i,\gamma ^{(j)}_i,1^{(j)}_i)\) be the i-th share of \(s^{(j)}\). We define \(\mathsf{MULT}(i,s^{(1)}_i,\ldots ,s^{(d)}_i)=\mathsf{MULT}'(i,t^{(1)}_i,\ldots ,t^{(d)})\), that is, the same as the original scheme. Then, we define \(\mathsf{PROOF}(i\), \(s^{(1)}_i\), \(\ldots \), \(s^{(d)}_i)=(\mathsf{MULT}'(i\), \(\alpha ^{(1)}_i\), \(1^{(2)}_i\), \(\ldots \), \(1^{(d)}_i)\), \(\mathsf{MULT}'(i\), \(\gamma ^{(1)}_i, t^{(2)}_i, \ldots , t^{(d)}_i))\), which consists of an additive share of \(\alpha ^{(1)}\cdot 1\cdots 1\) and that of \(\gamma ^{(1)}\cdot s^{(2)}\cdots s^{(d)}=\alpha ^{(1)}\cdot s^{(1)}\cdot s^{(2)}\cdots s^{(d)}\). For \(m\in \mathbb F\) and \(\sigma =(\sigma _1,\sigma _2) \in \mathbb F^2\), \(\mathsf{VER}(m,\sigma )=1\) if and only if \(m\cdot \sigma _1=\sigma _2\).

Let \(m_i=\mathsf{MULT}(i,s^{(1)}_i,\ldots ,s^{(d)}_i)\) and \(\sigma _i=(\sigma _{i,1},\sigma _{i,2})=\mathsf{PROOF}(i,s^{(1)}_i,\ldots ,s^{(d)}_i)\). It is obvious that the correctness holds because \(m=\sum m_i=s^{(1)}\cdots s^{(d)}\), \(\sigma _1=\sum \sigma _{i,1}=\alpha ^{(1)}\cdot 1\cdots 1=\alpha \), and \(\sigma _2=\sum \sigma _{i,2}=\alpha ^{(1)} \cdot s^{(1)}\cdot s^{(2)}\cdots s^{(d)}\).

In the following, we prove the verifiability. Let \(T\in \mathcal{T}\). Let \(\varDelta _m=m-m'\), \(\varDelta _\alpha =\sigma _1-\sigma _1'\), and \(\varDelta _\beta =\sigma _2-\sigma _2'\) where \(m'\) and \(\sigma '=(\sigma _1',\sigma _2')\) is computed in Step 4 in \({Exp}\). \(\mathsf {Adv}\) can choose \((\varDelta _m,\varDelta _{\alpha },\varDelta _{\beta })\) arbitrarily by modifying \(m_i'\) and \(\sigma _i'\) for \(i\in T\) in Step 3 of \({Exp}\). The error occurs if \(\varDelta _m\not =0\) and \(\mathsf{VER}(m+\varDelta _m,(\sigma _{1}+\varDelta _{\alpha }, \sigma _2+\varDelta _{\beta }))=1\), that is, \(m\cdot \varDelta _\alpha +\alpha ^{(1)}\cdot \varDelta _m+(\varDelta _m\cdot \varDelta _{\alpha }-\varDelta _{\beta })=0\). For every choice of \((\varDelta _m,\varDelta _\alpha ,\varDelta _\beta )\) with \(\varDelta _m\not =0\), there is a unique \(\alpha ^{(1)}\in \mathbb F\) satisfying the above equation. Thus, for any d secrets \(s^{(1)},\ldots ,s^{(d)}\), any \(T\in \mathcal{T}\), and any unbounded adversary \(\mathsf {Adv}\), the probability of \(\mathsf{VER}\) outputting 1 is \(1/|\mathbb F|\).

We can choose E arbitrarily by using an extension field \(\mathbb F^E\) instead of \(\mathbb F\). \(\mathsf{SHARE}\) shares \(\alpha \in \mathbb F^E\), \(\gamma =\alpha \cdot s\in \mathbb F^E\), and \(1\in \mathbb F^E\) by using a scheme for \(\mathbb F^E\). \(\mathsf{PROOF}\) generates additive shares in \(\mathbb F^E\) and \(\mathsf{VER}\) checks the equality over \(\mathbb F^E\). It is easy to show taht \(\epsilon =1/|\mathbb F|^E\) holds for the modified scheme with almost a same proof. Therefore, we obtain arbitrarily chosen \(\epsilon \) by choosing a degree of the extension E such that \(E=\min \{E'\;|\;\epsilon \le 1/|\mathbb F|^{E'}\}\).    \(\square \)

Proof

(Theorem 3 ). The only-if part is obvious from Theorem 1. If \(\mathcal{T}\) is of type \(Q_d\), then there is a d-multiplicative \(\mathcal{T}\)-private secret sharing scheme for n players over a finite field. From Lemma 1, the if-part follows.    \(\square \)

5 Conclusion

In this paper, we have introduced the notion of \((\epsilon ,d)\)-verifiably multiplicative \(\mathcal{T}\)-private secret sharing, and clarified the conditions under which such scheme exists. Namely, we have shown that (0, d)-verifiably multiplicative \(\mathcal{T}\)-private secret sharing scheme exists if the adversary structure \(\mathcal{T}\) is of type \(Q_{d+1}\), and that, for arbitrarily small \(\epsilon >0\), \((\epsilon ,d)\)-verifiably multiplicative \(\mathcal{T}\)-private secret sharing scheme exists if the adversary structure \(\mathcal{T}\) is of type \(Q_d\). These feasibility results were obtained by presenting constructions of \((\epsilon ,d)\)-verifiably multiplicative and \(\mathcal{T}\)-private secret sharing with the corresponding parameters.

Since it has been shown in [3] that a d-multiplicative \(\mathcal{T}\)-private secret sharing scheme exists only if the adversary structure \(\mathcal{T}\) is of type \(Q_d\), our proposed construction for \(\epsilon >0\) made it clear that an \((\epsilon ,d)\)-verifiably multiplicative \(\mathcal{T}\)-private secret sharing scheme with \(\epsilon >0\) exists if and only if the adversary structure \(\mathcal{T}\) is of type \(Q_d\).

However, it is not made clear whether (0, d)-verifiably multiplicative \(\mathcal{T}\)-private secret sharing scheme can be constructed even when the adversary structure \(\mathcal{T}\) is of type \(Q_d\). To clarify the necessary and sufficient condition for the existence of (0, d)-verifiably multiplicative \(\mathcal{T}\)-private secret sharing scheme will be future challenge.