1 Introduction

The strategy of viral marketing for promoting new products or ideas is based on the observation that once a certain fraction of a social network adopts a product, we can expect a cascade of further adoptions [3, 16, 27]. Domingos and Richardson [12, 33] were the first to raise the following important algorithmic problem in the context of social network analysis: If a company can turn a subset of customers in a given network into early adopters, and the goal is to trigger a large cascade of further adoptions, which set of customers should they target?

The social network can be modelled by a node-weighted graph \(G= (V,E, t)\) with V(G) representing individuals in the social network, E(G) denoting the social connections, and t an integer-valued threshold function. Starting with an initial seed set or target set, that is, a subset \(S \subseteq V\) of nodes in the graph, that are activated by some external incentive, influence propagates deterministically in discrete time steps, and is said to activate nodes. For any unactivated node v, if the number of its activated neighbors at time step \(i-1\) is at least t(v), then node v will be activated in step i. A node once activated stays activated. Clearly the process terminates after at most \(|V|-1\) steps. We call the set of nodes that are activated when the process terminates as the activated set. The problem proposed by Domingo and Richardson [12, 33] can now be formulated as follows: Given a social network \(G= (V, E, t)\), and an integer k, find a subset \(S \subseteq V\) of size k so that the resulting activated set is as large as possible. In the context of viral marketing, the parameter k corresponds to the budget, and S is a target set that maximizes the size of the activated set. This influence maximization problem has been widely studied [2, 5, 14, 17,18,19, 22, 28].

Recent work [10, 20, 25] points to some flaws in the above model for viral marketing. The authors of [10, 20] observe that a limitation of the model is that there is no possibility of giving partial external incentives; indeed the initial seed set is activated wholly by external incentives, and the remaining nodes only by the internal network effect. The authors of [25] further critique the fact that the nodes in the seed set are assumed to be activated immediately by external incentives, regardless of their own thresholds of activation. They point out that this is unrealistic assumption, and suggest that it is likely that highly influential nodes have high thresholds, and cannot be activated by external incentives alone.

In this paper, we provide a new way to model a viral marketing strategy with a fixed budget, that addresses the flaws mentioned above. In particular, we model strategies in which each node in the target set is given some partial incentive, eg. a $10 coupon; for some people this may be enough for them to buy the product, for others, it reduces their resistance to buying it. We represent the initiator of the viral marketing strategy by a node external to the social network. We can now restate the influence maximization problem as follows: Suppose Alice, the external initiator, wants to join a new social network, and can make k friends, how should she choose these friends if her goal is to influence as many people as possible? In other words, to which k people already in the social network should Alice create links, so that she can activate the maximum number of people? If Alice creates a link to a node v, the threshold of v is only effectively reduced by one, and so v in turn is activated only if its threshold is one. We call our problem the Maximum Influence with Links problem (Max-Inf-Links).

Notice that the links added from the external node Alice correspond to the external incentive given to the endpoints of these links. The nodes that are the endpoints of these new links may not be immediately completely activated, but their thresholds are effectively reduced; this corresponds to their receiving partial incentives. Individuals with high thresholds cannot be activated only by external incentives, which better models reality. The Max-Inf-Links problem also has applications in epidemiology or the spread of diseases: if an infected person arrives from outside a community, the Max-Inf-Links problem corresponds to identifying the set of k people such that if the infected external person has contact with this set, the highest number of people in the community could potentially be infected. The problem can obviously be generalized to a set of external influencers wishing to infect or gain control of a network.

Observe that the solution to the Max-Inf-Links problem can be quite different from the solution to choosing an optimal seed set for a given network. For example, consider a clique \(K_n\) in which node 1 has threshold \(n-1\) and the remaining nodes have threshold 1. If the budget k is 1, the optimal target set is clearly the node x, as choosing it activates the entire network. However, if we choose to link to the node x, it does not get activated, since its threshold is \(n-1\), and therefore no node in the network gets activated. The optimal solution to the Max-Inf-Links problem is in fact to choose any of the other nodes in \(K_n\); this would activate the entire network. This would however be a sub-optimal seed set.

1.1 Our Results

It was shown recently that it is NP-hard to find the minimum number of links required for an external influencer to activate the entire network [25]. Since this is a special case of our Max-Inf-Links problem, it follows that our problem is NP-hard in general. We prove here that the Max-Inf-Links problem is NP-hard, even if all nodes have threshold 1 or 2, even in bipartite graphs, which have many applications in social networks. Note that the NP-hardness proof in [25] does not apply to bipartite graphs. In light of the hardness result, we study the complexity of the problem for social networks that can be represented as trees, cycles, and cliques. We show that optimal solutions can be found for the Max-Inf-Links problem with k links in time \(\Theta (kn)\) for paths, \(\Theta (kn^2)\) for cycles, \(\Theta (k^2n^2)\) for trees, and \(\Theta (n)\) for cliques. Note that k is always upper bounded by n. Our algorithms for paths, trees, and cycles rely on non-trivial dynamic programming formulations. Note that the algorithm for trees can be used for paths, but we are able to get a much faster implementation for paths by making careful use of the solution properties.

1.2 Related Work

The problem of identifying the most influential nodes in a social network has received a tremendous amount of attention [2, 5, 14, 17,18,19, 22, 28]. The algorithmic question of choosing a seed set of size k that activates the most number of nodes in the context of viral marketing was first posed by Domingos and Richardson [12]. Many natural heuristics were proposed for the problem, such as choosing the nodes of highest degree, or those central in terms of distance [23, 24]. Kempe et al. [23] started the study of this problem as a discrete optimization problem, and studied it in both the probabilistic independent cascade model and the threshold model of the influence diffusion process. They showed the NP-hardness of the problem in both models, and showed that a natural greedy strategy has a \((1 - 1/e - \epsilon )\)-approximation guarantee in both models; these results were generalized to a more general cascade model in [24]. Mossel and Roch [30] further generalized the results of [23, 24] by positively resolving their conjecture that whenever the local threshold functions are local and submodular, the resulting influence function is also a submodular function. Borgs et al. [2] recently obtained a significant improvement by giving an algorithm that obtains an approximation factor of \(1 - 1/e - \epsilon \) for any \(\epsilon > 0\), in time \(O((m+n)k \log (n) / \epsilon ^2)\). A large body of work studies algorithms that have performance guarantees and at the same time scale in practice to real-life and very large-scale social networks [31, 35, 36]. Influence diffusion under time window or deadline constraints has also been studied [11, 15, 26, 29].

In the Target Set Selection problem [1, 4, 32], the size of the target set or budget is not specified in advance, but the goal is to activate the entire network or a fixed fraction of nodes. Partial incentives were studied in the context of the target set selection problem in [8, 10, 20, 21, 25]. The closest formulation to our paper is the Minimum Links problem introduced in [25], where it is required to find the minimum number of links an external influencer needs to form to nodes in the network so that the entire network is eventually activated. It was shown in [25] that the Minimum Links problem is NP-hard, and in fact, it is even hard to approximate with ratio \(\epsilon \) for some constant \(\epsilon \). The authors gave linear time greedy algorithms for trees, cycles, and cliques.

Demaine et al. [10] were the first to introduce the study of the maximization of influence with partial incentives and a fixed budget [10]. However, they consider thresholds chosen uniformly at random, while we study arbitrary thresholds. Additionally, they allow arbitrary fractional influence to be applied externally on any node, while in our model, every node that receives a link has its threshold reduced by the same amount. Eftekhar et al. studied a model where nodes become seed nodes with a fixed probability [13]. Recently, this idea was extended by considering the idea of offering discounts to nodes, which would cause some nodes to be activated with a probability proportional to the amount of the discount [34, 37].

2 Notation and Preliminaries

Given a social network represented by an undirected graph \(G=(V, E, t)\), we introduce a set of external nodes U that are assumed to be already activated. We assume that all edges have unit weight; this is generally called the uniform weight assumption, and has previously been considered in many papers [4, 6, 7, 15, 25]. A link set for (G, U) is a set S of links between nodes in U and nodes in V, i.e. \(S \subseteq \{ (u, v) \mid u \in U; v \in V\}\). For a link set S, we define \(E(S) = \{v \in V\mid \exists (u, v) \in S \}\), that is, E(S) is the set of V-endpoints of links in S. For a node \(v \in V(G)\), define r(v) to be the number of links in S for which v is an endpoint. Since the set of external nodes U is already activated, observe that adding the link set S to G is equivalent to reducing the threshold of the node v by r(v). In the viral marketing scenario, the link set S represents giving v a partial incentive of r(v).

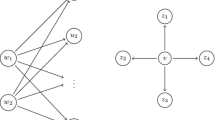
Given a link set S for a graph G, we define I(G, S) to be the set of nodes in G that are eventually activated as a result of adding the link set S, that is, by reducing the threshold of each node \(v \in E(S)\) by \(min \{ r(v), t(v) \}\), and then running the influence diffusion process. See Fig. 1 for an illustration. Observe that this is the same as the set of nodes activated by using U as the target set in the graph \(G'\), the graph obtained from G by adding the set U to the vertex set and the set S to the set of edges.

Fig. 1.
figure 1

Node \(\mu \) is the external influencer and is assumed to be activated. Links in the link set are shown with dashed edges. The given link set is an optimal link set of size 2 that activates 4 nodes: a, b, d, e.

Full size image

Definition 1

Maximum Influence with Links problem

( Max-Inf-Links ): Given a social network \(G=(V, E, t)\), and a set of external nodes U, and an integer k, find a link set S of size k that maximizes I(G, S) among all k-sized link sets. We denote by MI(G, k) the maximum number of people that can be influenced in G by an optimal link set of size k, that is, if S is an optimal solution to the Max-Inf-Links(G, k) problem, then \(MI(G, k) = |I(G,S)|\).

In our algorithms, we consider the case of a single influencer, that is, \(U = \{ \mu \}\). In this case, a link given to a vertex v reduces its threshold by 1. Since \(\mu \) must be an endpoint of each edge in the link set S, each such edge can be uniquely specified by a vertex in V. We therefore generally omit mention of \(\mu \) in the rest of the paper, and the link set S is referred to by its V-endpoints. For each such node \(v \in E(S)\), we say we give v a link, or that v receives a link.

3 NP-Hardness of Max-Inf-Links

In this section, we will prove that the decision version of the Max-Inf-Links problem is NP-hard even for bipartite graphs in which thresholds of all nodes are either one or two. It can be posed as follows: Given a social network \(G=(V,E,t)\), a set of external influencers A, and integers k and p, is there a link set S of size k such that \(|I(G, S)| = p\)? Note that in [25], the Min-Links problem (finding the smallest set of links which can activate the entire network) was shown to be NP-hard, even for graphs of degree 3 and threshold at most 2. This immediately implies the NP-hardness of the Max-Inf-Links problem as well. However, the reduction in [25] yielded a graph that was not bipartite. Here, we extend the result for bipartite graphs.

Theorem 1

The decision version of the Max-Inf-Links problem is NP-hard, even for a single external influencer, and bipartite graphs with all nodes having threshold 1 or 2.

Proof

We give a reduction from the Max-Clique problem: Given a graph \(G=(V,E)\) and an integer k, does G contain a clique of size at least k?

Given an instance of the Max-Clique problem (G, k), we construct a bipartite graph \(G'\) = (\(V_1 \cup V_2\), \(E'\), t) as follows. For every node \(v \in V\), we create a corresponding node v of threshold 1 in \(V_1\). For every edge \(\{u,v\} \in E\), we create a corresponding node (uv) of threshold 2 in \(V_2\). Next, for every edge \(\{u,v\} \in E\), we create the edges (u, (uv)) and (v, (uv)). Clearly, the transformation can be done in \(O(V+E)\) time. We show that G has a clique of size k if and only if \(G'\) has a link set of size k that can activate at least \(C_{k}^{2}+k\) nodes.

We show that G has a clique of size k if and only if \(G'\) has a link set of size k that can activate at least \(C_{k}^{2}+k\) nodes. Figure 2 illustrates the reduction.

Fig. 2.
figure 2

Reduction from G (top) to \(G'\) (bottom); thresholds in \(G'\) are indicated inside the circles representing the nodes.

Full size image

To do this, we first show that it suffices to consider link sets that contain only nodes in \(V_1\).

Claim

For any link set \(T \subseteq V_1 \cup V_2\), there exists a set \(S \subseteq V_1\) such that \(\left| S\right| \) \(\le \) \(\left| T\right| \) and \(|I(G',S)| \ge |I(G',T)|\).

Proof

Consider a node \(v \in V_2\) that receives a link in T, and is connected to \(v_1\) and \(v_2\) \(\in V_1\). We argue that we can either remove the link assigned to v, or assign that link to some other node in \(V_1\) while not decreasing the size of the activated set. The following four cases about the time of activation of v are exhaustive.

  1. Case 1:

    v is not activated by T: We can simply remove the link assigned to v.

  2. Case 2:

    v is activated before \(v_1\) and \(v_2\): Since v has threshold 2 while \(v_1\) and \(v_2\) are both of threshold 1, this is impossible with a single influencer, as the link v receives can only reduce its threshold by 1.

  3. Case 3:

    v is activated after \(v_1\) (or \(v_2\)) is activated and before \(v_2\) (rest. \(v_1\)) is activated: We can move the link assigned for v to \(v_2\) (resp. \(v_1\)); the same set of nodes will be activated eventually.

  4. Case 4:

    v is activated after \(v_1\) and \(v_2\) are activated: The link given to v is unnecessary and can be removed.

Claim

\(G'\) has a link set \(S \subseteq V_1 \) with \( |S| \le k\) and \(|I(G', S)| \ge C_{k}^{2}+k \) if and only if G has a clique of size k.

Proof

Suppose first that G has a clique \(V'\) of size k. We claim that \(V' \subseteq V_1\) is a link set such that \(|I(G', V')| = C^2_k +k\). Clearly, all nodes in \(V'\) are activated at round 1. Then since \(V'\) is a clique in G, it is easy to see that all nodes in \(V_2\) corresponding to the \(C^2_k\) edges between nodes in \(V'\) will be activated in round 2. This proves that \(|I(G',V')| \ge C_{k}^{2}+k\) .

Suppose next that there is a link set \(S \subseteq V_1\) such that \(|I(G', V')| = C^2_k +k\), then we claim that the corresponding set for S in G forms a clique of size k.

We claim that given \(S \subseteq V_1\) as a link set, it is impossible to activate any new node \(\in V_1\) except nodes in S and for any node (uv) \(\in V_2\) that gets activated, it must be that \(u \in S\) and \(v \in S\).

Suppose there exists a node \(d \in V_1-S\) such that d is eventually activated. Since d has threshold 1 and d doesn’t receive a link, in order for d to be activated, one of \(d\) \('\)s neighbors must be activated first. Let us say d is connected to (dx) and (dx) is activated before d. Node (dx) is of threshold 2, thus in order for (dx) to be activated, both d and x must be activated before (dx), a contradiction.

For the second part, suppose there exists a node (uv) \(\in V_2\) such that u \(\notin S \) and (uv) gets activated eventually. But from the previous analysis, we know that u can never be activated. Therefore (uv) cannot be activated either.

We have shown that with a set \(S \subseteq V_1\) of size k, only nodes in S can be activated for the nodes in \(V_1\); only those nodes which are connected to two nodes in S can be activated for nodes in \(V_2\). If \(|I(G',S)| \ge C_{k}^{2}\) + k, then for every pair of nodes in S, they must be connected in G, thus S must be a clique of size k in G.

This completes the proof of the reduction.    \(\Box \)

4 Optimal Algorithm for Trees

In contrast to the result of the previous section, in this section, we show that the Max-Inf-Links problem can be solved in polynomial time in trees. Let \(T= (V, E, t)\) be a tree with n nodes, \(V = \{1, 2, ... , n\}\) and \(t: t(v) \rightarrow \mathcal {Z}^{+}\). Fix an arbitrary root of the tree and order the children of every node in an arbitrary fashion. We define \(T_v\) and \(d_v\) to be the sub-tree rooted at node v, and the number of children of node v respectively. We define \(T_v^{-1}\) to be the same sub-tree as \(T_v\) except that the threshold of the root v is reduced by 1. Note that while in the input, all thresholds are \(\ge 1\), in a tree \(T_v^{-1}\), the threshold of v may be reduced to 0. We also define \(v_i\) to be \(i^{th}\) child of node v and \(T_{v_{i}}\) to be the sub-tree rooted at \(v_i\).

Given a tree \(T_v\), the optimal solution to the Max-Inf-Links problem for \(T_v\) may or may not activate the root. For example, in Fig. 3, for the tree on the left, it can be verified that every optimal link set of size 1 activates the root (one such link set gives a link to the root node a and activates a and d), but for the tree on the right, there is no link set of size 1 that activates the node a (an optimal solution gives a link to node b, and activates both b and c) . Let \(MIA(T_v, k) \) be the problem of finding an link set of at most k links to nodes in the sub-tree \(T_v\) that maximizes the number of influenced nodes while ensuring that root v is activated. Similarly, let \(MIB(T_v, k)\) be the problem of finding an link set of at most k links to nodes in the sub-tree \(T_v\) that maximizes the number of influenced nodes while ensuring that root v is not activated. Let \(A(T_v, k)\) and \(B(T_v, k)\) be the maximum number of nodes that can be influenced by an optimal solution to \(MIA(T_v, k)\) and \(MIB(T_v, k)\) respectively. Clearly, given a tree \(T = (V, E, t)\) rooted at node r, an optimal link set S for problem Max-Inf-Links \((T_{n}, k)\) either activates or does not activate the root r. Therefore:

$$MI(T_{n}, k) = max \{ A(T_r , k), B(T_r , k ) \}$$
Fig. 3.
figure 3

For the tree on the left, \(A(T, 1)=2\), and \(B(T,1)=1\) while for the tree on the right, \(A(T, 1)=-\infty \), and \(B(T,1)=1\)

Full size image

We start with link sets that do activate the root. We first prove a critical lemma that shows that any link set S that activates the root can be converted to an equivalent link set that gives a link to the root.

Lemma 1

Suppose S is a link set of size k for a tree \(T_v\) in which \(v= root(T)\) is activated, and \((\mu , v) \notin S\). Then there exists a link set \(S'\) with \((\mu , v) \in S'\) such that \(I(T, S') = I(T, S)\) and \(|S'| = k\).

Proof

We prove the lemma by induction on the height of the tree T. Clearly, the lemma is true for trees of height 0; the only way to activate the root in such a tree is to give a link to the root v.

Now consider a tree T of height h and a link set S for T that activates v without giving v a link. Clearly, there must exist a child c of v which is activated before v, and contributes to the activation of v. By the inductive hypothesis, we can assume that c is given a link in S. Consider \(S' =S - \{(\mu , c)\} \cup \{(\mu , v) \}\). Any node in \(T_v - T_c\) that was activated by S before v, is also activated in \(S'\) before v. Therefore v will be activated by \(S'\), and will subsequently activate c, and any nodes in \(T_c\) that were activated by c. All other children of v that were activated after v in S will also be activated after v by \(S'\). Therefore, \(I(T,S) = I(T,S')\). \(\Box \)

Lemma 1 tells us that an optimal link set S of size k that activates the root v of a tree \(T_v\) can be assumed to give a link to the root v. Then the remaining \(k-1\) links must be given to other nodes in \(T_v\), but since v is activated by S, it must be that at least \(t(v) -1\) children of v are activated before v and contribute to the activation of v. Observe that once v is activated, the thresholds of its remaining children are effectively reduced by 1. This, together with the links given by the link set S to nodes in the subtrees of the remaining children, may activate some of these children and subsequently other nodes in their subtrees. Let \(F_{v, d}\) be the forest of subtrees rooted at the first d children of v. We see that there exists some partition (C, D) of the roots of trees in \(F_{v, d_v}\) such that \(|C| \ge t(v) - 1\) and S activates the nodes in C before v, and subsequently v gets activated, which in turn reduces the thresholds of the nodes in D by one, perhaps contributing to their activation.

We formalize and generalize the above to find appropriate link sets for the forest \(F_{v, d_v}\). Let \(F_{v,d}\) be the forest consisting of the subtrees rooted at the first d children of v and let (C, D) be a partition of the roots of the d trees. Let F(C, D) be a forest derived from \(F_{v, d}\) by reducing the threshold of all nodes in D. We call a link set for F(C, D) a C-activating link set if it activates all nodes in C, and maximizes the total number of activated nodes in F(C, D). Given a forest F, and an integer i, we call a link set for F an i-first link set if it is a C-activating link set for some partition (C, D) of the roots of trees in F with \(|C| \ge i\). We now define \(MIA(F_{v, d}, i, k)\) to be the problem of finding an i-first link set of size k that maximizes the total number of activated nodes in F.

Next consider a link set that does not activate v. In this case, at most \(t(v)-1\) of v’s children can be activated, as otherwise v would also be activated. To find such a link set, we define \(MIB(F_{v, d}, i, k)\) to be the problem of finding a link set of size at most k that activates the most nodes in \(F_{v, d}\) while activating exactly i roots of trees in \(F_{v, d}\). Let \(A(F_{v, d},i, k)\) and \(B(F_{v,d}, i, k)\) be the number of influenced nodes by an optimal solution to \(MIA(F_{v, d},i, k)\). and \(MIB(F_{v, d},i, k)\) respectively.

We now give recursive formulations for \(A(T_v, k),\) \(B(T_v, k)\), \(A(F_{v,d}, i, k),\) and \(B(F_{v,d}, i, k)\); as we have already observed, they are inter-dependent. We start with a recursive formulation for A(v, k).

Lemma 2

$$\begin{aligned} \begin{array}{lcl} A(T_v , k) &{}=&{} \left\{ \begin{array}{ll} \text { 1+} A(F_{v, d_v},0, k) &{} \text {if } t(v) =0 \\ \text { 1+} A(F_{v, d_v},t(v)-1, k-1) &{} \text {if } 1 \le t(v) \le k \\ \text { } -\infty &{} \text {if } k < t(v) \end{array} \right. \\ \end{array} \end{aligned}$$

Proof

First suppose \(k \ge t(v) = 0\). In this case, there is no need to give v a link, and none of v’s children need to be activated before it. Therefore, \(A(T_v, k) = 1+ A(F_{v, d_v},0, k)\) as claimed.

Next suppose \(k \ge t(v) = 1\). Then by Lemma 1, there exists an optimal link set S in which root v receives a link, thereby activating v. It is then straightforward to see that \(S - \{v\}\) is also an optimal solution to problem \(MIA(F_{v, d_v},0, k-1)\). It follows that \( A(T_v, k) = 1+ A(F_{v, d_v},0, k-1)\) in this case.

Next, suppose \(1 < t(v) \le k\). Then giving root v a link does not suffice to activate v; in fact \(t(v) - 1\) of \(v'\)s children have to be activated before v, otherwise v cannot be activated. By Lemma 1, however, there exists an optimal link set S which gives root v a link. We claim that \(S - \{v\}\) is an optimal solution to problem \(MIA(F_{v, d_v},t(v)-1, k-1)\). Suppose not, let \(|S|= k\) and let \(S'\) be an optimal solution to \(MIA(F_{v, d_v},t(v)-1, k-1)\) which can activate more nodes than \(S - \{v\}\). With \(S'\), \(t(v)-1\) children of v have been activated. These activations, together with the link to v, are enough to activate node v, and would reduce the threshold of the remaining children of v by 1. Therefore \(S' \cup \{v \}\) activates v as well as all nodes activated by \(S'\) in \(F_{v, d(v)}\). Then \(S' \cup \{v\}\) will be a link set of k links which can activate more nodes in \(T_v\) than S, contradicting the optimality of S. Therefore: \(A(T_v, k) = 1 + A( F_{v, d_v},t(v)-1, k-1)\).

Finally suppose \(t(v) > k \ge 0\). Then we claim it is impossible to activate the root. If it were possible to activate the root using k links, then by Lemma 1, there is an optimal link set that activates the root and gives a link to v. Then the remaining \(k-1\) links must be given to nodes in \(F_{v, d_v}\). However using \(k-1< t(v)-1\) links, we can activate at most \(k-1\) children of v, and together with the link given to v, the reduction in threshold of v is \(< t(v)\), a contradiction. Thus in this case \(A(T_v, i) = - \infty \) as claimed. This completes the proof of the lemma.

   \(\Box \)

Lemma 3

\(A(F_{v, d},i, k) \) 

$$\begin{aligned} =\left\{ \begin{array}{ll} \text { } -\infty &{} \text {if } i>d \\ \text { } 0 &{} \text{ if } i=d = 0\\ \text { } \mathop {\max } \limits _{ 0 \le p \le k }\{A(F_{v, d-1},i-1, p) + A(T_{v_{d}},k-p) \} &{} \text {if } i = d >0\\ \text { } \max \left\{ \begin{aligned} &{} \mathop {\max } \limits _{ 0 \le p \le k } A(F_{v, d-1},i, p) + max\left\{ \begin{aligned} A(T_{v_{d}}^{-1}, k-p) \\ B(T_{v_{d}}^{-1}, k-p) \end{aligned} \right. \\ &{} \mathop {\max } \limits _{ 0 \le p \le k }\{A(F_{v, d-1},i-1, p) + A(T_{v_{d}},k-p) \} \end{aligned} \right. &{} \text {if } 0< i< d \\ \text { } \mathop {\max } \limits _{ 0 \le p \le k } A(F_{v, d-1},i, p) + max\left\{ \begin{aligned} A(T_{v_{d}}^{-1}, k-p) \\ B(T_{v_{d}}^{-1}, k-p) \end{aligned} \right. &{} \text {if } 0 = i < d \end{array} \right. \end{aligned}$$

Proof

If \(i > d\), clearly it is impossible to activate at least i of the first d children of v, therefore \(A(F_{v, d},i, k) = -\infty \). If \(i=d=0\), the forest \(F_{v, d}\) is empty, and therefore, no nodes can be influenced by any link set of any size.

If \(i = d\), this means that all children \(v_j\) with \(1 \le j \le d\) have to be activated before v. The optimal solution S will assign p links to \(F_{v, d-1}\) and \(k-p\) links to \(T_{v_d}\), for some p. It follows that \(A(F_{v, d}, i , k) = \mathop {\text {max}}\limits _{ 0 \le p \le k }\{ A(F_{v, d-1},i-1, p) + A(T_{v_{d}},k-p) \}\) If \(i < d\), and \(v_d\) is not activated before v by S, observe that \(v_d\) may or may not be activated after v. Besides, due to the fact that its parent has already been activated, the threshold of \(v_d\) is effectively reduced by one. An optimal link set S will assign p links to \(F_{v, d-1}\) and \(k-p\) links to \(T_{v_d}\), therefore we try all possibilities of p to find the best distribution. Therefore:

$$\begin{aligned} A(F_{v, d},i, k) = \mathop {\max } \limits _{ 0 \le p \le k }\{A(F_{v, d-1},i, p) + max\left\{ \begin{aligned} A(T_{v_{d}}^{-1}, k-p) \\ B(T_{v_{d}}^{-1}, k-p) \end{aligned} \right. \} \end{aligned}$$

Finally, if \(i < d\) and \(v_d\) is activated before v by S, at least \(i-1\) children of v in \(F_{v, d-1}\) are required to be activated before v. Since \(v_d\) contributes to the activation of v, the threshold of \(v_d\) remains unchanged.

$$\begin{aligned} A(F_{v, d}, i , k) = \mathop {\max } \limits _{ 0 \le p \le k }\{ A(F_{v, d-1},i-1, p) + A(T_{v_{d}},k-p) \} \end{aligned}$$

When \(i = 0\), we only need to consider the first of the two situations above. \(\Box \)

Next we consider link sets that do not activate the vertex v (the proof of Lemma 4 is omitted).

Lemma 4

$$\begin{aligned} \begin{array}{lcl} B(T_v, k) &{}=&{} \left\{ \begin{array}{ll} \text { } \mathop {\max } \limits _{ 0 \le i < min(t(v),d_v+1) } B(F_{v, d_v}, i, k) &{} \text {if } t(v) > 0 \\ \text { } -\infty &{} \text {if } t(v) = 0 \end{array} \right. \\ \end{array} \end{aligned}$$

Lemma 5

\(B(F_{v, d},i, k)\)

$$\begin{aligned} = \left\{ \begin{array}{ll} \text { }\max \left\{ \begin{aligned} &{} \mathop {\max } \limits _{ 0 \le p \le k }\{B(F_{v, d-1},i, p) + B(T_{v_{d}}, k-p)\} \\ &{} \mathop {\max } \limits _{ 0 \le p \le k }\{B(F_{v, d-1},i-1, p) + A(T_{v_{d}},k-p) \} \end{aligned} \right. &{} \text {if } 0< i, d \\ \text { } \mathop {\max } \limits _{ 0 \le p \le k }\{B(F_{v, d-1},i, p) + B(T_{v_{d}} , k-p)\} &{} \text {if } 0 = i < d\\ \text { } 0 &{} \text {if } d=0 \end{array} \right. \end{aligned}$$

Proof

Suppose \(i, d > 0\). Then in an optimal solution S to \(MIB(F_{v, d}, i, k)\), either \(v_d\) is activated or it is not. If \(v_d\) is activated, then some p links are given to nodes in \(F_{v, d-1}\) and exactly \(i-1\) nodes are activated by S in \(F_{v, d-1}\), while the remaining \(k-p\) links must constitute an optimal solution to \(MIA(T_{v_d}, k-p)\). That is, \(B(F_{v, d}, i, k) = B(F_{v, d-1},i-1, p) + A(T_{v_{d}},k-p)\). Alternatively, if \(v_d\) is not activated by S, then some p links are given to nodes in \(F_{v, d-1}\) and exactly i nodes are activated by S in \(F_{v, d-1}\), while the remaining \(k-p\) links must constitute an optimal solution to \(MIB(T_{v_d}, k-p)\). That is, \(B(F_{v, d}, i, k) = B(F_{v, d-1},i, p) + B(T_{v_{d}},k-p)\). If \(i=0\), this means no roots of trees in \(F_{v, d}\) are to be activated, which means neither \(v_d\) is activated, nor any roots in \(F_{v, d-1}\) . Finally, if the forest is empty (\(d=0\)), then clearly the maximum number of nodes that can be influenced is 0, regardless of i and k. \(\Box \)

Theorem 2

The Maximum Influence problem for a tree \(T_n=(V,E,t)\) using k links, can be solved in time \(O(n^2k^2)\).

Proof

The recursive definitions given in Lemmas 2 to  5 can be computed using dynamic programming to obtain an optimal solution to the Max-Inf-Links problem. In the worst case, for any node w with d children, we need to compute \(A(F_{v, p}, i, j)\) and \(B(F_{v, p}, i, j)\) for \(1 \le p \le d\), \(0\le i \le d\), and \(0 \le j \le k\). These are \(d^2k\) values, each of which can take \(\Theta (k)\) time to compute. The values \(A(T_v, k)\) and \(B(T_v, k)\) can be computed in constant time, and there are k such values. Using the result of [9], the sum of squares of degrees of a node in a graph is upper bounded by \(e(2e/(n-1) + n - 2)\), which for a tree is \(\Theta (n^2)\). Summing up the time over all vertices in the graph, we obtain a total time of \(O(n^2k^2)\). \(\Box \)

5 Faster Algorithm for Paths

The algorithm for trees in the previous section obviously also applies to paths. In this section, we give a \(\Theta (kn)\) algorithm for the Max-Inf-Links problem in a path, by exploiting its simpler structure. Let \(P_n = (V, E, t)\) be a path with n nodes, \(V = \{1, 2, ... , n\}\), \(E = \{(i, (i + 1)) \ |\ 1 \le i \le n-1 \}\), and \(t: t(v) \rightarrow \mathcal {Z^{+}}\) (the threshold function). For \(1 \le i \le j \le n\), we define \(P_{i, j}\) to be the sub-path of \(P_n\) consisting of all nodes in \(\{ i, \ldots , j\}\).

An optimal solution to Max-Inf-Links(\(P_{i, j}, k\)) may or may not activate the node i. Accordingly, let \(MIA(P_{i, j}, k)\) be the problem of finding a link set of size at most k for the sub-path \(P_{i, j}\) that maximizes the number of influenced nodes while ensuring that node i is activated. Similarly, let \(MIB(P_{i, j}, k)\) be the problem of finding a link set of size at most k for the sub-path \(P_{i, j}\) that maximizes the number of influenced nodes while ensuring that node i is not activated. Let A ( i ,  j ,  k ) and B ( i ,  j ,  k ) be the number of nodes that can be influenced by optimal solutions to \(MIA(P_{i, j}, k)\) and \(MIB(P_{i, j}, k)\) respectively.

The key idea of our algorithm is to break the path into subpaths containing only nodes of threshold 1 and 2, separated by nodes of threshold 3 or greater. We give recursive definitions for A(i, j, k) and B(i, j, k) when \(P_{i, j}\) has only nodes of threshold 1 or 2. As we will see, these definitions are inter-dependent. We need the following definition.

Definition 2

Given a path \(P_n\), fix i such that \(1 \le i \le n\). We define \(next(i) = min \{ j \mid i < j \le n+1 \text{ and } \text{ either } t(j) = 1 \text{ or } j = n+1\}\).

We see that next(i) is the first node after i to have threshold 1, unless i is the rightmost node in the path with threshold 1, in which case \(next(i) =n+1\). Clearly \(A(n+1,n, k) = B(n+1,n, k) = 0\) for all k. We now consider the case when \(1 \le i \le j \le n\). We start with the case when \(t(i) =2\).

Lemma 6

Given a sub-path \(P_{i, j}\) in which all nodes have threshold 1 or 2, and \(t(i) = 2\):

$$\begin{aligned} \begin{array}{lcl} A(i,j,k) = \left\{ \begin{array}{ll} 0 &{} \text {if}\,\, next(i)> j \\ 0 &{} \text {if }\,\, A(i+1, j, k-1) = 0 \\ 1 + A(i+1, j, k-1) &{} \text {if }\,\, A(i+1, j, k-1)> 0 \end{array} \right. \\ \text { }\\ B(i,j, k) = \left\{ \begin{array}{ll} 0 &{} \text {if}\,\, next(i) > j \\ max\left\{ \begin{aligned} &{} A(i+1, j, k) \\ &{} B(i+1, j, k) \end{aligned} \right. &{} \text {if}\,\, next(i) \le j \end{array} \right. \end{array} \end{aligned}$$

Proof

If \(next(i) >j\) then there is no way to activate any node in \(P_{i, j}\), therefore \(A(i, j, k) = B(i, j, k) = 0\) for every k. If instead \(next(i) \le j\), then it is possible to activate at least one node in \(P_{i, j}\). Observe that in any feasible solution for \(MIA(P_{i, j}, k)\), not only does node i need to receive a link, but its neighbor node \(i+1\) needs to be activated as well, therefore \(A(i, j, k) = 0\) if \(A(i+1, j, k-1) = 0\); otherwise \(A(i, j, k) = 1+A(i+1, j, k-1)\). Finally, note that any feasible solution for \(MIB(P_{i, j}, k)\) is a solution in which i does not receive a link, and the next node may or may not be activated, or it does receive a link, and the next node is not activated. That is \(B(i, j, k) = max \{A(i+1, j, k), B(i+1, j, k), B(i+1, j, k-1) \} = max \{A(i+1, j, k), B(i+1, j, k) \}\). \(\Box \)

Next we consider the case when node i has threshold 1. In this case, the optimal substructure of the problem is not so straightforward to prove. The difficulty arises because an optimal solution S to \(MIA(P_{i, j}, k)\) may or may not activate node \(i+1\). In the case when it does not activate node \(i+1\), we would like to claim that S consists of a link to i and and an optimal solution to \(MIB(P_{i+1, j}, k-1)\). However, we do not know whether or not \(i+2\) was activated in a solution to \(MIB(P_{i, j}, k)\). So when we combine such a solution with a link to node i, we may or may not activate node \(i+1\).The following technical lemma uncovers the structure of optimal solutions.

Lemma 7

Let \(P_{i, j}\) be a path with \(t(i) = 1\) and \(next(i) \le j\). If in every optimal solution for \(MIA(P_{i, j}, k)\), node i receives a link, then there exists an optimal solution S for \(MIA(P_{i, j}, k)\) in which neither \(i+1\) nor \(i+2\) receives a link.

Proof

Suppose in every optimal solution for \(MIA(P_{i, j},k)\), node i receives a link. Let S be an optimal solution for \(MIA(P_{i, j}, k)\) which uses the fewest links possible.

First we show that \(next(i) >i+2\). By assumption, node i receives a link in S. Observe that if \(next(i) = i+1\), then \(i+1\) cannot have a link since that would contradict the minimality of S. So we can simply move the link from node i to \(i+1\) and activate the same set of nodes, but this contradicts the assumption that in every optimal solution, node i must receive a link. Next suppose \(next(i) = i+2\). Then it is not possible that both \(i+1\) and \(i+2\) receive links, as this would contradict the minimality of S. If exactly one of \(i+1\) and \(i+2\) have a link, we can move the link to i to the node among \(i+1\) and \(i+2\) that does not have a link, thus creating a solution which activates exactly the same set of nodes, a contradiction. If neither \(i+1\) nor \(i+2\) has a link, and neither is activated, then the lemma is proved. Finally, if neither has a link, but one of them is activated, it must be that \(i+2\) is activated by node \(i+3\). In this case, we can move the link from node i to node \(i+1\), getting a solution that activates the same set of nodes, a contradiction to the assumption that every optimal solution must give i a link. We conclude that \(next(i)> i+2\), that is, there are at least two nodes in between i and next(i).

Fig. 4.
figure 4

The case when next(i) is not activated. At least one node in \(\{i+1, \ldots , next(i) - 1\}\) does not receive a link.

Full size image

We now show that we can always change S to a solution \(S'\) that does not activate \(i+1\) or \(i+2\) but activates the same number of nodes as S overall. Let \(S_1 = S \cap \{i+1, \ldots , next(i) -1 \}\) and \(S_2 = S \cap \{next(i), \ldots , j \}\). First suppose next(i) is not activated by S. Then next(i) did not get a link, and there must be at least one other node in \(\{ i+1 ,\ldots , next(i)-1\}\) that did not receive a link, as if all such nodes received a link, next(i) would be activated (see Fig. 4). Therefore \(|S_1| \le next(i) - i - 2\). Consider now the link set \(S'\) made by shifting all the links in \(S_1\) from \(i+1\) onwards to a consecutive sequence of nodes ending with next(i), that is, \(S' = \{i \} \cup \{ next(i) - |S_1| + 1, \ldots next(i) \} \cup S_2\). Then \(S'\) is the same size as S, it activates exactly the same number of nodes as S, and is therefore also optimal. Observe that \(next(i) - |S_1| + 1 >i+2\), since \(|S_1| \le next(i) - i - 2\). Thus \(S'\) is an optimal solution to \(MIA(P_{i, j}\) that does not give links to \(i+1\) and \(i+2\) as needed.

Fig. 5.
figure 5

The case when next(i) is activated either by a link or by \(next(i)+1\). At least two nodes in \(\{i+1, next(i)-1\}\) do not receive links.

Full size image

Next suppose next(i) is activated by S. If next(i) was activated by \(next(i)-1\), then all nodes in \(\{i+1, \ldots , next(i)-1\}\) must have received links, which contradicts either the minimality of S, or the assertion that i gets a link in every optimal solution. So we conclude that either next(i) received a link in S or was activated by \(next(i)+1\). Since S is minimal, there must exist at least one node in \(\{ i+1, \ldots , next(i)-1\}\) that did not receive a link. If there is exactly one such node p, then clearly every node in \(\{ i, \ldots , next(i)\}\) is activated by S, but then solution \(S'\) which moves the link given to i to node p also activates the same nodes, and contradicts the assertion that every optimal solution must give a link to i. Therefore, there must be two nodes in \(\{i+1, \ldots , next(i)-1\}\) that do not receive links (see Fig. 5). Therefore \(|S_1| \le next(i) - i - 3\). Consider now the link set \(S'\) made by shifting all the links in \(S_1\) from \(i+1\) onwards to a consecutive sequence of nodes ending with \(next(i)-1\), that is, \(S' = \{i \} \cup \{ next(i) - |S_1| , \ldots next(i) - 1\} \cup S_2\). Then \(S'\) is the same size as S, it activates exactly the same number of nodes as S, and is therefore also optimal. Observe that \(next(i) - |S_1| >i+2\), since \(|S_1| \le next(i) - i - 3\). Thus \(S'\) is an optimal solution to \(MIA(P_{i, j}, k)\) that does not give links to \(i+1\) and \(i+2\) as needed. \(\Box \)

The following lemma summarizes the optimal substructure of the problem when \(t(i) =1\).

Lemma 8

Given a sub-path \(P_{i, j}\) in which all nodes have threshold 1 or 2, and \(t(i) = 1\):

$$\begin{aligned} \begin{array}{lcl} A(i,j, k) = \left\{ \begin{array}{ll} \text {min}\{ k, j-i+1\} &{} \text {if}\,\, next(i)> j \\ max\left\{ \begin{aligned} &{} 1+A(i+1, j, k) \\ &{} 1+B(i+1, j, k-1) \end{aligned} \right. &{} \text {if}\,\, next(i) \le j \end{array} \right. \\ \text { }\\ B(i,j, k) = \left\{ \begin{array}{ll} 0 &{} \text {if }\,\, next(i) > j \\ B(i+1,j, k) &{} \text {if }\,\, next(i) \le j \end{array} \right. \end{array} \end{aligned}$$

Proof

First we prove the correctness of the recursive definitions for A(i, j, k). If \(next(i) > j\), then node i must receive a link, as it is not possible otherwise to activate any node in \(P_{i+1,j}\). Thus node i receives a link and is activated first. Inductively, we can show that node \(i+1\) is the second node which receives a link and gets activated (see Fig. 6). Therefore, all nodes in \(\{i, \ldots , i + min \{k,j-i+1 \} - 1\}\) must receive a link. Any node that does not receive a link cannot get activated, the maximum number of activated nodes is \(min \{k,n-i+1 \}\). This shows that \(A(i, j, k) = min \{k,n-i+1 \}\) in this case.

Fig. 6.
figure 6

An optimal link set S for \(MIA(P_{i, j}, 4)\): the case when \(t(i)=1\) and \(next(i)>j\)

Full size image

Otherwise, \(next(i) \le j\), that is, node i is not the rightmost node with threshold 1. First observe that either there exists an optimal solution for \(MIA(P_{i, j}, k)\) in which node i does not receive a link, or in every optimal solution for \(MIA(P_{i, j}, k)\), node i receives a link. In the first case, let S be an optimal solution for \(MIA(P_{i, j}, k)\) in which node i does not receive a link. It follows that its neighbor node \(i+1\) was also activated. Clearly S must be an optimal solution for \(MIA(P_{i+1, j}, k)\) (if not, and if \(S'\) is a solution for \(MIA(P_{i+1, j}, k)\) that activates more nodes than S, then \(S'\) is also a better solution for \(MIA(P_{i, j}, k)\), contradicting the optimality of S. Therefore, \(A(i, k) = 1 + A(i+1, k)\).

In the second case, by Lemma 7, we have an optimal solution \(S'\) in which nodes \(i+1\) and \(i+2\) do not receive links and are therefore not activated. Furthermore, using a cut-and-paste argument, it is straightforward to see that \(S'' = S' - \{i \}\) is an optimal solution for \(MIB(P_{i+1, j}, k-1)\). It follows that \(A(i, k) = 1 + B(i+1, k-1)\).

Finally, any solution in which node i is not activated, we can be sure that neither node i gets a link, nor does its neighbor, node \(i+1\) get activated. Therefore \(B(i, k) = B(i+1, k)\). This completes the proof. \(\Box \)

We now use the definitions of A(i, j, k) and B(i, j, k) to prove the main result of this section:

Theorem 3

Max-Inf-Links (\(P_n, k)\) can be solved in time \(\Theta (kn)\).

Proof

If \(P_n\) has no nodes of threshold \(> 2\), then clearly \(MI(P_n) = max \{ A(1, n, k), B(1, n, k) \}\). If not, let q be the largest index of a node in \(P_n\) such that \(t(q) \ge 3\). If \(t(q)>3\), then q cannot be activated, therefore, there is no need to give a link to q. That is, the optimal solution to the Max-Inf-Links problem with k links does not give node q a link, and instead uses \(\ell \) links to solve the Max-Influence problem on the path \(P_{1, q-1}\) and \(k- \ell \) links to solve the Max-Influence problem on the path \(P_{q+1, n}\) for some value of \(\ell \) such that \(0 \le \ell \le k\). Thus the optimal solution can be found by checking for all possible values of \(\ell \) between 0 and k, yielding:

$$MI(P_n, k) = max_{0 \le \ell \le k} \{ MI(P_{1, q-1}, \ell ) + MI(P_{q+1, n}, k - \ell ) \}$$

Finally if \(t(q) = 3\), then either there exists an optimal solution in which q is not activated, in which case \(MI(P_n, k)\) is defined identically to the case when \(t(q) > 3\), or in every optimal solution q is activated. In this case, let S be an optimal solution to \(MI(P_n, k)\). By assumption, q is activated. Since \(t(q) =3\), it must be that q gets a link, and also that \(q-1\) and \(q+1\) are activated. Let \(S =S_1 \cup \{q \} \cup S_2\) where \(S_1 = \{1, \ldots , q-1\} \cap S\) and \(S_2 = S \cap \{ q+1, n \}\), and let \(|S_1| = \ell \) and \(|S_2| = k - 1 - \ell \) We now claim that \(S_2\) is an optimal solution to \(MIA(P_{q+1, n}, k-1 - \ell )\). If there was a better solution to \(MIA(P_{q+1, n}, k-1 - \ell )\) than \(S_2\), we can replace \(S_2\) by the claimed better solution in S to get a better solution to Max-Inf-Links \((P_n, k)\), a contradiction to the optimality of S.

Next we claim that \(S_1\) is an optimal solution to Max-Inf-Links(\(P_{1, q-1}, \ell )\). Suppose instead that \(S_1\) activates \(\alpha \) nodes in \(P_{1, q-1}\) and there is another set of links \(S'\) of size \(\ell \) that activates \(\beta > \alpha \) nodes in \(P_{1, q-1}\). If \(S'\) activates \(q-1\), then clearly \(S' \cup \{q\} \cup S_2\) activates more nodes than S in \(P_n\), a contradiction to the optimality of S. If \(S'\) does not activate q, then \(S' \cup S_2\) does not activate node q but activates at least the same number of nodes in \(P_n\) as S does, a contradiction to the assertion that every optimal solution activates q. Therefore, we conclude that

$$MI(P_n, k) = max_{0 \le \ell \le k} \{ 1 + MI(P_{1, q-1}, \ell ) + A(P_{q+1, n}, k - 1 -\ell ) \}$$

Finally, we prove that the above formulation can be computed using dynamic programming in time \(\Theta (kn)\). For any sub-path\(P_{i,j}\) containing only nodes of threshold 1 and 2, the values of A(i, j, r), B(i, j, r) and MI(i, j, r) can be found using the definitions in Lemmas 8 and  6 for all \(0 \le r \le k\) in time \(\Theta (k (j-i+1)\). Since the total lengths of all sub-paths is at most n, the total time spent is \(\Theta (nk)\). Since there are O(n) such sub-paths, the recursive formulation for \(MI(P_n, k)\) above for a paths with no threshold limit takes another O(kn) time to compute.

   \(\Box \)

5.1 Cycles

By taking out a single node from the cycle, and considering the resulting path, we can obtain an algorithm for the Max-Inf-Linksproblem for cycles:

Theorem 4

The Max-Inf-Links problem for a cycle \(C_n\) using k links, can be solved in time \(\theta (kn^{2})\).

6 \(\Theta (n)\) Algorithm for Cliques

The following greedy algorithm can be shown to produce an optimal solution for cliques. We sort the nodes in order of threshold and examine nodes in order while we still have links to assign. When we process node i, if \(t(i) > i\), we stop assigning links and break. If \(t(i) < i\), we simply increment i and continue. Finally if \(t(i) = i\), we give a link to node i.

Theorem 5

Max-Inf-Links(\(K_n, k\)) can be solved in time \(\Theta (n)\).

7 Discussion

In this paper, we introduced and studied the Max-Influence-with-Links problem: given a social network G where every node v has a threshold t(v) to be activated, and an integer k, which k nodes in G should an already activated external influencer \(\mu \) befriend, so as to influence the maximum possible number of nodes in the network? We showed that the problem is NP-complete, even for a single influencer, and bipartite graphs with maximum threshold 2. In contrast, for the case of a single external influencer, we showed a linear time algorithm for cliques, \(\Theta (kn)\) algorithm for paths, \(\Theta (kn^2)\) algorithm for cycles, and a \(\Theta (k^2n^2)\) algorithm for trees. It seems straightforward to generalize our algorithms for any number k of external influencers. It would be interesting to study the complexity of the problem for graphs of bounded tree width, and the approximability of the problem for constant k. We are also interested in studying the case with non-uniform weights on the edges. Clearly, the problem remains NP-complete in general, but the complexity for special classes of graphs remains open.