Keywords

Introduction and Background

Given that proof has historically appeared solely in secondary school geometry (Fujita and Jones 2014; Herbst 2002), teachers tend to consider proof as residing within this content area (Furinghetti and Morselli 2011). An expansive body of research has documented the struggles that students experience with proof (e.g., Healy and Hoyles 2000) and the deleterious effects of traditional proof instruction in geometry (Schoenfeld 1989). Lampert’s (1990) work with fifth-grade students illustrated that it is possible for the teacher and students to co-construct a classroom environment where students make conjectures and engage in the development of valid mathematical arguments. Despite such proof of concept studies, teachers encounter similar struggles in identifying valid proofs (Knuth 2002a) and understanding the limits of empirical evidence (Martin and Harel 1989). Teachers also hold conceptions about the teaching of proof. For instance, in addition to formal proof, which was suitable only for some students, teachers also believed that proofs could be informal, consisting of empirical arguments (Knuth 2002b), which were suitable for all students. Indeed, teachers may harbor the conception that only students of perceived high ability can construct proofs (Furinghetti and Morselli 2011). Additionally, Dickerson and Doerr (2014) found that a group of 17 high school mathematics teachers stated that the most important proof purposes were: enhancing students’ understanding of mathematics and developing generalizing skills that could be used in other areas. Knuth (2002a) found that a group of 16 practicing secondary school mathematics teachers identified proof as having a number of different purposes (e.g., establishment of truth), but did not see how proof could promote understanding. Knuth (2002b) found that the majority of teachers in his study defined proof as a logical or deductive argument demonstrating the truth of an assertion. The remaining teachers defined proof as a convincing argument.

Although there are a number of different ways to define understanding, one way is via relational and instrumental understanding (Skemp 1976). Skemp defined relational understanding as knowing both what to do in particular situations as well as why it is important to do those things. Instrumental understanding, in contrast, involves knowing rules without the knowing the reasons behind these rules. DeVilliers’ (1991) work with 17 14-year-old pupils’ exploration of geometric ideas in a dynamic geometry system found that while they were convinced of the validity of the ideas after a few manipulations, they did desire to understand why these ideas held true. Thus, even when convinced that a mathematical idea is true, students are still interested in gaining a relational understanding of these ideas. Such findings suggest that students’ desire for relational understanding can be leveraged to motivate them to engage in proofs that serve an explanatory role.

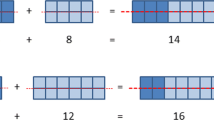
In 2010 Ireland implemented Project Maths, a reform of their secondary mathematics educational system intended to promote student learning through problem-solving, investigations, and the use of real-world contexts. Research involving teachers who piloted this reform suggest that it involves practices that are a significant departure from previous classroom instruction in Ireland (National Council for Curriculum and Assessment [NCCA] 2012). For instance, teachers spoke about rote learning , memorization, a focus on mathematical procedures, and a presentation of procedures without justification before implementation of Project Maths. Two representations of the Project Maths reform are the syllabi for junior certificate students (ages 12–15) and senior certificate students (ages 16–18), each of which contains content objectives separated by three ability levels listed in ascending order of difficulty: foundation level (FL), ordinary level (OL), and higher level (HL). The standards appearing in these syllabi were designed for teachers to use as they craft classroom instruction. Reasoning-and-proving (RP) processes (Stylianides 2008) involving identifying patterns (plausible and definite), constructing conjectures, and providing support for mathematical claims appear throughout these documents (Davis 2014), but are especially singled out in a section titled, Synthesis and Problem-Solving Skills, that appears in each content strand as seen in Fig. 14.1. Figure 14.1 reveals that students are expected to identify patterns and develop conjectures. Students are asked to craft arguments when they explain their findings, justify their conclusions, and draw relevant conclusions.

Fig. 14.1
figure 1

Synthesis and problem-solving skills from the syllabus for senior certificate students (NCCA 2014)

Full size image

In research reported elsewhere (Davis 2014) I found that junior certificate students were provided with fewer opportunities to develop conjectures and develop arguments than senior certificate students. In addition, each syllabus contained a preponderance of pattern identification, conjecture formulation, and proof construction outcomes that were not tied to specific mathematics content objectives. These standards were designed for teachers to use as they craft classroom instruction and given these disparities teachers may provide students with fewer opportunities to engage in RP during the enacted curriculum . The presence of RP processes in all content strands in this section of the syllabus led to questions surrounding teachers’ conception of the role of proof in different content strands.

The centrality of RP processes in the development of mathematical knowledge by mathematicians has been pointed out by Stylianides and Silver (2009) in citing the work of Polya (1954), Atiyah (1984/1986) and Schoenfeld (1983). Research by Stylianides (2008) on one set of middle school textbooks found that 10% of tasks involved pattern identification, 1% of tasks involved conjecturing, and 5% of tasks involved demonstrative arguments. Otten et al. (2013) examined six US geometry textbooks for the presence of RP processes and found that the majority of these elements appeared on introductory proof units with less than 5% of exercises in other chapters involving RP processes. Wong and Sutherland (this volume) also found that 13% of tasks in a popular Hong Kong grade 10 algebra textbook series involved RP processes. Research involving US students’ experiences with proof in geometry suggests that teachers skip tasks involving proof (Thompson and Senk 2014), rarely use technology such as dynamic geometry (Thompson and Senk), or reduce the cognitive demand of problems requiring arguments when enacted (Sears and Chávez 2014). Thus, given these findings it is likely that school students do not routinely experience pattern identification, conjecturing, and proof as a coordinate set of activities. Moreover, it is important to note that these RP processes do not necessarily have to follow a linear sequence. Karunakaran (this volume) has pointed out that mathematicians may interrupt their deductive logic in their process in order to complete their deductive arguments.

This study provides a unique contribution to the research body by using Stylianides’ (2008) framework to examine a group of Irish teachers’ mathematical, psychological, and pedagogical perspectives about RP processes and the connections between pattern identification and proof and the connections between conjecturing and proof. This study also sheds light on how mathematics teachers in transition from one set of educational experiences to another perceive RP processes. Specifically, this study was designed to answer the following research questions:

  1. 1.

    How does a group of Irish post-primary teachers perceive pattern identification and conjecturing and their roles in the development of proof arguments?

  2. 2.

    How does a group of Irish post-primary teachers define proof, position proof with regard to a mathematics content area, and envision the role of proof for students with different perceived abilities?

  3. 3.

    How does a group of Irish post-primary teachers conceive the role of proof in promoting understanding?

  4. 4.

    How does a group of Irish post-primary teachers perceive of the synthesis and problem-solving skills section of the syllabus that contains RP processes?

Methods

Stylianides (2008) introduced the term reasoning-and-proving (RP) to encompass the interconnected nature of four activities: pattern identification; conjecturing; constructing non-proof arguments; and developing proof arguments. These processes involve three components: mathematical, psychological, and pedagogical. The mathematical component consists of the examination of an activity for the presence of the aforementioned RP processes by a mathematically knowledgeable person. The psychological component seeks to understand how an individual who is engaged in solving a mathematical problem perceives RP processes. The pedagogical component has two subcomponents. First, it seeks to discern the relationship between the mathematical component of a problem with the solver’s psychological component of a problem. Second, it seeks to understand the teacher moves that will enable the mathematical component of a task to become transparent to the solver.

This study makes use of all three components within Stylianides’ (2008) framework. The focus of the psychological component is the teacher as solver and in the pedagogical component the teacher assumes the role of knowledgeable other with the interviewer seeking to understand the teacher moves that he or she takes to help students understand the mathematical nature of tasks involving RP processes. Participants were not presented with particular tasks, but in the course of the semi-structured interviews (described in more detail below) teachers either presented mathematical tasks as examples on their own or were pressed to provide examples. These tasks were then examined from a mathematical perspective to better understand the validity of the psychological component exhibited by the teachers and the nature of the teacher moves taken to make the mathematical perspective transparent to students (pedagogical component). If teachers did not provide examples and instead talked about RP processes in general, these descriptions were compared to their descriptions in Stylianides. This framework was chosen as the Project Maths syllabi contain these different RP processes (Davis 2014).

Post-primary teachers working with senior cycle mathematics students (ages 15–18) within a 50-mile radius of Limerick, Ireland were recruited for this study. The teaching experience and gender of these teachers appear in Table 14.1. teaching experience was broken down into three categories: low (0–5 years), medium (6–14 years), and high (15–30 years). Interview questions associated with each of the research questions appear in the Appendix. The semi-structured nature of the interviews enabled the author to follow-up on some teachers’ responses when they lacked sufficient details. Participants would occasionally provide examples from their classes where they engaged their students in RP processes. Twenty-two teachers were asked about pattern identification, 18 teachers were asked about conjecturing, and 21 teachers were asked about proof during semi-structured interviews lasting between 30 min and one hour during the 2012–2013 school year. The interview length varied as teachers were interviewed during the school day and had variable amounts of time for the interview. The variable interview lengths as well as the semi-structured nature of the interviews led to differing numbers of teachers answering the different questions associated with the interview questions. Each interview was audiotaped and transcribed and coded using HyperResearch (Researchware 2011) qualitative analysis software. Qualitative data analysis methods of analytic induction and constant comparison were used to identify and refute interpretations for themes and relationships appearing within the data (Miles et al. 2014).

Table 14.1 Participating teachers’ experience and gender
Full size table

Results

Pattern Identification

Seventeen out of twenty-two teachers most closely connected pattern to a specific mathematics unit, Sequences and Series, as seen in the following interview excerpt.

  • Interviewer: Is the identification of patterns connected to the construction of proofs at all?

  • Aidan: Um, I’m being brutally honest but, I haven’t taught the patterns, sequences, series [sic] section yet.

This excerpt also illustrates an important problem with connecting patterns with a specific unit, namely, students may experience a great deal of instruction before engaging in pattern identification. It also promotes in teachers a perspective that patterns are not a unifying mathematical activity that occurs across a variety of mathematics content areas. This stands in contrast to the Synthesis and Problem-Solving Skills section that appears in each content strand of the syllabus. The particular unit mentioned by the teacher in this excerpt provides students with opportunities to identify patterns in arithmetic and geometric sequences. Indeed, in the senior cycle ordinary level teacher handbook for Project Maths this is the only unit out of twelve that contains the word “patterns” in its title.

Additionally, sixteen of the teachers did not see pattern identification as a step leading towards proof. Indeed, for eight of these teachers the identification of plausible patterns was synonymous with proof, especially for students learning mathematics at the FL and OL.

  • Cassidy: Ah, another example that I can think of is okay when I’m doing the laws of indices. You know and you work away with them and then you come to this one and any number to the power of 0 is equal to 1. And, I kind of turn around to them and I say well, I mean do you not think that looks a bit crazy? Where are they getting that from you know? Anything to the power of 0 equals 1. So I go back and I’d say, “Well actually I’ll show you where it comes from. You know you don’t need to learn this or anything off by heart but just it’s interesting to look at.” And maybe I’ll [do] 2 cubed and 2 squared and 2 to the power of 1. And then I’ll get them to type into their calculators, uhm 2 to the power of minus 1, 2 to the power of minus 2, 2 to the power of minus 3 and we’ll take a look at the kind of pattern that emerges. And if you work it from either side, from let’s say the positive powers to the negative powers you can easily see by the pattern when you have 2 to the power of 0 what you should get is 1, uhm, as your answer.

  • Interviewer: So does that prove that any number to the 0 power is 1?

  • Cassidy: Well, you can try other numbers. And you keeping getting the same answers so we have done it, we’ll do 2 and I’ll say, “Okay we’ll check out to see if this works for three and then it does prove that any number to the power of 0 equals 1.” I think anyway. I think it proves it enough to them that they can accept it then.

  • Interviewer: Okay, proves that it is always true.

  • Cassidy: Yes.

  • Interviewer: You use the words “enough for them” would it be different for you?

  • Cassidy: No. Personally, I would accept that.

Indeed, the excerpt above suggests that Cassidy was not likely to see pattern identification as a necessary step in moving towards a proof, as pattern identification appeared to be sufficient for her in showing that a mathematical idea always held true. According to the teachers, HL students, on the other hand, were more likely to spend less time with pattern identification and focus more on the construction of proofs. In the excerpt below, Ashling confirms the different types of RP activities in her classroom for students of different perceived abilities. In this excerpt, “activity” refers to an opportunity for students to identify a mathematical pattern.

  • Interviewer: So with the ordinary level classroom you’d focus more on the activity?

  • Ashling: Yes.

  • Interviewer: So, given a finite amount of time in the classroom, you focus more on the activity and then less time on the formal proof?

  • Ashling: Yes.

  • Interviewer: Okay.

  • Ashling: But in the ordinary group [sic].

  • Interviewer: Okay, with the ordinary level. And maybe with the higher level it’s less time on the activity and more time on the proof?

  • Ashling: Yes.

Conjecturing

Out of 18 teachers asked about conjecturing, nine teachers were not able to define it at all. Four teachers provided incorrect definitions such as checking the reasonableness of an answer, assumptions when beginning a proof (2 teachers), and corollary. Two teachers were able to provide correct definitions of conjecture. Three teachers’ responses were coded as unknown as it was not possible to categorize their definitions. Due to time constraints during the interview I only provided five of the nine teachers with the definition of a conjecture as an educated guess. Even when provided with the definition these teachers did not connect conjecturing with the object of proof development. Consider the excerpt below.

  • Interviewer: Some people define a conjecture as a reasonable guess, or a reasonable hypothesis of what might happen.

  • Seamus: An educated guess.

  • Interviewer: Yeah, more or less. So does that play a role in the construction of a proof?

  • Seamus: It does, yeah.

  • Interviewer: Can you give an example of where students have done that in your classroom?

  • Seamus: Well they can rule something out. I know we were talking about the different methods of approaching a question. Well you could use conjecture quickly to rule something out whether it will work or not to solve the proof.

In this excerpt, the teacher considers conjecturing as a way to rule out a method to construct a proof. One of the four teachers who incorrectly defined conjecturing also connected this act to problem-solving. When cast in this light conjecturing was seen as a check on the reasonableness of the answer or how to approach the solving of a problem. The other three teachers connected conjecturing to proof, but in nonstandard ways like the following: valid assumptions that can be made at the beginning of a proof; confusing conjecture with corollary; and confusing conjecture with axiom. None of the 18 teachers asked about conjecturing saw a connection to proof in terms of the object of a proof. The excerpt below is an example of this phenomenon.

  • Interviewer: So I hear you talking about conjectures in terms of making sure that the answer that you get from the calculator is reasonable, so going back to the example from geometry where the sum of the two interior angles equals the exterior angle, you show them a lot of examples in an ordinary level class. Do you then ask them to make a guess about whether they think it’s always true or do you just go right to the proof then?

  • Simon: Personally I would say that I ordinarily go right to the proof.

Proof Development

Eleven out of 21 teachers defined proof as a logical derivation similar to what was found by Knuth (2002b). This is seen in the following excerpts from Ashling and Murtagh.

  • Interviewer: Our study is really focusing on reasoning-and-proving so something we have been asking teachers is your definition of what a mathematical proof is. So how would you define that?

  • Ashling: A set of logical steps and come out with an answer that’s true.

  • Interviewer: So the focus of our study is really on reasoning-and-proving . And so, what we’ve been asking the teachers for is their definition of a mathematical proof.

  • Murtagh: I suppose a proof involves a number of logical steps that you follow to reach a conclusion. There might be some prerequisite knowledge in those steps or there might be some previous theorems or proofs that you already understand, or there might be an axiom that doesn’t need to be proved, but you take those pieces of information and you piece them together until you can reach a logical conclusion about what you set out to prove to begin with.

Five teachers were not able to define a proof, but were only able to describe proof techniques such as proof by contradiction or provided theorems as definitions of proofs such as the irrationality of two. An example of the latter is seen below.

  • Interviewer: …How would you define what a mathematical proof is?

  • Shauna: Mathematical proof?

  • Interviewer: Ah huh.

  • Shauna: Well, something that has been well, discovered, years ago that um, say for example like um, like there’s, the angles of a triangle add up to 180. That can be proven pretty easily and it doesn’t necessarily have to be just taken as a given. You know you can take up all the triangle [sic] into the three angles and see that yourself or measure them with a protractor. You know in junior ones they’d cut off all the angles at the three corners and then actually put them together, make them 180. Things like that, but also then there’s lots of ones then that are taken, that’s given really without proving it like say the area of a triangle is half b times c. It would be a lot more complicated to prove that, but it can be done.

Shauna’s response also implies that a proof can be constructed through a series of examples such as cutting the corners off a set of triangles and showing that they form 180°. Four additional teachers considered a set of examples to denote a proof and one teacher’s definition was connected to a pattern and especially how that pattern could be converted into a proof. If teachers did not provide specific examples of proof within a content area, they were asked which content areas proof appears in. These teachers were then asked a follow-up question about other content areas where proof appears. If teachers embedded their proof examples in a specific content area then teachers were asked about other content areas where proof can occur in school mathematics . The most popular content area mentioned by 20 out of 22 teachers in which proof occurred was geometry.

  • Kaitlin: Well, it’s again I think proof, I think Geometry, very much Geometry, I think theorems I mean that’s what I think when I think proof. Do you know? But other than that I don’t really.

The next most frequent category was number (6 out of 22 teachers), followed by trigonometry (4 out of 22 teachers), and algebra (2 out of 22 teachers). A total of 18 teachers were asked a follow-up question about proof in other areas. Of these teachers only four mentioned algebra or provided valid examples of proof in algebra; four teachers mentioned calculus such as the use of first principles to prove differentiation formulas. In order to further probe teachers’ understanding of proof in other content areas a total of ten teachers were asked specifically about proof in the statistics and probability content strand. One teacher replied that she did not know if proof appeared in this content strand. Two teachers provided invalid examples of proof in statistics and probability, three teachers did not answer the question, and three teachers stated that proof did not appear in this content strand. This suggests that teachers either do not construct proofs for probability ideas such as the addition rule or, if they do justify these ideas, they do not consider them to be proofs. That is, their definitions for proof while devoid explicitly of a content area as in the logical derivation definition above may indeed be context dependent.

A total of 15 teachers were either asked about proof for students with different perceived ability levels or described proof experiences for students of different perceived ability levels. Fourteen teachers stated that HL students had very different proof experiences than OL and FL students. For instance, Catherine noted that she would use the word “proof” among HL students and not with FL students because the use of this terminology would inspire anxiety in FL students. Hugh stated that HL students worked on more difficult proofs and four teachers noted that these proofs would be more abstract than those worked on by OL or FL students. Kerry not only noted that HL students would be asked to create proofs, but that they also would be expected to create diagrams to assist in developing proofs. Additionally, Kian noted, that HL students would be assessed on their ability to prove on the high stakes exams given at the end of the senior cycle. However, due to the presence of proof on these exams for HL students Fiona admitted that she would delay the instruction of proof until right before the exams. Brian and Iona admitted that because HL students would be asked to reproduce proofs that they had already seen the students would resort to memorizing these proofs with less of an emphasis on understanding. Aidan noted that neither FL nor OL students were asked to construct proofs in his classroom. As four teachers stated, OL students would most likely encounter proof through teacher led presentations. Three teachers stated that FL students’ experiences with proof centered around applying the results of a theorem to find an answer such as a missing angle.

Connection Between Proof and Understanding

In order to ascertain teachers’ conceptions about proof a total of twelve teachers were asked if proof promotes understanding. Two teachers felt that proof did not promote students’ understanding of mathematical ideas. Hugh’s definition of understanding focused on applying mathematical ideas. He elaborated that as the development of a proof did not involve its application, proof was disconnected from understanding. Four teachers felt that proof was tied to understanding, but that understanding was compartmentalized to developing a proof. That is, a proof required understanding on the part of students, but that understanding did not necessarily apply to other areas of mathematics . Two other teachers stated that proof was connected to understanding the origin of mathematical objects. Two other teachers noted that the results of proof were used in solving problems oftentimes set within real-world contexts and therefore promoted understanding. One teacher stated that proof involved verification of mathematical ideas (e.g., knowing that), but not necessarily knowing why mathematical ideas were true. This delineation is similar to Skemp’s (1976) descriptions of instrumental and relational thinking. The last teacher believed that proof promoted understanding due to the fact that constructing a proof required making connections. This work enabled students to make connections across different mathematical ideas, which for this teacher was emblematic of understanding.

Connection to Syllabus Vis-à-Vis Synthesis and Problem-Solving

Recall that the Synthesis and Problem-Solving section of the syllabus contained a number of reasoning-and-proving components. A total of 22 teachers were asked what the section of the syllabus titled Synthesis and Problem-Solving meant to them in order to understand teachers’ perceptions of this section of the syllabus. Twenty of the teachers did not connect this section to RP. Nearly all of the teachers did not recognize this section as connected to the syllabus. Instead they parsed this title into its constituents: problem-solving and synthesis. They described problem-solving as best they could, but when it came to synthesis eight teachers did not know how to define this terminology. Two teachers did connect problem-solving and synthesis to a component of RP, proof. These connections are seen in the following two excerpts.

  • Nora: Synthesis, I’m not sure about that word, but um, problem-solving I suppose, trying to work through some logical steps to get from start to the end of the problem, I suppose.

  • Kerry: Ah, I suppose kind of understanding the question and reading the words and, um, creating if you like, like I said, an equation or a table and making sense of or, the synthesis part is kind of the creating the table or drawing the graph, and then they’re analyzing, and they’re arriving at their answer, or they’re justifying their answer saying why it’s true or not true. So that would be my understanding of the synthesis and the problem-solving.

Discussion

Teachers’ Perceptions of RP and Students’ Abilities

The Project Maths leaving certificate syllabus distinguishes different content goals for students at the FL, OL, and HL levels. However, the syllabus makes no distinctions when it comes to students’ experiences with three key RP processes: pattern identification, conjecture development, and the development of arguments. It is expected that all of these students be given opportunities to engage in all three of these processes. Yet, the interviews suggested that there is a bifurcation in classroom experiences for FL/OL and HL students, neither of which supports the goals of the syllabus nor promotes the interconnected nature of RP processes. FL and OL students were less likely to engage in the construction of arguments and HL students were less likely to identify patterns due to the influence of high stakes exams. FL/OL students’ experiences in RP typically involved pattern identification. A sizeable minority of teachers felt that this pattern identification was sufficient for these students to show that mathematical ideas always held true and that pattern identification promoted student understanding. Yet the examples given of patterns suggested that they showed that something was true but not necessarily why it was true. The presence of pattern identification as a form of proof is similar to an empirical proof scheme as noted in previous research (Knuth 2002b; Martin and Harel 1989). While HL students were more likely to engage in the construction of proofs, these arguments were likely to be memorized by students and taught in a way to promote their quick recall due to high stakes assessments. This memorization is akin to the instrumental understanding (Skemp 1976) displayed by sixth grade students in Askevold and Lekaus (this volume). These results are similar to the beliefs held by a group of grade 10 geometry students in the United States with respect to proof (Schoenfeld 1989). The influence of these high stakes examinations could be harnessed by Project Math personnel to more closely promote the goals of the leaving certificate syllabus by including questions where FL, OL, and HL engage in pattern identification, conjecturing, and proof development across of range of content areas.

Teachers’ Perceptions of RP as an Interconnected Set of Processes

The results of this study suggest that teachers do not view RP as a set of interconnected actions. Pattern identification was not connected to conjecturing or proof and for some teachers, pattern was synonymous with proof suggesting that for these teachers empirical arguments appeared to constitute valid proofs as researchers have found at the high school level in the USA (Knuth 2002b). Conjecturing was not connected to pattern identification or to proof. Indeed, teachers struggled to define conjecture and when provided with a definition they were more likely to connect it to problem-solving than proof or pattern identification. Teachers’ disconnections are further supported by their responses that pattern occurred primarily in one mathematical unit and proof appeared predominantly in geometry. The latter finding is similar to what has been reported in the body of research around proof (e.g., Herbst 2002). This fixation on proof in geometry also appears in curriculum from other places around the world such as Hong Kong (Wong and Sutherland, this volume). These findings as well as teachers’ struggles to describe the synthesis and problem-solving section appearing within each content strand of the syllabus suggest that teachers are not attending to this section of the leaving certificate syllabus. While Stylianides (2008) saw RP processes as interconnected and part and parcel to the work of mathematicians, the teachers in this study did not. This may reflect how these teachers themselves experienced instruction as students in secondary mathematics classrooms in Ireland or in the university where instruction may focus more on finished proofs and not how those proofs were developed (Stylianou et al. 2015). Consequently, professional development for Irish post-primary teachers could be fashioned around these processes to assist these individuals in understanding the synthesis and problem-solving skills that appear in each content strand, point out the ubiquitous of these processes, and provide examples to teachers for how they can implement these pattern identification, conjecturing, and developing arguments in the secondary mathematics classroom across a variety of different content strands.

Teachers’ Perceptions of Proof

The teachers interviewed for this study held a number of perceptions about proof. The majority of teachers defined proof as a logical derivation similar to teachers from Knuth’s (2002b) study had found. This study provides more evidence of teachers’ struggle with proof. That is, teachers struggled in defining a proof, considered proof techniques such as proof by contradiction to be a definition of proof, or confused a proof with the products of a proof (e.g., theorems). Five teachers saw examples as valid proof, which resonates with previous research studies (e.g., Knuth 2002b). Additionally, the teachers in this study tended to connect proof with geometry similar to previous research (Furinghetti and Morselli 2011). Taken as a group these findings suggest that teachers may be fixated on the instructional aspects of proof. That is, they may see proof primarily through their work with students and not as learners of mathematics or as individuals who engage in mathematical work and make use of proof in that work. This is seen in their definitions of proof as methods to complete a proof (e.g., proof by contradiction) or the use of examples to illustrate the result of a proof that they use in their daily work with students.

This work builds on a previous study completed by Knuth (2002a) and Dickerson and Doerr (2014) as it seeks to describe teachers’ perceptions with regard to the connections between proof development and understanding and it also seeks to further explicate teachers’ conceptions with regard to a lack of connection between proof and understanding. Knuth found that a group of sixteen teachers did not view understanding as a role that proof can take in mathematics . However, the vast majority (16/17) of teachers interviewed by Dickerson and Doerr saw proof as promoting understanding in a number of different ways. This study found the number of teachers making connections between proof and understanding to lie between these two studies. This study found that five teachers did not connect proof construction to understanding. Four of these teachers saw understanding as connected to the use of mathematics to solve problems set within real-world contexts, so called applications of mathematics. Recall that this was one of the goals of the Project Maths reform .

Seven teachers saw proof as connected to understanding. That understanding was constrained to proof construction for several teachers, but three teachers saw proof as promoting understanding in a number of interesting ways such as the origin of mathematical ideas and connections across mathematical ideas. In addition, teachers also saw proof as promoting students problem-solving capabilities. These findings suggest other ways that teachers perceive the connections between proof and understanding besides those described by Dickerson and Doerr (2014) such as proofs developing transferrable thinking skills or metacognitive thinking skills. Additionally, these findings suggest that while teachers may harbor unproductive conceptions around proof such as seeing it as limited to geometry, they can also possess progressive conceptions such as linking proof with understanding. Such connections to understanding can be leveraged by those wishing to engineer professional development to help teachers see the value of engaging all students in the development of support for mathematical claims.

Conclusion

This study examined the mathematical, psychological, and pedagogical components of RP processes as seen through the eyes of a group of Irish post-primary teachers. Although mathematicians invoke these processes as they develop mathematical ideas, teachers themselves did not see these processes as connected at all. This study serves as another testament to the disjuncture between school mathematics and mathematics as practiced by mathematicians (Schoenfeld 1989). While this study adds to our understanding of teachers’ perceptions about RP processes and their interconnectedness, it also speaks more broadly to curriculum reform and teachers’ perceptions . Although RP processes appear in the leaving certificate syllabus, teachers were not cognizant of this component of the syllabus as it did not contain specific mathematics content. This finding serves as a strong argument in favor of interweaving valued mathematical processes with content standards in the design of national curriculum documents.