Updatable Tokenization: Formal Definitions and Provably Secure Constructions

Abstract

Tokenization is the process of consistently replacing sensitive elements, such as credit cards numbers, with non-sensitive surrogate values. As tokenization is mandated for any organization storing credit card data, many practical solutions have been introduced and are in commercial operation today. However, all existing solutions are static yet, i.e., they do not allow for efficient updates of the cryptographic keys while maintaining the consistency of the tokens. This lack of updatability is a burden for most practical deployments, as cryptographic keys must also be re-keyed periodically for ensuring continued security. This paper introduces a model for updatable tokenization with key evolution, in which a key exposure does not disclose relations among tokenized data in the past, and where the updates to the tokenized data set can be made by an untrusted entity and preserve the consistency of the data. We formally define the desired security properties guaranteeing unlinkability of tokens among different time epochs and one-wayness of the tokenization process. Moreover, we construct two highly efficient updatable tokenization schemes and prove them to achieve our security notions.

This work has been supported in part by the European Commission through the Horizon 2020 Framework Programme (H2020-ICT-2014-1) under grant agreement number 644371 WITDOM and through the Seventh Framework Programme under grant agreement number 321310 PERCY, and in part by the Swiss State Secretariat for Education, Research and Innovation (SERI) under contract number 15.0098.

1 Introduction

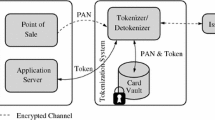
Increasingly, organizations outsource copies of their databases to third parties, such as cloud providers. Legal constraints or security concerns thereby often dictate the de-sensitization or anonymization of the data before moving it across borders or into untrusted environments. The most common approach is so-called tokenization which replaces any identifying, sensitive element, such as a social security or credit card number, by a surrogate random value.

Government bodies and advisory groups in Europe [6] and in the United States [9] have explicitly recommended such methods. Many domain-specific industry regulations require this as well, e.g., HIPAA [13] for protecting patient information or the Payment Card Industry Data Security Standard (PCI DSS) [10] for credit card data. PCI DSS is an industry-wide set of guidelines that must be met by any organization that handles credit card data and mandates that instead of the real credit card numbers only the non-sensitive tokens are stored.

For security, the tokenization process should be one-way in the sense that the token does not reveal information about the original data, even when the secret keys used for tokenization are disclosed. On the other hand, usability requires that a tokenized data set preserves referential integrity. That is, when the same value occurs multiple times in the input, it should be mapped consistently to the same token.

Many industrial white papers discuss solutions for tokenization [11, 12, 14], which rely on (keyed) hash functions, encryption schemes, and often also non-cryptographic methods such as random substitution tables. However, none of these methods guarantee the above requirements in a provably secure way, backed by a precise security model. Only recently an initial step towards formal security notions for tokenization has been made [5].

However, all tokenization schemes and models have been static so far, in the sense that the relation between a value and its tokenized form never changes and that the keys used for tokenization cannot be changed. Thus, key updates are a critical issue that has not yet been handled. In most practical deployments, all cryptographic keys must be re-keyed periodically for ensuring continued security. In fact, the aforementioned PCI DSS standard even mandates that keys (used for encryption) must be rotated at least annually. Similar to proactively secure cryptosystems [8], periodic updates reduce the risk of exposure when data leaks gradually over time. For tokenization, these key updates must be done in a consistent way so that already tokenized data maintains its referential integrity with fresh tokens that are generated under the updated key. None of the existing solutions allows for efficient key updates yet, as they would require to start from scratch and tokenize the complete data set with a fresh key. Given that the tokenized data sets are usually large, this is clearly not desirable for real-world applications. Instead the untrusted entity holding the tokenized data should be able to re-key an already tokenized representation of the data.

Our Contributions. As a solution for these problems, this paper introduces a model for updatable tokenization (UTO) with key evolution, distinguishes multiple security properties, and provides efficient cryptographic implementations. An updatable tokenization scheme considers a data owner producing data and tokenizing it, and an untrusted host storing tokenized data only. The scheme operates in epochs, where the owner generates a fresh tokenization key for every epoch and uses it to tokenize new values added to the data set. The owner also sends an update tweak to the host, which allows to “roll forward” the values tokenized for the previous epoch to the current epoch.

We present several formal security notions that refine the above security goals, by modeling the evolution of keys and taking into consideration adaptive corruptions of the owner, the host, or both, at different times. Due to the temporal dimension of UTO and the adaptive corruptions, the precise formal notions require careful modeling. We define the desired security properties in the form of indistinguishability games which require that the tokenized representations of two data values are indistinguishable to the adversary unless it trivially obtained them. An important property for achieving the desired strong indistinguishability notions is unlinkability and we clearly specify when (and when not) an untrusted entity may link two values tokenized in different epochs. A further notion, orthogonal to the indistinguishability-based ones, formalizes the desired one-wayness property in the case where the owner discloses its current key material. Here the adversary may guess an input by trying all possible values; the one-wayness notion ensures that this is also its best strategy to reverse the tokenization.

Finally, we present two efficient UTO constructions: the first solution ($\mathsf {UTO}_\mathsf {SE}$) is based on symmetric encryption and achieves one-wayness, and indistinguishability in the presence of a corrupt owner or a corrupt host. The second construction ($\mathsf {UTO}_\mathsf {DL}$) relies on a discrete-log assumption, and additionally satisfies our strongest indistinguishability notion that allows the adversary to (transiently) corrupt the owner and the host. Both constructions share the same core idea: First, the input value is hashed, and then the hash is encrypted under a key that changes every epoch.

We do not claim the cryptographic constructions are particularly novel. The focus of our work is to provide formal foundations for key-evolving and updatable tokenization, which is an important problem in real-world applications. Providing clear and sound security models for practitioners is imperative for the relevance of our field. Given the public demands for data privacy and the corresponding interest in tokenization methods by the industry, especially in regulated and sensitive environments such as the financial industry, this work helps to understand the guarantees and limitations of efficient tokenization.

Related Work. A number of cryptographic schemes are related to our notion of updatable tokenization: key-homomorphic pseudorandom functions (PRF), oblivious PRFs, updatable encryption, and proxy re-encryption, for which we give a detailed comparison below.

A key-homomorphic PRF [3] enjoys the property that given $\mathsf {PRF}_a(m)$ and $\mathsf {PRF}_b(m)$ one can compute $\mathsf {PRF}_{a+b}(m)$. This homomorphism does not immediately allow convenient data updates though: the data host would store values $\mathsf {PRF}_a(m)$, and when the data owner wants to update his key from a to b, he must compute $\varDelta _m = \mathsf {PRF}_{b-a}(m)$ for each previously tokenized value m. Further, to allow the host to compute $\mathsf {PRF}_{b}(m) = \mathsf {PRF}_a(m) + \varDelta _m$, the owner must provide some reference to which $\mathsf {PRF}_a(m)$ each $\varDelta _m$ belongs. This approach has several drawbacks: (1) the owner must store all previously outsourced values m and (2) computing the update tweak(s) and its length would depend on the amount of tokenized data. Our solution aims to overcome exactly these limitations. In fact, tolerating (1) + (2), the owner could simply use any standard PRF, re-compute all tokens and let the data host replace all data. This is clearly not efficient and undesirable in practice.

Boneh et al. [3] also briefly discuss how to use such a key-homomorphic PRF for updatable encryption or proxy re-encryption. Updatable encryption can be seen as an application of symmetric-key proxy re-encryption, where the proxy re-encrypts ciphertexts from the previous into the current key epoch. Roughly, a ciphertext in [3] is computed as $C = m + \mathsf {PRF}_a(N)$ for a nonce N, which is stored along with the ciphertext C. To rotate the key from a to b, the data owner pushes $\varDelta = b-a$ to the data host which can use $\varDelta$ to update all ciphertexts. For each ciphertext, the host then uses the stored nonce N to compute $\mathsf {PRF}_{\varDelta }(N)$ and updates the ciphertext to $C' = C + \mathsf {PRF}_{\varDelta }(N) = m + \mathsf {PRF}_b(N)$. However, the presence of the static nonce prevents the solution to be secure in our tokenization context. The tokenized data should be unlinkable across epochs for any adversary not knowing the update tweaks, and we even guarantee unlinkability in a forward-secure manner, i.e., a security breach at epoch e does not affect any data exposed before that time.

In the full version of their paper [4], Boneh et al. present a different solution for updatable encryption that achieves such unlinkability, but which suffers from similar efficiency issues as mentioned above: the data owner must retrieve and partially decrypt all of his ciphertexts, and then produce a dedicated update tweak for each ciphertext, which renders the solution unpractical for our purpose. Further, no formal security definition that models adaptive key corruptions for such updatable encryption is given in the paper.

The Pythia service proposed by Everspaugh et al. [7] mentions PRFs with key rotation which is closer to our goal, as it allows efficient updates of the outsourced PRF values whenever the key gets refreshed. The core idea of the Pythia scheme is very similar to our second, discrete-logarithm based construction. Unfortunately, the paper does not give any formal security definition that covers the possibility to update PRF values nor describes the exact properties of such a key-rotating PRF. As the main goal of Pythia is an oblivious and verifiable PRF service for password hashing, the overall construction is also more complex and aims at properties that are not needed here, and vice-versa, our unlinkability property does not seem necessary for the goal of Pythia.

While the aforementioned works share some relation with updatable tokenization, they have conceptually quite different security requirements. Starting with such an existing concept and extending its security notions and constructions to additionally satisfy the requirements of updatable tokenization, would reduce efficiency and practicality, for no clear advantage. Thus, we consider the approach of directly targeting the concrete real-world problem more suitable.

An initial study of security notions for tokenization was recently presented by Diaz-Santiago et al. [5]; they formally define tokenization systems and give several security notions and provably secure constructions. In a nutshell, their definitions closely resemble the conventional definitions for deterministic encryption and one-way functions adopted to the tokenization notation. However, they do not consider adaptive corruptions and neither address updatable tokens, which are the crucial aspects of this work.

2 Preliminaries

In this section, we recall the definitions of the building blocks and security notions needed in our constructions.

Deterministic Symmetric Encryption. A deterministic symmetric encryption scheme $\mathsf {SE}$ consists of a key space $\mathcal {K}$ and three polynomial-time algorithms $\mathsf {SE{.}KeyGen}, \mathsf {SE{.}Enc},\mathsf {SE{.}Dec}$ satisfying the following conditions:  

$\mathsf {SE{.}KeyGen}$::

The probabilistic key generation algorithm $\mathsf {SE{.}KeyGen}$ takes as input a security parameter $\lambda$ and produces an encryption key $s{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE{.}KeyGen}(\lambda )$.

$\mathsf {SE{.}Enc}$::

The deterministic encryption algorithm takes a key $s\in \mathcal {K}$ and a message $m\in \mathcal {M}$ and returns a ciphertext $C\leftarrow \mathsf {SE{.}Enc}({s},{m})$.

$\mathsf {SE{.}Dec}$::

The deterministic decryption algorithm $\mathsf {SE{.}Dec}$ takes a key $s\in \mathcal {K}$ and a ciphertext C to return a message $m\leftarrow \mathsf {SE{.}Dec}({s},{C})$.

 

For correctness we require that for any key $s\in \mathcal {K}$, any message $m\in \mathcal {M}$ and any ciphertext $C\leftarrow \mathsf {SE{.}Enc}({s},{m})$, we have $m\leftarrow \mathsf {SE{.}Dec}({s},{C})$.

We now define a security notion of deterministic symmetric encryption schemes in the sense of indistinguishability against chosen-plaintext attacks, or IND-CPA security. This notion was informally presented by Bellare et al. in [1], and captures the scenario where an adversary that is given access to a left-or-right (LoR) encryption oracle is not able to distinguish between the encryption of two distinct messages of its choice with probability non-negligibly better than one half. Since the encryption scheme in question is deterministic, the adversary can only query the LoR oracle with distinct messages on the same side (left or right) to avoid trivial wins. That is, queries of the type $(m^i_0, m^i_1), (m^j_0, m^j_1)$ where $m^i_0 = m^j_0$ or $m^i_1 = m^j_1$ are forbidden. We do not grant the adversary an explicit encryption oracle, as it can obtain encryptions of messages of its choice by querying the oracle with a pair of identical messages.

Definition 1

A deterministic symmetric encryption scheme $\mathsf {SE}= (\mathsf {SE{.}KeyGen},\mathsf {SE{.}Enc},\mathsf {SE{.}Dec})$ is called IND-CPA secure if for all polynomial-time adversaries $\mathcal {A}$, it holds that for some negligible function $\epsilon$.

Hash Functions. A hash function $\mathsf {H}:\mathcal {D}\rightarrow \mathcal {R}$ is a deterministic function that maps inputs from domain $\mathcal {D}$ to values in range $\mathcal {R}$. For our second and stronger construction we assume the hash function to behave like a random oracle.

In our first construction we use a keyed hash function, i.e., $\mathsf {H}$ gets a key $hk {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {H}{.}\mathsf {KeyGen}(\lambda )$ as additional input. We require the keyed hash function to be pseudorandom and weakly collision-resistant for any adversary not knowing the key hk. We also need $\mathsf {H}$ to be one-way when the adversary is privy of the key, i.e., $\mathsf {H}$ should remain hard to invert on random inputs.

 

Pseudorandomness::

A hash function is called pseudorandom if no efficient adversary $\mathcal {A}$ can distinguish $\mathsf {H}$ from a uniformly random function $f: \mathcal {D}\rightarrow \mathcal {R}$ with non-negligible advantage. That is, $\left| \Pr [\mathcal {A}^{\mathsf {H}(hk,\cdot )}(\lambda )]-\Pr [\mathcal {A}^{f(\cdot )}(\lambda )]\right|$ is negligible in $\lambda$, where the probability in the first case is over $\mathcal {A}$’s coin tosses and the choice of $hk {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {H}{.}\mathsf {KeyGen}(\lambda )$, and in the second case over $\mathcal {A}$’s coin tosses and the choice of the random function f.

Weak collision resistance::

A hash function $\mathsf {H}$ is called weakly collision-resistant if for any efficient algorithm $\mathcal {A}$ the probability that for $hk {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {H}{.}\mathsf {KeyGen}(\lambda )$ and $(m,m') {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathcal {A}^{\mathsf {H}(hk,\cdot )}(\lambda )$ the adversary returns $m \ne m'$, where $\mathsf {H}(hk,m) = \mathsf {H}(hk,m')$, is negligible (as a function of $\lambda$).

One-wayness::

A hash function $\mathsf {H}$ is one-way if for any efficient algorithm $\mathcal {A}$ the probability that for $hk {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {H}{.}\mathsf {KeyGen}(\lambda )$, $m {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathcal {D}$ and $m'{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathcal {A}(hk, \mathsf {H}(hk,m))$ returns $m'$, where $\mathsf {H}(hk,m) = \mathsf {H}(hk,m')$, is negligible (as a function of $\lambda$).

 

Decisional Diffie-Hellman Assumption. Our second construction requires a group $(\mathbb {G},g,p)$ as input where $\mathbb {G}$ denotes a cyclic group $\mathbb {G}= \langle g \rangle$ of order p in which the Decisional Diffie-Hellman (DDH) problem is hard w.r.t. $\lambda$, i.e., p is a $\lambda$-bit prime. More precisely, a group ($\mathbb {G},g,p)$ satisfies the DDH assumption if for any efficient adversary $\mathcal {A}$ the probability $| \Pr [\mathcal {A}(\mathbb {G},p,g,g^a, g^b,g^{ab})]-$ $\Pr [\mathcal {A}(\mathbb {G},p,g,g^a, g^b,g^c)]|$ is negligible in $\lambda$, where the probability is over the random choice of p, g, the random choices of $a,b,c \in \mathbb {Z}_p$, and $\mathcal {A}$’s coin tosses.

3 Formalizing Updatable Tokenization

An updatable tokenization scheme contains algorithms for a data owner and a host. The owner de-sensitizes data through tokenization operations and dynamically outsources the tokenized data to the host. For this purpose, the data owner first runs an algorithm $\mathsf {setup}$  to create a tokenization key. The tokenization key evolves with epochs, and the data is tokenized with respect to a specific epoch e, starting with $e=0$. For a given epoch, algorithm $\mathsf {token}$ takes a data value and tokenizes it with the current key ${k}_{e}$. When moving from epoch e to epoch $e+1$, the owner invokes an algorithm $\mathsf {next}$ to generate the key material ${k}_{e+1}$ for the new epoch and an update tweak ${\varDelta }_{e+1}$. The owner then sends ${\varDelta }_{e+1}$ to the host, deletes ${k}_{e}$ and ${\varDelta }_{e+1}$ immediately, and uses ${k}_{e+1}$ for tokenization from now on. After receiving ${\varDelta }_{e+1}$, the host first deletes ${\varDelta }_{e}$ and then uses an algorithm $\mathsf {upd}$ to update all previously received tokenized values from epoch e to $e+1$, using ${\varDelta }_{e+1}$. Hence, during some epoch e the update tweak from $e-1$ to e is available at the host, but update tweaks from earlier epochs have been deleted.

Definition 2

An updatable tokenization scheme $\mathsf {UTO}$ consists of a data space $\mathcal {X}$, a token space $\mathcal {Y}$, and a set of polynomial-time algorithms $\mathsf {UTO{.}setup}$, $\mathsf {UTO{.}next}$, $\mathsf {UTO{.}token}$, and $\mathsf {UTO{.}upd}$ satisfying the following conditions:

 

$\mathsf {UTO{.}setup}$::

The algorithm $\mathsf {UTO{.}setup}$ is a probabilistic algorithm run by the owner. On input a security parameter $\lambda$, this algorithm returns the tokenization key for the first epoch ${k}_{0}{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {UTO{.}setup}(\lambda )$.

$\mathsf {UTO{.}next}$::

This probabilistic algorithm is also run by the owner. On input a tokenization key ${k}_{e}$ for some epoch e, it outputs a tokenization key ${k}_{e+1}$ and an update tweak ${\varDelta }_{e+1}$ for epoch $e+1$. That is, $({k}_{e+1}, {\varDelta }_{e+1}) {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {UTO{.}next}({k}_{e})$.

$\mathsf {UTO{.}token}$::

This is a deterministic injective algorithm run by the owner. Given the secret key ${k}_{e}$ and some input data $x \in \mathcal {X}$, the algorithm outputs a tokenized value ${y}_{e}\in \mathcal {Y}$. That is, ${y}_{e} \leftarrow \mathsf {UTO{.}token}({k}_{e}, x)$.

$\mathsf {UTO{.}upd}$::

This deterministic algorithm is run by the host and uses the update tweak. On input the update tweak ${\varDelta }_{e+1}$ and some tokenized value ${y}_{e}$, $\mathsf {UTO{.}upd}$ updates ${y}_{e}$ to ${y}_{e+1}$, that is, ${y}_{e+1} \leftarrow \mathsf {UTO{.}upd}( {\varDelta }_{e+1}, {y}_{e})$.

 

The correctness condition of a UTO scheme ensures referential integrity inside the tokenized data set. A newly tokenized value from the owner in a particular epoch must be the same as the tokenized value produced by the host using update operations. More precisely, we require that for any $x\in \mathcal {X}$, for any ${k}_{0}{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {UTO{.}setup}(\lambda )$, for any sequence of tokenization key/update tweak pairs $({k}_{1},{\varDelta }_{1}), \dots , ({k}_{e},{\varDelta }_{e})$ generated as $({k}_{j+1},{\varDelta }_{j+1}){\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {UTO{.}next}({k}_{j})$ for $j=0,\dots ,e-1$ through repeated applications of the key-evolution algorithm, and for any ${y}_{e}\leftarrow \mathsf {UTO{.}token}({k}_{e},x)$, it holds that

$$\begin{aligned} \mathsf {UTO{.}token}({k}_{e+1},x) = \mathsf {UTO{.}upd}({\varDelta }_{e+1},{y}_{e}). \end{aligned}$$

3.1 Privacy of Updatable Tokenization Schemes

The main goal of UTO is to achieve privacy for data values, ensuring that an adversary cannot gain information about the tokenized values and cannot link them to input data tokenized in past epochs. We introduce three indistinguishability-based notions for the privacy of tokenized values, and one notion ruling out that an adversary may reverse the tokenization and recover the input value from a tokenized one. All security notions are defined through an experiment run between a challenger and an adversary $\mathcal {A}$. Depending on the notion, the adversary may issue queries to different oracles, defined in the next section.

At a high level, the four security notions for UTO are distinguished by the corruption capabilities of $\mathcal {A}$.  

IND-HOCH::

Indistinguishability with Honest Owner and Corrupted Host: This is the most basic security criterion, focusing on the updatable dynamic aspect of UTO. It considers the owner to be honest and permits corruption of the host during the interaction. The adversary gains access to the update tweaks for all epochs following the compromise and yet, it should (roughly speaking) not be able to distinguish values tokenized before the corruption.

IND-COHH::

Indistinguishability with Corrupted Owner and Honest Host: Modeling a corruption of the owner at some point in time, the adversary learns the tokenization key of the compromised epoch and all secrets of the owner. Subsequently $\mathcal {A}$ may take control of the owner, but should not learn the correspondence between values tokenized before the corruption. The host is assumed to remain (mostly) honest.

IND-COTH::

Indistinguishability with Corrupted Owner and Transiently Corrupte Host: As a refinement of the first two notions, $\mathcal {A}$ can transiently corrupt the host during multiple epochs according to its choice, and it may also permanently corrupt the owner. The adversary learns the update tweaks of the specific epochs where it corrupts the host, and learns the tokenization key of the epoch where it corrupts the owner. Data values tokenized prior to exposing the owner’s secrets should remain unlinkable.

One-Wayness::

This notion models the scenario where the owner is corrupted right at the first epoch and the adversary therefore learns all secrets. Yet, the tokenization operation should be one-way in the sense that observing a tokenized value does not give the adversary an advantage for guessing the corresponding input from $\mathcal {X}$.

 

3.2 Definition of Oracles

During the interaction with the challenger in the security definitions, the adversary may access oracles for data tokenization, for moving to the next epoch, for corrupting the host, and for corrupting the owner. In the following description, the oracles may access the state of the challenger during the experiment. The challenger initializes a UTO scheme with global state $({k}_{0}, {\varDelta }_{0}, e)$, where ${k}_{0}\leftarrow \mathsf {UTO{.}setup}(\lambda )$, ${\varDelta }_{0}\leftarrow \bot$, and $e\leftarrow 0$. Two auxiliary variables $e_h^*$ and $e_o^*$ record the epochs where the host and the owner were first corrupted, respectively. Initially $e_h^* \leftarrow \bot$ and $e_o^* \leftarrow \bot$.

 

$\mathcal {O}_\mathsf {token} (x)$::

On input a value $x\in \mathcal {X}$, return ${y}_{e}\leftarrow \mathsf {UTO{.}token}({k}_{e},x)$ to the adversary, where ${k}_{e}$ is the tokenization key of the current epoch.

$\mathcal {O}_\mathsf {next}$::

When triggered, compute the tokenization key and update tweak of the next epoch as $({k}_{e+1}, {\varDelta }_{e+1}) \leftarrow \mathsf {UTO{.}next}({k}_{e})$ and update the global state to $({k}_{e+1}, {\varDelta }_{e+1}, e+1)$.

::

When invoked, return ${\varDelta }_{e}$ to the adversary. If called for the first time ($e_h^* = \bot$), then set $e_h^* \leftarrow e$. This oracle models the corruption of the host and may be called multiple times.

::

When invoked for the first time ($e_o^* = \bot$), then set $e_o^* \leftarrow e$ and return ${k}_{e}$ to the adversary. This oracle models the corruption of the owner and can only be called once. After this call, the adversary no longer has access to $\mathcal {O}_\mathsf {token}$ and $\mathcal {O}_\mathsf {next}$.

 

Note that although corruption of the host at epoch e exposes the update tweak ${\varDelta }_{e}$, the adversary should not be able to compute update tweaks of future epochs from this value. To obtain those, $\mathcal {A}$ should call again in the corresponding epochs; this is used for IND-HOCH security and IND-COTH security, with different side-conditions. A different case arises when the owner is corrupted, since this exposes all relevant secrets of the challenger. From that point the adversary can generate tokenization keys and update tweaks for all subsequent epochs on its own. This justifies why the oracle can only be called once. For the same reason, it makes no sense for an adversary to query the $\mathcal {O}_\mathsf {token}$ and $\mathcal {O}_\mathsf {next}$ oracles after the corruption of the owner. Furthermore, observe that does not return ${\varDelta }_{e}$ according to the assumption that the owner deletes this atomically with executing the $\mathsf {next}$ algorithm.

We are now ready to formally define the security notions for $\mathsf {UTO}$ in the remainder of this section.

3.3 IND-HOCH: Honest Owner and Corrupted Host

The IND-HOCH notion ensures that tokenized data does not reveal information about the corresponding original data when $\mathcal {A}$ compromises the host and obtains the update tweaks of the current and all future epochs. Tokenized values are also unlinkable across epochs, as long as the adversary does not know at least one update tweak in that timeline.

Definition 3

(IND-HOCH). An updatable tokenization scheme $\mathsf {UTO}$ is said to be IND-HOCH secure if for all polynomial-time adversaries $\mathcal {A}$ it holds that for some negligible function $\epsilon$.

This experiment has two phases. In the first phase, $\mathcal {A}$ may query $\mathcal {O}_\mathsf {token}$, $\mathcal {O}_\mathsf {next}$ and ; it ends at an epoch $\tilde{e}$ when $\mathcal {A}$ outputs two challenge inputs $\tilde{x}_0$ and $\tilde{x}_1$. The challenger picks one at random (denoted by $\tilde{x}_{d}$), tokenizes it, obtains the challenge $\tilde{y}_{d,\tilde{e}}$ and starts the second phase by invoking $\mathcal {A}$ with $\tilde{y}_{d,\tilde{e}}$. The adversary may then further query $\mathcal {O}_\mathsf {token}$, $\mathcal {O}_\mathsf {next}$, and and eventually outputs its guess $d'$ for which data value was tokenized. Note that only the first host corruption matters for our security notion, since we are assuming that once corrupted, the host is always corrupted. For simplicity, we therefore assume that $\mathcal {A}$ calls once in every epoch after $e_h^*$.

The adversary wins the experiment if it correctly guesses $d$ while respecting two conditions that differ depending on whether the adversary corrupted the host (roughly) before or after the challenge epoch:

• (a) If $e_h^* \le \tilde{e}+1$, then $\mathcal {A}$ first corrupts the host before, during, or immediately after the challenge epoch and may learn the update tweaks to epoch $e_h^*$ and later ones. In this case, it must not query the tokenization oracle on the challenge inputs in epoch $e_h^*-1$ or later.

  In particular, if this restriction was not satisfied, when $e_h^*\le \tilde{e}$, the adversary could tokenize data of its choice, including $\tilde{x}_0$ and $\tilde{x}_1$, during any epoch from $e_h^*-1$ to $\tilde{e}$, subsequently update the tokenized value to epoch $\tilde{e}$, and compare it to the challenge $\tilde{y}_{d,\tilde{e}}$. This would allow $\mathcal {A}$ to trivially win the security experiment.

  For the case $e_h^* = \tilde{e}+1$, recall that according to the experiment, the update tweak ${\varDelta }_{e}$ remains accessible until epoch $e+1$ starts. Therefore, $\mathcal {A}$ learns the update tweak from $\tilde{e}$ to $\tilde{e}+1$ and may update $\tilde{y}_{d,\tilde{e}}$ into epoch $\tilde{e}+1$. Hence, from this time on it must not query $\mathcal {O}_{\mathsf {token}}$ with the challenge inputs either.

• (b) If $e_h^* > \tilde{e}+1 \vee e^*_h = \bot$, i.e., the host was first corrupted after epoch $\tilde{e}+1$ or not at all, then the only restriction is that $\mathcal {A}$ must not query the tokenization oracle on the challenge inputs during epoch $\tilde{e}$. This is an obvious restriction to exclude trivial wins, as tokenization is deterministic.

  This condition is less restrictive than case (a), but it suffices since the adversary cannot update tokenized values from earlier epochs to $\tilde{e}$, nor from $\tilde{e}$ to a later epoch. The reason is that $\mathcal {A}$ only gets the update tweaks from epoch $\tilde{e}+2$ onwards.

3.4 IND-COHH: Corrupted Owner and Honest Host

The IND-COHH notion models a compromise of the owner in a certain epoch, such that the adversary learns the tokenization key and may generate tokenization keys and update tweaks of all subsequent epochs by itself. Given that the tokenization key allows to derive the update tweak of the host, this implicitly models some form of host corruption as well. The property ensures that data tokenized before the corruption remains hidden, that is, the adversary does not learn any information about the original data, nor can it link such data with data tokenized in other epochs.

Definition 4

(IND-COHH). An updatable tokenization scheme $\mathsf {UTO}$ is said to be IND-COHH secure if for all polynomial-time adversaries $\mathcal {A}$ it holds that for some negligible function $\epsilon$.

During the first phase of the IND-COHH experiment the adversary may query $\mathcal {O}_\mathsf {token}$ and $\mathcal {O}_\mathsf {next}$, but it may not corrupt the owner. At epoch $\tilde{e}$, the adversary produces two challenge inputs $\tilde{x}_0$ and $\tilde{x}_1$. Again, the challenger selects one at random and tokenizes it, resulting in the challenge $\tilde{y}_{d,\tilde{e}}$. Subsequently, $\mathcal {A}$ may further query $\mathcal {O}_\mathsf {token}$ and $\mathcal {O}_\mathsf {next}$, and now may also invoke . Once the owner is corrupted (during epoch $e_o^*$), $\mathcal {A}$ knows all key material of the owner and may generate tokenization keys and update tweaks of all subsequent epochs by itself. Thus, from this time on, we remove access to the $\mathcal {O}_\mathsf {token}$ or $\mathcal {O}_\mathsf {next}$ oracles for simplicity.

The adversary ends the experiment by guessing which input challenge was tokenized. It wins when the guess is correct and the following conditions are met:

• (a) $\mathcal {A}$ must have corrupted the owner only after the challenge epoch ($e_o^* > \tilde{e}$) or not at all ($e^*_o = \bot$). This is necessary since corruption during epoch $\tilde{e}$ would leak the tokenization key ${k}_{\tilde{e}}$ to the adversary. (Note that corruption before $\tilde{e}$ is ruled out syntactically.)

• (b) $\mathcal {A}$ must neither query the tokenization oracle with any challenge input ($\tilde{x}_0$ or $\tilde{x}_1$) during the challenge epoch $\tilde{e}$. This condition eliminates that $\mathcal {A}$ can trivially reveal the challenge input since the tokenization operation is deterministic.

On the (Im)possibility of Additional Host Corruption. As can be noted, the IND-COHH experiment does not consider the corruption of the host at all. The reason is that allowing host corruption in addition to owner corruption would either result in a non-achievable notion, or it would give the adversary no extra advantage. To see this, we first argue why additional host corruption capabilities at any epoch $e_h^*\le \tilde{e}+1$ is not allowed. Recall that such a corruption is possible in the IND-HOCH experiment if the adversary does not make any tokenization queries on the challenge values $\tilde{x}_0$ or $\tilde{x}_1$ at any epoch $e\ge e_h^*-1$. This restriction is necessary in the IND-HOCH experiment to prevent the adversary from trivially linking the tokenized values of $\tilde{x}_0$ or $\tilde{x}_1$ to the challenge $\tilde{y}_{d,\tilde{e}}$. However, when the owner can also be corrupted, at epoch $e_o^*>\tilde{e}$, that restriction is useless. Note that upon calling the adversary learns the owner’s tokenization key and can simply tokenize $\tilde{x}_0$ and $\tilde{x}_1$ at epoch $e_o^*$. The results can be compared with an updated version of $\tilde{y}_{d,\tilde{e}}$ to trivially win the security experiment.

Now we discuss the additional corruption of the host at any epoch $e_h^*>\tilde{e}+1$. We note that corruption of the owner at epoch $e_o^* > \tilde{e}$ allows the adversary to obtain the tokenization key of epoch $e_o^*$ and compute the tokenization keys and update tweaks of all epochs $e > e_o^*+1$. Thus, the adversary then trivially knows all tokenization keys from $e_o^*+1$ onward and modeling corruption of the host after the owner is not necessary. The only case left is to consider host corruption before owner corruption, at an epoch $e_h^*$ with $\tilde{e}+1< e_h^* < e_o^*$. However, corrupting the host first would not have any impact on the winning condition. Hence, without loss of generality, we assume that the adversary always corrupts the owner first, which allows us to fully omit the oracle in our IND-COHH experiment.

We stress that the impossibility of host corruption at any epoch $e_h^*\le \tilde{e}+1$ only holds if we consider permanent corruptions, i.e., the adversary, upon invocation of is assumed to fully control the host and to learn all future update tweaks. In the following security notion, IND-COTH, we bypass this impossibility by modeling transient corruption of the host.

3.5 IND-COTH: Corrupted Owner and Transiently Corrupted Host

Extending both of the above security properties, the IND-COTH notion considers corruption of the owner and repeated but transient corruptions of the host. It addresses situations where some of the update tweaks received by the host leak to $\mathcal {A}$ and the keys of the owner are also exposed at a later stage.

Definition 5

(IND-COTH). An updatable tokenization scheme $\mathsf {UTO}$ is said to be IND-COTH secure if for all polynomial-time adversaries $\mathcal {A}$ it holds that for some negligible function $\epsilon$.

Observe that the owner can only be corrupted after the challenge epoch, just as in the IND-COHH experiment. As before, $\mathcal {A}$ then obtains all key material and, for simplicity, we remove access to the $\mathcal {O}_\mathsf {token}$ or $\mathcal {O}_\mathsf {next}$ oracles from this time on. The transient nature of the host corruption allows to grant $\mathcal {A}$ additional access to before the challenge, which would be impossible in the IND-COHH experiment if permanent host corruption was considered.

Compared to the IND-HOCH definition, here $\mathcal {A}$ may corrupt the host and ask for a challenge input to be tokenized after the corruption. Multiple host corruptions may occur before, during, and after the challenge epoch. But in order to win the experiment, $\mathcal {A}$ must leave out at least one epoch and miss an update tweak. Otherwise it could trivially guess the challenge by updating the challenge output or a challenge input tokenized in another epoch to the same stage. In the experiment this is captured through the conditions under (c). In particular:

 

(c-i):

If $\mathcal {A}$ calls $\mathcal {O}_{\mathsf {token}}$ with one of the challenge inputs $\tilde{x}_0$ or $\tilde{x}_1$ before triggering the challenge, it must not corrupt the host and miss the update tweak in at least one epoch from this point up to the challenge epoch. Thus, the latest epoch before the challenge epoch where $\mathcal {A}$ queries $\mathcal {O}_{\mathsf {token}}(\tilde{x}_0)$ or $\mathcal {O}_{\mathsf {token}}(\tilde{x}_1)$, denoted $e_{\mathsf {last}}$, must be smaller than the last epoch before $\tilde{e}$ where the host is not corrupted.

(c-ii):

Likewise if $\mathcal {A}$ queries $\mathcal {O}_{\mathsf {token}}$ with a challenge input $\tilde{x}_0$ or $\tilde{x}_1$ after the challenge epoch, then it must not corrupt the host and miss the update tweak in at least one epoch after $\tilde{e}$. Otherwise, it could update the challenge $\tilde{y}_{d,\tilde{e}}$ to the epoch where it calls $\mathcal {O}_{\mathsf {token}}$. The first epoch after the challenge epoch where $\mathcal {A}$ queries $\mathcal {O}_{\mathsf {token}}(\tilde{x}_0)$ or $\mathcal {O}_{\mathsf {token}}(\tilde{x}_1)$, denoted $e_{\mathsf {first}}$, must be larger than or equal to the first epoch after $\tilde{e}$ where the host is not corrupted.

(c-iii):

If $\mathcal {A}$ calls , it must not obtain at least one update tweak after the challenge epoch and before, or during, the epoch of owner corruption $e_o^*$. Otherwise, $\mathcal {A}$ could tokenize $\tilde{x}_0$ and $\tilde{x}_1$ with the tokenization key of epoch $e_o^*$, exploit the exposed update tweaks to evolve the challenge value $\tilde{y}_{d,\tilde{e}}$ to that epoch, and compare the results.

 

PRF-style vs. IND-CPA-style Definitions. We have opted for definitions based on indistinguishability in our model. Given that the goal of tokenization is to output random looking tokens, a security notion in the spirit of pseudorandomness might seem like a more natural choice at first glance. However, a definition in the PRF-style does not cope well with adaptive attacks: in our security experiments the adversary is allowed to adaptively corrupt the data host and corrupt the data owner, upon which it gets the update tweaks or the secret tokenization key. Modeling this in a PRF vs. random function experiment would require the random function to contain a key and to be compatible with an update function that can be run by the adversary. Extending the random function with these “features” would lead to a PRF vs. PRF definition. The IND-CPA inspired approach used in this paper allows to cover the adaptive attacks and consistency features in a more natural way.

Relation Among the Security Notions. Our notion of IND-COTH security is the strongest of the three indistinguishability notions above, as it implies both IND-COHH and IND-HOCH security, but not vice-versa. That is, IND-COTH security is not implied by IND-COHH and IND-HOCH security. A distinguishing example is our $\mathsf {UTO}_\mathsf {SE}$ scheme. As we will see in Sect. 4.1, $\mathsf {UTO}_\mathsf {SE}$ is both IND-COHH and IND-HOCH secure, but not IND-COTH secure.

The proof of Theorem 1 below can be found in the full version of this paper.

Theorem 1

(IND-COTH $\Rightarrow$ IND-COHH + IND-HOCH). If an updatable tokenization scheme $\mathsf {UTO}$ is IND-COTH secure, then it is also IND-COHH secure and IND-HOCH secure.

3.6 One-Wayness

The one-wayness notion models the fact that a tokenization scheme should not be reversible even if an adversary is given the tokenization keys. In other words, an adversary who sees tokenized values and gets hold of the tokenization keys cannot obtain the original data. Because the keys allow one to reproduce the tokenization operation and to test whether the output matches a tokenized value, the resulting security level depends on the size of the input space and the adversary’s uncertainty about the input. Thus, in practice, the level of security depends on the prior knowledge of the adversary about $\mathcal {X}$.

Our definition is similar to the standard notion of one-wayness, with the difference that we ask the adversary to output the exact preimage of a tokenized challenge value, as our tokenization algorithm is an injective function.

Definition 6

(One-Wayness). An updatable tokenization scheme $\mathsf {UTO}$ is said to be one-way if for all polynomial-time adversaries $\mathcal {A}$ it holds that

$$\begin{aligned} \Pr [~x&= \tilde{x}:x \leftarrow \mathcal {A} (\lambda , {k}_{0},\tilde{y}), \\&\qquad \qquad \tilde{y}\leftarrow \mathsf {UTO{.}token}({k}_{0},\tilde{x}), \tilde{x} {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathcal {X}, {k}_{0}{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {UTO{.}setup}(\lambda )] \le 1/|\mathcal {X}|. \end{aligned}$$

4 UTO Constructions

In this section we present two efficient constructions of updatable tokenization schemes. The first solution ($\mathsf {UTO}_\mathsf {SE}$) is based on symmetric encryption and achieves one-wayness, IND-HOCH and IND-COHH security; the second construction ($\mathsf {UTO}_\mathsf {DL}$) relies on a discrete-log assumption, and additionally satisfies IND-COTH security. Both constructions share the same core idea: First, the input value is hashed, and then the hash is encrypted under a key that changes every epoch.

4.1 An UTO Scheme Based on Symmetric Encryption

We build a first updatable tokenization scheme $\mathsf {UTO}_\mathsf {SE}$, that is based on a symmetric deterministic encryption scheme $\mathsf {SE}= (\mathsf {SE{.}KeyGen},\mathsf {SE{.}Enc},\mathsf {SE{.}Dec})$ with message space $\mathcal {M}$ and a keyed hash function $\mathsf {H}: \mathcal {K}\times \mathcal {X}\rightarrow \mathcal {M}$. In order to tokenize an input $x\in \mathcal {X}$, our scheme simply encrypts the hashed value of x. At each epoch e, a distinct random symmetric key $s_{e}$ is used for encryption, while a fixed random hash key $hk$ is used to hash x. Both keys are chosen by the data owner. To update the tokens, the host receives the encryption keys of the previous and current epoch and re-encrypts all hashed values to update them into the current epoch. More precisely, our $\mathsf {UTO}_\mathsf {SE}$ scheme is defined as follows:

 

$\mathsf {UTO{.}setup}(\lambda )$::

Generate keys $s_0{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE{.}KeyGen}(\lambda )$, $hk{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {H}{.}\mathsf {KeyGen}(\lambda )$ and output ${k}_{0} \leftarrow (s_0,hk)$.

$\mathsf {UTO{.}next}({k}_{e})$::

Parse ${k}_{e}$ as $(s_e,hk)$. Choose a new key $s_{e+1}{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE{.}KeyGen}(\lambda )$ and set ${k}_{e+1} \leftarrow (s_{e+1},hk)$ and ${\varDelta }_{e+1} \leftarrow (s_{e},s_{e+1})$. Output $({k}_{e+1},{\varDelta }_{e+1})$.

$\mathsf {UTO{.}token}({k}_{e},x)$::

Parse ${k}_{e}$ as $(s_e,hk)$ and output ${y}_{e}\leftarrow \mathsf {SE{.}Enc}({s_e},{\mathsf {H}(hk,{x})})$.

$\mathsf {UTO{.}upd}({\varDelta }_{e+1},{y}_{e})$::

Parse ${\varDelta }_{e+1}$ as $(s_{e},s_{e+1})$ and output the updated value ${y}_{e+1} \leftarrow \mathsf {SE{.}Enc}({s_{e+1}},{\mathsf {SE{.}Dec}({s_e},{{y}_{e}})})$.

 

This construction achieves IND-HOCH, IND-COHH, and one-wayness but not the stronger IND-COTH notion. The issue is that a transiently corrupted host can recover the static hash during the update procedure and thus can link tokenized values from different epochs, even without knowing all the update tweaks between them.

Theorem 2

The $\mathsf {UTO}_\mathsf {SE}$ as defined above satisfies the IND-HOCH, IND-COHH and one-wayness properties based on the following assumptions on the underlying encryption scheme $\mathsf {SE}$ and hash function $\mathsf {H}$:

$\mathsf {UTO}_\mathsf {SE}$	$\mathsf {SE}$	$\mathsf {H}$
IND-COHH	IND-CPA	Weak collision resistance
IND-HOCH	IND-CPA	Pseudorandomness
One-wayness	–	One-wayness

The proof of Theorem 2 can be found in the full version of this paper.

4.2 An UTO Scheme Based on Discrete Logarithms

Our second construction $\mathsf {UTO}_\mathsf {DL}$ overcomes the limitation of the first scheme by performing the update in a proxy re-encryption manner using the re-encryption idea first proposed by Blaze et al. [2]. That is, the hashed value is raised to an exponent that the owner randomly chooses at every new epoch. To update tokens, the host is not given the keys itself but only the quotient of the current and previous exponent. While this allows the host to consistently update his data, it does not reveal the inner hash anymore and guarantees unlinkability across epochs, thus satisfying also our strongest notion of IND-COTH security.

More precisely, the scheme makes use of a cyclic group $(\mathbb {G},g,p)$ and a hash function $\mathsf {H}: \mathcal {X}\rightarrow \mathbb {G}$. We assume the hash function and the group description to be publicly available. The algorithms of our $\mathsf {UTO}_\mathsf {DL}$ scheme are defined as follows:

 

$\mathsf {UTO{.}setup}(\lambda )$::

Choose ${k}_{0}{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathbb {Z}_p$ and output ${k}_{0}$.

$\mathsf {UTO{.}next}({k}_{e})$::

Choose ${k}_{e+1}{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathbb {Z}_p$, set ${\varDelta }_{e+1} \leftarrow {k}_{e+1}/{k}_{e}$, and output $({k}_{e+1},$ ${\varDelta }_{e+1})$.

$\mathsf {UTO{.}token}({k}_{e},x)$::

Compute ${y}_{e}\leftarrow \mathsf {H}(x)^{{k}_{e}}$, and output ${y}_{e}$.

$\mathsf {UTO{.}upd}({\varDelta }_{e+1}, {y}_{e})$::

Compute ${y}_{e+1} \leftarrow {y}_{e}^{{\varDelta }_{e+1}}$, and output ${y}_{e+1}$.

 

Our $\mathsf {UTO}_\mathsf {DL}$ scheme is one-way and satisfies our strongest notion of IND-COTH security, from which IND-HOCH and IND-COHH security follows (see Theorem 1). The proof of Theorem 3 below can be found in the full version of this paper.

Theorem 3

The $\mathsf {UTO}_\mathsf {DL}$ scheme as defined above is IND-COTH secure under the DDH assumption in the random oracle model, and one-way if $\mathsf {H}$ is one-way.