Keywords

1 Introduction

Quadrotor UAV (Unmanned Aerial Vehicle) has been developed for various military and civil missions, due to its simple structure, VTOL (Vertical Taskoff and Landing) and great maneuverability [1]. Quadrotor UAV is a typically coupled and underactuated nonlinear system. Its control system usually consist of attitude part and position part, whose position part guarantee the Quadrotor UAV to track the desired positions by changing the attitudes and total thrust, and the attitude part guarantee the quadrotor UAV to track the desired attitudes determined that given by position controller. It means that the position control performance is affected by the attitude tracking performance, besides several maneuver tasks require high attitude tracking performance. Unfortunately, it is not easy to achieve high attitude tracking performance, due to the coupled character and parameter uncertainties. Moreover, external disturbances also bring more challenge. Many techniques have been proposed to solve the above problem. Tradition method such as PID, LQ control [2], robust feedback linearization [3], robust control [4] etc. are adopted to improve the attitude tracking performance for quadrotor UAV to some extent, but they can’t achieve high performance because of ignoring the coupled character and parameter uncertainties during controller design. So many novel controller methods are proposed. The work [5] proposed a robust disturbance rejection control method based on robust disturbance observer (DOB), robust DOB was designed to compensate the uncertainty. In [6], An robust control method was addressed, adaptation laws were designed to learn and compensate the modeling error and external disturbance. In [7], A proportional-integral control method was proposed based on additive-state-decomposition (ASD) dynamic inversion design. By ASD and a new definition of output, the considered uncertain system is transformed into a first-order system, in which all original uncertainties were lumped into a new disturbance at the new defined output. And a dynamic inversion control was applied to reject the lumped disturbance.

In this brief, an adaptive nonsmooth attitude tracking controller is developed for quadrotor with dynamic uncertainties, integrating the nonsmooth control and adaptive control technology. Compared with the aforementioned method, the proposed method has fast transient, high-precision performances and simpler controller structures.

2 Preliminaries

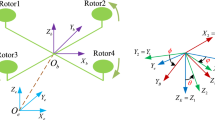
2.1 Model Dynamics of Quadrotor UAV Attitude System

An attitude system model of the rigid-body quadrotor UAV with dynamic uncertainties can be written as (see [1,2,3,4]):

$$ \begin{aligned} \ddot{\phi } & = \dot{\theta }\dot{\psi }{{\left( {I_{\text{y}} - I_{\text{z}} } \right)} \mathord{\left/ {\vphantom {{\left( {I_{\text{y}} - I_{\text{z}} } \right)} {I_{\text{x}} }}} \right. \kern-0pt} {I_{\text{x}} }} + {{blU_{\phi } } \mathord{\left/ {\vphantom {{blU_{\phi } } {I_{\text{x}} }}} \right. \kern-0pt} {I_{\text{x}} }} + \Delta_{\phi } \\ \ddot{\theta } & = \dot{\phi }\dot{\psi }{{\left( {I_{\text{z}} - I_{\text{x}} } \right)} \mathord{\left/ {\vphantom {{\left( {I_{\text{z}} - I_{\text{x}} } \right)} {I_{y} }}} \right. \kern-0pt} {I_{y} }} + {{blU_{\theta } } \mathord{\left/ {\vphantom {{blU_{\theta } } {I_{\text{y}} }}} \right. \kern-0pt} {I_{\text{y}} }} + \Delta_{\theta } \\ \dot{\psi } & = \dot{\phi }\dot{\theta }{{\left( {I_{\text{x}} - I_{\text{y}} } \right)} \mathord{\left/ {\vphantom {{\left( {I_{\text{x}} - I_{\text{y}} } \right)} {I_{z} }}} \right. \kern-0pt} {I_{z} }} + {{dU_{\psi } } \mathord{\left/ {\vphantom {{dU_{\psi } } {I_{\text{z}} }}} \right. \kern-0pt} {I_{\text{z}} }} + \Delta_{\psi } \\ \end{aligned} $$
(1)

Where \( \phi \in {\text{R}}, \) \( \theta \in {\text{R}}, \) \( \psi \in {\text{R}} \) denote the Euler angles (roll, pitch, yaw) respectively, \( I_{x} \in {\text{R}}^{+} \), \( I_{y} \in {\text{R}}^{+} \), \( I_{z} \in {\text{R}}^{+} \) are the moments of inertia of quadrotor, \( b \) is the lift coefficient, \( d \) is the drag coefficient, \( l \in {\text{R}}^{+} \) is the distance from the epicenter of the quadrotor UAV to the rotor axis, \( \Delta_{\varphi } \in {\text{R}}, \) \( \Delta_{\theta } \in {\text{R}}, \) \( \Delta_{\psi } \in {\text{R}} \) denote the uncertainties caused by bounded external disturbance. And \( U_{\phi } \), \( U_{\theta } \), \( U_{\psi } \) are given as follows:

$$ \begin{aligned} U_{\phi } & = \omega_{ 2}^{ 2} - \omega_{ 4}^{ 2} \\ U_{\theta } & = - \omega_{ 1}^{ 2} + \omega_{ 3}^{ 2} \\ U_{\psi } & = \omega_{ 1}^{ 2} - \omega_{ 2}^{ 2} { + }\omega_{ 3}^{ 2} - \omega_{ 4}^{ 2} \\ \end{aligned} $$
(2)

Where \( \omega_{i} \in {\text{R}},i = 1,2,3,4 \) denote the angular speed of the rotor \( i \). For the design procedure of adaptive nonsmooth attitude tracking controller, the dynamic model will be transformed as follow.

Define \( k_{1} = bl \), \( k_{2} = d \), \( p_{x1} = I_{x} /k_{1} \), \( p_{y1} = I_{y} /k_{1} \), \( p_{z1} = I_{z} /k_{1} \) \( p_{x2} = I_{x} /k_{2} \), \( p_{y2} = I_{y} /k_{2} \), \( p_{z2} = I_{z} /k_{2} \), we can write Eq. (1) in the following form

$$ \begin{aligned} U_{\varphi } = p_{x1} \ddot{\varphi } - \dot{\theta }\dot{\psi }p_{y1} + \dot{\theta }\dot{\psi }p_{z1} + T_{\varphi } \hfill \\ U_{\theta } = p_{y1} \ddot{\theta } - \dot{\varphi }\dot{\psi }p_{z1} + \dot{\theta }\dot{\psi }p_{x1} + T_{\theta } \hfill \\ U_{\psi } = p_{z2} \dot{\psi } - \dot{\varphi }\dot{\theta }p_{x2} + \dot{\varphi }\dot{\theta }p_{y2} + T_{\psi } \hfill \\ \end{aligned} $$
(3)

With: \( T_{\varphi } = p_{x1} \Delta_{\varphi } \), \( T_{\theta } = p_{y1} \Delta_{\theta } \), \( T_{\psi } = p_{z2} \Delta_{\psi } \).

Then Eq. (3) can be represented as:

$$ \varvec{U} = {\varvec{M}}{\ddot{\varvec{q}}} + {\varvec{C}}\left( {\dot{\varvec{q}}} \right) + \varvec{T} $$
(4)

where, \( \varvec{q} = \left[ {\begin{array}{*{20}c} \varphi & \theta & \psi \\ \end{array} } \right]^{\text{T}} \), \( {\dot{\varvec{q}}} = \left[ {\begin{array}{*{20}c} {\dot{\varphi }} & {\dot{\theta }} & {\dot{\psi }} \\ \end{array} } \right]^{\text{T}} \), \( {\ddot{\varvec{q}}} = \left[ {\begin{array}{*{20}c} {\ddot{\varphi }} & {\ddot{\theta }} & {\ddot{\psi }} \\ \end{array} } \right]^{\text{T}} \), \( \varvec{C}\left( {{\dot{\varvec{q}}}} \right) = \left[ {\begin{array}{*{20}c}-\ { \dot{\theta }\dot{\psi }p_{y1} + \dot{\theta }\dot{\psi }p_{z1} } &\ -\ {\dot{\varphi }\dot{\psi }p_{z1} + \dot{\theta }\dot{\psi }p_{x1} } &\ -\ {\dot{\varphi }\dot{\theta }p_{x2} + \dot{\varphi }\dot{\theta }p_{y2} } \\ \end{array} } \right]^{\text{T}} \), \( \varvec{U} = \left[ {\begin{array}{*{20}c} {U_{\varphi } } & {U_{\theta } } & {U_{\psi } } \\ \end{array} } \right]^{\text{T}} \), \( \varvec{T} = \left[ {\begin{array}{*{20}c} {T_{\varphi } } & {T_{\theta } } & {T_{\psi } } \\ \end{array} } \right]^{\text{T}} \), \( {\varvec{M}} = {\text{diag}}\left( {\begin{array}{*{20}c} {p_{x1} } & {p_{y1} } & {p_{z2} } \\ \end{array} } \right). \)

If we notate: \( \varvec{p} = \left[ {\begin{array}{*{20}c} {p_{x1} } & {p_{y1} } & {p_{z1} } & {p_{x2} } & {p_{y2} } & {p_{z2} } & {T_{\varphi } } & {T_{\theta } } & {T_{\psi } } \\ \end{array} } \right]^{\text{T}} \) and \( \varvec{\varPhi}\triangleq\varvec{\varPhi}\left( {\begin{array}{*{20}c} {\dot{\varvec{q}}} & {\ddot{\varvec{q}}} \\ \end{array} } \right) = \left[ {\begin{array}{*{20}c} {\ddot{\varphi }} &\ -\ {\dot{\theta }\dot{\psi }} &\ -\ {\dot{\theta }\dot{\psi }} & {} & {} & {} & 1 & {} & {} \\ {\dot{\theta }\dot{\psi }} & {\ddot{\theta }} & - {\dot{\varphi }\dot{\psi }} & {} & {} & {} & {} & 1 & {} \\ {} & {} & {} & - {\dot{\varphi }\dot{\theta }} & {\dot{\varphi }\dot{\theta }} & {\dot{\psi }} & {} & {} & 1 \\ \end{array} } \right] \).

Equation (3) could be derived as:

$$ \varvec{U} = \varvec{\varPhi p} $$
(5)

Then the dynamic model of the quadrotor UAV with uncertainties could be represented as:

$$ \varvec{U} =\varvec{\varPhi}\left( {\varvec{p}_{\text{n}} + \varvec{p}_{\text{u}} } \right) $$
(6)

Where \( \varvec{p}_{\text{n}} \) is the parameter vector of nominal system, \( \varvec{p}_{\text{u}} \) is the unknown parameter vector of the quadrotor UAV dynamic model.

2.2 New Version of Barbalate’s Lemma

Theorem 1. If \( x\left( t \right) \) is a uniformly continuous function and if there exist a lower bounded scalar function \( V \) and a continuous positive definite and radially unbounded scalar function \( M \) such that \( - \dot{V} \ge M\left( {x\left( t \right)} \right), \) then \( x\left( t \right) \to 0 \) as \( t \to \infty \) [8].

3 Adaptive Nonsmooth Attitude Tracking Control of Quadrotor UAV

Assumption 1.

The reference attitude trajectory \( \varvec{q}_{\text{r}} \in C^{2} \), and the sample rate of the controller is fast enough, so \( {\dot{\varvec{p}}} \approx 0 \)

Backstepping approach will be adopted to design the adaptive nonsmooth attitude tracking controller (ANSATC) as follow.

Step 1. Let \( \varvec{x}_{1} \triangleq \varvec{q} \) and \( \varvec{x}_{2} \triangleq {\dot{\varvec{q}}}, \) lead to \( {\dot{\varvec{x}}}_{1} = \varvec{x}_{2} \). Define \( \varvec{z}_{ 1}\ =\ \varvec{x}_{1} - \varvec{x}_{{ 1 {\text{r}}}} \) and \( \varvec{z}_{2} = \varvec{x}_{2} -\varvec{\beta}, \) where \( \varvec{x}_{{ 1 {\text{r}}}} = \varvec{q}_{\text{r}} \) and \( \varvec{\beta} \) is the auxiliary part which will be designed later.

Consider the candidate Lyapunov function as follow

$$ V_{ 1} = {{\varvec{z}_{ 1}^{\text{T}} \varvec{z}_{1} } \mathord{\left/ {\vphantom {{\varvec{z}_{ 1}^{\text{T}} \varvec{z}_{1} } 2}} \right. \kern-0pt} 2} $$
(7)

Differentiating \( V_{ 1} \) versus time along the trajectories of system (1) yields

$$ \dot{V}_{ 1} = {\varvec{z}}_{ 1}^{\text{T}} {\dot{\varvec{z}}}_{1} $$
(8)

With the definitions above, it could be derived as

$$ \dot{V}_{ 1} = \varvec{z}_{ 1}^{\text{T}} \left( {\varvec{x}_{2} - \varvec{x}_{{ 2 {\text{r}}}} } \right) = \varvec{z}_{ 1}^{\text{T}} \varvec{z}_{2} { + }\varvec{z}_{ 1}^{\text{T}} \left( {\varvec{\beta}- \varvec{x}_{{ 2 {\text{r}}}} } \right) $$
(9)

\( \varvec{\beta} \) is designed as

$$ \varvec{\beta}= \varvec{x}_{{ 2 {\text{r}}}} - \varvec{K}_{1} \text{sig} \left( {\varvec{z}_{1} } \right)^{\alpha } $$
(10)

Where, \( \varvec{K}_{1} \in {\text{R}}_{ + }^{3 \times 3} \) is a diagonal positive-definite gain matrix, \( \alpha \in {\text{R}}^{+}, 0 < \alpha < 1 \). And the notation \( \text{sig} \left( {\varvec{z}_{1} } \right)^{\alpha } \) is defined as [9]

$$ \text{sig} \left( {{\varvec{z}}_{1} } \right)^{\alpha } \triangleq \left[ {\begin{array}{*{20}c} {\left| {z_{1\varphi } } \right|^{\alpha } \text{sign} \left( {z_{1\varphi } } \right)} & {\left| {z_{1\theta } } \right|^{\alpha } \text{sign} \left( {z_{1\theta } } \right)} & {\left| {z_{1\psi } } \right|^{\alpha } \text{sign} \left( {z_{1\psi } } \right)} \\ \end{array} } \right]^{\text{T}} $$
(11)

From (10) and (11), \( \dot{V}_{ 1} \) could be deduced as

$$ \dot{V}_{ 1} = \varvec{z}_{ 1}^{\text{T}} \varvec{z}_{2} - \varvec{K}_{1} \varvec{z}_{ 1}^{\text{T}} \text{sig} \left( {\varvec{z}_{1} } \right)^{\alpha } $$
(12)

It is easy to deduce that \( \dot{V}_{ 1} = \varvec{K}_{1} \varvec{z}_{ 1}^{\text{T}} \text{sig} \left( {\varvec{z}_{1} } \right)^{\alpha } \le 0 \) as \( \varvec{z}_{2} = 0 \).

Step 2. We define parameter matrixes of the nominal system as \( \varvec{M}_{\text{n}} \), \( \varvec{C}_{\text{n}} \) and \( \varvec{T}_{\text{n}} \), and consider an desired system (parameters are known, without external disturbances) as the nominal system, from (4) and (6) it is easily obtained that

$$ \varvec{U} = \varvec{\varPhi p}_{\text{u}} + \varvec{M}_{\text{n}} {\ddot{\varvec{q}}} + \varvec{C}_{\text{n}} \left( {\dot{\varvec{q}}} \right) $$
(13)

Where \( \varvec{T}_{\text{n}} = 0, \) \( \varvec{M}_{\text{n}} \) is a diagonal positive-definite matric. Then consider a new candidate Lyapunov function as follow

$$ V = V_{1} + {{\left( {\varvec{z}_{2}^{\text{T}} \varvec{M}_{n} \varvec{z}_{2} + \bar{\varvec{p}}^{\text{T}} \varvec{\varGamma \bar{p}}} \right)} \mathord{\left/ {\vphantom {{\left( {\varvec{z}_{2}^{\text{T}} \varvec{M}_{n} \varvec{z}_{2} + \bar{\varvec{p}}^{\text{T}}\varvec{\varGamma}{\bar{\varvec{p}}}} \right)} 2}} \right. \kern-0pt} 2} $$
(14)

Where \( \bar{\varvec{p}}\ {\mathbf{=}}\ \varvec{p} - \hat{\varvec{p}} \), \( \hat{\varvec{p}} \) is the estimation result obtained by adaption laws, which will be designed next. \( \varvec{\varGamma}\in {\text{R}}_{ + }^{3 \times 3} \) is a diagonal positive-definite gain matrices.

Differentiating \( V \) with respect to time and from (12) yields

$$ \dot{V} = {\varvec{z}}_{ 1}^{\text{T}} {\varvec{z}}_{2} - \varvec{K}_{1} {\varvec{z}}_{ 1}^{\text{T}} \text{sig} \left( {{\varvec{z}}_{1} } \right)^{\alpha } + \varvec{z}_{2}^{\text{T}} \varvec{M}_{n} {\dot{\varvec{z}}}_{2} + \bar{\varvec{p}}^{\text{T}}\varvec{\varGamma}{{\dot{\bar{\varvec{p}}}}} $$
(15)

Substituting Eq. (13) into (15), we obtain

$$ \begin{aligned} \dot{V} & = \varvec{z}_{ 1}^{\text{T}} \varvec{z}_{2} - \varvec{K}_{1} \varvec{z}_{ 1}^{\text{T}} \text{sig} \left({\varvec{z}_{1} } \right)^{\alpha } + \varvec{z}_{2}^{\text{T}}\varvec{M}_{n} {\dot{\varvec{z}}}_{2} + \bar{\varvec{p}}_{{\mathbf{u}}}^{\text{T}} {\varvec{\varGamma}} {\dot{\bar{\varvec{p}}}}_{\text{u}} \\ & = \varvec{z}_{ 1}^{\text{T}} \varvec{z}_{2} - \varvec{K}_{1} {\varvec{z}}_{ 1}^{\text{T}} \text{sig} \left({\varvec{z}_{1} } \right)^{\alpha } + \varvec{z}_{2}^{\text{T}} \left[ { - \varvec{C}_{\text{n}} \left( {\dot{\varvec{q}}} \right) - \varvec{\varPhi p}_{\text{u}} - \varvec{M}_{\text{n}} {\dot{\varvec{\beta}}} + \varvec{U}} \right] + \bar{\varvec{p}}_{{\mathbf{u}}}^{\text{T}} {\varvec{\varGamma}\dot{\bar{\varvec{p}}}_{\text{u}}} \\ \end{aligned} $$
(16)

Design \( {\varvec{U}} \) as follow

$$ \varvec{U} = \varvec{U}_{\text{nsc}} - \varvec{z}_{1} + \varvec{M}_{\text{n}} {\dot{\varvec{\beta}}} + \varvec{C}_{\text{n}} \left( {\dot{\varvec{q}}} \right) +\varvec{\varPhi}\hat{\varvec{p}}_{\text{u}} $$
(17)

Where \( \varvec{U}_{\text{nsc}} = - \varvec{K}_{2} \text{sig} \left( {\varvec{z}_{2} } \right)^{\alpha } \), \( \varvec{K}_{2} \in {\text{R}}_{ + }^{3 \times 3} \) is a diagonal positive-definite gain matrices.

From (16), (17) can be derived as

$$ \dot{V} = - \varvec{K}_{1} \varvec{z}_{1} \text{sig} \left( {\varvec{z}_{1} } \right)^{\alpha } - \varvec{K}_{2} \text{sig} \left( {\varvec{z}_{2} } \right)^{\alpha } + \left( {\dot{\bar{\varvec{p}}}_{{\mathbf{u}}}^{\text{T}}\varvec{\varGamma}- \varvec{z}_{2}^{\text{T}}\varvec{\varPhi}} \right)\bar{\varvec{p}}_{\text{u}} $$
(18)

We let \( {\dot{\bar{\varvec{p}}}}_{{\mathbf{u}}}^{\text{T}}\varvec{\varGamma}- \varvec{z}_{2}^{\text{T}}\varvec{\varPhi}= 0, \) from Assumption 1 we can deduce the adaptation laws as follow [10]

$$ {\dot{\hat{{\varvec{p}}}}}_{{\mathbf{u}}}^{\text{T}} = - \varvec{z}_{2}^{\text{T}} \varvec{\varPhi \varGamma }^{-1} $$
(19)

And we get \( \dot{V} \le 0 \). For the system analysis, we define scalar function \( N\left( {{\varvec{z}}_{1}^{\text{T}} ,{\varvec{z}}_{2}^{\text{T}} } \right) \) as

$$ N\left( {\varvec{z}_{1}^{\text{T}} ,\varvec{z}_{2}^{\text{T}} } \right) = \varvec{K}_{1} \varvec{z}_{1} \text{sig} \left( {\varvec{z}_{1} } \right)^{\alpha } + \varvec{K}_{2} \text{sig} \left( {\varvec{z}_{2} } \right)^{\alpha } $$
(20)

From (14) and (20), it is easily to deduce that the infimum of \( V \) (\( \inf \left\{ V \right\}) \) exists, and supremum of \( V \) satisfies \( \sup \left\{ V \right\} \le V\left( 0 \right) \), so \( \varvec{z}_{1} \), \( \varvec{z}_{2} \), \( \bar{\varvec{p}}_{\text{u}} \) are bounded.

From (10), we can obtain

$$ {\dot{\varvec{z}}}_{ 1}\ =\ \varvec{z}_{2} - \varvec{K}_{1} \text{sig} \left( {\varvec{z}_{1} } \right)^{\alpha } $$
(21)

From (10), (13) and (17), we can obtain

$$ \varvec{M}_{\text{n}} {\dot{\varvec{z}}}_{2} = - \varvec{z}_{1} - K_{2} sig\left( {\varvec{z}_{2} } \right) + {\varPhi \bar{\varvec{p}}}_{\text{u}} $$
(22)

From (21) and (22), we can easily deduce that \( {\varvec{z}}_{1} \) and \( \varvec{z}_{2} \) are bounded, so \( \varvec{z}_{1} \), \( \varvec{z}_{2} \) are uniformly continuous function and \( N\left( {\varvec{z}_{1}^{\text{T}}, \varvec{z}_{2}^{\text{T}} } \right) \) is radially unbounded. By Theorem 1 we can obtain that then \( \varvec{z}_{1} \to 0,\ \varvec{z}_{2} \to 0 \) as \( t \to \infty \), which means the real attitude will tracking reference attitude trajectory without error as \( t \to \infty \).

Remark 1. When \( \alpha = 1, \) the adaptive nonsmooth controller in (17) will become a type of normal adaptive controller, and it will become a PD controller when \( \alpha = 1 \) and \( \hat{\varvec{p}}_{\text{u}}\ {\mathbf{=}}\ 0 \).

4 Simulation Results

The parameters of the quadrotor VAU are \( m = 2\,{\text{kg}} \), \( l = 0.2\,{\text{m}} \), \( I_{x} = 1.25\,{\text{kg}} \cdot {\text{m}}^{ 2} \), \( I_{y} = 1.25\,{\text{kg}} \cdot {\text{m}}^{ 2} \), \( I_{z} = 2.5\,{\text{kg}} \cdot {\text{m}}^{ 2} \), \( b = 2.98 \times 10^{-6}\,{{{\text{N}} \cdot {\text{s}}^{2} } \mathord{\left/ {\vphantom {{{\text{N}} \cdot {\text{s}}^{2} } {{\text{rad}}^{2} }}} \right. \kern-0pt} {{\text{rad}}^{2} }} \), \( d = 1.14 \times 10^{-7}\,{{{\text{N}} \cdot {\text{s}}^{2} } \mathord{\left/ {\vphantom {{{\text{N}} \cdot {\text{s}}^{2} } {{\text{rad}}^{2} }}} \right. \kern-0pt} {{\text{rad}}^{2} }} \). And the sampling rate of controller is 10 kHz. For simplicity, the altitude control of the quadrotor UAV is ignored, which means the quadrotor UAV is holding the altitude eternally. The reference attitude trajectory could be represented as \( \varphi_{\text{r}} = \left( {{\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0pt} 6}} \right)\sin \left( {2\pi } \right)\left( {\text{rad}} \right), \) \( \theta_{\text{r}} = \left( {{\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0pt} 6}} \right)\sin \left( {2\pi } \right)\left( {\text{rad}} \right), \) \( \psi_{\text{r}} = 0. \)

And \( \Delta_{\phi } = 10\% {{m{\kern 1pt} g{\kern 1pt} l} \mathord{\left/ {\vphantom {{m{\kern 1pt} g{\kern 1pt} l} {I_{x} }}} \right. \kern-0pt} {I_{x} }}, \) \( \Delta_{\theta } = 10\% {{m{\kern 1pt} g{\kern 1pt} l} \mathord{\left/ {\vphantom {{m{\kern 1pt} g{\kern 1pt} l} {I_{y} }}} \right. \kern-0pt} {I_{y} }}, \) with the assumption that the parameters are unknown to controller and the nominal parameters are given as \( k_{{1{\text{n}}}} = 0.8k_{1} \), \( k_{{2{\text{n}}}} = 0.6k_{2} \), \( I_{\text{xn}} = 0.7I_{\text{x}} \), \( I_{\text{yn}} = 0.7I_{\text{y}} \), \( I_{\text{zn}} = 0.7I_{\text{z}} \). Four experiments are designed with \( \varvec{K}_{1} = 5 \times {\text{diag}}\left( {\begin{array}{*{20}c} 1 & 1 & 1 \\ \end{array} } \right) \), \( \varvec{K}_{2} = 4 \times 10^{6} \times \text{diag} \left( {\begin{array}{*{20}c} 1 & 1 & 1 \\ \end{array} } \right) \), and the different part of the experiments are shown as Table 1, which represent normal PD controller (Method 1), normal adaptive controller (Method 2), nonsmooth controller (Method 3), and the proposed method (Method 4) respectively.

Table 1. Table of experiment parameters.
Full size table

The simulation results are illustrated in Fig. 1. Figure 1(a) presents the tracking results of \( \phi \), it is clearly that the proposed method (Method 4) has fastest transient and most precise tracking performances among the four experiments. The similar tracking results of \( \theta \) are shown in Fig. 1(b). And the tracking results of \( \psi \) are shown in Fig. 1(c). Figure 2 shows the control input of the four experiments, which are all continuous without chattering.

Fig. 1.
figure 1

Results of simulations

Full size image
Fig. 2.
figure 2

Comparison of control input

Full size image

Further, to evaluate the relationship between tracking performance and control parameter \( \alpha \), four experiments are carried out with \( \alpha = 1 \), \( \alpha = 0.9 \), \( \alpha = 0.8 \) and \( \alpha = 0.7. \) Figure 3 illustrates the tracking result of \( \phi \), we can easily find that tracking performance are the best when \( \alpha = 0.7, \) which means attitude tracking performance can be improved by reducing \( \alpha \). But \( \alpha \) could not be arbitrary small, because an arbitrary small may lead to chatting in real system.

Fig. 3.
figure 3

Tracking result comparison of \( \phi \) with different \( \alpha \)

Full size image

5 Conclusion

In this paper, an adaptive nonsmooth attitude tracking control of quadrotor UAV based on backstepping approach is presented. A dynamic model was built considering the dynamic uncertainties, an ANSATC was designed in detail, and the system stability is analyzed. Finally the effectiveness of the ANSATC was validated via serial simulations, which showed satisfactory transient and precise tracking performance while rejecting dynamic uncertainties.