1 Introduction

In recent years, the quadrotor UAV has attracted the attention of many researchers, thanks to its simple operation procedure and some unique advantages, such as vertical take-off and landing, hovering, etc. Stable flight is one of the most concerned issues in quadrotor systems. To achieve this goal, research on the controller design of quadrotor drones has been done.

Currently, many control methods have been applied to the design of attitude controller of quadrotor, such as proportional-integral-derivative control [1], active disturbance rejection control [2], \(H_\infty \) synthesis technique [3], model predictive control [4], model reference adaptive control [5] and linear quadratic control [6]. Among these control techniques, SMC is a well-known control technique that is widely utilized to construct the robust controller for nonlinear system. In [7,8,9], an integral SM was adopted to design attitude controller for a quadrotor. In [10,11,12], several adaptive SMC strategies have been considered to stabilize attitude channels of a quadrotor system. In [13,14,15], a terminal SMC was presented to design robust flight control system for a quadrotor. However, there is a problem of singularity in terminal SMC. Therefore, a nonsingular terminal SMC was proposed to address this problem [16, 17]. In addition, backstepping control is also a widely used control approach based on recursive design idea, which has been introduced to design quadrotor controller. In [18,19,20,21], a backstepping approach was applied to the attitude dynamics of a quadrotor. Then, the attitude trajectory tracking is achieved. However, the problem of explosion of complexity exists in the backstepping. To overcome this issue, command filter [22,23,24], tracking differentiator [25], optimization technique [26] were applied to the backstepping control, respectively. In [27, 28], two adaptive backstepping methods were introduced to design attitude controller of a quadrotor. Furthermore, to fully combine the advantages of SMC and backstepping control, some researches focus on backstepping sliding mode control (BSSMC) of quadrotor UAV. In [29,30,31], a BSSMC was developed to accomplish the attitude stabilization for a quadrotor. In [32, 33], a backstepping control combined with nonsingular terminal SMC was employed to construct an attitude controller for a quadrotor UAV.

When a quadrotor system flies outdoors, it will always encounter external disturbance, such as wind. Therefore, it is necessary to consider the suppression of disturbance in controller design. In [12, 30], the stabilization of quadrotor system was guaranteed by selecting that the controller gain was greater than the upper bound of disturbance. In [17, 33], by designing an adaptive law for the upper bound of disturbance in the developed controller, the disturbance could be suppressed. As a result, the stability of the closed-loop system could be achieved. Such an idea of disturbance rejection does not require the prior information of disturbance, but the adaptive algorithm may cause parameter drift of the estimated state. Moreover, designing disturbance observer is an effective method to compensate for disturbance in the design of controller. In [10, 13, 16, 19, 20, 24, 25, 28, 29, 31, 32, 34, 35], the disturbance observer designed have been integrated into quadrotor controller to eliminate disturbance, where an same assumption that disturbance changes slowly was given in [19, 28, 32]. This means the compensation of disturbance with rapid change may not be realized in [19, 28, 32]. Meanwhile, the estimation error of disturbance was only asymptotically convergent in [10, 24, 29, 34, 35]. Although the finite-time convergence of the estimation error of disturbance was guaranteed in [13, 16], the convergence time was not provided. In [20, 25, 31], an extended state observer was employed to estimate disturbance, which stabilized the disturbance observation error within a bounded range in finite time. Moreover, some intelligent techniques, such as neural network [36], fuzzy logic system [37] and reinforcement learning [37], combined with the classical algorithms have been applied to the estimation of disturbance.

It is worth noting that the aforementioned works have considered the convergence analysis of steady-state tracking error, but the transient performance of tracking error is not fully considered. To further highlight the gap identified in the literature, a comparative table, i.e. Table 1, is given, where Item A denotes method of disturbance rejection; Item B denotes prior information of disturbance; Item C denotes convergence of disturbance observation error; Item D denotes steady-state performance of tracking error; Item E denotes transient performance of tracking error; Item F denotes evaluation index.

Table 1 The comparison of disturbance rejection and tracking performance in literature
Full size table

In this paper, to eliminate the adverse effects of external disturbance acting on quadrotor systems, a BSSMC technique based on disturbance observer with finite-time convergence is proposed and then the three attitude angles of the quadrotor drone is stabilized. Moreover, the \(L_2\) performance of the transient tracking error is guaranteed. Therefore, the proposed method has the potential to be extended to other fields to realize practical applications, such as robots and unmanned vehicles. The main contributions of this paper are as follows:

  1. (i)

    Compared with the existing DO with asymptotical convergence in [10, 24, 28, 29, 34, 35] and the FTDO without convergence time in [13, 16, 20, 25, 31], in this paper, the proposed FTDO not only guarantees the disturbance observation error converge to zero in finite time, but also gives an explicit reaching time.

  2. (ii)

    Unlike the works [29, 31, 32] that only focus the steady-state performance of the tracking error using BSSMC based on DO, the transient performance in term of \(L_2\) norm and the steady-state performance of the tracking error are considered simultaneously in this paper.

  3. (iii)

    Compared with [8, 9, 11, 15, 18,19,20,21,22,23,24,25,26, 29, 30, 32, 36], several statistical indexes are used to quantitatively evaluate the performance of the proposed method in terms of control signal, observation error and tracking error in the comparative simulations.

The remainder of this paper is organized as follows. The dynamics description of the quadrotor is given in Sect. 2. Section 3 recalls some preliminary lemmas. Section 4 introduces the design of the proposed controller based on finite-time disturbance observer and stability analysis. In Sect. 5, the simulation results are presented. Finally, the main conclusions of the paper are presented in Sect. 6.

2 Problem formulation

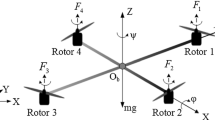
The sketch of the quadrotor UAV is shown in Fig. 1, where \(\{O_e: X_e-Y_e-Z_e\}\) and \(\{O_b: X_b-Y_b-Z_b\}\) represent the earth and body frames, respectively. Let \([x\; y\; z]\) denotes the position output of the quadrotor and \([\phi \; \theta \; \varphi ]\) represents attitude output of the quadrotor, where \(\phi \) is the roll angle, defined as the angle between the projection of the axis \(O_bZ_b\) of the body frame system on the \(O_e-Z_e-X_e\) plane of the earth frame system and the axis \(O_eZ_e\); \(\theta \) is the pitch angle, defined as the angle between the projection of the axis \(O_bY_b\) of the body frame system on the \(O_e-Y_e-Z_e\) plane of the earth frame system and the axis \(O_eY_e\); \(\varphi \) is the yaw angle, defined as the angle between the projection of the axis \(O_bX_b\) of the body frame system on the \(O_e-X_e-Y_e\) plane of the earth frame system and the axis \(O_eX_e\). In order to maintain the balance of the body, the diagonal rotors (e.g. Rotors 1 and 4) of the quadrotor drone rotate in the same direction, while the adjacent rotors (e.g. Rotors 2 and 3) rotate in the opposite direction.

Fig. 1
figure 1

Quadrotor UAV

Full size image

In the following, the derivation process of the attitude dynamic model of the quadrotor system will be introduced in detail.

Let \([{\bar{p}}\; {\bar{q}}\; {\bar{r}}]\) represent angular velocity of quadrotor in the coordinate system B. The angular motion dynamics of the quadrotor are [27]

$$\begin{aligned} \begin{array}{l} \displaystyle M_x=I_x\dot{{\bar{p}}}+(I_z-I_y){\bar{q}}{\bar{r}}, \\ \displaystyle M_y=I_y\dot{{\bar{q}}}+(I_x-I_z){\bar{p}}{\bar{r}},\\ \displaystyle M_z=I_z\dot{{\bar{r}}}+(I_y-I_x){\bar{p}}{\bar{q}}, \end{array} \end{aligned}$$
(1)

where \(M_x, M_y, M_z\) are the components of the resultant torque acting on quadrotor in the three directions of x, y, z, respectively, and \(I_x\), \(I_y\), \(I_z\) are the moments of inertia of the quadrotor around x, y, z, respectively.

Let \(M_{lx}, M_{ly}, M_{lz}\) denote the components of the lifting torque of the quadrotor in the three directions of x, y, z, respectively, which can be expressed as [27]

$$\begin{aligned} \begin{array}{l} \displaystyle M_{lx}=LF_\phi , \\ \displaystyle M_{ly}=LF_\theta ,\\ \displaystyle M_{lz}=fF_\varphi , \end{array} \end{aligned}$$
(2)

where L is the distance from the center of the rotor to the center of the quadrotor, f is the scaling factor from force to moment and \(F_\phi \), \(F_\theta \), and \(F_\varphi \) are control inputs of attitude channel.

Moreover, the quadrotor is subject to gyroscopic torque during flight, whose components \(M_{gx}, M_{gy}, M_{gz}\) around the x, y, and z axes, respectively, are given by [27]

$$\begin{aligned} \begin{array}{l} \displaystyle M_{gx}=I_r{\bar{q}}\Omega , \\ \displaystyle M_{gy}=-I_r{\bar{p}}\Omega ,\\ \displaystyle M_{gz}=0. \end{array} \end{aligned}$$
(3)

In (3), \(I_r\) is the inertia of each propeller and \(\Omega \) is the algebraic sum of the four rotors.

Considering (1)–(3), the angular dynamics of the quadrotor can be rewritten in the following form.

$$\begin{aligned} \begin{array}{l} \displaystyle I_x\dot{{\bar{p}}}=(I_y-I_z){\bar{q}}{\bar{r}}-I_r{\bar{q}}\Omega +LF_\phi , \\ \displaystyle I_y\dot{{\bar{q}}}=(I_z-I_x){\bar{p}}{\bar{r}}+I_r{\bar{p}}\Omega +LF_\theta ,\\ \displaystyle I_z\dot{{\bar{r}}}=(I_x-I_y){\bar{p}}{\bar{q}}+fF_\varphi . \end{array} \end{aligned}$$
(4)

Notice that the angular velocity \([{\bar{p}}\; {\bar{q}}\; {\bar{r}}]\) in the coordinate system \(\{O_b: X_b-Y_b-Z_b\}\) can be converted to the angular velocity \([{\dot{\phi }}\; {\dot{\theta }}\; {\dot{\varphi }}]\) in the coordinate system \(\{O_e: X_e-Y_e-Z_e\}\) by [9]

$$\begin{aligned} \left[ \begin{array}{ccc} \displaystyle {\dot{\phi }} \\ \displaystyle {\dot{\theta }} \\ \displaystyle {\dot{\varphi }} \\ \end{array} \right] = \left[ \begin{array}{ccc} \displaystyle 1 &{} \displaystyle \sin \phi \tan \theta &{} \displaystyle \cos \phi \tan \theta \\ \displaystyle 0 &{} \displaystyle \cos \phi &{} -\displaystyle \sin \phi \\ \displaystyle 0 &{} \displaystyle \frac{\sin \phi }{\cos \theta } &{} \displaystyle \frac{\cos \phi }{\cos \theta } \\ \end{array} \right] \left[ \begin{array}{c} \displaystyle {\bar{p}} \\ \displaystyle {\bar{q}} \\ \displaystyle {\bar{r}} \\ \end{array} \right] . \end{aligned}$$
(5)

To ensure flight safety, the attitude angles of the quadrotor are always kept small on purpose during the flight. Thus, it follows from (5) that \([{\dot{\phi }}\; {\dot{\theta }}\; {\dot{\varphi }}]^T\approx [{\bar{p}}\; {\bar{q}}\; {\bar{r}}]^T\). In consequence, the attitude dynamics of the quadrotor subjected to external disturbance can be derived from (4),

$$\begin{aligned} \begin{array}{l} \displaystyle \ddot{\phi }=\frac{(I_y-I_z){\dot{\theta }}{\dot{\varphi }}-I_r{\dot{\theta }}\Omega +LF_\phi }{I_x}+d_\phi , \\ \displaystyle \ddot{\theta }=\frac{(I_z-I_x){\dot{\phi }}{\dot{\varphi }}+I_r{\dot{\phi }}\Omega +LF_\theta }{I_y}+d_\theta ,\\ \displaystyle \ddot{\varphi }=\frac{(I_x-I_y){\dot{\phi }}{\dot{\theta }}+fF_\varphi }{I_z}+d_\varphi , \end{array} \end{aligned}$$
(6)

where \(d_\phi \), \(d_\theta \), \(d_\varphi \) are the external disturbances acting on the three attitudes of the quadrotor system in the form of acceleration, respectively. Note that the moment of inertia of the rotor is much smaller than that of the UAV, so the terms \(\frac{I_r{\dot{\theta }}\Omega }{I_x}\) and \(\frac{I_r{\dot{\phi }}\Omega }{I_y}\) can be ignored in the controller design [15]. As a result, (6) can be further derived as

$$\begin{aligned} \begin{array}{l} \displaystyle \ddot{\phi }=\frac{(I_y-I_z){\dot{\theta }}{\dot{\varphi }}+LF_\phi }{I_x}+d_\phi , \\ \displaystyle \ddot{\theta }=\frac{(I_z-I_x){\dot{\phi }}{\dot{\varphi }}+LF_\theta }{I_y}+d_\theta ,\\ \displaystyle \ddot{\varphi }=\frac{(I_x-I_y){\dot{\phi }}{\dot{\theta }}+fF_\varphi }{I_z}+d_\varphi . \end{array} \end{aligned}$$
(7)

3 Preliminaries

Lemma 1

For the following system

$$\begin{aligned} {\dot{\zeta }}=f(\zeta ),\quad t\ge 0, \quad \zeta (0)=\zeta _0, \end{aligned}$$
(8)

suppose that there exists a continuous, positive definite function \(V(\zeta )\) such that \({\dot{V}}(\zeta )\le -\beta V^{\alpha }(\zeta )\) with positive scalars \(\alpha \in (0,1)\) and \(\beta >0\). Then, the solution of system (8) will converge to zero in finite time \(T\le \frac{1}{\beta (1-\alpha )}V^{1-\alpha }(\zeta _0)\) with \(V(\zeta _0)\) being the initial value of \(V(\zeta )\) [39].

Lemma 2

Let \(V(\zeta )\) be a non-negative scalar function of time on \([0, \infty )\), which satisfies the differential inequality \({\dot{V}}(\zeta )\le -\gamma V(\zeta )\), where \(\gamma \) is a positive constant. Then \(V(\zeta )\le {\underline{e}}^{-\gamma t}V(\zeta _0), \forall t\in [0, \infty )\), where \({\underline{e}}\) is the base of the natural logarithm and \(V(\zeta _0)\) is the initial value of \(V(\zeta )\) [40].

Lemma 3

The Rayleigh quotient of symmetric matrix \(A \in {\mathbb {R}}^{n\times n}\) is defined as \(R_A=\frac{X^TAX}{X^TX}\) with \(X \in {\mathbb {R}}^n\) and \(X\ne 0\). Then we have \(\uplambda _{\min }(A) \le R_A\le \uplambda _{\max }(A)\), i.e., \(\uplambda _{\min }(A)X^TX \le X^TAX\le \uplambda _{\max }(A)X^TX\), where \(\uplambda _{\min }(\cdot )\) and \(\uplambda _{\max }(\cdot )\) are the minimum eigenvalue and maximum eigenvalue of A, respectively [41].

Lemma 4

Suppose that: (i) the function \(f_1(\tau )\) is monotone on the interval \([a, \infty )\) and \(\lim _{\tau \rightarrow \infty }f_1(\tau )=0\), and (ii) the function \(f_2(\tau )\) is integrable on [a, b] for all \(b>a\), and the integral function \(F_2(\tau )=\int _{a}^{\infty } f_2(\tau ) d\tau \) is bounded on \([a, \infty )\), then the improper integral \(\int _{a}^{\infty } f_1(\tau )f_2(\tau ) d\tau \) is convergent [42].

4 Controller design and stability analysis

The control objective is to design an attitude controller to guarantee that the tracking errors of the attitude angles \(\phi \), \(\theta \) and \(\varphi \) in (7) can be stabilized in the presence of external disturbance and to guarantee that the \(L_2\) performance of the tracking error is achieved.

Assumption 1

It is assumed that the derivatives of the disturbances \(d_\phi \), \(d_\theta \) and \(d_\varphi \) in (7) are uniformly bounded, and satisfy \( \vert {\dot{d}}_\phi \vert \le \delta _\phi \), \( \vert {\dot{d}}_\theta \vert \le \delta _\theta \) and \( \vert {\dot{d}}_\varphi \vert \le \delta _\varphi \) with known positive constants \(\delta _\phi \), \(\delta _\theta \), \(\delta _\varphi \).

Remark 1

Assumption 1 is reasonable, since there is no disturbance that changes infinitely fast in the real world. Moreover, to ensure that the derivative of Lyapunov function is negative, the boundedness of derivative of disturbance needs to be guaranteed.

Remark 2

It can be seen from the dynamic model (7) of the quadrotor that the disturbance acts on the quadrotor system in the form of acceleration. Therefore, the bound of derivative of disturbance could be obtained approximately by measuring the additional acceleration on quadrotor system.

4.1 Controller design

In this section, the design of FTDO and attitude controller will be given, respectively. The FTDO will be first introduce. Let \(\hbar _\chi ={\dot{\chi }}\), where \(\chi =\phi , \theta , \varphi \). Define observation error as

$$\begin{aligned} \begin{array}{l} \displaystyle e_{\chi 1}=\hbar _\chi -{\hat{\hbar }}_\chi , \\ \displaystyle e_{\chi 2}=d_\chi -{\hat{d}}_\chi , \end{array} \end{aligned}$$
(9)

where \({\hat{\hbar }}_\chi \) and \({\hat{d}}_\chi \) are the estimates of \(\hbar _\chi \) and \(d_\chi \), respectively. The FTDO of attitude channel of the quadrotor is designed as

$$\begin{aligned} \begin{array}{l} \begin{aligned} \displaystyle \dot{{\hat{\hbar }}}_\chi &{}=W_\chi F_\chi +Y_\chi +\xi _1 \vert e_{\chi 1} \vert ^\frac{1}{2}\textrm{sign}(e_{\chi 1})+\xi _2(e_{\chi 1})+{\hat{d}}_\chi , \\ \displaystyle \dot{{\hat{d}}}_\chi &{}=\xi _3\textrm{sign}(e_{\chi 1})+\xi _4(e_{\chi 1}), \end{aligned} \end{array} \end{aligned}$$
(10)

where \(\xi =l, p, q\) are the observer parameter to be designed; \(\xi =l\), \(W_\chi =\frac{L}{I_x}\), \(Y_\chi =\frac{I_y-I_z}{I_x}{\dot{\theta }}{\dot{\varphi }}\) when \(\chi =\phi \); \(\xi =p\), \(W_\chi =\frac{L}{I_y}\), \(Y_\chi =\frac{I_z-I_x}{I_y}{\dot{\phi }}{\dot{\varphi }}\) when \(\chi =\theta \); \(\xi =q\), \(W_\chi =\frac{f}{I_z}\), \(Y_\chi =\frac{I_x-I_y}{I_z}{\dot{\phi }}{\dot{\theta }}\) when \(\chi =\varphi \); \(\textrm{sign}(\cdot )\) denotes signum function. Then the error dynamics of the observer can be obtained by (7), (9) and (10)

$$\begin{aligned} \begin{array}{l} \displaystyle {\dot{e}}_{\chi 1}=-\xi _1 \vert e_{\chi 1} \vert ^\frac{1}{2}\textrm{sign}(e_{\chi 1})-\xi _2(e_{\chi 1})+e_{\chi 2}, \\ \displaystyle {\dot{e}}_{\chi 2}=-\xi _3\textrm{sign}(e_{\chi 1})-\xi _4(e_{\chi 1})+{\dot{d}}_\chi . \end{array} \end{aligned}$$
(11)

Then, the design of attitude controller is introduced. Define tracking error as

$$\begin{aligned} E_\chi =\chi _d-\chi , \end{aligned}$$
(12)

where \(\chi _d\) is desired attitude. Furthermore, define

$$\begin{aligned} {\tilde{E}}_\chi =-{\dot{\chi }}+\kappa _\chi , \end{aligned}$$
(13)

where \(\kappa _\chi \) is defined as

$$\begin{aligned} \kappa _\chi =c_\chi E_\chi +{\dot{\chi }}_d, \end{aligned}$$
(14)

with \(c_\chi \) as a positive constant. Therefore, the time derivative of \(E_\chi \) can be obtained

$$\begin{aligned} \begin{aligned} {\dot{E}}_\chi&={\dot{\chi }}_d-{\dot{\chi }}, \\&={\dot{\chi }}_d+{\tilde{E}}_\chi -c_\chi E_\chi -{\dot{\chi }}_d \\&=-c_\chi E_\chi +{\tilde{E}}_\chi . \end{aligned} \end{aligned}$$
(15)

The sliding surface is designed as

$$\begin{aligned} s_\chi =n_\chi E_\chi +{\tilde{E}}_\chi , \end{aligned}$$
(16)

whose derivative with respect to time is

$$\begin{aligned} \begin{aligned} {\dot{s}}_\chi&=n_\chi {\dot{E}}_\chi +\dot{{\tilde{E}}}_\chi \\&=n_\chi (-c_\chi E_\chi +{\tilde{E}}_\chi )+{\dot{\kappa }}_\chi -\ddot{\chi }, \end{aligned} \end{aligned}$$
(17)

where \(n_\chi \) is a positive constant. The attitude controller is designed as

$$\begin{aligned} \begin{aligned} F_\chi&=\frac{1}{W_\chi }(n_\chi (-c_\chi E_\chi +{\tilde{E}}_\chi )+{\dot{\kappa }}_\chi -Y_\chi -{\hat{d}}_\chi \\&\quad +E_\chi +h_\chi s_\chi ), \end{aligned} \end{aligned}$$
(18)

where \(h_\chi \) is a positive constant.

4.2 Stability analysis

Theorem 1

Consider the attitude dynamic model of the quadrotor UAV in (7), if the attitude control law is designed as (18) with the FTDO (10), then we can conclude:

  1. (i)

    the observation error (9) of disturbance will be guaranteed to converge to zero in finite time.

  2. (ii)

    the attitude output tracking error (12) of the closed-loop system has a global asymptotic stability property;

  3. (iii)

    the bound of the transient attitude tracking error in terms of \(L_2\) norm (denoted by \(\vert \vert \cdot \vert \vert _2\)) satisfies

    $$\begin{aligned} \vert \vert E_\chi \vert \vert _2 \le \sqrt{\Xi _{\chi 1}+ \Xi _{\chi 2}+ \Xi _{\chi 3}+ \Xi _{\chi 4}}, \end{aligned}$$
    (19)

    where

    $$\begin{aligned} \Xi _{\chi 1}= & {} \frac{2+2(n_\chi +c_\chi )^2\uplambda _\chi (n_\chi +c_\chi )}{\uplambda _\chi +\uplambda _\chi (n_\chi +c_\chi )^2}\chi ^2_d(0), \end{aligned}$$
    (20)
    $$\begin{aligned} \Xi _{\chi 2}= & {} \frac{2}{\uplambda _\chi +\uplambda _\chi (n_\chi +c_\chi )^2}({\dot{\chi }}_d(0))^2, \end{aligned}$$
    (21)
    $$\begin{aligned} \Xi _{\chi 3}= & {} \frac{4(n_\chi +c_\chi )}{\uplambda _\chi +\uplambda _\chi (n_\chi +c_\chi )^2}\chi _d(0){\dot{\chi }}_d(0), \end{aligned}$$
    (22)
    $$\begin{aligned} \Xi _{\chi 4}= & {} \frac{-2\uplambda _\chi M_E}{\uplambda _\chi +\uplambda _\chi (n_\chi +c_\chi )^2}. \end{aligned}$$
    (23)

Proof

Define the following Lyapunov function candidate

$$\begin{aligned} {\bar{V}}_{\chi }=\frac{1}{2}E^2_\chi +\frac{1}{2}s^2_\chi . \end{aligned}$$
(24)

The time derivative of \({\bar{V}}_{\chi }\) is

$$\begin{aligned} \dot{{\bar{V}}}_\chi =E_\chi {\dot{E}}_\chi +s_\chi {\dot{s}}_\chi . \end{aligned}$$
(25)

Applying (15) and (17) to (25) yields

$$\begin{aligned} \begin{aligned} \dot{{\bar{V}}}_\chi&=E_\chi (-c_\chi E_\chi +{\tilde{E}}_\chi ) \\&\quad +s_\chi (n_\chi (-c_\chi E_\chi +{\tilde{E}}_\chi )+{\dot{\kappa }}_\chi -\ddot{\chi }). \end{aligned} \end{aligned}$$
(26)

Substituting attitude dynamics (7) of the quadrotor into (26), we have

$$\begin{aligned} \begin{aligned} \dot{{\bar{V}}}_\chi&=E_\chi (-c_\chi E_\chi +{\tilde{E}}_\chi )+s_\chi (n_\chi (-c_\chi E_\chi +{\tilde{E}}_\chi ) \\&\quad +{\dot{\kappa }}_\chi -W_\chi F_\chi -Y_\chi +d_\chi ). \end{aligned} \end{aligned}$$
(27)

Substituting the designed attitude controller (18) into (27), we obtain

$$\begin{aligned} \dot{{\bar{V}}}_\chi =-c_\chi E^2_\chi +E_\chi {\tilde{E}}_\chi +s_\chi (-E_\chi -h_\chi s_\chi +{\hat{d}}_\chi -d_\chi ).\nonumber \\ \end{aligned}$$
(28)

According to (9), \(e_{\chi 2}=-({\hat{d}}_\chi -d_\chi )\). In the following, we will discuss the convergence of the observation error of the disturbance. Define the following Lyapunov function candidate

$$\begin{aligned} \begin{aligned} V_{\chi }&=2\xi _3 \vert e_{\chi 1} \vert +\xi _4e^2_{\chi 1}+\frac{1}{2}e^2_{\chi 2}+\frac{1}{2}(\xi _1 \vert e_{\chi 1} \vert ^\frac{1}{2}\textrm{sign}(e_{\chi 1})\\&\quad +\xi _2e_{\chi 1}-e_{\chi 2})^2. \end{aligned} \end{aligned}$$
(29)

\(V_{\chi }\) is everywhere continuous and differentiable everywhere except on the subspace \(\{(e_{\chi 1},e_{\chi 2})\in {\mathbb {R}}^2 \vert e_{\chi 1}=0\}\). The derivative of \(V_{\chi }\) with respect to time is

$$\begin{aligned} \begin{aligned} {\dot{V}}_{\chi }=&\,2\xi _3\frac{e_{\chi 1}}{ \vert e_{\chi 1} \vert }{\dot{e}}_{\chi 1}+2\xi _4e_{\chi 1}{\dot{e}}_{\chi 1}+e_{\chi 2}{\dot{e}}_{\chi 2} \\&+\left( \frac{1}{2}\xi ^2_1\textrm{sign}(e_{\chi 1}){\dot{e}}_{\chi 1}+\xi _1\xi _2 \vert e_{\chi 1} \vert ^\frac{1}{2}\textrm{sign}(e_{\chi 1}){\dot{e}}_{\chi 1} \right. \\&-\xi _1 \vert e_{\chi 1} \vert ^\frac{1}{2}\textrm{sign}(e_{\chi 1}){\dot{e}}_{\chi 2}+\frac{1}{2}\xi _1\xi _2 \vert e_{\chi 1} \vert ^{-\frac{1}{2}}e_{\chi 1}{\dot{e}}_{\chi 1} \\&+\xi ^2_2e_{\chi 1}{\dot{e}}_{\chi 1}-\xi _2e_{\chi 1}{\dot{e}}_{\chi 2}-\frac{1}{2}\xi _1 \vert e_{\chi 1} \vert ^{-\frac{1}{2}}{\dot{e}}_{\chi 1}e_{\chi 2} \\&\left. -\xi _2{\dot{e}}_{\chi 1}e_{\chi 2}+e_{\chi 2}{\dot{e}}_{\chi 2}\right) . \end{aligned} \end{aligned}$$
(30)

Since \(\textrm{sign}(e_{\chi 1})=\frac{e_{\chi 1}}{ \vert e_{\chi 1} \vert }\), (30) can be rewritten as

$$\begin{aligned} \begin{aligned} {\dot{V}}_{\chi }=\,&\left( 2\xi _3+\frac{\xi ^2_1}{2}\right) \frac{e_{\chi 1}}{ \vert e_{\chi 1} \vert }{\dot{e}}_{\chi 1}+(2\xi _4+\xi ^2_2)e_{\chi 1}{\dot{e}}_{\chi 1}\\&\quad +\frac{3}{2}\xi _1\xi _2\frac{e_{\chi 1}{\dot{e}}_{\chi 1}}{ \vert e_{\chi 1} \vert ^\frac{1}{2}} -\xi _2({\dot{e}}_{\chi 1}e_{\chi 2}+e_{\chi 1}{\dot{e}}_{\chi 2}) \\&\quad -\xi _1\left( \frac{1}{2}\frac{{\dot{e}}_{\chi 1}e_{\chi 2}}{ \vert e_{\chi 1} \vert ^\frac{1}{2}}+\frac{e_{\chi 1}}{ \vert e_{\chi 1} \vert ^\frac{1}{2}}{\dot{e}}_{\chi 2}\right) \\&\quad +2e_{\chi 2}{\dot{e}}_{\chi 2}. \end{aligned} \end{aligned}$$
(31)

Substituting \({\dot{e}}_{\chi 1}\) and \({\dot{e}}_{\chi 2}\) in (11) to (31) yields

$$\begin{aligned} {\dot{V}}_{\chi }= & {} -\left( 2\xi _1\xi _3+\frac{1}{2}\xi ^3_1\right) \vert e_{\chi 1} \vert ^\frac{1}{2}-\left( 2\xi _2\xi _3+\frac{1}{2}\xi ^2_1\xi _2\right) \frac{e^2_{\chi 1}}{ \vert e_{\chi 1} \vert } \nonumber \\{} & {} +\left( 2\xi _3+\frac{1}{2}\xi ^2_1\right) \frac{e_{\chi 1}e_{\chi 2}}{ \vert e_{\chi 1} \vert }-(2\xi _1\xi _4+\xi _1\xi ^2_2) \vert e_{\chi 1} \vert ^\frac{3}{2} \nonumber \\{} & {} -(2\xi _2\xi _4+\xi ^3_2)e^2_{\chi 1}+(2\xi _4+\xi ^2_2)e_{\chi 1}e_{\chi 2} \nonumber \\{} & {} -\frac{3}{2}\xi ^2_1\xi _2 \vert e_{\chi 1} \vert -\frac{3}{2}\xi _1\xi ^2_2 \vert e_{\chi 1} \vert ^\frac{3}{2}+\frac{3}{2}\xi _1\xi _2\frac{e_{\chi 1}}{ \vert e_{\chi 1} \vert ^\frac{1}{2}}e_{\chi 2} \nonumber \\{} & {} +\xi _1\xi _2\frac{e_{\chi 1}}{ \vert e_{\chi 1} \vert ^\frac{1}{2}}e_{\chi 2}+\xi ^2_2e_{\chi 1}e_{\chi 2}-\xi _2e^2_{\chi 2} \nonumber \\{} & {} +\xi _2\xi _3 \vert e_{\chi 1} \vert +\xi _2\xi _4e^2_{\chi 1}-\xi _2e_{\chi 1}{\dot{d}}_\chi \nonumber \\{} & {} +\frac{1}{2}\xi ^2_1\frac{e_{\chi 1}}{ \vert e_{\chi 1} \vert }e_{\chi 2}+\frac{1}{2}\xi _1\xi _2\frac{e_{\chi 1}}{ \vert e_{\chi 1} \vert ^\frac{1}{2}}e_{\chi 2}-\frac{1}{2}\xi _1\frac{e^2_{\chi 2}}{ \vert e_{\chi 1} \vert ^\frac{1}{2}}\nonumber \\{} & {} +\xi _1\xi _3 \vert e_{\chi 1} \vert ^\frac{1}{2}+\xi _1\xi _4 \vert e_{\chi 1} \vert ^\frac{3}{2}-\xi _1\frac{e_{\chi 1}}{ \vert e_{\chi 1} \vert ^\frac{1}{2}}{\dot{d}}_\chi \nonumber \\{} & {} -2\xi _3\frac{e_{\chi 1}}{ \vert e_{\chi 1} \vert }e_{\chi 2}-2\xi _4e_{\chi 1}e_{\chi 2}+2e_{\chi 2}{\dot{d}}_\chi . \end{aligned}$$
(32)

Obviously, (32) is a complex polynomial equation. For convenience, we transform (32) in the following form

$$\begin{aligned} \begin{aligned} {\dot{V}}_{\chi }&=-\left( 2\xi _1\xi _3+\frac{1}{2}\xi ^3_1\right) \vert e_{\chi 1} \vert ^\frac{1}{2}+\xi _1\xi _3 \vert e_{\chi 1} \vert ^\frac{1}{2} \\&\quad -(2\xi _1\xi _4+\xi _1\xi ^2_2) \vert e_{\chi 1} \vert ^\frac{3}{2}-\frac{3}{2}\xi _1\xi ^2_2 \vert e_{\chi 1} \vert ^\frac{3}{2}\\&\quad +\xi _1\xi _4 \vert e_{\chi 1} \vert ^\frac{3}{2} +\left( 2\xi _3+\frac{1}{2}\xi ^2_1\right) \frac{e_{\chi 1}e_{\chi 2}}{ \vert e_{\chi 1} \vert }\\&\quad +\frac{1}{2}\xi ^2_1\frac{e_{\chi 1}}{ \vert e_{\chi 1} \vert }e_{\chi 2} -2\xi _3\frac{e_{\chi 1}}{ \vert e_{\chi 1} \vert }e_{\chi 2} \\&\quad +\frac{3}{2}\xi _1\xi _2\frac{e_{\chi 1}}{ \vert e_{\chi 1} \vert ^\frac{1}{2}}e_{\chi 2}+\xi _1\xi _2\frac{e_{\chi 1}}{ \vert e_{\chi 1} \vert ^\frac{1}{2}}e_{\chi 2}\\&\quad +\frac{1}{2}\xi _1\xi _2\frac{e_{\chi 1}}{ \vert e_{\chi 1} \vert ^\frac{1}{2}}e_{\chi 2} -\left( 2\xi _2\xi _3+\frac{1}{2}\xi ^2_1\xi _2\right) \frac{e^2_{\chi 1}}{ \vert e_{\chi 1} \vert } \\&\quad -\frac{3}{2}\xi ^2_1\xi _2 \vert e_{\chi 1} \vert +\xi _2\xi _3 \vert e_{\chi 1} \vert \\&\quad +(2\xi _4+\xi ^2_2)e_{\chi 1}e_{\chi 2}+\xi ^2_2e_{\chi 1}e_{\chi 2}-2\xi _4e_{\chi 1}e_{\chi 2} \\&\quad -\frac{1}{2}\xi _1\frac{e^2_{\chi 2}}{ \vert e_{\chi 1} \vert ^\frac{1}{2}}-(2\xi _2\xi _4+\xi ^3_2)e^2_{\chi 1}+\xi _2\xi _4e^2_{\chi 1}\\&\quad -\xi _2e^2_{\chi 2} +2e_{\chi 2}{\dot{d}}_\chi -\xi _2e_{\chi 1}{\dot{d}}_\chi -\xi _1\frac{e_{\chi 1}}{ \vert e_{\chi 1} \vert ^\frac{1}{2}}{\dot{d}}_\chi . \\ \end{aligned} \end{aligned}$$
(33)

Furthermore, (33) follows from \( \vert {\dot{d}}_\chi \vert \le \delta _\chi \), \(e_{\chi 1}\le \vert e_{\chi 1} \vert \) and \(e_{\chi 2}\le \vert e_{\chi 2} \vert \) that

$$\begin{aligned} \begin{aligned} {\dot{V}}_{\chi }&\le -\left( \xi _1\xi _3+\frac{1}{2}\xi ^3_1\right) \vert e_{\chi 1} \vert ^\frac{1}{2}-\left( \xi _1\xi _4+\frac{5}{2}\xi _1\xi ^2_2\right) \vert e_{\chi 1} \vert ^\frac{3}{2}\\&\quad -\frac{\xi _1}{2}\frac{e^2_{\chi 2}}{ \vert e_{\chi 1} \vert ^\frac{1}{2}} +\xi ^2_1 \vert e_{\chi 2} \vert +3\xi _1\xi _2 \vert e_{\chi 1} \vert ^\frac{1}{2} \vert e_{\chi 2} \vert \\&\quad -(\xi _2\xi _3+2\xi ^2_1\xi _2) \vert e_{\chi 1} \vert -(\xi _2\xi _4+\xi ^3_2) \vert e_{\chi 1} \vert ^2\\&\quad -\xi _2 \vert e_{\chi 2} \vert ^2 +2\xi ^2_2 \vert e_{\chi 1} \vert \vert e_{\chi 2} \vert +2\delta _\chi \vert e_{\chi 2} \vert \\&\quad +\xi _2\delta _\chi \vert e_{\chi 1} \vert +\xi _1\delta _\chi \vert e_{\chi 1} \vert ^\frac{1}{2}. \end{aligned} \end{aligned}$$
(34)

Define \(\Pi _\chi =[ \vert e_{\chi 1} \vert ^\frac{1}{2}, e_{\chi 1}, e_{\chi 2}]^T\). Then (34) can be rewritten as

$$\begin{aligned} {\dot{V}}_{\chi }\le -\frac{1}{ \vert e_{\chi 1} \vert ^\frac{1}{2}}\Pi _\chi ^T\Lambda _{\chi 1}\Pi _\chi -\Pi _\chi ^T\Lambda _{\chi 2}\Pi _\chi , \end{aligned}$$
(35)

where

$$\begin{aligned}{} & {} \Lambda _{\chi 1}\\{} & {} \quad =\frac{1}{2} \begin{bmatrix} 2\xi _1\xi _3+\xi ^3_1-2\xi _1\delta _\chi &{} 0 &{} -\xi ^2_1-2\delta _\chi \\ 0 &{} 2\xi _1\xi _4+5\xi _1\xi ^2_2 &{} -3\xi _1\xi _2 \\ -\xi ^2_1-2\delta _\chi &{} -3\xi _1\xi _2 &{} \xi _1 \end{bmatrix}, \\{} & {} \Lambda _{\chi 2}= \begin{bmatrix} \xi _2\xi _3+2\xi ^2_1\xi _2-\xi _2\delta _\chi &{} 0 &{} 0 \\ 0 &{} \xi _2\xi _4+\xi ^3_2 &{} -\xi ^2_2 \\ 0 &{} -\xi ^2_2 &{} \xi _2 \end{bmatrix}, \end{aligned}$$

If the matrices \(\Lambda _{\chi 1}\) and \(\Lambda _{\chi 2}\) are positive definite, i.e., the following inequality holds,

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \xi _1\xi _3+\frac{\xi ^3_1}{2}-\xi _1\delta _\chi>0, \\ \displaystyle \langle \Sigma _{\chi 1} \rangle>0, \\ \displaystyle \xi _2\xi _3+2\xi ^2_1\xi _2-\xi _2\delta _\chi>0, \\ \displaystyle \langle \Sigma _{\chi 2} \rangle >0, \end{array} \right. \end{aligned}$$
(36)

where \(\langle \cdot \rangle \) denotes the determinant of matrix \(\cdot \), then (35) can be derived as

$$\begin{aligned} \begin{aligned} {\dot{V}}_{\chi }&\le -\frac{1}{ \vert e_{\chi 1} \vert ^\frac{1}{2}}\Pi _\chi ^T\Lambda _{\chi 1}\Pi _\chi . \\ \end{aligned} \end{aligned}$$
(37)

Notice that (29) can be written as:

$$\begin{aligned} V_{\chi }=\Theta _\chi ^T\Gamma _\chi \Theta _\chi , \end{aligned}$$
(38)

where

$$\begin{aligned} \Theta _\chi = \begin{bmatrix} \vert e_{\chi 1} \vert ^\frac{1}{2}\textrm{sign}(e_{\chi 1}) \\ e_{\chi 1} \\ e_{\chi 2} \end{bmatrix}, \end{aligned}$$

and

$$\begin{aligned} \Gamma _\chi =\frac{1}{2} \begin{bmatrix} 4\xi _3+\xi ^2_1 &{} \xi _1\xi _2 &{} -\xi _1 \\ \xi _1\xi _2 &{} 2\xi _4+\xi ^2_2 &{} -\xi _2 \\ -\xi _1 &{} -\xi _2 &{} 2 \end{bmatrix}. \end{aligned}$$

by simply calculating, we have \(\Pi _\chi ^T\Pi _\chi =\Theta _\chi ^T\Theta _\chi \). According to (37) and Lemma 3, it is obtained that

$$\begin{aligned} \begin{aligned} {\dot{V}}_{\chi }&\le -\frac{1}{ \vert e_{\chi 1} \vert ^\frac{1}{2}}\uplambda _{\min }(\Lambda _{\chi 1})\Pi _\chi ^T\Pi _\chi \\&\le -\frac{1}{ \vert e_{\chi 1} \vert ^\frac{1}{2}}\uplambda _{\min }(\Lambda _{\chi 1})\Theta _\chi ^T\Theta _\chi . \end{aligned} \end{aligned}$$
(39)

Meanwhile, by virtue of Lemma 3, we get from (38)

$$\begin{aligned} \begin{aligned} \Theta _\chi ^T\Theta _\chi&\ge \frac{\Theta _\chi ^T\Gamma _\chi \Theta _\chi }{\uplambda _{\max }(\Gamma _\chi )} \\&\ge \frac{V_{\chi }}{\uplambda _{\max }(\Gamma _\chi )}, \end{aligned} \end{aligned}$$
(40)

and

$$\begin{aligned} \begin{aligned} \uplambda _{\min }(\Gamma _\chi )(\Theta _\chi ^T\Theta _\chi )&\le \Theta _\chi ^T\Gamma _\chi \Theta _\chi \\&\le V_{\chi }, \end{aligned} \end{aligned}$$
(41)

i.e.,

$$\begin{aligned} \begin{aligned} V^\frac{1}{2}_{\chi }&\ge \sqrt{\uplambda _{\min }(\Gamma _\chi )}(\Theta _\chi ^T\Theta _\chi )^\frac{1}{2} \\&\ge \sqrt{\uplambda _{\min }(\Gamma _\chi )} \vert e_{\chi 1} \vert ^\frac{1}{2}. \end{aligned} \end{aligned}$$
(42)

(42) can be further rewritten as

$$\begin{aligned} \begin{aligned} \frac{1}{ \vert e_{\chi 1} \vert ^\frac{1}{2}}&\ge \frac{\sqrt{\uplambda _{\min }(\Gamma _\chi )}}{V^\frac{1}{2}_{\chi }}. \end{aligned} \end{aligned}$$
(43)

Using (39) and (40), one has

$$\begin{aligned} \begin{aligned} {\dot{V}}_{\chi } \le -\frac{1}{ \vert e_{\chi 1} \vert ^\frac{1}{2}}\uplambda _{\min }(\Lambda _{\chi 1})\frac{V_{\chi }}{\uplambda _{\max }(\Gamma _\chi )}. \end{aligned} \end{aligned}$$
(44)

Combining (43) and (44), it is obtained that:

$$\begin{aligned} {\dot{V}}_{\chi } \le -\rho _\chi V^\frac{1}{2}_{\chi }, \end{aligned}$$
(45)

where

$$\begin{aligned} \rho _\chi =\frac{\uplambda _{\min }(\Lambda _{\chi 1})\sqrt{\uplambda _{\min }(\Gamma _\chi )}}{\uplambda _{\max }(\Gamma _\chi )}>0. \end{aligned}$$

By comparing Lemma 1 it follows easily that \(V_{\chi }\) with initial value \(V_{\chi }(0)\), \(e_{\chi 1}\) and \(e_{\chi 2}\) will converge to zero in finite time and the reaching time is given by

$$\begin{aligned} T_\chi \le \frac{2V^\frac{1}{2}_{\chi }(0)}{\rho _\chi }, \end{aligned}$$
(46)

which indicates the \(e_{\chi 1}\) and \(e_{\chi 2}\) will converge to zero in finite time. Then, term \({\hat{d}}_\chi -d_\chi \) in (28) will vanish at \(t\ge T_\chi \). Therefore, (28) can be rewritten as

$$\begin{aligned} \dot{{\bar{V}}}_\chi =-c_\chi E^2_\chi +E_\chi {\tilde{E}}_\chi +s_\chi (-E_\chi -h_\chi s_\chi ). \end{aligned}$$
(47)

According to (16), \({\tilde{E}}_\chi =s_\chi -n_\chi E_\chi \). Thereby, (47) is further derived as

$$\begin{aligned} \begin{aligned} \dot{{\bar{V}}}_\chi =&-c_\chi E^2_\chi +E_\chi (s_\chi -n_\chi E_\chi )-s_\chi E_\chi -h_\chi s^2_\chi \\ =&-c_\chi E^2_\chi -n_\chi E^2_\chi -h_\chi s^2_\chi \\ \le&-\uplambda _\chi {\bar{V}}_\chi , \end{aligned} \end{aligned}$$
(48)

where \(\uplambda _\chi =\min \{2(c_\chi +n_\chi ), 2h_\chi \}\). Note that \(\min \{a,b\}\) means to select the minimum from a and b. Using Lemma 2, we have

$$\begin{aligned} {\bar{V}}_\chi \le {\bar{V}}_\chi (0){\underline{e}}^{-\uplambda _\chi t}, t\ge 0, \end{aligned}$$
(49)

where \({\bar{V}}_\chi (0)\) is the initial value of \({\bar{V}}_\chi \). Obviously, the tracking error \(E_\chi \) will converge to zero asymptotically from (24) and (49).

In the following, we will derive the bound of the attitude transient tracking error in terms of \(L_2\) norm. From the definition of \({\bar{V}}_\chi \) (24)

$$\begin{aligned} \frac{1}{2}E^2_\chi +\frac{1}{2}s^2_\chi \le {\bar{V}}_\chi (0){\underline{e}}^{-\uplambda _\chi t}. \end{aligned}$$
(50)

According to (12), (13), (14) and (16), \(s^2_\chi \) can be expressed by

$$\begin{aligned} s_\chi= & {} n_\chi E_\chi +{\tilde{E}}_\chi \nonumber \\= & {} n_\chi E_\chi +c_\chi E_\chi +{\dot{\chi }}_d-{\dot{\chi }} \nonumber \\= & {} n_\chi E_\chi +c_\chi E_\chi +{\dot{E}}_\chi . \end{aligned}$$
(51)

Substituting (51) into (50), we have

$$\begin{aligned} {\bar{V}}_\chi (0){\underline{e}}^{-\uplambda _\chi t}\ge & {} \frac{1}{2}E^2_\chi +\frac{1}{2}(n_\chi E_\chi +c_\chi E_\chi +{\dot{E}}_\chi )^2 \nonumber \\= & {} \frac{1}{2}E^2_\chi +\frac{1}{2}(n_\chi +c_\chi )^2E^2_\chi +\frac{1}{2}({\dot{E}}_\chi )^2 \nonumber \\{} & {} +(n_\chi +c_\chi )E_\chi {\dot{E}}_\chi . \end{aligned}$$
(52)

Integrating both sides of (52) yields

$$\begin{aligned} \begin{aligned}&\int _{0}^{\infty } {\bar{V}}_\chi (0){\underline{e}}^{-\uplambda _\chi t}\textrm{d}t \ge \int _{0}^{\infty } \left( \left( \frac{1}{2}+\frac{1}{2}(n_\chi +c_\chi )^2\right) E^2_\chi \right. \\&\quad \left. +\frac{1}{2}({\dot{E}}_\chi )^2+(n_\chi +c_\chi )E_\chi {\dot{E}}_\chi \right) \textrm{d}t \\&\quad = \int _{0}^{\infty } \left( \frac{1}{2}+\frac{1}{2}(n_\chi +c_\chi )^2\right) E^2_\chi \textrm{d}t \\&\qquad +\int _{0}^{\infty } (n_\chi +c_\chi )E_\chi {\dot{E}}_\chi \textrm{d}t\\&\qquad +\int _{0}^{\infty } \frac{1}{2}({\dot{E}}_\chi )^2 \textrm{d}t. \end{aligned} \end{aligned}$$
(53)

Note that according to the definition of \(L_2\) norm, the expression of \(\vert \vert E_\chi \vert \vert _2\) is

$$\begin{aligned} \vert \vert E_\chi \vert \vert _2=\sqrt{\int _{0}^{\infty }\vert \vert E_\chi \vert \vert ^2 \textrm{d}t}, \end{aligned}$$
(54)

where \(\vert \vert E_\chi \vert \vert \) is defined as Euclidean norm of \(E_\chi \), given by

$$\begin{aligned} \vert \vert E_\chi \vert \vert =\sqrt{E_\chi E_\chi }. \end{aligned}$$
(55)

Hence, (53) implies

$$\begin{aligned} \begin{aligned} \frac{1}{\uplambda _\chi }{\bar{V}}_\chi (0) \ge&\left( \frac{1}{2}+\frac{1}{2}(n_\chi +c_\chi )^2\right) \vert \vert E_\chi \vert \vert ^2_2 \\&+\frac{1}{2}(n_\chi +c_\chi )(E^2_\chi (\infty )-E^2_\chi (0)) \\&+\int _{0}^{\infty } \frac{1}{2}({\dot{E}}_\chi )^2 \textrm{d}t. \end{aligned} \end{aligned}$$
(56)

From (49), \(E_\chi (\infty )\rightarrow 0\), i.e., \(E^2_\chi (\infty )\rightarrow 0\). If we set all initial states of the quadrotor system to be zero, we have \(\chi (0)={\dot{\chi }}(0)=0\), where \(\chi (0)\) and \({\dot{\chi }}(0)\) denote initial values of \(\chi \) and its derivative, respectively. Therefore, \(E_\chi (0)=\chi _d(0)-\chi (0)=\chi _d(0)\) from (12). Furthermore, (56) can be written as

$$\begin{aligned} \begin{aligned} \frac{1}{\uplambda _\chi }{\bar{V}}_\chi (0) \ge&\left( \frac{1}{2}+\frac{1}{2}(n_\chi +c_\chi )^2\right) \vert \vert E_\chi \vert \vert ^2_2 \\&-\frac{1}{2}(n_\chi +c_\chi )\chi ^2_d(0)+\frac{1}{2}\int _{0}^{\infty }({\dot{E}}_\chi )^2 \textrm{d}t. \end{aligned} \end{aligned}$$
(57)

Next, we will calculate the improper integral \(\int _{0}^{\infty } ({\dot{E}}_\chi )^2 \textrm{d}t\). To derive the convergence of \(\int _{0}^{\infty } ({\dot{E}}_\chi )^2 \textrm{d}t\), we construct an auxiliary equation as

$$\begin{aligned} G_a(E_\chi )=\int _{0}^{\infty } ({\dot{E}}_\chi )^2 \textrm{d}t \int _{0}^{\infty } ({\underline{e}}^{-t})^2 \textrm{d}t. \end{aligned}$$
(58)

Applying Cauchy–Schwarz inequality [43] to (58), we have

$$\begin{aligned} G_a(E_\chi ) \ge \left( \int _{0}^{\infty } {\dot{E}}_\chi {\underline{e}}^{-t} \textrm{d}t\right) ^2, \end{aligned}$$
(59)

Let

$$\begin{aligned} g_1(t) = {\underline{e}}^{-t}, \end{aligned}$$
(60)

and

$$\begin{aligned} g_2(t) = {\dot{E}}_\chi . \end{aligned}$$
(61)

Obviously, \(g_1(t)\) is a monotone function on \([0, \infty )\) and

$$\begin{aligned} \lim _{t \rightarrow \infty } g_1(t) = 0. \end{aligned}$$
(62)

Moreover, \(g_2(t)\) is integrable on [0, c] for all \(c>0\), and the integral function \(G_2(x)=\int _{0}^{\infty } g_2(t)\textrm{d}t\) is bounded on \([0, \infty ]\). Therefore, the improper integral \(\int _{0}^{\infty } {\dot{E}}_\chi {\underline{e}}^{-t} \textrm{d}t\) in (59) is convergent by comparing with Lemma 4. Let \(M_E\) be the convergent value of the improper integral \(\int _{0}^{\infty } {\dot{E}}_\chi {\underline{e}}^{-t} \textrm{d}t\), then we get

$$\begin{aligned} \int _{0}^{\infty } {\dot{E}}_\chi {\underline{e}}^{-t} \textrm{d}t=M_E. \end{aligned}$$
(63)

Combining (58), (59) and (63), the following inequality holds

$$\begin{aligned} \int _{0}^{\infty } ({\dot{E}}_\chi )^2 \textrm{d}t \int _{0}^{\infty } ({\underline{e}}^{-t})^2 \textrm{d}t \ge M^2_E. \end{aligned}$$
(64)

Note that

$$\begin{aligned} \int _{0}^{\infty } ({\underline{e}}^{-t})^2 \textrm{d}t = \frac{1}{2}. \end{aligned}$$
(65)

Substituting (65) into (64), it is obtained that

$$\begin{aligned} \int _{0}^{\infty } ({\dot{E}}_\chi )^2 \textrm{d}t \ge 2M^2_E. \end{aligned}$$
(66)

Considering (66) and (57), it follows that

$$\begin{aligned} \vert \vert E_\chi \vert \vert ^2_2 \le \frac{2{\bar{V}}_\chi (0)+\uplambda _\chi (n_\chi +c_\chi )\chi ^2_d(0)-2\uplambda _\chi M^2_E}{\uplambda _\chi +\uplambda _\chi (n_\chi +c_\chi )^2}. \nonumber \\ \end{aligned}$$
(67)

Thereby, the bound of the transient tracking error \(E_\chi \) in terms of \(L_2\) norm can be obtained by

$$\begin{aligned} \vert \vert E_\chi \vert \vert _2 \le \sqrt{\frac{2{\bar{V}}_\chi (0)+\uplambda _\chi (n_\chi +c_\chi )\chi ^2_d(0)-2\uplambda _\chi M^2_E}{\uplambda _\chi +\uplambda _\chi (n_\chi +c_\chi )^2}}.\nonumber \\ \end{aligned}$$
(68)

In addition, according to (24), \({\bar{V}}_\chi (0)\) is given by

$$\begin{aligned} {\bar{V}}_\chi (0) = \frac{1}{2}E^2_\chi (0)+\frac{1}{2}s^2_\chi (0). \end{aligned}$$
(69)

From (12), we have

$$\begin{aligned} \begin{aligned} E^2_\chi (0) =&(\chi _d(0) - \chi (0))^2 \\ =&\chi ^2_d(0). \end{aligned} \end{aligned}$$
(70)

Using (51) and (70), we get

$$\begin{aligned} \begin{aligned} s^2_\chi (0)&= (n_\chi E_\chi (0)+c_\chi E_\chi (0)+{\dot{E}}_\chi (0))^2 \\&= ((n_\chi +c_\chi )\chi _d(0)+{\dot{\chi }}_d(0))^2 \\&= (n_\chi +c_\chi )^2\chi ^2_d(0)+({\dot{\chi }}_d(0))^2 \\&\quad +2(n_\chi +c_\chi )\chi _d(0){\dot{\chi }}_d(0). \end{aligned} \end{aligned}$$
(71)

Substituting (70) and (71) into (69), \({\bar{V}}_\chi (0)\) is derived as

$$\begin{aligned} \begin{aligned} {\bar{V}}_\chi (0)&= \chi ^2_d(0)+(n_\chi +c_\chi )^2\chi ^2_d(0)+({\dot{\chi }}_d(0))^2 \\&\quad +2(n_\chi +c_\chi )\chi _d(0){\dot{\chi }}_d(0). \end{aligned} \end{aligned}$$
(72)

Combining (68) and (72), we obtain

$$\begin{aligned} \vert \vert E_\chi \vert \vert _2 \le \sqrt{\beta _{\chi 1}+ \beta _{\chi 2}+ \beta _{\chi 3}+ \beta _{\chi 4}}, \end{aligned}$$
(73)

where \(\beta _{\chi i}=\Xi _{\chi i}, i=1, \cdots , 4\).

This completes the proof. \(\square \)

Remark 3

It is worth mentioning that although the signum function is involved in the Lyapunov function candidate, \(V_{\chi }\) in (29) is a continuous function. In the following, we analyze the continuity on the left and right of the point \(e_{\chi 1}=0\) in the signum function.

  1. (i)

    When \(e_{\chi 1}=0\), it is easy to get \(V_{\chi }=e^2_{\chi 1}\);

  2. (ii)

    When \(e_{\chi 1}\rightarrow 0^-\), we obtain \( \vert e_{\chi 1} \vert ^\frac{1}{2}\textrm{sign}(e_{\chi 1})\rightarrow 0^-\). Therefore, \(V_{\chi }\rightarrow {e^2_{\chi 1}}^+\);

  3. (iii)

    When \(e_{\chi 1}\rightarrow 0^+\), we obtain \( \vert e_{\chi 1} \vert ^\frac{1}{2}\textrm{sign}(e_{\chi 1})\rightarrow 0^+\). Therefore, \(V_{\chi }\rightarrow {e^2_{\chi 1}}^-\); Synthesizing (i), (ii) and (iii), it is concluded that (29) is a continuous function.

Remark 4

Note that the generalized Lyapunov theory only requires continuity and not differentiability of \(V_{\chi }\) along the solution trajectories [44, 45]. Moreover, \(e_{\chi 1}\) cannot be stabilized on the set \(\{(e_{\chi 1},e_{\chi 2})\in {\mathbb {R}}^2 \vert e_{\chi 1}=0\}\) \({\setminus } (0, 0)\), since \({\dot{e}}_{\chi 1}=e_{\chi 2}\ne 0\) from the first equation in (11) if only \(e_{\chi 1}=0\). Therefore, the equilibrium point \(e_{\chi 1}=e_{\chi 2}=0\) can be reached in finite time.

Remark 5

The saturation function given by

$$\begin{aligned} y_{\textrm{output}}=\left\{ \begin{array}{ll} c_{\max }, &{} \quad c_{\max } \le x_{\textrm{input}}, \\ x_{\textrm{input}}, &{}\quad c_{\min }< x_{\textrm{input}} < c_{\max }, \\ c_{\min }, &{} \quad x_{\textrm{input}} \le c_{\min }, \end{array} \right. \end{aligned}$$
(74)

where \(x_{\textrm{input}}\) and \(y_{\textrm{output}}\) are the input and output of saturation function, respectively, and \(c_{\max }\) and \(c_{\min }\) are the upper bound and lower bound of saturation function, respectively, can be used to replace signum function in (10) to reduce chattering of the designed observer.

Remark 6

The consideration for the mechanism of the auxiliary equation. In the derivation of the \(L_2\) norm bound of the tracking error, the determination of convergence of the improper integral \(\int _{0}^{\infty } ({\dot{E}}_\chi )^2 \textrm{d}t\) is very important. Firstly, we need to introduce a related function according to the conditions in Lemma 4. Obviously, a potential function is \(g_1(t)={\underline{e}}^{-t}\). Secondly, the relationship between the integral of the product of two functions and the integral of one of them can be found from Cauchy–Schwarz inequality. The above two ideas impel us to obtain the auxiliary equation (58) by repeated verification and trial and error.

Remark 7

The guideline for tuning of control parameters. Overall, the tuning parameters including the observer gains and the controller gains are obtained through trial and error based on tracking results. In the proposed controller, the control gains \(c_\chi \), \(n_\chi \) and \(h_\chi \) are easy to be determined, since the conditions of selection are relaxed. It is found that the values of the gains \(c_\chi \), \(n_\chi \) and \(h_\chi \) have a direct effect on the overshoot, tracking error and its convergence rate, but the effect of \(h_\chi \) is the most obvious in all three channels. It is worth mentioning that the effect of \(c_\chi \), \(n_\chi \) on the above three indexes is very weak in the pitch channel. In the designed observer, the first and third inequalities are relatively simple from the conditions (36). Therefore, we first choose suitable parameters \(\xi _1\) and \(\xi _3\) to satisfy the first inequality, then \(\xi _2\) can be chosen from the third inequality. Finally, \(\xi _4\) can be determined according to the second and fourth inequalities. We find that \(\xi _2\) and \(\xi _3\) have a greater effect on the adaption mechanism of disturbance than \(\xi _1\) and \(\xi _4\). Based on the above analysis and consideration, to obtain the better control parameters, \(h_\chi \), \(\xi _2\) and \(\xi _3\) should be tuned carefully, while \(c_\chi \), \(n_\chi \), \(\xi _1\) and \(\xi _4\) can be tuned roughly.

5 Simulation

The parameters of the quadrotor system are set as follows [46]: \(I_x=0.16\,\textrm{kg}\,\textrm{m}^2\), \(I_y=0.16\,\textrm{kg}\,\textrm{m}^2\), \(I_z=0.32\,\textrm{kg}\,\textrm{m}^2\), \(L=0.4\,\textrm{m}\), \(f=0.05\,\textrm{m}\). The initial attitude angles of the quadrotor are set as \([0\; 0\; 0]~\textrm{rad}\).

The quadrotor is required to track the following reference signals:

$$\begin{aligned} \phi _d= & {} \left\{ \begin{array}{ll} 0.1-\sqrt{0.1^2(1-\frac{t^2}{12^2})}, &{}\quad 0 \le t \le 12, \\ 0.1+\sqrt{0.1^2(1-\frac{(t-16)^2}{4^2})}, &{}\quad 12 < t \le 20, \end{array} \right. \end{aligned}$$
(75)
$$\begin{aligned} \theta _d= & {} 0.1\cos (\frac{\pi }{3}t+\frac{\pi }{4})+0.2\sin (0.35t+0.27)+0.2,\nonumber \\ \end{aligned}$$
(76)
$$\begin{aligned} \phi _d= & {} \left\{ \begin{array}{ll} 0.012(t-4.5)^2, &{}\quad 0 \le t \le 10, \\ \frac{3.63}{t}, &{}\quad 10 < t \le 20, \end{array} \right. \end{aligned}$$
(77)

where the desired signal in the roll channel is an elliptical trajectory [47]. The external disturbances acting on the quadrotor are set as

$$\begin{aligned} d_\phi= & {} 0.78{\underline{e}}^{-\frac{t}{4}}(\frac{t-1}{2})^2+\tanh (3t+0.35), \end{aligned}$$
(78)
$$\begin{aligned} d_\theta= & {} \left\{ \begin{array}{ll} 0.017(t-5)^3+0.1, &{}\quad 0 \le t \le 8, \\ -0.38(t-20), &{}\quad 8 < t \le 20, \end{array} \right. \end{aligned}$$
(79)
$$\begin{aligned} d_\varphi= & {} \left\{ \begin{array}{ll} 0, &{}\quad 0 \le t \le 3, \\ 1.21(1-\sin (2\pi \frac{t-3}{13})), &{}\quad 3< t \le 16, \\ \frac{650}{(t-2)^2}+0.28, &{}\quad 16 < t \le 20. \end{array} \right. \end{aligned}$$
(80)
Fig. 2
figure 2

The observation results for the given disturbances

Full size image
Fig. 3
figure 3

The observation errors for the given disturbances

Full size image

5.1 Compared with other FTDO

A comparative simulation with the FTDO in [13, 16] is carried out to highlight the observation performance of the proposed FTDO.

The observation results and observation errors for the external disturbances (78)–(80) are shown in Figs. 2 and 3, respectively. It can be seen that the given disturbances can be estimated online by the two observers, which indicates that the compensation for the disturbances can be effectively achieved in the controllers (18). However, the observation result in the roll channel have oscillations at the initial stage when using the FTDO in [13, 16]. Meanwhile, the observation results obtained by the FTDO in [13, 16] have greater overshoot when the disturbance is switched in the pitch and yaw channels.

To quantitatively evaluate the observation performance of the two FTDOs, the indexes including the mean value of absolute value of the error (MAE), the root mean square of the error (RMSE) and the standard deviation of the error (SDE) are used. The indexes MAE and RMSE are used to measure the accuracy of the observation/tracking error, while the index SDE is used to measure the degree of oscillation of the observation/tracking results. Note that the evaluation of index SDE is based on indexes MAE and RMSE. The values of the MAE, RMSE and SDE of the two observers are listed in Table 2. It can be seen that the MAE, RMSE and SDE of the proposed FTDO are smaller than that of the FTDO in [13, 16] in the roll and pitch channels. In the yaw channel, the MAE of the FTDO in [13, 16] is obviously smaller than that of the proposed observer, while the RMSE and SDE are roughly equal.

Table 2 The quantitative evaluations of the observation errors
Full size table
Fig. 4
figure 4

The control inputs with/without the designed FTDO

Full size image
Fig. 5
figure 5

The tracking results for the attitude angles

Full size image

5.2 Compared with pure BSSMC without FTDO

To illustrate the effectiveness of the designed FTDO on the control performance, a comparative simulation between the proposed BSSMC with the FTDO and the pure BSSMC without the FTDO is performed. According to the designed controller (18), the BSSMC scheme without the FTDO can be derived as

$$\begin{aligned} F_\chi= & {} T_\chi (n_\chi (-c_\chi E_\chi +{\tilde{E}}_\chi )+{\dot{\kappa }}_\chi -G_\chi \nonumber \\ {}{} & {} +E_\chi +h_\chi s_\chi ). \end{aligned}$$
(81)

It is worth mentioning that the controller gains \(c_\chi \), \(n_\chi \) and \(h_\chi \) of the two controllers are chosen to be the same.

The control inputs provided by the two controllers are depicted in Fig. 4. The tracking results for the desired attitude signals (75)–(77) are shown in Fig. 5, where we find that the tracking result for the desired yaw attitude trajectory (77) is good. However, an obvious steady-state tracking error is produced when using the pure BSSMC in the roll channel. There is also a small tracking error produced by the pure BSSMC between 8 s and 12 s in the pitch channel. On the contrary, the proposed controller synthesized with the FTDO can ensure that the desired attitude signals are closely followed in the three channels. The corresponding tracking errors of three attitude angles are plotted in Fig. 6.

Fig. 6
figure 6

The tracking errors for the attitude angles

Full size image

In this quantitative evaluation, in addition to the indexes MAE, RMSE and SDE, we also consider the sum of square of control signal (SSC) as a measure of the energy consumed in the tracking of the reference trajectories. It should be noted that all four indexes need to be considered to comprehensively evaluate the advantages of the proposed control scheme. The MAE, RMSE, SDE and SSC are listed in Table 3, where we find that the performance of the BSSMC with the FTDO are better than that of the pure BSSMC in all four indexes in the roll channel. Besides, it is worth noting that the MAE of the BSSMC with the FTDO is smaller than half of that of the pure BSSMC in the case of roughly equal energy consumption in the pitch and yaw channels. These statistical results show that the designed FTDO has a positive effect on the tracking performance of the quadrotor system.

Table 3 The quantitative evaluations of the tracking errors and control inputs using BSSMC with/without the FTDO
Full size table
Fig. 7
figure 7

The output signals of the two controllers

Full size image
Fig. 8
figure 8

The tracking results for the attitude angles

Full size image

5.3 Compared with adaptive finite-time SMC in [11]

The following uncertainties in physical parameter are considered in the proposed control scheme, then a comparative simulation with the controller in [11] is performed under the external disturbances (78)–(80).

$$\begin{aligned} {\bar{I}}_\alpha =80\%I_\alpha , \alpha =x, y,z, \quad {\bar{L}}=90\%L, \quad {\bar{f}}=90\%f.\nonumber \\ \end{aligned}$$
(82)

The outputs of the two controller are shown in Fig. 7. The corresponding tracking results and tracking errors are plotted in Figs. 8 and  9, respectively. It can be observed from Figs. 8 and 9 that the tracking performance of the proposed controller is slightly better than that of the controller in [11] in the roll channel, while a similar tracking performance is obtained by the two controller in the pitch and yaw channels.

Fig. 9
figure 9

The tracking errors for the attitude angles

Full size image

The MAE, RMSE, SDE and SSC of the two control algorithms are given in Table 4. In the roll channel, the values of the four indexes of the proposed controller are smaller than that of the controller in [11], especially the energy required by the proposed controller is much less than that of the controller in [11]. In the pitch channel, much more energy is consumed by the control scheme in [11], but it is only slightly better than the proposed controller in indexes RMSE and SDE. In the yaw channel, the comprehensive performance of the two controllers is roughly equal by evaluating the four indexes.

Table 4 The quantitative evaluations of the tracking errors and control inputs using the proposed controller and the controller in [11]
Full size table

5.4 Compared with LQR in [6]

Moreover, we consider the comparison between the proposed controller and LQR in terms of the tracking performance for the reference trajectories (75)–(77) in the presence of the external disturbances (78)–(80) and the white Gaussian noise [48]. Note that a weak noise and a strong noise are applied to the feedback channel of the closed-loop system respectively, which are subject to \(X~\sim ~\aleph (0, 0.000001)\) and \(X~\sim ~\aleph (0, 0.00002)\), where X denotes noise signal, \(\aleph \) denotes Gaussian distribution, 0 is the mean of the distribution, 0.000001 and 0.00002 are the covariance of the distribution.

The control inputs, tracking results and tracking errors for the three desired attitude angles under the noise are depicted in Figs. 10, 11 and 12, respectively. It should be noted that in order to fairly compare the tracking performance of the two control algorithms, their SSCs should be as close as possible. In this sense, a saturation operator is applied to the roll and pitch controllers of the quadrotor. When there is a weak noise in the feedback channel, the tracking of reference trajectories (75)–(77) can be achieved by both controllers under the defined disturbances (78)–(80). However, the tracking performance in the roll channel decreases more significantly as the noise increases. Meanwhile, the tracking error in the pitch channel increases slightly when LQR is applied to the quadrotor from Fig. 12.

Fig. 10
figure 10

The control inputs of the two controllers under the noise

Full size image
Fig. 11
figure 11

The tracking results of the two controllers under the noise

Full size image
Fig. 12
figure 12

The tracking errors of the two controllers under the noise

Full size image

According to the above results, the MAE, RMSE, SDE and SSC under the weak and strong noises are shown in Tables 5 and 6, respectively. When the noise increases, these indexes become worse, especially the value of the SSC increases significantly. This means that the quadrotor system needs to receive more energy to maintain a stable tracking performance. It is worth pointing out that the tracking performance of the roll channel degrades fastest when the strong noise is applied to the quadrotor system. Overall, the proposed controller outperforms LQR in the terms of comprehensive performance from the comparative results in Figs. 10, 11 and 12 and the statistical results in Tables 5 and 6.

Table 5 The quantitative evaluations of the tracking errors and control signals using the proposed controller and LQR under the small noise
Full size table
Table 6 The quantitative evaluations of the tracking errors and control signals using the proposed controller and LQR under the strong noise
Full size table

6 Conclusion

This article investigates the robust attitude trajectory tracking problem of a quadrotor drone in the presence of external disturbance. A nonlinear disturbance observer with finite-time convergence is proposed to estimate external disturbance. Then, a backstepping sliding mode control strategy based on the designed disturbance observer is proposed to guarantee the tracking errors of the three attitude angles of quadrotor to converge to zero asymptotically. In addition, the bound of the attitude transient tracking error in terms of \(L_2\) norm is derived by constructing an auxiliary equation. The comparative simulations are carried out to verify the effectiveness of the proposed control scheme and several statistical indexes are used to quantitatively evaluate the performance in terms of observation error, tracking error and control signal. However, there exist two limitations in the proposed method: (1) the bound of disturbance’s derivative needs to be known in the stability analysis of closed-loop systems and (2) the chattering phenomenon could occur in the designed disturbance observer. In future work, we will focus on the estimation of bound of disturbance’s derivative and the suppress of chattering phenomenon.