Keywords

3.1 Introduction

There are a lot of problems in the real world that involve a set of potential solutions, from which the one with the best quality is termed as the optimal solution, and the method of searching for such a solution is known as mathematical optimization. The quality of solutions is represented by the ability to maximize or minimize a certain function, called the objective function, while the pool of possible solutions that can satisfy the required objective is called the search space. One can traverse all possible solutions, examine the result of the objective function in each case, and select the best solution. However, many real problems are intractable using this exhaustive search strategy. In these problems, the search space expands exponentially with the input size, and exact optimization algorithms are impractical. The historical alternative in such situations is to resort to heuristics, similar to simple rules of thumb that humans would utilize in a search process. Heuristic algorithms implement such heuristics to explore the otherwise prohibitively large search space, but they do not guarantee finding the actual optimal solution, since not all areas of the space are examined. However, a close solution to the optimal is returned, which is “good enough” for the problem at hand.

The next step would be to generalize those heuristics in higher-level algorithmic frameworks that are problem independent and that provide strategies to develop heuristic optimization algorithms. The latter are known as metaheuristics [1]. Early metaheuristics were based on the concept of evolution, where the best solutions among a set of candidate solutions are selected in successive iterations, and new solution are generated by applying genetic operators such as crossover and mutation to the parent solutions.

Similar to and including evolutionary algorithms, many metaheuristics were based on a metaphor, inspired by some physical or biological processes. Many recent metaheuristics mimic the biological swarms in performing their activities, in particular, the important tasks of foraging, preying, and migration. Popular examples of developed metaheuristic algorithms in this category include particle swarm optimization (PSO) [2], which is inspired by the movement of swarms of birds or fishes; ant colony optimization (ACO) [3, 4], which is inspired by the foraging behavior of ants, where ants looking for food sources in parallel employ the concept of pheromone to indicate the quality of the found solutions; and artificial bee colony (ABC) algorithm, inspired by the intelligent foraging behavior of honeybees [5, 6].

The idea of deriving metaheuristics from natural-based metaphors proved so appealing that much more of such algorithms have been and continue to be developed. A few more examples include cuckoo search (CS) [7, 8], biogeography-based optimization (BBO) [9], animal migration optimization (AMO) [10], chicken swarm optimization (CSO) [11], grey wolf optimization (GWO) [12], krill herd (KH) [13], and monarch butterfly optimization (MBO) [14], which is inspired by the migration behavior of monarch butterfly. The bat algorithm (BA) [15] also belongs to the metaheuristics that are based on animal behavior, inspired by the echolocation behavior of bats in nature. On the other hand, several metaphor-based metaheuristics are derived from physical phenomena such as simulated annealing (SA) [16] which is inspired by the annealing process of a crystalline solid.

The aforementioned metaheuristics are classified as stochastic optimization techniques. To avoid searching the whole solution space, they include a randomization component to explore new solution areas. Though these random operators are essential, they can introduce two types of problems. First, if the randomization is too strong, the metaheuristic algorithm might keep moving between candidate solutions, loosely examining each localized region and failing to exploit promising solutions and find the best solution. Second, if the search process is too localized, exploiting the first found good solutions very well but failing to explore more regions, the algorithm might indeed miss the real optimal solution (called the global optimum) and trap into some local optima.

The perfect balance between exploitation and exploration is essential to all metaheuristics. In fact, it is whether and how this balance is achieved that distinguishes most metaheuristics from each other and forms a source of new attempts to improve existing algorithms, possibly by hybridizing ideas from more than one metaheuristic strategy [18].

In this paper, we follow this path and introduce a new hybrid metaheuristic that augments the popular ABC algorithm with a feature from the MBO algorithm so as to make the correct balance between randomization of local search and global search.

The rest of this article is organized as follows. Section 3.2 describes the proposed HAM method, while Sect. 3.3 explains the setup of experimental evaluation. Section 3.4 presents and discusses the obtained results, and finally Sect. 3.5 concludes the paper.

3.2 Proposed HAM Algorithm

This section introduces the HAM algorithm, which is based on the standard artificial bee colony algorithm [5, 6] and monarch butterfly optimization algorithm [14]. The ABC algorithm was proposed by Karaboga for optimizing numerical problems in 2005, and several developments were based on this algorithm [19,20,21]. The MBO algorithm was proposed by Gai-Ge, Suash, and Zhihua in 2015. It is a new nature-inspired metaheuristic optimization algorithm that works by simplifying and idealizing the migration behavior of monarch butterfly individuals between two distinct lands, namely, northern USA (Land1) and southern Canada (Land2). For more details about the two algorithms, please refer to [5, 14].

The exploitation and exploration concepts are undoubtedly considered exceedingly important characteristics in metaheuristic algorithms. In fact, the best metaheuristic algorithm is the one that strikes a balance between these two mechanisms, as a consequence of enhancing the solving of (low- and high-dimensional) optimization problems. The mechanism of exploitation is based on current knowledge to seek better solutions, while the mechanism of exploration is based on searching the entire area of the problem for an optimal solution.

Particularly, by analyzing the standard MBO algorithm, it could be noticed it has an effective capability of exploring the search space; nevertheless, it does possess a weak ability to exploit the search space due to the intermittent use of Levy flight by the updating operators which in turn drives the algorithm to large random steps or moves. On the other hand, the ABC algorithm has the capability of exploring the search space, as well as it has a decent capability in finding the local optima through the employee and onlooker phases. So these two phases in ABC algorithm classed as a local search process. The ABC algorithm is mostly dependent on selecting the solutions that improve the local search. While the global search in the ABC algorithm is implemented through the scout phase, which leads to reducing the speed convergence during the search process.

The main idea of the hybrid proposed algorithm is based on two ameliorations: firstly, the main objective in modifying the MBO algorithm improves the exploitation versus exploration balance, by modifying the butterfly adjusting operator in order to increase the search diversity and balance the insufficiency of ABC algorithm in global search efficacy. Algorithm 1 shows the amended version of the operator. The second enhancement is done by replacing the modified butterfly adjusting operator of MBO with the employee phase of ABC algorithm. The enhanced operator is called the “employee bee adjusting operator,” and the resulting modified phase is called the “employee bee adjusting phase.”

The main objective of the employee bee adjusting phase is to update all the solutions in the bee population, whereas each solution is a D-dimensional vector. While the initialization phase is used to define all the variables that would be defined in the standard ABC algorithm and assign them suitable values. Although the HAM algorithm is essentially founded on all the parameters of the original ABC algorithm, it uses three new control variables: limit1, limit2, and the maximum walk step variable S max; these three variables are used in the employee bee adjusting phase.

Algorithm 1 : Employee bee adjusting phase

Begin For i = 1 to SN do Calculate the walk step dx by Equation (1); Calculate the weighting factor by Equation (2); For j = 1 to D do If rand ≥ limit1 then Generate the j th element by Equation (3); Else Randomly select a food Source (r) by Equation (4); If rand < limit2 then Generate the j th element by Equation (5); Else Generate the j th element by Equation (6); If rand < BAR then Generate the j th element by Equation (7); End if End if End if End for j Evaluate the fitness value of the candidate solution x i . Apply a greedy selection process between x i and x best If solution x i does not improve, trial i = trial i + 1, Otherwise trial i = 0. End for i End

In Algorithm 1 above, each employee bee of the employee bee adjusting phase has been assigned to an independent food source whereby it generates a new solution either by a new mutation operators or through Levy flight. The mutation operators are based on the two control variables: limit1 and limit2. The focal point of limt1 and limit2 is to fine-tune the exportation versus exploitation through improving the global search diversity. As shown in Algorithm 1, the first step is to use the Levy flight to compute a walking step “dx” for the i th bee by Eq. 3.1, and then it uses the Eq. 3.2 to compute the weighting factor “∝,” where t is the current generation and S max represents the max walk step that a bee individual can move in one step. Then, the Algorithm 1 uses Eq. 3.3 to update the solution element, when (rand ≥ limit1), for each element j of the D dimensions.

$$ {dx}_k=\mathrm{levy}\left({x}_j^t\right) $$
(3.1)
$$ \propto \kern0.5em ={S}_{\mathrm{max}}/{t}^2 $$
(3.2)
$$ {x}_{i,j}^{t+1}={x}_{\mathrm{best},j}^t $$
(3.3)

\( {x}_{i,j}^{t+1} \) represents the location of the solution i, the j th element of solution x i at generation t + 1, while \( {x}_{\mathrm{best},j}^t \) represents the best location among the food sources, the j th element of x best at generation t, so far with respect to the i th bee. On the other hand, if (rand < limit1) then another set of updates are performed. First, a random food source (equivalent to a random solution or bee) is selected from the current population using Eq. 3.4. Then, depending on whether a randomly generated value is smaller than limit2, Eq. 3.5 is used to update the solution elements, as follows:

$$ r=\mathrm{round}\left(\left({\mathrm{SN}}^{\ast}\operatorname{rand}\right)+0.5\right)\kern10em $$
(3.4)
$$ {x}_{i,j}^{t+1}={x}_{r,j}^t+{0.5}^{\ast }{\operatorname{rand}}^{\ast}\left({x}_{\mathrm{worst},j}^t-{x}_{r2,j}^t-{x}_{\mathrm{best},j}^t\right)\kern5.25em $$
(3.5)

\( {x}_{i,j}^{t+1} \) represents the location of the solution i, the j th element of solution x i at generation t + 1. \( {x}_{\mathrm{best},j}^t \) represents the best location among the food sources, the j th element of x best at generation t. And \( {x}_{\mathrm{worst},j}^t \) signifies the worst location among the food sources, the j th element of x worst at generation t. \( {x}_{r,j}^t \) represents the location of the solution r calculated by Eq. 3.4, the j th element of x r at generation t. The t in Eq. 3.5 is the current generation number.

On the other hand, if the randomly generated value was bigger than limit2, the solution elements are updated by Eq. 3.6, where \( {x}_{i,j}^{t+1} \) is the j th element of solution x i at generation t + 1, which represents the location of the solution i; \( {x}_{\mathrm{best},j}^t \) is the j th element of x best at generation t, which represents the best location among the food sources so far; \( {x}_{\mathrm{worst},j}^t \) is the j th element of x worst at generation t, which represents the worst location among the food sources so far, while \( {x}_{r,j}^t \) is the j th element of x r at generation t, which represents the location of the solution r calculated by Eq. 3.4.

$$ {x}_{i,j}^{t+1}={x}_{r,j}^t+{0.5}^{\ast }{\operatorname{rand}}^{\ast}\left({x}_{\mathrm{best},j}^t-{x}_{r3,j}^t-{x}_{\mathrm{worst},j}^t\right) $$
(3.6)

The HAM algorithm also used the Levy flight function but with a smaller probability of execution to reduce its impact on the exploitation process. Assuming the execution path has already passed the tests of limit1 and limit2 control variables, then the algorithm performs another random check against the BAR parameter, right after the update by Eq. 3.6 to further change the value of \( {x}_{i,j}^{t+1} \) occasionally by the amount ∝ × (dx k  − 0.5), as per Eq. 3.7.

$$ {x}_{i,j}^{t+1}={x}_{i,j}^{t+1}+\propto \times \left({dx}_k-0.5\right) $$
(3.7)

Finally, the employee bee adjusting phase tests the limits of the newly created solution to make sure it is within the permissible limits for the optimization problem, and after that it evaluates the fitness value that is produced by the new solution and uses the greedy selection process between the best and the new solutions to select the better one. In the case that the resulted solutions are not improved, then a trial counter is increased by one. The HAM algorithm relies on the implementation of the original ABC algorithm without any change, which can be found in [22].

3.3 Experimental Evaluation

In this section, we lay out the experimental setup through which we have evaluated the proposed algorithm, HAM.

3.3.1 General Setup

3.3.1.1 Hardware and Software Implementation

All the experiments have been conducted on a laptop with an Intel Core i5 2.4 GHz processor and RAM 8 GB. The proposed HAM algorithm is a software implementation based on the implementation of ABC and MBO. The software implementation tests were carried out in MATLAB R2009b (V7.9.0.529) on a windows 7 box.

3.3.1.2 Parameters

For fair comparison purposes, we set all common control parameters to the same values. This includes mounting the dimensionality of search space to 10 and the population size to 50 for all methods. And here below, we present the parameters for all methods in this work.

The control variables that have been set across all experiments of HAM algorithm are as follows: limit1 is set to 0.8, limit2 is set to 0.5, migration period Per i is set to 1.2, migration ratio p is set to 0.4167, and finally S max is set to 1.0. Moreover, the ABC algorithm has had the following parameter settings: limit was set to 100, and the colony size was set to 100, employed bees = 50 and onlooker bees = 50. Finally, the variables for MBO algorithm were fixed as follows: the butterfly adjusting rate BAR is set to 0.4167, max step S max is set to 1, the migration period Per i  = 1.2, and the migration ratio p = 0.4167, as per the setup in the original work of MBO [14].

3.3.2 Benchmark Function

This paper uses a set of eight test functions for global numerical optimization. These functions are listed in Table 3.1 alongside their respective equations and properties.

Table 3.1 Benchmark functions used for evaluating the proposed algorithm
Full size table

3.4 Results

Table 3.2 lists the optimization results when applying the eight optimization test functions to ABC, MBO, and our HAM methods. The listed values are the optimal values of the objective function achieved by each algorithm after iterating over 50 generations. The mean values in the table are averaged over 20 runs (each run constitutes 50 iterations) and listed along the standard deviation. The min values, however, are the best results achieved by each algorithm at all. By the “best result,” we mean the closest result to the actual optimal value of the function.

Table 3.2 The min, mean, and standard deviation of test function values found by ABC, MBO, and the proposed HAM algorithms, averaged over 20 experimental runs. The dimensions set to 10
Full size table

It is evident from Table 3.2 that the HAM algorithm can reach a better optimum on average, at least with respect to the set of benchmark functions used in the experiments (HAM has better average results in the case of seven out of eight test functions). For ease of recognition, the best average result is marked with bold font and shaded in a gray cell. The min values are bold font to identify the absolute best minimum achieved for each function. Note that this value is meaningful because it happened that the minimum achieved values by the algorithms for the selected benchmark functions are closest to the real optimum. With respect to the set of test functions used in our evaluations, HAM could achieve the best result in six out of eight cases.

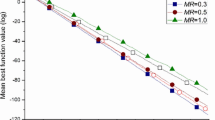
On another perspective, we also graphed the optimization process of each algorithm (for each benchmark function) as the value of the so-far best solution versus the current iteration, which shows the search path in terms of selected best solution per iteration. The curve of this kind is expected to decline overall at a slope that reflects the convergence speed of the algorithm (there is no degradation during the process of any included metaheuristic algorithm, as the best solution is either improved or kept unchanged at all iterations). Therefore, these graphs can be called the convergence plots of the algorithms. Because of the large number of plots, we include hereby representative samples of the convergence plots in Fig. 3.1, which compares the convergence of HAM with the two most related metaheuristic techniques: ABC and MBO.

Fig. 3.1
figure 1figure 1

Performance of ABC, MBO, and HAM algorithms for (a) F1, (b) F2, (c) F3, and (d) F4 benchmark functions

Full size image

Figures 3.1a–d shows that the HAM algorithm enjoys not only a superior overall performance in terms of the quality of the found optimal solution but also a faster convergence especially in the earlier stages. Although the starting points of the algorithms are close to each other in the plots of the four testing functions in the figure, the proposed HAM method does not trap into a quick local optimum, unlike the original ABC and MBO algorithms, for example.

3.5 Conclusion

The proposed algorithm in the article, HAM, is founded on two metaheuristics algorithms, which are the artificial bee colony and monarch butterfly optimization algorithms. It is worth to mention that HAM is the first novelty hybrid algorithm born of these two algorithms. In addition HAM is composite of three phases: employee bee adjusting phase, onlooker phase, and scout phase. The initial phase is a modified version of the adjusting operator in MBO algorithm, while the second and last (onlooker and scout) phases are identical to those original equivalents found in ABC algorithm.

The crux of HAM development aims at finding a higher convergence speed and best optimal solutions than its predecessors by enhancing diversification of MBO that has been used to augment good intensification ability of ABC. In future works, we intend to utilize HAM algorithm as a neural network trainer as well as to extend the method for solving multi-objective optimization problems to serve many other various purposes.