Abstract
We present a unified framework for obtaining black-box constructions of Universal Composable (UC) protocol in trusted setup models. Our result is analogous to the unified framework of Lin, Pass, and Venkitasubramaniam [STOC’09, Asiacrypt’12] that, however, only yields non-black-box constructions of UC protocols. Our unified framework shows that to obtain black-box constructions of UC protocols, it suffices to implement a special purpose commitment scheme that is, in particular, concurrently extractable using a given trusted setup. Using our framework, we improve black-box constructions in the common reference string and tamper-proof hardware token models by weakening the underlying computational and setup assumptions.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Combined Setup
- Trusted Setup Model
- Universal Composability (UC)
- Commitment Scheme
- Concurrently Extractable
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Secure multi-party computation (MPC) protocols enable a set of m mutually distrustful parties with private inputs \(x_1, \cdots , x_m\) to jointly compute a function f, learn the output \(f(x_1, \cdots , x_m)\) and nothing else. In the classical stand-alone setting, security of MPC protocols is analyzed where a single instance of a protocol runs in isolation. However, such analysis falls short of guaranteeing security in more realistic, concurrent, settings, where multiple instances of different protocols co-exist and are subject to coordinated attacks. To address this, Canetti formulated the Universally Composable (UC) framework [1] for reasoning about the security of protocols in arbitrary execution environments that dynamically interact with the analyzed protocol. The UC framework formulates, so far, the most stringent and realistic model of protocol execution, and provides a strong composability property —known as the universal composition theorem— that protocols shown secure in the UC framework remain secure when executed concurrently within arbitrary larger complex system.
Unfortunately, these strong properties come at a price: Many natural functionalities cannot be realized with UC security in the plain model, where the only setup provided is authenticated communication channels; some additional trusted setup is necessary [2, 3]. Following Canetti and Fischlin [2], Canetti et al. [4] demonstrated the feasibility of UC-secure protocols realizing general functionalities, in the Common Reference String (CRS) Model, where a trusted entity samples a single CRS from a prescribed distribution that can be referenced to by all executions of the designed protocol. Since its conception, a long line of work have focused on designing UC secure protocols under various trusted setups, from CRS, to public key infrastructure, to tamper-proof hardware tokens, and many others (see for example [5,6,7,8,9,10,11]), and led to a comprehensive understanding on what are the minimal trusted setups and computational assumptions needed for achieving UC security.
Black-box vs Non-black-box Construction: A basic distinction between cryptographic constructions is whether they make only black-box use of the underlying primitives or not. Black-box constructions only call the designated input/output interface of the underlying primitives, whereas non-black-box constructions depend on specifics of the code implementing the primitives. Typically, non-black-box constructions are more versatile for demonstrating feasibility of cryptographic tasks and minimizing underlying primitives. However, black-box constructions are more modular and tend to be more efficient. A natural theoretical direction seeks to narrow the gap between what is achieved via non-black-box and black-box constructions for important cryptographic tasks, under minimal assumptions (as done in, for example [12,13,14,15,16,17,18,19,20,21,22]), which leads to new constructions, techniques, and understanding.
For the task of achieving UC security with trusted setups, there still remain significant gaps between what is achievable via non-black-box and black-box constructions. First, generic approaches for achieving UC-security have been developed using non-black-box techniques. Lin et al. [11, 23] presented a unified framework for developing UC-secure protocols in general trusted setup models. In particular, they identified a (simple) “minimal primitive” called UC-puzzles that give non-black-box constructions of UC-secure protocols for general functionalities. At a high-level this primitive facilitates concurrent simulation, which is a necessary condition to achieve UC-security. Moreover, an important consequence of the unified framework was the weakening of trusted infrastructure and other assumptions in many models. It also significantly reduced the complexity of designing UC-secure protocols, as UC puzzles are often easy (if not trivial) to attain using trusted setups. Thus a natural question we ask in this work is,
Can we have a unified framework for developing
black-box constructions of UC-secure protocols, under general setup?
Thus far, no generic approach using black-box techniques exist, and, in fact, to the best of our knowledge, there are only a few black-box constructions [21, 22, 24] of UC-secure protocols for specific trusted-setup, namely the CRS and tamper-proof hardware tokens models, which fall short in the following ways:
-
In the CRS model, the state-of-the-art non-black-box constructions assume only the existence of semi-honest secure Oblivious Transfer (OT) protocols, whereas black-box constructions are based on either the existence of enhanced trapdoor permutations [4], or specific assumptions, such as, Strong RSA, DDH, DLIN [25,26,27]. All these assumption imply CCA encryption and semi-honest OT. This raises the question:
Can we have black-box constructions of UC-secure protocols in the CRS model, from weaker assumptions?
Hazay and Venkitasubramaniam [21] gave partial answer to this question in the stronger “local CRS model”. They gave black-box construction of UC-protocols from public-key encryption and semi-honest OT; however, every execution of their protocols needs to rely on an independently sampled local CRS. In contrast, the CRS model as defined originally [4] considers a single CRS that is shared by all concurrent executions. Clearly, having a trusted entity sampling a single CRS once and for all is a much more realistic setup than sampling a CRS for every protocol execution.
-
In the tamper-proof hardware token model, Footnote 1 unconditionally UC-secure protocols exist using stateful tokens [28, 29]. When relying on much weaker (and more realistic) stateless tokens, computational assumptions are necessary [28]. Following a body of works [28, 30,31,32,33,34], Hazay et al. [22] showed that the minimal assumption of one-way functions suffices. However, all UC-protocols using stateless tokens require each instance of protocol execution to create a token that has specific information of the instance (namely, the session id) hardwired inside. This means parties must have the capability to create customized tokens. In this work, we consider a even weaker model of tokens, namely stateless and instance-independent tokens, which runs codes sampled from a universal distribution, independent of protocol instances. We believe that this model is more realistic as tokens with instance-independent codes may be obtained and distributed ahead of protocol execution, and can potentially be reused across different execution instances. We ask,
Can we have UC-secure protocols using stateless and instance-independent tokens?
1.1 Our Result
In this work, we present a unified framework for obtaining black-box construction of UC-secure protocols under general trusted setup, assuming semi-honest OT. At a high-level, our framework reduces the task of achieving UC-security to that of constructing a UC-special-purpose commitment scheme \(\mathsf{CECom} \) with the following properties.
-
\(\mathsf{CECom} \) is straight-line concurrently extractable w.r.t. opening, that is, there is a straight-line extraction strategy E that can extract values from any concurrent committer \(C^*\) with the guarantee that \(C^*\) cannot successfully open to any values different from what E extracts.
-
\(\mathsf{CECom} \) is hiding against resetting receivers.
We observe that comparing with UC commitments, UC-special-purpose commitments are weaker in the sense that it does not guarantee simulation-extractability nor equivocation, but stronger in the sense that they are resettably hiding.
Given such a commitment scheme \(\mathsf{CECom} \) under trusted setup \(\mathcal {T}\), our unified framework shows how to construct general UC-secure protocols that make use of 4 independent instances of \(\mathcal {T}\) and black-box use of \(\mathsf{CECom} \). We model the 4 independent instances of \(\mathcal {T}\) as a single trusted-setup:
-
The quadruple-\(\mathcal {T}\) trusted setup \(\mathsf{4}\mathcal {T}\) simply runs 4 independent instances of \(\mathcal {T}\) internally, and make them available to all parties.
In fact, for many specific trusted setups, 4 independent instances can be emulated using just a single instance. For example, in the CRS model, 4 reference strings can be concatenated into one. In the tamper proof token model, operations related to tokens are captured by an ideal functionality that allows parties to create an arbitrary number of tokens, transfer them, and execute them. One single such ideal functionality provides the same functionality as 4 of them. In these cases, our unified framework shows that to obtain black-box UC-secure protocols, it suffices to focus on constructing UC-special-purpose commitment schemes.
Theorem 1 (Main Theorem, Informal)
Let \(\mathcal {T}\) be any trusted-setup. Assume the existence of a UC-special-purpose commitment scheme \(\mathsf{CECom} \) under \(\mathcal {T}\), and a constant-round semi-honest oblivious transfer protocol. Then, for every well-formed functionality \(\mathcal {F}\), there is a black-box construction of a protocol \(\pi \) that UC-realizes \(\mathcal {F}\) in the \(\mathsf{4}\mathcal {T}\)-trusted setup model. Moreover, if \(\mathsf{CECom} \) has \(r_{\textsc {cec}}\) rounds, then \(\pi \) has \(O(r_{\textsc {cec}})\) rounds.
We remark that we rely on our setup in an “instance independent” way. In particular, in the CRS model, four references strings are sampled at the beginning and all instances rely on the same reference strings. Whereas in the token model, our result implies that we require tokens with “instance-independent” code. Technically, we follow the Joint Universal Composition (JUC) paradigm [1] and show that our protocol \(\pi \) when executed concurrently implement directly the multi-session extension \(\hat{F}\) of the functionality \(\mathcal {F}\), using a single instance of \(\mathsf{4}\mathcal {T}\).
 The unified framework (dubbed as the LPV framework) of [11, 23] formulated the notion of UC puzzles and showed how to use them to obtain non-black-box constructions of UC-protocols. Roughly speaking, UC puzzle is a protocol between a sender and a receiver with two properties: (i) soundness guarantees that the puzzle is hard to solve for an honest receiver, yet (ii) concurrent simulation guarantees that the view of a concurrent sender can be simulated while obtaining all puzzle solutions. From there, the LPV framework shows how to use the UC puzzles to construct protocols that can be concurrently simulated by following the Feige-Shamir paradigm with the puzzle solutions as trapdoors.
The unified framework (dubbed as the LPV framework) of [11, 23] formulated the notion of UC puzzles and showed how to use them to obtain non-black-box constructions of UC-protocols. Roughly speaking, UC puzzle is a protocol between a sender and a receiver with two properties: (i) soundness guarantees that the puzzle is hard to solve for an honest receiver, yet (ii) concurrent simulation guarantees that the view of a concurrent sender can be simulated while obtaining all puzzle solutions. From there, the LPV framework shows how to use the UC puzzles to construct protocols that can be concurrently simulated by following the Feige-Shamir paradigm with the puzzle solutions as trapdoors.
In comparison, our unified framework requires constructing UC-special purpose commitment, which captures the capability of concurrent extraction. While it is known that using non-black-box techniques concurrent extraction can be achieved through concurrent simulation, as done implicitly in the LPV framework, these techniques often require the use of zero-knowledge or witness indistinguishable proofs, and are not suitable for black-box constructions. This is why in our framework, we directly require a concurrently extractable commitment scheme to start with.
Next, using the generic framework, we improve black-box construction of UC secure protocols in the CRS and tamper-proof hardware token model.
 In this work, we follow the JUC framework [1] for modeling concurrent security of protocols. In particular, we show that for every functionality \(\mathcal {F}\), the concurrent execution of our protocol \(\pi _{\mathcal {F}}\) that implements \(\mathcal {F}\) securely computes the multi-session extension of \(\mathcal {F}\). This means that all instances of execution of \(\pi _{\mathcal {F}}\) refer to the same trusted setup, for example, the same CRS. This model should be compared with the Global UC (GUC) framework of [7], where a trusted setup is not only available to all protocol instances, but also to the environment. This means the trusted setup can be shared between arbitrary, even potentially unknown, protocols. Therefore, protocols secure in the GUC framework provide stronger composition guarantees. However, this comes at a price, in particular, it is known that general GUC protocols in the CRS model is infeasible. In the tamper-proof hardware model, the protocols by [22] are secure in the GUC framework, but their tokens are instance-dependent.
In this work, we follow the JUC framework [1] for modeling concurrent security of protocols. In particular, we show that for every functionality \(\mathcal {F}\), the concurrent execution of our protocol \(\pi _{\mathcal {F}}\) that implements \(\mathcal {F}\) securely computes the multi-session extension of \(\mathcal {F}\). This means that all instances of execution of \(\pi _{\mathcal {F}}\) refer to the same trusted setup, for example, the same CRS. This model should be compared with the Global UC (GUC) framework of [7], where a trusted setup is not only available to all protocol instances, but also to the environment. This means the trusted setup can be shared between arbitrary, even potentially unknown, protocols. Therefore, protocols secure in the GUC framework provide stronger composition guarantees. However, this comes at a price, in particular, it is known that general GUC protocols in the CRS model is infeasible. In the tamper-proof hardware model, the protocols by [22] are secure in the GUC framework, but their tokens are instance-dependent.
Black-box UC Protocols in the CRS Model. In the CRS model, UC-special purpose commitment scheme is trivial to construct, simply use any public key encryption scheme. (In fact, even public key encryption with an interactive encryption phase suffices.) Thus, plugging into our unified framework, we immediately obtain black-box UC-protocols in the CRS model, from public key encryption and semi-honest OT.
Theorem 2
Assuming the existence of a public-key encryption scheme and a semi-honest oblivious-transfer protocol, there exists a fully black-box construction of UC-secure protocols for general functionalities in the CRS model. Moreover, if both underlying primitives have constant rounds, then the UC-secure protocols also have constant rounds.
Previous black-box constructions in the CRS model either relies on the existence of a trapdoor permutation [4], or specific algebraic or number theoretic assumptions, such as, DDH [27], Strong RSA [26], and DLin [26]. Note that all these assumptions imply CCA encryption, which is used in all previous constructions. In comparison, our construction only relies on a public key encryption scheme and a semi-honest OT protocol, which are not known to imply CCA encryption. Instead, in our construction, we use the public key encryption scheme to implement an interactive CCA encryption scheme, where the encryption phase is interactive (while the key generation and decryption procedures remain the same). Our notion of interactive CCA encryption should be compared with that of Dodis and Fiore [35]. Our notion is stronger in the sense that the receiver in the interactive encryption phase does not need to know the secret key, whereas in the notion by [35], only receivers knowing the secret key can “receive” the encryption. In particular, their notion is insufficient for constructing UC-secure protocols in the CRS model.
On the other hand, comparing with non-black-box constructions, the best non-black-box construction assumes only the existence of semi-honest OT [11]. We thus narrow the gap in assumptions between non-black-box and black-box constructions, and leaving open the question whether public key encryption can be eliminated for black-box constructions.
Since the common reference string used in our protocols is simply the public keys of the encryption scheme, we obtain as a corollary UC secure protocols in the Uniform Reference String (URS) model assuming public key encryptions with pseudorandom public key (also referred to as dense public-key cryptosystems [36]), which also implies semi-honest OT [37].
Corollary 1
Assuming the existence of an public-key encryption scheme with pseudorandom public keys, there exists a fully black-box construction of UC-secure protocols for general functionalities in the URS model. Moreover, if both underlying primitives have constant rounds, then the UC-secure protocols also have constant rounds.
Using the same techniques, we believe we can also obtain black-box UC-secure protocols in the public key infrastructure model.
Black-box UC Protocols in the Tamper Proof Hardware Token Model. Extending the work of [22], we show how to construct a UC-special purpose commitment scheme using tamper-proof hardware tokens, with black-box use of a one-way function. The tokens used in our protocols are stateless and instance independent, in the sense, every token implements a stateless function that is sampled from a predefined distribution. Thus, plugging this commitment scheme into our unified framework, we immediately obtain black-box UC-protocols in the token model from semi-honest OT.
Theorem 3
Assuming the existence of semi-honest oblivious-transfer. Then, there is black-box construction of UC-secure protocols for general functionalities in the tamper-proof hardware token model, using stateless and instance-independent hardware tokens.
In contrast, previous works [22, 28, 34] either rely on stateful or instance-dependent tokens.
We believe that our framework will yield analogous improvements in other setups such as, PUF [38], global random oracle models [39], etc., and we leave it as future work to explore these instantiations.
1.2 Our Techniques
We now give an overview of our techniques. Recall that our main theorem states that for a given trusted setup \(\mathcal {T}\), we can obtain black-box UC protocols in the \(\mathsf{4}\mathcal {T}\) model from semi-honest OT and UC-special-purpose commitment schemes in the \(\mathcal {T}\) model, where UC-special-purpose commitment schemes are concurrently extractable commitment schemes that are also resettably hiding. We prove this theorem in two steps. For simplicity of this overview, our discussion below will only use the concurrently extractability property of the commitments, and not the resettable hiding property. For the use of resettable hiding property, see Remark 2 at the bottom of this overview.
From CCA Commitment to Black-box UC Protocols in Trusted Setup Models. We first show that a black-box construction of UC-secure protocols in \(\mathsf{4}\mathcal {T}\)-model can be obtained from semi-honest OT and CCA-secure commitment schemes [40] in \(\mathsf{4}\mathcal {T}\)-model. We recall here that CCA-secure commitment schemes are a stronger variant of non-malleable commitment schemes that additionally require the hiding property to hold even against adversaries that have access to the committed-value oracle, which can break arbitrary commitments sent by the adversary using brute force.
CCA-secure commitments were originally proposed for the purpose of constructing concurrent secure protocol in the plain model (without any trusted setups) that satisfy a weaker security notion called angel-based security [41] or UC with super-polynomial time helpers [40]. In these models, to circumvent the aforementioned impossibility results of UC security [2, 3], the security definition is modified by allowing the adversary/simulator to have access to a super-polynomial time helper H or angel. Since the helper can be implemented in super-polynomial time, these models imply super-polynomial-time simulation security [42]. The security in these models can be realized in the plain model [19, 20, 40, 41, 43, 44], and in particular black-box constructions of protocols satisfying UC-security with super-polynomial time helpers in the plain model can be obtained from CCA-secure commitment schemes and semi-honest OT protocol [19, 20].
Our starting point is the work of [19] which builds upon techniques in [13, 14, 45], and show how to obtain UC-secure protocols with a super-polynomial time helper starting from semi-honest OT and CCA-secure commitments in a black-box way. We show that a direct extension of this yields an analogous result where we rely on CCA-secure commitments in \(\mathsf{4}\mathcal {T}\)-model as opposed to CCA-commitments in the plain model. Moreover, the helper H is a super-polynomial machine that breaks \(\mathsf {CCACom} \) commitments in \(\mathsf{4}\mathcal {T}\)-model.
In our next step, we eliminate access to super-polynomial helpers to guarantee standard UC-security. Suppose that the \(\mathsf {CCACom} \) is also straight-line concurrently extractable, i.e., there exists a (polynomial-time) extractor E that by simulating the \(\mathsf{4}\mathcal {T}\)-setup for the concurrent committer can extract the committed values in a straight-line way, then we can simply remove the super-polynomial time helper H by simulating the trusted setup (in polynomial time), achieving UC-security. Then, we will be able to emulate H with standard UC-simulation in \(\mathsf{4}\mathcal {T}\)-model.
From Concurrently Extractable Commitments to CCA-secure Commitments in Trusted Setup Models. We next show that a black-box CCA-secure commitment scheme (with straight-line concurrent extractability as required in the above step) in \(\mathsf{4}\mathcal {T}\)-model can be obtained from a straight-line concurrent extractable commitment scheme in \(\mathcal {T}\)-model.
Our high-level approach is to use the well-known Naor-Yung paradigm [46] that has been used to construct many CCA-secure encryption schemes. Recall that in the Naor-Yung technique, the sender encrypts a single message twice and proves “consistency” (i.e., the plaintext encrypted in both ciphertexts are equal) using a simulation-sound (non-interactive) zero-knowledge proof. Similarly, we consider a commitment scheme where, at a very high-level, the committer commits to a single message twice using a concurrently extractable commitment scheme and proves consistency. However, since our goal is to obtain black-box constructions, the committer of our protocol cannot use generic zero-knowledge proofs for proving consistency. We address this problem using the elegant technique of Choi et al. [45], developed in the context of constructing black-box non-malleable encryption from just public key encryption, and later extended to the context of constructing black-box non-malleable commitments by Wee [17]. Their techniques combine the cut-and-choose technique with Shamir’s secret sharing scheme.
In more detail, we consider the following scheme as the starting point. Let \(\mathsf{CECom} \) be a straight-line concurrently extractable commitment scheme in \(\mathcal {T}\)-model, and \(\mathsf {ECom}\) be a straight-line (stand-alone) extractable commitment scheme in \(\mathcal {T}\)-model (\(\mathsf {ECom}\) can be obtained from \(\mathsf{CECom} \) trivially). Let v be the message to be committed, and \(\mathcal {T}_0, \mathcal {T}_1, \mathcal {T}_2\) be three independent instances of \(\mathcal {T}\).
- Stage 1. :
-
The receiver R commits to a random subset \(\varGamma \subset [10\lambda ]\) of size \(\lambda \) using \(\mathsf {ECom}\) and trusted setup \(\mathcal {T}_0\).
- Stage 2. :
-
The committer C computes a \((\lambda +1)\)-out-of-\(10\lambda \) Shamir’s secret sharing \({\varvec{s}} = (s_1, \ldots , s_{10\lambda })\) of value v. Next, for each \(j\in [10\lambda ]\), C commits to \(s_j\) in parallel, using \(\mathsf{CECom} \) and the setup \(\mathcal {T}_1\). We will refer to commitments made in this stage as “commitments in the first row”.
- Stage 3. :
-
For each \(j\in [10\lambda ]\), C commits to \(s_j\) in parallel, using \(\mathsf{CECom} \) and the setups \(\mathcal {T}_2\). We will refer to commitments made in this stage as “commitments in the second row”.
- Stage 4 (Cut and Choose). :
-
R decommits the Stage 1 commitment to \(\varGamma \). For each \(j\in \varGamma \), C decommits both the \(j{^{th}}\) commitment in the first row and the \(j{^{th}}\) one in the second row, and R checks whether the two commitments are correctly decommitted to the same value \(s_j\).
- Decommitment. :
-
To decommit, simply decommit all commitments in the first row. If the shares \({\varvec{s}} = (s_1, \ldots , s_{10\lambda })\) committed in the first row is 0.9-close to a valid codeword of v, then the committed value is v, otherwise, it is set to \(\bot \).
Note that this scheme works in \(\mathsf{3}\mathcal {T}\)-model since it uses three instances of \(\mathcal {T}\). We remark that, similar to the scheme by Naor and Yung, this scheme satisfies the following two properties.
-
1.
The committer is required to commit to the same value in the two rows of the commitments. Specifically, it is guaranteed by the values revealed in the cut-and-choose stage (i.e., Stage 4) and the hiding of \(\mathsf {ECom}\), that the shares that are committed in the two rows are very “close” (that is, agree in most coordinates). This “closeness” ensures that there is a way of reconstructing the committed value from the shares committed in the second row. (We remark that this reconstruction works differently from that in the actual decommitment.)
-
2.
The commitments made in the two rows are “independent” since they are generated using two independent instances of \(\mathcal {T}\). When considering man-in-the-middle adversaries playing the roles of receiver and sender in the different executions, this independence will allow us to extract commitments made by the adversary from one row “correctly” while maintaining the “hiding” property of the commitments received by the adversary made in the other row.
Now, we rely on the following hybrid experiments to prove the CCA security.
-
\(H_0\) The real experiment, where an adversary tries to break the hiding property of the above scheme in the “left” interaction while interacting with the committed-value oracle in the “right” interaction.
-
\(H_1\) Follows the experiment as in \(H_0\) with the following exceptions:
-
1.
In the left interaction, the committed subset \(\varGamma \) is extracted from the adversary in Stage 1 using the extractability of \(\mathsf {ECom}\), and then \(0^{\left| {s_j} \right| }\) is committed in the \(j{^{th}}\) commitment of the second row for every \(j\not \in \varGamma \)
-
2.
In the right interaction, the committed-value oracle is emulated in polynomial time as follows. All shares committed to in the first row are extracted relying on the extractability of the underlying \(\mathsf{CECom} \) scheme and then the committed value is reconstructed from those extracted shares.
Notice that in this experiment, the setups \(\mathcal {T}_0\) and \(\mathcal {T}_1\) are simulated for extraction.
-
1.
-
\(H_2\) Follows experiment \(H_1\) with the following exceptions:
-
1.
In the left interaction, \(0^{\left| {s_j} \right| }\) is committed in the \(j{^{th}}\) commitment of the first row for every \(j\not \in \varGamma \).
-
2.
In the right interaction, the committed-value oracle is emulated in polynomial time by extracting shares from the second row and reconstructing the committed value.
In this experiment, the setups \(\mathcal {T}_0\) and \(\mathcal {T}_2\) are simulated for extraction. We notice that in this experiment, only \(|\varGamma | = \lambda \) shares are set and revealed in the left execution for both rows. Hence from the perfect privacy of the underlying Shamir secret sharing scheme, the committed value in the left interaction is hidden.
-
1.
Intuitively, \(H_0\) and \(H_1\) are indistinguishable because (i) in \(H_1\) the committed value oracle is emulated correctly using the shares extracted from the first rows, which defines the committed values, and thus (ii) the only difference in the adversary’s view are the values committed to in the second row on the left (which are committed using the setup \(\mathcal {T}_2\)), and the setup \(\mathcal {T}_2\) is not simulated in these hybrids. Additionally, at first sight, \(H_1\) and \(H_2\) also seem indistinguishable because (i) in \(H_2\) the committed-value oracle seems to be emulated correctly using values extracted from the second row thanks of the closeness, and thus (ii) the only difference in the adversary’s view is the values committed in the first row on the left (which are committed using the setup \(\mathcal {T}_1\)) and the setup \(\mathcal {T}_1\) is not simulated in \(H_2\).
Unfortunately, we cannot show the indistinguishability between the above hybrids since the above scheme does not guarantee simulation soundness. The problem is that if we simulate \(\mathcal {T}_0\) on the left (as in \(H_1, H_2\)), we can no longer rely on the hiding property of \(\mathsf {ECom}\) on the right, so we cannot show the closeness of the two rows on the right directly. This is problematic because when showing the indistinguishability between \(H_1\) and \(H_2\), we need to use the closeness of the two rows to argue that the committed-value oracle can be emulated correctly even from the second row.
To address this problem, we add a non-malleable commitment scheme into the above scheme. Specifically, we modify the scheme so that the second row is generated by using a commitment scheme that is both non-malleable and straight-line concurrently extractable, and additionally require the committer to commit to the decommitment of the first rows when generating the second row (i.e., we require the committer to commit to \((s_j, d_j)\) in the second row, where \(d_j\) is the decommitment of the \(j{^{th}}\) commitment in the first row). With these modifications, we can prove the closeness of the two rows in \(H_1\) as follows.
-
1.
First, we observe that, since the decommitments of the first row are committed in the second row, the closeness of the two rows can be verified by seeing only the committed values of the second row. In particular, the closeness holds between the two rows if the second row is “consistent”, meaning that a correct decommitment of the first row is committed in most coordinates.
-
2.
Based on this observation, we show the closeness in \(H_1\) as follows. First, we show the consistency of the second row in \(H_0\) using the hiding property of \(\mathsf {ECom}\). (Recall that we do not break \(\mathsf {ECom}\) in \(H_0\) and can use its hiding property in \(H_0\).) Next, when we move to \(H_1\) from \(H_0\), we use the non-malleability of the second row to argue that the committed values of the second row on the right does not change non-negligibly, which implies that the second row on the right remains consistent in \(H_1\). (Here we use the ability to efficiently verify the consistency condition given the committed values of the second row). Now, since the consistency condition implies the closeness, we conclude that the closeness holds in \(H_1\) as desired.
Given the closeness in \(H_1\), we can show the indistinguishability between \(H_1\) and \(H_2\) as follows. Consider an intermediate hybrid where the left interaction is generated as in \(H_1\) but the committed-value oracle is emulated using the second row as in \(H_2\). Then, we first use the closeness in \(H_1\) to argue that this intermediate hybrid is indistinguishable from \(H_1\). Next, observing that the setup \(\mathcal {T}_1\) is not simulated in this intermediate hybrid and \(H_2\), we show that this intermediate hybrid is also indistinguishable from \(H_2\) by using the hiding property of the second row on the left.
Finally, to complete the proof, we argue that the non-malleable commitment scheme that we use above (i.e., a commitment scheme that is both non-malleable and straight-line concurrently extractable) can be obtained without any additional assumptions. We know that constant-round black-box non-malleable commitments in the plain model can be obtained from one-way functions in a black-box way [18], which in turn can be obtained from semi-honest OT (which we assume to exist in the main theorem). Then, our idea is to combine this non-malleable commitments and \(\mathsf{CECom} \) in \(\mathcal {T}\)-model in a similar manner as in the protocol above (i.e., by using secret sharing and cut-and-choose technique). Now, non-malleability follows analogous to the plain-model non-malleability of the underlying scheme and straight-line concurrent extractability follows from the properties of the latter. The resulting non-malleable commitment is proven secure in the \(\mathsf{2}\mathcal {T}\)-model; thus, if this scheme is plugged into our first protocol (as the commitment used in the second row), the final protocol will be in the \(\mathsf{4}\mathcal {T}\)-model.
Remark 1
We remark that several issues arise when making the preceding high-level argument formal. For example, one subtlety that we ignore is the case that the concurrently extractable commitment scheme that we use is only computationally binding (which is the case in our instantiation for the token model.) This subtlety makes the above argument complicated because the closeness of the two rows is hard to define if the shares that are committed in the rows are not uniquely determined. In our formal proof, we address this subtlety by defining the closeness property only w.r.t. the shares that are extracted from the rows.
Remark 2
As noted at the beginning of this overview, we actually assume the existence of concurrently extractable commitment scheme that is also resettably hiding. We use this requirement when constructing straight-line concurrently extractable non-malleable commitment schemes. Moreover, we obtain such schemes by combining a non-malleable commitment in the plain model and concurrently extractable commitment in \(\mathcal {T}\)-model. In the actual argument, we additionally use plain-model extractable commitments, and rely on its plain-model (i.e. rewinding based) extractability in the analysis. However relying on a rewinding analysis in the presence of trusted setups is subtle. Specifically, since the adversary might have an arbitrary unbounded-round interaction with the setups, the interaction with the setups can be rewound when the extractor rewinds the adversary. To circumvent this, we simply assume that the schemes in the setup models remain secure even when they are rewound (i.e., reset). In the two concrete setup models we consider, CRS and tamper-proof hardware model, we show that achieving resettable hiding is not hard.
2 Definitions of Commitments in Trusted-Setup Models
In this work, we consider commitment protocols that use trusted setups, meaning that the honest committer and receiver communicate with the setup \(\mathcal {T}\) for committing and decommitting, and the security of the commitment scheme relies on that \(\mathcal {T}\) is never controlled by the adversary — we say such a protocol is in the trusted setup \(\mathcal {T}\)-model, or simply in \(\mathcal {T}\)-model.
For clarity, we indicate the parts related to trusted-setup models in red in the definitions we give below; removing them gives the definitions in the plain model.
2.1 Trusted Setups
We model a trusted-setup \(\mathcal {T}\) as an ideal functionality in the UC model, which is simply given by an Interactive Turning Machine (ITM) \(\mathcal {M} \). Different from UC, which models the execution of arbitrary protocol in arbitrary environment, for commitments, we only need to consider the execution of security games that define different properties, such as, hiding, binding, and CCA security. Therefore, below we describe a much simpler model of execution.
In a security game with setup \(\mathcal {T}\), a set of m (honest or corrupted) parties \(\left\{ {P_i} \right\} _{i \in [m]}\), and an adversary A, the setup \(\mathcal {T}\) can concurrently communicate with all entities following the rules described below:
-
Whenever a party \(P_i\), or a subroutine invoked by \(P_i\), sends a message m to \(\mathcal {T}\), \(\mathcal {T}\) receives input \((\mathsf {ID}, m)\), where \(\mathsf {ID}\) is the identifier of \(P_i\) or its subroutine. The identifiers of all parties and their subroutines are adaptively chosen by the adversary A at the beginning of their invocation.
-
The adversary can communicate with \(\mathcal {T}\) either directly according to the code of \(\mathcal {T}\), or indirectly by acting as a party with identifier \(\mathsf {ID}\).
-
All identifiers (of all parties and their subroutines and of parties acted by A) must be distinct.
2.2 Commitments in \(\mathcal {T}\)-Model
First we define the structure of a commitment scheme.
Definition 1 (Commitment Schemes)
A commitment scheme  is a pair of \(\mathsf{PPT} \) ITMs \(\langle C,R \rangle \) with the following properties:
is a pair of \(\mathsf{PPT} \) ITMs \(\langle C,R \rangle \) with the following properties:
-
1.
The commitment scheme has two stages, a commit stage and a reveal stage, where C and R receive as common input a security parameter \(1^n\) and C receives a private input \(v \in \{0,1\}^n\) that is the string to be committed.
-
2.
The commit stage results in a joint output c, called the commitment, a private output for C, d, called the decommitment string.

 .
. -
3.
In the reveal stage, upon receiving pair (v, d), the receiver R decides to accept or reject deterministically, depending only on (c, v, d).
We let \(\mathsf {open}\) denote the function that verifies the validity of (v, d); the receiver accepts (v, d) if \(\mathsf {open}(c, v, d) = 1\), and rejects otherwise,
If C and R do not deviate from the protocol, then R should accept with probability 1 during the reveal stage.
We define the binding and hiding property of a commitment scheme in trusted setup models naturally as in the plain model.Footnote 2 (We provide their formal definition in the full version.) We say that a commitment c is accepting if R does not abort at the end of commit stage, and is valid if there exists an accepting decommitment.
Next we define the resettably hiding property of a commitment scheme. Roughly speaking, a commitment scheme  is resettably hiding if its hiding property holds even against any cheating receiver that can “reset” an honest committer
is resettably hiding if its hiding property holds even against any cheating receiver that can “reset” an honest committer  and restart the interaction with them from an arbitrary point of the interaction.
and restart the interaction with them from an arbitrary point of the interaction.
Definition 2 (Resettably Hiding)
A commitment scheme \(\langle C,R \rangle \)  is computationally (resp. statistically) resettably hiding if for every non-uniform \(\mathsf{PPT}\) machine (resp. for every machine) \(R^*\), the view of \(R^*\) in the following two games, Game 0 and Game 1, are computationally indistinguishable over \(\lambda \in N\) (resp. statistically indistinguishable over \(\lambda \in N\)).
is computationally (resp. statistically) resettably hiding if for every non-uniform \(\mathsf{PPT}\) machine (resp. for every machine) \(R^*\), the view of \(R^*\) in the following two games, Game 0 and Game 1, are computationally indistinguishable over \(\lambda \in N\) (resp. statistically indistinguishable over \(\lambda \in N\)).
-
Game b (\(b\in \{0,1\}\)): Let C(b) be a committer that upon receiving \((v_0, v_1)\) gives a commitment to \(v_b\) by using \(\langle C,R \rangle \). Let F denote the forest of execution threads, initialized as empty. Then, in Game b, \(R^*\) can interact with C(b)
 in an arbitrary number of interactions as below: \(R^*\) specifies a prefix \(\rho \) of execution in F, and starts interacting with C(b)
in an arbitrary number of interactions as below: \(R^*\) specifies a prefix \(\rho \) of execution in F, and starts interacting with C(b)  from \(\rho \), where \(R^*\), C and
from \(\rho \), where \(R^*\), C and  use fresh randomness after \(\rho \).
use fresh randomness after \(\rho \).
In the rest of the paper, by default we refer to commitment schemes as ones that are statistically binding and computationally hiding, and will specify explicitly when considering commitment schemes that are computationally binding. In addition, we consider tag-based commitment schemes.
Definition 3 (Tag-based Commitment Schemes)
A commitment scheme \(\langle C,R \rangle \) is tag-based w.r.t. \(l(\lambda )\)-bit identities if, in addition to the security parameter \(1^\lambda \), the committer and the receiver also receive a “tag” —a.k.a. identity— \(\mathsf {id}\) of length \(l(\lambda )\) as common input. In \(\mathcal {T}\)-model, the tag is set to the identity of the committer input. 

2.3 Concurrent Non-malleable Commitments in \(\mathcal {T}\)-Model
Next we define the concurrent non-malleability of a commitment scheme. Roughly speaking, a commitment scheme is non-malleable if a man-in-the-middle adversary, who receives a commitment in the left interaction, cannot commit to a value that is related to the values committed in the left interaction. A commitment scheme is concurrent non-malleable if it is non-malleable even when the man-in-the-middle adversary can give multiple commitments concurrently.
Formally, the concurrent non-malleability of a commitment scheme is defined as follows. Let \(\langle C,R \rangle \) be a tag-based commitment scheme; 
 . Let \(M^*\) be a man-in-the-middle adversary and consider the following experiment. On input security parameter \(\lambda \in \mathbb {N}\) and auxiliary input \(z\in \{0,1\}^*\), \(M^*\) participates in one left and m right interactions simultaneously. In the left interaction, \(M^*\) interacts with the committer of \(\langle C,R \rangle \) and receives a commitment to value v using identity \(id\in \left\{ {0,1} \right\} ^\lambda \) of its choice,
. Let \(M^*\) be a man-in-the-middle adversary and consider the following experiment. On input security parameter \(\lambda \in \mathbb {N}\) and auxiliary input \(z\in \{0,1\}^*\), \(M^*\) participates in one left and m right interactions simultaneously. In the left interaction, \(M^*\) interacts with the committer of \(\langle C,R \rangle \) and receives a commitment to value v using identity \(id\in \left\{ {0,1} \right\} ^\lambda \) of its choice,  . In the right interaction, \(M^*\) interacts with the receiver of \(\langle C,R \rangle \) and gives commitments using identity \(\widetilde{\mathsf {id}}_0, \ldots , \widetilde{\mathsf {id}}_m\) of its choice, where the commitments can be scheduled arbitrarily by \(M^*\),
. In the right interaction, \(M^*\) interacts with the receiver of \(\langle C,R \rangle \) and gives commitments using identity \(\widetilde{\mathsf {id}}_0, \ldots , \widetilde{\mathsf {id}}_m\) of its choice, where the commitments can be scheduled arbitrarily by \(M^*\),  . Let \(\widetilde{v}_1, \ldots , \widetilde{v}_m\) be the values that \(M^*\) commits to on the right. If any of the right commitments is invalid or undefined, its committed value is defined to be \(\bot \). For any i, if \(\mathsf {id}= \widetilde{\mathsf {id}}_i\), set \(\widetilde{v}_i = \bot \). Let \(\mathsf {c}\hbox {-}\mathsf {mim}(\langle C,R \rangle , M^*, v, z)\) denote a random variable that describes \(\widetilde{v}_1, \ldots , \widetilde{v}_m\) and the view of \(M^*\) in the above experiment.
. Let \(\widetilde{v}_1, \ldots , \widetilde{v}_m\) be the values that \(M^*\) commits to on the right. If any of the right commitments is invalid or undefined, its committed value is defined to be \(\bot \). For any i, if \(\mathsf {id}= \widetilde{\mathsf {id}}_i\), set \(\widetilde{v}_i = \bot \). Let \(\mathsf {c}\hbox {-}\mathsf {mim}(\langle C,R \rangle , M^*, v, z)\) denote a random variable that describes \(\widetilde{v}_1, \ldots , \widetilde{v}_m\) and the view of \(M^*\) in the above experiment.
Definition 4
A commitment scheme \(\langle C,R \rangle \)  is concurrent non-malleable if for any \(\mathsf{PPT} \) man-in-the-middle adversary \(M^*\), the following are computationally indistinguishable.
is concurrent non-malleable if for any \(\mathsf{PPT} \) man-in-the-middle adversary \(M^*\), the following are computationally indistinguishable.
-
\(\left\{ {\mathsf {c}\hbox {-}\mathsf {mim}(\langle C,R \rangle , M^*, v_0, z)} \right\} _{\lambda \in \mathbb {N}, v_0\in \left\{ {0,1} \right\} ^{\lambda },v_1\in \left\{ {0,1} \right\} ^{\lambda }, z\in \left\{ {0,1} \right\} ^*}\)
-
\(\left\{ {\mathsf {c}\hbox {-}\mathsf {mim}(\langle C,R \rangle , M^*, v_1, z)} \right\} _{\lambda \in \mathbb {N}, v_0\in \left\{ {0,1} \right\} ^{\lambda }, v_1\in \left\{ {0,1} \right\} ^{\lambda }, z\in \left\{ {0,1} \right\} ^*}\)
We remark that the above definition captures “one-many” setting, where the adversary participates in one left and m right interactions simultaneously. We can easily generalize the definition so that it captures “many-many” setting, where the adversary participates in m left and m right interactions simultaneously. It is known that the “one-many” version of the definition implies the “many-many” one [47].
2.4 CCA Commitments in Trusted-Setup Models
The notion of CCA security for statistically-binding and computationally hiding tag-based commitment schemes was introduced in [40]. We here adapt the definition of CCA security in the plain model of [19] to trusted setup models.
Roughly speaking, a (statistically binding) commitment scheme is CCA secure if the commitment scheme retains its hiding property even if the receiver has access to a committed-value oracle. Let \(\mathsf {CCACom} \) be a tag-based commitment scheme with \(l(\lambda )\)-bit identities; 
 . A committed-value oracle
. A committed-value oracle  of \(\mathsf {CCACom} \) acts as follows in interaction with an adversary A,
of \(\mathsf {CCACom} \) acts as follows in interaction with an adversary A, 
 : It participates with A in many sessions of the commit phase of \(\mathsf {CCACom} \) as an honest receiver, using identities chosen adaptively by A. At the end of each session, if the session is accepting and valid, it returns to A the unique committed value in that session (by the statistical binding property of the commitment scheme, there exists such a unique value when the commitment is valid except with negligible probability; if not output \(\bot \)); otherwise, it sends \(\bot \).
: It participates with A in many sessions of the commit phase of \(\mathsf {CCACom} \) as an honest receiver, using identities chosen adaptively by A. At the end of each session, if the session is accepting and valid, it returns to A the unique committed value in that session (by the statistical binding property of the commitment scheme, there exists such a unique value when the commitment is valid except with negligible probability; if not output \(\bot \)); otherwise, it sends \(\bot \).
More precisely, let \(\mathsf{IND}_b(\mathsf {CCACom}, A, \lambda , z)\), where \(b\in \{0,1\}\), denote the output of the following probabilistic experiment: on common input \(1^\lambda \) and auxiliary input z,  (adaptively) chooses a pair of challenge values \((v_0\), \(v_1)\in \{0,1\}^\lambda \) —the values to be committed to— and an identity \(\mathsf {id}\), and receives a commitment to \(v_b\) using identity \(\mathsf {id}\),
(adaptively) chooses a pair of challenge values \((v_0\), \(v_1)\in \{0,1\}^\lambda \) —the values to be committed to— and an identity \(\mathsf {id}\), and receives a commitment to \(v_b\) using identity \(\mathsf {id}\),  . Finally, the experiment outputs the output y of
. Finally, the experiment outputs the output y of  ; the output y is replaced by \(\bot \) if the identity of the commitment that A receives is the same as the identity of any of the commitments that A sends to
; the output y is replaced by \(\bot \) if the identity of the commitment that A receives is the same as the identity of any of the commitments that A sends to  (that is, any execution where the adversary queries the decommitment oracle on a commitment using the same identity as the commitment it receives, is considered invalid).
(that is, any execution where the adversary queries the decommitment oracle on a commitment using the same identity as the commitment it receives, is considered invalid).
Definition 5 (CCA-security)
Let \(\mathsf {CCACom} \) be a tag-based statistically binding commitment scheme  . We say that \(\mathsf {CCACom} \) is CCA-secure, if for every \(\mathsf{PPT}\) ITM A, the following ensembles are computationally indistinguishable:
. We say that \(\mathsf {CCACom} \) is CCA-secure, if for every \(\mathsf{PPT}\) ITM A, the following ensembles are computationally indistinguishable:
-
\(\left\{ {\mathsf{IND}_0(\mathsf {CCACom}, A, \lambda , z)} \right\} _{\lambda \in N, z \in \{0,1\}^*}\)
-
\(\left\{ {\mathsf{IND}_1(\mathsf {CCACom}, A, \lambda , z)} \right\} _{\lambda \in N, z \in \{0,1\}^*}\)
k-Robustness. Roughly speaking, k-robustness states the committed-value oracle can be simulated efficiently for an attacker, without “disturbing” any k-round interaction that the attacker participates in.
Consider a man-in-the-middle adversary A that participates in an arbitrary left interaction with B of a limited number of rounds, while having access to a committed-value oracle  ;
; 
 \(\mathsf {CCACom} \) is k-robust if the (joint) output of every k-round interaction, with an adversary having access to the oracle
\(\mathsf {CCACom} \) is k-robust if the (joint) output of every k-round interaction, with an adversary having access to the oracle  , can be simulated without the oracle. In other words, having access to the oracle does not help the adversary in participating in any k-round protocols
, can be simulated without the oracle. In other words, having access to the oracle does not help the adversary in participating in any k-round protocols  .
.
Definition 6
(
k
-Robustness). Let \(\mathsf {CCACom} \) be a statistically binding commitment scheme  . We say that \(\mathsf {CCACom} \) is k -robust, if for every \(\mathsf{PPT}\) adversary A, there exists a \(\mathsf{PPT}\) simulator S, such that, the following holds.
. We say that \(\mathsf {CCACom} \) is k -robust, if for every \(\mathsf{PPT}\) adversary A, there exists a \(\mathsf{PPT}\) simulator S, such that, the following holds.
-
Simulation: For every \(\mathsf{PPT}\) k-round ITM B that interacts only with A, the following two ensembles are computationally indistinguishable.
-
−

-
− \(\left\{ {\mathsf {output}_{B, S}[{\langle B(1^\lambda , x), S(1^\lambda , z) \rangle }]} \right\} _{\lambda \in N, x,z\in \{0,1\}^{\mathrm{poly}(\lambda )}}\)
where \(\mathsf {output}_{X,Y}[{\langle X(x), Y(y) \rangle }]\) denote the joint output of an interaction between ITMs X and Y on private input x and y respectively, and with uniformly and independently chosen random inputs to each machine.
-
We say that \(\mathsf {CCACom} \) is \(\mathrm{poly}\)-robust if it is k-robust against arbitrary polynomial \(k(\lambda )\).
2.5 Concurrent Extractability w.r.t. Commitment in \(\mathcal {T}\)-Model
We now define concurrent extractability w.r.t. commitment. Extraction w.r.t. commitment is defined only for statistically binding commitments and guarantees to extract from (malicious) committers the statistically defined committed values.
Definition 7 (Concurrent Extractability w.r.t. Commitment)
Let \(\mathsf {CCACom} \) be a statistically binding commitment scheme  . We say that \(\mathsf {CCACom}\) is straight-line concurrently extractable w.r.t. commitment, if there exists a universal \(\mathsf{PPT}\) simulator S, such that,
. We say that \(\mathsf {CCACom}\) is straight-line concurrently extractable w.r.t. commitment, if there exists a universal \(\mathsf{PPT}\) simulator S, such that,
-
Simulation of Committed-value Oracle: for every \(\mathsf{PPT}\) adversary A, the following two ensembles are computationally indistinguishable.
-
−

-
− \(\left\{ {{\langle S(1^\lambda ), A(1^\lambda ,z) \rangle }} \right\} _{\lambda \in N, z\in \{0,1\}^{\mathrm{poly}(\lambda )}}\)
-
We say that \(\mathsf {CCACom} \) is straight-line extractable w.r.t. commitment if the above condition holds for attackers that sends only a single commitment to  .
.
Claim 1
If a statistically binding commitment scheme \(\mathsf {CCACom} \) in \(\mathcal {T}\)-model is straight-line concurrently extractable w.r.t. commitment, then it is also k-robust for any polynomial \(k(\lambda )\).
Due to space restrictions, we defer the proof of claim to the full version. At a very high level, straight-line concurrent extractability w.r.t. commitment implies \(\mathrm{poly}\)-robustness as it essentially guarantees that  can be simulated in a straight-line, and straight-line simulation does not “disturb” the concurrent interaction with B, no matter how many rounds the interaction has.
can be simulated in a straight-line, and straight-line simulation does not “disturb” the concurrent interaction with B, no matter how many rounds the interaction has.
2.6 Concurrent Extractability w.r.t. Opening in \(\mathcal {T}\)-Model
We now introduce the new notion of straight-line concurrent extractability w.r.t. opening. This notion is defined for any computationally binding and computationally hiding commitment scheme. Roughly speaking, it requires the commitment scheme to have an efficient extractor E satisfying the following two properties: (1) when interacting with any efficient attacker A acting as a concurrent committer, the value v that E extracts for each commitment that A sends is guaranteed to be consistent with the value \(v'\) that A opens to (i.e., \(v' = \bot \) or \(v = v'\)), even if A receives the extracted values v’s. (2) The messages that E send statistically emulate that of honest receivers, for even computationally unbounded attackers.
Definition 8
Let \(\mathsf{CECom} \) be any computationally hiding and computationally binding commitment scheme in a trusted-setup \(\mathcal {T}\)-model. We say that \(\mathsf{CECom} \) is straight-line concurrently extractable w.r.t. opening if there exists a universal \(\mathsf{PPT} \) extractor E with the following properties:
-
Syntax and Statistical Emulation: For any (potentially unbounded) adversary A, it holds that the view of A in the following real and simulated games are statistically close.
-
− In the real game, A (acting as a concurrent committer) interacts with honest receivers R in multiple sessions of \(\mathsf{CECom} \). At the end of each session, if A sends a decommitment, R replies with the decision of whether the decommitment is accepted. All parties have access to \(\mathcal {T}\).
-
− In the simulated game, E emulates the honest receivers and trusted-setup for A in a straight-line.
At the end of the commit stage of each session j, E outputs a value \(v_j\) on its special output tape.
-
-
Concurrent Extractability w.r.t. Opening: For any PPT adversary A, consider another simulated game where A interacts with E as described above, and at the end of the commit stage of each session j, it receives the value \(v_j\) that E outputs on its special output tape. The probability that in any session j, A successfully decommits to a value \(v_j'\ne \bot \) that is different from the value \(v_j\) that E outputs is negligible, that is, if \(\mathsf {open}(c_j, v_j', d_j) = 1\) then \(v_j = v_j'\) with overwhelming probability.
3 Robust \(\mathsf {CCACom}\) from \(\mathsf{CECom} \) w.r.t Opening
In this section, given a commitment scheme \(\mathsf{CECom} \) that is straight-line concurrently extractable w.r.t. opening in \(\mathcal {T}\)-model, we construct a robust CCA-secure commitment scheme \(\mathsf {CCACom} \) that uses a related trusted-setup \(\mathsf{4}\mathcal {T}\), called the quadruple-\(\mathcal {T}\) trusted-setup, which runs four independent copies of \(\mathcal {T}\) internally.
The \(\mathsf{x}\mathcal {T}\) Trusted Setup: \(\mathsf{x}\mathcal {T}\), parameterized by an integer x, is an ITM that upon invocation invokes internally x instances of \(\mathcal {T}\)—denoted as \(\mathcal {T}_0\), \(\mathcal {T}_1, \cdots , \mathcal {T}_{x-1}\). In an experiment with \(\mathsf{x}\mathcal {T}\), all parties and adversaries can interact with any instance, by pre-pending to every message to/from copy \(\mathcal {T}_i\) with the index \(i \in \{ 0, \cdots , x-1 \}\). That is, upon receiving input i||v from party P, \(\mathsf{x}\mathcal {T}\) activates internally the copy \(\mathcal {T}_i\) with input v from party P, and upon receiving output o from \(\mathcal {T}_i\), returns i||o to P. Additionally, each copy \(\mathcal {T}_i\) can interact with the adversary as its code specifies, with all messages exchanged of form \(i||\mathsf{mesg}\).
Theorem 4
Let \(\mathcal {T}\) be any trusted setup, and \(\mathsf{4}\mathcal {T}\) the corresponding quadruple-\(\mathcal {T}\) trusted setup. There is a fully black-box construction of a \(\mathrm{poly}\)-robust CCA-secure commitment scheme \(\mathsf {CCACom} \) in the \(\mathsf{4}\mathcal {T}\)-trusted setup model from any one-way function and any commitment scheme \(\mathsf{CECom} \) in the \(\mathcal {T}\)-trusted setup model that is straight-line concurrently extractable w.r.t. opening and resettably hiding. Moreover, if \(\mathsf{CECom} \) has \(r_{\textsc {cec}}\) rounds, then \(\mathsf {CCACom} \) has \(O(r_{\textsc {cec}})\) rounds.
Proof. In our protocol \(\mathsf {CCACom} \), we use the following building blocks:
-
A standard constant-round statistically-binding commitment scheme \({{\textsf {com}}} \) in the plain model, which is known from one-way functions [48].
-
A \(r_{\textsc {cec}}\)-round commitment scheme \(\mathsf{CECom} \) that is (straight-line) concurrently extractable w.r.t. opening in the \(\mathcal {T}\)-trusted setup model.
-
A commitment scheme \(\mathsf {ECom}\) that is straight-line extractable w.r.t. opening in the \(\mathcal {T}\)-model, which is implied by \(\mathsf{CECom} \) in \(\mathcal {T}\)-model.
-
A \(O(r_{\textsc {cec}})\)-round concurrent non-malleable commitment scheme \(\mathsf {NMCom}\) in the double-\(\mathcal {T}\), \(\mathsf{2}\mathcal {T}\), trusted-setup model that is also straight-line concurrently extractable w.r.t. commitment.
Such a commitment scheme can be constructed from any concurrent non-malleable commitment scheme in the plain model, and any commitment scheme in \(\mathcal {T}\)-model that is straight-line concurrently extractable w.r.t. opening and resettably hiding. (Note that the \(\mathsf {CCACom} \) protocol itself does not directly rely on the resettable hiding property of \(\mathsf{CECom} \).) Due to space limitations, we provide our construction in the full version.
Next, we present our protocol \(\mathsf {CCACom} \) formally.
Commit Phase of \(\mathsf {CCACom} \) . On common inputs \(1^{\lambda }\) and identities \(\mathsf {ID}_C, \mathsf {ID}_R\), and private input \(v\in \{0,1\}^{\lambda }\) to C, the committer C and receiver R interact with each other as follows:
- Stage 1. :
-
R commits to a random subset \(\varGamma \subset [10\lambda ]\) of size \(\lambda \) using \(\mathsf {ECom}\) and trusted setup \(\mathcal {T}_0\). We will refer to \(\mathcal {T}_0\) as the ECom-setup.
- Stage 2 (The Com Row). :
-
C computes a \((\lambda +1)\)-out-of-\(10\lambda \) Shamir’s secret sharing \({\varvec{s}} = (s_1, \ldots , s_{10\lambda })\) of value v. Next, for each \(j\in [10\lambda ]\), C commit to \(s_j\) in parallel, using \({{\textsf {com}}} \). We will refer to commitments made in this stage as “commitments in the com row”.
Let \(\phi _j\) and \(d_j\) be the commitment and decommitment for share \(s_j\).
- Stage 3 (The CECom Row). :
-
For each \(j\in [10\lambda ]\), C commits to \((s_j, d_j)\) in parallel, using the protocol \(\mathsf{CECom} \) and the setup \(\mathcal {T}_1\). We will refer to commitments made in this stage as “commitments in the CECom row”, and \(\mathcal {T}_1\) as the CECom-setup.
Let \(\psi _j\) and \(e_j\) be the commitment and decommitment for \((s_j, d_j)\).
- Stage 4 (The NMCom Row). :
-
For each \(j\in [10\lambda ]\), C commits to \((s_j, d_j, e_j)\) in parallel, using the protocol \(\mathsf {NMCom}\) and the setups \(\mathcal {T}_2\) and \(\mathcal {T}_3\) to emulate the double-\(\mathcal {T}\) setup \(\mathsf{2}\mathcal {T}\). We will refer to commitments made in this stage as “commitments in the NMCom row”, and \(\mathcal {T}_2, \mathcal {T}_3\) as the NMCom-setup.
- Stage 5 (Cut and Choose). :
-
R decommits the Stage 1 commitment to \(\varGamma \). For each \(j\in \varGamma \), C decommits the \(j{^{th}}\) commitment in the NMCom row to \((s_j, d_j, e_j)\). R accepts if for every \(j \in \varGamma \), the decommitment to the \(j{^{th}}\) NMCom commitment is accepting, and \((s_j, d_j)\) is a valid decommitment to commitment \(\phi _j\) in the Stage 2, and \(((s_j, d_j), e_j)\) is a valid decommitment to \(\psi _j\) in Stage 3.
Decommit Phase. C sends v and the decommitments \((s_1, d_1), \cdots , (s_{10\lambda }, d_{10\lambda })\) to all \({{\textsf {com}}} \) commitments \(\phi _1, \cdots , \phi _{10\lambda }\). R checks all decommitments and does the following. If for any \(i \in [10\lambda ]\), the decommitment \((s_i,d_i)\) is invalid w.r.t. \(\phi _i\), set \(s_i\) to \(\bot \). R accepts the decommitments if and only if  , where
, where  for
for  is defined as follows:
is defined as follows:

Clearly, The round complexity of the above protocol is \(O(r_{\textsc {cec}})\). The statistical binding property of \(\mathsf {CCACom} \) follows directly from that of \({{\textsf {com}}} \) in Stage 2. Thus, it remains to show that \(\mathsf {CCACom} \) is CCA secure and \(\mathrm{poly}\)-robust; for the latter property, we show the stronger property of straight-line concurrently extractability w.r.t. commitment, which implies \(\mathrm{poly}\)-robustness by Claim 1.
Proposition 1
\(\mathsf {CCACom} \) in the \(\mathsf{4}\mathcal {T}\)-trusted setup model is CCA secure and straight-line concurrently extractable w.r.t. commitment.
Due to space restrictions, we prove only CCA security below, and defer the proof of straight-line concurrently extractable w.r.t. commitment in the full version.
Proof of CCA Security. For any \(\mathsf{PPT} \) adversary A, we need to show that the outputs of the games \(\mathsf{IND}_0\) and \(\mathsf{IND}_1\) are indistinguishable (cf. Definition 5).
-
\(\left\{ {\mathsf{IND}_0(\mathsf {CCACom}, A, \lambda , z)} \right\} _{\lambda \in N, z \in \{0,1\}^*}\)
-
\(\left\{ {\mathsf{IND}_1(\mathsf {CCACom}, A, \lambda , z)} \right\} _{\lambda \in N, z \in \{0,1\}^*}\)
Towards showing the indistinguishability, for each \(b\in \{0,1\}\), we consider the following hybrid experiments \(H_0^b \cdots H_{7}^b\); we use \(\mathsf {H}_{k}^{b}(\lambda ,z)\) to denote the random variable representing the view of A in the execution of \(H_{k}^{b}(\lambda ,z)\). Throughout the hybrids, we will keep the invariant that certain bad events do not happen except with negligible probabilities. Roughly speaking, we would like to maintain that in all hybrids, in every right session, the shares that A commits to in the com, CECom, and/or NMCom rows are “consistent”, so that, we can efficiently emulate the  oracle by extracting from either the CECom rows or from the NMCom rows. Below, we first define these bad events.
oracle by extracting from either the CECom rows or from the NMCom rows. Below, we first define these bad events.
 We say that a vector of shares
We say that a vector of shares  is inconsistent w.r.t. a transcript \(\mathsf{Trans}\) of protocol \(\mathsf {CCACom} \), if
is inconsistent w.r.t. a transcript \(\mathsf{Trans}\) of protocol \(\mathsf {CCACom} \), if
-
Either, more than 0.1 fraction of
 are \(\bot \), that is, \(|\varLambda _1 = \{ j | \tilde{s}_j = \bot \}| > \lambda \).
are \(\bot \), that is, \(|\varLambda _1 = \{ j | \tilde{s}_j = \bot \}| > \lambda \). -
or,
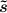 is 0.8-close to a valid codeword
is 0.8-close to a valid codeword  , yet 0.1-far from it, that is, \(|\varLambda _2 = \{ j | \tilde{s}_j \ne w_j \}|> \lambda \), and additionally
, yet 0.1-far from it, that is, \(|\varLambda _2 = \{ j | \tilde{s}_j \ne w_j \}|> \lambda \), and additionally  agrees with the shares \(\{ {s_j} \}_{j \in \varGamma }\) opened to in Stage 5 in transcript \(\mathsf{Trans}\).
agrees with the shares \(\{ {s_j} \}_{j \in \varGamma }\) opened to in Stage 5 in transcript \(\mathsf{Trans}\).
 is defined for hybrids below where the extractor
is defined for hybrids below where the extractor  of \(\mathsf{CECom} \) is used to extract values from the CECom rows (i.e., \(H_1^b, H_2^b, H_3^b\)). Let \(\{ {({\tilde{s}}^k_j, d^k_j)} \}_{j \in [10\lambda ]}\) denote the values extracted by
of \(\mathsf{CECom} \) is used to extract values from the CECom rows (i.e., \(H_1^b, H_2^b, H_3^b\)). Let \(\{ {({\tilde{s}}^k_j, d^k_j)} \}_{j \in [10\lambda ]}\) denote the values extracted by  from the \(\mathsf{CECom} \) commitment in right session k. Set
from the \(\mathsf{CECom} \) commitment in right session k. Set

Event \(\mathrm{Bad}_{CEC}\) occurs if there is an accepting right session k in which the shares \(\{ {\tilde{s}^k_j} \}_{10\lambda }\) extracted from the CECom row is inconsistent w.r.t. the transcript of this session.
 is defined for all hybrids below and concerns the values committed to in the \(\mathsf {NMCom}\) commitments on the right. Let \(\{ {(({{\hat{s}}}^k_j, d^k_j), e^k_j)} \}_{j \in [10\lambda ]}\) denote the values committed to in the NMCom row in right session k. (Since \(\mathsf {NMCom}\) is statistically binding, the committed values are well-defined.) Set
is defined for all hybrids below and concerns the values committed to in the \(\mathsf {NMCom}\) commitments on the right. Let \(\{ {(({{\hat{s}}}^k_j, d^k_j), e^k_j)} \}_{j \in [10\lambda ]}\) denote the values committed to in the NMCom row in right session k. (Since \(\mathsf {NMCom}\) is statistically binding, the committed values are well-defined.) Set

where \(\psi ^k_j\) and \(\phi ^k_j\) are respectively the \(j{^{th}}\) commitment in the CECom row and in the com row in the \(k{^{th}}\) right session. Event \(\mathrm{Bad}_{\text {NM}}\) occurs if there is an accepting right session k, in which the shares \(\{ {{\hat{s}}^k_j} \}_{10\lambda }\) extracted from the values committed in the NMCom row are inconsistent w.r.t. the transcript of this session.
-
Hybrid \(H_{0}^{b}(\lambda ,z)\) is the same as experiment \(\mathsf{IND}_b(\mathsf {CCACom}, A, \lambda , z)\).
-
Hybrid \(H_{1}^{b}(\lambda ,z)\) is the same as \(H_{0}^{b}(\lambda ,z)\) except that on the right the
 oracle is emulated efficiently using the extractor
oracle is emulated efficiently using the extractor  of \(\mathsf{CECom} \) as follows:
of \(\mathsf{CECom} \) as follows:-
1.
Generate the receiver messages of \(\mathsf {CCACom} \) honestly, except for messages in the CECom-rows.
-
2.
Use
 to emulate (i) the \(\mathsf{CECom} \) receivers in the CECom-rows and in Stage 5 when A open some of the \(\mathsf{CECom} \) commitments, and (ii) the CECom-setup \(\mathcal {T}_1\). By definition, at the end of each CECom-row, say in the right session k,
to emulate (i) the \(\mathsf{CECom} \) receivers in the CECom-rows and in Stage 5 when A open some of the \(\mathsf{CECom} \) commitments, and (ii) the CECom-setup \(\mathcal {T}_1\). By definition, at the end of each CECom-row, say in the right session k,  outputs a vector of values \(\{ {({\tilde{s}}^k_j, {d}^k_j)} \}_{j \in [10\lambda ]}\) on its special output tape. Set
outputs a vector of values \(\{ {({\tilde{s}}^k_j, {d}^k_j)} \}_{j \in [10\lambda ]}\) on its special output tape. Set  , where
, where  is described in Eq. (2).
is described in Eq. (2). -
3.
At the end of each right session k, emulate the committed value that
 returns, by returning the value
returns, by returning the value  reconstructed from the shares
reconstructed from the shares  where \(\widetilde{\mathsf {Value}}\) is defined as
where \(\widetilde{\mathsf {Value}}\) is defined as  (4)
(4)
-
1.
We first show that bad events \(\mathrm{Bad}_{\text {NM}}\) and \(\mathrm{Bad}_{CEC}\) occur in \(H_1^b\) with negligible probability.
Lemma 1
For every \(b\in \{ 0,1 \}\), it holds that, the probabilities that event  and \(\mathrm{Bad}_{\text {CEC}}\) occur are negligible in \(H_1^b\).
and \(\mathrm{Bad}_{\text {CEC}}\) occur are negligible in \(H_1^b\).
Proof
We first bound the probability of \(\mathrm{Bad}_{CEC}\) occurring. Suppose for contradiction that there is an accepting right session k in which the shares  extracted from the CECom row is inconsistent. The inconsistency condition states that
extracted from the CECom row is inconsistent. The inconsistency condition states that
-
Either,
 contains more than \(\lambda \) \(\bot \), i.e., \(|\varLambda _1 = \{ j \ | \ \tilde{s}^k_j = \bot \}| \ge \lambda \).
contains more than \(\lambda \) \(\bot \), i.e., \(|\varLambda _1 = \{ j \ | \ \tilde{s}^k_j = \bot \}| \ge \lambda \). -
Or,
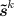 is 0.8-close to
is 0.8-close to  , yet 0.1-far from it, i.e., \(|\varLambda _2 = \{ j \ | \ \tilde{s}^k_j \ne w^k_j \}| > \lambda \), and
, yet 0.1-far from it, i.e., \(|\varLambda _2 = \{ j \ | \ \tilde{s}^k_j \ne w^k_j \}| > \lambda \), and  agree with the shares opened in Stage 5 of right session k.
agree with the shares opened in Stage 5 of right session k.
In case 1, for this session to be accepting, it must happen that none of the locations in \(\varLambda _1\) was opened in Stage 5, that is, \(\varLambda _1 \cap \varGamma ^k = \emptyset \), where \(\varGamma ^k\) is the subset opened in Stage 5 of right session k; otherwise, the attacker must manage to open to a non-\(\bot \) share for some \(j \in \varLambda _1\), which contradicts with the concurrent extractability w.r.t. opening property of \(\mathsf{CECom} \). Similarly, in case 2, it must be that \(\varLambda _2 \cap \varGamma ^k = \emptyset \), as otherwise, the attacker must manage to open to a share \(\tilde{s}^k_j = w^k_j\) for some \(j \in \varLambda _2\). In both cases, A manage to form a set, \(\varLambda _1\) or \(\varLambda _2\), of size \(\lambda \) that does not intersect with \(\varGamma ^k\) also of size \(\lambda \), which violates hiding of the \(\mathsf {ECom}\) commitment to \(\varGamma ^k\). (See the full version for a formal argument).
We next bound the probability of \(\mathrm{Bad}_{\text {NM}}\) occurring in \(H_1^b\) by using the following hybrid \(G_1^b, G^b_2\).
-
Hybrids \(G_1^b, G_2^b\) are identical to \(H^b_1\) except that on the right the values committed to in the \(\mathsf {NMCom}\) commitments are extracted using the committed-value oracle
 in \(G_1^b\) and using the extractor
in \(G_1^b\) and using the extractor  in \(G_2^b\). That is,
in \(G_2^b\). That is,-
− On the right, \(G_1^b\) (resp. \(G_2^b\)) forwards all \(\mathsf {NMCom}\) commitments to
 (resp.
(resp.  ). By definition,
). By definition,  (resp.
(resp.  ) returns after every NMCom row the values committed to in this row. \(G_1^b\) (resp. \(G_2^b\)) ignores these values.
) returns after every NMCom row the values committed to in this row. \(G_1^b\) (resp. \(G_2^b\)) ignores these values.
-
Since \(G_2^b\) is completely efficient, it follows from the same argument as above that event \(\mathrm{Bad}_{\text {NM}}\) does not occur w.r.t. the values extracted by  except for negligible probability. Then, by the concurrent extractability w.r.t. commitment of \(\mathsf {NMCom}\), \(G_1^b\) and \(G_2^b\) are indistinguishable and hence \(\mathrm{Bad}_{\text {NM}}\) does not occur w.r.t. the values returned by
except for negligible probability. Then, by the concurrent extractability w.r.t. commitment of \(\mathsf {NMCom}\), \(G_1^b\) and \(G_2^b\) are indistinguishable and hence \(\mathrm{Bad}_{\text {NM}}\) does not occur w.r.t. the values returned by  , except for negligible probability in \(G_1^b\). Finally, since
, except for negligible probability in \(G_1^b\). Finally, since  emulates the receivers of \(\mathsf {NMCom}\) perfectly for A, the views of A in \(H_1^b\) and \(G_1^b\) are identical. Thus, event \(\mathrm{Bad}_{\text {NM}}\) (w.r.t. the values committed to in the \(\mathsf {NMCom}\) commitments) occurs with only negligible probability in \(H_1^b\). \(\blacksquare \)
emulates the receivers of \(\mathsf {NMCom}\) perfectly for A, the views of A in \(H_1^b\) and \(G_1^b\) are identical. Thus, event \(\mathrm{Bad}_{\text {NM}}\) (w.r.t. the values committed to in the \(\mathsf {NMCom}\) commitments) occurs with only negligible probability in \(H_1^b\). \(\blacksquare \)
Now, we are ready to show the indistinguishability between \(H_0^b\) and \(H_1^b\).
Lemma 2
For every \(b\in \{ 0,1 \}\), it holds that,
Proof
We show that both \(H^b_0\) and \(H^b_1\) are indistinguishable from the following simulated hybrid \(G^b\).
-
Hybrid \(G^b\) is the same as \(H_{1}^{b}(\lambda ,z)\) except for the following:
-
− On the right, it emulates the right receiver messages as \(H_1^b\) does (i.e., the \(\mathsf{CECom} \) receivers of commitments in CECom-rows and the CECom-setup are simulated using
 , and other receiver messages are generated honestly). However, at the end of each right session k, committed value that
, and other receiver messages are generated honestly). However, at the end of each right session k, committed value that  returns is emulated differently: It extracts the shares \({\varvec{s}} = (s_1, \ldots , s_{10\lambda })\) committed to in the com row by brute force, and reply
returns is emulated differently: It extracts the shares \({\varvec{s}} = (s_1, \ldots , s_{10\lambda })\) committed to in the com row by brute force, and reply  , where \(\mathsf {Value}\) is defined in Eq. (1). (That is, \(G^b\) returns to A the actual committed value in each right session.)
, where \(\mathsf {Value}\) is defined in Eq. (1). (That is, \(G^b\) returns to A the actual committed value in each right session.)
-
Claim 2
For every \(b \in \{ 0,1 \}\), it holds that,
Proof
The only difference between these two hybrids lies in how the committed values of the right sessions are extracted: in \(H_{1}^b\), they are reconstructed from the shares extracted from the CECom-rows, whereas in \(G^b\), the actually committed value is extracted by brute-force. Thus it suffices to show that in \(H_{1}^b\) the values \(\{ {\tilde{v}^k} \}\) reconstructed from the shares extracted from the CECom-rows are the actual committed values \(\{ {v^k} \}\) with overwhelming probability. Since Lemma 1 gives that event \(\mathrm{Bad}_{CEC}\) occurs with negligible probability in \(H_1^b\), it suffices to argue that when \(\mathrm{Bad}_{CEC}\) does not occur, \(\tilde{v}^k = v^k\) for every right session k. Recall that if \(\mathrm{Bad}_{CEC}\) does not occur, in any accepting right session k the shares  extracted from the CECom row is consistent, so they satisfy the following condition.
extracted from the CECom row is consistent, so they satisfy the following condition.
-
1.
\(\left| {\varLambda _1} \right| \le \lambda \), where \(\varLambda _1 := \{ j | \tilde{s}^k_j = \bot \}\), and
-
2.
if
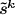 is 0.8-close to a valid codeword \({\varvec{w}} = (w_1, \ldots , w_{10\lambda })\) such that \(w_j\) equals the value revealed in Stage 5 for each \(j\in \varGamma ^k\), then \(\left| {\varLambda _2} \right| \le \lambda \), where \(\varLambda _2 := \{ j | \tilde{s}^k_j \ne w_j \}\).
is 0.8-close to a valid codeword \({\varvec{w}} = (w_1, \ldots , w_{10\lambda })\) such that \(w_j\) equals the value revealed in Stage 5 for each \(j\in \varGamma ^k\), then \(\left| {\varLambda _2} \right| \le \lambda \), where \(\varLambda _2 := \{ j | \tilde{s}^k_j \ne w_j \}\).
Let  be the share that are committed to in the com row in the right session k. We consider two cases.
be the share that are committed to in the com row in the right session k. We consider two cases.
-
Case 1.
 is 0.9-close to a valid codeword \({\varvec{w}} = (w_1, \ldots , w_{10\lambda })\)
.
is 0.9-close to a valid codeword \({\varvec{w}} = (w_1, \ldots , w_{10\lambda })\)
.
Since \(\left| {\varLambda _1} \right| \le \lambda \),
 and
and  are 0.9-close (this follows from Eq. (2)), so
are 0.9-close (this follows from Eq. (2)), so  is 0.8-close to
is 0.8-close to  . Hence,
. Hence,  if \(w_j\) equals to the value revealed in Stage 5 for every \(j\in \varGamma \), and
if \(w_j\) equals to the value revealed in Stage 5 for every \(j\in \varGamma \), and  otherwise.
otherwise. -
Case 2.
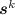 is 0.1-far from any valid codeword.
is 0.1-far from any valid codeword.
We have
 if
if  is 0.2-far from any valid codeword, or is 0.8-close to a valid codeword \({\varvec{w}} = (w_1, \ldots , w_{10\lambda })\) but \(w_j\) does not equal the value revealed in Stage 5 for some \(j\in \varGamma ^k\). Now, we argue that
is 0.2-far from any valid codeword, or is 0.8-close to a valid codeword \({\varvec{w}} = (w_1, \ldots , w_{10\lambda })\) but \(w_j\) does not equal the value revealed in Stage 5 for some \(j\in \varGamma ^k\). Now, we argue that  cannot be 0.8-close to a valid codeword \({\varvec{w}} = (w_1, \ldots , w_{10\lambda })\) such that \(w_j\) equals the value that is revealed in Stage 5 for every \(j\in \varGamma ^k\). Assume for contradiction that
cannot be 0.8-close to a valid codeword \({\varvec{w}} = (w_1, \ldots , w_{10\lambda })\) such that \(w_j\) equals the value that is revealed in Stage 5 for every \(j\in \varGamma ^k\). Assume for contradiction that  is 0.8-close to such \({\varvec{w}} = (w_1, \ldots , w_{10\lambda })\). Then, since \(\left| {\varLambda _2} \right| \le \lambda \), it follows that
is 0.8-close to such \({\varvec{w}} = (w_1, \ldots , w_{10\lambda })\). Then, since \(\left| {\varLambda _2} \right| \le \lambda \), it follows that  is actually 0.9-close to
is actually 0.9-close to  . However, since we have \(\tilde{s}^k_j = s_j^k\) for every \(j\in \{ j | \tilde{s}^k_j \ne \bot \}\) (this follows from Eq. (2)), and we have \(\tilde{s}^k_j \ne \bot \) for every \(j\in \{ j | \tilde{s}^k_j = w_j \}\) (this is because
. However, since we have \(\tilde{s}^k_j = s_j^k\) for every \(j\in \{ j | \tilde{s}^k_j \ne \bot \}\) (this follows from Eq. (2)), and we have \(\tilde{s}^k_j \ne \bot \) for every \(j\in \{ j | \tilde{s}^k_j = w_j \}\) (this is because 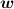 is a valid codeword), 0.9-closeness between
is a valid codeword), 0.9-closeness between  and
and  implies that
implies that  is also 0.9-close to
is also 0.9-close to  . This is contradiction because we assume that
. This is contradiction because we assume that  is 0.1-far from any valid codeword.
is 0.1-far from any valid codeword.
Hence, we have  , i.e., \(v^k = \tilde{v}^k\), in both cases. \(\blacksquare \)
, i.e., \(v^k = \tilde{v}^k\), in both cases. \(\blacksquare \)
Claim 3
For every \(b \in \{ 0,1 \}\), it holds that,
Proof
Note that the only difference between \(G^b\) and \(H_0^b\) is that in the former the \(\mathsf{CECom} \) receivers and the CECom-setup are simulated by  , whereas in the latter, they are emulated honestly. It follows directly from the statistical emulation property of
, whereas in the latter, they are emulated honestly. It follows directly from the statistical emulation property of  that these two hybrids are statistically close. (Note that the statistical emulation property of
that these two hybrids are statistically close. (Note that the statistical emulation property of  applies to even computationally unbound committers, which is the case here as hybrid \(H_0^b\) and \(G^b\) are not efficient.) \(\blacksquare \)
applies to even computationally unbound committers, which is the case here as hybrid \(H_0^b\) and \(G^b\) are not efficient.) \(\blacksquare \)
It follows from the above claims and a standard hybrid argument that hybrids \(H^b_0\) and \(H^b_1\) are indistinguishable. This concludes the proof of Lemma 2. \(\blacksquare \)
-
Hybrid \(H_{2}^{b}(\lambda ,z)\) is the same as \(H_{1}^{b}(\lambda ,z)\) except that on the left it uses the extractor
 of \(\mathsf {ECom}\) to extract a subset \(\varGamma '\) from Stage 1 of the left session. More precisely,
of \(\mathsf {ECom}\) to extract a subset \(\varGamma '\) from Stage 1 of the left session. More precisely,-
− Use the extractor
 of \(\mathsf {ECom}\) to emulate (i) the receiver of \(\mathsf {ECom}\) in Stage 1 of the left session and in Stage 5 when A opens this \(\mathsf {ECom}\) commitment, as well as (ii) the ECom-setup.
of \(\mathsf {ECom}\) to emulate (i) the receiver of \(\mathsf {ECom}\) in Stage 1 of the left session and in Stage 5 when A opens this \(\mathsf {ECom}\) commitment, as well as (ii) the ECom-setup.By definition, at the end of Stage 1 in the left session,
 outputs a value \(\varGamma '\), interpreted as a subset, on its special output tape.
outputs a value \(\varGamma '\), interpreted as a subset, on its special output tape. -
− Furthermore, in Stage 5, if A opens successfully to a set \(\varGamma \) and \(\varGamma \ne \varGamma '\), abort and output \(\textsf {ERR}\).
-
Lemma 3
For every \(b\in \{ 0,1 \}\), it holds that,
Proof
The only difference between these two hybrids lies in that in \(H^b_2\), the receiver of \(\mathsf {ECom}\) in the left session and the ECom-setup are emulated, and the hybrid aborts if the extracted subset \(\varGamma '\) disagree with the subset that A opens to. Since \(H^b_2\) is completely efficient, it follows from the extractability w.r.t. opening property of  that the subset \(\varGamma \) that A opens to must agree with the extracted subset \(\varGamma '\) except for negligible probability. Moreover, conditioned on not aborting, since the extracted subset \(\varGamma '\) is never used otherwise, it follows from the statistical emulation property of
that the subset \(\varGamma \) that A opens to must agree with the extracted subset \(\varGamma '\) except for negligible probability. Moreover, conditioned on not aborting, since the extracted subset \(\varGamma '\) is never used otherwise, it follows from the statistical emulation property of  that
that  statistically emulates the receiver of \(\mathsf {ECom}\) and the ECom-setup. Therefore, \(H^b_1\) and \(H^b_2\) are statistically close. \(\blacksquare \)
statistically emulates the receiver of \(\mathsf {ECom}\) and the ECom-setup. Therefore, \(H^b_1\) and \(H^b_2\) are statistically close. \(\blacksquare \)
Then, since the two hybrids \(H^b_1\) and \(H^b_2\) are statistically close, and by Lemma 1, bad events \(\mathrm{Bad}_{\text {NM}}, \mathrm{Bad}_{\text {CEC}}\) do not happen in \(H^b_1\), they do not happen in \(H^b_2\) either.
Lemma 4
For every \(b\in \{ 0,1 \}\), it holds that, the probabilities that event  and \(\mathrm{Bad}_\mathrm{CEC}\) occur are negligible in \(H^b_2\).
and \(\mathrm{Bad}_\mathrm{CEC}\) occur are negligible in \(H^b_2\).
- Hybrid :
-
\(H_{3}^{b}(\lambda ,z)\) is the same as \(H_{2}^{b}(\lambda ,z)\) except that in the NMCom-row on the left, the left committer commits to 0 instead of \(((s_j, d_j), e_j)\) for every \(j\not \in \varGamma \).
Note that both \(H^b_2\) and \(H^b_3\) are completely efficient. Thus, it follows directly from the hiding property of the left \(\mathsf {NMCom}\) commitments that \(H^b_2\) and \(H^b_3\) are indistinguishable.
Lemma 5
For every \(b\in \{ 0,1 \}\), it holds that,
Moreover, we argue that the bad events \(\mathrm{Bad}_{\text {NM}}\) and \(\mathrm{Bad}_\mathrm{CEC}\) do not occur in \(H_3^b\) either.
Lemma 6
For every \(b\in \{ 0,1 \}\), it holds that, the probabilities that event  and \(\mathrm{Bad}_\mathrm{CEC}\) occur are negligible in \(H^b_3\).
and \(\mathrm{Bad}_\mathrm{CEC}\) occur are negligible in \(H^b_3\).
It follows from the hiding property of the left \(\mathsf {NMCom}\) commitments that if event \(\mathrm{Bad}_{CEC}\) does not occur in \(H^b_2\), then it does not occur in \(H^b_3\) either. Furthermore, it follows from the concurrent non-malleability property of \(\mathsf {NMCom}\) that the values committed to in the \(\mathsf {NMCom}\) commitments are indistinguishable in \(H_2^b\) and \(H_3^b\). Therefore, it follows from Lemma 4 that \(\mathrm{Bad}_{\text {NM}}\) almost never occurs in \(H^b_3\).
- Hybrid :
-
\(H_{4}^{b}(\lambda ,z)\) is the same as \(H_{3}^{b}(\lambda ,z)\) except that on the right A interacts with the
 oracle.
oracle.The only difference between \(H_4^b\) and \(H_3^b\) lies in that in the former A interacts with
 on the right, whereas in the latter
on the right, whereas in the latter  is emulated using the extractor
is emulated using the extractor  of \(\mathsf{CECom} \). This difference is the same as that between \(H_0^b\) and \(H_1^b\). Furthermore, as in \(H_1^b\), event \(\mathrm{Bad}_{CEC}\) does not occur in hybrid \(H^b_3\) by Lemma 6. Thus, it follows from the same proof that \(H^b_3\) and \(H^b_4\) are statistically close.
of \(\mathsf{CECom} \). This difference is the same as that between \(H_0^b\) and \(H_1^b\). Furthermore, as in \(H_1^b\), event \(\mathrm{Bad}_{CEC}\) does not occur in hybrid \(H^b_3\) by Lemma 6. Thus, it follows from the same proof that \(H^b_3\) and \(H^b_4\) are statistically close.
Lemma 7
For every \(b\in \{ 0,1 \}\), it holds that,
Given that \(H^b_3\) and \(H^b_4\) are statistically close, it follows from Lemma 6 that event \(\mathrm{Bad}_{\text {NM}}\) occurs with only negligible probability in \(H^b_4\).
Lemma 8
For every \(b\in \{ 0,1 \}\), it holds that, the probability that event \(\mathrm{Bad}_{\text {NM}}\) occur is negligible in \(H^b_4\).
- Hybrid :
-
\(H_{5}^{b}(\lambda ,z)\) is the same as \(H_{4}^{b}(\lambda ,z)\) except that on the right, it uses the committed-value oracle
 of \(\mathsf {NMCom}\) to emulate
of \(\mathsf {NMCom}\) to emulate  as follows:
as follows: - 1.:
-
Emulate the receivers of \(\mathsf {CCACom} \) honestly for A, except that all \(\mathsf {NMCom}\) commitments are forwarded to
 , which emulates the receivers of \(\mathsf {NMCom}\) perfectly. By definition of
, which emulates the receivers of \(\mathsf {NMCom}\) perfectly. By definition of  , at the end of each NMCom-row, say in the right session k,
, at the end of each NMCom-row, say in the right session k,  returns the vector of committed values, parsed as \(\{ {({{\hat{s}}}^k_j, {d}^k_j), e^k_j} \}_{j \in [10\lambda ]}\). Set
returns the vector of committed values, parsed as \(\{ {({{\hat{s}}}^k_j, {d}^k_j), e^k_j} \}_{j \in [10\lambda ]}\). Set  , where
, where  is described in Eq. (3).
is described in Eq. (3). - 2.:
-
At the end of each right session k, emulate the committed value that
 returns, by returning the value
returns, by returning the value  , where \(\widetilde{\mathsf {Value}}\) is defined in Eq. (4).
, where \(\widetilde{\mathsf {Value}}\) is defined in Eq. (4).
Lemma 9
For every \(b\in \{ 0,1 \}\), it holds that,
Proof
Note that in \(H^b_5\), the receivers of \(\mathsf {CCACom} \) are emulated perfectly for A. Therefore, the only difference between \(H^b_5\) and \(H^b_4\) lies in how the committed values of the right sessions are extracted: in \(H^b_5\) they are reconstructed from the values committed to in the NMCom-rows, whereas in \(H^b_4\), the actually committed values are extracted by brute-force by  . Thus it suffices to show that in \(H_5^b\) the values \(\{ {\hat{v}^k} \}\) reconstructed from the values committed to in the NMCom-rows are the actual committed values \(\{ {v^k} \}\) with overwhelming probability. By Lemma 8, event \(\mathrm{Bad}_{\text {NM}}\) does not occur in \(H_4^b\), except for negligible probability. Then, it follows from the same argument as in the proof of Claim 2 that when \(\mathrm{Bad}_{\text {NM}}\) does not occur, \(\hat{v}^k = v^k\) for every right session k. \(\blacksquare \)
. Thus it suffices to show that in \(H_5^b\) the values \(\{ {\hat{v}^k} \}\) reconstructed from the values committed to in the NMCom-rows are the actual committed values \(\{ {v^k} \}\) with overwhelming probability. By Lemma 8, event \(\mathrm{Bad}_{\text {NM}}\) does not occur in \(H_4^b\), except for negligible probability. Then, it follows from the same argument as in the proof of Claim 2 that when \(\mathrm{Bad}_{\text {NM}}\) does not occur, \(\hat{v}^k = v^k\) for every right session k. \(\blacksquare \)
Given that \(H^b_5\) and \(H^b_4\) are statistically close, it follows from Lemma 8 that event \(\mathrm{Bad}_{\text {NM}}\) occurs with negligible probability in \(H^b_5\).
Lemma 10
For every \(b\in \{ 0,1 \}\), it holds that, the probability that event \(\mathrm{Bad}_{\text {NM}}\) occur is negligible in \(H^b_5\).
- Hybrid :
-
\(H_{6}^{b}(\lambda ,z)\) is the same as \(H_{5}^{b}(\lambda ,z)\) except that on the right, it uses the universal simulator
 of \(\mathsf {NMCom}\) to emulate
of \(\mathsf {NMCom}\) to emulate  .
.It follows directly from the concurrent extractability w.r.t. commitment property of \(\mathsf {NMCom}\) that \(H_6^b\) and \(H_5^b\) are indistinguishable.
Lemma 11
For every \(b\in \{ 0,1 \}\), it holds that,
- Hybrid :
-
\(H_{7}^{b}(\lambda ,z)\) is the same as \(H_{6}^{b}(\lambda ,z)\) except that on the left, the left committer (i) commits to 0 instead of \(s_j\) for every \(j\not \in \varGamma \) in the com-row, and (ii) commits to 0 instead of \((s_j, d_j)\) for every \(j\not \in \varGamma \) in the CECom-row.
Note that both \(H^b_6\) and \(H^b_7\) are completely efficient. Thus, it follows directly from the hiding property of the left \({{\textsf {com}}} \) commitments and \(\mathsf{CECom} \) commitments that \(H^b_7\) and \(H^b_6\) are indistinguishable.
Lemma 12
For every \(b\in \{ 0,1 \}\), it holds that,
Finally, notice that in hybrid \(H_7^b\), in the left session, the committer commits to 0 in all of the com, CECom, and NMCom rows. This means A receives no information about whether \(v_0\) or \(v_1\) is committed in \(H_{7}^b(\lambda ,z)\). Thus, the views of A in \(\mathsf {H}_{7}^{0}(\lambda ,z)\) and \(\mathsf {H}_{7}^{1}(\lambda ,z)\) are identically distributed.
Lemma 13
It holds that,
Given the lemmas, it follows from a hybrid argument that for every b, \(\{ \mathsf {H}_{0}^{b}(\lambda ,z) \} \approx \{ \mathsf {H}_{7}^{b}(\lambda ,z) \}\). Furthermore, given that \(\mathsf {H}_{7}^{0}(\lambda ,z)\) and \(\mathsf {H}_{7}^{1}(\lambda ,z)\) are identically distributed, we conclude that \(\{ \mathsf {H}_{0}^{0}(\lambda ,z) \} \approx \{ \mathsf {H}_{0}^{1}(\lambda ,z) \}\) and thus the \(\mathsf {CCACom} \) protocol is CCA-secure.
4 From CCA Commitments to UC Secure Protocols
We assume familiarity with the models of UC, Externalized UC (EUC), and Angel-based security/UC with super-polynomial helpers. See the full version for more details on these models.
4.1 The General Transformation
In this session, we show that given any commitment scheme \(\mathsf{CECom} \) in \(\mathcal {T}\)-model that is straight-line concurrently extractable w.r.t. opening, we can UC-realize every functionality in the \(\mathsf{4}\mathcal {T}\)-trusted-setup model. Formally,
Theorem 5
(UC-secure Protocols in \(\mathsf{4}\mathcal {T}\) -trusted-setup model from \(\mathsf{CECom} \) in \(\mathcal {T}\) -model). Let \(\mathcal {T}\) be any trusted-setup, and \(\mathsf{4}\mathcal {T}\) the corresponding quadruple-\(\mathcal {T}\) setup. Then, for every well-formed functionality \(\mathcal {F}\), there is a fully black-box construction of a protocol \(\pi \) that UC-realizes \(\mathcal {F}\) in the \(\mathsf{4}\mathcal {T}\)-trusted setup model, from the following primitives:
-
a O(1)-round semi-honest secure oblivious transfer protocol, and
-
a commitment scheme \(\mathsf{CECom} \) in \(\mathcal {T}\)-model that is straight-line concurrently extractable w.r.t. opening and resettably hiding.
Moreover, if \(\mathsf{CECom} \) has \(r_{\textsc {cec}}\) rounds, \(\pi \) has \(O(r_{\textsc {cec}})\) rounds.
We achieve the theorem in three steps.
- Step 1: :
-
Starting from a \(r_{\textsc {cec}}\)-round commitment scheme \(\mathsf{CECom} \) that is straight-line concurrently extractable w.r.t. opening and resettably hiding in the \(\mathcal {T}\)-model, by Theorem 4, there is fully black-box construction of a CCA-secure commitment scheme \(\mathsf {CCACom} \) in \(\mathsf{4}\mathcal {T}\)-model that is also straight-line concurrently extractable w.r.t. commitment, and the scheme has \(r_{\textsc {cca}}= O(r_{\textsc {cec}})\) rounds. Recall that by Claim 1, such a scheme is also \(\mathrm{poly}\)-robust.
- Step 2: :
-
Given a \(\mathrm{poly}\)-robust CCA-secure commitment scheme \(\mathsf {CCACom} \), it follows from the work of Lin and Pass [19] that every well-formed functionality \(\mathcal {F}\) can be EUC-realized w.r.t. the shared functionality \(\bar{\mathcal{H}}_{\mathsf {CCACom}}\) defined by \(\mathsf {CCACom} \). Roughly speaking, \(\bar{\mathcal{H}}_{\mathsf {CCACom}}\) runs the committed-value oracle of \(\mathsf {CCACom} \) for every party with the restriction that when invoked by a party with identity \(\mathsf {ID}= (P_i, sid)\) (consisting of party ID \(P_i\) and session ID sid), it only breaks \(\mathsf {CCACom} \) commitments with exactly the same identity \(\mathsf {ID}\). Since we here consider robust CCA-secure \(\mathsf {CCACom} \) in \(\mathsf{4}\mathcal {T}\)-model, all parties also have access to \(\mathsf{4}\mathcal {T}\). Thus, we let \(\bar{\mathcal{H}}_{\mathsf {CCACom}}\) run also the setup \(\mathsf{4}\mathcal {T}\). A formal description of the functionality is in Fig. 1.
Therefore, honest parties interact with \(\bar{\mathcal{H}}_{\mathsf {CCACom}}\) to access \(\mathsf{4}\mathcal {T}\), while corrupted parties, adversaries A/S, and environment Z can interact with \(\bar{\mathcal{H}}_{\mathsf {CCACom}}\) to access both \(\mathsf{4}\mathcal {T}\) and the committed-value oracles
 . We note that since the work of [19] considers CCA secure commitment schemes in the plain model, their helper functionalities only run the committed-value oracle, and the honest parties never access the helper functionality. Their construction and security proof extends directly to our case where the honest parties access the helper functionality for \(\mathsf{4}\mathcal {T}\) only, but not
. We note that since the work of [19] considers CCA secure commitment schemes in the plain model, their helper functionalities only run the committed-value oracle, and the honest parties never access the helper functionality. Their construction and security proof extends directly to our case where the honest parties access the helper functionality for \(\mathsf{4}\mathcal {T}\) only, but not  .
.
Theorem 6
([19]). Assume the existence of a \(r_{\textsc {cca}}\)-round \(\mathrm{poly}\)-robust CCA-secure commitment scheme \(\mathsf {CCACom} \) in the \(\mathsf{4}\mathcal {T}\)-trusted-setup model, and a constant-round semi-honest secure oblivious transfer protocol. Then, for every well-formed functionality \(\mathcal {F}\), there is a fully black-box construction of a \(O(r_{\textsc {cec}})\)-round protocol \(\pi \) that \(\bar{\mathcal{H}}_{\mathsf {CCACom}}\)-EUC-realizes \(\mathcal {F}\).
- Step 3: :
-
Finally, we move from EUC-security w.r.t. shared functionality \(\bar{\mathcal{H}}_{\mathsf {CCACom}}\) back to UC-security w.r.t. \(\mathsf{4}\mathcal {T}\)-trusted-setup, by crucially relying on the fact that \(\mathsf {CCACom} \) is straight-line concurrently extractable w.r.t. commitment.
Theorem 7
Let \(\mathsf {CCACom} \) be any commitment scheme that is CCA-secure and straight-line concurrently extractable w.r.t. commitment in the \(\mathsf{4}\mathcal {T}\)-trusted-setup model. For every well-formed functionality \(\mathcal {F}\), if protocol \(\pi \) \(\bar{\mathcal{H}}_{\mathsf {CCACom}}\)-EUC-realizes \(\mathcal {F}\), then \(\pi \) UC-realizes \(\mathcal {F}\) in the \(\mathsf{4}\mathcal {T}\)-trusted-setup model.
To show that \(\pi \) UC-realizes \(\mathcal {F}\) in the \(\mathsf{4}\mathcal {T}\)-trusted-setup model, we need to show that its multi-session extension \(\hat{\pi }\) UC-realizes the multi-session extension \(\hat{\mathcal {F}}\) of \(\mathcal {F}\) in the \(\mathsf{4}\mathcal {T}\)-hybrid model. This follows from the following two simple observations.
First, combining the universal composition theorem of EUC with Theorem 6 gives that \(\hat{\pi }\) \(\bar{\mathcal{H}}_{\mathsf {CCACom}}\)-EUC-realizes \(\hat{F}\). That is, for any \(\mathsf{PPT} \) adversary \(\mathcal {A} \), there exists a \(\mathsf{PPT}\) simulator S, such that, for every \(\mathsf{PPT} \) environment Z, it holds that
where \(\bar{\mathcal{H}}\) is a short hand for \(\bar{\mathcal{H}}_{\mathsf {CCACom}}\).
By definition of EUC, the above indistinguishability holds for arbitrary A and Z that may or may not access the shared functionality \(\bar{\mathcal{H}}\). Consider the special case where \(\mathcal {A} \) never accesses  in \(\bar{\mathcal{H}}\) (but may access \(\mathsf{4}\mathcal {T}\) in \(\bar{\mathcal{H}}\)), and Z never accesses \(\bar{\mathcal{H}}\) at all. In this case, in the real execution, honest parties of \(\hat{\pi }\) and \(\mathcal {A} \) may access \(\mathsf{4}\mathcal {T}\) in \(\bar{\mathcal{H}}\), and no party accesses
in \(\bar{\mathcal{H}}\) (but may access \(\mathsf{4}\mathcal {T}\) in \(\bar{\mathcal{H}}\)), and Z never accesses \(\bar{\mathcal{H}}\) at all. In this case, in the real execution, honest parties of \(\hat{\pi }\) and \(\mathcal {A} \) may access \(\mathsf{4}\mathcal {T}\) in \(\bar{\mathcal{H}}\), and no party accesses  in \(\bar{\mathcal{H}}\). Note that this is simply an execution \({\textsc {exec}}_{\hat{\pi }, \mathcal {A}, Z}(\lambda , z)\) of \(\hat{\pi }\) with adversary \(\mathcal {A} \) and environment Z in the \(\mathsf{4}\mathcal {T}\)-hybrid-model. On the other hand, in the ideal execution, only the simulator S interacts with \(\bar{\mathcal{H}}\) and no other party interacts with \(\bar{\mathcal{H}}\) at all.
in \(\bar{\mathcal{H}}\). Note that this is simply an execution \({\textsc {exec}}_{\hat{\pi }, \mathcal {A}, Z}(\lambda , z)\) of \(\hat{\pi }\) with adversary \(\mathcal {A} \) and environment Z in the \(\mathsf{4}\mathcal {T}\)-hybrid-model. On the other hand, in the ideal execution, only the simulator S interacts with \(\bar{\mathcal{H}}\) and no other party interacts with \(\bar{\mathcal{H}}\) at all.
Next, to show that \(\pi \) UC-realizes \(\mathcal {F}\) in \(\mathsf{4}\mathcal {T}\) trusted-setup model, we need to show that \(\hat{\pi }\) UC-emulates the ideal protocol \(\mathcal {I} _{\hat{\mathcal {F}}}\) of \(\hat{F}\) in the \(\mathsf{4}\mathcal {T}\)-hybrid model. That is, for any \(\mathsf{PPT} \) adversary \(\mathcal {A} \), there exists a \(\mathsf{PPT}\) simulator \(S'\), such that, for any \(\mathsf{PPT} \) environment Z, it holds that
As discussed above, for any \(\mathcal {A} \), Z, \(\lambda \) and z, the experiments \({\textsc {exec}}_{\hat{\pi },\mathcal {A},Z}(\lambda , z)\) and \({\textsc {exec}}^{\bar{\mathcal{H}}}_{\hat{\pi },\mathcal {A},Z}(\lambda , z)\) are identically distributed. We now use the simulator S for \(\mathcal {A} \) in the EUC model to construct the a simulator \(S'\) for \(\mathcal {A} \) in the UC model satisfying that
The only difference between these two ideal executions is that in the former Z interacts with \(S'\) and in the latter Z interacts with S who interacts with \(\bar{\mathcal{H}}\) (no other party accesses \(\bar{\mathcal{H}}\)). Construct \(S'\) as follows: It internally runs S and emulates (the committed-value oracle of \(\mathsf {CCACom} \) and the setup \(\mathsf{4}\mathcal {T}\) in) \(\bar{\mathcal{H}}\) for S, using the simulator  of \(\mathsf {CCACom} \). It follows directly from the concurrent extractability w.r.t. commitment property of \(\mathsf {CCACom} \) that the simulation is indistinguishable and so are the above two experiments. It then follows from a hybrid argument that \(S'\) is a valid simulator for \(\mathcal {A} \) in the UC model. Therefore, we conclude that \(\pi \) UC-realizes \(\mathcal {F}\) in the \(\mathsf{4}\mathcal {T}\)-trusted setup model.
of \(\mathsf {CCACom} \). It follows directly from the concurrent extractability w.r.t. commitment property of \(\mathsf {CCACom} \) that the simulation is indistinguishable and so are the above two experiments. It then follows from a hybrid argument that \(S'\) is a valid simulator for \(\mathcal {A} \) in the UC model. Therefore, we conclude that \(\pi \) UC-realizes \(\mathcal {F}\) in the \(\mathsf{4}\mathcal {T}\)-trusted setup model.
Combining the above three steps gives a protocol \(\pi \) that UC-realizes an arbitrary functionality \(\mathcal {F}\) in the \(\mathsf{4}\mathcal {T}\)-trusted setup model. In addition, it is easy to see that the protocol has \(O(r_{\textsc {cca}}) = O(r_{\textsc {cec}})\) rounds. This concludes Theorem 5.
4.2 Instantiation of CECom in the CRS Model
In this section we present our \(\mathsf{CECom} \) in the \(\mathcal {F}_\mathsf {CRS}\)-hybrid model.
 We will require a perfectly-correct semantically-secure public-key encryption scheme \((\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\) for this construction.
We will require a perfectly-correct semantically-secure public-key encryption scheme \((\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\) for this construction.
- Common Reference String. :
-
The common reference string is set to \(\mathsf {pk}\) where \((\mathsf {pk},\mathsf {sk})\) is sampled according to \(\mathsf {Gen}(1^\kappa )\).
- Input. :
-
C and R have as common input \(1^{\lambda }\) and identities \(\mathsf {sid}\), and C has private input \(v\in \{0,1\}^{\lambda }\).
- Commit Phase of \(\mathsf{CECom} _\mathsf {CRS}\).:
-
\(\mathrm{Sen}\) queries \(\mathcal {F}_\mathsf {CRS}\) to obtain the \(\mathsf {CRS}= \mathsf {pk}\). Then it samples randomness r and sends \(c = \mathsf {Enc}_\mathsf {pk}(v;r)\) to the receiver.
- Decommitment Phase. :
-
The sender simply reveals v, r.
From semantic security and correctness of the underlying encryption scheme, \(\mathsf{CECom} _\mathsf {CRS}\) is statistically binding, computationally hiding, straight-line concurrently extractable w.r.t. commitment, and resettably-hiding in the \(\mathcal {F}_\mathsf {CRS}\)-model. Therefore we have the following lemma:
Lemma 14
Assume the existence of public-key encryption scheme. Then, there exists a computationally-hiding statistically-binding commitment scheme that is (1) Straight-line concurrently extractable w.r.t commitment, and (2) Resettably-hiding in the Common Reference String Model.
Instantiation of \(\mathsf{CECom} \) in the Uniform Reference String Model. An immediate corollary to our instantiation in the CRS model is an instantiation in the uniform reference string (URS) model. Recall that in the URS model, the reference string is sampled as uniformly random. We can rely on the same construction as in the CRS model if the we rely on a dense public-key encryption scheme where additionally the distribution of the sampled public-keys are pseudorandom. More precisely we have the following corollary.
Corollary 1
Assume the existence of a dense public-key encryption scheme. Then, there exists a computationally-hiding statistically-binding commitment scheme that is (1) Straight-line concurrently extractable w.r.t commitment, and (2) Resettably-hiding in the Uniform Reference String Model.
4.3 Instantiation of CECom in the Tamper Proof Hardware Model
We assume familiarity of the global tamper proof model of [22], where operations related to tokens are captured by the ideal functionality \(\mathcal {F}_\mathsf {gwrap}\).
A simple extractable commitment based on tokens can be achieved as follows: The receiver chooses a function F from a pseudorandom function family that maps \(\{0,1\}^m\) to \(\{0,1\}^n\) bits where \(m \gg n\), and incorporates it into a token that it sends to the sender. Next, the sender commits to its input b by first sampling a random string \(u \in \{0,1\}^m\) and querying the PRF token on u to receive the value v. It sends as its commitment the string \({{\textsf {com}}} _b = (\mathsf {Ext}(u;r)\oplus b,r,v)\) where \(\mathsf {Ext}(\cdot ,\cdot )\) is a strong randomness extractor. Hiding follows from the fact that the PRF is highly compressing, while binding follows from the pseudorandomness of the underlying PRF. Extraction on the other hand can be achieved by allowing the simulator to observe the queries made by the sender to the token and waiting for a query to give the answer v. First, we remark that this commitment only achieves commitment w.r.t opening as the extraction procedure does not know when the commitment is correct. This is however not an issue as our general framework can rely on \(\mathsf{CECom} \) that has straight-line extractability w.r.t opening. A larger issue however is to handle resettability of tokens. A resetting receiver can leak information by creating a stateful token and rewinding the committer. We tackle this problem by observing that resettable hiding of our protocol can be solved by using a commitment scheme with “reusable” tokens. Such a scheme was presented in [22] and we here rely on a milder variant of this protocol.

Input. C and R receive as common inputs \(1^{\lambda }\) and identity \((\mathsf {sid},\mathsf {ssid})\), and individual inputs \(\mathsf {pid}_C\) and \(\mathsf {pid}_R\) respectively. C also receives as private input \(v\in \{0,1\}^{\lambda }\).
Commit Phase of \(\mathsf{CECom} _{\mathsf {TK}}\)
-
Round 1. The Receiver creates the following tokens and sends it to the sender.
-
− For every \(l \in [2\kappa ]\), Receiver chooses a random PRF keys \(\gamma _{b,l}\) (\(l \in [\kappa ], b \in \{0,1\}\)) from a PRF family \(\mathcal {F}\) from \(5\kappa \) bits to \(\kappa \). Then, for every (b, l), the Receiver creates the tokens \({\mathsf {TK}}^{{\mathsf {PRF}},l}\) by sending the message \(\{\mathsf {create},\mathsf {sid},\mathsf {ssid},\mathrm{Rec},\mathrm{Sen},\mathsf {tid}_{b,l}, M_{b,l}\}\), that on input x, outputs \({\mathsf {PRF}}_{\gamma _{b,l}}(x)\), where \(M_{b,l}\) is the functionality.
-
-
Round 2. \(\mathrm{Sen}\rightarrow \mathrm{Rec}\): \(\mathrm{Sen}\) picks \(\kappa \) random bits \(h_1,\ldots ,h_k\). For every \(i \in [\kappa ]\), run \({\mathsf {TK}}_{i,h_i}\) on input u and check if all token output the same value v. It they don’t output the receiver halts. Otherwise, it commits by transmitting \((\text {Ext}(u)\oplus m ,v)\) to the sender, where \(\text {Ext} : \{0, 1\}^{5\kappa }\times \{0, 1\}^d \rightarrow \{0, 1\}\) is a \((2\kappa +1,2^{-\kappa })\) randomness extractor and the seed has length d (for simpler exposition we drop the seed in the expression above).
-
Decommitment Phase. The sender simply reveals u and m.
The following properties follow directly from the pseudorandomness of the underlying PRF and the fact that the function is highly compressing. We provide formal proofs in the full version.
Proposition 1
\(\mathsf{CECom} _{\mathsf {TK}}= {\langle C,R \rangle }\) presented above is a computationally binding commitment scheme in the \(\mathcal {F}_\mathsf {gwrap}\)-model.
Proposition 2
\(\mathsf{CECom} _{\mathsf {TK}}\) is statistically hiding commitment scheme in the \(\mathcal {F}_\mathsf {gwrap}\)-model.
We can further show a stronger hiding property.
Proposition 3
\(\mathsf{CECom} _{\mathsf {TK}}\) is straight-line concurrently extractable w.r.t. opening in \(\mathcal {F}_\mathsf {gwrap}\)-model.
Proposition 4
\(\mathsf{CECom} _{\mathsf {TK}}\) is resettably-hiding in \(\mathcal {F}_\mathsf {gwrap}\)-model.
Notes
- 1.
In the tamper-proof hardware model, parties are assumed to have tamper-proof hardware tokens that only provide input/output (i.e. black-box) access to the token holder.
- 2.
As described in Sect. 2.1, in the binding game with \(\mathcal {T}\), R, and \(C^*\), R can interact with the trusted setup \(\mathcal {T}\) using an identity \(\mathsf {ID}_R\) chosen by \(C^*\), and \(C^*\) can interact with \(\mathcal {T}\) directly according to \(\mathcal {T}\)’s code, or indirectly as any parties with identities different from \(\mathsf {ID}_R\). Similarly, in the hiding game with \(\mathcal {T}\), C, and \(R^*\), C can interact with the trusted setup \(\mathcal {T}\) using an identity \(\mathsf {ID}_C\) chosen by \(R^*\), and \(R^*\) can interact with \(\mathcal {T}\) directly according to \(\mathcal {T}\)’s code, or indirectly as any parties with identities different from \(\mathsf {ID}_C\).
References
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: FOCS, pp. 136–145 (2001)
Canetti, R., Fischlin, M.: Universally composable commitments. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 19–40. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_2
Canetti, R., Kushilevitz, E., Lindell, Y.: On the limitations of universally composable two-party computation without set-up assumptions. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 68–86. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-39200-9_5
Canetti, R., Lindell, Y., Ostrovsky, R., Sahai, A.: Universally composable two-party and multi-party secure computation. In: STOC (2002)
Groth, J., Ostrovsky, R.: Cryptography in the multi-string model. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 323–341. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74143-5_18
Barak, B., Canetti, R., Nielsen, J.B., Pass, R.: Universally composable protocols with relaxed set-up assumptions. In: FOCS, pp. 186–195 (2004)
Canetti, R., Dodis, Y., Pass, R., Walfish, S.: Universally composable security with global setup. IACR Cryptology ePrint Archive 2006/432 (2006)
Kalai, Y.T., Lindell, Y., Prabhakaran, M.: Concurrent composition of secure protocols in the timing model. J. Cryptol. 20(4), 431–492 (2007)
Katz, J.: Universally composable multi-party computation using tamper-proof hardware. In: Naor, M. (ed.) EUROCRYPT 2007. LNCS, vol. 4515, pp. 115–128. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-72540-4_7
Canetti, R., Pass, R., Shelat, A.: Cryptography from sunspots: how to use an imperfect reference string. In: FOCS, pp. 249–259 (2007)
Lin, H., Pass, R., Venkitasubramaniam, M.: A unified framework for concurrent security: universal composability from stand-alone non-malleability. In: STOC, pp. 179–188 (2009)
Kilian, J.: Founding cryptography on oblivious transfer. In: 20th ACM STOC, pp. 20–31. ACM Press, May 2008
Ishai, Y., Kushilevitz, E., Lindell, Y., Petrank, E.: Black-box constructions for secure computation. In: STOC, pp. 99–108 (2006)
Haitner, I.: Semi-honest to malicious oblivious transfer—the black-box way. In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 412–426. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78524-8_23
Ishai, Y., Prabhakaran, M., Sahai, A.: Founding cryptography on oblivious transfer – efficiently. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 572–591. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_32
Pass, R., Wee, H.: Black-box constructions of two-party protocols from one-way functions. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 403–418. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00457-5_24
Wee, H.: Black-box, round-efficient secure computation via non-malleability amplification. In: 51st FOCS, pp. 531–540. IEEE Computer Society Press, October 2010
Goyal, V., Lee, C., Ostrovsky, R., Visconti, I.: Constructing non-malleable commitments: a black-box approach. In: FOCS, pp. 51–60 (2012)
Lin, H., Pass, R.: Black-box constructions of composable protocols without set-up. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 461–478. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_27
Kiyoshima, S.: Round-efficient black-box construction of composable multi-party computation. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8617, pp. 351–368. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44381-1_20
Hazay, C., Venkitasubramaniam, M.: On black-box complexity of universally composable security in the CRS model. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9453, pp. 183–209. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48800-3_8
Hazay, C., Polychroniadou, A., Venkitasubramaniam, M.: Composable security in the tamper-proof hardware model under minimal complexity. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9985, pp. 367–399. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53641-4_15
Pass, R., Lin, H., Venkitasubramaniam, M.: A unified framework for UC from only OT. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 699–717. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34961-4_42
Damgård, I., Nielsen, J.B.: Improved non-committing encryption schemes based on a general complexity assumption. In: Bellare, M. (ed.) CRYPTO 2000. LNCS, vol. 1880, pp. 432–450. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44598-6_27
Damgård, I., Groth, J.: Non-interactive and reusable non-malleable commitment schemes. In: STOC, pp. 426–437 (2003)
Choi, S.G., Katz, J., Wee, H., Zhou, H.-S.: Efficient, adaptively secure, and composable oblivious transfer with a single, global CRS. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 73–88. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36362-7_6
Lindell, Y.: Highly-efficient universally-composable commitments based on the DDH assumption. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 446–466. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20465-4_25
Goyal, V., Ishai, Y., Sahai, A., Venkatesan, R., Wadia, A.: Founding cryptography on tamper-proof hardware tokens. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 308–326. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11799-2_19
Moran, T., Segev, G.: David and Goliath commitments: UC computation for asymmetric parties using tamper-proof hardware. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 527–544. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_30
Chandran, N., Goyal, V., Sahai, A.: New constructions for UC secure computation using tamper-proof hardware. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 545–562. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_31
Döttling, N., Kraschewski, D., Müller-Quade, J.: Unconditional and composable security using a single stateful tamper-proof hardware token. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 164–181. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_11
Döttling, N., Mie, T., Müller-Quade, J., Nilges, T.: Implementing resettable UC-functionalities with untrusted tamper-proof hardware-tokens. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 642–661. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_36
Döttling, N., Kraschewski, D., Müller-Quade, J., Nilges, T.: General statistically secure computation with bounded-resettable hardware tokens. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9014, pp. 319–344. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46494-6_14
Choi, S.G., Katz, J., Schröder, D., Yerukhimovich, A., Zhou, H.-S.: (Efficient) Universally composable oblivious transfer using a minimal number of stateless tokens. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 638–662. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_27
Dodis, Y., Fiore, D.: Interactive encryption and message authentication. In: Abdalla, M., De Prisco, R. (eds.) SCN 2014. LNCS, vol. 8642, pp. 494–513. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10879-7_28
De Santis, A., Persiano, G.: Zero-knowledge proofs of knowledge without interaction (extended abstract). In: 33rd FOCS, pp. 427–436. IEEE Computer Society Press, October 1992
Gertner, Y., Kannan, S., Malkin, T., Reingold, O., Viswanathan, M.: The relationship between public key encryption and oblivious transfer. In: 41st FOCS, pp. 325–335. IEEE Computer Society Press, November 2000
van Dijk, M., Rührmair, U.: Physical unclonable functions in cryptographic protocols: security proofs and impossibility results. IACR Cryptology ePrint Archive 2012/228 (2012)
Canetti, R., Jain, A., Scafuro, A.: Practical UC security with a global random oracle. In: CCS, pp. 597–608 (2014)
Canetti, R., Lin, H., Pass, R.: Adaptive hardness and composable security in the plain model from standard assumptions. In: FOCS, pp. 541–550 (2010)
Prabhakaran, M., Sahai, A.: New notions of security: achieving universal composability without trusted setup. In: STOC, pp. 242–251 (2004)
Pass, R.: Simulation in quasi-polynomial time, and its application to protocol composition. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 160–176. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-39200-9_10
Malkin, T., Moriarty, R., Yakovenko, N.: Generalized environmental security from number theoretic assumptions. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 343–359. Springer, Heidelberg (2006). https://doi.org/10.1007/11681878_18
Goyal, V., Lin, H., Pandey, O., Pass, R., Sahai, A.: Round-efficient concurrently composable secure computation via a robust extraction lemma. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9014, pp. 260–289. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46494-6_12
Choi, S.G., Dachman-Soled, D., Malkin, T., Wee, H.: Black-box construction of a non-malleable encryption scheme from any semantically secure one. In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 427–444. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78524-8_24
Naor, M., Yung, M.: Public-key cryptosystems provably secure against chosen ciphertext attacks. In: 22nd ACM STOC, pp. 427–437. ACM Press, May 1990
Lin, H., Pass, R., Venkitasubramaniam, M.: Concurrent non-malleable commitments from any one-way function. In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 571–588. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78524-8_31
Naor, M.: Bit commitment using pseudorandomness. J. Cryptol. 4, 151–158 (1991)
Acknowledgments
We sincerely thank the anonymous reviewers for their incredibly helpful and insightful comments and suggestions.
Huijia Lin was supported by NSF grants CNS-1528178, CNS-1514526, CNS-1652849 (CAREER), a Hellman Fellowship, the Defense Advanced Research Projects Agency (DARPA) and Army Research Office (ARO) under a subcontract No. 2017-002 through Galois. Muthuramakrishnan Venkitasubramaniam is supported by a Google Faculty Research Grant and NSF Awards CNS-1526377 and CNS-1618884. The views expressed are those of the authors and do not reflect the official policy or position of the Department of Defense, the National Science Foundation, the U.S. Government or Google.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Kiyoshima, S., Lin, H., Venkitasubramaniam, M. (2017). A Unified Approach to Constructing Black-Box UC Protocols in Trusted Setup Models. In: Kalai, Y., Reyzin, L. (eds) Theory of Cryptography. TCC 2017. Lecture Notes in Computer Science(), vol 10677. Springer, Cham. https://doi.org/10.1007/978-3-319-70500-2_26
Download citation
DOI: https://doi.org/10.1007/978-3-319-70500-2_26
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70499-9
Online ISBN: 978-3-319-70500-2
eBook Packages: Computer ScienceComputer Science (R0)



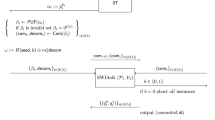


 .
. in an arbitrary number of interactions as below:
in an arbitrary number of interactions as below:  from
from  use fresh randomness after
use fresh randomness after 

 are
are 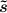 is 0.8-close to a valid codeword
is 0.8-close to a valid codeword  , yet 0.1-far from it, that is,
, yet 0.1-far from it, that is,  agrees with the shares
agrees with the shares  oracle is emulated efficiently using the extractor
oracle is emulated efficiently using the extractor  of
of  to emulate (i) the
to emulate (i) the  outputs a vector of values
outputs a vector of values  , where
, where  is described in Eq. (
is described in Eq. ( returns, by returning the value
returns, by returning the value  reconstructed from the shares
reconstructed from the shares  where
where 
 contains more than
contains more than 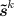 is 0.8-close to
is 0.8-close to  , yet 0.1-far from it, i.e.,
, yet 0.1-far from it, i.e.,  agree with the shares opened in Stage 5 of right session k.
agree with the shares opened in Stage 5 of right session k. in
in  in
in  (resp.
(resp.  ). By definition,
). By definition,  (resp.
(resp.  ) returns after every NMCom row the values committed to in this row.
) returns after every NMCom row the values committed to in this row.  , and other receiver messages are generated honestly). However, at the end of each right session k, committed value that
, and other receiver messages are generated honestly). However, at the end of each right session k, committed value that  returns is emulated differently: It extracts the shares
returns is emulated differently: It extracts the shares  , where
, where 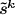 is 0.8-close to a valid codeword
is 0.8-close to a valid codeword  is 0.9-close to a valid codeword
is 0.9-close to a valid codeword  and
and  are 0.9-close (this follows from Eq. (
are 0.9-close (this follows from Eq. ( is 0.8-close to
is 0.8-close to  . Hence,
. Hence,  if
if  otherwise.
otherwise. is 0.1-far from any valid codeword.
is 0.1-far from any valid codeword.
 if
if  is 0.2-far from any valid codeword, or is 0.8-close to a valid codeword
is 0.2-far from any valid codeword, or is 0.8-close to a valid codeword  cannot be 0.8-close to a valid codeword
cannot be 0.8-close to a valid codeword  is 0.8-close to such
is 0.8-close to such  is actually 0.9-close to
is actually 0.9-close to  . However, since we have
. However, since we have  is a valid codeword), 0.9-closeness between
is a valid codeword), 0.9-closeness between  and
and  implies that
implies that  is also 0.9-close to
is also 0.9-close to  . This is contradiction because we assume that
. This is contradiction because we assume that  is 0.1-far from any valid codeword.
is 0.1-far from any valid codeword. of
of  of
of  outputs a value
outputs a value  oracle.
oracle. on the right, whereas in the latter
on the right, whereas in the latter  is emulated using the extractor
is emulated using the extractor  of
of  of
of  as follows:
as follows:  , which emulates the receivers of
, which emulates the receivers of  , at the end of each NMCom-row, say in the right session k,
, at the end of each NMCom-row, say in the right session k,  returns the vector of committed values, parsed as
returns the vector of committed values, parsed as  , where
, where  is described in Eq. (
is described in Eq. ( returns, by returning the value
returns, by returning the value  , where
, where  of
of  .
.
 . We note that since the work of [
. We note that since the work of [ .
.