Abstract
An active research trend is to exploit the consensus mechanism of cryptocurrencies to secure the execution of distributed applications. In particular, some recent works have proposed fair lotteries which work on Bitcoin. These protocols, however, require a deposit from each player which grows quadratically with the number of players. We propose a fair lottery on Bitcoin which only requires a constant deposit.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Recent research on blockchain technologies studies how to extend the applications of cryptocurrencies from simple transfers of money to complex financial transactions. The goal is to make financial agreements or “smart contracts” [24] between mutually distrusting participants, and automatically enforce them via the consensus mechanism of the cryptocurrency, without relying on a trusted third party. In particular, some works propose to run smart contracts on top of existing cryptocurrencies (mostly, on Bitcoin). Many of these approaches, e.g. [1, 6, 8, 16,17,18], implement fair computations, where a set of players contribute to compute a function without revealing their inputs; fairness, studied in various forms, guarantees e.g. that any player that aborts after learning the output pays a penalty to all players that did not learn the output. Other works implement decentralised authorization systems [10], and contracts which allow users to make statements, penalising those which make conflicting ones [22].
A particular kind of smart contract is the one which implements a lottery among a set a players. Intuitively, this is an application where each one of N players puts their bets in a pot, and a winner—uniformly chosen among the players—gets the whole pot. Secure protocols for multiparty lotteries on Bitcoin have been recently proposed by [2, 4, 5, 8]. These protocols enjoy a fairness property, which roughly guarantees that: (i) each honest player will have (on average) a non-negative payoff, even in the presence of adversaries who play against; (ii) when all the players are honest, the protocol behaves as an ideal lottery: one player wins the whole pot, while all the others lose their bets.
To obtain the result, these protocols require that, to bet e.g. 1 coin, each one of the N players must block a deposit of \(O(N^2)\) coins throughout the whole protocolFootnote 1. Since the deposit grows quadratically with N, these protocols are only practical for a small number of players. In this paper we address this issue.
Contributions. We propose a fair protocol for multiparty lotteries, whose deposit does not depend on the number N of players. More specifically, our protocol is fair for any choice of the deposit value (including zero), and for any adversarial strategy. Furthermore, if the deposit value is positive, an adversary who tries to attack the protocol with the goal of altering the payoff of honest players, can only lose money on average. Our protocol is based on a single-elimination tournament, i.e. a tree of \(N-1\) two-player matches where the loser of each match is eliminated. Overall, a complete run of the protocol requires O(N) transactions on-chain and \(O(\log N)\) time (assuming that the time to put transactions on the Bitcoin ledger dominates the time required for communications and local computations). Our protocol has been implemented as an Ethereum smart contract; an implementation on Bitcoin would require a variant of the mechanism for verifying the signature of transactions, to allow the malleability of input fields.
An extended version of this paper is available online at [7].
2 Statically Signing Chains of Transactions
The current signature mechanism of Bitcoin is known to be unsuitable for signing chains of transactions before they are put on the ledgerFootnote 2. Consider e.g. two players,  and
and  , and three transactions,
, and three transactions,  ,
,  and
and  , made as follows.
, made as follows.
-
transaction
 has
has  as input, while
as input, while  has
has  as input: hence the three transactions form a chain.
as input: hence the three transactions form a chain. -
the out-scripts of
 and
and  require signatures by both players
require signatures by both players  and
and  .
.
The players want to put the chain of transactions on the ledger, assuming that  is already there. Intuitively, the players have two possible ways of proceeding:
is already there. Intuitively, the players have two possible ways of proceeding:
- dynamic signing: :
-
both players sign
 and put it on the ledger. After that, they both sign
and put it on the ledger. After that, they both sign  and put it on the ledger.
and put it on the ledger. - static signing: :
-
 signs both
signs both  and
and  before these transactions are on the ledger, and sends her signatures to
before these transactions are on the ledger, and sends her signatures to  . Then,
. Then,  adds his own signatures, and puts both
adds his own signatures, and puts both  and
and  , one after the other, on the ledger.
, one after the other, on the ledger.
Without the segregated witnesses feature [19], only dynamic signing is feasible. Of course, in static signing, the addition of  ’s signature to the in-script of
’s signature to the in-script of  alters its in-script.Footnote 3 Note that this will not invalidate
alters its in-script.Footnote 3 Note that this will not invalidate  ’s signature of
’s signature of  (because the signature does not consider the in-script), so
(because the signature does not consider the in-script), so  can still be put on the ledger. However, altering the in-script changes the hash of
can still be put on the ledger. However, altering the in-script changes the hash of  , which is used in
, which is used in  to refer to the previous transaction. Because of this,
to refer to the previous transaction. Because of this,  ’s signature of
’s signature of  is no longer valid, hence
is no longer valid, hence  can not put
can not put  on the ledger.
on the ledger.
A possible solution to this problem is to allow partial signatures, which e.g. neglect the in part of transactions, as already done for the in-script part. Indeed, even if  (i.e., the hash of
(i.e., the hash of  ) is modified, the (partial) signature in
) is modified, the (partial) signature in  is still valid, because it neglects the in part. More in general, we define below a signature scheme for Bitcoin transactions, allowing users to choose which parts M of the transaction to include in the signature. In this way, once the transaction is signed, anyone can modify the parts not in M without invalidating the signature. The ability of modifying transactions while preserving their signatures is called transaction malleability: while in some circumstances it can cause security vulnerabilities [3], if used in a controlled manner it can extend the range of applications built upon Bitcoin [1]. Note that the unsigned parts of a transaction can be freely altered by adversaries; therefore, designing a secure protocol must take into account for this possibility. E.g., in the previous static signing example,
is still valid, because it neglects the in part. More in general, we define below a signature scheme for Bitcoin transactions, allowing users to choose which parts M of the transaction to include in the signature. In this way, once the transaction is signed, anyone can modify the parts not in M without invalidating the signature. The ability of modifying transactions while preserving their signatures is called transaction malleability: while in some circumstances it can cause security vulnerabilities [3], if used in a controlled manner it can extend the range of applications built upon Bitcoin [1]. Note that the unsigned parts of a transaction can be freely altered by adversaries; therefore, designing a secure protocol must take into account for this possibility. E.g., in the previous static signing example,  can alter
can alter  so to refer to some
so to refer to some  whose out-script can be satisfied by
whose out-script can be satisfied by  ’s signature. In this way
’s signature. In this way  becomes unredeemable. To protect against this attack,
becomes unredeemable. To protect against this attack,  could use a fresh key in
could use a fresh key in  , so that nothing else can be redeemed by her signature.
, so that nothing else can be redeemed by her signature.
We anticipate that our lottery protocol does not require the whole flexibility of the signature mechanism outlined below, but it only relies on the malleability of the in and in-script fields. While the malleability of in-script is already allowed by the segregated witnesses release, that of in fields would require support from the signature verification mechanism (e.g., a new signature flag or opcode).
Signature scheme for transaction malleability. Let

and denote with  the bitstring obtained by concatenating the parts of the transaction
the bitstring obtained by concatenating the parts of the transaction  mentioned in M. We then define:
mentioned in M. We then define:

Hereafter, we use \(\sigma \) as a meta-variable for the partial signatures \(({ sig}_{k}(\ldots ),M)\), and \(\varvec{\sigma }\) for arrays of such pairs (we will always use the same convention for arrays). When k and \(\varvec{\sigma }\) have the same size n, we define:

Transaction templates. The mechanism shown above allows to statically sign chains of transactions; further, we can also use it to statically sign chains of the form  , where the transaction
, where the transaction  depends on a parameter y such that (i) y is unknown at signing time (it will only be known later on), and (ii) y only affects those parts of
depends on a parameter y such that (i) y is unknown at signing time (it will only be known later on), and (ii) y only affects those parts of  not included in the partial signatures. Under these assumptions, instantiating y in a later moment will not invalidate any signature. More importantly, while there might be a large number of values for y (and so, a large number of chains that can be put on the ledger), only one partial static signature of
not included in the partial signatures. Under these assumptions, instantiating y in a later moment will not invalidate any signature. More importantly, while there might be a large number of values for y (and so, a large number of chains that can be put on the ledger), only one partial static signature of  is needed (as well as for
is needed (as well as for  and
and  ).
).
Parametric descriptions like the chain above are useful when designing complex protocols, where the actual chain (or graph) of transactions to be put on the ledger depend on events known after signatures have already been computed. We now introduce a general notation for expressing transactions with parameters and variants, which hereafter we name transaction templates. Our notation shows all the possible forms of the malleable transaction parts which are used in a protocol. Further, we will show how to statically sign such transactions (in all their forms). We anticipate that, for our lottery protocol, the number of possible transactions is large, while the number of needed static signatures is small.
Hereafter, we fix  in our signature scheme, so making the in and in-script fields malleable.Footnote 4
in our signature scheme, so making the in and in-script fields malleable.Footnote 4

The general form of transaction templates  is shown on the right. The template
is shown on the right. The template  is parametrized over an array of values \(\mathbf {x}\), in a given domain. Further, for its in and in-script fields, the template describes a few variants, each of which may take some additional parameters \(\mathbf {y}\). Note that out-scripts may only refer to the template parameters \(\mathbf {x}\), while in and in-scripts may also refer to their own variant parameters \(\mathbf {y}\). Further, the in field refers to another template. A template
is parametrized over an array of values \(\mathbf {x}\), in a given domain. Further, for its in and in-script fields, the template describes a few variants, each of which may take some additional parameters \(\mathbf {y}\). Note that out-scripts may only refer to the template parameters \(\mathbf {x}\), while in and in-scripts may also refer to their own variant parameters \(\mathbf {y}\). Further, the in field refers to another template. A template  can be instantiated to a transaction
can be instantiated to a transaction  , by choosing the variant i and the parameters. Here,
, by choosing the variant i and the parameters. Here,  is set to any redeemable transaction on the ledger which is an instantiation of the template in the in field of
is set to any redeemable transaction on the ledger which is an instantiation of the template in the in field of  .
.
The procedure for signing transaction templates is detailed in [7].
3 The Tournament Protocol
We introduce our lottery protocol for \(N = 2^L\) players; each player is represented by a bit-string in  , ranged over by
, ranged over by  . We assume that each player bets
. We assume that each player bets  in the lottery, and blocks a deposit of
in the lottery, and blocks a deposit of  , for an arbitrary \(d \ge 0\). Our protocol is based on a single-elimination tournament, where matches are organised as a complete binary tree of L levels. The tournament involves \(N-1\) two-player matches: the winners of the matches at level \(\ell \in 1..L-1\) play at the next level \(\ell -1\); the winner of the match at level 0 wins the whole
, for an arbitrary \(d \ge 0\). Our protocol is based on a single-elimination tournament, where matches are organised as a complete binary tree of L levels. The tournament involves \(N-1\) two-player matches: the winners of the matches at level \(\ell \in 1..L-1\) play at the next level \(\ell -1\); the winner of the match at level 0 wins the whole  stake.
stake.
Let  (i.e., sequences of n bits) be the set of tree paths. Intuitively, for every path in
(i.e., sequences of n bits) be the set of tree paths. Intuitively, for every path in  we have a two-player match. For any two paths \(\pi , \pi ' \in \varPi \), we write \(\pi \sqsubseteq \pi '\) when \(\pi \) is a prefix of \(\pi '\) (\(\sqsubset \) for proper prefixes).
we have a two-player match. For any two paths \(\pi , \pi ' \in \varPi \), we write \(\pi \sqsubseteq \pi '\) when \(\pi \) is a prefix of \(\pi '\) (\(\sqsubset \) for proper prefixes).
Key pairs and secrets. Our protocol requires players to exchange a certain number of Bitcoin transactions, together with their signatures. To this purpose, each player  generates all the following key pairs for every
generates all the following key pairs for every  and for every \(\pi \):
and for every \(\pi \):

The first component in each key pair above (e.g., \( Collect \)) is a distinct label. Note that each player generates \(O(N^2)\) key pairs. We assume that the private part of a key pair  is kept secret by
is kept secret by  , while the public part is communicated to the other players. For each set of key pairs
, while the public part is communicated to the other players. For each set of key pairs  , we denote with \(\mathbf{K }{(X,\cdots )}\) the set of key pairs
, we denote with \(\mathbf{K }{(X,\cdots )}\) the set of key pairs  . We denote with \(\epsilon \) the empty sequence.
. We denote with \(\epsilon \) the empty sequence.
The outcome of a match is randomly determined with a “coin toss” protocol, as in [2]. Intuitively, the players generate two random secrets, and exchange their hashes; then, they reveal the secrets: the winner is determined by a function of the two secrets (i.e., the parity of the sum of the lengths of the two secrets). Since a player may be involved in L distinct matches, we assume that each  generates L secrets (i.e., long random sequences of bits), one for each
generates L secrets (i.e., long random sequences of bits), one for each  . The secret of
. The secret of  at level \(\pi \) is denoted by
at level \(\pi \) is denoted by  ; its public hash
; its public hash  is denoted by
is denoted by  .
.
Overview of the protocol. Our protocol uses a number of transactions, the templates of which are in Fig. 1. The protocol is organised in three phases:
- initialization: :
-
the players exchange the public data, e.g. the static signatures and hashed secrets. Then, they collect all the bets, and put on the ledger the transactions for the leaves of the tournament tree.
- execution: :
-
this phase is organised in L rounds, one for each level of the tree. In each round \(\ell \), exactly \(2^{\ell }\) two-player matches are played, by the winners of the previous round. The possible executions of a single round are depicted in Fig. 3. The winner of the last round collects the whole stake.
- garbage collection: :
-
this allows players to recover from some potential interference, to be discussed in the proof of Theorem 5.
We now comment the protocol in Fig. 2. We denote the duration of each round with \(\tau _{ Round} = 6 \, \tau _{ Ledger}\), following Fig. 3. The transaction templates of Fig. 1 define some timelocks, which depend on a time \(\tau _1\) (chosen in the initialization phase), corresponding to the start of the execution phase.
Initialization phase. In step 1, all the players generate the signatures and secrets, and exchange the related public data. Step 2 is needed to prevent attacks where a player does not compute a hash from her own secret, but replays the hash of another player. In step 3 we choose the time \(\tau _1\) to be large enough so that the initialization can be completed within \(\tau _1\). In steps 4–5 the players exchange all the static signatures needed in the execution phase. Each player  contributes his own part of the signature, using his own keys
contributes his own part of the signature, using his own keys  . Steps 6–8 collect the bets from the transactions
. Steps 6–8 collect the bets from the transactions  in a single transaction
in a single transaction  . If
. If  is not confirmed on the ledger, e.g. because some player has already redeemed his bet, then all the other players redeem their original bets. In this way, they ensure that
is not confirmed on the ledger, e.g. because some player has already redeemed his bet, then all the other players redeem their original bets. In this way, they ensure that  can no longer appear on the ledger, hence the protocol is aborted. Step 8 also prevents an attack where
can no longer appear on the ledger, hence the protocol is aborted. Step 8 also prevents an attack where  is maliciously delayed so to make honest players lose. Finally, step 9 sets up the first level of the tournament, by splitting the stake in the
is maliciously delayed so to make honest players lose. Finally, step 9 sets up the first level of the tournament, by splitting the stake in the  among all the leaves of the tree, i.e.
among all the leaves of the tree, i.e.  .
.
To choose \(\tau _1\), note that the initialization phase requires:
-
at steps 1–6, to generate all the needed \(O(N^3)\) signatures and NL secrets, and share the related public parts. This costs \(O(N^3)\) time.
-
at step 7, to put on the ledger the transaction
 . This costs \(1 \; \tau _{ Ledger}\).
. This costs \(1 \; \tau _{ Ledger}\). -
after that, at step 9, to put all the transactions
 . This costs \(1 \; \tau _{ Ledger}\), because it can be done in parallel.
. This costs \(1 \; \tau _{ Ledger}\), because it can be done in parallel.
Therefore, we choose \(\tau _1\) such that \(\tau _1 \ge \mathsf{currentTime} + O(N^3) + 2 \tau _{ Ledger}\).
Execution phase. In this phase, the players play against each other. We recommend the reader to examine Fig. 3 for an overview of how matches are played. Matches correspond to the nodes of the tournament tree, and so they are indexed by tree paths \(\pi \). The match at \(\pi \) involves the winners of the two matches \(\pi 0\) and \(\pi 1\) of the previous round (i.e., the children of \(\pi \)). These winners are, respectively, the players  and
and  in the transactions
in the transactions  and
and  which are on the ledger at the start of the match (step 10). The goal of steps 10–15 is to put on the ledger a transaction
which are on the ledger at the start of the match (step 10). The goal of steps 10–15 is to put on the ledger a transaction  , where
, where  is the winner at \(\pi \).
is the winner at \(\pi \).
Step 11 starts by redeeming both  and
and  through the transaction
through the transaction  . Note that any player (not only
. Note that any player (not only  and
and  ) can perform this step, since everyone has the required signatures. At step 12, player
) can perform this step, since everyone has the required signatures. At step 12, player  is expected to reveal her secret
is expected to reveal her secret  ; otherwise, after a certain deadline, the other players can make
; otherwise, after a certain deadline, the other players can make  lose. If
lose. If  chooses to reveal her secret, she must put on the ledger the transaction
chooses to reveal her secret, she must put on the ledger the transaction  , which redeems
, which redeems  , through an input script containing
, through an input script containing  . Otherwise, after \(1 \tau _{ Ledger}\), the timelock on
. Otherwise, after \(1 \tau _{ Ledger}\), the timelock on  expires, allowing any other player to put
expires, allowing any other player to put  on the ledger at step 13. After that,
on the ledger at step 13. After that,  can be put on the ledger by any player, so making
can be put on the ledger by any player, so making  lose the match. At step 14, it is the turn of player
lose the match. At step 14, it is the turn of player  to reveal his secret
to reveal his secret  ; otherwise, similarly to the previous steps, the other players can make
; otherwise, similarly to the previous steps, the other players can make  lose after some time. If
lose after some time. If  chooses to reveal his secret, he must first compute the winner
chooses to reveal his secret, he must first compute the winner  of the match—this is possible because
of the match—this is possible because  knows both secrets
knows both secrets  and
and  . Then, he must put
. Then, he must put  on the ledger, which redeems
on the ledger, which redeems  , through an input script containing
, through an input script containing  . Otherwise, after \(1 \tau _{ Ledger}\), the timelock on
. Otherwise, after \(1 \tau _{ Ledger}\), the timelock on  expires, allowing any other player to put
expires, allowing any other player to put  on the ledger at step 13. After that,
on the ledger at step 13. After that,  can be put on the ledger by any player, so making
can be put on the ledger by any player, so making  lose the match.
lose the match.
After the last round of the execution phase, the tournament protocol is over. At this point, there is exactly one transaction  on the ledger, for some
on the ledger, for some  . This transaction can be redeemed by
. This transaction can be redeemed by  at any time, by putting on the ledger a transaction with in-script
at any time, by putting on the ledger a transaction with in-script  . Note that only
. Note that only  has the private key needed for this signature. In this way
has the private key needed for this signature. In this way  can obtain the whole stake of
can obtain the whole stake of  .
.
Garbage collection phase. As discussed in the proof of Theorem 5, a dishonest player can try to cheat by forging  transactions. When this happens, some legit
transactions. When this happens, some legit  transactions are left orphan on the ledger: garbage collection allows the players who contributed to these transactions to redeem their money back. In this way the protocol remains secure, as established later on by Theorem 5.
transactions are left orphan on the ledger: garbage collection allows the players who contributed to these transactions to redeem their money back. In this way the protocol remains secure, as established later on by Theorem 5.
4 Security of the Tournament Protocol
We assume that all the algorithms used by the players run in PPTIME with respect to a security parameter \(\eta \). A function \(f : \mathbb {N} \rightarrow \mathbb {R}\) is said to be negligible iff, for some constant \(c \in \mathbb {N}\), the inequation \(|f(\eta )| \le \eta ^{-c}\) holds asymptotically. We assume that all the cryptographic primitives (e.g., digital signatures, hash functions) are secure, up-to a negligible probability of attack.
We assume that Bitcoin works as a robust public transaction ledger, where every player can append valid transactions (which are confirmed in \(\tau _{ Ledger}\)), while invalid transactions cannot appear. Recent results [13] show that, in a backbone Bitcoin protocol, this assumption holds when the honest miners hold the majority of the hashing power (despite the negative results in [11]). For simplicity, we assume that transactions require no fees. All our results hold even when there is only one honest player.
Basic properties. Consider an arbitrary lottery protocol with N players, where each player bets a certain amount \( bet\) of bitcoins to have the chance to win \(N \cdot { bet}\). A run is a pair \((\beta ,\lambda )\), where \(\beta \) is the state of the blockchain when the protocol starts, and \(\lambda \) is the timed sequence of public events occurred in a (possibly partial) protocol execution. The component \(\lambda \) includes, e.g., the exchanged signatures and the transactions put on the ledger after \(\beta \). Each player  uses a strategy
uses a strategy  to choose which events to perform at any time in a run of the protocol. Roughly,
to choose which events to perform at any time in a run of the protocol. Roughly,  is a PPTIME algorithm which can observe the whole past \((\beta ,\lambda )\), and choose the next moves (not necessarily those prescribed by the protocol). We further allow
is a PPTIME algorithm which can observe the whole past \((\beta ,\lambda )\), and choose the next moves (not necessarily those prescribed by the protocol). We further allow  to access the local state of
to access the local state of  , including her private information. A strategy
, including her private information. A strategy  is honest when it follows the protocol; a player is honest when she uses an honest strategy. A run is maximal for
is honest when it follows the protocol; a player is honest when she uses an honest strategy. A run is maximal for  when she has performed all the enabled actions prescribed by
when she has performed all the enabled actions prescribed by  .
.
We say that a transaction is freely redeemable by  when (i)
when (i)  can use her knowledge (including private information) to compute the needed witness, and (ii)
can use her knowledge (including private information) to compute the needed witness, and (ii)  can freely choose the output script of the redeeming transaction. The wealth of
can freely choose the output script of the redeeming transaction. The wealth of  after a certain run \((\beta ,\lambda )\), denoted by
after a certain run \((\beta ,\lambda )\), denoted by  , is the amount of bitcoins freely redeemable at that time by
, is the amount of bitcoins freely redeemable at that time by  , but not by any other player.
, but not by any other player.
Lottery protocols usually require players to block a deposit of bitcoins throughout their execution (beyond the bet). Technically, we define the deposit of  as the minimum amount of bitcoins
as the minimum amount of bitcoins  such that, starting from \(\beta \),
such that, starting from \(\beta \),  can always perform a maximal run of the protocol (using an honest strategy), regardless of the behaviour of the other players. Then, we say that a lottery protocol is d-deposit if d is the maximum of the deposits of all players. Note that, by definition, it must be \(d \ge 0\): otherwise, should
can always perform a maximal run of the protocol (using an honest strategy), regardless of the behaviour of the other players. Then, we say that a lottery protocol is d-deposit if d is the maximum of the deposits of all players. Note that, by definition, it must be \(d \ge 0\): otherwise, should  lose the lottery, there would not be enough bitcoins to pay the other players.
lose the lottery, there would not be enough bitcoins to pay the other players.
The following Theorem 1 states that the tournament protocol requires constant  deposit; note instead that the protocols in [2, 4, 5, 8] require
deposit; note instead that the protocols in [2, 4, 5, 8] require  deposit.
deposit.
Theorem 1
The tournament protocol is d-deposit.
Lemma 1
For each level \(\ell = L..1\) of the execution phase:
-
1.
for every \(\pi \) such that \(|\pi |=\ell \), the ledger contains a transaction
 with value
with value  , for some
, for some  ;
; -
2.
the round starts within time \(\tau _1 + (L - \ell ) \cdot \tau _{ Round}\).
Theorem 2 exploits Lemma 1 to establish an upper bound to the completion time of our protocol. Note that a single honest player  is enough to guarantee termination: indeed, even if the other players do not cooperate,
is enough to guarantee termination: indeed, even if the other players do not cooperate,  can always put all the required transactions on the ledger, after the respective timeouts.
can always put all the required transactions on the ledger, after the respective timeouts.
Theorem 2
Assume that at least one player is honest, while the others can be adversaries with arbitrary strategies. Then:
-
1.
after \(\tau _1\), either
 is on the ledger, or the protocol is aborted without any honest players losing their wealth;
is on the ledger, or the protocol is aborted without any honest players losing their wealth; -
2.
after
 is on the ledger, a transaction
is on the ledger, a transaction  is put on the ledger within \(6 \, L \, \tau _{ Ledger}\), for some
is put on the ledger within \(6 \, L \, \tau _{ Ledger}\), for some  (who is the winner of the lottery).
(who is the winner of the lottery).
Payoff distribution. We now quantify the payoff of each player in a single run of the protocol where all the players are honest. The payoff of a player at a given point of an execution is the wealth difference between that point and the beginning of the protocol. Formally, given a run \((\beta ,\lambda )\) for  , this amounts to:
, this amounts to:

Then, Theorem 3 states that, once the  transaction has been put on the ledger, there are only two possible outcomes of the protocol: either a player loses
transaction has been put on the ledger, there are only two possible outcomes of the protocol: either a player loses  (her bet), or she wins
(her bet), or she wins  (the bets of all the other players).
(the bets of all the other players).
Theorem 3
If all players are honest, then, for all players  and for all maximal runs \((\beta ,\lambda )\) of
and for all maximal runs \((\beta ,\lambda )\) of  such that
such that  , we have
, we have  .
.
Theorem 4 below describes the probability distribution of the payoff of an honest player in contexts where the other players are adversaries. In particular, we will assume that adversaries follow rational strategies which, on average, will not make them lose money (but for a negligible amount). In order to define rational strategies, we introduce an auxiliary notion. Given a set of strategies \(\varvec{\Sigma }\) for all players and a blockchain state \(\beta \), we denote with  the expected payoff of
the expected payoff of  over all the runs \((\beta ,\lambda )\) which are maximal for each player
over all the runs \((\beta ,\lambda )\) which are maximal for each player  using
using  . Then, we say that player
. Then, we say that player  is rational in \(\varvec{\Sigma }\) iff for all \(\beta \), there exists a negligible f such that, for all \(\eta \),
is rational in \(\varvec{\Sigma }\) iff for all \(\beta \), there exists a negligible f such that, for all \(\eta \),  .
.
Theorem 4 states that the expected payoff of each player  in a given set of honest players
in a given set of honest players  is either \(-1\) or \(N-1\) with probabilities, respectively,
is either \(-1\) or \(N-1\) with probabilities, respectively,  or
or  , up-to a negligible error. This holds when either all the players are honest (and the deposit is arbitrary, potentially zero), or the adversaries are rational and the deposit is greater than zero.
, up-to a negligible error. This holds when either all the players are honest (and the deposit is arbitrary, potentially zero), or the adversaries are rational and the deposit is greater than zero.
Theorem 4
Let  be a set of players, and let \(\varvec{\Sigma }\) be such that
be a set of players, and let \(\varvec{\Sigma }\) be such that  is honest for all
is honest for all  . If (i)
. If (i) , or (ii) \(d>0\) and
, or (ii) \(d>0\) and  is rational for all
is rational for all  , then the payoff of each
, then the payoff of each  is distributed as follows, for all \(\beta \):
is distributed as follows, for all \(\beta \):

where \(f_1,f_2,f_3\) are negligible functions, and \(\lambda \) is a random variable, sampled so that \((\beta ,\lambda )\) is maximal with respect to \(\varvec{\Sigma }\).
In the presence of adversaries (i.e.,  ), the hypothesis (ii) is necessary. Indeed, if adversaries are not rational, they can simply increase the payoff of honest players by giving them money, or voluntarily losing by timeout. Instead, if \(d=0\), a rational adversary can interfere with the protocol and cause the payoff distribution to differ from the one given by Theorem 4. Remarkably, we will show in Theorem 5 that even if the adversary can alter the payoff distribution, she can not diminish the payoff average, which is at least negligible in all cases. Hence, the protocol is still secure.
), the hypothesis (ii) is necessary. Indeed, if adversaries are not rational, they can simply increase the payoff of honest players by giving them money, or voluntarily losing by timeout. Instead, if \(d=0\), a rational adversary can interfere with the protocol and cause the payoff distribution to differ from the one given by Theorem 4. Remarkably, we will show in Theorem 5 that even if the adversary can alter the payoff distribution, she can not diminish the payoff average, which is at least negligible in all cases. Hence, the protocol is still secure.
Honest strategies are rational. Theorem 5 below establishes that, even in the case of adversaries with arbitrary strategies, for any value of the deposit (including zero), our lottery protocol is secure, i.e. a player which follows the protocol does not lose money, on average.
Theorem 5
Honest strategies are rational in any set of strategies \(\varvec{\Sigma }\).
Proof
(Sketch). Without loss of generality, assume that only one player, say  , is honest, while the other \(N-1\) players are adversaries, with arbitrary (not necessarily rational) strategies \(\varvec{\Sigma }\). We need to prove that the average payoff of
, is honest, while the other \(N-1\) players are adversaries, with arbitrary (not necessarily rational) strategies \(\varvec{\Sigma }\). We need to prove that the average payoff of  is nonnegative, up to a negligible quantity. Before
is nonnegative, up to a negligible quantity. Before  is put on the ledger,
is put on the ledger,  can redeem her bet, so her payoff is zero. Hence, we only need to consider the case where
can redeem her bet, so her payoff is zero. Hence, we only need to consider the case where  has been put on the ledger. Hereafter, we inductively define proper transactions as follows:
has been put on the ledger. Hereafter, we inductively define proper transactions as follows:  is proper either if
is proper either if  , or all the inputs of
, or all the inputs of  are proper. Note that, in a run of the protocol where all the players are honest, all the transactions put on the ledger are proper.
are proper. Note that, in a run of the protocol where all the players are honest, all the transactions put on the ledger are proper.
We start by studying the possible attack strategies, which determine how adversaries put new transactions on the ledger, and how they redeem existing transactions. Adversaries can move their wealth through transactions unrelated to the protocol. Further, they can put on the ledger any transaction obtained by instantiating some transaction template of the protocol. In doing that, they can exploit the malleability of \(\mathsf{in}\) fields, and make them redeem some previous transaction unrelated to the protocol, consuming part of their wealth in the process. This results in an improper transaction. Its presence on the ledger is not a problem per se, unless it can be exploited to interfere with a proper protocol transaction—e.g., by preventing it to be redeemed, and causing the tournament behavior to diverge from the protocol. So, we now turn our attention to how proper transactions can be redeemed.
We first note that each \(\mathsf{out}\) script of the protocol transactions (except for the final transactions  and
and  ) requires a signature from every player, including the honest
) requires a signature from every player, including the honest  . Hence, adversaries can only redeem those transactions through the signatures exchanged during the initialization phase, i.e. using some instantiation of the protocol templates. Further, every transaction template uses its own public keys, so when a protocol transaction
. Hence, adversaries can only redeem those transactions through the signatures exchanged during the initialization phase, i.e. using some instantiation of the protocol templates. Further, every transaction template uses its own public keys, so when a protocol transaction  is redeemed by
is redeemed by  , then (exactly) one of the following cases applies:
, then (exactly) one of the following cases applies:
-
(a)
 is
is  and
and  is a leaf
is a leaf  , or
, or -
(b)
 has an outgoing edge to
has an outgoing edge to  , according to Fig. 3, or
, according to Fig. 3, or -
(c)
 is
is  with \(\pi \ne \epsilon \), and
with \(\pi \ne \epsilon \), and  is
is  , or
, or -
(d)
 is a final transaction.
is a final transaction.
For example, if  is a
is a  , then
, then  must provide a signature made with the keys of
must provide a signature made with the keys of  or
or  . So, as per item (b),
. So, as per item (b),  can only be redeemed by
can only be redeemed by  or
or  . By the above reasoning, and by carefully inspecting the protocol (Fig. 2) and the used transactions (Fig. 1), we see that improper transactions can not interfere with the protocol steps where a proper transaction
. By the above reasoning, and by carefully inspecting the protocol (Fig. 2) and the used transactions (Fig. 1), we see that improper transactions can not interfere with the protocol steps where a proper transaction  is redeemed by a single-input template instantiation
is redeemed by a single-input template instantiation  . Indeed, when such redemption happens,
. Indeed, when such redemption happens,  must be a proper protocol transaction as well. However, this reasoning does not extend to the case where the redeeming transaction
must be a proper protocol transaction as well. However, this reasoning does not extend to the case where the redeeming transaction  has multiple inputs. In our protocol, this is only possible when
has multiple inputs. In our protocol, this is only possible when  is a
is a  . Indeed, consider the case when a proper
. Indeed, consider the case when a proper  is on the ledger, as well as a proper
is on the ledger, as well as a proper  . If
. If  is redeemed by
is redeemed by  (as per item (b)), however, we have no guarantees that such
(as per item (b)), however, we have no guarantees that such  is redeeming both
is redeeming both  and
and  —because it is possible that
—because it is possible that  is instead redeeming the proper
is instead redeeming the proper  together with an improper transaction
together with an improper transaction  , which was forged by the adversaries. When this interference happens, the protocol continues with an improper
, which was forged by the adversaries. When this interference happens, the protocol continues with an improper  , and
, and  is left on the ledger as an “orphan”. Therefore, player
is left on the ledger as an “orphan”. Therefore, player  will not be able to participate in the current match. Note that, since
will not be able to participate in the current match. Note that, since  is the only multiple-input protocol transaction, this interference can only happen at the start of a match. After a match is started, the honest player
is the only multiple-input protocol transaction, this interference can only happen at the start of a match. After a match is started, the honest player  has at least 1 / 2 probability to win the match, since
has at least 1 / 2 probability to win the match, since  will always respect deadlines (so to avoid losing the match by timeout), and she chose her secret
will always respect deadlines (so to avoid losing the match by timeout), and she chose her secret  in a uniformly random way during initialization. So, either the adversaries lose by timeout, or reveal their secrets and the match proceeds in a fair way.
in a uniformly random way during initialization. So, either the adversaries lose by timeout, or reveal their secrets and the match proceeds in a fair way.
We can now estimate the average payoff of the honest player  , by tracking her composite bet throughout the tournament rounds (i.e., the sum gained by
, by tracking her composite bet throughout the tournament rounds (i.e., the sum gained by  so far, that she must invest in further rounds). We start by noting that, at the beginning of each round, at least one of the following must hold:
so far, that she must invest in further rounds). We start by noting that, at the beginning of each round, at least one of the following must hold:
-
1.
 has lost a previous match.
has lost a previous match. -
2.
there is an unspent
 on the ledger, and the adversaries do not interfere: hence,
on the ledger, and the adversaries do not interfere: hence,  is redeemed by
is redeemed by  , and
, and  participates in the match. In this case,
participates in the match. In this case,  has at least 1 / 2 probability to double her composite bet.
has at least 1 / 2 probability to double her composite bet. -
3.
there is an unspent
 on the ledger, and the adversaries do interfere: so,
on the ledger, and the adversaries do interfere: so,  is not redeemed (unlike its sibling
is not redeemed (unlike its sibling  ), and
), and  cannot participate in the match. The transaction
cannot participate in the match. The transaction  is left “orphan” on the ledger; after \(1 \, \tau _{ Ledger}\), player
is left “orphan” on the ledger; after \(1 \, \tau _{ Ledger}\), player  can collect the composite bet she earned so far, by putting
can collect the composite bet she earned so far, by putting  on the ledger. In this way
on the ledger. In this way  can redeem her current composite bet.
can redeem her current composite bet.
Since  is honest, she will reveal her secret for a match only after
is honest, she will reveal her secret for a match only after  has been put on the ledger (i.e., when adversaries can no longer interfere in the match). Note that the adversaries do not know the match result when they have to choose whether to interfere or not. Therefore, the whole tournament is similar to a game where
has been put on the ledger (i.e., when adversaries can no longer interfere in the match). Note that the adversaries do not know the match result when they have to choose whether to interfere or not. Therefore, the whole tournament is similar to a game where  tosses L fair coins in sequence, doubling up her bet every time she wins the flip, and losing the whole stake at the first loss. Her opponent can choose to stop her before any of the coin tosses, but in such case she is allowed to collect what she won so far. Since this coin game is fair, also the average payoff of
tosses L fair coins in sequence, doubling up her bet every time she wins the flip, and losing the whole stake at the first loss. Her opponent can choose to stop her before any of the coin tosses, but in such case she is allowed to collect what she won so far. Since this coin game is fair, also the average payoff of  in the tournament protocol is nonnegative. \(\square \)
in the tournament protocol is nonnegative. \(\square \)
5 Related Work
Several lottery protocols have been investigated outside the cryptocurrency setting, e.g. by [12, 14, 15, 21, 23]. In the last few years, some authors have proposed protocols that work on Bitcoin or similar cryptocurrencies.
Concurrently and independently of our work, Miller and Bentov [20] proposed a lottery protocol, that similarly to ours exploits a tournament tree and requires zero deposit. Two variants of the protocol are presented: the first one only relies on the SegWit feature [19], while the second one proposes a new signature verification opcode, called MULTIINPUT. The first variant requires players to statically sign a tree of \(O(2^N)\) transactions. To reduce this overhead, our protocol relies on a more flexible signature verification scheme, that allows malleability of in fields, resulting in O(N) transactions. This malleability introduces the interference issues discussed in Sect. 4. Such interferences do not make our protocol insecure, because the average payoff of honest players is non-negative, even for \(d = 0\) (Theorem 5), thanks to the garbage collection phase. However, such interferences are still undesirable, because adversaries can prevent honest players from completing the tournament. The second variant of the protocol in [20] achieves O(N) transactions and avoids interferences through a “controlled” malleability of in fields. This is obtained through the new MULTIINPUT opcode, which allows to malleate in fields (to achieve O(N) transactions), but only within a pre-specified set (to avoid interferences).
Table 1 summarises the comparison between our protocol and [20] (MB), and also with the protocols in [2] (ADMM), [8] (BK). We also consider a variant of ours and [2], called “2 players iterated”, which implement an N-players lottery by running \(N-1\) instances of a two-players protocol. Similarly to our tournament protocol, these instances are composed in a tree: only the winners of a level can play at the next one, and the winner of the root collects all the bets. In the iterated versions, the initialization phase is performed for every match (using independent keys/secrets), while in the non-iterated version the initialization is done only once, at the beginning.
The first row in Table 1 quantifies the deposit: this is constant (\(d \ge 0\)) in our protocol, zero in [20], while in the others it grows with the number of players. More specifically, the deposit is \(O(N^2)\) in [8] and in the non-iterated version of [2], while in the iterated version it is N: intuitively, an N-deposit at the last round is needed to guarantee that the final winner can collect the whole N stake.
The second row quantifies the completion time of the protocol, excluding the communication and computation time (which is marginal in practice, compared to the time required to put transactions on the ledger). Only the non-iterated version of [2] requires constant time; in [8] the time is linear in N, while in the other protocols the time is proportional to \(L = \log N\).
The number of off-chain and on-chain transactions required by each protocol is shown in the third and fourth rows. Not that all protocols require a linear number of on-chain transactions, except for [8] and the first version of [20], which require \(O(N^2)\) transactions.
The fifth row describes whether a protocol has an ideal behaviour, where only one player wins the whole stake, while the others lose their bets. More specifically, we call a protocol “all-or-nothing” if, assuming rational adversaries, the payoff of honest players is either \(-1\) or \(N-1\). The iterated versions of the protocols are not “all-or-nothing”: indeed, a rational adversary can simply stop playing after winning a match, collecting the partial winnings and making impossible for any other player to obtain the whole  stake (hence forcing some honest player to gain
stake (hence forcing some honest player to gain  ). Instead, our (non-iterated) protocol is “all-of-nothing” when \(d>0\) (Theorem 4).
). Instead, our (non-iterated) protocol is “all-of-nothing” when \(d>0\) (Theorem 4).
The last row describes which Bitcoin features a protocol requires to be actually implemented. All protocols make use of non-standard transactions, which are currently handled by a small fraction of the miners. Note that some recent works [6] address the issue of implementing complex protocols on Bitcoin by using only standard transactions. Both our protocol and the ones in [8, 20] also rely on the SegWit feature [19]. Additionally, our protocol requires the malleability of in-fields, as discussed in Sect. 2, while the second version of the protocol in [20] requires the MULTIINPUT opcode. This opcode would also allow to avoid the interferences outlined in the proof of Theorem 5. The protocol in [8] assumes resilience to malleability attacks, which can be obtained through [19].
The work [16] proposes a general model for secure multiparty computations on cryptocurrencies, which goes beyond the features provided by Bitcoin. Applying this model to lotteries, we would obtain a protocol where the deposit grows linearly in the number of dishonest players. This approach might also allow for reducing the number of rounds from \(\log N\) to a constant number.
6 Conclusions
We have presented a lottery protocol based on Bitcoin, where N players can place a bet, and one of them, uniformly chosen, wins all the bets. Our protocol is parametric w.r.t. the deposit \(d \ge 0\) that the players have to block throughout the protocol. For any value of d, our protocol ensures that honest players have a negligible average payoff, even in the presence of arbitrary adversaries (Theorem 5). Further, for \(d>0\), the payoff is distributed like an ideal lottery (Theorem 4): that is, the winner gets the sum of all the bets with probability close to  , while the other players lose their bets with probability close to
, while the other players lose their bets with probability close to  . This holds unless the adversaries follow strategies which (on average) make them lose money, and make honest players gain money. According to the terminology in [2], our protocol implements a fair lottery.
. This holds unless the adversaries follow strategies which (on average) make them lose money, and make honest players gain money. According to the terminology in [2], our protocol implements a fair lottery.
Although our protocol has been crafted for Bitcoin, the underlying ideas can be used to implement fair lotteries on other frameworks for smart contracts. This could allow to relax the rationality assumption of Theorem 4 when the deposit is zero. For instance, the implementations in Ethereum [9] of Miller and BentovFootnote 5 and of AtzeiFootnote 6 follow the structure of rounds of the tournament protocol.
Notes
- 1.
Concurrently and independently of our work, [20] proposes a lottery protocol for Bitcoin that requires zero deposit.
- 2.
- 3.
in-script and out-script are respectively referred as scriptPubKey and scriptSig in the Bitcoin documentation.
- 4.
Note that only the transactions related to our protocol need to use this form of malleability. Instead, signers of transactions unrelated to the protocol can simply choose non-malleable signatures, unless they are prepared to defend against malleability-related attacks. For instance, if
 and
and 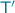 are standard transactions on the ledger with the same out-script, when
are standard transactions on the ledger with the same out-script, when  is redeemed by
is redeemed by 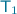 with a malleable in field, an adversary can also make
with a malleable in field, an adversary can also make  redeemed, by putting on the ledger a copy of
redeemed, by putting on the ledger a copy of  where the in field is changed to point to
where the in field is changed to point to 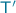 .
. - 5.
- 6.
References
Andrychowicz, M., Dziembowski, S., Malinowski, D., Mazurek, Ł.: Fair two-party computations via Bitcoin deposits. In: Böhme, R., Brenner, M., Moore, T., Smith, M. (eds.) FC 2014. LNCS, vol. 8438, pp. 105–121. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44774-1_8
Andrychowicz, M., Dziembowski, S., Malinowski, D., Mazurek, L.: Secure multiparty computations on Bitcoin. In: IEEE S&P, pp. 443–458 (2014)
Andrychowicz, M., Dziembowski, S., Malinowski, D., Mazurek, Ł.: On the malleability of Bitcoin transactions. In: Brenner, M., Christin, N., Johnson, B., Rohloff, K. (eds.) FC 2015. LNCS, vol. 8976, pp. 1–18. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48051-9_1
Andrychowicz, M., Dziembowski, S., Malinowski, D., Mazurek, L.: Secure multiparty computations on Bitcoin. Commun. ACM 59(4), 76–84 (2016)
Back, A., Bentov, I.: Note on fair coin toss via Bitcoin. http://www.cs.technion.ac.il/~idddo/cointossBitcoin.pdf (2013)
Banasik, W., Dziembowski, S., Malinowski, D.: Efficient zero-knowledge contingent payments in cryptocurrencies without scripts. In: Askoxylakis, I., Ioannidis, S., Katsikas, S., Meadows, C. (eds.) ESORICS 2016. LNCS, vol. 9879, pp. 261–280. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-45741-3_14
Bartoletti, M., Zunino, R.: Constant-deposit multiparty lotteries on Bitcoin. IACR Cryptology ePrint Archive, 2016/955 (2016). http://eprint.iacr.org/2016/955
Bentov, I., Kumaresan, R.: How to use Bitcoin to design fair protocols. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8617, pp. 421–439. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44381-1_24
Buterin, V.: Ethereum: a next generation smart contract and decentralized application platform (2013). https://github.com/ethereum/wiki/wiki/White-Paper
Crary, K., Sullivan, M.J.: Peer-to-peer affine commitment using Bitcoin. In: ACM Conference on Programming Language Design and Implementation, pp. 479–488 (2015)
Eyal, I., Sirer, E.G.: Majority is not enough: Bitcoin mining is vulnerable. In: Christin, N., Safavi-Naini, R. (eds.) FC 2014. LNCS, vol. 8437, pp. 436–454. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45472-5_28
Fouque, P.-A., Poupard, G., Stern, J.: Sharing decryption in the context of voting or lotteries. In: Frankel, Y. (ed.) FC 2000. LNCS, vol. 1962, pp. 90–104. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45472-1_7
Garay, J., Kiayias, A., Leonardos, N.: The Bitcoin backbone protocol: analysis and applications. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 281–310. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_10
Goldschlag, D.M., Stubblebine, S.G.: Publicly verifiable lotteries: applications of delaying functions. In: Hirchfeld, R. (ed.) FC 1998. LNCS, vol. 1465, pp. 214–226. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055485
Goldschlag, D.M., Stubblebine, S.G., Syverson, P.F.: Temporarily hidden bit commitment and lottery applications. Int. J. Inf. Secur. 9(1), 33–50 (2010)
Kiayias, A., Zhou, H.-S., Zikas, V.: Fair and robust multi-party computation using a global transaction ledger. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 705–734. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_25
Kumaresan, R., Bentov, I.: How to use Bitcoin to incentivize correct computations. In: ACM CCS, pp. 30–41 (2014)
Kumaresan, R., Moran, T., Bentov, I.: How to use Bitcoin to play decentralized poker. In: ACM CCS, pp. 195–206 (2015)
Lombrozo, E., Lau, J., Wuille, P.: Segregated witness (consensus layer), BIP 141. https://github.com/bitcoin/bips/blob/master/bip-0141.mediawiki
Miller, A., Bentov, I.: Zero-collateral lotteries in Bitcoin and Ethereum (2014). http://arxiv.org/abs/1612.05390
Rivest, R.L.: Electronic lottery tickets as micropayments. In: Hirschfeld, R. (ed.) FC 1997. LNCS, vol. 1318, pp. 307–314. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-63594-7_87
Ruffing, T., Kate, A., Schröder, D.: Liar, liar, coins on fire!: penalizing equivocation by loss of Bitcoins. In: ACM CCS, pp. 219–230 (2015)
Syverson, P.F.: Weakly secret bit commitment: applications to lotteries and fair exchange. In: IEEE CSFW, pp. 2–13 (1998)
Szabo, N.: Formalizing and securing relationships on public networks. First Monday 2(9) (1997)
Acknowledgments
The authors thank Patrick McCorry, Andrew Miller, and Iddo Bentov for their comments on a preliminary version of this paper. This work is partially supported by Aut. Reg. of Sardinia P.I.A. 2013 “NOMAD”.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Financial Cryptography Association
About this paper
Cite this paper
Bartoletti, M., Zunino, R. (2017). Constant-Deposit Multiparty Lotteries on Bitcoin. In: Brenner, M., et al. Financial Cryptography and Data Security. FC 2017. Lecture Notes in Computer Science(), vol 10323. Springer, Cham. https://doi.org/10.1007/978-3-319-70278-0_15
Download citation
DOI: https://doi.org/10.1007/978-3-319-70278-0_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70277-3
Online ISBN: 978-3-319-70278-0
eBook Packages: Computer ScienceComputer Science (R0)





 has
has  as input, while
as input, while  has
has  as input: hence the three transactions form a chain.
as input: hence the three transactions form a chain. and
and  require signatures by both players
require signatures by both players  and
and  .
. and put it on the ledger. After that, they both sign
and put it on the ledger. After that, they both sign  and put it on the ledger.
and put it on the ledger. signs both
signs both  and
and  before these transactions are on the ledger, and sends her signatures to
before these transactions are on the ledger, and sends her signatures to  . Then,
. Then,  adds his own signatures, and puts both
adds his own signatures, and puts both  and
and  , one after the other, on the ledger.
, one after the other, on the ledger.


 to
to  means that
means that  redeems
redeems  . Solid edges mean that any player can redeem; wavy edges mean that any player can redeem, but only after a timeout. Dashed edges mean that only the player who knows the secret on the label can redeem.
. Solid edges mean that any player can redeem; wavy edges mean that any player can redeem, but only after a timeout. Dashed edges mean that only the player who knows the secret on the label can redeem. . This costs
. This costs  . This costs
. This costs  with value
with value  , for some
, for some  ;
; is on the ledger, or the protocol is aborted without any honest players losing their wealth;
is on the ledger, or the protocol is aborted without any honest players losing their wealth; is on the ledger, a transaction
is on the ledger, a transaction  is put on the ledger within
is put on the ledger within  (who is the winner of the lottery).
(who is the winner of the lottery). is
is  and
and  is a leaf
is a leaf  , or
, or has an outgoing edge to
has an outgoing edge to  , according to Fig.
, according to Fig.  is
is  with
with  is
is  , or
, or is a final transaction.
is a final transaction. has lost a previous match.
has lost a previous match. on the ledger, and the adversaries do not interfere: hence,
on the ledger, and the adversaries do not interfere: hence,  is redeemed by
is redeemed by  , and
, and  participates in the match. In this case,
participates in the match. In this case,  has at least 1 / 2 probability to double her composite bet.
has at least 1 / 2 probability to double her composite bet. on the ledger, and the adversaries do interfere: so,
on the ledger, and the adversaries do interfere: so,  is not redeemed (unlike its sibling
is not redeemed (unlike its sibling  ), and
), and  cannot participate in the match. The transaction
cannot participate in the match. The transaction  is left “orphan” on the ledger; after
is left “orphan” on the ledger; after  can collect the composite bet she earned so far, by putting
can collect the composite bet she earned so far, by putting  on the ledger. In this way
on the ledger. In this way  can redeem her current composite bet.
can redeem her current composite bet. and
and 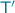 are standard transactions on the ledger with the same
are standard transactions on the ledger with the same  is redeemed by
is redeemed by 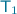 with a malleable
with a malleable  redeemed, by putting on the ledger a copy of
redeemed, by putting on the ledger a copy of  where the
where the 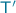 .
.