Keywords

1 Introduction

Multi-agent systems have been received considerable attention [1,2,3,4,5] due to their distinctive advantages in many aries in recent years, such as non-minimum phase switch stabilization [6, 7], containment control [8], near-optimal control [9], distributed optimal control [10], and network packet dropouts [11]. The consensus control is a popular problem of multi-agent systems which is to make the trajectory of all the agents run onto a common trajectory [12]. This techniques also have been widely applied to solve a lot of practical control problems.

The synchronization phenomenon is very common in the real world. Because of its widely applications in distributed sensor fusion, formation flying and so on, it has attracted many interest in the recent years. The synchronization control problem of multi-agent systems could be described as follows: the main attention is to keep synchronization by designing appropriate control laws on each agent by using the neighbor information of the agent. Reference [12] give a unified viewpoint between consensus of multi-agent systems and synchronization problem, in which the main unified viewpoint is the distributed control algorithm. Directed communication graphs was considered in [13] in handling the optimal synchronization phenomenon of discrete-time multi-agent systems based on riccati design method. Basical identical linear systems was studied in [14] under a directed interconnection and possibly time-varying structure.

Further more, [15] considered the synchronization problem of multi-agent systems which contains the external disturbance, and an internal model method is used to handle the case that the system matrices are also uncertain. In addition, the exosystem is a general case and a transformation is add to the exosystem matrix to solve the problem. This problem also called the output regulation problem, in which the disturbance generated by an exosystem is rejected and the outputs of each node also asymptotic reach to same trajectory of the leader’s output. A distributed leader-follower consensus control algorithms are presented in [16] to solve the output regulation problem for linear multi-agent systems, and this method is also used to obtain existing multi-agent coordination solutions to track an active leader with different dynamics and unmeasurable variables to allow the identical agents. Then [17] considered the discrete-time multi-agent systems and designed a stabilization region to keep the closed-loop systems without the external disturbance stable.

The purpose of this paper is to address distributed output synchronization problem for nonidentical discrete-time multi-agent systems with directed graphs. All the agents have different dynamics with others, and the disturbance generated by the leader node also influence the followers. For the discrete-time case, we should use the stabilization region regulator method which has been addressed in [17]. Then we use the variable restructured method to solve the output synchronization problem. At last, we give an example to improve the effectiveness of the result.

2 Preliminaries

Some basic concepts and notations in graph theory [18] should be introduced firstly. A weighted graph \(\mathcal {G}_l=(\mathcal {N}_l,\mathcal {E}_l,\mathcal {A}_l),\) where \(\mathcal {N}=\{v_1,v_2,\ldots ,v_N\}\) is the set of nodes, \(\mathcal {E}_l\) is the node set, and an edge of \(\mathcal {G}_l\) denoted by \(e_{ij}=(v_i,v_j)\in \mathcal {E}\) means that node \(v_i\) receives information from node \(v_j\). \(\mathcal {A}=[a_{ij}]\) is a weighted adjacency matrix, where \(a_{ii}=0\) and \(a_{ij}\ge 0\) for all \(i\ne j.\) \(a_{ij}>0\) if and only if there is an edge from vertex j to vertex i. The set of neighbors of node \(v_i\) is denoted by \(\mathcal {N}_i=\{v_j\in \mathcal {V}:(v_i,v_j)\in \mathcal {E}\}.\) The communication topology between agents could be expressed by a diagonal matrix \(\mathcal {D}_l=\mathrm {block~ diag}\{\varSigma _{j=1}^{n}a_{1j}, \varSigma _{j=1}^{n}a_{2j},\ldots , \varSigma _{j=1}^{n}a_{Nj}\},\) where \(\varSigma _{j=1}^{n}a_{ij}, i=1,2,\ldots ,N\) is called a degree matrix of \(\mathcal {G}_l.\) The Laplacian with the directed graph \(\mathcal {G}_l\) is defined as \(\mathcal {L}_l=\mathcal {D}_l-\mathcal {A}_l.\)

There is a sequence of edges with the form \((v_i, v_{k_1}),(v_{k_1}, v_{k_2}),\ldots ,(v_{k_j}, v_j)\in \mathcal {E}\) composing a direct path beginning with \(v_i\) ending with \(v_j\), then node \(v_j\) is reachable from node \(v_i\). A directed graph contains a directed spanning tree if there exists at least one agent which is called root node that has a directed path to every other agents. A node is reachable from all the other nodes of graph, the node is called globally reachable.

3 Problem Formulation

In this paper, two types of the system dynamics of the multi-agent systems are given. The leaders of the agents are given as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} x_i(k+1)=A_ix_i+B_iu_i+E_i\omega , &{} \hbox {} \\ y_i=C_ix_i+D_iu_i, &{} \hbox {i = 1,}\ldots \hbox {,N.} \end{array} \right. \end{aligned}$$
(1)

where \(x_i\in R^n\) and \(y_i\in R^p,\) are the state and output of the agents. \(u_i\in R^m\) is the unknown consensus protocol to be designed later. \(\omega \) is the exosystem state, and the exosystem is addressed as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \omega (k+1)=A_0\omega , &{} \hbox { } \\ y_r=Q\omega , &{} \hbox {} \end{array} \right. \end{aligned}$$
(2)

where \(\omega \in R^q\) is the disturbance to be rejected and/or the reference input to be tracked, and \(y_r\in R^p\) is the reference output.

The synchronization errors about the followers and the leader are given as follows:

$$\begin{aligned} e_i=y_i-y_r=C_ix_i+D_iu_i-Q\omega ,~~~~i=1,\ldots ,N. \end{aligned}$$
(3)

The output synchronization problem in networks of nonidentical discrete-time systems can be resolved if the following conditions are hold:

  1. 1.

    Under the appropriate distributed control law \(u_i,\) the nominal form of closed-loop system matrices are Hurwitz.

  2. 2.

    The output synchronization errors between the measured and reference outputs converge to zero, i.e.,

$$\begin{aligned} \lim _{k\rightarrow \infty } e_i(k)=0. \end{aligned}$$
(4)

4 Distributed Dynamic Feedback Design

The agents can only receive their neighbor’s information. We have to use the distributed control method. Thus the distributed dynamic state feedback control law is designed as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \eta _i(k+1)=A_0\eta _i+\theta L\mathop {\sum }\nolimits _{j=0}^Na_{ij}(\eta _i-\eta _j), &{} \hbox {} \\ z_i(k+1)=G_1z_i+G_2(y_i-Q\eta _i(k)), &{} \hbox {} \\ u_i=K_{1i}x_i+K_{2i}z_i, &{} \hbox {} \end{array} \right. \end{aligned}$$
(5)

in which \(z_i\in R^s\) is the state of the compensator, \(\eta _i\in R^p\) is the state of the distributed compensator. \((G_1,G_2)\) incorporate the p-copy internal model of the matrix \(A_0,\) which is defined as follows:

$$\begin{aligned} G_1=\mathrm {block~diag}\{\varsigma _1, \varsigma _2,\ldots , \varsigma _p\},\nonumber \\ G_2=\mathrm {block~diag}\{\sigma _1, \sigma _2, \ldots , \sigma _p\}, \end{aligned}$$
(6)

in which \(\sigma _i\) is a constant column vector, \(\varsigma _i\) is a constant square matrix, for any \(i=1,\ldots ,p\) such that the minimal polynomial of \(A_0\) divides the characteristic polynomial of \(\varsigma _i\) and \((\varsigma _i,\sigma _i)\) is controllable.

Let

$$\begin{aligned} min~det(\lambda I-A_0)=\lambda ^{s_m}+a_1\lambda ^{s_m-1}+\ldots +a_{s_m-1}\lambda +a_{s_m} \end{aligned}$$

be the minimal polynomial of \(A_0\). Choose \(\varsigma _i\) and \(\sigma _i\) in (6) as the following forms:

$$\begin{aligned} \varsigma _i=\varsigma =\left( \begin{array}{ccccc} 0 &{} 1 &{} \ldots &{} 0 &{} 0 \\ 0 &{} 0 &{} \ldots &{} 0 &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} \ldots &{} 0 &{} 1 \\ -a_{s_m} &{} -a_{s_m-1} &{} \ldots &{} -a_2 &{} -a_1 \\ \end{array} \right) ,~\sigma _i=\sigma =\left( \begin{array}{c} 0 \\ 0 \\ \vdots \\ 0 \\ 1 \\ \end{array} \right) , \end{aligned}$$
(7)

with \(s=ps_m,\) \(i=1,2,\ldots ,p\) and \(\varsigma _i\in R^{s_m\times s_m}, \sigma _i\in R^{s_m\times 1}.\)

Consider the distributed compensator \(\eta _i,\) we have:

$$\begin{aligned} \eta _i(k+1)=A_0\eta _i+\theta _iL\sum _{j=0}^Na_{ij}\eta _i-\theta _iL\sum _{j=0}^Na_{ij}\eta _j-\theta _iL a_{i0}\omega . \end{aligned}$$

Let \(\eta (k+1)=(\eta _1^T,\eta _2^T,\ldots ,\eta _N)^T,\) then one gets:

$$\begin{aligned} \eta (k+1)= & {} (I_N\otimes A_0)\eta (k)+(\theta I_N\otimes I_q)((\mathcal {D}+\mathcal {A}_0)\otimes L)\eta \nonumber \\&-(\theta I_N\otimes I_q)(\mathcal {A}\otimes L)\eta -(\theta I_N\otimes I_q)(\mathcal {A}_0\otimes L)\bar{\omega }, \end{aligned}$$
(8)

in which \(\bar{\omega }=1_N\otimes \omega .\) Then submitting the distributed control law into the system dynamics, one gets:

$$\begin{aligned} {x_i}(k+1)= & {} (A_i+B_iK_{1i})x_i+B_iK_{2i}z_i+E_i\omega \nonumber \\ y(k)= & {} (C_i+D_iK_{1i})x_i+D_iK_{2i}z_i\nonumber \\ z(k+1)= & {} G_2(C_i+D_iK_{1i})x_i+(G_1+G_2D_iK_{2i})z_i-Q_i\eta _i \end{aligned}$$
(9)

Let \(x(k)=(x_1(k),x_2(k),\ldots ,x_N(k))^T,\) and \(z(k)=(z_1(k),z_2(k),\ldots ,\) \(z_N(k))^T,\) we have

$$\begin{aligned} x(k+1)= & {} (A+BK_1)x+BK_2z+E\bar{\omega }\nonumber \\ z(k+1)= & {} (I_N\otimes G_1+(I_N\otimes G_2)DK_2)z+(I_N\otimes G_2)(C+DK_1)x, \end{aligned}$$
(10)

in which

$$\begin{aligned}&A=\mathrm {block ~diag}\{A_1,A_2,\ldots ,A_N\}\\&B=\mathrm {block ~diag}\{B_1,B_2,\ldots ,B_N\}\\&K_1=\mathrm {block ~diag}\{K_{11},K_{12},\ldots ,K_{1N}\}\\&K_2=\mathrm {block ~diag}\{K_{21},K_{22},\ldots ,K_{2N}\}\\&C=\mathrm {block ~diag}\{C_1,C_2,\ldots ,C_N\}\\&D=\mathrm {block ~diag}\{D_1,D_2,\ldots ,D_N\}\\&E=\mathrm {block ~diag}\{E_1,E_2,\ldots ,E_N\}. \end{aligned}$$

Then the compacted closed-loop system could be obtained as follows:

$$\begin{aligned} \rho (k+1)=\varLambda \rho (k)+\varGamma \varrho (k), \end{aligned}$$
(11)

in which \(\rho (k)=(x(k)^T, z(k)^T)^T,\) \(\varrho (k)=(\bar{\omega }(k)^T,\eta (k)^T)^T\) and

To obtain the main result, we give the following assumptions and lemmas.

Assumption 1:

The pairs \((A_i, B_i, C_i), i=1,\ldots ,N\) are stabilizable and detectable.

Assumption 2:

Let \(\lambda \in \sigma (A_0),\) where \(\sigma (A_0)\) is the spectrum of \(A_0,\)

$$\begin{aligned} Rank\left( \begin{array}{cc} A_i-\lambda I_n &{} B_i \\ C_i &{} D_i \\ \end{array} \right) =n+p. \end{aligned}$$
(12)

Assumption 3:

All the eigenvalues of \(A_0\) span in the interior of the unit circle.

Lemma 1

[8]: If the Assumptions 1, 2 and 3 hold, and the matrix pair \((G_1,G_2)\) incorporates a p-copy internal model of \(A_0\), then the matrix pair

$$\begin{aligned} \left( \begin{array}{cc} \left( \begin{array}{cc} A_i &{} \mathbf 0 \\ G_2C_i &{} G_1 \\ \end{array} \right) &{} \left( \begin{array}{c} B_i \\ G_2D \\ \end{array} \right) \\ \end{array} \right) \end{aligned}$$

is stabilizable.

Thus we obtain the following theorem.

Theorem 1:

If the node 0 in the topology graph \(\mathcal {G}_s\) is globally reachable, and the Assumption 1, 2 and 3 hold, the closed-loop system matrix \(\varLambda \) is stable under the distributed control law (5).

Proof: A transformation should be used as

$$\begin{aligned} \varLambda _t=(T\otimes I_n)\varLambda (T^{-1}\otimes I_n), \end{aligned}$$
(13)

in which T is chosen as follows: the \((2k-1)\)-th row is the k-th row of \(I_{2N}\) and the (2k)-th row of T is the \((k+N)\)-th row of \(I_{2N}\) with \(k=1,\ldots ,N,\) and

$$\begin{aligned} \varLambda _t=\mathrm {block~diag}\{\varLambda _{1t},\varLambda _{2t},\ldots ,\varLambda _{Nt}\}, \end{aligned}$$

with

$$\begin{aligned} \varLambda _{it}=\left( \begin{array}{cc} A_i+B_iK_{1i} &{} B_iK_{2i} \\ G_2(C_i+DK_{1i}) &{} G_1+G_2D_iK_{2i} \\ \end{array} \right) , i=1, \ldots , N. \end{aligned}$$

Then the matrix \(\varLambda _{it}\) can be rewritten as:

$$\begin{aligned} \begin{array}{cc} \left( \begin{array}{cc} A_i &{} \mathbf 0 \\ G_2C_i &{} G_1 \\ \end{array} \right) +\left( \begin{array}{c} B_i \\ G_2D \\ \end{array} \right) \\ \end{array} \left( \begin{array}{cc} K_{i1} &{} K_{i2} \\ \end{array} \right) \end{aligned}$$

Therefore, according to Lemma 1, there exist appropriate \(K_{1i}\) and \(K_{2i}\) such that the matrix \(\varLambda \) is stable.

Theorem 2:

Under the Assumption 1, 2 and 3, if the node 0 in the topology graph \(\mathcal {G}_s\) is globally reachable, then the distributed dynamic control law (5) could solve synchronization for nonidentical discrete-time systems.

Proof: The Sylvester equation, which can be written as follows:

$$\begin{aligned} \varXi (I_{2N}\otimes A_0)=\varLambda \varXi +\varGamma , \end{aligned}$$
(14)

with the unique solution \(\varXi .\) This theorem could be proved according to Theorem 1.

4.1 Example

To illustrate the validity of the proposed controller design strategy, we consider the system matrices of five agents as follows:

$$\begin{aligned} A_i=\left( \begin{array}{cc} 0 &{}1+0.1*i \\ 1 &{} 0 \\ \end{array} \right) , B_i=\left( \begin{array}{c} 0 \\ 1\\ \end{array} \right) ,C_i=\left( \begin{array}{cc} 1 &{} 0 \\ \end{array} \right) ,E_i=\left( \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} i \\ \end{array} \right) , \end{aligned}$$

and \(D_i\) are chosen as zero matrices. The leader’s system matrix is

$$\begin{aligned} A_0= \left( \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 1 &{} 0 &{} -1 \\ 0&{} 1 &{} 0 \\ \end{array} \right) . \end{aligned}$$
Fig. 1.
figure 1

The topology graph of five agents and leader

Full size image
Fig. 2.
figure 2

Synchronization error of the outputs

Full size image

Correspondingly, the internal model matrices are chosen as

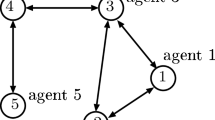
$$\begin{aligned} G_1=\left( \begin{array}{ccc} 0 &{} 1 &{} 0 \\ -1 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 \\ \end{array} \right) , G_2=\left( \begin{array}{c} 0 \\ 0 \\ 1 \\ \end{array} \right) . \end{aligned}$$

The agents communicate information with their neighbors. The information link can be shown in Fig. 1. At last, the tracking errors are shown in Fig. 2 by the appropriate distributed control law. It is shown that the outputs of the agents could reach on the same trajectories with the leader’s output.

5 Conclusion

Discrete-time multi-agent systems were studied in this paper, and distributed output synchronization problem has been solved by the appropriate distributed compensator and dynamic state feedback control law. Two main theorems were addressed and proved. At last, an example was shown to improve the main result.