23.1 Introduction

It is by no means a simple matter to develop a firm in a competitive environment, especially if there are disparities in firms’ market power. A firm has to strictly monitor changes occurring in the market and try to adapt its strategy to evolving circumstances. These changes and adaptation possibilities should be taken into account in evaluations that support decision-making processes. Real options are a tool which enables this (e.g., Dixit and Pindyck 1994; Luehrman 1998; Mun 2002).

The next key factor for firm’s success on the market is its ability to cope with competitors. The firm should closely follow competitor’s behaviors, try to understand them, and anticipate competitor’s moves. Of course the effect of competition should be incorporated into firm’s decision-making process, as well. The game theory provides tools to do that (Smit and Ankum 1993; Grenadier 2000; Smit and Trigeorgis 2004; Chevalier-Roignant and Trigeoris 2011; Trigeogris and Baldi 2013).

The main goal and the original contribution of this paper are to find and describe optimal investment strategies for asymmetric firms acting on a competitive market. Investment decision-making process is described as a game between two players, and the real options approach is used to find a value of an investment project; therefore, the paper falls in the area of the real options games (ROG). We also study the effect of a project risk level (measured by volatility) on the firm’s investment strategy and examine a case of symmetric firms as well.

The rest of the paper is structured as follows: Sect. 23.2 presents basic assumptions of a model of interaction between asymmetric firms and relations between model’s parameters. Section 23.3 contains the real options games analysis. Main results are summarized in the Sect. 23.4. The next two sections present key findings of sensitivity analysis devoted to the impact of the project risk (Sect. 23.5) and the market share (Sect. 23.6) on firm optimal policies resulting from real options games between them. Section 23.7 concludes.

23.2 The Model of Interaction Between Firms

We consider two risk-neutral firms (A and B) operating on a competitive market. Each of them can make a new investment. Both competitors share the same investment opportunity – it is a shared option (Smit and Trigeorgis 2004, 35). Each of the firms may exercise the option by paying investment expenditure I, I > 0. We assume that the lifetime of the investment project is infinite.

The investment project generates cash flows (Y t ), which evolve in accordance with the geometric Brownian motion, with drift α, α > 0 and volatility σ, σ > 0 under the risk-neutral measure. A risk-free asset yields a constant rate of return r; δ is a convenience yield (δ > 0), and it reflects an opportunity cost of delaying construction of the project and instead keeping the option to invest alive (Dixit and Pindyck 1994, p.149). The present value of the project is determined by the discounting and accumulating of its future cash flows. It is equal to \( V\left({Y}_0\right)=\frac{Y_0}{\delta } \) (Dixit and Pindyck 1994, 181).

Further, let μ be the total expected rate of return from owning the completed project. It is a sum of the expected percentage rate of growth of Y t (α) and the convenience yield (δ):

$$ \mu =\alpha +\delta. $$

Then again, according to CAPM, let μ be the expected rate of return from holding a financial asset (non-dividend paying) perfectly correlated with Y t; it complies with the following formula:

$$ \mu =r+\left({r}_{\mathrm{m}}-r\right) \cdot \frac{\sigma \cdot {\rho}_{\mathrm{m}}}{\sigma_{\mathrm{m}}}, $$

where r m is the expected return on the market, σ m is the standard deviation of r m, and ρ m is the correlation of the asset with the market portfolio.

Under the assumption of constant risk-free rate (r) and constant expected return on the market (r m), the significant links are between the project risk (σ), the opportunity cost of delaying investment (δ), and the expected percentage rate of change of cash flows (α) (Dixit and Pindyck 1994). We will assume that α is a fundamental fact about Y t and there exist links only between σ and δ according to:

$$ r+\left({r}_{\mathrm{m}}-r\right)\cdot \frac{\sigma \cdot {\rho}_m}{\sigma_{\mathrm{m}}}=\alpha +\delta. $$

Considering the implementation of the project, a firm chooses between three basic strategies: Wait, Invest, or Abandon. The primary criterion for investment decisions is the comparison between the investment option value, the benefits of instantaneous investment, and zero. However, for the shared option, a firm has to include its rivals’ decision into its decision-making process. A firm has to take into account both how its investment decision affects its competitor and how it itself may be impacted by rival reactions. Therefore, firms’ strategic choices could be described as non-zero sum games.

When firms are both active on a market, there is a market power asymmetry between them. Without loss of generality, we will assume that firm A has u market share dominance (0.5 < u < 1); firm B is left with (1 − u) share. While only the one firm decides to invest, it obtains the whole market, and the firm which is deferring investment losses its market share toward the investing firm.

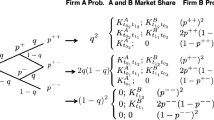
There are four possible cases of firms’ decisions. The decision to invest or to defer is made at time t = 0, and functions of payments are as follows:

  1. 1.

    Firms A and B invest immediately and simultaneously. They share the project’s benefits in accordance with their market shares; the payment for each firm is the net present value of the project:

$$ {\left.{NPV}_0^A:= NPV\left(u\cdot {Y}_t\right)\right|}_{t=0}=V\left(u\cdot {Y}_0\right)-I; $$
$$ {\left.{NPV}_0^B:= NPV\left(\left(1-u\right)\cdot {Y}_t\right)\right|}_{t=0}=V\left(\left(1-u\right)\cdot {Y}_0\right)-I, $$

where

u – the market share of firm A

  1. 2.

    Firms A and B defer and keep their investment options. The payment for each of them is the call option value from the Black-Scholes-Merton model (the underlying asset is the present value of the project determined with an appropriate part of project’s benefits (u · Y t for firm A or \( \left(1-u\right)\cdot {Y}_{\mathrm{t}} \) for firm B), and the exercise price is the investment expenditure I):

$$ {\left.{F}_0^A:= F\left(u\cdot {Y}_t\right)\right|}_{t=0}; $$
$$ {\left.{F}_0^B:= F\left(\left(1-u\right)\cdot {Y}_t\right)\right|}_{t=0}. $$
  1. 3.

    Firm A invests immediately and gains the whole market. Its payment is the net present value of the whole project:

$$ {\left.{NPV}_0:= NPV\left({Y}_t\right)\right|}_{t=0}=V\left({Y}_0\right)-I, $$

firm B defers and its payment is zero. It is forced to abandon the investment project.

  1. 4.

    Firm A defers and firm B invests immediately. Then their payments are opposite to these of the case 3.

To visualize values of these payments and to analyze games, let us assume a basic set of parameters: investment expenditure I = 6 (in monetary unit); expiration date T = 2 (years); risk-free rate r = 1.96% (YTM of treasury bonds with maturity date equal to expiration date of investment option); the expected percentage rate of change of project cash flows α = 1% (expert prediction); volatility of the project’s benefits σ = 60%; the expected return on the market r m = 6.03% (rate of return on market index WIG 2012–2016); the standard deviation of r m, σ m = 14.65%; and the correlation of the asset with the market portfolio ρ m = 0.5 (expert calculations). Assumptions about the parameters reflect a situation of a real company (a similar approach is used by authors of cited papers). Additionally we assume the firm A’s market share is u = 0.75 (so 0.25 of the market pie is left for firm B).

We are going to consider different initial values of the cash flows generated by the project Y 0 > 0, which enables us to formulate games and find most advantageous strategies for each firm under different present values of the project V 0 > 0.

Figure 23.1 presents the option values (\( {F}_0^{\mathrm{A}} \), \( {F}_0^{\mathrm{B}} \)), the benefits of instantaneous investment for the only investor (NPV0), and the benefits when the firms invest immediately and simultaneously (\( {\mathrm{NPV}}_0^{\mathrm{A}},{\mathrm{NPV}}_0^{\mathrm{B}} \)).

Fig. 23.1
figure 1

The investment option values (\( {F}_0^{\mathrm{A}} \), \( {F}_0^{\mathrm{B}} \)), the net present value for the only investor (NPV0), and the net present values when both firms invest immediately and simultaneously (\( {\mathrm{NPV}}_0^{\mathrm{A}},{\mathrm{NPV}}_0^{\mathrm{B}} \)) for different present values of the project (V 0) and regions of firms’ interactions. Base case parameters (Source: own study)

Full size image

23.3 Real Options Games Analysis

The type of the game, the way it is played, and the payments depend on the relationship between the values (payments): NPV0, \( {\mathrm{NPV}}_0^{\mathrm{A}} \),\( {\mathrm{NPV}}_0^{\mathrm{B}} \), \( {F}_0^{\mathrm{A}} \), \( {F}_0^{\mathrm{B}} \), and 0. For each firm we can identify four types of these relationships, which lead to seven ranges of the present value of the project’s benefits (V 0) (Fig. 23.1). In every region firms are playing different games, but these games have one general normal form, which is presented in Table 23.1.

Table 23.1 Payoff matrix
Full size table

We are going to determine a dominant strategy for each player in every game (if it exists) and indicate Nash equilibria. In the NE no player has anything to gain by changing only its own strategy. If the other player is rational, it is reasonable for each of them to expect its opponent to follow the recommendation of NE as well (Watson 2013, p.82). So the Nash equilibrium is a kind of prediction of how the game will be played for rational players. However, it is well known that the NE may, but not need to, give players the highest possible payoffs. In these cases, firms could consider negotiations as a way to achieve better results.

In region I the net present value of the project is very low; it is lower than investment option values for both competitors and lower than zero (\( {\mathrm{NPV}}_0^{\mathrm{A}}<{\mathrm{NPV}}_0<0<{F}_0^{\mathrm{A}} \) and \( {\mathrm{NPV}}_0^{\mathrm{B}}<{\mathrm{NPV}}_0<0<{F}_0^{\mathrm{B}} \)). Table 23.2 presents sample payoffs in the game for this region.

Table 23.2 Example of payoff matrix for region I (V 0 = 5)
Full size table

Keeping the investment option (waiting) is a dominant strategy for each firm. Since the strictly dominant strategy exists for each player, the game has the only one unique Nash equilibrium (W; W). Both players achieve the highest possible payments (\( {F}_0^{\mathrm{A}};{F}_0^{\mathrm{B}} \)). In this region of project benefits V 0, when they are really low, waiting is the optimal decision for both competitors.

The situation completely changes when the net present value of the project for the only investor exceeds the value of the investment option for firm B (only), but when both firms invest at the same time, the net present values of the project remain negative (\( {\mathrm{NPV}}_0^{\mathrm{A}}<0<{\mathrm{NPV}}_0<{F}_0^{\mathrm{A}} \) and \( {\mathrm{NPV}}_0^{\mathrm{B}}<0<{F}_0^{\mathrm{B}}<{\mathrm{NPV}}_0 \), region II). It is a very attractive situation for firm B and an awkward one for firm A.

Sample payoffs in the game for this region are presented in Table 23.3.

Table 23.3 Example of payoff matrix for region II (V 0 = 6.24)
Full size table

Firm A has a dominant strategy – Wait, so if it is a rational player it delays investment decision. There is no dominant strategy for firm B, but, under the assumption of common knowledge, the B’ best response to the A’ strategy Wait is the strategy Invest, and the strategy profile (W; I) is the Nash equilibrium. Therefore, firm B should invest and take the whole market.

The firm A could obviously anticipate it, and there arises a problem to find a way of arbitrating game which does take into account strategic inequalities but has a claim to fairness. There is also a circumstance which can strengthen A’s bargaining position – it can threaten to invest immediately as well and cause a loss for firm B. Actually, firm A also loses in this case, but its loss is smaller than B’ one.

So the firm A ought to negotiate with firm B an investment delaying. But implementation of negotiation’s outcome may be quite difficult, and moreover there occurs another problem concerning payoff transfers. A first idea of how to solve this problem – the Nash arbitration scheme – was proposed by Nash (1950). But the Nash arbitration scheme is neither superior nor the only possible one. Another interesting solution of the payoff transfer problem has been described by Kalai and Kalai (2009) and Kalai and Kalai (2013) as a cooperative-competitive value (coco value for short). The calculation of the coco value relies on a natural decomposition of game into cooperative and competitive components. The coco value is a sum of the maxmax payoff for cooperative team game (equal for both players) and the minmax one for the competitive game (the value of the zero-sum game) which is an adjustment compensating transfer from the strategically weaker player to the stronger one (Kalai and Kalai 2009, p.2).

Table 23.4 presents a decomposition of the game from Table 23.3 into two components. The cooperative payoffs are obtained as maxmax solution of the first decomposition component. But these equal payments should be adjusted in order to take into account the strategic position of both parties. The value of this compensation is the value of the competitive zero-sum game. So, the coco value is computed as:

$$ \mathrm{Coco}\ \mathrm{value}=\left(0.24;0.24\right)+\left(0.2;-0.2\right)=\left(0.44;0.04\right). $$

So, an interesting possibility of the game solution is a strategy profile (W; W) which is accompanied by payoff transfer of 0.02 from the firm A to the firm B.

Table 23.4 The coco decomposition of game in region II (V 0 = 6.24)
Full size table

At the first sight, it could appear unreasonable that B would be willing to obtain the cocopayoff of 0.04 instead of the payoff of 0.24 that it get by playing its best response to the A’s dominant strategy. But we should notice that it contains also a price of protection against losses which would be faced by both in the case of simultaneous investment.

In the region III firms’ positions remain also unsatisfactory (\( {\mathrm{NPV}}_0^A<0<{F}_0^A<{\mathrm{NPV}}_0 \) and \( {\mathrm{NPV}}_0^B<0<{F}_0^B<{\mathrm{NPV}}_0 \)). For initial values of the project benefits falling under the region III, the game has two pure nonequivalent and noninterchangeable equilibria, (W; I) and (I; W), and a mixed strategy equilibrium where each player Waits with probability p (p ∙ W, (1 − p) ∙ I; p ∙ W, (1 − p) ∙ I). This game has no dominant strategy for any player, so each of them may seek different equilibrium. Without coordination their decisions may lead to the strategy profile (I; I). Obviously (I; I) is not a good solution, since both A and B could be better off at strategy (W; W) getting positive payoffs instead of negative ones.

Sample payoffs in the game for this region are presented in Table 23.5.

Table 23.5 Example of payoff matrix for region III (V 0 = 8)
Full size table

It is interesting that the coco value in this game is (1;1) + (1;−1) = (2;0).

It means that firm A has the stronger strategic position than firm B, and if negotiations about deferring investment project are opened, firm B will have nothing to offer. So it seems that in this case, firm A should invest, and firm B is left to abandon the project.

We can observe a similar, or even better for A, situation in the regions IV and V (\( 0<{\mathrm{NPV}}_0^A<{F}_0^A<{\mathrm{NPV}}_0 \) or \( 0<{F}_0^A<{\mathrm{NPV}}_0^A<{\mathrm{NPV}}_0 \) and \( {\mathrm{NPV}}_0^B<0<{F}_0^B<{\mathrm{NPV}}_0 \)). Firm A obtains benefits whenever it is an only investor, or both firms invest simultaneously on the market. Firm B experiences losses or has to abandon the project. The dominant strategy for firm A is Invest, and the B′ best response is Wait which means Abandon in these cases.

Sample payoffs in the game for the region V are presented in Table 23.6.

Table 23.6 Example of payoff matrix for region V (V 0 = 14)
Full size table

For firm B situation changes only when benefits from immediate investment (for both competitors) become positive simultaneously (\( 0<{F}_0^{\mathrm{A}}<{\mathrm{NPV}}_0^{\mathrm{A}}<{\mathrm{NPV}}_0 \) and \( 0<{\mathrm{NPV}}_0^{\mathrm{B}}<{F}_0^{\mathrm{B}}<{\mathrm{NPV}}_0 \) or \( 0<{F}_0^{\mathrm{B}}<{\mathrm{NPV}}_0^{\mathrm{B}}<{\mathrm{NPV}}_0 \), regions VI and VII). It occurs for very large present values of project benefits V 0.

For both players the strategy profile (I; I) is the optimal one. Invest is the dominant strategy for both parties leading to the Nash equilibrium. The payoffs in this strategy profile are the best for both players. For high values of the project, Invest is the best natural decision. Sample payoffs in the game for the region VI are presented in Table 23.7.

Table 23.7 Example of payoff matrix for region VI (V 0 = 32)
Full size table

23.4 Conclusions

The subject of the last section was interactions between asymmetric firms on a competitive market connected with investment project execution. We have shown that for different present values of project benefits firms are playing different games. We have tried to identify the solution of every game and propose the best strategy for each firm. Our findings may be summarized as follows:

  1. 1.

    Decision: invest, wait, or cooperate is always on the part of the dominant company on a competitive market, but under some circumstances, the weaker party may have a very strong bargaining chip.

  2. 2.

    The precise recognition of the competitor situation is particularly important when an economic analysis of an investment project made by a dominant market party suggests deferring the investment project execution and keeping an investment option. Where it is found that the weaker competitor could benefit being the only investor on the market the stronger competitor should propose cooperation to the weaker one (delaying investment project execution) in order to avoid losses. An attractive incentive to engage in this cooperation may prove to be payoff transfer computed as the coco value.

  3. 3.

    When the economic analysis of an investment project made by the dominant firm recommends an immediate investment, the dominant firm has no reason to cooperate with the weaker firm which should abandon the project.

  4. 4.

    Invest is a profitable strategy for both firms only for really large present values of the investment project.

23.5 The Impact of the Project Risk

A project risk is one of the more important factors having a direct effect on an optimal policy of a firm. To study this issue, we relax the assumption about a fixed project risk level. The sensitivity analysis was performed for σϵ[10%; 120%], and its results provide a basis for following conclusions:

  1. 1.

    When a project risk is low, the dominant firm has no motivation to cooperate with the weaker one because in this case, the situation when the investment execution is profitable only for the weaker competitor (region II of the present values of the project benefits) does not appear. The dominant firm ought to conduct a project value analysis and follow its recommendation: Wait or Invest.

  2. 2.

    When a project risk is high, cooperation between competitors gains in significance. The region II of the present values of the project benefits becomes larger, and for the wider range of these values, the dominant party should be willing to offer cooperation to the weaker partner in order to delay investment project and keep investment option. In the case of high risk, the compensation to the weaker firm for delaying investment execution (calculated as the coco value) should be greater than in the case of low risk.

23.6 The Impact of Sharing of a Market

The degree of the asymmetry between firms’ market shares is the next significant factor which influences the type of games between firms and their optimal strategies. The sensitivity analysis was made for uϵ[0. 5; 1), and its findings are as follows:

  1. 1.

    The more significant the firms’ market power differences are, the narrower the range of present value of the project benefits which could be an incentive to cooperation between firms. Under strong asymmetry conditions, the dominant firm is not forced to cooperation with the weaker one. The dominant firm strategy takes on a monopoly character.

  2. 2.

    When the disparity between firms market shares is low and they are more or less the same, another kind of problematic interactions between firms becomes increasingly important.

For quite a wide range of present value of the project benefits, there are no dominant strategies in games between firms, and neither of them has a strategic advantage (region III, \( {\mathrm{NPV}}_0^i<0<{F}_0^i<{\mathrm{NPV}}_0 \) for i = A, B). Sample payoffs in the game for this region in the case of symmetric firms are presented in Table 23.8.

Table 23.8 Example of payoff matrix for region III, u = 0.5 (V 0 = 8)
Full size table

This game has two pure nonequivalent and noninterchangeable Nash equilibria: (W; I) and (I; W) and a mixed one. Both players may seek different equilibria deciding Invest and obtaining, as a result, the worst possible payments.

Furthermore, there arises a new kind of interactions between firms: a game of a prisoner’s dilemma nature. This kind of game we can observe for project values from a new region which is the intersection of regions IV and VI (\( 0<{\mathrm{NPV}}_0^i<{F}_0^i<{\mathrm{NPV}}_0 \) for i=A, B). Sample payoffs in the game for this region in the case of symmetric firms are presented in Table 23.9.

Table 23.9 Example of payoff matrix for a new region, the intersection of IV and VI, u = 0.5 (V 0 = 15)
Full size table

The game has a dominant strategy and one unique Nash equilibrium for each firm in this case (strategy profile (I; I)), but it does not seem to be a very happy choice, since both players would provide much higher payoffs choosing strategy: Wait.

In both cases coco values suggest cooperation but without any compensation. They are adequately equal, for the game from the Table 23.8:

$$ \mathrm{Coco}\ \mathrm{value}=\left(1;1\right)+\left(0;0\right)=\left(1;1\right). $$

For the game from the Table 23.9:

$$ \mathrm{Coco}\ \mathrm{value}=\left(4.5;4.5\right)+\left(0;0\right)=\left(4.5;4.5\right). $$

There is no dominant party in these relationships; thus, the teamwork could take the form of co-opetition, for example. The co-opetition is one of the types of interaction between firms on a market. It brings benefits from both the cooperation and competition, and it could mean investment expenditure sharing and then competing on the product market (e.g., Dagnino and Padula 2002; Rychłowska-Musiał 2017). This is particularly important because the range of present project values that determines prisoner’ dilemma interactions between firms extends when risk increases.

23.7 Final Remarks

The basis of firm’s strategic decisions should be not only attentive monitoring of changes occurring on the market and adaptation to evolving circumstances but also keeping track of competitor behaviors and incorporating them into firms’ decision-making processes.

The effect of competition should be reflected in investment project valuation methods. If they fail to take account of the competition impact, the investment project will be overvalued.

But even if we can compute the proper value of the project (as the net present value or the real option value) taking into account the externalities, it may not be the only basis for investment decision-making under competitive market conditions, as it was shown in the paper. To make the optimal strategic decision, a firm has to try to predict its rival’s decision and then to find the best response to it. Appropriate tools for solving these problems seem to be the real options games’ approach and the coco value concept as a complement to the analysis.